
几何综合题
一图形与证明中要求:会用归纳和类比进行简单的推理。
图形的认识中要求:会运用几何图形的相关知识和方法(两点之间的距离,等腰三角形、等边三角形、直角三角形的知识,全等三角形的知识和方法,平行四边形的知识,矩形、菱形和正方形的知识,直角三角形的性质,圆的性质)解决有关问题;能运用三角函数解决与直角三角形相关的简单实际问题;能综合运用几何知识解决与圆周角有关的问题;能解决与切线有关的问题。
图形与变换中要求:能运用轴对称、平移、旋转的知识解决简单问题。
二.基本图形及辅助线
解决几何综合题,是需要厚积而薄发,所谓的“几何感觉”,是建立在足够的知识积累的基础上的,熟悉基本图形及常用的辅助线,在遇到特定条件时能够及时联想到对应的模型,找到“新”问题与“旧”模型间的关联,明确努力方向,才能进一步综合应用数学知识来解决问题。在中档几何题目教学中注重对基本图形及辅助线的积累是非常必要的。
举例:
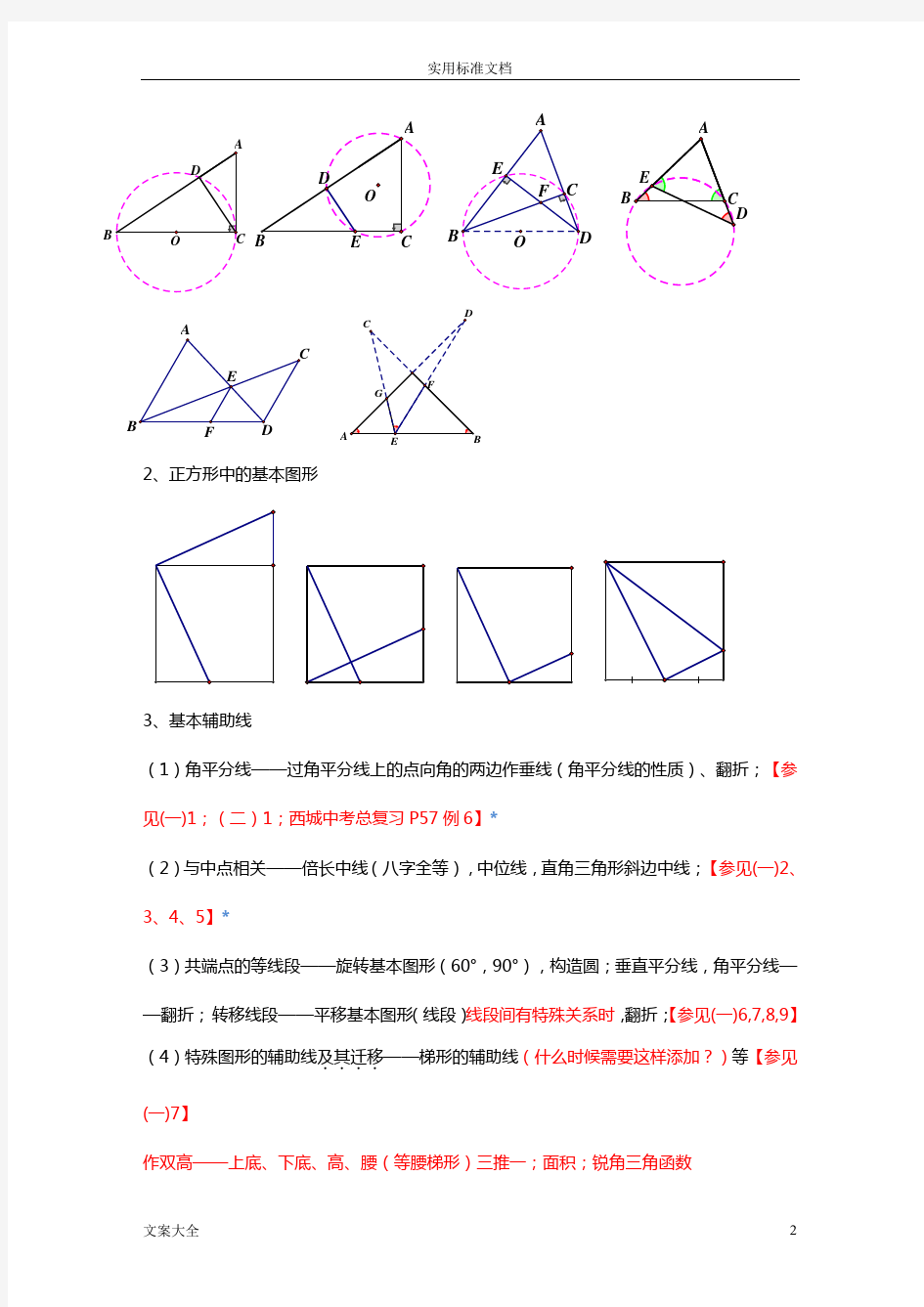
1、与相似及圆有关的基本图形
2、正方形中的基本图形
3、基本辅助线
(1)角平分线——过角平分线上的点向角的两边作垂线(角平分线的性质)、翻折;【参见(一)1;(二)1;西城中考总复习P57例6】*
(2)与中点相关——倍长中线(八字全等),中位线,直角三角形斜边中线;【参见(一)2、3、4、5】*
(3)共端点的等线段——旋转基本图形(60°,90°),构造圆;垂直平分线,角平分线——翻折;转移线段——平移基本图形(线段)线段间有特殊关系时,翻折;【参见(一)6,7,8,9】
(4)特殊图形的辅助线及其迁移
....
——梯形的辅助线(什么时候需要这样添加?)等【参见(一)7】
作双高——上底、下底、高、腰(等腰梯形)三推一;面积;锐角三角函数
平移腰——上下底之差;两底角有特殊关系(延长两腰);梯形——三角形
平移对角线——上下底之和;对角线有特殊位置、数量关系。(P5——2006北京,25*)……
注:在绘制辅助线时要注意同样辅助线的不同说法,可能会导致解题难度有较大差异。
三.题目举例
在几何综合题解题教学中,建议可以分为以下三个阶段:
第一阶段:基本图形、辅助线等的积累——在讲授综合题目前,搭配方法类似的中档题,或者给有阅读材料(小问递进启发)的综合题目,给学生入手点的启发。注重提升学生的迁移能力,培养转化数学思想方法。
第二阶段:反思与总结——引导学生在解题遇到困难时,记录思维卡点,分析问题所在;注重一题多解,并注重各种解法的可迁移性;在解题后,能够抽离出题目的基本型,将题目的图形,方法进行归类整理。
第三阶段:综合能力的提升——学生在遇到综合问题时能够联想到之前的经验,形成所谓的“几何感觉”。此时练习可以综合性较强的题目为主,要注重书写过程时抓住要点,简明有条理性。
(一)基本图形与辅助线的添加
#角平分线(【类】P5——2006北京,23;西城中考总复习P57-例6)
1、(2010宣武一模,23)已知: AC 平分MAN ∠
(1)在图1中,若?=∠120MAN ,?=∠=∠90ADC ABC ,AC AD AB ___+。(填
写“>”或“<”或“=”)
(2)在图2中,若?=∠120MAN ,?=∠+∠180ADC ABC ,则(1)中结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由; (3)在图3中:
①若?
=
∠60
MAN,?
=
∠
+
∠180
ADC
ABC,判断AD
AB+与AC的数量关系,并说明理由;
②若)
180
0(?
<
=
∠α
α
MAN,?
=
∠
+
∠180
ADC
ABC,则AC
AD
AB_____
=
+(用含α的三角函数表示,直接写出结果,不必证明)
23.解:(1) AB+AD = AC.--------------------------------------------------------------------------1分
(2) 仍然成立.
证明:如图2过C作CE⊥AM于E,CF⊥AN于F,
则∠CEA=∠CFA=90°.
∵AC平分∠MAN,∠MAN=120°,
∴∠MAC=∠NAC=60°.
又∵AC=AC,∴△AEC≌△AFC,
∴AE=AF,CE=CF.
∵在Rt△CEA中,∠EAC=60°,
∴∠ECA=30°,∴AC=2AE.
∴AE+AF=2AE=AC.∴ED+DA+AF=AC.
∵∠ABC+∠AD C=180°,∠CDE+∠ADC=180°,
∴∠CDE=∠CBF.
又∵CE=CF,∠CED=∠CFB,∴△CED≌△CFB.
∴ED=FB,∴FB+DA+AF=AC.
∴AB+AD=AC.----------------------------------------- 4分
(3)①AB+AD=3AC.
证明:如图3,方法同(2)可证△AGC≌△AHC.
∴AG=AH.
∵∠MAN=60°,∴∠GAC=∠HAC=30°.
∴AG=AH=
2
3AC.∴AG+AH=3AC.
∴GD+DA+AH=3AC.
方法同(2)可证△GDC≌△HBC.
∴GD=HB,∴HB+DA+AH=3AC.
∴AD+AB=3AC.-------------------------------------------------------------------------------------6分
②AB+AD=
2
cos
2
α·AC.-------------------------------------------------------------------7分
N
M
A
C
D
E
M
A
D
C
G
中位线/中线*2、(2010海淀一模,25)已知:AOB △中,2AB OB ==,COD △中,
3CD OC ==, ABO DCO =∠∠. 连接AD 、BC ,点M 、N 、P 分别为OA 、OD 、BC 的中点.
图1
图2
(1) 如图1,若A 、O 、C 三点在同一直线上,且60ABO =∠,则PMN △的形状是________________,此时
AD
BC
=________; (2) 如图2,若A 、O 、C 三点在同一直线上,且2ABO α=∠,证明PMN BAO △∽△,并计算
AD
BC
的值(用含α的式子表示); (3) 在图2中,固定AOB △,将COD △绕点O 旋转,直接写出PM 的最大值.
#直角三角形斜边中线3、(2011海淀一模,25)在Rt △ABC 中,∠ACB=90°,tan ∠BAC=1
2
. 点D 在边AC 上(不与A ,C 重合),连结BD ,F 为BD 中点.
(1)若过点D 作DE ⊥AB 于E ,连结CF 、EF 、CE ,如图1. 设CF kEF ,则k = ; (2)若将图1中的△ADE 绕点A 旋转,使得D 、E 、B 三点共线,点F 仍为BD 中点,如图2所示.求证:BE-DE=2CF ;
(3)若BC=6,点D 在边AC 的三等分点处,将线段AD 绕点A 旋转,点F 始终为BD
中点,求线段CF 长度的最大值.
B C
A D
E
F
B D E
A F
C
B
A
C
1
图2
图备图
25. 解:(1)k =1;
………….……………………………2分
(2)如图2,过点C 作CE 的垂线交BD 于点G ,设BD 与AC 的交点为Q .
由题意,tan ∠BAC =
12,∴ 1
2
BC DE AC AE ==. ∵ D 、E 、B 三点共线,∴ AE ⊥DB .
∵ ∠BQC =∠AQD ,∠ACB =90°, ∴ ∠QBC =∠EAQ. ∵ ∠ECA+∠ACG =90°,∠BCG+∠ACG =90°, ∴ ∠ECA =∠BCG . ∴ BCG ACE △∽△.
∴
1
2
BC GB AC AE ==. ∴ GB =DE. ∵ F 是BD 中点, ∴ F 是EG 中点. 在Rt ECG △中,1
2
CF EG =
, ∴ 2BE DE EG CF -==. ……………………5分
(3)情况1:如图,当AD =
1
3
AC 时,取AB 的中点M ,连结MF 和CM , ∵∠ACB =90°, tan ∠BAC =12
,且BC = 6, ∴AC =12,AB
=∵M 为AB 中点,∴CM
=∵AD =
1
3
AC , ∴AD =4.
∵M 为AB 中点,F 为BD 中点, ∴FM =
1
2
AD = 2. ∴当且仅当M 、F 、C 三点共线且M 在线段CF 上时CF 最大,此时CF =CM +FM
=2+分
情况2:如图,当AD =2
3
AC 时,取AB 的中点M ,
连结MF 和CM ,
类似于情况1,可知CF
的最大值为4+ …7分 综合情况1与情况2,可知当点D 在靠近点C 的
2
图B
D E
A
F
C
G
Q
三等分点时,线段CF
的长度取得最大值为4+.………8分
#直角三角形斜边中线+四点共圆(【类】西城中考总复习P61-17)*4、已知:在△ABC 中,∠ABC =90?, 点E 在直线AB 上, ED 与直线AC 垂直, 垂足为D ,且点M 为EC 中点, 连接
BM , DM .
(1)如图1,若点E 在线段AB 上,探究线段BM 与DM 及∠BMD 与∠BCD 所满足
的数量关系, 并直接写出你得到的结论;
(2)如图2,若点E 在BA 延长线上,你在(1)中得到的结论是否发生变化?写出
你的猜想并加以证明;
(3)若点E 在AB 延长线上,请你根据条件画出相应的图形,并直接写出线段BM
与DM 及∠BMD 与∠BCD 所满足的数量关系.
图1 图2
#倍长过中点的线段5、(2008年北京,25)请阅读下列材料:
问题:如图1,在菱形ABCD 和菱形BEFG 中,点A B E ,,在同一条直线上,P 是线段DF 的中点,连结PG PC ,.若60ABC BEF ∠=∠=,探究PG 与PC 的位置关系及PG
PC
的值.
B
E
D A
M
C
B E D A M
C E
B
A
C
M
小聪同学的思路是:延长GP 交DC 于点H ,构造全等三角形,经过推理使问题得到解决.
请你参考小聪同学的思路,探究并解决下列问题: (1)写出上面问题中线段PG 与PC 的位置关系及
PG
PC
的值; (2)将图1中的菱形BEFG 绕点B 顺时针旋转,使菱形BEFG 的对角线BF 恰好与菱形ABCD 的边AB 在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.
(3)若图1中2(090)ABC BEF αα∠=∠=<<,将菱形BEFG 绕点B 顺时针旋转任
意角度,原问题中的其他条件不变,请你直接写出
PG
PC 的值(用含α的式子表示). 解:(1)线段PG 与PC 的位置关系是 ;PG
PC = .
25.解:(1)线段PG 与PC 的位置关系是PG ⊥PC ;3=PC
PG
.
(2)猜想:(1)中的结论没有发生变化.
证明:如图,延长GP ,交AD 于点H ,连结CH 、CG . ∵P 是线段DF 的中点, ∴FP =DP .
由题意可知AD ∥FG . ∴∠GFP =∠HDP .
D
A
B E
F C
P
G 图1
D
C
G P
A
B E
F
图2
又∵∠GPF =∠HPD , ∴△GFP ≌△HDP . ∴GP =HP ,GF =HD . ∵四边形ABCD 是菱形,
∴CD =CB ,∠HDC =∠ABC =60°.
由∠ABC =∠BEF =60°,且菱形BEFG 的对角线BF 恰好与菱形ABCD 的边AB 在同一条直线上,可得∠GBC =60°.
∴∠HDC =∠GBC .∵四边形BEFG 是菱形, ∴GF =GB .∴HD =GB .∴△HDC ≌△GBC . ∴CH =CG ,∠DCH =∠BCG .
∴∠DCH +∠HCB =∠BCG +∠HCB =120°.
即∠HCG =120°.∵CH =CG ,PH =PG ,∴PG ⊥PC ,∠GCP =∠HCP =60°.
3=∴
PC PG
. (3))90tan(α-= PC
PG .
第25题答图
#共端点的等线段,旋转6、(2010西城一模,24)如图1,在□ABCD 中,AE ⊥BC 于E ,
E 恰为BC 的中点,2tan =B .
(1)求证:AD =AE ;
(2)如图2,点P 在BE 上,作EF ⊥DP 于点F ,连结AF .
求证:AF EF DF 2=-;
(3)请你在图3中画图探究:当P 为射线E C 上任意一点(P 不与点E 重合)时,作
EF ⊥DP 于点F ,连结AF ,线段DF 、EF 与AF 之间有怎样的数量关系?直接写
出你的结论.
24.证明:(1)在Rt △ABE 中,∠AEB=90°, ∴
2tan ==
BE
AE
B ∴BE AE 2=. ····································································· 1分 ∵E 为B
C 的中点,
∴BE BC 2=.
∴AE=BC .
∵ABCD 是平行四边形, ∴AD=BC .
∴AE=AD . ································································································································· 2分
(2)在DP 上截取DH =EF (如图8).
∵四边形ABCD 是平行四边形,AE ⊥BC , ∴∠EAD=90°. ∵EF ⊥PD ,∠1=∠2, ∴∠ADH =∠AEF .
图1
E
B
C
A
D
图3
E B
C
A D
图2
E
C
B A
F
P
H
E
C
B A
D
F
P
2
1
图8
B
A
D
H
∵AD =AE ,
∴△ADH ≌△AEF . ······································4分 ∴∠HAD =∠FAE ,AH =AF . ∴∠FAH ==90°.
在Rt △FAH 中, AH =AF ,∴AF FH 2=.
∴AF EF FD HD FD FH 2=-=-=. 即AF EF DF 2=
-. 5分
(3)按题目要求所画图形见图9, 线段DF 、EF 、AF 之间的数量关系为:AF EF DF 2=+.
利用平移变换转移线段,类比梯形平移对角线7、(2006年北京,25)我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形。请解答下列问题:
(1)写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称;
(2)探究:当等对角线四边形中两条对角线所夹锐角为60°时,这对60°角所对的两
边之和与其中一条对角线的大小关系,并证明你的结论。
25.解:(1)略.写对一种图形的名称给1分,最多给2分.
(2)结论:等对角线四边形中两条对角线所夹锐角为60时,这对60角所对的两边之和大于或等于一条对角线的长.
已知:四边形ABCD 中,对角线AC ,BD 交于点O ,AC BD =, 且60AOD ∠=. 求证:BC AD AC +≥.
证明:过点D 作DF AC ∥,在DF 上截取DE ,使DE AC =. 连结CE ,BE .
故60EDO ∠=,四边形ACED 是平行四边形. 所以BDE △是等边三角形,CE AD =. 所以DE BE AC ==.
①当BC 与CE 不在同一条直线上时(如图1),
在BCE △中,有BC CE BE +>.所以BC AD AC +>. ②当BC 与CE 在同一条直线上时(如图2), 则BC CE BE +=.因此BC AD AC +=. 综合①、②,得BC AD AC +≥.
即等对角线四边形中两条对角线所夹角为60时,这对60角所对的两边之和大于或等于其中一条对角线的长.
利用平移变换转移线段+作图8、(2011西城一模,25)在Rt △ABC 中,∠C =90°,D ,E 分别为CB ,CA 延长线上的点,BE 与AD 的交点为P .
(1)若BD=AC ,AE=CD ,在图1中画出符合题意的图形,并直接写出∠APE 的度数; (2)若3AC BD ,3CD =,求∠APE 的度数.
25.解:(1)如图9,∠APE= 45 °. ……………………2分
(2)解法一:如图
10,将AE 平移到DF ,连接
BF ,EF .……………………3分
则四边形AEFD 是平行四边形. ∴ AD ∥EF ,AD=EF . ∵
AC
,CD =,
∴ 3=BD
AC
,
3==DF CD AE CD . ∴
AC CD
BD DF
=
∵ ∠C =90°, ∴
18090BDF C ∠=?-∠=?.
∴ ∠C=∠BDF .
∴ △ACD ∽△BDF .………………5分
∴
AD AC
BF BD ==1=∠2. ∴ EF AD BF BF
==.
∵ ∠1+∠3=90°, ∴ ∠2+∠3=90°. ∴ BF ⊥AD .
∴ BF ⊥EF .…………………………………………………………6分 ∴ 在Rt △BEF 中,tan BF BEF EF ∠=
=
. ∴ ∠APE =∠BEF =30°.…………………………………………7分
解法二:如图11,将CA 平移到DF ,连接AF ,BF ,EF .………………3分
则四边形ACDF 是平行四边形. ∵ ∠C =90°,
∴ 四边形ACDF 是矩形,∠AFD =∠CAF = 90°,∠1+∠2=90°. ∵ 在Rt △AEF 中,tan 3AE AE AF CD ∠===
在Rt △BDF 中,tan 1BD BD DF AC ∠===
, ∴
3130∠=∠=?.
∴ ∠3+∠2=∠1+∠2=90°,即∠EFB =90°. ∴ ∠AFD =∠EFB . …………………4分
又∵
DF AF BF EF ==
∴ △ADF ∽△EBF . ………………………………………………5分 ∴ ∠4=∠5.…………………………………………………………6分 ∵ ∠APE+∠4=∠3+∠5,
∴ ∠APE =∠3=30°.………………………………………………7分
翻折全等+等腰(与角平分线类比)9、(2007年北京,25)我们知道:有两条边相等的三角形叫做等腰三角形.类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形. (1)请写出一个你学过的特殊四边形中是等对边四边形的图形的名称;
(2)如图,在ABC △中,点D E ,分别在AB AC ,上,设CD BE ,相交于点O ,若
60A ∠=°,1
2
DCB EBC A ∠=∠=
∠.请你写出图中一个与A ∠相等的角,并猜想图中哪个四边形是等对边四边形;
(3)在ABC △中,如果A ∠是不等于60°的锐角,点D E ,分别在AB AC ,上,且
1
2
DCB EBC A ∠=∠=
∠.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
25.解:(1)回答正确的给1分(如:平行四边形、等腰梯形等)。
(2)答:与∠A 相等的角是∠BOD (或∠COE ),四边形DBCE 是等对边四边形; (3)答:此时存在等对边四边形,是四边形DBCE 。
证法一:如图1,作CG ⊥BE 于G 点,作BF ⊥CD 交CD 延长线于F 点。 因为∠DCB=∠EBC=
1
2
∠A ,BC 为公共边, 所以△BCF ≌△CBG , 所以BF=CG ,
因为∠BDF=∠ABE+∠EBC+∠DCB ,∠BEC=∠ABE+∠A , 所以∠BDF=∠BEC , 可证△BDF ≌△CEG , 所以BD=CE
所以四边形DBCE 是等边四边形。
证法二:如图2,以C 为顶点作∠FCB=∠DBC ,CF 交BE 于F 点。
B O
A
D
E
C
B
O
A
D
E
C
F
B C
因为∠DCB=∠EBC=1
2
∠A,BC为公共边,
所以△BDC≌△CFB,
所以BD=CF,∠BDC=∠CFB,
所以∠ADC=∠CFE,
因为∠ADC=∠DCB+∠EBC+∠ABE,∠FEC=∠A+∠ABE,
所以∠ADC=∠FEC,
所以∠FEC=∠CFE,
所以CF=CE,
所以BD=CE,
所以四边形DBCE是等边四边形。
说明:当AB=AC时,BD=CE仍成立。只有此证法,只给1分。
(二)从题目中获得方法的启发,类比解决问题(上述画#的题目都有涉及这点)
由角平分线启发翻折,垂线1、(2006年北京,23)如图①,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形。请你参考这个作全等三角形的方法,解答下列问题:
(1)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA 的平分线,AD、CE相交于点F。请你判断并写出FE与FD之间的数量关系;
(2)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其它条件不变,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由。
23.解:图略(1)FE与FD之间的数量关系为FE=FD。
(2)答:(1)中的结论FE=FD仍然成立。
证法一:如下图,在AC上截取AG=AE,连结FG
因为∠1=∠2,AF为公共边可证△AEF≌△AGF所以∠AFE=∠AFG,
FE=FG
由∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线
可得∠2+∠3=60°
所以∠AFE =∠CFD =∠AFG =60°所以∠CFG =60°
由∠3=∠4及FC 为公共边,可得△CFG ≌△CFD 所以FG =FD 所以FE =FD 证法二:如下图,过点F 分别作FG ⊥AB 于点G ,FH ⊥BC 于点H 因为∠B =60°,且AD 、CE 分别是∠BAC 、∠BCA 的平分线, 所以可得∠2+∠3=60°,F 是△ABC 的内心 所以 ∠GEF =60°+∠1,FG =FH
又因为 ∠HDF =∠B +∠1 所以 ∠GEF =∠HDF 因此可证△EGF ≌△DHF 所以 FE =FD
启发利用重心分中线,中点相关内容2、(2010石景山一模,24)我们知道三角形三条中线的交点叫做三角形的重心.经过证明我们可得三角形重心具备下面的性质: 重心到顶点的距离与重心到该顶点对边中点的距离之比为2﹕1.请你用此性质解决下面的问题.
已知:如图,点O 为等腰直角三角形ABC 的重心, 90=∠CAB ,直线m 过点O ,过
C B A 、、三点分别作直线m 的垂线,垂足分别为点F E
D 、、.
(1)当直线m 与BC 平行时(如图1),请你猜想线段CF BE 、和AD 三者之间的数量关系并证明;
(2) 当直线m 绕点O 旋转到与BC 不平行时,分别探究在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段CF BE AD 、、三者之间 又有怎样的数量关系?请写出你的结论,不需证明.
m
O
F
E
D
C
B
A
A
B
C
D
E F
O m
m
A
B
(D)
E
F O 图1 图2 图3
B
A
24.(1)猜想:BE+CF=AD ………………………………1分 证明:如图,延长AO 交BC 于M 点, ∵点O 为等腰直角三角形ABC 的重心
∴AO=2OM 且AM ⊥BC 又∵EF ∥BC ∴AM ⊥EF ∵BE ⊥EF,CF ⊥EF ∴EB ∥OM ∥CF ∴EB=OM=CF
∴EB+CF=2OM=AD ………………………3分
(2)图2结论:BE+CF=AD 证明:联结AO 并延长交BC 于点G, 过G 做GH ⊥EF 于H 由重心性质可得AO=2OG
∵∠ADO=∠OHG=90°, ∠AOD=∠HOG
∴△AOD ∽△GOH ∴AD=2HG ………………………………5分 ∵O 为重心 ∴G 为BC 中点
∵GH ⊥EF,BE ⊥EF,CF ⊥EF ∴EB ∥HG ∥CF ∴H 为EF 中点 ∴HG=
2
1
(EB+CF) ∴EB+CF=AD …………………………………………7分 (3)CF -BE= AD ………………………………………8分
图1
G
B
图2
由特殊形解题启发构造哪些相等的角3、(2011南京,27)如图①,P 为△ABC 内一点,连接PA 、PB 、PC ,在△PAB 、△PBC 和△PAC 中,如果存在一个三角形与△ABC 相似,那么就称P 为△ABC 的自相似点.
⑴ 图②,已知Rt △ABC 中,∠ACB =90°,∠ABC >∠A ,CD 是AB 上的中线,过点
B 作BE ⊥CD ,垂足为E ,试说明E 是△AB
C 的自相似点.
⑵在△ABC 中,∠A <∠B <∠C .
①如图③,利用尺规作出△ABC 的自相似点P (写出作法并保留作图痕迹); ②若△ABC 的内心P 是该三角形的自相似点,求该三角形三个内角的度数.
(三) 一题多解与题目的变式及类题
1、*(西城中考总复习P64例5)点M 为正方形ABCD 的边AB (或延长线
上)任一点(不与A ,B 重合),90DMN ∠=?,射线MN 与ABC ∠的外角平分线交于点N ,求证:DM=MN.
【变式】
A 、方法类比,改变图形
B
B
B C
C C
①
②
③
高中立体几何典型500题及解析(二)(51~100题) 51. 已知空间四边形ABCD 中,AB=BC=CD=DA=DB=AC,M 、N 分别为BC 、AD 的中点。 求:AM 及CN 所成的角的余弦值; 解析:(1)连接DM,过N 作NE∥AM 交DM 于E ,则∠CNE 为AM 及CN 所成的角。 ∵N 为AD 的中点, NE∥AM 省 ∴NE=2 1AM 且E 为MD 的中点。 设正四面体的棱长为1, 则NC=21·23= 4 3且ME=2 1MD= 4 3 在Rt△MEC 中,CE 2=ME 2+CM 2= 163+41=16 7 ∴cos ∠CNE= 324 3 432167)43()43( 2222 22-=??-+=??-+NE CN CE NE CN , 又∵∠CNE ∈(0, 2 π) ∴异面直线AM 及CN 所成角的余弦值为3 2. 注:1、本题的平移点是N ,按定义作出了异面直线中一条的平行线,然后先在△CEN 外计算CE 、CN 、EN 长,再回到△CEN 中求角。 2、作出的角可能是异面直线所成的角,也可能是它的邻补角,在直观图中无法判定,只有通过解三角形后,根据这个角的余弦的正、负值来判定这个角是锐角(也就是异面直线所成的角)或钝角(异面直线所成的角的邻补角)。最后作答时,这个角的余弦值必须为正。
52. .如图所示,在空间四边形ABCD 中,点E 、F 分别是BC 、AD 上的点,已知AB=4,CD=20,EF=7, 3 1 ==EC BE FD AF 。求异面直线AB 及CD 所成的角。 解析:在BD 上取一点G ,使得3 1 =GD BG ,连结EG 、FG 在ΔBCD 中,GD BG EC BE = ,故EG//CD ,并且4 1==BC BE CD EG , 所以,EG=5;类似地,可证FG//AB ,且 4 3 ==AD DF AB FG , 故FG=3,在ΔEFG 中,利用余弦定理可得 cos ∠ FGE= 2 1 5327532222222- =??-+=??-+GF EG EF GF EG ,故∠FGE=120°。 另一方面,由前所得EG//CD ,FG//AB ,所以EG 及FG 所成的锐角等于AB 及CD 所成的角,于是AB 及CD 所成的角等于60°。 53. 在长方体ABCD -A 1B 1C 1D 1中,AA 1=c ,AB=a ,AD=b ,且a >b .求AC 1及BD 所成的角的余弦. A B C D E F G E D 1 C 1 B 1 A 1 A B D C O
中考数学复习几何压轴题 1.在△ABC 中,点D 在AC 上,点E 在BC 上,且DE ∥AB ,将△CDE 绕点C 按顺时针方向旋转得到△E D C ''(使E BC '∠<180°),连接D A '、E B ',设直线E B '与AC 交于点O . (1)如图①,当AC =BC 时,D A ':E B '的值为 ; (2)如图②,当AC =5,BC =4时,求D A ':E B '的值; (3)在(2)的条件下,若∠ACB =60°,且E 为BC 的中点,求△OAB 面积的最小值. 图① 图② 答 案 : 1;……………………………………………………………………………………………1分 (2)解:∵DE ∥AB ,∴△CDE ∽△CAB .∴AC DC BC EC =. 由旋转图形的性质得,C D DC C E EC '='=,,∴AC C D BC C E '='. ∵ D C E ECD ' '∠=∠,∴ , E AC D C E E AC ECD '∠+''∠='∠+∠即 D AC E BC '∠='∠. ∴E BC '?∽D AC '?.∴4 5 ==''BC AC E B D A .……………………………………………………4分 (3)解:作BM ⊥AC 于点M ,则BM =BC ·sin 60°=23. ∵E 为BC 中点,∴CE = 2 1 BC =2. △CDE 旋转时,点E '在以点C 为圆心、CE 长为半径的圆上运动. ∵CO 随着E CB '∠的增大而增大, ∴当E B '与⊙C 相切时,即C E B '∠=90°时E CB '∠最大,则CO 最大. O D E'O E' A D
2013中考数学压轴题动态几何题型精选解析(三) 例题如图1,在直角坐标系中,已知点A(0,2)、点B(﹣2,0),过点B和线段OA的中点C作直线BC,以线段BC为边向上作正方形BCDE. (1)填空:点D的坐标为,点E的坐标为. (2)若抛物线y=ax2+bx+c(a≠0)经过A、D、E三点,求该抛物线的解析式. (3)若正方形和抛物线均以每秒个单位长度的速度沿射线BC同时向上平移,直至正方形的顶点E落在y 轴上时,正方形和抛物线均停止运动. ①在运动过程中,设正方形落在y轴右侧部分的面积为s,求s关于平移时间t(秒)的函数关系式,并写出相应自变量t的取值范围. ②运动停止时,求抛物线的顶点坐标. 思路分析: (1)构造全等三角形,由全等三角形对应线段之间的相等关系,求出点D、点E的坐标; (2)利用待定系数法求出抛物线的解析式; (3)本问非常复杂,须小心思考与计算: ①为求s的表达式,需要识别正方形(与抛物线)的运动过程.正方形的平移,从开始到结束,总共历时秒,期间可以划分成三个阶段:当0<t≤时,对应图(3)a;当<t≤1时,对应图(3)b;当1<t≤时,对应图(3)c.每个阶段的表达式不同,请对照图形认真思考; ②当运动停止时,点E到达y轴,点E(﹣3,2)运动到点E′(0,),可知整条抛物线向右平移了3个单位,向上平移了个单位.由此得到平移之后的抛物线解析式,进而求出其顶点坐标. 解:(1)由题意可知:OB=2,OC=1. 如图(1)所示,过D点作DH⊥y轴于H,过E点作EG⊥x轴于G. 易证△CDH≌△BCO,∴DH=OC=1,CH=OB=2,∴D(﹣1,3); 同理△EBG≌△BCO,∴BG=OC=1,EG=OB=2,∴E(﹣3,2). ∴D(﹣1,3)、E(﹣3,2). (2)抛物线经过(0,2)、(﹣1,3)、(﹣3,2), 则 解得
高中空间立体几何典型 例题 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN
1 如图所示,正方体ABCD —A 1B 1C 1D 1中,侧面对角线AB 1,BC 1上分别有两点E ,F ,且B 1E=C 1F. 求证:EF ∥平面ABCD. 证明 方法一 分别过E ,F 作EM ⊥AB 于M ,FN ⊥BC 于N ,连接MN. ∵BB 1⊥平面ABCD , ∴BB 1⊥AB ,BB 1⊥BC , ∴EM ∥BB 1,FN ∥BB 1, ∴EM ∥FN. 又∵B 1E=C 1F ,∴EM=FN , 故四边形MNFE 是平行四边形,∴EF ∥MN. 又MN ?平面ABCD ,EF ?平面ABCD , 所以EF ∥平面ABCD. 方法二 过E 作EG ∥AB 交BB 1于G , 连接GF ,则B B G B A B E B 1111=, ∵B 1E=C 1F ,B 1A=C 1B , ∴B B G B B C E C 1111=,∴FG ∥B 1C 1∥BC , 又EG ∩FG =G ,AB ∩BC =B , ∴平面EFG ∥平面ABCD ,而EF ?平面EFG , ∴EF ∥平面ABCD . 2 已知P 为△ABC 所在平面外一点,G 1、G 2、G 3分别是△PAB 、△PCB 、△PAC 的重心.
(1)求证:平面G 1G 2G 3∥平面ABC ; (2)求S △3 21G G G ∶S △ABC . (1)证明 如图所示,连接PG 1、PG 2、PG 3并延长分别与边AB 、BC 、AC 交于点D 、E 、F , 连接DE 、EF 、FD ,则有PG 1∶PD =2∶3, PG 2∶PE =2∶3,∴G 1G 2∥DE . 又G 1G 2不在平面ABC 内, ∴G 1G 2∥平面ABC .同理G 2G 3∥平面ABC . 又因为G 1G 2∩G 2G 3=G 2, ∴平面G 1G 2G 3∥平面ABC . (2)解 由(1)知PE PG PD PG 21 =32,∴G 1G 2=32DE . 又DE =21AC ,∴G 1G 2=31 AC . 同理G 2G 3=31AB ,G 1G 3=3 1BC . ∴△G 1G 2G 3∽△CAB ,其相似比为1∶3, ∴S △3 21G G G ∶S △ABC =1∶9. 3如图所示,已知S 是正三角形ABC 所在平面外的一点,且SA =SB =SC ,SG 为△SAB 上的高, D 、 E 、 F 分别是AC 、BC 、SC 的中点,试判断S G 与平面DEF 的位置关系,并给予证明. 解 SG ∥平面DEF ,证明如下: 方法一 连接CG 交DE 于点H , 如图所示.
1.(1)操作发现· 如图,矩形ABCD 中,E 是AD 的中点,将△ABE 沿BE 折叠后得到△GBE ,且点G 在矩形ABCD 内部.小明将BG 延长交DC 于点F ,认为GF =DF ,你同意吗?说明理由. (2)问题解决 保持(1)中的条件不变,若DC =2DF ,求AB AD 的值; (3)类比探究 保持(1)中的条件不变,若DC =n ·DF ,求 AB AD 的值. 2.如图1所示,在直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,∠DCB =75o,以CD 为一边的
等边△DCE 的另一顶点E 在腰AB 上. (1)求∠AED 的度数; (2)求证:AB =BC ; (3)如图2所示,若F 为线段CD 上一点,∠FBC =30o. 求 DF FC 的值. 3.如图①,在等腰梯形ABCD 中,AD ∥BC ,AE ⊥BC 于点E ,DF ⊥BC 于点F .AD =2cm ,BC =6cm ,AE =4cm .点P 、Q 分别在线段AE 、DF 上,顺次连接B 、P 、Q 、C ,线段BP 、PQ 、QC 、CB 所围成的封闭图形记为M .若点P 在线段AE 上运动时,点Q 也随之在线段DF 上运动,使图形M 的形状发生改变,但面积始终.. 为10cm 2.设EP =x cm ,FQ =y cm ,A B C D E 图1 A B C D E 图2 F
解答下列问题: (1)直接写出当x =3时y 的值; (2)求y 与x 之间的函数关系式,并写出自变量x 的取值范围; (3)当x 取何值时,图形M 成为等腰梯形?图形M 成为三角形? (4)直接写出线段PQ 在运动过程中所能扫过的区域的面积. 4.如图①,将一张矩形纸片对折,然后沿虚线剪切,得到两个(不等边)三角形纸片△ABC ,△A 1B 1C 1. A B C D E F (备用图) A B C D E F Q P 图① 图 ① A C A 1 B 1 C 1
几何图形变换压轴题中考整理 1(黑龙江省哈尔滨市)已知:△ABC的高AD所在直线与高BE所在直线相交于点F.(1)如图l,若△ABC为锐角三角形,且∠ABC=45°,过点F作FG∥BC,交直线AB于点G,求证:FG+DC=AD; (2)如图2,若∠ABC=135°,过点F作FG∥BC,交直线AB于点G,则FG、DC、AD之间满足的数量关系是____________________________________; (3)在(2)的条件下,若AG=2 5,DC=3,将一个45°角的顶点与点B重合并绕点B旋转,这个角的两边分别交线段FG于M、N两点(如图3),连接CF,线段CF分别 3,求线段PQ的长. 与线段BM、线段BN相交于P、Q两点,若NG= 2 (湖北省随州市)如图①,已知△ABC是等腰三直角角形,∠BAC=90°,点D是BC 的中点.作正方形DEFG,使点A,C分别在DG和DE上,连接AE,BG.(1)试猜想线段BG和AE的数量关系,请直接写出你得到的结论. (2)将正方形DEFG绕点D逆时针方向旋转一定角度后(旋转角度大于0°,小于或等于360°),如图②,通过观察或测量等方法判断(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由. (3)若BC=DE=2,在(2)的旋转过程中,当AE为最大值时,求AF的值.
3、如图13-1,一等腰直角三角尺GEF 的两条直角边与正方形ABCD 的两条边分别重合在一起.现正方形ABCD 保持不动,将三角尺GEF 绕斜边EF 的中点O (点O 也是BD 中点)按顺时针方向旋转. (1)如图13-2,当EF 与AB 相交于点M ,GF 与BD 相交于点N 时,通过观察或测 量BM ,FN 的长度,猜想BM ,FN 满足的数量关系,并证明你的猜想; (2)若三角尺GEF 旋转到如图13-3所示的位置时,线段FE 的延长线与AB 的延长 线相交于点M ,线段BD 的延长线与GF 的延长线相交于点N ,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由. 3.在△ABC 中,点P 为BC 的中点. (1)如图1,求证:AP < 2 1 (AB +BC ); (2)延长AB 到D ,使得BD =AC ,延长AC 到E ,使得CE =AB ,连结DE . ①如图2,连结BE ,若∠BAC =60°,请你探究线段BE 与线段AP 之间的数量关系.写出你的结论,并加以证明; ②请在图3中证明:BC ≥ 2 1 DE . 图13-2 E A B D G F O M N C 图13-3 A B D G E F O M N C 图13- 1 A ( G ) B ( E ) C O D ( F )
2020 挑战压轴题中考数学 精讲解读篇 因动点产生的相似三角形问题 1.如图,在平面直角坐标系xOy中,将抛物线y=x2的对称轴绕着点P(0,2)顺时针旋转45°后与该抛物线交于A、B两点,点Q是该抛物线上一点. (1)求直线AB的函数表达式; (2)如图①,若点Q在直线AB的下方,求点Q到直线AB的距离的最大值;(3)如图②,若点Q在y轴左侧,且点T(0,t)(t<2)是射线PO上一点,当以P、B、Q为顶点的三角形与△PAT相似时,求所有满足条件的t的值. 2.如图,已知BC是半圆O的直径,BC=8,过线段BO上一动点D,作AD⊥BC 交半圆O于点A,联结AO,过点B作BH⊥AO,垂足为点H,BH的延长线交半圆O于点F. (1)求证:AH=BD; (2)设BD=x,BE?BF=y,求y关于x的函数关系式; (3)如图2,若联结FA并延长交CB的延长线于点G,当△FAE与△FBG相似时,求BD的长度.
3.如图,在平面直角坐标系xOy中,直线AB过点A(3,0)、B(0,m)(m>0),tan∠BAO=2. (1)求直线AB的表达式; (2)反比例函数y=的图象与直线AB交于第一象限内的C、D两点(BD<BC),当AD=2DB时,求k1的值; (3)设线段AB的中点为E,过点E作x轴的垂线,垂足为点M,交反比例函数y=的图象于点F,分别联结OE、OF,当△OEF∽△OBE时,请直接写出满足条件的所有k2的值. 4.如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=7,点D是边CA延长线的一点,AE⊥BD,垂足为点E,AE的延长线交CA的平行线BF于点F,连结CE交AB于点G. (1)当点E是BD的中点时,求tan∠AFB的值; (2)CE?AF的值是否随线段AD长度的改变而变化?如果不变,求出CE?AF的值;如果变化,请说明理由; (3)当△BGE和△BAF相似时,求线段AF的长.
立体几何坐标解法典型例题 1、如图,正三棱柱111ABC A B C -的所有棱长都为2,D 为1CC 中点. (Ⅰ)求证:1AB ⊥平面1A BD ; (Ⅱ)求二面角1A A D B --的大小; (Ⅲ)求点C 到平面1A BD 的距离. 2、如图,在Rt AOB △中, π6 OAB ∠=,斜边4AB =.Rt AOC △可以通过Rt AOB △以直线AO 为轴旋转得到,且二面角B AO C --的直二面角.D 是AB 的中点. (1)求证:平面COD ⊥平面AOB ; (2)求异面直线AO 与CD 所成角的大小. A B C D
3.(2010·上海松江区模拟)设在直三棱柱ABC -A 1B 1C 1中,AB =AC =AA 1=2,∠BAC =90°,E ,F 依次为C 1C ,BC 的中点. (1)求异面直线A 1B 、EF 所成角θ的正弦值; (2)求点B 1到平面AEF 的距离. 4.四棱锥S ABCD -中,底面ABCD 为平行四边形,侧面SBC ⊥底面ABCD .已知45ABC =o ∠, 2AB = ,BC = SA SB == (Ⅰ)证明SA BC ⊥; (Ⅱ)求直线SD 与平面SAB 所成角的大小. D B C A S
5.如图,点P 是单位正方体ABCD -A 1B 1C 1D 1中异于A 的一个顶点,则AP →·AB → 的值为( ) A .0 B .1 C .0或1 D .任意实数 5.在棱长为1的正方体ABCD -A 1B 1C 1D 1中,M 、N 分别为A 1B 1和BB 1的中点,那么直线AM 与CN 所成角的余弦值等于( ) A.32 B.1010 C.35 D.25 <二>选择题辨析 [注]: ①两条异面直线在同一平面内射影一定是相交的两条直线.(×) ②直线在平面外,指的位置关系:平行或相交 ③若直线a 、b 异面,a 平行于平面,b 与的关系是相交、平行、在平面内. ④两条平行线在同一平面内的射影图形是一条直线或两条平行线或两点. ⑤在平面内射影是直线的图形一定是直线.(×) ⑥在同一平面内的射影长相等,则斜线长相等.(×) ⑦是夹在两平行平面间的线段,若,则的位置关系为相交或平行或异面. [注]: ①直线与平面内一条直线平行,则∥. (×) ②直线与平面内一条直线相交,则与平面相交. (×) ③若直线与平面平行,则内必存在无数条直线与平行. (√) ④两条平行线中一条平行于一个平面,那么另一条也平行于这个平面. (×) ⑤平行于同一直线的两个平面平行.(×) ⑥平行于同一个平面的两直线平行.(×) ⑦直线与平面、所成角相等,则∥.(×) [注]: ①垂直于同一平面....的两个平面平行.(×) ②垂直于同一直线的两个平面平行.(√) ③垂直于同一平面的两条直线平行.(√) αααb a ,b a =b a ,a αa αa αa αa ααa l αβαβ
2020年全国各地中考数学压轴题汇编(贵州专版) 几何综合 参考答案与试题解析 一.选择题(共6小题) 1.(2020?贵阳)如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD的周长为() A.24 B.18 C.12 D.9 解:∵E是AC中点, ∵EF∥BC,交AB于点F, ∴EF是△ABC的中位线, ∴EF=BC, ∴BC=6, ∴菱形ABCD的周长是4×6=24. 故选:A. 2.(2020?遵义)如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E、F,连接PB、PD.若AE=2,PF=8.则图中阴影部分的面积为() A.10 B.12 C.16 D.18 解:作PM⊥AD于M,交BC于N.
则有四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形, ∴S △ADC =S △ABC ,S △AMP =S △AEP ,S △PBE =S △PBN ,S △PFD =S △PDM ,S △PFC =S △PCN , ∴S △DFP =S△PBE=×2×8=8, ∴S 阴=8+ 8=16, 故选:C. 3.(2020?贵阳)如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为() A.B.1 C.D. 解:连接BC, 由网格可得AB=BC=,AC=,即AB2+BC2=AC2, ∴△ABC为等腰直角三角形, ∴∠BAC=45°, 则tan∠BAC=1, 故选:B. 4.(2020?遵义)如图,四边形ABCD中,AD∥BC,∠ABC=90°,AB=5,BC=10,连接AC、BD,以BD为直径的圆交AC于点E.若DE=3,则AD的长为()
第三课时 几何代数综合题1.已知:如图①,在矩形ABCD 中,AB=5,AD=320 ,AE ⊥BD ,垂足是 E.点F 是点E 关于AB 的对称点,连接 AF 、BF. (1)求AE 和BE 的长; (2)若将△ABF 沿着射线BD 方向平移,设平移的距离为 m (平移距离指点B 沿BD 方向所经过的线段长度).当点F 分别平移到线段AB 、AD 上时,直接写出相应的m 的值. (3)如图②,将△ABF 绕点B 顺时针旋转一个角(0°<<180°),记旋转中的△ABF 为△A ′BF ′,在旋转过程 中,设A ′F ′所在的直线与直线 AD 交于点P.与直线BD 交于点Q.是否存在这样的P 、Q 两点,使△DPQ 为等腰三角形?若存在,求出此时DQ 的长;若不存在,请说明理由 . 解:(1)在Rt △ABD 中,AB=5,AD = ,由勾股定理得:BD === . ∵S △ABD =BD?AE =AB?AD , ∴AE===4. 在Rt △ABE 中,AB=5,AE=4,由勾股定理得: BE=3.(2)设平移中的三角形为△ A ′ B ′F ′,如答图2所示:由对称点性质可知,∠ 1=∠2.由平移性质可知,AB ∥A ′B ′,∠4=∠1,BF=B ′F ′=3. ①当点F ′落在AB 上时,∵AB ∥A ′B ′, ∴∠3=∠4,∴∠3=∠2, ∴BB ′=B ′F ′=3,即m=3; ②当点F ′落在AD 上时,∵AB ∥A ′B ′, ∴∠6=∠2,∵∠1=∠2,∠5=∠1, ∴∠5=∠6,又易知A ′B ′⊥AD , ∴△B ′F ′D 为等腰三角形, ∴B ′D=B ′F ′=3, ∴BB ′=B D ﹣B ′D =﹣3=,即m=. (3)存在.理由如下:
目录 第一部分函数图象中点的存在性问题 1.1 因动点产生的相似三角形问题 例1 上海市中考第24题 例2 苏州市中考第29题 例3 黄冈市中考第25题 例4 义乌市中考第24题 例5 临沂市中考第26题 例6 苏州市中考第29题 1.2 因动点产生的等腰三角形问题 例1 上海市虹口区中考模拟第25题 例2 扬州市中考第27题 例3 临沂市中考第26题 例4 湖州市中考第24题 例5 盐城市中考第28题 例6 南通市中考第27题 例7 江西省中考第25题 1.3 因动点产生的直角三角形问题 例1 山西省中考第26题 例2 广州市中考第24题 例3 杭州市中考第22题 例4 浙江省中考第23题 例5 北京市中考第24题 例6 嘉兴市中考第24题 例7 河南省中考第23题 1.4 因动点产生的平行四边形问题 例1 上海市松江区中考模拟第24题 例2 福州市中考第21题 例3 烟台市中考第26题 例4 上海市中考第24题 例5 江西省中考第24题 例6 山西省中考第26题 例7 江西省中考第24题 1.5 因动点产生的梯形问题 例1 上海市松江中考模拟第24题 例2 衢州市中考第24题 例4 义乌市中考第24题
例5 杭州市中考第24题 例7 广州市中考第25题 1.6 因动点产生的面积问题 例1 苏州市中考第29题 例2 菏泽市中考第21题 例3 河南省中考第23题 例4 南通市中考第28题 例5 广州市中考第25题 例6 扬州市中考第28题 例7 兰州市中考第29题 1.7 因动点产生的相切问题 例1 上海市杨浦区中考模拟第25题 例2 河北省中考第25题 例3 无锡市中考第28题 1.8 因动点产生的线段和差问题 例1 天津市中考第25题 例2 滨州市中考第24题 例3 山西省中考第26题 第二部分图形运动中的函数关系问题 2.1 由比例线段产生的函数关系问题 例1 宁波市中考第26题 例2 上海市徐汇区中考模拟第25题 例3 连云港市中考第26题 例4 上海市中考第25题 2.2 由面积公式产生的函数关系问题 例1 菏泽市中考第21题 例2 广东省中考第22题 例3 河北省中考第26题 例4 淮安市中考第28题 例5 山西省中考第26题 例6 重庆市中考第26题 第三部分图形运动中的计算说理问题 3.1 代数计算及通过代数计算进行说理问题 例1 南京市中考第26题 例2 南昌市中考第25题 3.2几何证明及通过几何计算进行说理问题 例1 上海市黄浦区中考模拟第24题 例2 江西省中考第24题
中考数学几何选择填空压轴题精选配答案 Pleasure Group Office【T985AB-B866SYT-B182C-BS682T-STT18】
2016中考数学几何选择填空压轴题精选(配答案)一.选择题(共13小题) 1.(2013蕲春县模拟)如图,点O为正方形ABCD的中心,BE平分∠DBC交DC 于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则以下四个结论中正确结论的个数为() ①OH=BF;②∠CHF=45°;③GH=BC;④DH2=HEHB. A .1个B . 2个C . 3个D . 4个 2.(2013连云港模拟)如图,Rt△ABC中,BC=,∠ACB=90°,∠A=30°,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连结BE1交CD1于D2;过D2作 D2E2⊥AC于E2,连结BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点E4、E5、…、E2013,分别记△BCE1、△BCE2、△BCE3、…、△BCE2013的面积为S1、S2、S3、…、S2013.则S2013的大小为() A .B . C . D . 3.如图,梯形ABCD中,AD∥BC,,∠ABC=45°,AE⊥BC于点E,BF⊥AC于点F,交AE于点G,AD=BE,连接DG、CG.以下结论: ①△BEG≌△AEC;②∠GAC=∠GCA;③DG=DC;④G为AE中点时,△AGC的面积有最大值.其中正确的结论有() A .1个B . 2个C . 3个D . 4个 4.如图,正方形ABCD中,在AD的延长线上取点E,F,使DE=AD,DF=BD,连接BF分别交CD,CE于H,G下列结论:
中考数学压轴题(几何综合题) 1、如图1,△ABC中,∠ACB=90°,AC=4厘米,BC=6厘米,D是BC的中点.点E从A 出发,以a厘米/秒(a>0)的速度沿AC匀速向点C运动,点F同时以1厘米/秒的速度从C出发,沿CB匀速向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,过点E作AC的垂线,交AD于点G,连接EF,FG.设它们运动的时间为t秒(t>0).(1)当t=2时,△ECF∽△BCA,求a的值; (2)当a=1 2 时,以点E、F、D、G为顶点的四边形是平行四边形,求t的值; (3)当a=2时,是否存在某个时间,使△DFG是直角三角形?若存在,请求出t的值; 若不存在,请说明理由. 解:(1)∵t=2,∴CF=2厘米,AE=2a厘米, ∴EC=(4-2a ) 厘米. ∵△ECF∽△BCA.∴EC CF CB AC = ∴422 64 a - =.∴ 1 2 a=. (2)由题意,AE=1 2 t厘米,CD=3厘米,CF=t厘米. ∵EG∥CD,∴△AEG∽△ACD.∴EG AE CD AC =, 1 2 34 t EG =.∴EG= 3 8 t. ∵以点E、F、D、G为顶点的四边形是平行四边形,∴EG=DF. 当0≤t<3时,3 3 8 t t =-, 24 11 t=. 当3<t≤6时,3 3 8 t t=-, 24 5 t=. 综上 24 11 t=或 24 5 (3)由题意,AE=2t厘米,CF=t厘米,可得:△AEG∽△ACD AG=5 2 t厘米,EG= 3 2 t,DF=3-t厘米,DG=5- 5 2 t(厘米). G D B A C F E (第27题) D B A C 备用图 图1
中考数学几何选择填空压轴题精选 一.选择题(共13小题) 1.(2013?蕲春县模拟)如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE 的延长线于点H,连接OH交DC于点G,连接HC.则以下四个结论中正确结论的个数为() ①OH=BF;②∠CHF=45°;③GH=BC;④DH2=HE?HB. A.1个B.2个C.3个D.4个 2.(2013?连云港模拟)如图,Rt△ABC中,BC=,∠ACB=90°,∠A=30°,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连结BE1交CD1于D2;过D2作D2E2⊥AC于E2,连结BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点E4、E5、…、E2013,分别记△BCE1、△BCE2、△BCE3、…、△BCE2013的面积为S1、S2、S3、…、S2013.则S2013的大小为() A.B.C.D. 3.如图,梯形ABCD中,AD∥BC,,∠ABC=45°,AE⊥BC于点E,BF⊥AC于点F,交AE于点G,AD=BE,连接DG、CG.以下结论:①△BEG≌△AEC;②∠GAC=∠GCA;③DG=DC;④G为AE中点时,△AGC的面积有最大值.其中正确的结论有() A.1个B.2个C.3个D.4个 4.如图,正方形ABCD中,在AD的延长线上取点E,F,使DE=AD,DF=BD,连接BF分别交CD,CE于H,G下列结论: ①EC=2DG;②∠GDH=∠GHD;③S△CDG=S?DHGE;④图中有8个等腰三角形.其中正确的是() A.①③B.②④C.①④D.②③ 5.(2008?荆州)如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使BC与DC重合,得到△DCF,连EF交CD于M.已知BC=5,CF=3,则DM:MC的值为() A.5:3B.3:5C.4:3D.3:4 6.如图,矩形ABCD的面积为5,它的两条对角线交于点O1,以AB,AO1为两邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交BD于点02,同样以AB,AO2为两邻边作平行四边形ABC2O2.…,依此类推,则平行四边形ABC2009O2009的面积为() A.B.C.D. 7.如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值是() A.B.6C.D.3 8.(2013?牡丹江)如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②;③△PMN为等边三角形;④当∠ABC=45°时,BN=PC.其中正确的个数是() A.1个B.2个C.3个D.4个 9.(2012?黑河)Rt△ABC中,AB=AC,点D为BC中点.∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论: ①(BE+CF)=BC; ②S△AEF≤S△ABC; ③S四边形AEDF=AD?EF; ④AD≥EF; ⑤AD与EF可能互相平分, 其中正确结论的个数是() A.1个B.2个C.3个D.4个
近年来中考数学压轴题大集合 【一】函数与几何综合的压轴题 1.〔2004安徽芜湖〕如图①,在平面直角坐标系中,AB 、CD 都垂直于x 轴,垂足分别为B 、D 且AD 与B 相交于E 点.:A (-2,-6),C (1,-3) (1) 求证:E 点在y 轴上; (2) 假如有一抛物线通过A ,E ,C 三点,求此抛物线方程. (3) 假如AB 位置不变,再将DC 水平向右移动k (k >0)个单位,如今AD 与BC 相交于E ′点, 如图②,求△AE ′C 的面积S 关于k 的函数解析式. [解]〔1〕 〔本小题介绍二种方法,供参考〕 方法一:过E 作EO ′⊥x 轴,垂足O ′∴AB ∥EO ′∥DC ∴,EO DO EO BO AB DB CD DB ' '''== 又∵DO ′+BO ′=DB ∴1EO EO AB DC ' ' += ∵AB =6,DC =3,∴EO ′=2 又∵DO EO DB AB ' '=,∴2 316 EO DO DB AB ''=?=?= ∴DO ′=DO ,即O ′与O 重合,E 在y 轴上 方法二:由D 〔1,0〕,A 〔-2,-6〕,得DA 直线方程:y =2x -2① 再由B 〔-2,0〕,C 〔1,-3〕,得BC 直线方程:y =-x -2② 联立①②得 2 x y =?? =-? ∴E 点坐标〔0,-2〕,即E 点在y 轴上 〔2〕设抛物线的方程y =ax 2+bx +c (a ≠0)过A 〔-2,-6〕,C 〔1,-3〕 E 〔0,-2〕三点,得方程组426 32a b c a b c c -+=-?? ++=-??=-? 解得a =-1,b =0,c =-2 ∴抛物线方程y =-x 2-2 〔3〕〔本小题给出三种方法,供参考〕 由〔1〕当DC 水平向右平移k 后,过AD 与BC 的交点E ′作E ′F ⊥x 轴垂足为F 。 同〔1〕可得:1E F E F AB DC ''+=得:E ′F =2 图①
空间向量与立体几何典型例题 一、选择题: 1.(2008全国Ⅰ卷理)已知三棱柱111ABC A B C -的侧棱与底面边长都相等,1A 在底面ABC 内的射影为ABC △的中心,则1AB 与底面ABC 所成角的正弦值等于( C ) A . 13 B C D .23 1.解:C .由题意知三棱锥1A ABC -为正四面体,设棱长为a ,则1AB = ,棱柱的高 1 3AO a ===(即点1B 到底面ABC 的距离),故1AB 与底面ABC 所成角的正弦值为113 AO AB =. 另解:设1,,AB AC AA u u u r u u u r u u u r 为空间向量的一组基底,1,,AB AC AA u u u r u u u r u u u r 的两两间的夹角为0 60 长度均为a ,平面ABC 的法向量为111133 OA AA AB AC =--u u u r u u u r u u u r u u u r ,11AB AB AA =+u u u r u u u r u u u r 211112,,33 OA AB a OA AB ?===u u u r u u u r u u u r u u u r 则1AB 与底面ABC 所成角的正弦值为11 1 13OA AB AO AB ?=u u u u r u u u r u u u r u u u r . 二、填空题: 1.(2008全国Ⅰ卷理)等边三角形ABC 与正方形ABDE 有一公共边AB ,二面角 C AB D -- M N ,分别是AC BC ,的中点,则EM AN ,所成角的余弦值等于 6 1 . 1.答案: 1 6 .设2AB =,作CO ABDE ⊥面, OH AB ⊥,则CH AB ⊥,CHO ∠为二面角C AB D -- cos 1CH OH CH CHO ==?∠=,结合等边三角形ABC 与正方形ABDE 可知此四棱锥为正四棱锥,则AN EM ==11(),22AN AC AB EM AC AE =+=-u u u r u u u r u u u r u u u u r u u u r u u u r , 11()()22AN EM AB AC AC AE ?=+?-=u u u r u u u u r u u u r u u u r u u u r 12 故EM AN ,所成角的余弦值1 6 AN EM AN EM ?=u u u r u u u u r u u u r u u u u r 另解:以O 为坐标原点,建立如图所示的直角坐标系, 则点(1,1,0),(1,1,0),(1,1,0),A B E C ----,
中考数学几何专题知识点总结78点中考数学 几何压轴题 1 同角或等角的余角相等 2 过一点有且只有一条直线和已知直线垂直 3 过两点有且只有一条直线 4 两点之间线段最短 5 同角或等角的补角相等 6 直线外一点与直线上各点连接的所有线段中,垂线段最短 7 平行公理经过直线外一点,有且只有一条直线与这条直线平行 8 如果两条直线都和第三条直线平行,这两条直线也互相平行 9 同位角相等,两直线平行 10 内错角相等,两直线平行 11 同旁内角互补,两直线平行 12两直线平行,同位角相等 13 两直线平行,内错角相等 14 两直线平行,同旁内角互补 15 定理三角形两边的和大于第三边
16 推论三角形两边的差小于第三边 17 三角形内角和定理三角形三个内角的和等于180° 18 推论1 直角三角形的两个锐角互余 19 推论2 三角形的一个外角等于和它不相邻的两个内角的和 20 推论3 三角形的一个外角大于任何一个和它不相邻的内角 21 全等三角形的对应边、对应角相等 22边角边公理 有两边和它们的夹角对应相等的两个三角形全等 23 角边角公理有两角和它们的夹边对应相等的两个三角形全等 24 推论有两角和其中一角的对边对应相等的两个三角形全等 25 边边边公理有三边对应相等的两个三角形全等 26 斜边、直角边公理 有斜边和一条直角边对应相等的两个直角三角形全等 27 定理1 在角的平分线上的点到这个角的两边的距离相等 28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上 29 角的平分线是到角的两边距离相等的所有点的集合 30 等腰三角形的性质定理等腰三角形的两个底角相等 31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边
第一部分函数图象中点的存在性问题 §1.1因动点产生的相似三角形问题 例1 2014 年衡阳市中考第 28 题 例2 2014 年益阳市中考第 21 题 例3 2015 年湘西州中考第 26 题 例4 2015 年张家界市中考第 25 题 例5 2016 年常德市中考第 26 题 例6 2016 年岳阳市中考第 24 题 例 72016年上海市崇明县中考模拟第25 题 例 82016年上海市黄浦区中考模拟第26 题 §1.2因动点产生的等腰三角形问题 例9 2014 年长沙市中考第 26 题 例10 2014 年张家界市第 25 题 例11 2014 年邵阳市中考第 26 题 例12 2014 年娄底市中考第 27 题 例13 2015 年怀化市中考第 22 题 例14 2015 年长沙市中考第 26 题 例15 2016 年娄底市中考第 26 题 例 162016年上海市长宁区金山区中考模拟第25 题例 172016年河南省中考第 23 题
§1.3因动点产生的直角三角形问题 例19 2015 年益阳市中考第 21 题 例20 2015 年湘潭市中考第 26 题 例21 2016 年郴州市中考第 26 题 例22 2016 年上海市松江区中考模拟第 25 题 例23 2016 年义乌市绍兴市中考第 24 题 §1.4因动点产生的平行四边形问题 例24 2014 年岳阳市中考第 24 题 例25 2014 年益阳市中考第 20 题 例26 2014 年邵阳市中考第 25 题 例27 2015 年郴州市中考第 25 题 例28 2015 年黄冈市中考第 24 题 例29 2016 年衡阳市中考第 26 题 例 302016年上海市嘉定区宝山区中考模拟中考第24 题例 312016年上海市徐汇区中考模拟第 24 题 §1.5因动点产生的面积问题 例32 2014 年常德市中考第 25 题 例33 2014 年永州市中考第 25 题
2018年全国各地中考数学压轴题汇编(广西专版) 几何综合 参考答案与试题解析 一.选择题(共8小题) 1.(2018?广西)如图,分别以等边三角形ABC的三个顶点为圆心,以边长为半径画弧,得到的封闭图形是莱洛三角形,若AB=2,则莱洛三角形的面积(即阴影部分面积)为() A.B.C.2D.2 解:过A作AD⊥BC于D, ∵△ABC是等边三角形, ∴AB=AC=BC=2,∠BAC=∠ABC=∠ACB=60°, ∵AD⊥BC, ∴BD=CD=1,AD=BD=, ∴△ABC的面积为=, S扇形BAC==π, ∴莱洛三角形的面积S=3×π﹣2×=2π﹣2, 故选:D. 2.(2018?桂林)如图,在正方形ABCD中,AB=3,点M在CD的边上,且DM=1,△AEM与△ADM关于AM所在的直线对称,将△ADM按顺时针方向绕点A旋转90°得到△
ABF,连接EF,则线段EF的长为() A.3 B.C.D. 解:如图,连接BM. ∵△AEM与△ADM关于AM所在的直线对称, ∴AE=AD,∠MAD=∠MAE. ∵△ADM按照顺时针方向绕点A旋转90°得到△ABF, ∴AF=AM,∠FAB=∠MAD. ∴∠FAB=∠MAE ∴∠FAB+∠BAE=∠BAE+∠MAE. ∴∠FAE=∠MAB. ∴△FAE≌△MAB(SAS). ∴EF=BM. ∵四边形ABCD是正方形, ∴BC=CD=AB=3. ∵DM=1, ∴CM=2. ∴在Rt△BCM中,BM==, ∴EF=, 故选:C. 解法二:如图,过E作HG∥AD,交AB于H,交CD于G,作EN⊥BC于N,则∠AHG=∠MGE=90°, 由折叠可得,∠AEM=∠D=90°,AE=AD=3,DM=EM=1, ∴∠AEH+∠MEG=EMG+∠MEG=90°, ∴∠AEH=∠EMG, ∴△AEH∽△EMG,
中考数学压轴题专题十动态几何问题 试题特点 用运动的观点来探究几何图形变化规律的问题称为动态几何问题,此类问题的显著特点是图形中的某个元素(如点、线段、三角形等)或整个图形按照某种规律运动,图形的各个元素在运动变化过程中互相依存、和谐统一,体现了数学中“变”与“不变” 、“一般” 与“特殊”的辩证思想.其主要类型有:1.点的运动(单点运动、多点运动);2.线段 (直线)的运动;3.图形的运动(三角形运动、四边形运动、圆运动等). 方式趋势 动态几何题已成为中考试题的一大热点题型.在近几年各地的中考试卷中,以动点问题、平面图形的平移、翻折、旋转、剪拼问题等为代表的动态几何题频频出现在填空、选择、解答等各种题型中,总体呈现源于教材、高于教材,入口宽、难易适度、梯度分明,考查同学们对图形的直觉能力以及从变化中看到不变实质的数学洞察力. 热点解析 一、点的运动 4 【题1】(2011 盐城)如图1,已知一次函数y=-x+7 与正比例函数y=x 的图象3 交于点A ,且与x 轴交于点B. (1)求点A 和点B 的坐标; (2)过点A 作AC⊥y轴于点C,过点B 作直线l∥y 轴,动点P 从点O 出发,以每秒1 个单位长的速度,沿O-C-A 的路线向点A 运动;同时直线l 从点B 出发,以相同速度向左平移,在平移过程中,直线l 交x 轴于点R,交线 段BA 或线段AO 于点Q.当点P 到达点A 时,点P 和直线l 都停止运动.在运 动过程中,设动点P 运动的时间为t 秒. ①当t 为何值时,以A、P、R 为顶点的三角形的面积为8? ②是否存在以A 、P、Q 为顶点的三角形是等腰三角形?若存在,请说明 理由. 求t 的值;若不存在, 4 【思路】(1)联立方程y=-x+7 和y=3x 即可求出点A 的坐标,令-x+7=0 即 3 可得点B 的坐标. (2)①只要把三角形的面积用t 表示,求出即可.应注意分P 在OC 上运动和P 在CA