
高三数学第二轮专题复习系列(8)-- 空间向量、立体几何复习与检测
一、大纲解读
立体几何的主要内容是空间几何体,点线面之间的位置关系,空间向量与立体几何.其考查内容主要是空间两直线的位置关系、直线与平面的位置关系、两平面的位置关系;异面直线所成的角、二面角、线面角;几何体的表面积和体积、空间几何体的三视图和直观图等.其中线面平行与垂直判定定理与性质定理、面面平行与垂直判定定理与性质定理是考查的重点.对于理科生来说,空间向量作为一种新的快捷有效的工具已被广泛应用于解决立体几何综合问题,是高考的焦点所在.
二、高考预测
一般来说立体几何有两个左右的选择题或填空题和一道解答题,约20-25分,占整章试卷的15%. 选择题或填空题考查的是空间几何体和点线面位置关系的基本问题,与三视图相结合考查是一种典型题型;解答题近年已成为一个较为固定的模式,以多面体(少数为旋转题)为载体,考查点线面的位置关系的判断推理,求空间角和距离,求有关最值和体积一般分步设问,难度逐渐增大,但都可以用基本方法解决,理科生要会用空间向量来解决这类问题.
三.重点剖析
立体几何的重点内容是柱锥台球的表面积和体积,空间几何体的三视图和直观图,平面的基本性质,空间线面位置关系,空间向量的基本问题,空间向量与立体几何,特别是用空间向量解决立体几何中的线面平行与垂直的证明,求解异面直线所成的角、二面角、线面角,以及简单的距离计算.
重点一:空间几何体的三视图、体积与表面积
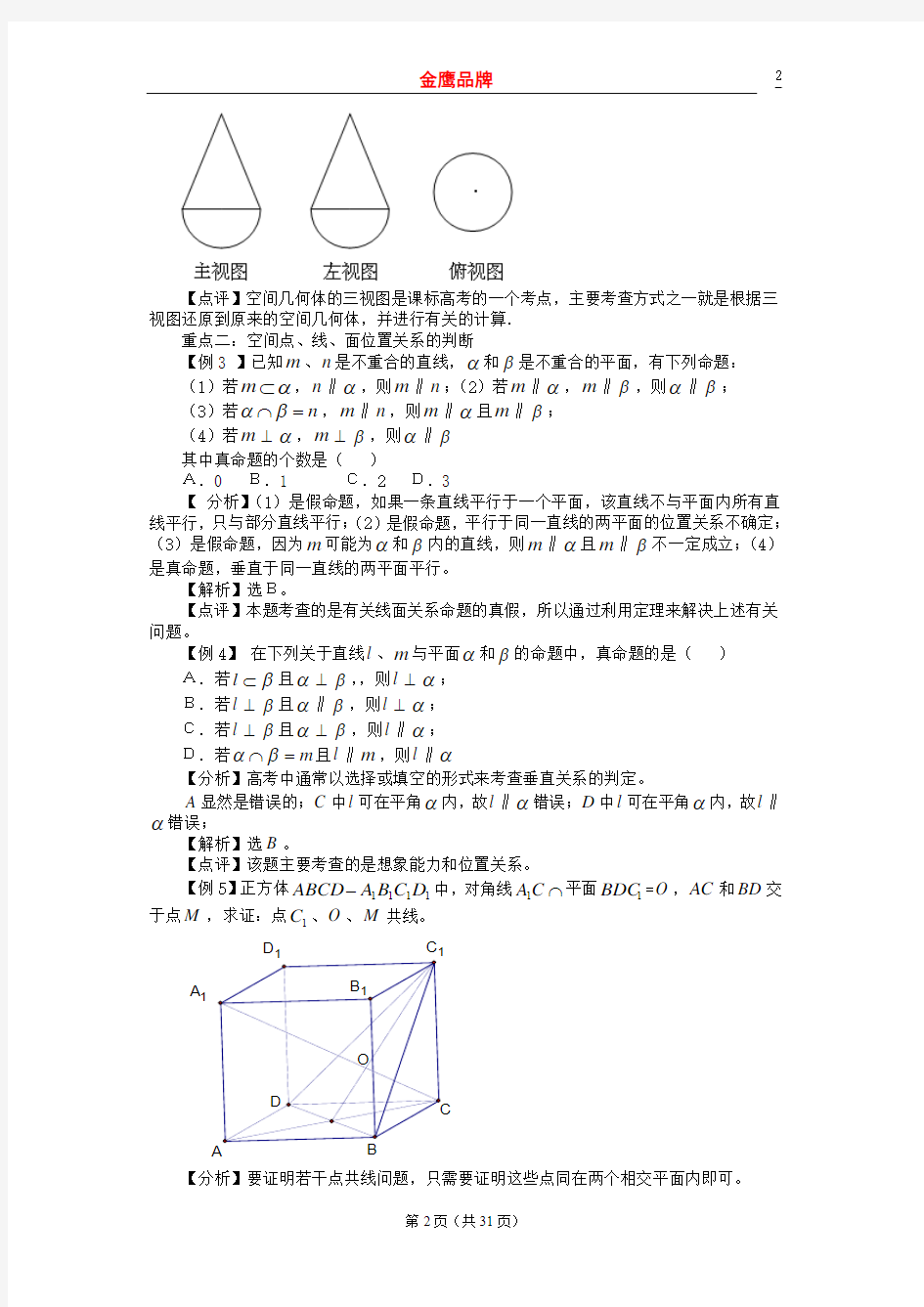
【例1】 一个空间几何体的主视图、左视图、俯视图为直角三角形,边长如图所示,那么这个几何体的体积为( )
A.1
B.2
C.3
D.4
【分析】根据三个试图可以知道这个几何体是一个一条侧棱和底面垂直,底面是直角三角形的三棱锥。
【解析】该几何体是底面两直角边长分别是1,2的直角三角形,高为3的三棱锥,故其体积为11
123132
?
???=。 【点评】主试图和侧视图的高就是实际几何体的高。
【例2】已知一个几何体是由上下两部分构成的组合体,其三视图如下,若图中圆的半径为1,等腰三角形的腰长为5,则该几何体的体积是 ( )
A.
43π B.2π C.83π D.103
π 【分析】这个空间几何体是一个圆锥和一个半球组成的组合体,把其中的数量关系找
出来按照圆锥和球的体积计算公式计算就行.
【解析】A 这个几何体是一个底面半径为1,高为2的圆锥和一个半径为1的半球组成
的组合体,故其体积为2
311441213233
πππ??+
??=.
【点评】空间几何体的三视图是课标高考的一个考点,主要考查方式之一就是根据三视图还原到原来的空间几何体,并进行有关的计算.
重点二:空间点、线、面位置关系的判断
【例3 】已知m 、n 是不重合的直线,α和β是不重合的平面,有下列命题: (1)若α?m ,n ∥α,则m ∥n ;(2)若m ∥α,m ∥β,则α∥β; (3)若n =?βα,m ∥n ,则m ∥α且m ∥β; (4)若m ⊥α,m ⊥β,则α∥β 其中真命题的个数是( )
A.0 B.1 C.2 D.3 【 分析】(1)是假命题,如果一条直线平行于一个平面,该直线不与平面内所有直线平行,只与部分直线平行;(2)是假命题,平行于同一直线的两平面的位置关系不确定;(3)是假命题,因为m 可能为α和β内的直线,则m ∥α且m ∥β不一定成立;(4)是真命题,垂直于同一直线的两平面平行。
【解析】选B。
【点评】本题考查的是有关线面关系命题的真假,所以通过利用定理来解决上述有关问题。
【例4】 在下列关于直线l 、m 与平面α和β的命题中,真命题的是( )
A.若β?l 且α⊥β,,则l ⊥
α; B.若l ⊥β且α∥β,则l ⊥α; C.若l ⊥β且α⊥β,则l ∥α; D.若m =?βα且l ∥m ,则l ∥α
【分析】高考中通常以选择或填空的形式来考查垂直关系的判定。
A 显然是错误的;C 中l 可在平角α内,故l ∥α错误;D 中l 可在平角α内,故l ∥α
错误;
【解析】选B 。
【点评】该题主要考查的是想象能力和位置关系。
【例5】正方体1111D C B A ABCD -中,对角线?C A 1平面1BDC =O ,AC 和BD 交
于点M ,求证:点1C 、O 、M 共线。
O
C 1
D 1
B 1
A 1
C
D
A
B
【分析】要证明若干点共线问题,只需要证明这些点同在两个相交平面内即可。
【证明】如图所示,由A A 1∥C C 1,则11CC AA 确定平面C AA 1。
C A 1?平面C AA 1,C A O 1∈,∴∈O 平面C AA 1。 又C A 1?平面1BDC =O ,∴∈O 平面1BDC 。 ∴O 在平面1BDC 与平面C AA 1的交线上。 又M B
D AC =?,∴平面C AA 1?平面1BDC =M C 1, ∴∈O M C 1,即O 、1C 、M 三点共线。
【点评】该题的考向是点共线的问题,一般转化为证明这些点是某两个平面的公共点,这样就可以根据公理2证明这些点都是在这两个平面的交线上。
重点三:空间线面位置关系的证明和角的计算
【例6】 1111D C B A ABCD -是边长为a 正方体,计算下列问题:(1)1AD 与C B 1所成角的大小;(2)若
E 、
F 、
G 、
H 为对应棱的中点,求EF ,GH 所成的角。
【分析】该题可以采用平移法,即将EF ,GH 平移到11B D 和1AB 即可。
【解析】(1)连1BC ,则1AD ∥1BC ,所以1BC ⊥C B 1,则1AD ⊥C B 1,即1AD 与
C B 1所成角为090;
(2)连1AB ,11D B ,则EF ∥11D B ,GH ∥1AB ,A B D 11∠即为EF 和GH 所成
的角,
因为A B D 11?为正三角形,∴A B D 11∠=060,即EF 和GH 所成的角为060。
E
F
H
G
C 1
D 1
B 1
A 1
C
D
A
B
图2
【点评】掌握此类基本题的解法,也是反映同学们的立体几何基础。
【例7】如图,四棱锥P ABCD -中,PA ⊥底面ABCD , PC ⊥AD .底面ABCD
为梯形,//AB DC ,AB BC ⊥.PA AB BC ==,点
E 在棱PB 上,且2PE EB =.
(1)求证:平面PAB ⊥平面PCB ; (2)求证:PD ∥平面EAC ; (3)(理)求平面AEC 和平面PBC 所成锐二面角的余弦值.
【分析】(1)根据两个平面垂直的判定定理,寻找一个面对一条直线垂直于另一个平面;(2)根据线面平行的判定定理,寻找线线平行;(3)可以利用传统的方法作出二面角的平面角解决,也可以利用空间向量的方法解决。
【解析】(1)∵PA ⊥底面ABCD ,∴PA BC ⊥.又AB BC ⊥,PA AB A = ,∴BC ⊥平面PAB .
又BC ?平面PCB ,∴平面PAB ⊥平面PCB .
(2)∵PA ⊥底面ABCD , ∴PA AD ⊥,又PC AD ⊥,∴AD ⊥平面PAC ,∴AC AD ⊥.
在梯形A B C D 中,由A B B C ⊥,AB BC =,得4
BAC π
∠=
,∴
4
DCA BAC π
∠=∠=
.
又AC AD ⊥,故D A C ?为等腰直角三角形.∴(
)
22
22DC AC AB AB =
==.
连接BD ,交AC 于点M ,则
2.DM DC MB AB == 在BPD ?中,2PE DM
EB MB
==,∴//PD EM
又PD ?平面EAC ,EM ?平面EAC , ∴PD ∥平面EAC .
(3)方法一:在等腰直角PAB ?中,取PB 中点N ,连结AN ,则AN PB ⊥.∵平面PAB ⊥平面PCB ,且平面PAB 平面PCB =PB ,∴AN ⊥平面PBC .
在平面PBC 内,过N 作NH ⊥直线CE 于H ,连结AH ,由A
N C E ⊥、NH CE ⊥,得CE ⊥平面ANH ,故AH CE ⊥.∴AHN ∠就是二面角A CE P --的平面角.
M
E A
B
C
D
P
H
N
H N
P
B
C
E
在Rt PBC ?中,设CB a =,则222PB PA AB a =
+=,12
33
BE PB a ==
,1266NE PB a ==,22113
CE CB BE a =+=,
由NH CE ⊥,EB CB ⊥可知:NEH ?∽CEB ?,∴NH CB
NE CE
=,代入解得:22
a
NH =.
在
Rt AHN
?中,
2
2
A N
a
=,∴
tan 11AN
AHN NH
∠=
=,
13
cos 6
111AHN ∠=
=
+. ∴平面AEC 和平面PBC 所成锐二面角的余弦值为3
6
. 方法二:以A 为原点,,AB AP 所在直线分别为y 轴、z 轴,如图建立空间直角坐标
系.
设PA AB BC a ===,则()0,0,0A ,()0,,0B a ,(),,0C a a ,()0,0,P a ,
20,,33a a E ?? ???
.
设()1,,1x y =n 为平面EAC 的一个法向量,则11,AC AE ⊥⊥uuu r uu u r n n ,∴0,20.3
3ax ay ay a +=??
?+=??,
解得11,22x y =
=-,∴111
(,,1)22
=-n . 设()2',',1x y =n 为平面PBC 的一个法向量,则22,BC BP ⊥⊥uu u r uu r
n n ,
又(),0,0BC a = ,(0,,)BP a a =- ,∴'
'0,0,
ax ay a =??-+=?,解得'0,'1x y ==,∴()20,1,1=n . 1212123
cos ,6
?==
n n n n n n . ∴平面AEC 和平面PBC 所成锐二面角的余弦值为
3
6
. 【点评】求二面角的平面角的方法通常有:一是根据线面垂直关系作出二面角的平面角,通过解三角形解决;二是用空间向量的方法来求解,方法是:求出两个平面的法向量
→
1n 和→
2n ,然后利用数量积公式计算出锐二面角,其公式为12cos ,n n =→→→
→?2
121|
|n n n n ,当然
考虑到二面角的取值范围是[]0,π,所以,二面角的平面角θ与这两个平面的法向量的夹角相等或互补。
四 扫雷先锋
错误之一:概念理解错误
【例8】空间四边形ABCD 中,AB =CD 且成0
60的角,点 M 、N 分别为BC 、AD 的中点,求异面直线AB 和MN 成的角.
【错解】如图所示,取AC 的中点P ,连PM ,PN ,MN 。
∵ M、N 分别为BC 、AD 的中点,∴MP∥AB,且MP=
21 AB ;NP∥CD,且NP=2
1
CD 。 又AB=CD , 且AB ,CD 所成的角为060, ∴MP=NP 且直线MP 于NP 成060角,∴
∠MPN=060,即MPN ?使等边三角形, ∴∠PMN=060,即直线AB 和MN 成的角为060.
【剖析】上面的解法遗漏了当直线PM 与PN 成060角,而∠MPN=0
120的情形,此时直线AB 和MN 所成角为030.为防止遗漏或错误,在解题过程中应正确理解定义.
【点评】题目中的错误,是同学们最易忽视的,有时看到一例题目,似乎会做,但是,不经过缜密的思考,就会出现“千里之堤,溃于蚁穴”的慨叹.
错误之二:忽视分类讨论错误
【例9】点M是线段AB 的中点,若A 、B 到平面α的距离分别为4cm 和6cm ,则点M 到平面α的距离为——————
【错解】如图1,分别过点A 、B 、M 作平面α的垂线,/
AA ,/
BB ,MH ,垂足分别为
H B A ,,//.
则线段/
AA ,/
BB ,MH 的长分别为点,A 、B 、M 到平面α的距离,由题设知,/
AA =4cm ,/BB =6cm ,
因此,MH=
)(52
6
42//cm BB AA +=+ 【剖析】不少同学在解此类问题时,总认为A 、B 在α的同侧,只注意检验计算是否
正确,并没有发现异侧的情况,缺乏分类讨论的意识.事实上,如图2 ,若A 、B 在α异侧,则MH=1cm .
【点评】分类讨论是数学中一种重要的思想方法,它在立体几何中应用非常广泛.但
A
B
C
M
N
D
P A
M
H
B
/B
/
A
图2
α
α A
M H
B
/
A
/
B
图1
不少同学不能正确的利用这种思想方法,经常片面地考虑问题,使问题出现漏解.
五 规律总结
1.空间几何体的三视图“长对正、高平齐、宽相等”的规律。
2.在计算空间几何体体积时注意割补法的应用。
3.注意多面体中的特征图和旋转体的轴截面在解题的应用。
4.空间平行与垂直关系的关系的证明要注意转化:线线平行 线面平行 面面平行,线线垂直 线面垂直 面面垂直。
5.求异面直线所成的角θ的方法
(文科)求异面直线所成的角的最关键是要找出一个点,把其作为角的顶点,然后把两条直线“平行平移”过来,这个角就完成了。这个点有时很好找,中点、交点、对称点等。若用平移转化烦琐或无法平移时,可考虑是否异面垂直,即可通过证明垂直的位置关系得到90°的数量关系。
(理科)利用空间向量法:
cos |cos ,|a b θ=<>r r =121212222222
111222||||||||
x x y y z z a b a b x y z x y z ++?=
?++?++r r r r (其中θ(090θ<≤o o
)
为异面直线a b ,所成角,,a b r r
分别表示异面直线a b ,的方向向量)。
6.直线与平面所成的角
(文科)在斜线上找到任意一点,过该点向平面作垂线,找到斜线在该平面上的射影,则斜线和射影所成的角便是直线与平面所成的角。
(理科)直线AB 与平面所成角sin ||||
AB m AB m β?=
(m
为平面α的法向量). 7.(理科)二面角
方法一:常见的方法有三垂线定理法和垂面法;
方法二:向量法:二面角l αβ--的平面角cos ||||
m n arc m n θ?=
或cos ||||m n arc m n π?- (m ,n
为平面α,β 的法向量)
。 8.(理科)空间距离
(1)点与点的距离、点到直线的距离,一般用三垂线定理“定性”; (2)给出公垂线的两条异面直线的距离,先进行论证(先定性),后计算(后定量); (3)线面距、面面距都转化为点面距;
(4)求点面距: ||||
AB n d n ?=
(n
为平面α的法向量,AB 是经过面α的一条斜线,A α∈)。
六 能力突破
例1 如图在直三棱柱ADE-BCF 中,面ABFE 和面ABCD 都为正方形,且互相垂直, M 为AB 的中点, O 为DF 中点.
(1)求证:OM∥平面BCF ;
(2)求证:平面MDF⊥平面EFCD ; (3)(理科)求二面角F-DM-C 的正切值。
A
B
C
G
F
O
D
E
M
【分析】问题(1)是证明线面平行,则可以利用线面 平行的判定定理;问题(2)是证明面面垂直,方法
比较多,当然最好的办法是用线面垂直的判定定理来证明。
【解析】(1)取FC 的中点G , 连结OG 、BG 。∵O 为DF 的中点, ∴OG//DC 且OG=2
1
DC . 在正方形ABCD 中, M 为AB 中. ∴MB//DC 且MB=2
1
DC. ∴OG//MB 且OG=MB , ∴四边形OMBG 为平行四边形. ∴OM//BG , 又∵BG ?平面BFC , OM ?平面BFC ,
∴OM//平面BCF.
(2)在直三棱柱ADE-BCF 中, DC⊥平面BCF, ∴DC⊥BG , 在等腰△FBC 中, ∵BF=BC, ∴G 为FC 的中点, ∴BG⊥FC , ∴BG⊥平面EFCD. 又∵OM//BG , ∴OM⊥平面EFCD. 又∵OM ?平面MDF, ∴平面MDF⊥平面EFCD. (3)过B 作BH⊥DM 交DM 的延长线于H , 连结FH . ∵平面EFBA⊥平面ABCD, FB⊥AB. ∴FB⊥平面ABCD .
∴BH 为FN 在平面ABCD 上的射影. ∴FH⊥DH (三垂线定理). ∴∠FHB 为二面角F-DM-C 的平面角, 设AB=1 , 则BH=BMsin∠AMD=
5
1
2
5121=?,∴tan∠FHB=5=BH BF . ∴二面角F-DM-C 的正切值为5。
【点评】该题主要是能够熟练应用判定定理来证明相关的问题,因此要熟悉定理并能灵活应用。
【例2】 如图, 己知四棱锥P-ABCD 的底面为直角梯形, AD//BC , ∠BCD=90°, PA=PB, PC=PD 。
(1)证明: CD 与平面PAD 不垂直; (2)证明:平面PAB⊥平面ABCD ; (3)(理科)如果CD=AD+BC , 二面角P-BC-A 等于60°, 求二面角P-CD-A 的大小。
【分析】问题(1)需要利用反证法来证明,问题(2)仍用面面垂直的判定定理来证明。
【解析】(1)若CD⊥平面PAD, 则CD⊥PD, 由己知PC=PD 得∠PCD=∠PDC<90°, 这与CD⊥PD 矛盾,所以CD 与平面QAD 不垂直.
(2)取AB 、CD 的中点E 、F , 连结PE 、PF 、EF, EF 为 直角梯形的中位线, EF⊥CD.
由PA=PB , PC=PD 得 PE⊥AB. 又PF∩EF=F
A
B
C
G
F
O
D
E
M
P
B
C
F
D A
E
∴CD⊥平面PEF , 由PE ?平面PEF 得 CD⊥PE , 又AB⊥PE 且梯形两腰AB 、CD 必相交。
∴PE⊥平面ABCD, 又PE ?平面PAB , ∴平面PAB ⊥平面ABCD. (3)由(2)及二面角定义可知∠PFE 为二面角P-CD-A 的平面角. 作EG⊥BC 于G , 连PG.
∴BC⊥PG. ∴∠PGE 为二面角P-CD-A 的平面角, 即∠PGE=60°. 由己知 得 EF=
21(AD+BC)= 21CD. 又EG=CF=2
1
CD. ∴EF=EG。 易证得R t △PEF≌R t △PEG , ∴∠PFE=∠PGE =60°即为所求。
【点评】会添加辅助线,并注意一定的逻辑推理,这是立体几何大题的解题所应该注意的地方。
【例3】已知四棱锥P-ABCD 的底面为直角梯形,AB∥DC,⊥=∠PA DAB ,90 底面ABCD ,且PA=AD=DC=
2
1
AB=1,M 是PB 的中点。 (1)证明:面PAD⊥面PCD ;
(2)求AC 与PB 所成的角余弦值; (3)(理科)求面AMC 与面BMC 所成二面角的余弦值。
【分析】本小题主要考查直线与平面垂直、直线与平面所成角和二面角的有关知识及思维能力和空间想象能力.考查应用向量知识解决数学问题的能力。
【解析】方法一:
(1)证明:∵PA⊥面ABCD ,CD⊥AD,∴由三垂线定理得:CD⊥PD。因而,CD 与面PAD 内两条相交直线AD ,PD 都垂直,∴CD⊥面PAD 。又CD ?面PCD ,∴面PAD⊥面PCD.
(2)解:过点B 作BE//CA ,且BE=CA ,则∠PBE 是AC 与PB 所成的角.
连结AE ,可知AC=CB=BE=AE=2,又AB=2,所以四边形ACBE 为正方形. 由PA⊥面ABCD 得∠PEB=90°,在Rt△PEB 中BE=2,PB=5, 5
10
cos =
=
∠∴PB BE PBE 。
(3)解:作AN⊥CM,垂足为N ,连结BN 。在Rt△PAB 中,AM=MB ,又AC=CB , ∴△AMC≌△BMC,∴BN⊥CM,故∠ANB 为所求二面角的平面角.
∵CB⊥AC,由三垂线定理,得CB⊥PC,在Rt△PCB 中,CM=MB ,所以CM=AM 。 在等腰三角形AMC 中,AN·MC=AC AC CM ?-2
2
)2
(
, A
D
C
B
E
P
M
N
5
6
2
5223
=?=∴AN . ∴AB=2,32
2cos 222-=??-+=
∠∴BN AN AB BN AN ANB 方法二:(理科)因为PA⊥PD,PA⊥AB,AD⊥AB,以A 为坐标原点AD 长为单位长度,
如图建立空间直角坐标系,则各点坐标为A (0,0,0)B (0,2,0),C (1,1,0),D (1,0,0),P (0,0,1),M (0,1,)2
1
.
(1)证明:因DC AP DC AP DC AP ⊥=?==所以故,0),0,1,0(),1,0,0(。 由题设知AD⊥DC,且AP 与AD 是平面PAD 内的两条相交直线,由此得DC⊥面PAD. 又DC 在面PCD 上,故面PAD⊥面PCD. (2)解:因),1,2,0(),0,1,1(-==PB AC
.
510
|
|||,cos ,2
,5||,2||=??>=<=?==PB AC PB
AC PB AC PB AC PB AC 所以故
(3)解:在MC 上取一点N (x ,y ,z ),则存在,R ∈λ使,MC NC λ=
.2
1
,1,1),21,0,1(),,1,1(λλ==-=∴-=---=z y x MC z y x NC 。
要使5
4
,0210,==-=?⊥λ解得即只需z x MC AN MC AN 。
),5
2
,1,51(),52,1,51(,,
0),5
2
,1,51(,54=?-===?=MC BN BN AN MC AN N 有此时能使点坐标为时可知当λ
ANB MC BN MC AN MC BN MC AN ∠⊥⊥=?=?所以得由.,0,0为所求二面角
的平面角。
30304
||,||,.
555
2cos(,).
3||||
AN BN AN BN AN BN AN BN AN BN ==?=-?∴==-?
【点评】建立空间直角坐标系,通过代数计算得到几何值,这种问题是近几年中高考
的重点内容。
七、高考风向标
考查方向一:空间几何体的三视图以及面积、体积的计算
例1右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( ) A .9π B .10π C .11π D .12π
分析:本题考查三视图、球和圆锥的表面积等基础知识,考查空间想象能力和运算能力.三视图是课标高考相对于大纲高考的新增内容,是课标高考的一个热点内容.解题的关键是由这个三视图想象出这个空间几何体是如何构成的.
解析:D 该几何体下面是一个底面半径为1,母线长为3的圆柱,上面是一个半径为1的球,其表面积是2
2
213214112ππππ??+??+?=.
点评:本题容易出错的答复有两个,一是不能由这个三视图想象出这个空间几何体,二是用错球的表面积公式、圆柱的侧面积公式或在计算圆柱的表面积时忽视了上下底面.
考查方向二:空间线面位置关系的判断
例2(08年安徽理4)已知,m n 是因为两条不同直线,,,αβγ是三个不同平面,下列命题中正确的是( )
A .,,m n m n αα若则‖‖‖
B .,,αγβγαβ⊥⊥若则‖
C .,,m m αβαβ若则‖‖‖
D .,,m n m n αα⊥⊥若则‖
分析:考查空间线面位置关系的判断.本题主要用到的是“两条直线如果和同一个平面垂直,则这两条直线平行”,这是空间直线和平面垂直的性质定理,是空间线面位置关系的主要定理之一。 解析:D ,m n 均为直线,其中,m n 平行α,,m n 可以相交也可以异面,故A 不正确;m ⊥α,n ⊥α则同垂直于一个平面的两条直线平行.
点评:对空间线面位置关系的判定定理生疏或者不会结合图形进行分析是本题解答错误或不会解答的主要原因.在空间直线和直线的平行关系、平面和平面之间的平行关系具有传递性,但是直线和平面之间的平行关系没有传递性,本题中A 、C 两个选择支就是针对这个问题而设计的。在平面上和同一条直线垂直的两条直线平行,但在空间这个结论不成立,同时在空间和同一个平面垂直的两个平面也不平行,本题的选择支B 就是针对这个问题设计的。
考查方向三:空间垂直与平行关系的证明
例3如图,在四面体ABCD 中,BD AD CD CB ⊥=,,点F E ,分别是BD AB ,的中点,求证:
(1)直线EF 面ACD ;
(2)面⊥EFC 面BCD .
分析:根据线面平行的判定定理和面面垂直的判定定理,寻找需要的直线。
B C A
F
D
E 俯视图
正(主)视图 侧(左)视图
2 3
2 2
证明:(1)∵E、F 分别是AB 、BD 的中点, ∴EF 是△ABD 的中位线,∴EF//AD. 又∵EF ?面ACD ,AD ?面ACD ,∴直线EF//面ACD .
(2)//EF AD EF BD AD BD ??⊥?⊥?
C CB C
D F BD F BD =?
?⊥??
为中点
BD CEF EFC BCD BD BCD ?⊥??⊥???面面面面 C F EF F =
点评:本题考查空间直线与平面、平面与平面的位置关系的判定,考查空间想象能力、推理论证能力.主要检测考生对空间线面位置关系的判定和性质定理的掌握程度.
考查方向四:全面考查立体几何的综合性试题 例4 如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图.它的正视图和俯视图在下面画出(单位:cm )
(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图; (2)按照给出的尺寸,求该多面体的体积;
(3)在所给直观图中连结BC ',证明:BC '∥面EFG .
分析:根据图中的数据和图中反应的线面位置关系解决。
解析:(1)如图
(2)所求多面体体积
V V V =-长方体正三棱锥1144622232??
=??-???? ???
2284(cm )3
=.
(3)证明:在长方体ABCD A B C D ''''-中, 连接AD ',则AD BC ''∥.
因为E G ,分别为AA ',A D ''中点, 所以AD EG '∥,从而EG BC '∥. 又BC '?平面EFG , 所以BC '∥面EFG .
点评:本题考查立体几何初步的基本知识和方法.立体几何初步中的主要问题是空间几何体的三视图、直观图、表面积和体积计算,空间线面位置关系的证明,本题把这些问题糅合在一起综合检测考生对立体几何初步的掌握程度,这可以说是针对立体几何初步而设计的一道典型试题。在画俯视图时不标明尺寸,或是只画一个矩形;在计算体积时没有
4
6
4 2
2
E D A
B C
F G B '
C '
D '
2
4
6 4
2
2 2
4
6 2
2
(俯视图)
(正视图)
(侧视图)
A
B
C D
E F
G
A '
B '
C '
D '
体积分割的思想意识,或是忽视了锥体体积公式中的
1
3
,在空间几何体的体积计算中“割补法”是最重要的技巧之一,在复习中要认真体会。
例4 如图
,已知四棱锥P ABCD -,底面ABCD 为菱形,PA ⊥
平面ABCD ,60ABC ∠=
,E F ,分别是BC PC ,的中点. (1)证明:AE PD ⊥;
(2)若H 为PD 上的动点,EH 与平面PAD 所成最大角的正切值为
6
2
,求二面角E AF C --的余弦值.
分析:第一问转化为证明线面垂直;第二问根据EH 与平面PAD 所成最大角的正切值为
6
2
可以找出四棱锥的底面边长和高之间的关系,然后用传统的方法作出二面角的平面角解决,或是用空间向量的方法解决。
证明:(1)由四边形ABCD 为菱形,60ABC ∠=
,可得ABC △为正三角形. 因为E 为BC 的中点,所以AE BC ⊥.又BC AD ∥,因此AE AD ⊥. 因为PA ⊥平面ABCD ,AE ?平面ABCD ,所以PA AE ⊥.
而PA ?平面PAD ,AD ?平面PAD 且PA AD A = ,所以AE ⊥平面PAD . 又PD ?平面PAD ,所以AE PD ⊥.
解:(2)设2AB =,H 为PD 上任意一点,连接AH EH ,,如图
.
由(1)知AE ⊥平面PAD ,则EHA ∠为EH 与平面PAD 所成的角.
在Rt EAH △中,3AE =,所以当AH 最短时,EHA ∠最大,即当AH PD ⊥时,
EHA ∠最大.此时36
tan 2
AE EHA AH AH ∠=
==,因此2AH =.又2AD =,所以45ADH ∠= ,所以2PA =.
解法一:因为PA ⊥平面ABCD ,PA ?平面PAC ,所以平面PAC ⊥平面ABCD . 过E 作EO AC ⊥于O ,则EO ⊥平面PAC ,过O 作OS AF ⊥于S ,连接ES ,
则ESO ∠为二面角E AF C --的平面角,在Rt AOE △中,3
sin 302
EO AE == ,
3cos302AO AE == ,又F 是PC 的中点,在Rt ASO △中,32
sin 454
SO AO == ,
又22
3930484
SE EO SO =+=+=
,在Rt ESO △中,P
B
E C D
F A
H
O S P
B
E
C
D
F A
32154cos 530
4
SO ESO SE ∠===,即所求二面角的余弦值为15
5.
解法二:由(1)知AE AD AP ,,两两垂直,以A 为坐标原点,建立如图
所示的空间直角坐标系,因为E F ,分别为BC PC ,的中点,所
以
(000)(310)(310)(020)A B C D -,,,,,,,,,,,,
31(002)(300)122P E F ??
? ??
?,,,,,,,,, 所以31(300)122AE AF ??
== ? ??
? ,,,,,.
设平面AEF 的一法向量为111()x y z =,,m ,则00AE AF ?=??=??
,
,
m m 因此11113031
022
x x y z ?=?
?++=??,
. 取11z =-,则(021)=-,,m ,因为BD AC ⊥,BD PA ⊥,PA AC A = ,所以BD ⊥平面AFC ,故BD 为平面AFC 的一法向量.又(330)BD =-
,,,所以
2315
cos 5512BD BD BD
?<>==
=?
,m m m .因为二面角E AF C --为锐角,所以所求二面角的余弦值为
15
5
. 点评:本题考查空间线面位置关系的有关定理、线面角、二面角等基础知识,考查用空间向量解决立体几何问题的方法,考查转化的数学思想,考查空间想象、逻辑思维、运算求解等能力.本题第一问是一个证明线线垂直问题,证明的基本思想是转化为证明线面垂直,只要考生熟悉这个转化策略,熟悉空间线面位置关系的有关定理,解决起来困难不大;第二问以一个动态的情境给出,确定动点H 的位置是解决的关键所在,这就要求有一定的逻辑推理能力和分析问题的能力,这个地方能有效地检测考生的思维层次,是一个设计优秀的试题.
八、沙场练兵 一、选择题
P
B
E C
D F A y
z x
1.一条直线与一个平面所成的角等于
3π,另一直线与这个平面所成的角是6
π
. 则这两条直
线的位置关系( )
A .必定相交
B .平行
C .必定异面
D .不可能平行 1.D
2.在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1∶3,则锥 体被截面所分成的两部分的体积之比为( )
A .1∶3
B .1∶9
C .1∶33
D .1∶)133(- 2.D
3.正方体1111ABCD A BC D -中,P 、Q 、R 分别是AB 、AD 、11B C 的中点.那么,正方体的过P 、Q 、R 的截面图形是( )
A .三角形
B .四边形
C .五边形
D .六边形 3.D
4.正四棱锥的侧棱长与底面边长都是1,则侧棱与底面所成的角为( ) A .75° B .60° C .45° D .30° 4.C
5.对于直线m 、n 和平面α,下面命题中的真命题是( ) A .如果m n m ,,αα??、n 是异面直线,那么α//n B .如果m n m ,,αα??、n 是异面直线,那么α与n 相交
C .如果m n m ,//,αα?、n 共面,那么n m //
D .如果m n m ,//,//αα、n 共面,那么n m // 5.C