
勾股定理、
了解勾股定理的几种证明方法,运用勾股定理及逆定理解决问题,系统梳理勾股定理中的重要考点。
二、知识要点
1.勾股定理
内容: ,即222
a b c +=。
2.勾股定理的证明
常见的是拼图法,思路是:①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变 ②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理
3.勾股定理的适用范围
勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于 三角形。 4.勾股定理的应用
①已知直角三角形的任意两边长,求第三边
②知道直角三角形一边,可得另外两边之间的数量关系
③可运用勾股定理解决一些实际问题
5.勾股定理的逆定理
如果三角形三边长,,a b c 满足222a b c +=,那么这个三角形是 ,其中c 为斜边。 这是判定一个三角形是否是直角三角形的一种重要方法。
6.勾股数
①能够构成直角三角形的三边长的三个正整数称为勾股数,即222a b c +=中,,,a b c 为正整数时,称,,a b c 为一组勾股数
②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25等
7.勾股定理及其逆定理的应用
勾股定理及其逆定理在解决一些实际问题或具体的几何问题中,是密不可分的一个整体.通常既要通过逆定理判定一个三角形是直角三角形,又要用勾股定理求出边的长度,二者相辅相成,完成对问题的解决。 三、典型例题
例1、勾股定理的证明
(2011中考)我国汉代数学家赵爽为了证明勾股定理,创
制了一幅“弦图”,后人称其为“赵爽弦图”(如图1).图
2由弦图变化得到,它是用八个全等的直角三角形拼接而
成,记图中正方形A B C D ,正方形E F G H ,正方形
M N K T 的面积分别为123,,S S S ,若12310S S S ++=,则
2S 的值是 .
例2、勾股定理的直接用法
在Rt△ABC 中,∠C=90°
(1)已知6,10a c ==,求b , (2)已知40,9a b ==,求c ; (3)已知25,15c b ==,求b 。
变式:图示是一种“羊头”形图案,其作法是,从正方形1开
始,以它的一边为斜边,向外作等腰直角三角形,然后再以其
直角边为边,分别向外作正方形2,和2′,…,依次类推,若
正方形7的边长为1cm ,则正方形1的边长为__________cm.
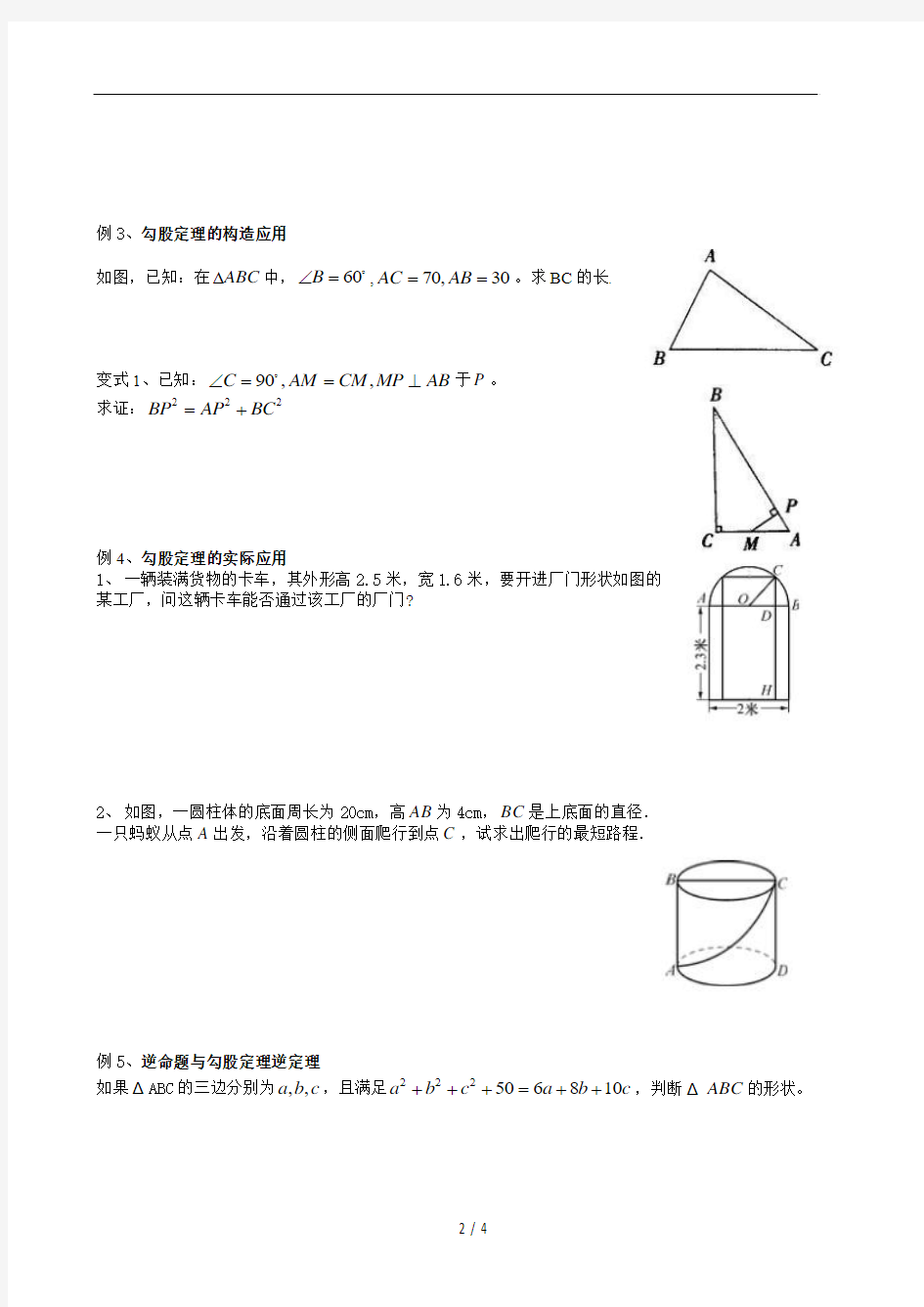
例3、勾股定理的构造应用
如图,已知:在ABC ?中,60B ∠= ,70,30AC AB ==。求BC 的长.
变式1、已知:90,,C AM CM MP AB ∠==⊥ 于P 。
求证:222
BP AP BC =+
例4、勾股定理的实际应用
1、 一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的
某工厂,问这辆卡车能否通过该工厂的厂门?
2、 如图,一圆柱体的底面周长为20cm ,高AB 为4cm ,BC 是上底面的直径.
一只蚂蚁从点A 出发,沿着圆柱的侧面爬行到点C ,试求出爬行的最短路程.
例5、逆命题与勾股定理逆定理
如果ΔABC 的三边分别为,,a b c ,且满足222506810a b c a b c +++=++,判断ΔABC 的形状。
变式:如图正方形A B C D ,E 为BC 中点,F 为AB 上一点,且
14
BF AB =
。 请问FE 与DE 是否垂直?请说明。
例6、如图,正方形ABCD 的四个顶点分别在四条平行线1234
,,,l l l l 上,这四条直线中相邻两条之间的距离依次为
()123123,,0,0,0h h h h h h >>>。
(1)求证:13h h >;
(2)设正方形ABCD 的面积为S ,求证:()2
2121S h h h =++; (3)若
12312
h h +=,当1h 变化时,说明正方形ABCD 的面积S 随1h 的变化情况
四、思维拓展
如图,C 为线段BD 上一动点,分别过点,B D 作,AB BD ED BD ⊥⊥,连接,A C E C ,已知
5,1,8AB DE BD ===,设CD x = (1)用含x 的代数式表示AC CE +的长;
(2)请问点C 满足什么条件时,AC CE +的值最小?
(3)根据(2)中的规律和结论,请构图求出代数式
9)12(422+-++x x 的最小值.
五、课后练习
1、在射线、角和等腰三角形中,它们( )轴对称图形
A .都是
B .只有一个是
C .只有一个不是
D .都不是
2、三角形内有一点,到三角形三边的距离都相等,同时与三角形三顶点的距离也都相等,则这个三角形一定是( )
A .等腰三角形
B .等腰直角三角形
C .非等腰三角形
D .等边三角形
3、如图:在∠GAH 的两边上,AB BC CD DE EF ====,
若
∠A =18°,则∠GEF 的度数是( )
A .80°
B .90°
C .100°
D .108°
4、如图,E 是等边△ABC 中AC 边上的点,∠1=∠2, BE CD =,则对△ADE 的形状最准确的判断是( )
A .等腰三角形
B .等边三角形
C .不等边三角形
D .不能确定形
状
5、已知等腰三角形三边的长分别是42,1,156x x x -+-,则它的周长是 。
6、等腰△ABC 中,,6AB AC BC cm ==则△ABC 的周长的取值范围是
7、如图,等边△ABC 中,O 点是∠ABC 及∠ACB 的角平分线的交点,OM ∥AB 交BC 于M ,ON ∥AC 交BC 于N ,求证:,M N 是BC 的三等分点。
8、在锐角△ABC 中,D 是BC 上任意一点,,E F 分别在AB 、BC 上,且满足,D E D B D F
D C ==,若
055A ∠=,则的度数多少?
类型一:勾股定理的直接用法 1、在Rt△ABC中,∠C=90° (1)已知a=6,c=10,求b,(2)已知a=40,b=9,求c;(3)已知c=25,b=15,求a. 思路点拨:写解的过程中,一定要先写上在哪个直角三角形中,注意勾股定理的变形使用。 解析:(1) 在△ABC中,∠C=90°,a=6,c=10,b= b=9,c=°,a=40,(2) 在△ABC中,∠C=90 (3) 在△ABC中,∠C=90°,c=25,b=15,a= 举一反三 【变式】:如图∠B=∠ACD=90°, AD=13,CD=12, BC=3,则AB的长是多少? °ACD=90 【答案】∵∠13, CD=12 = AD 222 ∴AC-=ADCD 22-=1312 =25 =5 ∴AC =3 °且BC又∵∠ABC=90 ∴由勾股定理可得 -222 ACBC AB= 22 =53- =16 = 4 AB∴ 4. 的长是∴AB 类型二:勾股定理的构造应用
. BC的长中,、如图,已知:在,,. 求: 2 ,则有角的直角三角形,为此作于D,想到构造含思路点拨:由条件 的DC的长,进而求出BC,再由勾股定理计算出AD、,. 长 ,则因:作,D于解析 (∴的两个锐角互余) 中,如果一个锐角等于∴(在,
. 那么它所对的直角边等于斜边的一半) 根据勾股定理,在中, . 根据勾股定理,在中, . . ∴ . 求证: . P于,,如图,已知:】1【变式举一反三 解析:连结BM,根据勾股定理,在中, . 中,则根据勾股定理有而在
. ∴ 又∵(已知), ∴. 中,根据勾股定理有在 , ∴. 【变式2】已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。求:四边形ABCD的面积。 分析:如何构造直角三角形是解本题的关键,可以连结AC,或延长AB、DC交于F,或延长AD、BC交于点E,根据本题给定的角应选后两种,进一步根据本题给定的边选第三种较为简单。 解析:延长AD、BC交于E。 ∵∠A=∠60°,∠B=90°,∴∠E=30°。 CE=2CD=4,∴AE=2AB=8, 22222BE==8= -4∴BE。=AE=48-AB,
中考数学勾股定理知识点-+典型题及解析 一、选择题 1.图中不能证明勾股定理的是( ) A . B . C . D . 2.勾股定理是几何中的一个重要定理,在我国算书《网醉算经》中就有“若勾三,股四,则弦五”的记载.如图1,是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,BC=5,点D ,E ,F ,G ,H ,I 都在矩形KLMJ 的边上,则矩形KLMJ 的面积为( ) A .121 B .110 C .100 D .90 3.如图,在ABC 中,90A ∠=?,6AB =,8AC =,ABC ∠与ACB ∠的平分线交于点O ,过点O 作⊥OD AB 于点D ,若则AD 的长为( )
A .2 B .2 C .3 D .4 4.已知△ABC 是腰长为1的等腰直角三角形,以Rt △ABC 的斜边AC 为直角边,画第二个等腰Rt △ACD ,再以Rt △ACD 的斜边AD 为直角边,画第三个等腰Rt △ADE ,…,依此类推,第n 个等腰直角三角形的面积是( ) A .2n ﹣2 B .2n ﹣1 C .2n D .2n+1 5.如图,正方形ABCD 和正方形CEFG 边长分别为a 和b ,正方形CEFG 绕点C 旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE 2+BG 2=2a 2+2b 2,其中正确结论有( ) A .0个 B .1个 C .2个 D .3个 6.如图是我国数学家赵爽的股弦图,它由四个全等的直角三角形和小正方形拼成的一个大正方形.已知大正方形的面积是l3,小正方形的面积是1,直角三角形的较短直角边长为a ,较长直角边长为b ,那么()2 a b +值为( ) A .25 B .9 C .13 D .169 7.我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知90A ∠=?正方形ADOF 的边长是2,4BD =,则CF 的长为( ) A .6 B .2 C .8 D .10 8.有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了上图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2020次后形成的图形中所有的正方形的面积和是( )
一.填空题(共9小题) 1.△ABC是等腰三角形,腰上的高为8cm,面积为40cm2,则该三角形的周长是cm. 2.如图,在△ABC中,AB=BC=8,AO=BO,点M是射线CO上的一个动点,∠AOC=60°,则当△ABM为直角三角形时,AM的长为. 3.如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=. 4.如图,在Rt△ABC中,∠ACB=90,AC=3,BC=4,分别以AB、AC、BC为边在AB同侧作正方形ABEF,ACPQ,BDMC,记四块阴影部分的面积分别为S1、S2、S3、S4,则S1+S2+S3+S4=. 5.如图,Rt△ABC中,∠ACB=90°,AC=2,BC=.分别以AB,AC,BC为边,向外作正方形ABDE,正方形ACFG,正方形BCMN,连接GE,DN.则图中阴影的总面积是.
6.有一棵9米高的大树,树下有一个1米高的小孩,如果大树在距地面4米处折断(未完全折断),则小孩至少离开大树米之外才是安全的. 7.如图,A在线段BG上,ABCD和DEFG都是正方形,面积分别为7平方厘米和11平方厘米,则△CDE的面积等于平方厘米. 8.等腰△ABC的底边BC=8cm,腰长AB=5cm,一动点P在底边上从点B开始向点C以0.25cm/秒的速度运动,当点P运动到PA与腰垂直的位置时,点P运动的时间应为秒. 9.Rt△ABC中,∠BAC=90°,AB=AC=2.以AC为一边,在△ABC外部作等腰直角三角形ACD,则线段BD的长为. 二.解答题(共3小题) 10.已知△ABC中,AB=AC. (1)如图1,在△ADE中,若AD=AE,且∠DAE=∠BAC,求证:CD=BE; (2)如图2,在△ADE中,若∠DAE=∠BAC=60°,且CD垂直平分AE,AD=3,CD=4,求BD的长; (3)如图3,在△ADE中,当BD垂直平分AE于H,且∠BAC=2∠ADB时,试探究CD2,BD2,AH2之间的数量关系,并证明.
数学数学勾股定理试题及解析 一、选择题 1.△ABC 中,AB=15,AC=13,高AD=12,则△ABC 的周长为( ) A .42 B .32 C .42或32 D .37或33 2.如图,在Rt ABC ?中,90, 5 ,3ACB AB cm AC cm ?∠=== ,动点P 从点B 出发,沿射线BC 以1 /cm s 的速度移动,设运动的时间为t 秒,当?ABP 为等腰三角形时,t 的值不可能为( ) A .5 B .8 C .254 D .258 3.如图,四边形ABCD 中,AC ⊥BD 于O ,AB =3,BC =4,CD =5,则AD 的长为( ) A .1 B .32 C .4 D .23 4.如图,已知直线a ∥b ,且a 与b 之间的距离为4,点A 到直线a 的距离为2,点B 到直线b 的距离为3,AB 230=.试在直线a 上找一点M ,在直线b 上找一点N ,满足MN ⊥a 且AM +MN +NB 的长度和最短,则此时AM +NB =( ) A .6 B .8 C .10 D .12 5.如图,设正方体ABCD-A 1B 1C 1D 1的棱长为1,黑、白两个甲壳虫同时从点A 出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA 1→A 1D 1→…,白甲壳虫爬行的路线是AB→BB 1→…,并且都遵循如下规则:所爬行的第n+2与第n 条棱所在的直线必须
既不平行也不相交(其中n 是正整数).那么当黑、白两个甲壳虫各爬行完第2017条棱分别停止在所到的正方体顶点处时,它们之间的距离是( ) A .0 B .1 C .3 D .2 6.我国古代数学家赵爽的“勾股方圆图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是25,小正方形的面积是1,直角三角形的两直角边分别是a 和b ,那么ab 的值为( ) A .49 B .25 C .12 D .10 7.如图所示,有一个高18cm ,底面周长为24cm 的圆柱形玻璃容器,在外侧距下底1cm 的点S 处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm 的点F 处有一只苍蝇,则急于捕获苍蝇充饥的蜘蛛所走的最短路径的长度是( ) A .16cm B .18cm C .20cm D .24cm 8.下列各组线段能构成直角三角形的一组是( ) A .30,40,60 B .7,12,13 C .6,8,10 D .3,4,6 9.勾股定理是“人类最伟大的十个科学发现之一”.我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”.2002年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是( ) A . B . C . D . 10.为了庆祝国庆,八年级(1)班的同学做了许多拉花装饰教室,小玲抬来一架2.5米长的梯子,准备将梯子架到2.4米高的墙上,则梯脚与墙角的距离是( ) A .0.6米 B .0.7米 C .0.8米 D .0.9米 二、填空题 11.如图,ACB △和ECD 都是等腰直角三角形,CA CB =,CE CD =,ABC 的顶
勾股定理(3)勾股定理及逆定理的综合 民棊市在“I日城改中卄划在市内一块如囲17-3-7所示的三角率空她上胛植 某秒耳良以灵比药填^其中ZApl5(T,Jl£f = l?(}来川C = 30米■已知这 棘常皮需平方米倍价a亓+则胸买这种茸皮至少需要元. 乳如图17-3-8所示,艮方形片附?门中用"=乩班:=仁将桩方形沿At?折養? 点D蔣应”址刚巫獰部 分^AfC的面积是 _____________ 10. 17-3-9所示,把长方殛AHCD迓片祈是使点B蒋在点D如点<?摧在C'处,折痕EF与BD交 于点O?已知AE = 1趴AD=]盒则折锻EF的怅为___________ ? 1134EJ 17^3-10 所示*在ZXABC 屮上丸CH = g(TMC二EGP 是ZV1迟C 内的一点,且PB=UPC=2:尸人"3,桁△円垃骁点C旋转后,与△AFC重合,连播P严,则PP f = _______________ ,Z-BPC的度数为________ * 12. 等慣三角形的一边氏蹙12,另一边快挺10*则其面积均_____________ , 13. 如图1Z-311所吾*公路昭N和公賂PQ在点P处交汇*且ZQPN=30\点A赴有一所中学.AP = 1仙m.假没拖拉机行餐时J剤出】00m以内空受到噪音的申响?那么检拉机牲公路上沿PN方向 行观时?学校抠否会受剰囁芦喲叙诸说明理由,如廉覺烹鞘’已知拖拉机的速度为 18km/h f W么学 校受影响的时间为多少秒? 14. 如图L7-3-1Z所示’在-篷直妁公貉MN的同一旁冇两个新开堤区片*為巳知4fi = 10千米,直銭AE与公路 MJV的夹甬Z_4CWW = 3OJ新开发区B到公路肋片的跑离EC=3千米. (D滾新开发区A到公路阿挖的距离* ■熄)现磐在丽闻上某点尸处向新开发区AE修两条公賂尸使点尸到新开发IKA,B的亜离之彌故矩■诸似用尺规悴團在亜呻找出点户的位豎:不用证期「不写作搖,谏苗作囲痕迹4并求出此 ■ 时PA+PB的值. “、 估' 3] 17 3 12图17-i 8ffl 17 3 !>
中考数学勾股定理知识归纳总结附解析 一、选择题 1.在ABC ?中,D 是直线BC 上一点,已知15AB =,12AD =,13AC =,5CD =,则BC 的长为( ) A .4或14 B .10或14 C .14 D .10 2.如图,在△ABC 中,∠BAC =90°,AC =2AB ,点D 是AC 的中点,将一块锐角为45°的直角三角板ADE 如图放置,连接BE ,EC .下列判 断:①△ABE ≌△DCE ;②BE =EC ;③BE ⊥EC ;④EC =3DE .其中正确的有( ) A .1个 B .2个 C .3个 D .4个 3.如图,在等腰三角形ABC 中,AC=BC=5,AB=8,D 为底边上一动点(不与点A ,B 重合),DE ⊥AC ,DF ⊥BC ,垂足分别为E 、F ,则DE+DF= ( ) A .5 B .8 C .13 D .4.8 4.如果正整数a 、b 、c 满足等式222+=a b c ,那么正整数a 、b 、c 叫做勾股数.某同学将自己探究勾股数的过程列成下表,观察表中每列数的规律,可知x y +的值为( ) A .47 B .62 C .79 D .98 5.如图,在△ABC 中,∠A =90°,P 是BC 上一点,且DB =DC ,过BC 上一点P ,作PE ⊥AB 于E ,PF ⊥DC 于F ,已知:AD :DB =1:3,BC =46,则PE+PF 的长是( ) A .6 B .6 C .42 D .26
6.如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD 、正方形EFGH 、正方形MNKT 的面积分别为S 1、S 2、S 3.若S 1+S 2+S 3=15,则S 2的值是( ) A .3 B .154 C .5 D .152 7.如图,已知AB AC =,则数轴上C 点所表示的数为( ) A .3- B .5- C .13- D .15- 8.如图,在Rt △ABC 中,∠A=90°,AB=6,AC=8,现将Rt △ABC 沿BD 进行翻折,使点A 刚好落在BC 上,则CD 的长为( ) A .10 B .5 C .4 D .3 9.如图, 在ABC 中,CE 平分ACB ∠,CF 平分ABC 的外角ACD ∠,且EF //BC 交AC 于M ,若CM 4=,则22CE CF +的值为( ) A .8 B .16 C .32 D .64 10.如图,△ABC 中,AB =AC ,AD 是∠BAC 的平分线.已知AB =5,AD =3,则BC 的长 为( )
“二次函数+勾股定理型”的压轴题分析 一、基础题(15分钟内自主学会得30分,提示、互助中学会得25分,听懂20分,书写规范另外奖励5至10分) 如图1,已知抛物线与x 轴交于)0,1(-A 、)0,3(B 两点,与y 轴交于点)3,0(C . (1)求抛物线的解析式; (2)设抛物线的顶点为D ,在其对称轴的右侧抛物线上是否存在点P ,使得PDC ?是等腰三角形?若存在,求出符合条件的点P 的坐标;若不存在,请说明理由. (3)若点M 是抛物线上一点,以B 、C 、D 、M 为顶点的四边形是直角梯形,试求出点M 的坐标.
二、提高题(15分钟内自主学会得30分,提示、互助中学会得25分,听懂20分,书写规范另外奖励5至10分) 已知抛物线c bx ax y ++=2与x 轴相交于)0,1(-A 、)0,2(B 两点,与y 轴交于点)2,0(-C .如图2所示. (1)求这个抛物线的表达式及其顶点M (2)若点N 为线段BM 上一点(如图3),过点N 作x 轴的垂线,垂足为点Q ,当点N 在线段BM 上运动时(点N 不与点B 、点M 重合),设OQ 的长为t ,四边形NQAC 的面积为S ,求S 关于t 的函数关系式,并写出自变量的取值范围;
(3)在对称轴右侧的抛物线上是否存在点P ,使P A C ?为直角三角形?若存在,求出所有符合条件的点P 的坐标,若不存在请说明理由. 三、拓展题(15分钟内自主学会得30分,提示、互助中学会得25分,听懂20分,书写规范另外奖励5至10分) 已知抛物线c bx ax y ++=2 与x 轴相交于A 、B 两点(点A 在点B 左侧),与y 轴交于点C (如图4),且当2=x 和0=x 时,y 的值相等.直线73-=x y 与这条抛物线相交于两点,其中一点的横坐标为4,另一点是这条抛物线的顶点M . (1)求这个抛物线的表达式;
几种简单证明勾股定理的方法 ——拼图法、定理法 江苏省泗阳县李口中学沈正中 据说对社会有重大影响的10大科学发现,勾股定理就是其中之一。早在4000多年前,中国的大禹曾在治理洪水的过程中利用勾股定理来测量两地的地势差。迄今为止,关于勾股定理的证明方法已有500余种,各种证法融几何知识与代数知识于一体,完美地体现了数形结合的魅力。让我们动起手来,拼一拼,想一想,娱乐几种,去感悟数学 的神奇和妙趣吧! 一、拼图法证明(举例12种) 拼法一:用四个相同的直角三角形(直角边为a 、b ,斜边为c )按图2拼法。 问题:你能用两种方法表示左图的面积吗?对比两种不同的表示方法,你发现了什么? 分析图2:S 正方形=(a+b )2= c 2 + 4×2 1ab 化简可得:a 2+b 2 = c 2 拼法二:做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像左 图那样拼成两个正方形。 从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即 a 2+ b 2+4×21ab = c 2+4×21ab 整理得 a 2+b 2 = c 2 拼法三:用四个相同的直角三角形(直角边为a 、b ,斜边为c )按图3拼法。 问题:图3是由三国时期的数学家赵爽在为《周髀算经》作注时给出的。在图3中用同样的办法研究,你有什么发现?你能验证a 2+b 2=c 2吗? 分析图3:S 正方形= c 2 =(a-b )2+ 4×21ab 化简可得:a 2+b 2 = c 2 图1 图2 图3 图4 b a b a b a b a c b a c b a c b a c b a c b a c b a
初二数学直角三角形的判别导学案 执笔人:孙丹 参与人:曲明 林娇 【学习目标】 1、知识技能目标:我要学会通过边长判断一个三角形是否是直角三角形,并能进行简单应用; 2、过程方法目标:我要积极参与到直角三角形判别条件的探索过程,发展自己的推理能力; 3、情感态度目标:我要了解勾股定理的历史及应用,体会其文化价值。 【教学重难点】:会根据直角三角形的判别条件灵活解决问题 【教学过程】: 一、复习巩固: 1、求下图中的边长 2、如图1,从电线杆离地面3米处向地面拉一条长为5米的拉线,这条拉线在地面的定点距离电线杆底部有 米。 二、自主学习 1、尺规作图:作一个三角形,使得它的边长分别为: 3cm ,4cm 、5cm 。画完后猜想你作的是什么三角形?用量角器量一量。 2、猜想下列三组数据能否组成直角三角形?为什么? (1)5,12,13; (2)8,15,17; (3)7,24,25。 3、总结得出勾股定理的逆定理:如果三角形的三边长a 、b 、c 满足______________,那么这个三角形是直角三角形。并把满足2 2 2 c b a =+的三个正整数,称为勾股数。 三、典例讲解 一个零件的形状如图,按规定这个零件中∠A 与∠BDC 都应为直角,工人师傅量得零件各边尺寸:AD = 4,AB = 3, DC = 12 , BC=13,这个零件符合要求吗? A D 四、巩固练习 A 类1、下列几组数能否作为直角三角形的三边长?说说你的理由. ⑴9,12,15; ⑵15,36,39; ⑶12,35,36; ⑷12,18,22. 2、已知?ABC 中,BC=41, AC=40, AB=9, 则此三角形为_______三角形。 3、直角三角形的两直角边分别为5厘米、12厘米,则斜边上的高是_______。 4、如图3所示的一块地,已知AD =4m ,CD =3m , AD ⊥DC ,AB =13m ,BC =12m ,则这块地的面积是__________2 m . B 类5、如图,AD=7,AB =25,BC =10,DC =26,DB =24,求四边形ABCD 的面积. 6、如图,已知在△ABC 中,CD ⊥AB 于D ,AC =20,BC =15,DB =9. (1)求DC 的长. (2)求AB 的长. (3)求证: △ABC 是直角三角形. 五、课堂小结 六、课堂检测 A 类如图,在四边形ABCD 中,AD ⊥DC ,AD =8,DC =6,C B =24,AB =26.则四边形ABCD 的面积为____________. B 类已知:如图,∠ABD=∠C=90°,AD=12,AC=B C ,∠DAB=30°,求BC 的长.
《勾股定理》教材分析 一、课标要求: 1、体验勾股定理的探索过程,会运用勾股定理解决简单问题; 2、会运用勾股定理的逆定理判定直角三角形; 3、通过具体的例子,了解定理的含义,了解逆命题、逆定理的概念,知道原命题成立其逆命题不一定成立。 二、中考要求: 1、已知直角三角形的两边长,会求第三边长。 2、会用勾股定理解决简单问题;会用勾股定理逆定理判定三角形是否为直角三角形。 3、了解定义、命题、定理含义;了解逆命题的概念,会识别两个互逆命题,并知道原命题成立,逆命题不一定成立。 三、 本章结构图: 互逆定理 四、 本章的地位和作用 五、本章课时安排: 本章教学时间约需要7课时,具体安排如下: 18.1 勾股定理 3课时 18.2 勾股定理的逆定理 2课时 18.3 小结 2课时
六、本章重要的数学思想和方法 1. 在定理、逆定理探究过程中所体现出来的由特殊到一般的思想 2.数形结合思想:面积法证明数学问题及由数到形、由形到数 3、整体的方法. 4.分类讨论思想 5.方程思想贯穿始终 6.转化思想:化斜为直,化空间为平面,化曲为直 七、教学内容设计 八、数学思想的贯穿 2、数形结合思想 例1、我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形。如果大正方形的面积是13,小正方形的面积是1,直角三角形的两条直角边分别为a,b. 那么( a+b)2的值为_____ 例2 如图,高速公路的同侧有A、B两个村庄,他们到高速公路所在直线MN的距离分别为AA1=2km,BB1=4km,A1B1=8km。现要在高速公路上
勾股定理应用的教学设计 教学目标 1 ?会用勾股定理进行简单的计算。 2.通过探究,会运用勾股定理解释生活中的实际问题 教学重点 勾股定理的应用。 教学难点 实际问题向数学问题的转化 教学过程 通过小组合作学习探究,研究勾股定理在实际中的应用 一、 复习旧知 复习勾股定理以及一些简单的计算 ⑴勾股定理: ____________________________________________________ (2)求出下列直角三角形中未知的边. 通过四个问题,让学生明白勾股定理在实际生活中的应用,以及如何去使用勾股定理 问题1.有一个边长为1米正方形的洞口,想用一个圆形盖去盖住这个洞口, 则圆形盖半径至 少为多少米? ? 问题2.如图所示,一旗杆在离地面 5 m 处断裂,旗杆顶部落在离底部 12 m 处,问旗杆 折断前有多咼? 合作探究 B A 2 C C C
问题4.如图,一个5米长的梯子AB 斜着靠在竖直的墙A0上,这时A0的距离为3米. ① 球梯子的底端B 距墙角0多少米? ② 如果梯的顶端A 沿墙下滑1米至C,请同学们猜一猜,底端 B 也将滑动1米吗? 算一算,底端滑动的距离。(结果保留 1位小数). 三. 深化新知 “引葭赴岸”是《九章算术》中的一道题“今有池方一丈,葭生其中央,出水一尺 , 引 葭赴岸,适与岸齐。问水深、葭长各几何?” 四、课堂小结 本节课你有什么收获?你认为用勾股定理解决实际问题的关键是什么? 五、运用新知 1校园里有两棵树,相距15米,一棵树高10米,另一棵树高18米,一只小鸟从一棵树 的顶端飞到另一棵树的顶端,小鸟至少要飞 ___________ 米。 2如图,一根12米高的电线杆两侧各用 15米的铁丝固定,两个固定点之间的距离 问题3.如下图,要将楼梯铺上地毯,则需要 _____ 米长的地毯.
勾股定理经典例题详解 知识点一:勾股定理 如果直角三角形的两直角边长分别为:a,b,斜边长为c,那么a2+b2=c2.即直角三角形中两直角边的平方和等于斜边的平方. 要点诠释:(1)勾股定理揭示的是直角三角形平方关系的定理。 (2)勾股定理只适用于直角三角形,而不适用于锐角三角形和钝角三角。 (3)理解勾股定理的一些变式: c2=a2+b2, a2=c2-b2, b2=c2-a2,c2=(a+b)2-2ab 知识点二:用面积证明勾股定理 方法一:将四个全等的直角三角形拼成如图(1)所示的正方形。 图(1)中,所以。 方法二:将四个全等的直角三角形拼成如图(2)所示的正方形。 图(2)中,所以。 方法三:将四个全等的直角三角形分别拼成如图(3)—1和(3)—2所示的两个形状相同的正方形。
在(3)—1中,甲的面积=(大正方形面积)—(4个直角三角形面积), 在(3)—2中,乙和丙的面积和=(大正方形面积)—(4个直角三角形面积), 所以,甲的面积=乙和丙的面积和,即:. 方法四:如图(4)所示,将两个直角三角形拼成直角梯形。 ,所以。 知识点三:勾股定理的作用 1.已知直角三角形的两条边长求第三边;2.已知直角三角形的一条边,求另两边的关系; 3.用于证明平方关系的问题; 4.利用勾股定理,作出长为 的线段。 2. 在理解的基础上熟悉下列勾股数 满足不定方程x2+y2=z2的三个正整数,称为勾股数(又称为高数或毕达哥拉斯数),显然,以x,y,z为三边长的三角形一定是直角三角形。 熟悉下列勾股数,对解题是会有帮助的: ①3、4、5②5、12、13;③8、15、17;④7、24、25;⑤10、24、26;⑥9、 40、41.
初二数学勾股定理常考压轴题专题练习汇总(含解析) 一.选择题(共8小题) 1.直角三角形两直角边长度为5,12,则斜边上的高( ) A.6B.8C.D. 2.下列说法中正确的是( ) A.已知a,b,c是三角形的三边,则a2+b2=c2 B.在直角三角形中两边和的平方等于第三边的平方 C.在Rt△ABC中,∠C=90°,所以a2+b2=c2 D.在Rt△ABC中,∠B=90°,所以a2+b2=c2 3.如图,是台阶的示意图.已知每个台阶的宽度都是30cm,每个台阶的高度都是15cm,连接AB,则AB等于( ) A.195cm B.200cm C.205cm D.210cm 4.如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是( ) A.10尺B.11尺C.12尺D.13尺 5.如图所示,在数轴上点A所表示的数为a,则a的值为( )
A.﹣1﹣B.1﹣C.﹣D.﹣1+ 6.一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了( ) A.1.5米B.0.9米C.0.8米D.0.5米 7.在△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长为( ) A.2B.2.6C.3D.4 8.如图,是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么(a+b)2的值为( ) A.13B.19C.25D.169 二.填空题(共5小题)
勾股定理及直角三角形的判定 知识要点分析 1、勾股定理 222,即直角三角形两直角边的平方和等于+b=c,斜边为a、bc,那么一定有a如果直角三角形两直角边分别为斜边的平方。 2、勾股定理的验证 勾股定理的证明方法很多,其中大多数是利用面积拼补的方法证明的。我们也可将勾股定理理解为:以两条直角边分别为边长的两个正方形的面积之和等于以斜边为边长的正方形的面积。因此,证明勾股定理的关键是想办法把以两条直角边分别为边长的两个正方形作等面积变形,使它能拼成以斜边为边长的正方形。另外,用拼图的方法,并利用两种方法表示同一个图形的面积也常用来验证勾股定理。 222,那么这个三角形是直角三角形,此结论是勾股定理的逆定理+b=cb、c有关系:a3、如果三角形的三条边a、(它与勾股定理的条件和结论正好相反)。其作用是利用边的数量关系判定直角三角形,运用时必须在已知三角形三条边长的情况下。我们还可以理解为:如果三角形两条短边的平方和等于最长边的平方,那么这个三角形是直角三角形,并且两条短边是直角边,最长边是斜边。 4、勾股数 222的三个正整数a、b、c称为勾股数。满足条件a+b =c友情提示:(1)3,4,5是勾股数,又是三个连续正整数,并不是所有三个连续正整数都是勾股数;(2)每组勾股数的相同倍数也是勾股数。 【典型例题】 考点一:勾股定理 例1:在△ABC中,∠C=90°, (1)若a=3,b=4,则c=__________; (2)若a=6,c=10,则b=__________; (3)若c=34,a:b=8:15,则a=________,b=_________. 例2:已知三角形的两边长分别是3、4,如果这个三角形是直角三角形,求第三边的长。 解: 考点二:勾股定理的验证 例3:如图所示,图(1)是用硬纸板做成的两个直角三角形,两直角边的长分别是a和b,斜边长为c,图(2) 是以c为直角边的等腰三角形。请你开动脑筋,将它们拼成一个能证明勾股定理的图形。 (1)画出拼成的这个图形的示意图,写出它是什么图形。 (2)用这个图形证明勾股定理。 (3)假设图(1)中的直角三角形有若干个,你能用图(1)中所给的直角三角形拼出另一种能证明勾股定理的图形吗?请画出拼接后的示意图。(无需证明)
勾股定理知识归纳总结及解析 一、选择题 1.如图,已知ABC 中,4AB AC ==,6BC =,在BC 边上取一点P (点P 不与点B 、C 重合),使得ABP △成为等腰三角形,则这样的点P 共有( ). A .1个 B .2个 C .3个 D .4个 2.如图,在矩形纸片ABCD 中,AD =9,AB =3,将其折叠,使点D 与点B 重合,折痕为EF ,那么折痕EF 的长为( ) A .3 B .6 C .10 D .9 3.如图,已知ABC 中,10,86,AB AC BC AB ===,的垂直平分线分别交,AC AB 于 ,,D E 连接BD ,则CD 的长为( ) A .1 B . 54 C . 74 D .254 4.如图,在ABC 中,90A ∠=?,6AB =,8AC =,ABC ∠与ACB ∠的平分线交于点O ,过点O 作⊥OD AB 于点D ,若则AD 的长为( ) A 2 B .2 C 3 D .4 5.如图,设正方体ABCD-A 1B 1C 1D 1的棱长为1,黑、白两个甲壳虫同时从点A 出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA 1→A 1D 1→…,白甲壳虫爬行的路线是AB→BB 1→…,并且都遵循如下规则:所爬行的第n+2与第n 条棱所在的直线必须
既不平行也不相交(其中n 是正整数).那么当黑、白两个甲壳虫各爬行完第2017条棱分别停止在所到的正方体顶点处时,它们之间的距离是( ) A .0 B .1 C .3 D .2 6.如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD 、正方形EFGH 、正方形MNKT 的面积分别为S 1、S 2、S 3.若S 1+S 2+S 3=15,则S 2的值是( ) A .3 B . 154 C .5 D . 152 7.下列四组数中不能构成直角三角形的一组是( ) A .1,2,6 B .3,5,4 C .5,12,13 D .3,2,13 8.下列长度的三条线段能组成直角三角形的是( ) A .9,7,12 B .2,3,4 C .1,2,3 D .5,11,12 9.在直角三角形ABC 中,90C ∠=?,两直角边长及斜边上的高分别为,,a b h ,则下列关系式成立的是( ) A . 222221a b h += B . 222111 a b h += C .2h ab = D .222h a b =+ 10.如图,在△ABC ,∠C =90°,AD 平分∠BAC 交CB 于点D ,过点D 作DE ⊥AB ,垂足恰好是边AB 的中点E ,若AD =3cm ,则BE 的长为( )
勾股定理的证明 【证法1】(课本的证明) 做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形. 从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即 ab c ab b a 21 4214222?+=?++, 整理得 222c b a =+. 【证法2】(邹元治证明) 以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积 等于ab 21. 把这四个直角三角形拼成如图所示形状,使 A 、E 、 B 三点在一条直线上,B 、F 、 C 三点在一条直线上,C 、G 、 D 三点在一条直线上. ∵ Rt ΔHA E ≌ Rt ΔEBF, ∴ ∠AHE = ∠BE F . ∵ ∠AEH + ∠AHE = 90o, ∴ ∠AEH + ∠BEF = 90o. ∴ ∠HEF = 180o―90o= 90o. ∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2. ∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA . ∵ ∠HGD + ∠GHD = 90o, ∴ ∠EHA + ∠GHD = 90o. 又∵ ∠GHE = 90o, ∴ ∠DHA = 90o+ 90o= 180o. ∴ ABCD 是一个边长为a + b 的正方形,它的面积等于(a +∴ ()2 2 21 4c ab b a +?=+. ∴ 2 22c b a =+. 【证法3】(赵爽证明) 以a 、b 为直角边(b>a ), 以c 为斜 边作四个全等的直角三角形,则每个直角
一、教材分析 勾股定理是直角三角形的一条非常重要的性质,也是几何中最重要的定理之一。它揭示了三角形三条边之间的数量关系,主要用于解决直角三角形中的计算问题,是解直角三角形的主要根据之一,同时在实际生活中具有广泛的用途,“数学源于生活,又用与生活”是这章书所体现的主要思想。教材在编写时注意培养学生的动手操作能力和分析问题的能力,通过实际操作,使学生获得较为直观的印象;通过联系比较、探索、归纳,帮助学生理解勾股定理,以利于进行正确的应用。 2、教学目标 <1> 通过对几种常见的勾股定理验证方法,进行分析和欣赏。理解数学知识之间的内在联系,体会数形结合的思想方法,进一步感悟勾股定理的文化价值。 <2> 通过拼图活动,尝试验证勾股定理,培养学生的动手实践和创新能力。 <3>让学生经历查询资料、自主探究、合作交流、观察比较、计算推理、动手操作等过程,获得一些研究问题的方法,取得成功和克服困难的经验,培养学生良好的思维品质,增进他们数学学习的信心。 <4> 掌握勾股定理及其逆定理,并能运用这两个定理解决实际问题. 重点: <1> 分析和欣赏几种常见的验证勾股定理的方法。 <2>勾股定理和逆定理的探索和应用。 难点: <1> “数形结合”思想方法的理解和应用。 <2> 通过拼图,探求验证勾股定理的新方法。 4、教法和学法: 在整个教学过程中,本课的教法和学法体现如下特点: 1、以学生自我探索、合作交流为主,充分发挥教师的主导作用,运用各种手段激发学生学习欲望和兴趣,组织学生活动,让学生主动参与学习全过程。 2、切实体现学生的主体地位,让学生通过观察、分析、讨论、操作、归纳,理解定理,提高学生动手操作能力,以及分析问题和解决问题的能力。 3、通过学生自己得到获得新知的成功感受,从而激发学生钻研新知的欲望。 二、学情分析: 八年级的学生虽然缺乏七年级学生那种强烈的新奇感,但他们已具备了一定的动手能力,分析归纳能力,而且勾股定理是在学生已经掌握了直角三角形的有关性质的基础上学习的,所以只要教师能通过各种教学手段调动学生的学习积极性,并进行适当的引导,他们能够就勾股定理这一主题展开探索,在探索中理解并掌握勾股定理。 三、课程设计 1.课时安排 勾股定理2课时 直角三角形的判定1课时 勾股定理的运用2课时 复习2课时 勾股定理的“无字证明”2课时 共9课时 四、注意事项
新人教版八年级下第十七章 勾股定理提高练习与常考难题和培优题压轴题(含解析) 一.选择题(共8小题) 1.直角三角形两直角边长度为5,12,则斜边上的高() A.6 B.8 C.D. 2.下列说法中正确的是() A.已知a,b,c是三角形的三边,则a2+b2=c2 B.在直角三角形中两边和的平方等于第三边的平方 C.在Rt△ABC中,∠C=90°,所以a2+b2=c2 D.在Rt△ABC中,∠B=90°,所以a2+b2=c2 3.如图,是台阶的示意图.已知每个台阶的宽度都是30cm,每个台阶的高度都是15cm,连接AB,则AB等于() A.195cm B.200cm C.205cm D.210cm 4.如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是() A.10尺B.11尺C.12尺D.13尺 5.如图所示,在数轴上点A所表示的数为a,则a的值为()
A.﹣1﹣B.1﹣C.﹣D.﹣1+ 6.一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了() A.1.5米B.0.9米C.0.8米D.0.5米 7.在△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长为() A.2 B.2.6 C.3 D.4 8.如图,是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么(a+b)2的值为() A.13 B.19 C.25 D.169 二.填空题(共5小题) 9.将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图
【证法1】(课本的证明) 做8个全等的直角三角形,设它们的两条直角边长分别为a、b,斜边长为c,再做三个边长分别为a、b、c的正方形,把它们像上图那样拼成两个正方形. 从图上可以看到,这两个正方形的边长都是a + b,所以面积相等. 即 a^2+b^2+4*(ab/2)=c^2+4*(ab/2), 整理得到:a^2+b^2=c^2。 【证法2】 以a、b 为直角边,以c为斜边做四个全等的直角三角形,则每个直角三角形的面积等于 ab/2.把这四个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上,B、F、C三点在一条直线上,C、G、D三点在一条直线上. ∵ RtΔHAE ≌ RtΔEBF, ∴∠AHE = ∠BEF. ∵∠AEH + ∠AHE = 90o, ∴∠AEH + ∠BEF = 90o. ∴∠HEF = 180o―90o= 90o. ∴四边形EFGH是一个边长为c的 正方形. 它的面积等于c^2. ∵ RtΔGDH ≌ RtΔHAE, ∴∠HGD = ∠EHA. ∵∠HGD + ∠GHD = 90o, ∴∠EHA + ∠GHD = 90o. 又∵∠GHE = 90o, ∴∠DHA = 90o+ 90o= 180o. ∴ ABCD是一个边长为a + b的正方形,它的面积等于(a+b)^2. ∴(a+b)^2=c^2+4*(ab/2),∴ a^2+b^2=c^2。
【证法3】 以a、b 为直角边(b>a),以c为斜边作四个全等的直角三角形,则每个直角三角形的面积等于ab/2. 把这四个直角三角形拼成如图所示形状. ∵ RtΔDAH ≌ RtΔABE, ∴∠HDA = ∠EAB. ∵∠HAD + ∠HAD = 90o, ∴∠EAB + ∠HAD = 90o, ∴ ABCD是一个边长为c的正方形,它的面积等于c^2. ∵ EF = FG =GH =HE = b―a , ∠HEF = 90o. ∴ EFGH是一个边长为b―a的正方形,它的面积等于(b-a)^2. ∴(b-a)^2+4*(ab/2)=c^2,∴ a^2+b^2=c^2。 【证法4】 以a、b 为直角边,以c为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab/2. 把这两个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上. ∵ RtΔEAD ≌ RtΔCBE, ∴∠ADE = ∠BEC.
初二数学勾股定理提高练习与常考难题和培优题压轴题(含解 析) 一.选择题(共8小题) 1.直角三角形两直角边长度为5,12,则斜边上的高() A.6 B.8 C.D. 2.下列说法中正确的是() A.已知a,b,c是三角形的三边,则a2+b2=c2 B.在直角三角形中两边和的平方等于第三边的平方 C.在Rt△ABC中,∠C=90°,所以a2+b2=c2 D.在Rt△ABC中,∠B=90°,所以a2+b2=c2 3.如图,是台阶的示意图.已知每个台阶的宽度都是30cm,每个台阶的高度都是15cm,连接AB,则AB等于() A.195cm B.200cm C.205cm D.210cm 4.如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是() A.10尺B.11尺C.12尺D.13尺 5.如图所示,在数轴上点A所表示的数为a,则a的值为()
A.﹣1﹣B.1﹣C.﹣D.﹣1+ 6.一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了() A.1.5米B.0.9米C.0.8米D.0.5米 7.在△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长为() A.2 B.2.6 C.3 D.4 8.如图,是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么(a+b)2的值为() A.13 B.19 C.25 D.169 二.填空题(共5小题)