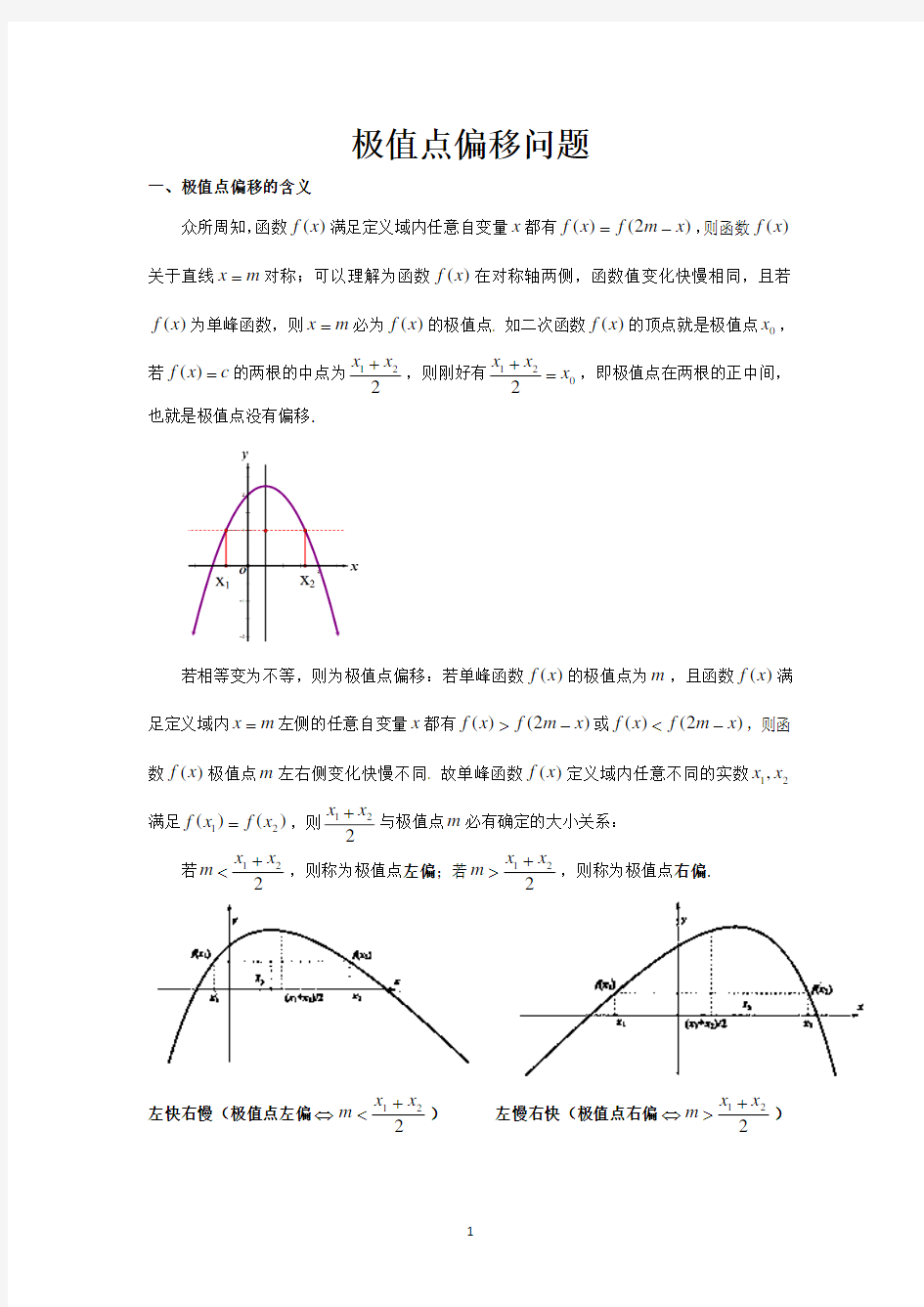

极值点偏移问题总结 一、 判定方法 1、极值点偏移的定义 对于函数)(x f y =在区间),(b a 内只有一个极值点0x ,方程0)(=x f 的解分别为 21x x 、,且b x x a <<<21, (1)若 02 12x x x ≠+,则称函数)(x f y =在区间),(21x x 上极值点0x 偏移; (2) 若0212 x x x >+,则函数)(x f y =在区间),(21x x 上极值点0x 左偏,简称极值点0 x 左偏; (3)若02 12 x x x <+,则函数)(x f y =在区间),(21x x 上极值点0x 右偏,简称极值点0 x 右偏。 2、极值点偏移的判定定理 证明:(1)因为可导函数)(x f y =,在区间),(b a 上只有一个极大(小)值点0x ,则函数)(x f y =的单调递增(减)区间为),(0x a ,单调递减(增)区间为),(0b x ,又 b x x a <<<21,有 ),(221b a x x ∈+由于0)2('21>+x x f ,故),(2 02 1x a x x ∈+,所以02 1)(2 x x x ><+,即函数极大(小)值点0x 右(左)偏。
证明:(1)因为对于可导函数)(x f y =,在区间),(b a 上只有一个极大(小)值点0x ,则函数)(x f y =的单调递增(减)区间为),(0x a ,单调递减(增)区间为),(0b x ,又 b x x a <<<21,有01x x <,且0202x x x <-,又)2()(201x x f x f -<,故2012)(x x x -><,所以 02 1)(2 x x x ><+,即函数极大(小)值点0x 右(左)偏. 结论(2)证明略。 二、 运用判定定理判定极值点偏移的方法 1.方法概述: (1)求出函数()f x 的极值点; (2)构造一元差函数00()()()F x f x x f x x =+-- (3)确定函数()F x 的单调性; (4)结合(0)0F =,判断()F x 的符号,从而确定00(),()f x x f x x -+的大小关系。 2.抽化模型 答题模板:若已知函数()f x 满足12()()f x f x =,0x 为()f x 的极值点,求证:1202x x x +< (1)讨论函数()f x 的单调性并求出()f x 的极值点0x ; 假设此处()f x 在()0,x -∞上单调递减,在()0,x +∞ 上单调递增。 (2)构造00()()()F x f x x f x x =+--;
极值点偏移问题的两种常见解法之比较 浅谈部分导数压轴题的解法 在高考导数压轴题中,不断出现极值点偏移问题,那么,什么是极值点偏移问题?参考陈宽宏、邢友宝、赖淑明等老师的文章,极值点偏移问题的表述是:已知函数()y f x =是连续函数,在区间12(,)x x 内有且只有一个极值点0x ,且 12()()f x f x =,若极值点左右的“增减速度”相同,常常有极值点12 02 x x x += ,我们称这种状态为极值点不偏移;若极值点左右的“增减速度”不同,函数的图象不具有对称性,常常有极值点12 02 x x x +≠的情况,我们称这种状态为“极值点偏移”. 极值点偏移问题常用两种方法证明:一是函数的单调性,若函数()f x 在区间(,)a b 内单调递增,则对区间(,)a b 内的任意两个变量12x x 、, 1212()()f x f x x x . 二是利用“对数平均不等式”证明,什么是“对数平均”?什么又是“对数平均不等式”? 两个正数a 和b 的对数平均数定义:,,(,)ln ln ,, a b a b L a b a b a a b -?≠? =-??=? 对数平均数与算术平均数、 (,)2 a b L a b +≤≤,(此式记为对数平均不等式) 下面给出对数平均不等式的证明: i )当0a b =>时,显然等号成立 ii )当0a b ≠>时,不妨设0a b >>, ln ln a b a b --, ln ln a b a b -<-, 只须证:ln a b < 1x =>,只须证:1 2ln ,1x x x x ≤-> 设1 ()2ln ,1f x x x x x =-+>,则222 21(1)()10x f x x x x -'=--=- <,所以()f x
含参数的极值点偏移问题,在原有的两个变元12,x x 的基础上,又多了一个参数,故思路很自然的就会想到:想尽一切办法消去参数,从而转化成不含参数的问题去解决;或者以参数为媒介,构造出一个变元的新的函数. ★例1. 已知函数x ae x x f -=)(有两个不同的零点12,x x ,求证:221>+x x . 不妨设12x x >,记12t x x =-,则0,1t t e >>, 因此只要证明:1 21 t t e t e +?>-01)1(2>+--?t t e e t , 再次换元令x t x e t ln , 1=>=,即证),1(,01 ) 1(2ln +∞∈>+-- x x x x 构造新函数2(1) ()ln 1 x F x x x -=- +,0)1(=F 求导2 ' 22 14(1)()0(1)(1)x F x x x x x -=- =>++,得)(x F 在),1(+∞上递增, 所以0)(>x F ,因此原不等式122x x +>获证.
★例 2. 已知函数()ln f x x ax =-,a为常数,若函数() f x有两个零点 12 ,x x,证明: 2 12 . x x e ?> 法二:利用参数a作为媒介,换元后构造新函数: 不妨设 12 x x >, ∵ 1122 ln0,ln0 x ax x ax -=-=,∴ 12121212 ln ln(),ln ln() x x a x x x x a x x +=+-=-, ∴12 12 ln ln x x a x x - = - ,欲证明2 12 x x e >,即证 12 ln ln2 x x +>. ∵ 1212 ln ln() x x a x x +=+,∴即证 12 2 a x x > + , ∴原命题等价于证明12 1212 ln ln2 x x x x x x - > -+ ,即证:112 212 2() ln x x x x x x - > + ,令1 2 ,(1) x t t x =>,构造 2(1) ln, 1 )1 ( t t g t t t - =-> + ,此问题等价转化成为例1中思路2的解答,下略. 法三:直接换元构造新函数: 1222 1211 ln ln ln , ln x x x x a x x x x ==?=设2 12 1 ,,(1) x x x t t x <=>, 则11 21 11 ln ln ln , ln ln tx t x x tx t t x x + ==?=, 反解出: 1211 ln ln ln ln,ln ln ln ln ln 111 t t t t x x tx t x t t t t ===+=+= --- , 故2 1212 1 ln ln2ln2 1 t x x e x x t t + >?+>?> - ,转化成法二,下同,略.
极值点偏移问题专题(0)——偏移新花样(拐点偏移) 例1已知函数()22ln f x x x x =++,若正实数1x ,2x 满足()()12+=4f x f x , 求证:122x x +≥。 证明:注意到()1=2f ,()()()12+=21f x f x f ()()()12+=21f x f x f ()2 =+210f x x x '+> ()22 =2f x x ''-+,()1=0f '',则(1,2)是()f x 图像的拐点,若拐点(1,2)也是()f x 的 对称中心,则有12=2x x +,证明122x x +≥则说明拐点发生了偏移,作图如下 想到了“极值点偏移”,想到了“对称化构造”,类似地,不妨将此问题命名为“拐点偏移”,仍可用“对称化构造”来处理. 不妨设1201x x <≤≤,要证 ()() 1221212 212x x x x f x f x +≥?≥-≥?≥- ()() ()() 11114242f x f x f x f x ?-≥-?≥+- ()()()2F x f x f x =+-,(]0,1x ∈,则 ()()()()222212212F x f x f x x x x x '''=--????=++-+-+ ? ?-????
() ( ) 1 4110 2 x x x ?? =--≥ ? ? - ?? , 得() F x在(]0,1上单增,有()()() 1214 F x F ≤=+=,得证。 2、极值点偏移PK拐点偏移常规套路 1、极值点偏移(()00 f x '=) 二次函数()() 12120 2 f x f x x x x =?+= 2、拐点偏移() () f x ''= ()()() 12 0120 22 f x f x f x x x x +=?+= 极值点偏移问题专题(1)——对称化构造(常规套路) 例1(2010 天津)已知函数()e x f x x- =. (1)求函数() f x的单调区间和极值; (2)已知函数() g x的图像与() f x的图像关于直线1 x=对称,证明:当1 x>时, ()() 12201 120 2 2 f x f x x x x x x x =?>- ?+> ()()() 120201 120 22 2 f x f x f x x x x x x x +=?>- ?+>
一:极值点偏移(俗称峰谷偏)问题的定义 对于可导函数在区间(a,b)上只有一个极大(小)值点,方程(f(x)=m)的解分别为且< 1) 若)()(x b f x a f -=+,则)(x f 的图象关于直线2 b a x += 对称;特别地,若)()(x a f x a f -=+(或f(x)=f(2a-x)),则)(x f 的图象关于直线a x =对称 2) 若函数f(x)满足 有下列之一成立: ①f(x)在 递增,在(a,2a)递减,且f(a-x)<(>)f(a+x)(f(x)<(>)f(2a-x)) ②f(x)在(0,a)递减,在(a,2a)递增,且f(a-x)>(<)f(x+a)(f(x)>(<)f(2a-x)) 则函数f(x)在(0,2a)的图象关于直线x=a 偏移(偏对称)(俗称峰谷偏函数)其中① 极大 值左偏(或右偏)也称峰偏左(或右)②极小值偏左(或偏右)也称谷偏左(或右); 性质: 1) )(x f 的图象关于直线a x =对称若 则 <=> ,( =0, ); 2)已知函数是满足条件的极大值左偏(峰偏左)若则 则 ,及 极值点偏移解题步骤: ①求函数f(x)的极值点; ②构造函数F(x)=f(x+)-f( (F(x)=f( )-f( , F(x)=f(x+)-f( , F(x)=f(x)-f( )确定F(x)单调性 ③结合F(0)=0(F(-)=0,F(判断F(x)符号从而确定f(x+),f( ( f(x+) 与f( f(x)与f(的大小关系; 答题模式: 已知函数y=f(x)满足,为函数y=f(x)的极值点,求证: ①求函数f(x)的极值点; ②构造函数F(x)=f(x+)-f( 确定F(x)单调性 ③判断F(x)符号从而确定f(x+),f( 的大小关系; 假设F(x)在(0,+单调递增则F(x)>F(0)=0,从而得到x>0时f(x+)>f( ④ 极值点偏移问题 沈阳市第十一中学数学组:赵拥权 一:极值点偏移(俗称峰谷偏)问题的定义 对于可导函数在区间(a,b )上只有一个极大(小)值点,方程(f(x)=m)的解 分别为 且 < 2) 若函数f(x)满足 有下列之一成立: ①f(x)在 递增,在(a,2a)递减,且f(a-x)<(>)f(a+x)(f(x)<(>)f(2a-x)) ②f(x)在(0,a)递减,在(a,2a)递增,且f(a-x)>(<)f(x+a)(f(x)>(<)f(2a-x)) 则函数f(x)在(0,2a)的图象关于直线x=a 偏移(偏对称)(俗称峰谷偏函数)其中① 极大值左偏(或右偏)也称峰偏左(或右)②极小值偏左(或偏右)也称谷偏左(或右); 性质: 1) )(x f 的图象关于直线a x 对称若 则 <=> ,( =0, ); 2)已知函数是满足条件的极大值左偏(峰偏左)若 则则 ,及 极值点偏移解题步骤: ①求函数f(x)的极值点; ②构造函数F(x)=f(x+)-f( (F(x)=f()-f(, F(x)=f(x+)-f( , F(x)=f(x)-f( )确定F(x)单调性 ③结合F(0)=0(F(-)=0,F(判断F(x)符号从而确定f(x+),f(( f(x+)与f( f(x)与f(的大小关系; 答题模式: 已知函数y=f(x)满足 ,为函数y=f(x)的极值点,求证: ①求函数f(x)的极值点; ②构造函数F(x)=f(x+)-f( 确定F(x)单调性 极值点偏移问题的处理策略 所谓极值点偏移问题,是指对于单极值函数,由于函数极值点左右的增减速度不同,使得函数图像 没有对称性。若函数()f x 在0x x =处取得极值,且函数()y f x =与直线y b =交于1(,)A x b ,2(,)B x b 两点,则AB 的中点为12(,)2x x M b +,而往往1202 x x x +≠.如下图所示. 极值点没有偏移 此类问题在近几年高考及各种模考,作为热点以压轴题的形式给出,很多学生对待此类问题经常是束手无策。而且此类问题变化多样,有些题型是不含参数的,而更多的题型又是含有参数的。不含参数的如何解决?含参数的又该如何解决,参数如何来处理?是否有更方便的方法来解决?其实,处理的手段有很多,方法也就有很多,我们先来看看此类问题的基本特征,再从几个典型问题来逐一探索! 【问题特征】 【处理策略】 一、不含参数的问题. 例1.(2010天津理)已知函数()()x f x xe x R -=∈ ,如果12x x ≠,且12()()f x f x = , 证明:12 2. x x +> 【解析】法一:()(1)x f x x e -'=-,易得()f x 在(,1)-∞上 单调递增,在(1,)+∞上单调递减, x →-∞时,()f x →-∞,(0)0f =,x →+∞时,()0f x →, 函 数()f x 在1x =处取得极大值(1)f ,且 1 (1)f e =,如图所示. 由1212()(),f x f x x x =≠,不妨设12x x <,则必有1201x x <<<, 构造函数()(1)(1),(0,1]F x f x f x x =+--∈, 则 21 ()(1)(1)(1)0x x x F x f x f x e e +'''=++-= ->,所以()F x 在(0,1]x ∈上单调递增, ()(0)0F x F >=,也即(1)(1)f x f x +>-对(0,1]x ∈恒成立. 由1201x x <<<,则11(0,1]x -∈, 所以11112(1(1))(2)(1(1))()()f x f x f x f x f x +-=->--==,即12(2)()f x f x ->,又因为 122,(1,)x x -∈+∞,且()f x 在(1,)+∞上单调递减, 所以122x x -<,即证12 2. x x +> 极值点偏移问题的处理策略及探究 所谓极值点偏移问题,是指对于单极值函数,由于函数极值点左右的增减速度不同,使得函数图像没有对称性。若函数()f x 在0x x =处取得极值,且函数()y f x =与直线y b =交于1(,)A x b ,2(,)B x b 两点,则AB 的中点为12(,)2x x M b +,而往往1202 x x x +≠.如下图所示. 极值点没有偏移 此类问题在近几年高考及各种模考,作为热点以压轴题的形式给出,很多学生对待此类 问题经常是束手无策。而且此类问题变化多样,有些题型是不含参数的,而更多的题型又是含有参数的。不含参数的如何解决?含参数的又该如何解决,参数如何来处理?是否有更方便的方法来解决?其实,处理的手段有很多,方法也就有很多,我们先来看看此类问题的基本特征,再从几个典型问题来逐一探索!【问题特征】 【处理策略】 一、不含参数的问题. 例1.(2010天津理)已知函数()()x f x xe x R -=∈,如果12x x ≠,且12()()f x f x =, 证明:12 2. x x +> 【解析】法一:()(1)x f x x e -'=-,易得()f x 在(,1)-∞上 单调递增,在(1,)+∞上单调递减,x →-∞时, ()f x →-∞,(0)0f =,x →+∞时,()0f x →,函 数()f x 在1x =处取得极大值(1)f ,且1 (1)f e = ,如图所示.由1212()(),f x f x x x =≠,不妨设12x x <,则必有1201x x <<<,构造函数()(1)(1),(0,1]F x f x f x x =+--∈,则21 ()(1)(1)1)0x x x F x f x f x e e +'''=++-= ->,所以()F x 在(0,1]x ∈上单调递增, ()(0)0F x F >=,也即(1)(1)f x f x +>-对(0,1]x ∈恒成立. 由1201x x <<<,则11(0,1]x -∈, 所以11112(1(1))(2)(1(1))()()f x f x f x f x f x +-=->--==,即12(2)()f x f x ->,又因为122,(1,)x x -∈+∞,且()f x 在(1,)+∞上单调递减,所以122x x -<,即证12 2. x x +>法二:欲证122x x +>,即证212x x >-,由法一知1201x x <<<,故122,(1,)x x -∈+∞,又因为()f x 在(1,)+∞上单调递减,故只需证21()(2)f x f x <-,又因为12()()f x f x =,故也即证11()(2)f x f x <-,构造函数()()(2),(0,1)H x f x f x x =--∈,则等价于证明 ()0H x <对(0,1)x ∈恒成立. 由221()()(2)(1)0x x x H x f x f x e e --'''=+-= ->,则()H x 在(0,1)x ∈上单调递增,所以()(1)0H x H <=,即已证明()0H x <对(0,1)x ∈恒成立,故原不等式122x x +>亦成立. 法三:由12()()f x f x =,得1 212x x x e x e --=,化简得212 1 x x x e x -= …①,不妨设21x x >,由法一知,121o x x <<<.令21t x x =-,则210,t x t x >=+,代入①式, 极值点偏移问题的处理策略及探究 所谓极值点偏移问题,是指对于单极值函数,由于函数极值点左右的增减速度不同,使 得函数图像没有对称性。若函数()f x 在0x x =处取得极值,且函数()y f x =与直线y b =交于1(,)A x b ,2(,)B x b 两点,则AB 的中点为12(,)2x x M b +,而往往1202 x x x +≠.如下图所示. 极值点没有偏移 此类问题在近几年高考及各种模考,作为热点以压轴题的形式给出,很多学生对待此类问题经常是束手无策。而且此类问题变化多样,有些题型是不含参数的,而更多的题型又是含有参数的。不含参数的如何解决?含参数的又该如何解决,参数如何来处理?是否有更方便的方法来解决?其实,处理的手段有很多,方法也就有很多,我们先来看看此类问题的基本特征,再从几个典型问题来逐一探索! 【问题特征】 【处理策略】 一、不含参数的问题. 例1.(2010天津理)已知函数()()x f x xe x R -=∈ ,如果12x x ≠,且12()()f x f x = , 证明:12 2. x x +> 【解析】法一:()(1)x f x x e -'=-,易得()f x 在(,1)-∞上单调递增,在(1,)+∞上单调递减,x →-∞时, ()f x →-∞,(0)0f =,x →+∞时,()0f x →, 函 数()f x 在1x =处取得极大值(1)f ,且1 (1) f e =,如图所示. 由1212()(),f x f x x x =≠,不妨设12x x <,则必有1201x x <<<, 构造函数()(1)(1),(0,1]F x f x f x x =+--∈, 则21 ()(1)(1)(1)0x x x F x f x f x e e +'''=++-= ->,所以()F x 在(0,1]x ∈上单调递增,()(0)0F x F >=,也即(1)(1)f x f x +>-对(0,1]x ∈恒成立. 由1201x x <<<,则11(0,1]x -∈, 所以11112(1(1))(2)(1(1))()()f x f x f x f x f x +-=->--==,即12(2)()f x f x ->,又因为122,(1,)x x -∈+∞,且()f x 在(1,)+∞上单调递减, 所以122x x -<,即证12 2. x x +> 法二:欲证122x x +>,即证212x x >-,由法一知1201x x <<<,故122,(1,)x x -∈+∞,又因为()f x 在(1,)+∞上单调递减,故只需证21()(2)f x f x <-,又因为12()()f x f x =, 故也即证11()(2)f x f x <-,构造函数()()(2),(0,1)H x f x f x x =--∈,则等价于证明 ()0H x <对(0,1)x ∈恒成立. 由221()()(2)(1)0x x x H x f x f x e e --'''=+-= ->,则()H x 在(0,1)x ∈上单调递增,所以()(1)0H x H <=,即已证明()0H x <对(0,1)x ∈恒成立,故原不等式122x x +>亦成立. 法三:由12()()f x f x =,得1 212x x x e x e --=,化简得212 1 x x x e x -= … , 此文档下载后即可编辑 极值点偏移问题专题(0)——偏移新花样(拐点偏移) 例1已知函数()22ln f x x x x =++,若正实数1x ,2x 满足()()12+=4f x f x , 求证:122x x +≥。 证明:注意到()1=2f ,()()()12+=21f x f x f ()()()12+=21f x f x f ()2 =+210f x x x '+> ()2 2 =2f x x ''- +,()1=0f '',则(1,2)是()f x 图像的拐点,若拐点(1,2)也是()f x 的对称中心,则有12=2x x +,证明122x x +≥则说明拐点发生了偏移,作图如下 想到了“极值点偏移”,想到了“对称化构造”,类似地,不妨将此问题命名为“拐点偏移”,仍可用“对称化构造”来处理. 不妨设1201x x <≤≤,要证 ()() 1221212 212x x x x f x f x +≥?≥-≥?≥- ()() ()() 11114242f x f x f x f x ?-≥-?≥+- ()()()2F x f x f x =+-,(]0,1x ∈,则 ()()()()222 212212F x f x f x x x x x '''=--????=++-+-+ ? ?-???? ()()141102x x x ??=--≥ ? ?-?? , 得()F x 在(]0,1上单增,有()()()1214F x F ≤=+=,得证。 2、极值点偏移PK 拐点偏移常规套路 1、 极值点偏移(()00f x '=) 二次函数()()121202f x f x x x x =?+= 2、拐点偏移()()00f x ''= ()()()12012022f x f x f x x x x +=?+= ()()12201120 22f x f x x x x x x x =?>-?+>()()()120201 120 222f x f x f x x x x x x x +=?>-?+> 一题弄懂极值点偏移5大套路 已知()2 1ln 2 f x x x mx x =- -,m ∈R .若()f x 有两个极值点1x ,2x ,且12x x <,求证:2 12e x x >(e 为自然对数的底数). 解法一:齐次构造通解偏移套路 证法1:欲证2 12e x x >,需证12ln ln 2x x +>. 若()f x 有两个极值点1x ,2x ,即函数()f x '有两个零点.又()ln f x x mx '=-,所以,1x , 2x 是方程()0f x '=的两个不同实根. 于是,有1122 ln 0 ln 0x mx x mx -=?? -=?,解得1212ln ln x x m x x +=+. 另一方面,由1122 ln 0 ln 0x mx x mx -=??-=?,得()2121ln ln x x m x x -=-, 从而可得, 2112 2112 ln ln ln ln x x x x x x x x -+=-+. 于是,()()22 21211112221 1 1ln ln ln ln ln 1x x x x x x x x x x x x x x ??+ ?-+??+= =--. 又120x x <<,设2 1x t x =,则1t >.因此,()121ln ln ln 1 t t x x t ++=-,1t >. 要证12 ln ln 2x x +>,即证:()1ln 21t t t +>-, 1t >.即:当1t >时,有() 21ln 1 t t t -> +.设函数()()21ln 1t h t t t -=-+,1t ≥,则()()()() ()()2 22 212111011t t t h t t t t t +---'=-=≥++, 所以,()h t 为()1.+∞上的增函数.注意到,()10h =,因此,()()10h t h ≥=. 于是,当1t >时,有()21ln 1 t t t ->+.所以,有12ln ln 2x x +>成立,2 12e x x >. 解法二 变换函数能妙解 证法2:欲证2 12e x x >,需证12ln ln 2x x +>.若()f x 有两个极值点1x ,2x ,即函数() f x '有两个零点.又()ln f x x mx '=-,所以,1x ,2x 是方程()0f x '=的两个不同实根.显然0m >,否则,函数()f x '为单调函数,不符合题意. 一题弄懂极值点偏移5大套路 已知()21ln 2 f x x x mx x =--,m ∈R .若()f x 有两个极值点1x ,2x ,且12x x <,求证:212e x x >(e 为自然对数的底数). 解法一:齐次构造通解偏移套路 证法1:欲证212e x x >,需证12ln ln 2x x +>. 若()f x 有两个极值点1x ,2x ,即函数()f x '有两个零点.又()ln f x x mx '=-,所以,1x ,2x 是方程()0f x '=的两个不同实根. 于是,有1122ln 0ln 0x mx x mx -=??-=?,解得1212 ln ln x x m x x +=+. 另一方面,由1122ln 0ln 0x mx x mx -=?? -=?,得()2121ln ln x x m x x -=-, 从而可得,21122112 ln ln ln ln x x x x x x x x -+=-+. 于是,()()22212111122211 1ln ln ln ln ln 1x x x x x x x x x x x x x x ??+ ?-+??+==--. 又120x x <<,设21 x t x =,则1t >.因此,()121ln ln ln 1t t x x t ++=-,1t >. 要证12ln ln 2x x +>,即证:()1ln 21t t t +>-,1t >.即:当1t >时,有()21ln 1 t t t ->+.设函数()()21ln 1t h t t t -=-+,1t ≥,则()()()() ()()222212111011t t t h t t t t t +---'=-=≥++, 所以,()h t 为()1.+∞上的增函数.注意到,()10h =,因此,()()10h t h ≥=. 于是,当1t >时,有()21ln 1 t t t ->+.所以,有12ln ln 2x x +>成立,212e x x >. 导数压轴题分类(2)---极值点偏移问题 极值点偏移问题常见的处理方法有⑴构造一元差函数()()()x x f x f F --=02x 或者 ()()()x x f x x f x F --+=00。其中0x 为函数()x f y =的极值点。⑵利用对数平均不等式。 2 ln ln ab b a b a b a +< --< 。⑶变换主元等方法。 任务一、完成下面问题,总结极值点偏移问题的解决方法。 1.设函数2 2 ()ln ()f x a x x ax a R =-+-∈ (1)试讨论函数()f x 的单调性; (2)()f x m =有两解12,x x (12x x <),求证:122x x a +>. 解析:(1)由2 2 ()ln f x a x x ax =-+-可知 2222(2)()()2a x ax a x a x a f x x a x x x --+-'=-+-== 因为函数()f x 的定义域为(0,)+∞,所以 ① 若0a >时,当(0,)x a ∈时,()0f x '<,函数()f x 单调递减, 当(,)x a ∈+∞时,()0f x '>,函数()f x 单调递增; ② 若0a =时,当()20f x x '=>在(0,)x ∈+∞内恒成立,函数()f x 单调递增; ③ 若0a <时,当(0,)2 a x ∈-时,()0f x '<,函数()f x 单调递减, 当(,)2 a x ∈-+∞时,()0f x '>,函数()f x 单调递增; (2)要证122x x a +>,只需证12 2x x a +>, (x)g =22 2(x)2,g (x)20(x)(x)a a f x a g f x x '''=-+-=+>∴=则为增函数。 只需证:12 x x ( )()02 f f a +''>=,即证()2121221212221+0+0a x x a x x a x x x x a -+->?-+->++(*) 又2222 111222ln ,ln ,a x x ax m a x x ax m -+-=-+-=两式相减整理得: 1212212ln ln 1(x x a)0x x x x a -- ++-=-,把1212212 ln ln 1 (x x a)x x a x x -+-=-代入(*)式,即证: 2 例1已知函数f x =2ln x x x,若正实数x i, X2满足f X i +f x? =4 , 求证:x1x2 -2。 证明:注意到f 1 =2,f +f x2 =2f 1 f x1 +f x2 =2f 1 2 f x = +2x 10 x 不妨设0 :::X1乞1乞X2,要证 x-i x2- 2 二x2_ 2「% -1 二f x2- f 2 -论 =4-f 为-f 2-凶 =4 一f % f 2 - % F x = f x f 2 -x , x 0,1 1,则 F x 二f x -f2-x +1 |「丄+2(2_x)+1 丿l2—x 极值点偏移问题专题(0)偏移新花样(拐点偏移) 2 r x = 22,C 1 =0,则(1,2 )是f X图像的拐点,若拐点(1,2 )也是f x的x 移”,仍可用“对称化构造”来处理. = 4(1—x) ------------ —1 >0 , (x(2—x)丿 得F x在0,11上单增,有Fx乞F1=2'1=4,得证。 2、极值点偏移PK拐点偏移常规套路 1、极值点偏移(「x0 =0) (1) 求函数f x的单调区间和极值; (2) 已知函数g x的图像与f x的图像关于直线x=1对称,证明:当x 1时, f x g x ; (3) 如果x^=x2,且f x1二f x2,证明: x1x2 2 ? 二次函数f % A f x2 = xi x^ -2x0 2、拐点偏移f x o =0 f x = f x2 = x22x0_ x1 =x1x22x0例1( 2010天津) 已知函数f x i;二xe* ? 』)上/ ’枉(L+?)±\ r y(x)有极大值解:(l)/,(x)=e_I(l-x) r得f (刃在(YD /(1) = - ’无驗卜值; e (2)g(x]的團像与f(x)的團像关于直线x“对称”则g[x)的跡式为$ = /(2-x), 构iim^F(x)=/(x)-g(x) = /(x)-/(2-x) F(x) = r[x) + /(2-x) 二严(1_工)+严(T 当Q1 时宀―I A O r严-「A0 ’则r(x)>0 ,得F⑴在(l J+ao)±fflS P fl| F(x)>F(l)=O F?/(x)>^(x). (3)由才(坷)=子(花)「结合门刘的单调性可设坯弋让码'将七代入(2 )中不等式得 /(2-巧)f又画<1 , 2-X2 <1 r f又/(码)=/(旳)r故/*(码)A 『(划在(YD±1]上单堵「故^>2-^ t遍+冯>2 + 来源:微信公众号中学数学研讨部落 点评:该题的三问由易到难,层层递进,完整展现了处理极值点偏移问题的一般方法一一对称化构造的全过程,直观展示如下: 例1是这样一个极值点偏移问题:对于函数 f x二xe",已知f = f X2,为X2, 证明X| x22. 再次审视解题过程,发现以下三个关键点: (1)为,x2的范围0 :::x ■■■■ 1 x2 ; (2)不等式f x ■ f 2 -x x 1 ; (3 )将X2代入(2 )中不等式,结合f x的单调性获证结论. 把握以上三个关键点,就可轻松解决一些极值点偏移问题. 2 极值点偏移问题总结 一、判定方法 1、极值点偏移的定义 对于函数在区间内只有一个极值点,方程的解分别为 )(x f y =),(b a 0x 0)(=x f ,且, 21x x 、b x x a <<<21(1)若 ,则称函数在区间上极值点偏移;02 12x x x ≠+)(x f y =),(21x x 0x (2) 若,则函数在区间上极值点左偏,简称极值点 0212 x x x >+)(x f y =),(21x x 0x 左偏; 0x (3)若,则函数在区间上极值点右偏,简称极值点02 12 x x x <+)(x f y =),(21x x 0x 0 x 右偏。 2、极值点偏移的判定定理 判定定理1 对于可导函数,在区间上只有一个极大(小)值点,方)(x f y =),(b a 0x 程的解分别为,且, 0)(=x f 21x x 、b x x a <<<21(1)若, 则,即函数在区间上极大(小)0)2( '21>+x x f 021)(2x x x ><+)(x f y =),(21x x 值点右(左)偏; 0x (2)0若, 则,即函数在区间上极大(小)0)2( '21<+x x f 021)(2 x x x <>+)(x f y =),(21x x 值点左(右)偏。 0x 证明:(1)因为可导函数,在区间上只有一个极大(小)值点,)(x f y =),(b a 0x 则函数的单调递增(减)区间为,单调递减(增)区间为,又 )(x f y =),(0x a ),(0b x ,有 由于,故,所以b x x a <<<21),(221b a x x ∈+02('21>+x x f ),(2 021x a x x ∈+,即函数极大(小)值点右(左)偏。02 1)(2 x x x ><+0x 高中数学复习:极值点偏移问题 一、 判定方法 1、极值点偏移的定义 对于函数)(x f y =在区间),(b a 内只有一个极值点0x ,方程0)(=x f 的解分别为 21x x 、,且b x x a <<<21, (1)若 02 12x x x ≠+,则称函数)(x f y =在区间),(21x x 上极值点0x 偏移; (2) 若0212 x x x >+,则函数)(x f y =在区间),(21x x 上极值点0x 左偏,简称极值点 0x 左偏; (3)若 02 12 x x x <+,则函数)(x f y =在区间),(21x x 上极值点0x 右偏,简称极值点0x 右偏。 2、极值点偏移的判定定理 证明:(1)因为可导函数)(x f y =,在区间),(b a 上只有一个极大(小)值点0x ,则函数)(x f y =的单调递增(减)区间为),(0x a ,单调递减(增)区间为),(0b x ,又 b x x a <<<21,有 ),(221b a x x ∈+由于0)2('21>+x x f ,故),(2 021x a x x ∈+,所以02 1)(2 x x x ><+,即函数极大(小)值点0x 右(左)偏。 证明:(1)因为对于可导函数)(x f y =,在区间),(b a 上只有一个极大(小)值点 0x ,则函数)(x f y =的单调递增(减)区间为),(0x a ,单调递减(增)区间为),(0b x , 又b x x a <<<21,有01x x <,且0202x x x <-,又)2()(201x x f x f -<,故 2012)(x x x -><,所以 02 1)(2 x x x ><+,即函数极大(小)值点0x 右(左)偏. 结论(2)证明略。 二、 运用判定定理判定极值点偏移的方法 1.方法概述: (1)求出函数()f x 的极值点; (2)构造一元差函数00()()()F x f x x f x x =+-- (3)确定函数()F x 的单调性; (4)结合(0)0F =,判断()F x 的符号,从而确定00(),()f x x f x x -+的大小关系。 2.抽化模型 答题模板:若已知函数()f x 满足12()()f x f x =,0x 为()f x 的极值点,求证:1202x x x +< (1)讨论函数()f x 的单调性并求出()f x 的极值点0x ; 假设此处()f x 在()0,x -∞上单调递减,在()0,x +∞ 上单调递增。 极值点偏移问题专题(0)——偏移新花样(拐点偏移) 例1已知函数()22ln f x x x x =++,若正实数1x ,2x 满足()()12+=4f x f x , 求证:122x x +≥。 证明:注意到()1=2f ,()()()12+=21f x f x f ()()()12+=21f x f x f ()2= +210f x x x '+> ()2 2=2f x x ''-+,()1=0f '',则(1,2)是()f x 图像的拐点,若拐点(1,2)也是()f x 的 对称中心,则有12=2x x +,证明122x x +≥则说明拐点发生了偏移,作图如下 想到了“极值点偏移”,想到了“对称化构造”,类似地,不妨将此问题命名为“拐点偏移”,仍可用“对称化构造”来处理. 不妨设1201x x <≤≤,要证 ()() 1221212212x x x x f x f x +≥?≥-≥?≥ - ()()()() 11114242f x f x f x f x ?-≥-?≥ + - ()()()2F x f x f x =+ -,(]0,1x ∈,则 ()()() ()222212212F x f x f x x x x x '''=--????=++-+-+ ? ?-???? ()()1 41102x x x ??=--≥ ? ?-?? , 得()F x 在(]0,1上单增,有()()()1214F x F ≤=+=,得证。 2、极值点偏移PK 拐点偏移常规套路 1、 极值点偏移(()00f x '=) 二次函数()()121202f x f x x x x =?+= 2、拐点偏移()()00f x ''= ()()()12012022f x f x f x x x x + = ?+= 今天带来极值点偏移系列 第3篇文章,供大家参考 () ()12201 120 22f x f x x x x x x x =? >-?+ >()()()120201 120 222f x f x f x x x x x x x + = ? >-?+>高中数学极值点偏移问题
极值点偏移问题的处理策略及探究
极值点偏移问题的处理策略及探究
《极值点偏移问题的处理策略及探究》
极值点偏移问题专题(完整资料).doc
极值点偏移问题专题(三)一一题学懂极值点偏移5大套路
极值点偏移问题专题(三)一一题学懂极值点偏移5大套路
导数压轴题分类___极值点偏移问题
极值点偏移问题专题
极值点偏移问题(最新整理)
高中数学复习:极值点偏移问题
极值点偏移问题专题(一)拐点偏移PK极值点偏移常规套路