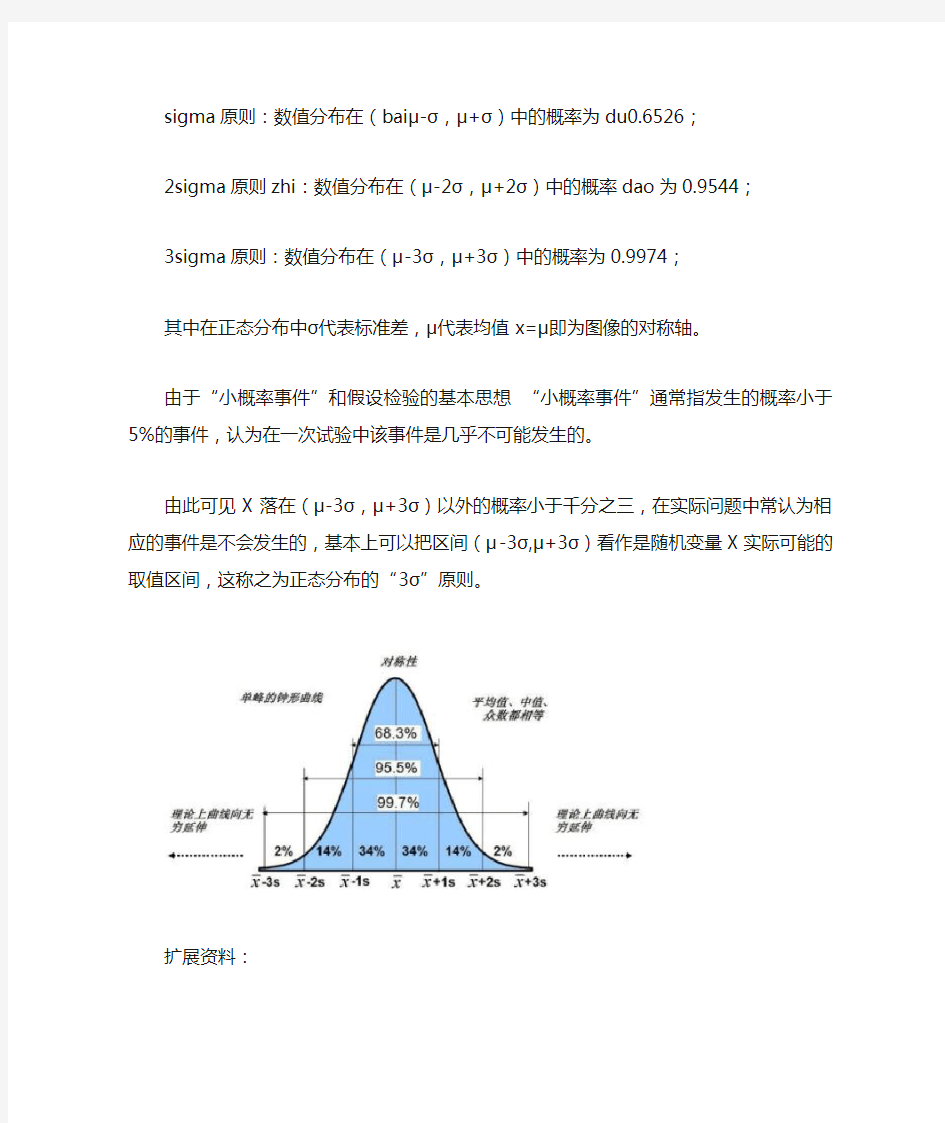

sigma原则:数值分布在(baiμ-σ,μ+σ)中的概率为du0.6526;
2sigma原则zhi:数值分布在(μ-2σ,μ+2σ)中的概率dao为0.9544;
3sigma原则:数值分布在(μ-3σ,μ+3σ)中的概率为0.9974;
其中在正态分布中σ代表标准差,μ代表均值x=μ即为图像的对称轴。
由于“小概率事件”和假设检验的基本思想“小概率事件”通常指发生的概率小于5%的事件,认为在一次试验中该事件是几乎不可能发生的。
由此可见X落在(μ-3σ,μ+3σ)以外的概率小于千分之三,在实际问题中常认为相应的事件是不会发生的,基本上可以把区间(μ-3σ,μ+3σ)看作是随机变量X实际可能的取值区间,这称之为正态分布的“3σ”原则。
扩展资料:
曲线应用
综述
1、估计频数分布一个服从正态分布的变量只要知道其均数与标准差就可根据公式即可估计任意取值范围内频数比例。
2、制定参考值范围
(1)正态分布法适用于服从正态(或近似正态)分布指标以及可以通过转换后服从正态分布的指标。
(2)百分位数法常用于偏态分布的指标。表3-1中两种方法的单双侧界值都应熟练掌握。
3、质量控制:为了控制实验中的测量(或实验)误差,常以作为上、下警戒值,以作为上、下控制值。这样做的依据是:正常情况下测量(或实验)误差服从正态分布。
4、正态分布是许多统计方法的理论基础。检验、方差分析、相关和回归分析等多种统计方法均要求分析的指标服从正态分布。许多统计方法虽然不要求分析指标服从正态分布,但相应的统计量在大样本时近似正态分布,因而大样本时这些统计推断方法也是以正态分布为理论基础的。
sigma原则:数值分布在(μ—σbai,μ+σ)中的概率du为0.6526
2sigma原则zhi:数值分dao布在(μ—2σ,μ+2σ)中的概率为0.9544
3sigma原则:数值分布在(μ—3σ,μ+3σ)中的概率为0.9974
其中在正态分布中σ代表标准差,μ代表均值x=μ即为图像的对称轴。
3σ准则又称为拉依达准则,它是先假设一组检测数据只含有随机误差,对其进行计算处理得到标准偏差,按一定概率确定一个区间,认为凡超过这个区间的误差,就不属于随机误差而是粗大误差,含有该误差的数据应予以剔除。且3σ适用于有较多组数据的时候。
可以认为,数值分布几乎全部集中在(μ-3σ,μ+3σ)区间内,超出这个范围的可能性仅占不到0.3%.
第五章假设检验 一、选择题 1.单项选择题 (1)将由显著性水平所规定的拒绝域平分为两部分,置于概率分布的两边,每边占显著性水平的 1 /2,这是(B )。 A.单侧检验 B.双侧检验 C.右单侧检验 D.左单侧检验 (2)检验功效定义为(B )。 A.原假设为真时将其接受的概率 B.原假设不真时将其舍弃的概率 C.原假设为真时将其舍弃的概率 D.原假设不真时将其接受的概率 (3)符号检验中,(+)号的个数与(-)号的个数相差较远时,意味着(C )。 A.存在试验误差(随机误差) B.存在条件误差 C.不存在什么误差 D.既有抽样误差,也有条件误差 (4)得出两总体的样本数据如下: 甲:8,6,10,7,8; 乙:5,11,6,9,7,10 秩和检验中,秩和最大可能值是(C )。 A.15 B.48 C.45 D.66 2.多项选择题 (1)显著性水平与检验拒绝域的关系是(ABD )。 A.显著性水平提高(α 变小),意味着拒绝域缩小 B.显著性水平降低,意味着拒绝域扩大 C.显著性水平提高,意味着拒绝域扩大 D.显著性水平降低,意味着拒绝域扩大化 E.显著性水平提高或降低,不影响拒绝域的变化 (2)β 错误(ACDE )。A. 是在原假设不真实的条件下发生的 B.是在原假设真实的条件下发生的 C.决定于原假设与实际值之间的差距 D. 原假设与实际值之间的差距越大,犯β 错误的可能性就越小 E.原假设与实际值之间的差距越小,犯β错误的可能性就越大 二、计算题 1.某牌号彩电规定无故障时间为10000 小时,厂家采取改进措施,现在从新批量彩电中抽取100 台,
ο n ο n 60 16 测得平均无故障时间为 10150 小时,标准差为 500 小时,能否据此判断该彩电无故障时间有显著增加(α =0.01)? 解:假设检验为H 0:μ0=10000,H 1:μ0<10000(使用寿命应该使用单侧检验)。n =100 可近似采用 x - μ0 正态分布的检验统计量z = 。查出α=0.01 水平下的反查正态概率表得到临界值 2.34 到 2.36 之间 (因为表中给出的是双侧检验的接受域临界值,因此本题的单侧检验显著性水平应先乘以 2,再查到对应的临界值)。计算统计量值 z = 3 。因为z =3>2.36(>2.34),所以拒绝原假设。 2. 假设某产品的重量服从正态分布,现在从一批产品中随机抽取 16 件,测得平均重量为 820 克,标准差为 60 克,试以显著性水平 α=0.01 与 α=0.05,分别检验这批产品的平均重量是否是 800 克。 解:假设检验为H 0:μ0=800,H 1:μ0≠800(产品重量应该使用双侧检验)。采用t 分布的检验统计量 t = x - μ0 。查出α=0.05 和 0.01 两个水平下的临界值(df =n -1=15)为 2.131 和 2.947。t = 820 - 800 =1.667。因为 t < 2.131 < 2.947 ,所以在两个水平下都接受原假设。 3. 某市全部职工中,平常订阅某种报纸的占 40%,最近从订阅率来看似乎出现降低的现象,随机抽 200 户职工家庭进行调查,有 76 户职工订阅该报纸,问报纸的订阅率是否显著降低(α=0.05)? 解:假设检验为H :P =40%,H :P <40%。采用成数检验统计量 z = α=0.05 1 水平下的临界值为 1.64 和 1.65 之间。计算统计量值 z ≈ -0.577 ,z =-0.577>- 1.64,所以接受原假设。p 值为 0.48 和 0.476 之间[因为本题为单侧检验, p 值= (1- F ( z )) 2 ] 。显然 p 值>0.05,所以接受原假设。 4. 某加油站经理希望了解驾车人士在该加油站的加油习惯。在一周内,他随机地抽取 100 名驾车人士 调查,得到如下结果:平均加油量等于 13.5 加仑,样本标准差是 3.2 加仑,有 19 人购买无铅汽油。试问: (1) 以 0.05 的显著性水平,是否有证据说明平均加油量并非 12 加仑? (2) 计算(1)的 p -值; (3) 以 0.05 的显著性水平来说,是否有证据说明少于 20%的驾车者购买无铅汽油? (4) 计算(3)的 p -值; (5) 在加油量服从正态分布假设下,若样本容量为 25,计算(1)和(2)。
总结正态性检验的几种方法 1.1 正态性检验方法 1)偏度系数 样本的偏度系数(记为1g )的计算公式为 ()233133 1(1)(2)(1)(2)n i i n n g x x n n s n n s μ==-=----∑, 其中s 为标准差,3μ为样本的3阶中心距,即()331 1n i i x x n μ==-∑。 偏度系数是刻画数据的对称性指标,关于均值对称的数据其偏度系数为0,右侧更分散的数据偏度系数为正,左侧更分散的数据偏度系数为负。 (2)峰度系数 样本的峰度系数(记为2g ),计算公式为 ()2424 122 44(1)(1)3(1)(2)(3)(2)(3)(1)(1)3(1)(2)(3)(2)(3)n i i n n n g x x n n n s n n n n n n n n s n n μ=+-=-------+-=------∑, 其中s 为标准差,4μ为样本的3阶中心距,即()441 1n i i x x n μ==-∑。 当数据的总体分布为正态分布时,峰度系数近似为0,;当分布为正态分布的尾部更分散时,峰度系数为正;否则为负。当峰度系数为正时,两侧极端数据较多,当峰度系数为负时,两侧极端数据较少。 (3)QQ 图 QQ 图可以帮助我们鉴别样本的分布是否近似于某种类型的分布。现假设总体为正态分布()2 ,N μσ,对于样本12,,,n x x x L ,其顺序统计量是(1)(2)(),,,n x x x L 。设()x Φ为标准正 态分布()0,1N 的分布函数,1 ()x -Φ是反函数,对应正态分布的QQ 图是由以下的点 1()0.375,,1,2,,0.25i i x i n n -??-??Φ= ? ?+???? L , 构成的散点图,若样本数据近似为正态分布,在QQ 图上这些点近似地在直线上 y x σμ=+, 附近,此直线的斜率是标准差σ,截距式均值,μ,所以利用正态QQ 图可以做直观的正态性检验。若正态QQ 图上的点近似地在一条直线上,可以认为样本的数据来自正态分布总
如何检验数据是否服从正态分布 一、图示法 1、P-P图 以样本的累计频率作为横坐标,以安装正态分布计算的相应累计概率作为纵坐标,把样本值表现为直角坐标系中的散点。如果资料服从整体分布,则样本点应围绕第一象限的对角线分布。 2、Q-Q图 以样本的分位数作为横坐标,以按照正态分布计算的相应分位点作为纵坐标,把样本表现为指教坐标系的散点。如果资料服从正态分布,则样本点应该呈一条围绕第一象限对角线的直线。 以上两种方法以Q-Q图为佳,效率较高。 3、直方图 判断方法:是否以钟形分布,同时可以选择输出正态性曲线。 4、箱式图 判断方法:观测离群值和中位数。 5、茎叶图 类似与直方图,但实质不同。 二、计算法 1、偏度系数(Skewness)和峰度系数(Kurtosis) 计算公式: g1表示偏度,g2表示峰度,通过计算g1和g2及其标准误σg1及σg2然后作U检验。两种检验同时得出U
第三章 假设检验 3.2 一种元件,要求其使用寿命不低于1000(小时),现在从一批这种元件中随机抽取25件,测得其寿命平均值为950(小时)。已知这种元件寿命服从标准差 100σ=(小时)的正态分布,试在显著水平0.05下确定这批元件是否合格。 {}01001:1000, H :1000 X 950 100 n=25 10002.5 V=u 0.05H x u αμμσμα-≥<====->=提出假设:构造统计量:此问题情形属于u 检验,故用统计量:此题中:代入上式得: 拒绝域: 本题中:0.950.950 u 1.64u 0.0u H =>∴即,拒绝原假设认为在置信水平5下这批元件不合格。 3.4某批矿砂的五个样品中镍含量经测定为(%): 3.25 3.27 3.24 3.26 3.24 设测定值服从正态分布,问在0.01α=下能否接受假设,这批矿砂的镍含量为 010110 2: 3.25 H :t 3.252, S=0.0117, n=5 0.3419 H x μμμμσ==≠==提出假设:构造统计量:本题属于未知的情形,可用检验,即取检验统计量为:本题中,代入上式得:否定域为:1-20.99512 0 V=t>t (1)0.01,(4) 4.6041, 3.25n t t t H ααα- ??-?? ?? ==<∴Q 本题中,接受认为这批矿砂的镍含量为。
3.5确定某种溶液中的水分,它的10个测定值0.452%,0.035%,X S == 2N(,),μσ设总体为正态分布试在水平5%检验假设: 0101() H :0.5% H :0.5%() H :0.04% H :0.0.4% i ii μμσσ≥<≥< {}0.95()0.452% S=0.035%-4.1143 (1)0.05 n=10 t (9) 1.833i t X n ασα==-==1-构造统计量:本文中未知,可用检验。取检验统计量为X 本题中,代入上式得: 0.452%-0.5% 拒绝域为: V=t >t 本题中,0 1 4.1143H <=∴t 拒绝 {}2 2 2 002 2 2212210.95 2()nS S 0.035% n=10 0.04%100.035%7.65630.04% V=(1)(1)(9)16.919 ii n n αα μχσσχχχχ χ χ--= ==*==>--==Q 2 构造统计量:未知,可选择统计量本题中,代入上式得: () () 否定域为: 本题中, 210 (1)n H αχ-<-∴接受 3.9设总体116(,4),,,X N X X μ:K 为样本,考虑如下检验问题:
正态性检验的几种方法 一、引言 正态分布是自然界中一种最常见的也是最重要的分布。因此,人们在实际使用统计分析时,总是乐于正态假定,但该假定是否成立,牵涉到正态性检验。目前,正态性检验主要有三类方法:一是计算综合统计量,如动差法、Shapiro-Wilk 法(W 检验)、D ’Agostino 法(D 检验)、Shapiro-Francia 法(W ’检验)。二是正态分布的拟合优度检验,如2χ检验、对数似然比检验、Kolmogorov-Smirov 检验。三是图示法(正态概率图Normal Probability plot),如分位数图(Quantile Quantile plot ,简称QQ 图)、百分位数(Percent Percent plot ,简称PP 图)和稳定化概率图(Stablized Probability plot ,简称SP 图)等。而本文从不同角度出发介绍正态性检验的几种常见的方法,并且就各种方法作了优劣比较,还进行了应用。 二、正态分布 2.1 正态分布的概念 定义1若随机变量X 的密度函数为 ()()()+∞∞-∈= -- ,,21 2 2 2x e x f x σμπ σ 其中μ和σ为参数,且()0,,>+∞∞-∈σμ 则称X 服从参数为μ和σ的正态分布,记为()2,~σμN X 。 另我们称1,0==σμ的正态分布为标准正态分布,记为()1,0~N X ,标准正态分布随机变量的密度函数和分布函数分别用()x ?和()x Φ表示。 引理1 若()2,~σμN X ,()x F 为X 的分布函数,则()?? ? ??-Φ=σμx x F 由引理可知,任何正态分布都可以通过标准正态分布表示。 2.2 正态分布的数字特征
第七章假设检验 第一节二项分布 二项分布的数学形式·二项分布的性质 第二节统计检验的基本步骤 建立假设·求抽样分布·选择显著性水平和否定域·计算检验统计量·判定第三节正态分布 正态分布的数学形式·标准正态分布·正态分布下的面积·二项分布的正态近似法 第四节中心极限定理 抽样分布·总体参数与统计量·样本均值的抽样分布·中心极限定理 第五节总体均值和成数的单样本检验 σ已知,对总体均值的检验·学生t分布(小样本总体均值的检验)·关于总体成数的检验 一、填空 1.不论总体是否服从正态分布,只要样本容量n足够大,样本平均数的抽样分布就趋于()分布。 2.统计检验时,被我们事先选定的可以犯第一类错误的概率,叫做检验的( ),它决定了否定域的大小。 3.假设检验中若其他条件不变,显著性水平的取值越小,接受原假设的可能性越(),原假设为真而被拒绝的概率越()。 4.二项分布的正态近似法,即以将B(x;n,p)视为()查表进行计算。 5.已知连续型随机变量X~N(0,1),若概率P{X ≥λ}=0.10,则常数λ=()。 6.已知连续型随机变量X~N(2,9),函数值 9772 .0 )2( = Φ ,则概率 }8 {< X P= ()。 二、单项选择 1.关于学生t分布,下面哪种说法不正确()。 A 要求随机样本 B 适用于任何形式的总体分布 C 可用于小样本 D 可用样本标准差S代替总体标准差σ 2.二项分布的数学期望为()。 A n(1-n)p B np(1- p) C np D n(1- p)。 3.处于正态分布概率密度函数与横轴之间、并且大于均值部分的面积为()。 A 大于0.5 B -0.5 C 1 D 0.5。
单样本T检验 按规定苗木平均高达1.60m以上可以出圃,今在苗圃中随机抽取10株苗木,测定的苗木高度如下: 1.75 1.58 1.71 1.64 1.55 1.72 1.62 1.83 1.63 1.65 假设苗高服从正态分布,试问苗木平均高是否达到出圃要求?(要求α=0.05) 解:1)根据题意,提出: 虚无假设H0:苗木的平均苗高为H0=1.6m; 备择假设H1:苗木的平均苗高H1>1.6m; 2)定义变量:在spss软件中的“变量视图”中定义苗木苗高, 之后在“数据视图”中输入苗高数据; 3)分析过程 在spss软件上操作分析,输出如下:
表1.1:单个样本统计量 表1.2:单个样本检验 由图1.1和表1.1数据分析可知,变量苗木苗高成正态分布,平均值为1.6680m,标准差为0.0843,说明样本的离散程度较小,标准误为0.0267,说明抽样误差较小。 由表1.3数据分析可知,T检验值为2.55,样本自由度为9,t检
验的p值为0.031<0.05,说明差异性显著,因此,否定无效假设H0,取备择假设H1。 由以上分析知:在显著水平为0.05的水平上检验,苗木的平均苗高大于1.6m,符合出圃的要求。 独立样本T检验 从两个不同抚育措施育苗的苗圃中各以重复抽样的方式抽得样本如下: 样本1苗高(CM):52 58 71 48 57 62 73 68 65 56 样本2苗高(CM):56 75 69 82 74 63 58 64 78 77 66 73 设苗高服从正态分布且两个总体苗高方差相等(齐性),试以显著水平α=0.05检验两种抚育措施对苗高生长有无显著性影响。 解:1)根据题意提出: 虚无假设H0:两种抚育措施对苗木生长没有显著的影响; 备择假设H1:两种抚育措施对苗高生长影响显著; 2)在spss中的“变量视图”中定义变量“苗高1”,“抚育措施”,之后在“数据视图”中输入题中的苗高数据,及抚育措施,其中措施一定义为“1”措施二定义为“2”; 3)分析过程 在spss软件上操作分析输出分析数据如下;
正态分布检验 一、正态检验的必要性[1] 当对样本是否服从正态分布存在疑虑时,应先进行正态检验;如果有充分的理论依据或根据以往积累的信息可以确认总体服从正态分布时,不必进行正态检验。 当然,在正态分布存疑的情况下,也就不能采用基于正态分布前提的参数检验方 法,而应采用非参数检验。 二、图示法 1、P-P图 以样本的累计频率作为横坐标,以安装正态分布计算的相应累计概率作为纵坐标,把样本值表现为直角坐标系中的散点。如果资料服从整体分布,则样本点应围绕第一象限的对角线分布。 2、Q-Q图 以样本的分位数作为横坐标,以按照正态分布计算的相应分位点作为纵坐标,把样本表现为指教坐标系的散点。如果资料服从正态分布,则样本点应该呈一条围绕第一象限对角线的直线。 Q-Q图为佳,效率较高。 以上两种方法以 3、直方图 判断方法:是否以钟形分布,同时可以选择输出正态性曲线。 4、箱式图 判断方法:观测离群值和中位数。 5、茎叶图 类似与直方图,但实质不同。 三、计算法 1、峰度(Kurtosis)和偏度(Skewness) (1)概念解释 峰度是描述总体中所有取值分布形态陡缓程度的统计量。这个统计量需要与正态分布相比较,峰度为0表示该总体数据分布与正态分布的陡缓程度相同;峰度大于0表示该总体数据分布与正态分布相比较为陡峭,为尖顶峰;峰度小于0表示该总体数据分布与正态分布相比
较为平坦,为平顶峰。峰度的绝对值数值越大表示其分布形态的陡缓程度与正态分布的差异 程度越大。 峰度的具体计算公式为: 注:SD就是标准差σ。峰度原始定义不减3,在SPSS中为分析方便减3后与0作比较。 偏度与峰度类似,它也是描述数据分布形态的统计量,其描述的是某总体取值分布的对称性。这个统计量同样需要与正态分布相比较,偏度为0表示其数据分布形态与正态分布的偏斜程度相同;偏度大于0表示其数据分布形态与正态分布相比为正偏或右偏,即有一条长尾巴拖在右边,数据右端有较多的极端值;偏度小于0表示其数据分布形态与正态分布相比为负偏或左偏,即有一条长尾拖在左边,数据左端有较多的极端值。偏度的绝对值数值越大表示其分布形态的偏斜程度越大。 偏度的具体计算公式为: 各种正态分布,尽管μ和σ可以分别取不同的值,但偏度都等于0,峰度都等于3,它们的密度函数曲线的形状都是一样的[1]。(SPSS中峰度减3与0比较 (2)适用条件 样本含量应大于200。 (3)检验方法 计算得到的峰度、偏度根据正态分布的值3、0(SPSS中为0、0)来直观判断是 否接近。 应对二者分别进行U检验来定量描述显著性,方法如下[2]:峰度U检验:|峰度-3| / 峰度标准差 <= U0.05 = 1.96(SPSS中将3替换为0)偏度U检验:|偏度-0| / 偏度标准差 <= U0.05 = 1.96 如果上述都成立,则可认为在0.05显著水平符合正态分布(下例偏度可判断不符合。
假设检验 一、单样本总体均值的假设检验 .................................................... 1 二、独立样本两总体均值差的检验 ................................................ 2 三、两匹配样本均值差的检验 ........................................................ 4 四、单一总体比率的检验 ................................................................ 5 五、两总体比率差的假设检验 .. (7) 一、单样本总体均值的假设检验 例题: 某公司生产化妆品,需要严格控制装瓶重量。标准规格为每瓶250 克,标准差为1 克,企业的质检部门每日对此进行抽样检验。某日从生产线上随机抽取16 瓶测重,以95%的保证程度进行总体均值的假设检验。 x t μ-= data6_01 样本化妆品重量 SPSS 操作: (1)打开数据文件,依次选择Analyze (分析)→Compare Means (比较均值)→One Sample T Test (单样本t 检验),将要检验的变量置入Test Variable(s)(检验变量); (2)在Test Value (检验值)框中输入250;点击Options (选项)按钮,在
Confidence Interval(置信区间百分比)后面的框中,输入置信度(系统默认为95%,对应的显著性水平设定为5%,即0.05,若需要改变显著性水平如改为0.01,则在框中输入99 即可); (3)点击Continue(继续)→OK(确定),即可得到如图所示的输出结果。 图中的第2~5 列分别为:计算的检验统计量t 、自由度、双尾检验p-值和样本均值与待检验总体均值的差值。使用SPSS 软件做假设检验的判断规则是:p-值小于设定的显著性水平?时,要拒绝原假设(与教材不同,教材的判断标准是p
Shapiro-Wilk 检验含义:Shapiro —Wilk 检验法是S.S.Shapiro 与 M.B.Wilk提出用顺序统计量W来检验分布的正态性,对研究的对象总体先提出假设认为总体服从正态分布,再将样本量为n的样本按大小顺序排列编秩,然后由确定的显著性水平a ,以及根据样本量为n时所对应的系数a i,根据特定公式计算出检验统计量W.最后查特定的正态性W检 验临界值表,比较它们的大小,满足条件则接受假设认为总体服从正态分布,否则拒绝假设,认为总体不服从正态分布? W检验全称Shapiro-Wilk检验,是一种基于相关性的算法。计算可得到一个相关系数,它越接近1就越表明数据和正态分布拟合得越好。 w检验是检验样本容量8< n < 50,样本是否符合正态分布的一种方法。 计算式为: E-Lj k -訓 其检验步骤如下: ①将数据按数值大小重新排列,使x1
正态分布是许多检验的肚础,比如F检验,t检验,卡方检验等在总体不是正太分布是没有任何盘义。因此,対一个样本是否来口正态总、体的检验是至关巫要的。当然,我们无法证明某个数据的确来口正态总体,但如果使用效率高的检验还?无法否认总体是正太的检验,我『]就没有理山否认那些和正太分布有关的检验有意义,下而我就对正态性检验方法进行简单的归纳和比较。 一.图示法 1.P-P 图 以样本的累计频率作为横坐标,以按照正态分布计算的相应累计概率作为纵坐标,以样本值表现为直角坐标系的散点。如果数据服从 F态分布,则样本点应鬧绕第一象限的对角线分布。 2.Q-Q 图 以样本的分位数作为横坐标,以按照正态分布计算的相应分位点作为纵坐标,把样本表现为直角坐标系的散点。如果数据服从正太分布,则样本点应围绕第一彖限的对角线分布。 以上两种方法以Q-Q图为佳,效率较高。 3.直方图 判断方法:是否以钟型分布,同时可以选择输出正态性曲线。 4.箱线图 判断方法;观察矩形位置利中位数,若矩形位于中间位置且中位数位于矩形的中间位迓,则分布较为对称,否则是偏态分布。 5.茎叶图
spss 数据正态分布检验方法及意义判读 要观察某一属性的一组数据是否符合正态分布,可以有两种方法(目前我知道这两种,并且这两种方法只是直观观察,不是定量的正态分布检验): 1:在spss里的基本统计分析功能里的频数统计功能里有对某个变量各个观测值的频数直方图中可以选择绘制正态曲线。具体如下:Analyze-----Descriptive S tatistics-----Frequencies,打开频数统计对话框,在Statistics里可以选择获得各种描述性的统计量,如:均值、方差、分位数、峰度、标准差等各种描述性统计量。在Charts里可以选择显示的图形类型,其中Histograms选项为柱状图也就是我们说的直方图,同时可以选择是否绘制该组数据的正态曲线(With nor ma curve),这样我们可以直观观察该组数据是否大致符合正态分布。如下图: 从上图中可以看出,该组数据基本符合正态分布。 2:正态分布的Q-Q图:在spss里的基本统计分析功能里的探索性分析里面可以通过观察数据的q-q图来判断数据是否服从正态分布。 具体步骤如下:Analyze-----Descriptive Statistics-----Explore打开对话框,选择Plots选项,选择Normality plots with tests选项,可以绘制该组数据的q-q 图。图的横坐标为改变量的观测值,纵坐标为分位数。若该组数据服从正态分布,则图中的点应该靠近图中直线。 纵坐标为分位数,是根据分布函数公式F(x)=i/n+1得出的.i为把一组数从小到大排序后第i个数据的位置,n为样本容量。若该数组服从正态分布则其q-q图应该与理论的q-q图(也就是图中的直线)基本符合。对于理论的标准正态分布,其q-q图为y=x直线。非标准正态分布的斜率为样本标准差,截距为样本均值。 如下图:
正态性检验的一般方法 姓名:蓝何忠 学号:1101200203 班号:1012201 正态性检验的一般方法 【摘要】:正态分布是自然界中一种最常见的也是最重要的一种分布.因此,人们在实际使用统计分析时,总是乐于正态假定,但该假定是否成立,牵涉到正态性检验.在一般性的概率统计教科书中,只是把这个
问题放在一般性的分布拟合下作简短处理,而这种万精油式的检验方法,对正态性检验不具有特效.鉴于此,该文从不同角度出发介绍正态性检验的几种常见的方法,并且就各种方法作了优劣比较, 【引言】一般实际获得的数据,其分布往往未知。在数据分析中,经常要判断一组数据的分布是否来自某一特定的分布,比如对于连续性分布,常判断数据是否来自正态分布,而对于离散分布来说,常判断是否来自二项分布.泊松分布,或判断实际观测与期望数是否一致,然后才运用相应的统计方法进行分析。 几种正态性检验方法的比较。 2?一、拟合优度检验: (1)当总体分布未知,由样本检验总体分布是否与某一理论分布一致。 H0: 总体X的分布列为p{X=}=,i=1,2,…… H1:总体 X. 的分布不为 构造统计量 为真时H0发生的理为为样本中发生的实际频数,其中论频数。2)检验原理(2?意味着对于,=,观测频数与期望频数完全一致,若=0,则即完全拟合。 2?观察频数与期望频数越接近,则值越小。 2?当原假设为真时,有大数定理,与不应有较大差异,即值应较小。
2?若值过大,则怀疑原假设。 2?拒绝域为R={d} ,判断统计量是否落入拒绝域,得出结论。 二、Kolmogorov-Smirnov正态性检验: Kolmogorov-Smirnov检验法是检验单一样本是否来自某一特定它的 检验方法是以样本数比如检验一组数据是否为正态分布。分布。. 据的累积频数分布与特定理论分布比较,若两者间的差距很小,则推论该样本取自某特定分布族。即对于假设检验问题: H0:样本所来自的总体分布服从某特定分布 H1:样本所来自的总体分布不服从某特定分布 统计原理:Fo(x)表示分布的分布函数,Fn(x)表示一组随机样本的累计概率函数。 #}n1,2,,x{x?,i?i?)F(x n n : x)差距的最大值,定义如下式Fn为Fo(x)与(D设 D=max|Fn(x)-Fo(x)| P{Dn>d}=a. a,对于给定的位健康男性在未进食前的血糖浓度如表所示,试测验这组35例如: =6的正态分布,标准差数据是否来自均值μ=80σ87 77 92 68 80 78 84 77 81 80 80 77 92 86 76 80 81 75 77 72 81 90 84 86 80 68 77 87 76 77 78 92 75 80 78 n=35 检验过程如下:健康成人男性血糖浓度服从正态分布 H0:假设健康成人男性血糖浓度不服从正态分布 H1: 计算过程如表:
参数估计和假设检验习题 1.设某产品的指标服从正态分布,它的标准差σ已知为150,今抽了一个容量为26的样本,计算得平均值为1637。问在5%的显著水平下,能否认为这批产品的指标的期望值μ为1600? 解: 01:1600, :1600,H H μμ=≠标准差σ已知,拒绝域为2 Z z α>,取0.05,α=26,n = 0.0250.9752 1.96z z z α===, 由检验统计量 1.25 1.96Z = ==<,接受0:1600H μ=, 即,以95%的把握认为这批产品的指标的期望值μ为1600. 2.某纺织厂在正常的运转条件下,平均每台布机每小时经纱断头数为O.973根,各台布机断头数的标准差为O.162根,该厂进行工艺改进,减少经纱上浆率,在200台布机上进行试验,结果平均每台每小时经纱断头数为O.994根,标准差为0.16根。问,新工艺上浆率能否推广(α=0.05)? 解: 012112:, :,H H μμμμ≥< 3.某电器零件的平均电阻一直保持在2.64Ω,改变加工工艺后,测得100个零件的平均电阻为2.62Ω,如改变工艺前后电阻的标准差保持在O.06Ω,问新工艺对此零件的电阻有无显著影响(α=0.05)? 解: 01: 2.64, : 2.64,H H μμ=≠已知标准差σ=0.16,拒绝域为2 Z z α>,取0.0252 0.05, 1.96z z αα===, 100,n = 由检验统计量 3.33 1.96Z = ==>,接受1: 2.64H μ≠, 即, 以95%的把握认为新工艺对此零件的电阻有显著影响. 4.有一批产品,取50个样品,其中含有4个次品。在这样情况下,判断假设H 0:p ≤0.05是否成立(α=0.05)? 解: 01:0.05, :0.05,H p H p ≤>采用非正态大样本统计检验法,拒绝域为Z z α>,0.950.05, 1.65z α==, 50,n = 由检验统计量0.9733Z = ==<1.65,接受H 0:p ≤0.05. 即, 以95%的把握认为p ≤0.05是成立的. 5.某产品的次品率为O.17,现对此产品进行新工艺试验,从中抽取4O0件检验,发现有次品56件,能否认为此项新工艺提高了产品的质量(α=0.05)? 解: 01:0.17, :0.17,H p H p ≥<采用非正态大样本统计检验法,拒绝域为Z z α<-,400,n = 0.950.05, 1.65z α=-=-,由检验统计量 400 1.5973i x np Z -= = =-∑>-1.65, 接受0:0.17H p ≥, 即, 以95%的把握认为此项新工艺没有显著地提高产品的质量. 6.从某种试验物中取出24个样品,测量其发热量,计算得x =11958,样本标准差s =323,问以5%的显著水平是否可认为发热量的期望值是12100(假定发热量是服从正态分布的)?
学院数学与信息科学学院 专业信息与计算科学 年级 2011级 姓名姚瑞娟 论文题目单个正态总体的检验假设 指导教师韩英波职称副教授成绩 2014年3月10日
目录 摘要 (1) 关键词 (1) Abstrac (1) Keywords (1) 前言 (1) 1 假设检验的基本步骤 (2) 1.1 建立假设 (2) 1.2 建立假设选择检验统计量,给出拒绝域形式 (2) 2 单个正态总体均值的检验 (3) 2.1 δ已知时的μ检验 (4) 2.2 δ未知时的t检验 (6) 3 单个正态总体方差的检验 (8) 参考文献 (9)
单个正态总体的假设检验 学生姓名:姚瑞娟学号:20115034036 数学与信息科学学院信息与计算科学专业 指导老师:韩英波职称:副教授 摘要:本文介绍了假设检验的基本步骤,如何建立假设检验,判断假设是否正确.此外,从2δ已知和2δ未知详细的讲述了单个正态总体μ的检验,还有单个正态总体方差的检验,及与它们相关的应用举例. 关键词:正态分布;假设检验;均值;方差;拒绝域;接受域;原假设; Hypothesis test of one normal population Abstract:It introduces the basic steps of hypothesis test in this paper, and how to build hypothesis and correct judgment test. In addition, it detailed introduces the single hypothesis test from variance is known and unknown. There is a single of normal population variance test and the related application. Keywords:normal distribution;price value;hypothesis test;variance;rejected region;receptive regions;the original hypothesis 前言 假设检验是由K.Pearson于20世纪初提出的,之后由费希尔进行了细化,并最终由奈曼和E.Pearson提出了较完整的假设检验理论.统计推断的一个重要内容就是假设检验.然而,正态分布正态分布是最重要的一种概率分布,正态分布概念是由德国的数学家和天文学家Moiré于1733年受次提出的,但由于德国数学家Gauss率先将其应用于天文学家研究,故正态分布又叫高斯分布,高斯这项工作对后世的影响极大他使正态分布同时有了”高斯分布”的名称,后世之所以多将最小二乘法的发明权归之于他.也是出于这一工作,高斯是一个伟大的数学家,重要的贡献不胜枚举.但现今德国10马克的印有高斯头像的钞票,其上还印有正态
一、图示法 1、P-P图 以样本的累计频率作为横坐标,以安装正态分布计算的相应累计概率作为纵坐标,把样本值表现为直角坐标系中的散点。如果资料服从整体分布,则样本点应围绕第一象限的对角线分布。 2、Q-Q图 以样本的分位数作为横坐标,以按照正态分布计算的相应分位点作为纵坐标,把样本表现为指教坐标系的散点。如果资料服从正态分布,则样本点应该呈一条围绕第一象限对角线的直线。 以上两种方法以Q-Q图为佳,效率较高。 3、直方图 判断方法:是否以钟形分布,同时可以选择输出正态性曲线。 4、箱式图 判断方法:观测离群值和中位数。 5、茎叶图 类似与直方图,但实质不同。 二、计算法 1、偏度系数(Skewness)和峰度系数(Kurtosis) 计算公式: g 1表示偏度,g 2 表示峰度,通过计算g1和g2及其标准误σ g1 及σ g2 然后作U 检验。两种检验同时得出U<=,即p>的结论时,才可以认为该组资料服从正态分布。由公式可见,部分文献中所说的“偏度和峰度都接近0……可以认为……近似服从正态分布”并不严谨。 2、非参数检验方法
非参数检验方法包括Kolmogorov-Smirnov检验(D检验)和Shapiro- Wilk (W检验)。 SAS中规定:当样本含量n≤2000时,结果以Shapiro – Wilk(W检验)为准,当样本含量n >2000时,结果以Kolmogorov – Smirnov(D检验)为准。 SPSS中则这样规定:(1)如果指定的是非整数权重,则在加权样本大小位于3和50之间时,计算Shapiro-Wilk统计量。对于无权重或整数权重,在加权样本大小位于3 和 5000 之间时,计算该统计量。由此可见,部分SPSS教材里面关于“Shapiro – Wilk适用于样本量3-50之间的数据”的说法是在是理解片面,误人子弟。(2)单样本Kolmogorov-Smirnov检验可用于检验变量(例如income)是否为正态分布。 对于此两种检验,如果P值大于,表明资料服从正态分布。 三、SPSS操作示例 SPSS中有很多操作可以进行正态检验,在此只介绍最主要和最全面最方便的操作: 1、工具栏--分析—描述性统计—探索性 2、选择要分析的变量,选入因变量框内,然后点选图表,设置输出茎叶图和直方图,选择输出正态性检验图表,注意显示(Display)要选择双项(Both)。 3、Output结果 (1)Descriptives:描述中有峰度系数和偏度系数,根据上述判断标准,数据不符合正态分布。 S k =0,K u =0时,分布呈正态,Sk>0时,分布呈正偏态,Sk<0时,分布呈负偏 态,时,Ku>0曲线比较陡峭,Ku<0时曲线比较平坦。由此可判断本数据分布为正偏态(朝左偏),较陡峭。 (2)Tests of Normality:D检验和W检验均显示数据不服从正态分布,当然在此,数据样本量为1000,应以W检验为准。
第三节 两个正态总体的假设检验 上一节介绍了单个正态总体的数学期望与方差的检验问题,在实际工作中还常碰到两个正态总体的比较问题. 1.两正态总体数学期望假设检验 (1) 方差已知,关于数学期望的假设检验(Z 检验法) 设X ~N (μ1,σ12),Y ~N (μ2,σ22),且X ,Y 相互独立,σ12与σ22 已知,要检验的是 H 0:μ1=μ2;H 1:μ1≠μ2.(双边检验) 怎样寻找检验用的统计量呢从总体X 与Y 中分别抽取容量为n 1,n 2的样本X 1,X 2,…, 1n X 及Y 1,Y 2,…,2n Y ,由于 2111~,X N n σμ?? ??? ,2222~,Y N n σμ?? ???, E (X -Y )=E (X )-E (Y )=μ1-μ2, D (X -Y )=D (X )+D (Y )= 22 121 2 n n σσ+, 故随机变量X -Y 也服从正态分布,即 X -Y ~N (μ1-μ2, 22 121 2 n n σσ+). 从而 X Y ~N (0,1). 于是我们按如下步骤判断. (a ) 选取统计量 Z X Y , () 当H 0为真时,Z ~N (0,1). (b ) 对于给定的显著性水平α,查标准正态分布表求z α/2使 P {|Z |>z α/2}=α,或P {Z ≤z α/2}=1-α/2. () (c ) 由两个样本观察值计算Z 的观察值z 0: z 0 x y . (d ) 作出判断: 若|z 0|>z α/2,则拒绝假设H 0,接受H 1; 若|z 0|≤z α/2,则与H 0相容,可以接受H 0. 例8.7 A ,B 两台车床加工同一种轴,现在要测量轴的椭圆度.设A 车床加工的轴的椭
Z 假设检验 例1 (Z 值右侧检验) 某种元件的寿命X (以h 计)服从正态分布N (μ,δ2 ), 已知δ2 =10000,μ未知,现在测得16只元件的寿命如下: 159 280 101 212 224 379 179 264 222 362 168 250 149 260 485 170 取α=0.05,问是否有理由认为元件的平均寿命大于225h ? 解:按题意需检验 H 0:μ≤μ0=225 ,H 1 :μ>225 由题设得Z 0.05=1.65 , n=16,x =241.5, z 0.66 x = = = 得,Z 0.05=1.65 > z=0.66 即z 值没有落在拒绝域内,故接受H 0 。认为元件的平均寿命不大于225h.
例2(t值右侧检验)某种元件的寿命X(以h计)服从正态分布 N(μ,δ2 ), δ2 ,μ均未知,现在测得16只元件的寿命如下: 159280101212224379179264 222362168250149260485170 取α=0.05,问是否有理由认为元件的平均寿命大于225 h? 解:按题意需检验 H0:μ≤μ0=225 ,H1:μ>225 由题设得t0.05 (15)=1.75 , n=16, χ=241.5, 0.67 t=== 得,t0.05 (15)=1.75 > z=0.67 即z值没有落在拒绝域内,故接受H0。认为元件的平均寿命不大于225 h.
例3 某厂生产的某种型号的电池,其寿命(以h 计)长期以来服从方差δ2 =5000的正态分布,现有一批这种电池,从他的生产情况来看,寿命的波动性有所改变。现随机取26只电池,测出其寿命的样本方差S 2=9200。问根据这一数据能否推断这批电池的寿命的波动性较以往的有显著的变化(取α=0.02)? 解:本题要求在水平α=0.02下检验假设 H0: δ2 = 5000 , H0: δ2 ≠ 5000 现在n = 26 , 22/20.01(1)(25)44.314n αχχ-== , 221/20.99(25)(25)11.524αχχ-== . 即拒绝域为, 2 2 (1)44.314n S δ -≥ ,或 2 20 (1)11.524n S δ -≤ 由观察值S 2 = 9200 得 2 2 0(1)4644.314n S δ-=>, 所以拒绝H 0。认为这批电池寿命波动性较以往的有显著的变化。