
在立体几何中引入向量之前,求角与距离是一个难点,在新课标中,从向量的角度来研究空间的点、线、面的关系,我们只要通过两个向量的数量积运算、运用向量的模、平面的法向量就可以解决常见的角与距离的问题。而且,运用向量来解题思路简单、步骤清楚,对学生来说轻松了很多。
重点:用空间向量数量积及夹角公式求异面直线所成角。 难点:建立恰当的空间直角坐标系
关键:几何问题转换为代数问题及正确写出空间向量的坐标。 Ⅰ、空间直角坐标系的建立
空间向量的数量积公式(两种形式)、夹角公式和空间向量的数量积的几何性质。(用媒体分步显示下列内容) 1. 向量的数量积公式(包括向量的夹角公式):
若与的夹角为θ(0≤θ≤π),且={x 1,y 1,z 1},={x 2,y 2,z 2},则 ⑴ a ·b =|a ||b |cos θ 或 a ·b = x 1x 2+y 1y 2+z 1z 2 ⑵若a 与b 非零向量 cos θ
=
22
22
22
21
21
21
212121x z z y y x x z
y x z y ++?++++
2. 向量的数量积的几何性质:
⑴两个非零向量与垂直的充要条件是·=0
⑵两个非零向量a 与b 平行的充要条件是a ·b =±|a ||b | 利用空间向量知识求异面直线所成角的一般步骤: (1)根据图形建立合理的空间直角坐标系; (2)确定关键点的坐标; (3)求空间向量的夹角; (4)得出异面直线的所成角。
D 1
x
y o
. M
x
y
o
. M
平面直角坐标系
空间直角坐标系
z
用向量解决角的问题 ①两条异面直线a 、b 间夹角
在直线a 上取两点A 、B ,在直线b 上取两点C 、D ,若直线a 与b 的夹角为θ,
则cos |cos ,|AB CD θ=<>u u u r u u u
r =。
注意,由于两向量的夹角范围为[]??180,0,而异面直线所成角的范围为
()?<
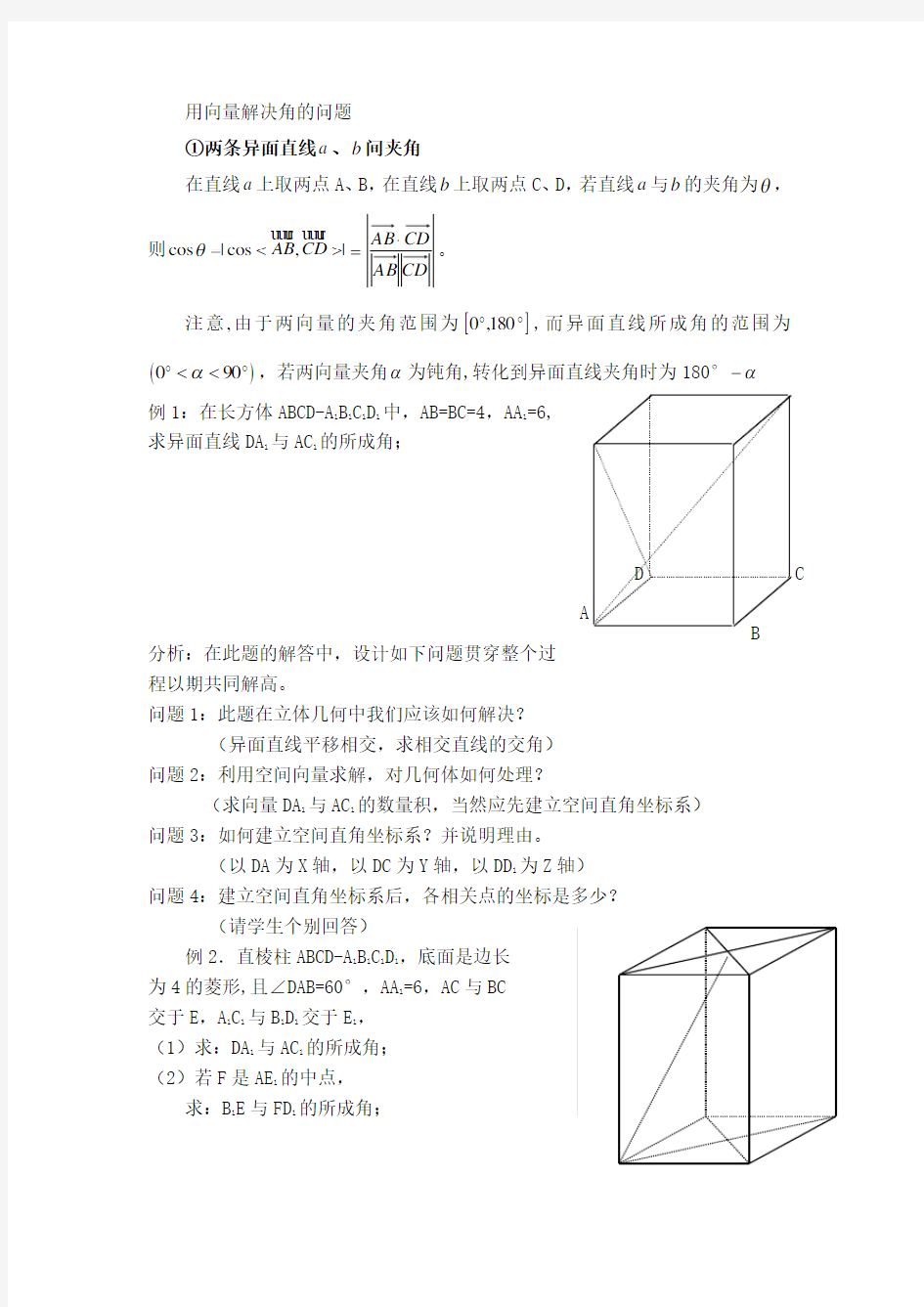
例1:在长方体ABCD-A 1B 1C 1D 1中,AB=BC=4,AA 1=6, 求异面直线DA 1与AC 1的所成角;
分析:在此题的解答中,设计如下问题贯穿整个过程以期共同解高。
问题1:此题在立体几何中我们应该如何解决?
(异面直线平移相交,求相交直线的交角) 问题2:利用空间向量求解,对几何体如何处理?
(求向量DA 1与AC 1的数量积,当然应先建立空间直角坐标系) 问题3:如何建立空间直角坐标系?并说明理由。
(以DA 为X 轴,以DC 为Y 轴,以DD 1为Z 轴) 问题4:建立空间直角坐标系后,各相关点的坐标是多少?
(请学生个别回答)
例2.直棱柱ABCD-A 1B 1C 1D 1,底面是边长 为4的菱形,且∠DAB=60°,AA 1=6,AC 与BC 交于E ,A 1C 1与B 1D 1交于E 1, (1)求:DA 1与AC 1的所成角; (2)若F 是AE 1的中点,
求:B 1E 与FD 1的所成角;
②直线a 与平面α所成的角θ(如图11-)
可转化成用向量→
a 与平面α的法向量→
n 的夹角ω表示,由向量平移得:若
平面α的法向量→
n 是向量的一个重要内容,是求直线与平面所成角、求点到平面距离的必备工具.由α⊥→n 可知,要求得法向量→
n ,只需在平面α上找出两
个不共线向量→
a 、→
b ,最后通过解方程组?????=?=?→→→→0
0n b n a 得到→n .
例4、 在直三棱柱111C B A ABC -中,底面是等腰直角三角形,?=∠90ACB ,侧棱21=AA ,D 、E 分别是1CC 与B A 1的中点,点E 在平面ABD 上的射影是ABD ?的重 心G ,求直线B A 1与平面ABD 所成角正弦值.
例8.三棱柱111B A O OAB -,平面⊥11O OBB 平面OAB ,?=∠601OB O ,
?=∠90AOB 且21==OO OB ,3=OA ,求:二面角O AB O --1的余弦值大小.
x
图1-2
图1-1
图1-3
B 1
例9. 如图,在底面是直角梯形的四棱锥S —
A BCD 中,AD//BC ,∠A BC=900,
S A ⊥面A BCD ,S A =21,A B=BC=1,A D=2
1
。求侧面SCD 与面SB A 所成的二面
角的余弦值大小。
用向量解决距离问题
①两点B A ,间距离||AB
由?→
??→??→
??=AB AB AB 2
可算出;
若→
→
?→
?+=b a AB ,则由数量积得→
→→→?→
??+??
?
??+??? ??=b a b a AB 22
2
2
,
若已知两点坐标,则可直接用两点间距离公式. ②点P 到直线AB 的距离
过点P 作直线AB 的垂线PD ,垂足为D ,则由AB PD ⊥且点D B A ,,共线得
AB AD AB PD λ==?,0,解出D 点后再求||PD 。
例1、直角坐标系中的三点()3,1,0A ,()
0,0,3B ,()0,2,0C ,求点A 到直线BC
的距离。
解:过A 作BC AH ⊥,垂足为H 设?→
??→
?=BC BH λ,∵()
0,2,3-=?→
?BC
∴()()
0,2,30,2,3λλλ-=-=?→?BH ,则H 点坐标为(
0,2,33λλ-
∴=
?→?AH (
)
3,12,33---λλ,又∵0=??→
??→?BC AH ,
∴02433=-++-λλ,75=λ,∴???
? ??-=?→?3,73,732AH ,7
24
=?→?AH ③异面直线a 、b 的距离
可先设a 、b 的公垂线段EF (a E ∈、b F ∈),再由垂直向量性质得??
???=?=??→
?
→?→?
→00
EF b EF a ,从而得到E 、F 的坐标,最后算出所求?→
?EF .
例2、正方体1111D C B A ABCD -的边长为1,求异面直线C A 1、BD 的距离?
分析:从正方体条件得,运用坐标向量的方法较好. 建立直角坐标系,设EF 是所求的公垂线,令?→
??→?=BD BE λ、
?→
??→
?=C A k F A 11,则()0,1,1-=?→
?λBE 、E 的坐标为()0,,1λλ-,
同理()k k k F -1,,,再由0=??→??→?BD EF 、01=??→
??→?C A EF ,算得
21=λ、32=k ,最后算出?→?EF 、6
6=?→?EF . 这个方法不但能求出直线上的点的坐标,也能求出空间向量的表示式,是向量运用中常用的一个小技巧. ④点P 到平面α的距离h
先设平面α的斜线为PA ()α∈A ,再求α的法向量→
n ,运用向量平移,不
难得到推论“h 等于?→?PA 在法向量→n 上的射影→
→
?→
??
n
n PA
最后由此算出所求距离.
例3、正四棱柱1111D C B A ABCD -,1=AB ,
21=AA ,E 是1CC 的中点,求点1D 到平面BDE 的距离分析:如图建立直角坐标系,得各点坐标,
设平面BDE 的法向量为),,(z y x n =→
,
由??
???=?=??→
?→?→?→0
0DB n DE n ,得???=+=+00y x z y ;令1=y ,得法向量)1,1,1(--=→n ∴?→?E D 1在→
n 上的投影为3
3
21=
?
→
→
?→
?n
n E D ,∴点1D 到平面BDE 的距离为332.
此类题目,是在立体几何学习中的必须解决的重点题和难题,传统的解题方法很多,也很复杂。运用平面法向量的知识,能直接算出所求距离,避免繁复的逻辑推理。
④两平行平面,αβ之间的距离
由平行平面间的距离定义知道,平面α上任意一点A 到β的距离就是α到β的距离,因此,我们也可把α到β的距离转化为A 到β的距离,运用求点与面距离的方法来求。
1、(2011年高考陕西卷理科16)(本小题满分12分) 如图:在,ABC ∠V 0
中,ABC=60,∠0
BAC=90
AD BC 是上的高,沿AD 把ABD V 折起,
使∠0
BDC=90(Ⅰ)证明:平面⊥ADB BDC 平面;
(Ⅱ)设E BC DB u u r u u u r
为的中点,求AE 与夹角的余弦值。
2、(2011年高考北京卷理科16)(本小题共14分)
如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,底面
ABCD 是菱形,2,60AB BAD =∠=o .
(Ⅰ)求证:BD ⊥平面;PAC (Ⅱ)若,PA AB =求PB 与AC 所成角的余弦值; (Ⅲ)当平面PBC 与平面PDC 垂直时,求PA 的长.
3、(2011年高考全国新课标卷理科18) (本小题满分12分)
如图,四棱锥P—ABCD中,底面ABCD为平行四
边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
(Ⅰ)证明:PA⊥BD;
(Ⅱ)若PD=AD,求二面角A-PB-C的余弦值。
分析:(1)要证明线线垂直只要证明线面垂直或者用向量去证明;(2)求二面角的余弦只需建立适当的坐标系,有空间向量来完成。
7.1平面直角坐标系 7.1.1有序数对 教学三维目标 知识与技能: 1.理解有序数对的意义。 2.能用有序数对表示实际生活中物体的位置 过程与方法: 1.学生经历有序数对的学习过程,培养学生的概括能力,发展学生的数感。 2. 体会具体-抽象-具体的数学学习过程 情感态度与价值观: 1.通过在游戏中学习有序数对,培养学生合作交流意识和探索精神. 2.经历用有序数对表示位置的过程,体验数、符号是描述现实世界的重要手段 . 教学重点:有序数对及平面内确定点的方法. 教学难点:利用有序数对表示平面内的点. 教学课型:新授课 教学课时:1课时 教学方法:启发、讨论、交流 教学准备:三角尺粉笔多媒体 教学过程: 一、问题与情境 情景引入:游戏“找朋友” 问题: (1)只给一个数据如“第3列”你能确定好朋友的位置吗? (2)给两个数据如“第3列第2排”你能确定好朋友的位置吗?为什么?(3)你认为需要几个数据能确定一个位置?
二、合作探究 1.【提出问题】 请在教室找到如下表用数对表示的同学位置: 发现:在教室里排数与列数的先后顺序没有约 定的情况下,不能确定参加数学问题讨论的同学 假设约定“列数在前,排数在后”,你能找到参加数学问题讨论的同学的座位吗? 思考: (1)(2,4)和(4,2)在同一个位置吗? (2)如果约定“排数在前,列数在后”,刚才那些同学对应的有序数对会变化吗? 2. 【师生归纳】 思考:在生活中还有用有序数对表示一个位置的例子吗? 3. 【例题讲解】 例1:如图,甲处表示2街与5巷的十字路口,乙处表示5街5巷的十字路口,如果用(2,5)表示甲处的位置,那么(2,5)→(3,5)→(4,5)→(5,5)→(5,4)→(5,3)→(5,2)表示从甲处到乙处的一种路线,请你用有序数对写出几种从甲处到乙处的路线。 3街4街5街6街2巷 1巷 1街2街6巷 5巷 4巷 3巷 变式练习:设计一个容易用有序数对描述的图形,并用自己的语言描述这个图形 有序数对: 我们把有顺序的两个数a 与b 组成的数对,叫做有序数对。 记作(a ,b )
(易错题精选)初中数学函数之平面直角坐标系难题汇编附答案 一、选择题 1.如图,小手盖住的点的坐标可能为( ) A.(-1,1) B.(-1,-1) C.(1,1) D.(1,-1) 【答案】D 【解析】 【详解】 解:根据第四象限的坐标特征,易得小手盖住的点的横坐标为正,纵坐标为负,选项D符合此特征, 故选:D 2.若点P(x,y)在第三象限,且点P到x轴的距离为3,到y轴的距离为2,则点P的坐标是( ) A.(-2,3) B.(-2,-3) C.(2,-3) D.(2,3) 【答案】B 【解析】【分析】根据点P到x轴的距离为3,则这一点的纵坐标是3或-3,到y轴的距离为2,那么它的横坐标是2或-2,再根据点P所处的象限即可确定点P的坐标. 【详解】∵点P到x轴的距离为3, ∴点的纵坐标是3或-3, ∵点P到y轴的距离为2, ∴点的横坐标是2或-2, 又∵点P在第三象限, ∴点P的坐标为:(-2,-3), 故选B. 【点睛】本题考查了点的坐标的几何意义,横坐标的绝对值就是点到y轴的距离,纵坐标的绝对值就是到x轴的距离. 3.在平面直角坐标系内,若点P(3﹣m,m﹣1)在第二象限,那么m的取值范围是 () A.m>1 B.m>3 C.m<1 D.1<m<3 【答案】B 【解析】 【分析】
由第二象限点的横坐标为负数、纵坐标为正数得出关于m 的不等式组,解之可得答案. 【详解】 ∵点P (3﹣m ,m ﹣1)在第二象限, ∴3-010m m ??-?<① >② , 解不等式①,得:m >3, 解不等式②,得:m >1, 则m >3, 故选:B . 【点睛】 本题主要考查象限内点的坐标符号特点及解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键. 4.如图,动点P 从()0,3出发,沿箭头所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角.当点P 第2018次碰到矩形的边时,点P 的坐标为( ) A .()1,4 B .()5,0 C .()7,4 D .()8,3 【答案】C 【解析】 【分析】 理解题意,由反射角与入射角的定义作出图形,观察出反弹6次为一个循环的规律,解答即可. 【详解】 如图, 经过6次反弹后动点回到出发点(0,3), ∵2018÷6=336…2,
用空间向量解立体几何题型与方法 平行垂直问题基础知识 (1) 线面平行: l ∥α? a ⊥u? a ·u =0? a 1a 3+ b 1b 3+c 1c 3= 0 (2) 线面垂直: l ⊥α? a ∥u? a =ku? a 1=ka 3,b 1= kb 3,c 1=kc 3 (3) 面面平行: α∥β? u ∥v? u =kv? a 3=ka 4,b 3=kb 4,c 3=kc 4 (4) 面面垂直: α⊥β? u ⊥v? u ·v = 0? a 3a 4+b 3b 4+c 3c 4=0 例 1、如图所示,在底面是矩形的四棱锥 P-ABCD 中, PA ⊥底面 ABCD , 的中点, PA =AB =1, BC =2. (1) 求证: EF ∥平面 PAB ; (2) 求证:平面 PAD ⊥平面 PDC. [证明] 以 A 为原点, AB ,AD ,AP 所在直线分别为 x 轴,y 轴,z 轴,建立 空 A(0,0,0),B(1,0,0),C(1,2,0), D(0,2,0),P(0,0,1),所以 E 12,1,12 , uuur uuur uuur 1),PD =(0,2,-1),AP =(0,0,1),AD =(0,2,0), uuur ∥AB ,即 EF ∥AB. 又 AB? 平面 PAB , EF? 平面 PAB ,所以 EF ∥平面 PAB. uuur uuur uuur uuur (2)因为 AP ·DC =(0,0,1) (1,0·,0)= 0, AD ·DC =(0,2,0) (1,0·,0)=0, uuur uuur uuur uuur 所以 AP ⊥ DC , AD ⊥ DC ,即 AP ⊥DC ,AD ⊥DC. 又 AP ∩ AD = A ,AP? 平面 PAD ,AD? 平面 PAD ,所以 DC ⊥平面 PAD.因为 DC? 平面 PDC , 直线 l 的方向向量为 a =(a 1,b 1,c 1).平面 α, β的法向量 u = (a 3,b 3,c 3), v =(a 4,b 4,c 4) 1 uuur 1 uuur F 0 , 1, 2 ,EF = -2, 0, 0 ,PB = (1,0, uuur uuur E , F 分别是 PC , PD 间直角坐标系如图所示,则 DC =(1,0,0), AB =(1,0,0). uuur 1uuur uuur (1)因为 EF =- 2AB ,所以 EF
平面直角坐标系动点问题 (一)找规律 1.如图1,一只跳蚤在第一象限及x 轴、y 轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是( ) 图1 A .(4,0) B .(5,0) C .(0,5) D .(5,5) 图2 2、如图2,所有正方形的中心均在坐标原点,且各边与x 轴或y 轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A 1,A 2,A 3,A 4,…表示,则顶点A 55的坐标是( ) A 、(13,13) B 、(﹣13,﹣13) C 、(14,14) D 、(﹣14,﹣14) 3.如图3,在平面直角坐标系中,有若干个横、纵坐标分别为整数的点,其顺序按图中点的坐标分别为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…的规律排列,根据这个规律,第2019个点的横坐标为 . 4.在平面直角坐标系中,一蚂蚁从原点O 出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如下图所示。 图3 (1)填写下列各点的坐标:1A (____,____),3A (____,____),12A (____,____); (2)写出点n A 4的坐标(n 是正整数); (3)指出蚂蚁从点100A 到101A 的移动方向.
5.观察下列有序数对:(3,﹣1)(﹣5,)(7,﹣)(﹣9,)…根据你发现的规律,第100个有序数对是 . 6、观察下列有规律的点的坐标: 依此规律,A 11的坐标为 ,A 12的坐标为 . 7、以0为原点,正东,正北方向为x 轴,y 轴正方向建立平面直角坐标系,一个机器人从原点O 点出发,向正东方向走3米到达A 1点,再向正北方向走6米到达A 2,再向正西方向走9米到达A 3,再向正南方向走12米到达A 4,再向正东方向走15米到达A 5,按此规律走下去,当机器人走到A 6时,A 6的坐标是 . 8、如图,将边长为1的正三角形OAP 沿x 轴正方向连续翻转2019次,点P 依次落在点 201921,,,P P P 的位置,则点2019P 的横坐标为 . 9、如图,在平面直角坐标系上有个点P (1,0),点P 第1次向上跳动1个单位至点P 1(1,1),紧接着第2次向左跳动2个单位至点P 2(﹣1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P 第100次跳动至点P 100的坐标是 .点P 第2019次跳动至点P 2019的坐标是 . 图4 图5 10、如图5,已知A l (1,0),A 2(1,1),A 3(﹣1,1),A 4(﹣1,﹣1),A 5(2,﹣1),….则点A 2019的坐标为 .
向量法解立体几何 立体几何的计算和证明常常涉及到二大问题:一是位置关系,它主要包括线线垂直,线面垂直,线线平行,线面平行;二是度量问题,它主要包括点到线、点到面的距离,线线、线面所成角,面面所成角等。 一、基本工具 1.数量积: cos a b a b θ?= 2.射影公式:向量a 在b 上的射影为 a b b ? 3.直线0Ax By C ++=的法向量为 (),A B ,方向向量为 (),B A - 4.平面的法向量(略) 二、用向量法解空间位置关系 1.平行关系 线线平行?两线的方向向量平行 线面平行?线的方向向量与面的法向量垂直 面面平行?两面的法向量平行 2.垂直关系 线线垂直(共面与异面)?两线的方向向量垂直 线面垂直?线与面的法向量平行 面面垂直?两面的法向量垂直 三、用向量法解空间距离 1.点点距离
点()111,,P x y z 与()222,,Q x y z 的 距离为PQ =u u u r 2.点线距离 求点()00,P x y 到直线:l 0Ax By C ++=的距离: 方法:在直线上取一点(),Q x y , 则向量PQ u u u r 在法向量(),n A B =上的射影 PQ n n ?u u u r = 即为点P 到l 的距离. 3.点面距离 求点()00,P x y 到平面α的距离: 方法:在平面α上去一点(),Q x y ,得向量PQ u u u r , 计算平面α的法向量n , 计算PQ u u u r 在α上的射影,即为点P 到面α的距离. 四、用向量法解空间角 1.线线夹角(共面与异面) 线线夹角?两线的方向向量的夹角或夹角的补角 2.线面夹角 求线面夹角的步骤: ① 先求线的方向向量与面的法向量的夹角,若为锐角角即可,若为钝角,则取其补角; ②再求其余角,即是线面的夹角. 3.面面夹角(二面角) 若两面的法向量一进一出,则二面角等于两法向量的夹角;法
培优训练三:平面直角坐标系(压轴题) 一、坐标与面积: 【例1】如图,在平面直角坐标中,A(0,1),B(2,0),C(2,1.5). (1)求△ABC的面积; (2)如果在第二象限内有一点P(a,0.5),试用a的式子表示四边形ABOP的面积; (3)在(2)的条件下,是否存在这样的点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由. 【例2】在平面直角坐标系中,已知A(-3,0),B(-2,-2),将线段AB平移至线段CD. 图2 (1)如图1,直接写出图中相等的线段,平行的线段; (2)如图2,若线段AB移动到CD,C、D两点恰好都在坐标轴上,求C、D的坐标;(3)若点C在y轴的正半轴上,点D在第一象限内,且S△ACD=5,求C、D的坐标;
(4)在y 轴上是否存在一点P ,使线段AB 平移至线段PQ 时,由A 、B 、P 、Q 构成的四边形是平行四边形面积为10,若存在,求出P 、Q 的坐标,若不存在,说明理由; 【例3】如图,△ABC 的三个顶点位置分别是A (1,0),B (-2,3),C (-3,0). (1)求△ABC 的面积; (2)若把△ABC 向下平移2个单位长度,再向右平移3个单位长度,得到△A B C ''',请你在图中画出△A B C '''; (3)若点A 、C 的位置不变,当点P 在y 轴上什么位置时,使2ACP ABC S S =V V ; (4)若点B 、C 的位置不变,当点Q 在x 轴上什么位置时,使2BCQ ABC S S =V V . 【例4】如图1,在平面直角坐标系中,A (a ,0),C (b ,2),且满足2(2)20a b ++-=,过C 作CB ⊥x 轴于B .
空间向量与立体几何 一、知识网络: 二.考纲要求: (1)空间向量及其运算 ① 经历向量及其运算由平面向空间推广的过程; ② 了解空间向量的概念,了解空间向量的基本定理及其意义,掌握空间向量的正交分解及其坐标表示; ③ 掌握空间向量的线性运算及其坐标表示; ④ 掌握空间向量的数量积及其坐标表示,能运用向量的数量积判断向量的共线与垂直。 (2)空间向量的应用 ① 理解直线的方向向量与平面的法向量; ② 能用向量语言表述线线、线面、面面的垂直、平行关系; ③ 能用向量方法证明有关线、面位置关系的一些定理(包括三垂线定理); ④ 能用向量方法解决线线、线面、面面的夹角的计算问题,体会向量方法在研究几何问题中的作用。 三、命题走向 本章内容主要涉及空间向量的坐标及运算、空间向量的应用。本章是立体几何的核心内容,高考对本章的考查形式为:以客观题形式考查空间向量的概念和运算,结合主观题借助空间向量求夹角和距离。 预测10年高考对本章内容的考查将侧重于向量的应用,尤其是求夹角、求距离,教
材上淡化了利用空间关系找角、找距离这方面的讲解,加大了向量的应用,因此作为立体几何解答题,用向量法处理角和距离将是主要方法,在复习时应加大这方面的训练力度。 第一课时 空间向量及其运算 一、复习目标:1.理解空间向量的概念;掌握空间向量的加法、减法和数乘; 2.了解空间向量的基本定理; 3.掌握空间向量的数量积的定义及其性质;理解空间向量的夹角的概念;掌握空间向量的数量积的概念、性质和运算律;了解空间向量的数量积的几何意义;能用向量的数量积判断向量的共线与垂直。 二、重难点:理解空间向量的概念;掌握空间向量的运算方法 三、教学方法:探析类比归纳,讲练结合 四、教学过程 (一)、谈最新考纲要求及新课标高考命题考查情况,促使积极参与。 学生阅读复资P128页,教师点评,增强目标和参与意识。 (二)、知识梳理,方法定位。(学生完成复资P128页填空题,教师准对问题讲评)。 1.空间向量的概念 向量:在空间,我们把具有大小和方向的量叫做向量。如位移、速度、力等。 相等向量:长度相等且方向相同的向量叫做相等向量。 表示方法:用有向线段表示,并且同向且等长的有向线段表示同一向量或相等的向量。 说明:①由相等向量的概念可知,一个向量在空间平移到任何位置,仍与原来的向量相等,用同向且等长的有向线段表示;②平面向量仅限于研究同一平面内的平移,而空间向量研究的是空间的平移。 ②向量加法的平行四边形法则在空间仍成立。 3.平行向量(共线向量):如果表示空间向量的有向线段所在的直线互相平行或重合, 则这些向量叫做共线向量或平行向量。a 平行于b 记作a ∥b 。 注意:当我们说a 、b 共线时,对应的有向线段所在直线可能是同一直线,也可能是平 行直线;当我们说a 、b 平行时,也具有同样的意义。 共线向量定理:对空间任意两个向量a (a ≠)、b ,a ∥b 的充要条件是存在实数λ使b =λa (1)对于确定的λ和a ,b =λa 表示空间与a 平行或共线,长度为 |λa |,当λ>0时与
建立空间直角坐标系,解立体几何高考题 立体几何重点、热点: 求线段的长度、求点到平面的距离、求直线与平面所成的夹角、求两异面直线的夹角、求二面角、证明平行关系和垂直关系等. 常用公式: 1 、求线段的长度: 222z y x AB ++==()()()2 12212212z z y y x x -+-+-= 2、求P 点到平面α的距离: PN = ,(N 为垂足,M 为斜足,为平面α的法向量) 3、求直线l 与平面α所成的角:|||||sin |n PM ?= θ,(l PM ?,α∈M ,为α的法向量) 4、求两异面直线AB 与CD 的夹角:cos = θ 5、求二面角的平面角θ:|||||cos |21n n ?= θ,( 1n ,2n 为二面角的两个面的法向量) 6、求二面角的平面角θ:S S 射影 = θ cos ,(射影面积法) 7、求法向量:①找;②求:设, 为平面α内的任意两个向量,)1,,(y x =为α的法向量, 则由方程组?????=?=?0 n b n a ,可求得法向量.