
应变张量
变形
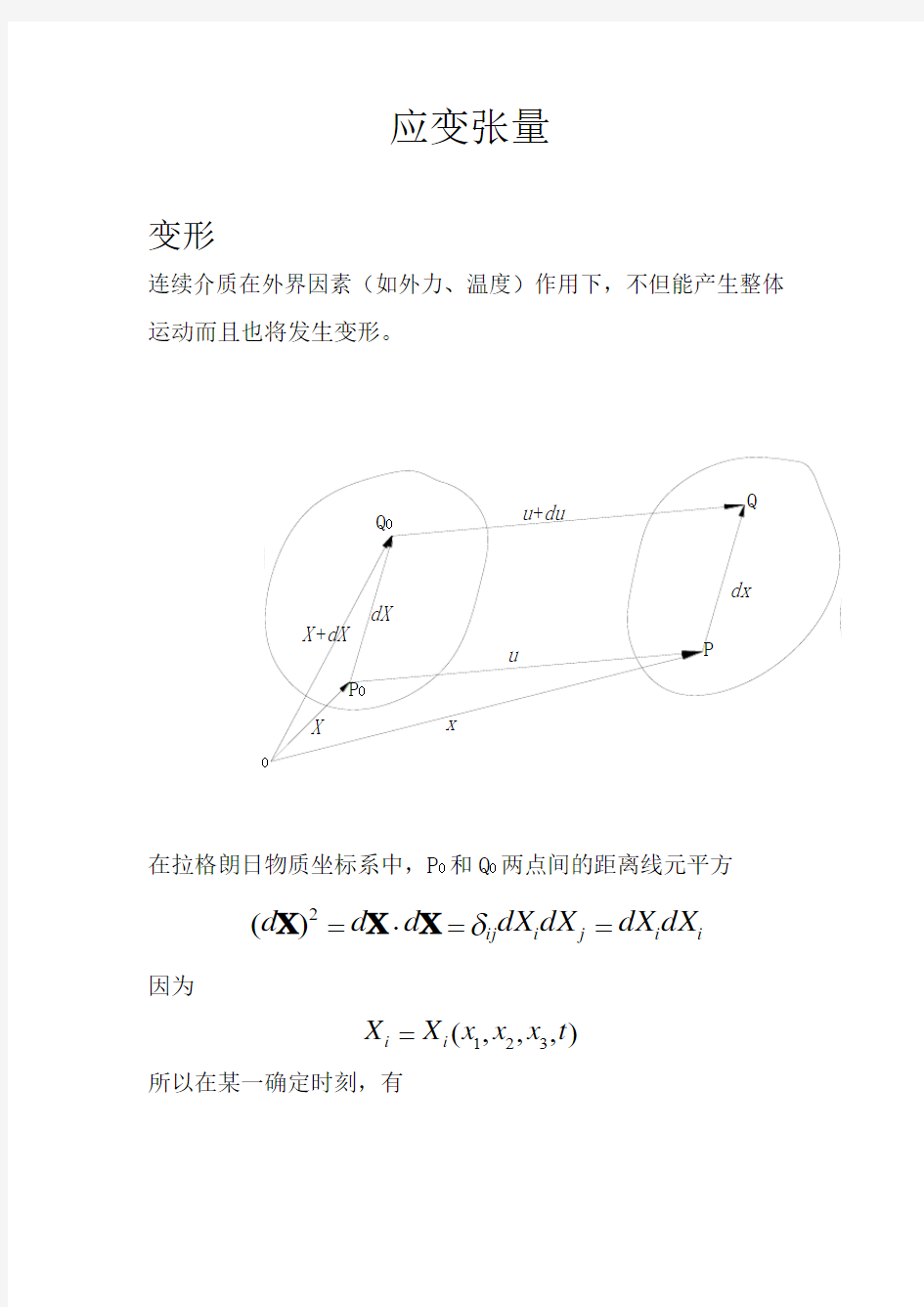
连续介质在外界因素(如外力、温度)作用下,不但能产生整体运动而且也将发生变形。
在拉格朗日物质坐标系中,P 0和Q 0两点间的距离线元平方
i i j i ij dX dX dX dX d d d ==?=δX X X 2)(
因为
),,,(321t x x x X X i i =
所以在某一确定时刻,有
j j
i
i dx x X dX ??=
写成不变性形式
x H X d d ?=
其中j i j
i x e e x X ??=?=X H 。于是
j i ij j i j
k
i k k k dx dx C dx dx x X x X dX dX d =????==2
)(X (2.7a )
x C x X d d d ??=2
)((2.7b )
其中
j
k
i k ij x X x X C ????=
(2.7c )
H H C T ?=(2.7d)
我们称它为柯西变形张量。
类似的在欧拉空间坐标系中,P 和Q 两点线元平方
j i ij dX dX G d =2)(x (2.9a )
不变形式
X G X x d d d ??=2)((2.9b)
其中
j k
i k ij X x X x G ????=
(2.9c )
F F
G T ?=(2.9d)
我们称为格林变形张量。
对于连续介质,我们用相邻两个物质点的距离线元的平方差
22)()(X x d d -来度量其变现。那么
X
E X X x d d dX dX E dX dX X x X x d d j i ij j
i ij j
k
i k ??==-????=-22)(
)()(22δ(2.10a)
或者
x
e x X x d d dx dx e dx dx x X x X d d j i ij j
i j
k
i k ij ??==????-
=-22)()()(22δ(2.10b)
其中
)(21ij j
k
i k ij X x X x E δ-????=(2.10c )
称为拉格朗日有限变形张量或格林有限变形张量,
)`(21j
k
i k ij ij x X x X e ????-=δ(2.10d )
称为欧拉有限变形张量或阿尔曼西有限变形张量。 由图
i i i X x u -=(2.11)
对于拉格朗日物质坐标系
ij j
i
j i j i j i X x X X X x X u δ-??=??-??=?? 则
j i
ij j i X u X x ??+=??δ(2.12a )
同样对于欧拉空间坐标系
j i
ij j i x u x X ??-=??δ(2.12b )
把式(2.12a )和式(2.12b )中的j
i
X x ??和
j
i x X ??分别代入式(2.10c )
和(2.10d )得到:
)(21j
k
i k i j j i ij X u X u X u X u E ????+??+??=(2.13a)
)(21j
k
i k i j j i ij x u x u x u x u e ????-??+??=(1.13b)
拉格朗日有限变形张量表征物质点P 0的领域的变形。在一些实际问题中(例如弹性固体的小变形问题),连续介质发生变形时,位移梯度分量
j
i
X u ??和
j
i x u ??的大小与1相比都是高阶小量。因此,
在线性连续介质理论中可以把j
k i k X u X u ????和
j
k i k x u x u ????中的非线性项和
略去不计。那么可得到无限小应变张量:
)(21i j
j i ij X u X u E ??+??=(2.14a )
)(21i
j j i
ij x u x u e ??+??=(2.14b )
它们常被称为拉格朗日应变张量和欧拉应变张量。写成不变形式:
)(21
X X ?+?=u u E (2.14c )
)(2
1
x x ?+?=u u e (2.14d )
矩阵形式
[]??
??
????
???????
?
??????+????+????+??????+????+????+????=33
1
3321
33113322
212
2113311
2
211
1)(21)(21)(21)
(21)(21)(21X u X u X u X u X u X u X u X u X u X u X u X u X u X u X u E (2.14e) []??
??
????
???????
?
??????+????+????+??????+????+????+????=33
1
3321
33113322
212
2113311
2211
1)(21)(21)(21)
(21)(21)(21x u x u x u x u x u x u x u x u x u x u x u x u x u x u x u e (2.14f) 在小变形弹性理论中,由于x 与X 差别很小,通常认为x=X ,
j
i
j i x u X u ??=??。这样,我们就没有必要再去区分拉格朗日应变张量和
欧拉应变张量,统称为应变张量。
首先考察主对角线元素。设线元i i ds d e X =,这里ds 为线元的长度,i e 为i d X 方向内的单位矢量。*ds 代表i d X 变形后i d x 长度,于是
i i i i i
i ds ds
d ds d ds d d ds ds
e E e X
E X X E X ??=??=??=-*22
22)(2)(22)()((2.15a ) 对于小变形
)
(2)
)(()()(22ds ds ds ds ds ds ds ds ds -≈-+=-*
***(2.15b )
于是
i i ds
ds
ds e E e ??=-* (2.16) 上式表明,关于线元每单位长度上的长度变化可由应变张量E 度量。比如:
1
1
1111X u E ??=
=??e E e (2.17) 它表示线元1X d 的单位伸长率,也称为沿1X 方向的法向应变。 再考察非对角线元素的几何意义。令i i i ds d e X =,于是:
2
121122121212cos X E X e e X X x x 2
1d d ds ds ds ds d d d d ??=?-=?-?*
*θ(2.18a)
即
212112212cos e E e ??=*
*ds ds ds ds θ (2.18b)
若令1212-2
γπ
θ=
,则称12γ为剪切应变,它可以用来度量1X d 和
2X d 间的夹角的微小减少量。因为:
121212sin )-2
cos(
cos γγπ
θ==
由于小变形情况
12
γ<<1,因而1212sin γγ≈,111≈*
ds ,
122≈*
ds ds ,故
12211222E =??=e E e γ(2.19a)
即 12122
1
γ=E
由此可见,12E 表示原来在1X 和2X 方向内的两个线微元之间夹角的减少量之半。综上所述,应变张量矩阵[E]的主对角线元素表示连续介质内某一点附近的法向应变,而非对角线元素则表示其剪切应变。
主应变
应变张量的第一不变量I 1的几何意义。
dV
dV e E E E E I ii )
(1312111?==++==(2.22a)
这里e 表示单位体积的体积变化率,称之为膨胀系数(膨胀率),有时也成为体积应变。
应力矢量、应力张量
在连续介质力学中重要的公理之一就是关于接触力形式的柯西假设。柯西假设在运动过程中的时刻t 对于任何物质坐标X 和与之对应的接触面S 上的单位法矢量n ,表面力的存在形式为:
),,(n X t t t =(3.1)
为了研究物体内部一点P 的应力状态,设想在P 的附近给定一个单位法矢量为
),,()cos ,cos ,(cos 32321n e n e n e n 1???==ααα(3.3)
的平截面。如图
e 设在ABC 上受到的作用力为A Δt ,在PBC ,PCA ,PAB 上的作用力分别为11ΔA t -、22ΔA t -、33ΔA t -,作用于微小四面体ABCP 上单位质量的体力为b 。
对于微小四面体ABCP ,柯西定律给出
a a a
b t t b t t b t t t t A h V m A
h A A V A A V A A A A i i i i Δ3
1
ΔΔΔ3
1
cos ΔΔΔΔΔΔΔΔΔΔ332211ρρραρρ===+-=+-=+---(3.4)
即
a b t t A h A h A A i i Δ3
1
Δ31cos ΔΔρρα=+-
a b t t h h i i ρρα3
1
31cos =+-(3.5)
当微小四面体体积趋于零时,即0Δ→A ,0→h ,则有
i i αcos t t =(3.6)
考虑到式(3.3),并令
i ij i i i i T T T T e e e e t =++=332211(3.7)
则式(3.6)可写成
n
T n e e e e T
n e e n e e n t t T i j j i j i j i i ?=?=?==?=?=??==)())((cos )())((cos ij ij i i ij ij i T n T t T T αα(3.8a ) 当T 对称时,则
n T T n t ?=?=(3.8b )
j i e e T ij T =(3.9a )
称为应力张量,其矩阵形式
[]????
?
?????=333231232221131211T T T T T T T T T T (3.9b)
如果物体中一点处的应力张量已知,那么由式(3.8)可以得到通过该点的任何截面上的应力矢量,因此应力张量完全地刻画了物体中一点的应力状态。
质量守恒定律
设ρ为物体的密度,dV 表示物质质点的体积,由于在运动过程中质量体积保持不变,所以
0)(=dV Dt
D
ρ (3.11a) 展开
0)(=+dV Dt
D dV Dt D ρρ (3.11b) 又由(2.32)
dV
div dV x v dV Dt D i
i )()(v =??= 于是(3.11b )可写为
=??+i
i
x v Dt D ρρ (3.12a) 其不变形式
=+v div Dt
D ρρ
(3.12b) 其中
ρρ
ρρρΔ?+??=??+??=v t
x v t Dt D i i (3.13)
把上式代入式(3.12a )
0)
(=??+??=??+??+??=??+x
v t x v x v t x v Dt D i i
i i i i i ρρρρρρρ(3.14a)
其不变形式
0)(=+??v ρρ
div t
(3.14b ) 式(3.12)和式(3.14)就是质量守恒定律的数学表达式——质量守恒方程,在连续介质力学中常称为连续性方程。
动量平衡定律
欧拉第一运动定律:D Dt
=m
f (3.17) 上式说明任意物体具有m 的动量的变化率等于作用于物体
上的合力f 。
设所研究物体在其体积V 上受有连续分布的体力b f 和在其体积的边界面S 上连续分布的接触力c f ,因此在物体上所受合力为
b c =+f f f (3.18a )
其中
b v dV
ρ=?f b (3.18b )b 是每单位质量的体力
c v dS =?f t (3.18c )
物体的动量为
v D dV dV
Dt
ρρ==??x
m v (3.19)
于是将式(3.18)和式(3.19)代入式(3.17)则
v
s v dV dS dV
ρρ=+?
??a t b (3.20)
其中22D Dt
=x
a 表示点x 的加速度。由式(3.8),可将上式改写成
S
v v dS dV dV ρρ+=?
??n T b a
利用高斯公式
S
v dS dV
=??
?n T T
则得
v
v v dV dV dV ρρ?+=?
??T b a
即
()0v
dV ρρ?+-=?
T b a
考虑到V 的任意性,则
0ρρ?+-=T b a
即
div ρρ+=T b a (3.21a )
上式称为柯西第一运动定律。其指标形式
,ji i i i T b a ρρ+=(3.21b )
展开得
31
112111123
32
122222123
132333
33123
T T T b a x x x T T T b a x x x T T T b a x x x ρρρρρρ???+++=??????+++=??????+++=???(3.21c )
特别的,在静止的情况下,物体的加速度为零,则式(3.21a )化为
0div ρ+=T b (3.22)
在弹性力学中,上式称为平衡方程。
动量矩平衡定律
对于任意物体下列关系是成立:
00
x x Dt
D l M =(3.24)
x M 其中表示物体绕0x 点的动量矩,表示作用于物体上的力对点0x 的合力矩。上式称为欧拉第二运动定律。
设作用于物体上的力矩只是由体力和接触力引起的,故其合力矩为
dS dV S V x t x x b x x l 00?-+?-=??)()(0ρ(3.25)
而物体的动量矩为
dV Dt
D V x x
x x M 0?-=?)(0
ρ(3.26)
将式(3.25)和式(3.26)代入式(3.24),并考虑到
dV
Dt D V d Dt
D Dt D dV Dt D dV Dt D Dt D V d Dt D Dt D dV Dt D dV Dt D Dt D dV Dt
D Dt D V V V V V V V V 222222)()
()()()
()()()()(x
x x x x x x x x x x x x x x x x x x x x
x x 0000000?-=?-+?-+?=?-+?-+?-=?-????????ρρρρρρρρ可得
dS
dV dV S V V
t x x b x x a x x 000?-+?-=?-???
)()()(ρρ(3.27)
其中22Dt
D x
a =表示点
x 的加速度。考虑到式(3.8)和高斯公式,则
x l
[][]{}[]{}{}{}0
))(()()())(()())(()())(()()()()()()()()()()()()()()(,000,00000=∈=∈=+-+-∈=-?+-+--∈=-?+--∈=∈-?---∈=-???-??-=-??-??-=?--??-+?-=?--?-+?-???????????????dV T dV T dV T a b T x x dV x x T x x T a b x x dV
x x T a b x x dV x x T a b x x dV
a dS dV a dV dS dV dV
dS dV ij ijk
V
il ij ljk V il
ij i
j
i
ij l
l
ljk V l
l
i
ij
l
l
i
ij i
j
l
l
ljk V l
l
ij
i
i j l l ljk V jlk
l
l
ij
i
i
j
l
l
ljk
V V S
V V
S
V V
S
V
k
k k
k k k
k
00
00
e e e e e e e x x T b x x x x T n b x x a x x T n x x b x x a x x t x x b x x δδρρρρρρρρρρρ考虑到体积的任意性,得
0=∈ij ijk T
因此,必为对称张量,即
ji ij T T =(3.28a)
或
T
T
T =(3.29a)
上式叫做柯西第二运动定律。柯西第二运动定律限定应力张量为对称张量,其中只有六个独立的分量。
ij T
能量守恒定律
在连续介质中,如果只研究力学量的影响,而不考虑热学效应,那么连续介质的能量守恒定律可以直接由运动方程导出。首先,将运动方程
Dt D v
b T ρ
ρ=+??
点乘速度矢量
Dt D v
v b T v ?
=+???ρρ)(
在体积V 上积分
dV
dV dV Dt D V V V b v T v v
v ?+???=????ρρ)(
考虑到
Dt
DK dV v Dt D dV Dt D dV Dt D dV Dt D dV
Dt D dV Dt D V V V V V V ==?=?-?=?=???????222)
(21)2()21
(ρρρρρρv v v v v v v v v v
上式表示在体积V 中的总动能dV v K V 2
2ρ
?=的时间变化率。
另外,考虑到
T
D v T T
W T D v T T W D v T T v v T T v :)(::)(:)()(:)()()()(;,;-???=--???=+-???=?-???=-==???ij i j i ij j i
ij j T v T v T v
这里利用了反对称张量W 与对称张量T 之间的双重点积为零的
性质。
吧式(3.31)和式(3.32)代会到式(3.30)中去,则得
dV dV dV Dt
DK
V V V b v T v T D ?+???=+???ρ)(:
运用高斯公式把上式右边的第一个体积分化为面积分,并李永华
柯西假设T n t ?=,则
dS dS dV S S V
v t T n T v ?=???=??????
)()(
将上式代入式(3.33),于是我们得到纯力学的能量方程
dV dV dV Dt
DK
V V V b v v t T D ?+?=+???ρ:
其中方程左边两项分别表示连续介质的动能和内能的时间变化率,右边两项分别表示接触力和体力所做的功率。若令U 表示内能,则能量方程(3.35)也可简洁地写成
Dt
W
D Dt DU Dt DK =+
其中
表示接触力和体力的功率,记号表示这个量不一定能
写成某个函数的全微分形式。
Dt
W
D
<连续介质力学> QM 复习提纲(2010.12) 一、基本要求 1、掌握自由指标与哑指标的判别方法及表达式按指标展开; 2、掌握ij 与ijk e 的定义、性质及相互关系; 3、掌握二阶张量坐标转换的计算; 4、掌握二阶张量特征值、特征向量与三个不变量的计算方法; 5、掌握哈密顿微分算子及其基本计算; 6、掌握小变形应变张量、转动张量及转动向量的计算; 7、掌握正应变的计算; 8、掌握正应力、剪应力及应力向量的计算; 9、掌握应力张量与应变张量的对称性; 10、掌握能量密度及能通量密度向量的计算; 11、掌握各向同性线弹性体的广义胡克定律的两种形式; 12、掌握应力张量与体积膨胀率的关系; 13、掌握各向同性线弹性体的应变能密度函数; 14、会对材料的各个弹性参数之间的关系进行相互推导; 15、掌握从质点的运动方程推导Navier 方程的过程; 16、掌握从质点的运动方程出发推导纵横波的方程的过程; 17、掌握地震波速度与泊松比的关系; 18、掌握非均匀平面简谐波的传播特征; 19、掌握P 波、SV 波入射到自由界面上的传播特征; 20、掌握利用自由界面边界条件确定反射系数和反射波位移场的方法; 21、掌握Reilaygh 波和Stonely 波的传播特征; 22、掌握P 波入射到两种弹性体接触面上的反射系数和透射系数的计算方法; 二、复习题 简答论述题 1、试解释“连续介质”所必须满足的条件。 2、简述弹性动力学基本假设。 3、说明应力、应变、正应力、正应变、剪应力及剪应变的含义。 4、说明杨氏模量、泊松比、体积模量与剪切模量的物理含义。 5、简述小变形应变张量的几何解释。
发信人: Rubik (韦小宝@好事多磨), 信区: Mathematics 标题: 个人体会-如何学习《连续介质力学》-基本概念zz 发信站: 吉林大学牡丹园站(2008年04月07日00:04:04 星期一), 站内信件 作者为baibing@SimWe 连续介质力学,也叫连续统理论,或者叫理性力学。叫连续介质力学,是因为他的框 架内一个最重要得假设是“介质是宏观连续的”,可以用连续的数学理论来处理,显 然这种命名方法带有物理,力学的的痕迹。 叫连续统理论,实际上是借用了数学上的概念。学数学的人都知道,数学中就有“连 续统”的概念,比如,连续的线段,连续的曲面,和连续的体。由于数学上这些概念 都是抽象出来的,没有物理意义的,可以叫连续统。很多人不知道连续统,连续介质 ,我想实际上可以理解为不同学科的不同称呼。但是,说连续介质,实际上表示考虑了具体物理特性的连续统。 叫理性力学,实际上是从力学研究的方法论上来命名的。以那种理性的,数学化的, 公理化的思维和方法来研究力学。看过连续介质力学书籍的人应该是深有体会的。里 面到处充满这理性的思维的魅力。 说明:本人2004年在中国科学院研究生院学习了王文标教授的《连续介质力学基础》课程。这是本人一年后的感悟,欢迎我得同学一同加入进来讨论。 不知道从什么时候开始,我养成了一个习惯,那就是每接触一个新的学科,总是希望 获得这门学科最权威而且是最经典,最全面的书籍。当然这样的书籍是找不到的。但是,相对而样比较好的书籍还是有的,力学更是这样。 《非线性连续统力学》,北航出版社,李松年,黄执中的作品,80年代中期写的。这本书我第一次看到的时候,惊为天人所写,前半部分写的是张量分析,后面是连续统 力学,两方面都比一般的连续介质力学全面,而且讲解浅显易懂。特别是其前言和结语写的尤为出色,不仅概括了这门学科的梗概,而且指出了这门学科的前景,真是绝 佳的资料。 A.C.ERIGEN的《连续统力学》,这是我目前见到的最经典的书,实际上前面一本书很大一部分是参考了这本书编写的,当然,加入了自己的内容(这是我读后才知道的) 。这一点都不奇怪, A.C.ERIGEN是连续统力学的鼻祖人物,也是集大成者。和钱伟长先生关系很好。 英国东英格兰大学的查德威克先生写的《连续介质力学简明理论和例题》,虽然这本书只有短短一百多页,但是用逼一般力学书籍夺得数学,比数学书籍少得多的数学非 常准确地阐释了连续介质力学理论,尤其是和数学地结合方面,能够让你从本质上, 从数学的角度认识和理解连续介质力学。而且有大量的习题。 陈志达先生的《理性力学》。大家都知道陈志达先生吧,中国矿业大学的老师,98年
关于损伤力学的建议与看法 在别的论坛看到关于损伤力学的讨论,想起来几年前毕业的一位师兄在其论文中对损伤力学的讨论,现在发出来大家探讨一下 原文如下: 1.3 材料疲劳分析的损伤力学方法 目前,对汽轮机转子破坏过程的研究,基本采用的是线弹性断裂力学方法,其研究的是转子结构中具有明确几何边界的宏观裂纹问题。它从整体出发,对裂纹前沿的应力、应变、位移和能量场的分析,以确定控制裂纹行为的力学参数,来实现对裂纹扩展和转子安全性进行预测。而对裂纹萌生的宏观位置往往根据经验进行人为的假定。 事实上,实际转子服役过程中裂纹的萌生寿命往往很长,有的占总寿命的80%~90%。在这个阶段,材料内部微细观结构逐渐劣化,并逐步发展成为宏观裂纹[25,26,27],况且有些损伤现象并不导致断裂力学所描述的临界开裂,而且崩溃、失稳等。因此,对上述转子损伤现象进行定量的数学描述,对于转子结构的裂纹萌生及寿命预估是非常重要的。也是断裂力学无法解决的。目前,对于无裂纹转子虽能大致估计其致裂寿命,但不能定量描述裂纹的形成发展过程及确切位置和形貌,而且由于往往采用线性损伤累积理论,不能正确地反映转子材料的实际损伤发展情况,因此,其分析结果往往与实际偏差较大。 近三十年发展起来的连续介质损伤力学[28],它采用唯象学方法,引入表征损伤的内部状态变量,将损伤纳入热力学框架,重点研究微观缺陷对材料宏观整体平均力学特性的影响,因此,用损伤力学理论导得的结果,既能反映材料微观结构的变化,又能说明材料宏观力学性能的实际变化情况。可用于分析微裂纹的演化,宏观裂纹形成直至构件的完全破坏的整个过程,弥补了微观研究和断裂力学研究的不足。因此,损伤力学对于研究汽轮机转子结构在各种载荷环境条件下的灾变事故的产生和发展,进而对其进行复现与防治,有着极其重要的意义。 1.3.1 损伤力学发展概况 损伤力学的发端被公认为是1958年Kachanov 在研究金属蠕变时所做的工作,他在当时提出了连续性因子与有效应力的概念,并利用后者给出了前者的演化方程。1963年Rabotnov又定义了损伤因子的概念。在其后的一二十年当中,以Lemaitre,Chaboche,Hult,Lechie,Krajcinovic,Rousselier等为代表的一批学者,针对损伤力学的基本概念、方法等做了大量开创性的工作,这不仅使其框架渐渐明晰充实,而且还把它的适用领域从最初的蠕变分析,推广到对于弹性、塑性、粘塑性、脆性及疲劳等损伤现象的分析[29,30,31];而其所描述的材料,也从金属扩展到复合材料、陶瓷、混凝土等非(纯)金属材料。由于损伤力学已表现出可观的理论价值与应用前景,这使其逐步上升为固体力学的一个新兴分支,并已成为目前国内外力学界所关注的一个十分活跃的研究领域。 然而,从损伤力学发展的现状来看,其相当一部分工作是关于基本理论的,而关于损伤力学算法的研究则显得相对薄弱。目前,关于构件损伤分析的算例,一部分是针对简单受力情形的(如控制应力或控制应变的一维拉伸或纯剪),而对于复杂的问题则采用的是损伤耦合的有限元法。对含裂纹体的损伤力学分析也是该领域中特别引人注目的一个专题。已有的一些工作表明:无论是对于蠕变、塑性、脆性,还是对于疲劳,计及损伤的裂纹性质都显著有别于经典断裂力学中的理想情形。 这些工作虽然已将损伤力学从理论研究向实际应用朝前推进了一大步,但已有的进展还显得不够充分,尚有待于人们进一步的努力。 1.3.2损伤力学研究方法 用损伤力学方法对材料的力学特性进行研究,首先要对材料变形过程进行宏观和微观的实验观察,根据材料损伤演变的微观现象及其宏观表现,采用唯象方法,选择适当的损伤参数,作为本构关系中的内变量建立方程。如何建立能够正确反映材料的损伤本质的损伤演化方程,是未来工作的核心。 ----------------------------------------------------------------------------------- 请问损伤力学如何学习? 前面有热力学的东西,头都大了! 张量也很令人费解! 有没有大侠指一条明路,谢谢!
连续介质力学基础 物质坐标和空间坐标 对于有限个质点组成的质点系统,我们可以采用给质点编号的方式区分各个质点;对于有无限个质点组成的系统,我们就采用坐标识别系统中各个质点。用于标示质点的坐标称为物质坐标132(,,)ξξξ;表示空间中几何点的坐标312(,,)x x x 则称为欧拉坐标。 两种坐标是通过连续介质的运动联系起来的:如果在时刻t 质点132(,,)ξξξ占据空间位置312(,,)x x x ,则二者之间具有函数关系: 123(,,,)k k x x t ξξξ= 由于这个函数必须是一一影射的,其反函数存在并且唯一: 123(,,,) k k x x x t ξξ= 因此,质点的位置矢量、速度等都可以等价地用物质坐标或空间坐标描述: (,)((),)t t =r ξr ξx 当我们采用物质坐标时,相应的基矢量: i i ?ξ ?=?r g 当我们采用空间(Euler )坐标时,相应的基矢量: i i x ?= ?r g 两者之间具有转换关系: k k i k i k i i x x ?x ξξξ ????===????r r g g j j m m ?x ξ?=?g g k k i k i i k i ?x x x ξξξ????===????r r g g j j m m x ?ξ ?=?g g 物质导数 质点的速度: D D k k k k (,t )()x (,t )v t t x t ???==???r r ξr x ξv g 算子D D t 称为物质导数(全导数)。它的含义是保持物质坐标不变时,张量随时间的变
化率。 Euler 坐标基底矢量的物质导数: k k m i i ik m k D v v Dt x ?==Γ?g g g i i k k i m mk k D v v Dt x ?==-Γ?g g g 物质坐标(Langrange )基底矢量的物质导数: ?(,)()i i D t Dt t ξ ??=??g r ξ 欧氏空间中矢量求偏导数的顺序是可以交换的,因此 ?(,)()i i i D t Dt t ξξ ???==???g r ξv 利用协变基与逆变基之间的关系,我们得到: () m i i i m ?D ????Dt ξ ?=??=???g v g g v g () m i i i m ?D ????Dt ξ ?=??=???g v g g g v Langrange 逆变基底矢量的物质导数可以由逆变基的定义式 j j i i ??δ?=g g 求得。显而易见: ??()0i m D Dt ?=g g 因此 i m i i m m ??D D ???Dt Dt ξ ??=-?=-??g g v g g g 该式左端是逆变基物质导数在协变基下的分量,因而 ????()???i i m i m m i i m D Dt ξ ξ ?=-??=-????=-??=-???g v g g g v v g g v g (物质坐标基底矢量的物质导数可表示为速度梯度与基矢量的点积;协变基的导数与哈密顿算子相邻;逆变基的导数与负的速度矢量相邻)
力学学科分类---力学是从物理学中独立出来的一个分支学科 力学分类 力学是研究物质机械运动的科学。机械运动亦即力学运动,是物质在时间、空间中的集团变化,包括移动、转动、流动、变形、振动、波动、扩散等。力学原是物理学的一个分支学科,当物理学摆脱了机械(力学) 的自然观而获得进一步发展时,力学则在人类生产和工程技术的推动下按自身逻辑进一步演化和发展,而从物理学中独立出来。它既是探索自然界一般规律的基础科学,又是一门为工程服务的技术科学,担负认识自然和改造自然的任务。力学的研究对象是以天然的或人工的宏观的物质机械运动为主。但由于本学科自身的发展和完善以及现代科技发展所促成的学科的相互渗透,有时力学也涉及微观各层次中的对象及其运动规律的研究。机械运动是物质的最基本的运动形式,但还不能脱离其他运动(热、电磁、原子、分子运动及化学运动等) 形式而独立存在,只是在研究力学问题时突出地甚至单独地考虑机械运动形式而已。如果需要考虑不同运动之间的相互作用,则力学与其他学科之间形成交叉学科或边缘学科。力学产生很早, 古希腊的阿基米德(约公元前287 —212) 是静力学的奠基人。在欧洲文艺复兴运动以后,人们对力和运动之间的关系逐渐有了正确的认识。英国科学家牛顿继承和发展了前人的研究成果,提出了物体运动三定律,标志着力学开始成为一门科学。到了20 世纪,力学更得到蓬勃的发展。到目前为止,已形成了几十个分支学科,诸如一般力学、固体力学、结构力学、物理力学、流体力学、空气动力学、流变学、爆炸力学、计算力学、连续介质力学、应用力学、岩土力学、电磁流体力学、生物力学,等等。为了充分发挥这些力学文献的作用,必须对其进行科学的分类。本文拟对力学文献的分类标准、分类体系和分类方法进行研究。 一、力学文献的分类标准 根据力学文献的属性,其分类标准很多,但根据读者(用户) 的检索需求和文献分类法的立类列类原则,主要采用以下9 种标准: 1.1 根据研究对象分 根据研究各种物体不同的运动,力学就形成了不同的分类。例如:当物体是液体或气体时,就是流体力学;当物体是固体时,就是固体力学;当研究固体在外界加力影响下,内部的变形和应力状态,以及它受力的性能时,就是弹塑性力学;当研究物体的整体运动的时候,而不去仔细考虑物体每一部分的情况便是一般力学。 1.2 根据研究方法分 根据研究方法,力学可以分为实验力学、理论力学、物理力学、理性力学和计算力学等。1.3 根据研究的时代分 根据研究的时代,力学可以分为经典力学和近代力学。从牛顿至哈密顿的理论体系称为经典
张量 张量是用来描述矢量、标量和其他张量之间线性 关系的几何对象。这种关系最基本的例子就是点积、 叉积和线性映射。矢量和标量本身也是张量。张量可 以用多维数值阵列来表示。张量的阶(也称度或秩) 表示阵列的维度,也表示标记阵列元素的指标值。例 如,线性映射可以用二位阵列--矩阵来表示,因此该 阵列是一个二阶张量。矢量可以通过一维阵列表示, 所以其是一阶张量。标量是单一数值,它是0阶张量。 张量可以描述几何向量集合之间的对应关系。例 如,柯西应力张量T 以v 方向为起点,在垂直于v 终点方向产生应力张量T(v),因此,张量表示了这两个 向量之间的关系,如右图所示。 因为张量表示了矢量之间的关系,所以张量必 须避免坐标系出现特殊情况这一问题。取一组坐标 系的基向量或者是参考系,这种情况下的张量就可 以用一系列有序的多维阵列来表示。张量的坐标以 “协变”(变化规律)的形式独立,“协变”把一种 坐标下的阵列和另一种坐标下的阵列联系起来。这 种变化规律演化成为几何或物理中的张量概念,其 精确形式决定了张量的类型或者是值。 张量在物理学中十分重要,因为在弹性力学、流体力学、广义相对论等领域中,张量提供了一种简洁的数学模型来建立或是解决物理问题。张量的概念首先由列维-奇维塔和格莱格里奥-库尔巴斯特罗提出,他们延续了黎曼、布鲁诺、克里斯托费尔等人关于绝对微分学的部分工作。张量的概念使得黎曼曲率张量形式的流形微分几何出现了替换形式。 历史 现今张量分析的概念源于卡尔?弗里德里希?高斯在微分几何的工作,概念的 制定更受到19世纪中叶代数形式和不变量理论的发展[2]。“tensor ”这个单词在 1846年被威廉·罗恩·哈密顿[3]提及,这并不等同于今天我们所说的张量的意思。 [注1]当代的用法是在1898年沃尔德马尔·福格特提出的[4]。 “张量计算”这一概念由格雷戈里奥·里奇·库尔巴斯特罗在1890年《绝对微分几何》中发展而来,最初由里奇在1892年提出[5]。随着里奇和列维-奇维塔1900年的经典著作《Méthodes de calcul différentiel absolu et leurs applications 》(绝对微分学的方法及其应用)出版而为许多数学家所知[6]。 在20世纪,这个学科演变为了广为人知的张量分析,1915年左右,爱因斯坦的广义相对论理论中广泛应用了这一理论。广义相对论完全由张量语言表述。爱因斯坦曾向几何学家马塞尔·格罗斯曼学习过张量方法,并学得很艰苦。[7]1915 年到1917年之间,列维·奇维塔 在与爱因斯坦互相尊重互相学习的氛围下,对爱因斯坦的张量表述给与了一些指正。 “我很佩服你的计算方法的风采,它必将使你在数学大道上策马奔腾,然而我们却只能步履蹒跚。”阿尔伯特·爱因斯坦,意大利相对论数学家[8]。 柯西应力张量是一个二阶张量。该张量的元素在三维笛卡尔坐标系下组成如下矩 阵: 312()()()111213212223313233 T T T =e e e σσσσσσσσσσ??=???????????? 该矩阵的各列表示作用在 e 1,e 2,e 3方向正方体表面上的应力(单位面积上的力)。
浅谈损伤力学专业:结构工程
浅谈损伤力学 摘要:本文主要简要介绍损伤的概念,损伤力学的研究内容,并简单介绍了损伤诱发的材料和结构物理力学性能改变、有效应力和等效应变以及有效应力和等效应变与真应力真应变的关系,同时,还包括损伤力学的研究方法、损伤诱发的各向异性、损伤的测量方法及其表征与演化模式刻画。此外,还叙述了损伤力学与实际工程的关系,以及作者对损伤力学方面文献的一点收获。 关键词损伤;损伤力学;各向同性;各向异性;损伤变量;有效应力;等效应变;演化 1、前言 损伤力学是固体力学的分支。研究材料或构件在各种加载条件下,其中损伤随变形而演化发展并最终导致破坏的过程中的力学规律。损伤力学认为,材料内部存在着分布的缺陷,如位错、微裂纹、微空洞、剪切带等,这些不同尺度的细结构是损伤的典型表现。物体中的损伤有多种,如脆性损伤、塑性损伤、蠕变损伤、疲劳损伤等。损伤力学选取合适的损伤变量(可以是标量、矢量或张量),利用连续介质力学的唯象方法或细观力学、统计力学的方法,导出含损伤的材料的本构关系和损伤演化方程,形成损伤力学的初、边值问题的提法,并求解物体的应力变形场和损伤场。损伤力学近年来得到发展并应用于破坏分析、力学性能预计、寿命估计、材料韧化等方面。从1958 年P.M.卡恰诺夫提出完好度(损伤度)概念至今,损伤力学仍处在发展阶段。它与断裂力学一起组成破坏力学的主要框架,以研究物体由损伤直至断裂破坏的这样一类破坏过程的力学规律。 2、损伤力学的研究内容和方法 所谓损伤是指冶炼、冷热工艺过程或荷载、温度、环境等的作用,使材料的微细结构发生变化,引起微缺陷成胚、孕育、扩展和汇合,导致材料宏观力学性能的劣化,最终形成宏观开裂或材料破坏。从细观的物理学的观点来看,损伤是材料组分晶粒的错位、滑移、微孔洞、微裂隙等微缺陷形成和发展的结果;从宏观的、连续介质力学的观点来看,损伤又可认为是材料内部微细结构状态的一种不可逆的、耗能的演变过程。 损伤力学(Damage Mechanics——DM)主要研究材料内部微观缺陷的产生和发展所引起的宏观力学效应及最终导致材料破坏的过程和规律。它通过引入一种所谓“损伤变量”的内部状态变量来描述含微细观缺陷材料的力学效应——受损材料的力学行为,以便更好地预测工程材料的变形破坏和使用寿命等。 现如今损伤力学已经成为一门公认的固体力学新分支,它主要研究探讨以下
重庆大学学术型硕士研究生培养方案 力学 专业代码:080100 一、培养目标 本学科专业培养能够从事力学方面的教案、科研或相关工程设计工作的高层次人才。学位获得者应具备坚实的力学和数学基础理论和较宽广的专业知识;较为熟练地掌握一门外国语;了解本学科理论研究和工程应用的前沿动态;具有一定的理论分析、实验研究及数值分析能力,能结合与本学科相关的实际问题从事科学研究或工程技术工作,并取得较系统的研究成果。 二、学科、专业及研究方向简介 重庆大学工程力学专业创建于1978年。1981年获得固体力学硕士学位授权点,是全校最早的硕士授权点之一;1986年获得固体力学博士学位授权点,是原重庆大学八个最早获得博士学位授权点的学科之一;2003年获得力学博士学位授权一级学科;2007年力学一级学科被确立为重庆市重点学科。 重庆大学力学博士学位授权一级学科包括固体力学、工程力学、流体力学和一般力学与基础力学四个二级学科博士学位授权点;固体力学、工程力学、流体力学和一般力学与基础力学四个硕士学位授权点。本学科拥有先进的MTS材料实验机和并行计算机系统等一批重要设备,为力学理论、实验和数值研究提供必要的条件。近年来,本学科承担了数十项国家和省部级工程以及大量重点横向合作工程,获得了丰富的科研成果。 本学科主要研究领域: 1多场耦合理论与智能材料及结构力学 2生物材料力学与高性能复合材料制备 3材料与结构的强度与破坏 4超常环境下材料及其微结构特性的理论与测试 5纳M材料特性及其微结构机理、多尺度及跨尺度分析 6结构动态特性及失效 7结构运动与变形耦合动力学及控制 8微重力下晶体生长过程的流体动力学、热张力流和浮力流理论、方法及其应用 9输配电装备及系统安全的关键力学问题 10多孔介质力学及其应用 11生物力学 12振动测试理论与技术 13智能与虚拟仪器的研制与开发 14 可压缩流体动力学 15 超音速流和冲击波 16 线性波和非线性波 1 / 8 主要研究方向及其内容: 1材料的强度理论与破坏机理
1.吴鸿遥. 损伤力学. 北京:国防工业出版社,1990 2.杨光松. 连续介质损伤力学讲义. 北京:国防科技大学航天技术系,1990 3.谢和平. 岩石、混凝土损伤力学. 北京:中国矿业大学出版社,1990 4.楼志文. 损伤力学基础. 西安:西安交通大学出版社,1991 5.李灏. 损伤力学基础. 济南:山东科学技术出版社,1992 6.余天庆,钱济成. 损伤理论及其应用. 北京:国防工业出版社,1993 7.王光钦,高庆. 固体的损伤与断裂. 成都:成都科技大学出版社,1993 8.沈为. 损伤力学. 武汉:华中理工大学出版社,1995 9.杨光松. 损伤力学与复合材料损伤. 北京:国防工业出版社,1995 10.余寿文,冯西桥. 损伤力学. 北京:清华大学出版社,1997 11.王军. 损伤力学的理论与应用. 北京:科学出版社,1997 12.李兆霞. 损伤力学及其应用. 北京:科学出版社,2002 13.冯西桥, 余寿文著. 准脆性材料细观损伤力学. 北京:高等教育出版社,2002 14.唐雪松,郑健龙,蒋持平著. 连续损伤理论及应用. 北京:人民交通出版社,2006 15.张行. 断裂与损伤力学. 北京:北京航空航天大学出版社,2006 16.K L Reifsnider. Damage in Composite Materials: Basic Mechanisms, Accumulation, Tolerance, and Characterization. ASTM, 1982 17.L M Kachanov. Introduction to continuum damage mechanics. Dordrecht, Netherlands: Martinus Nijhoff Publishers, 1986 18.D Krajcinovic and J Lemaitre. Continuum Damage Mechanics-Theory and Applications. Wien, New York: Springer Verlag, 1987 19.R Viswanathan. Damage mechanisms and life assessment of high-temperature components. Metals Park, Ohio : ASM International, 1989. 20.J Lemaitre, J. –L. Chaboche. Mechanics of Solid Materials. Cambridge : Cambridge University Press, 1990 21.J Lemaitre, H Lippmann. A course on damage mechanics. Berlin: Springer, 1992 22.R Talreja. Damage Mechanics of Composite Materials (Composite Materials Series Vol. 9). Amsterdam: Elsevier,1994 23.D Krajcinovic. Damage Mechanics. Amsterdam: Elsevier Science Publishers, 1996 24.D L Mcdowell. Applications of Continuum Damage Mechanics to Fatigue and Fracture. West Conshohocken: ASTM publisher,1997 25.G Z Voyiadjis, J W Ju and J L Chaboche. Damage Mechanics in Engineering Materials. Amsterdam: Elsevier Science, 1998 26.M H Aliabadi. Nonlinear fracture and damage mechanics. Southampton, Boston: WIT Press, 2001 27.A llix and F Hild .Continuum damage mechanics of materials and structures. Amsterdam: Elsevier, 2002 28.P I Kattan, G Z Voyiadjis. Damage mechanics with finite elements:practical applications with computer tools. Berlin:Springer-Verlag,2002 29.K hémais Saanouni . Numerical Modelling in Damage Mechanics. London: Kogan Page Science , 2003
第六章连续介质力学方法 连续介质力学方法的出发点是支护结构与围岩相互作用,组成一个共同承载体系,其中围岩是主要的承载结构,支护结构是镶嵌在无限或半无限介质孔洞上的加劲环。它的特点能反映出隧道开挖后围岩的应力状态。 解析法:即根据所给定的边界条件,对问题的平衡方程、几何方程和物理方程直接求解。由于数学上的困难,现在还只能对少数问题求解。 数值法:主要是指有限元法。它把围岩和支护结构都划分为若干单元,然后根据能量原理建立单元刚度矩阵,并形成整个系统的总体刚度矩阵,从而求出系统上各个节点的位移和单元的应力。它不但可以模拟各种施工过程和各种支护效果,同时可以分析复杂的地层情况(如断层、节理等地质构造以及地下水等)和材料的非线性等。 6.1 解析法 以均匀内压水工隧洞的计算为例,说明解析法计算的基本思路。 (1)衬砌应力的分析 水工隧洞衬砌厚度一般在20 cm以上、故力学分析中可将其视为厚壁圆筒。如图6.1.1 (a)所示。在均匀内水压力作用下,厚壁圆筒的内力分析是轴对称问题。 衬砌的径向应变为: 近似按平面应变问题分析衬砌,则由平面问题极坐标解的物理方程可写为: 作用在单元体上的外荷载为零,且在轴对称情况下单元体内力分量中的剪应力也为零,故根据平面问题极坐标解的静力平衡力程式,有:
(2)洞室围岩应力 分析均匀内力圆形水工隧洞围岩的应力仍可采用厚壁圆筒原理。 由式(6.1.16)可知:内水压力使围岩产生的切向应力σt是拉应力。若σt 的量值大于围岩中原来存在的压应力,且差值超过岩体的抗拉强度,则当衬砌抗拉强度不足时岩体将与衬砌一起发生开裂。将式(6.1.16)中的r0理解为毛洞半径,Pa理解为内压力,则该式就成为无衬砌圆形水工隧洞围岩应力的计算式。 (3)衬砌与围岩共同作用的计算 分析均匀内力圆形水工隧洞围岩的应力仍可采用厚壁圆筒原理。
张量分析在连续介质力学中的应用 薛玉洁 (中国矿业大学力学与建筑工程学院,桥梁与隧道工程,ZS13030047) 摘要:本研究将叙述张量分析在连续介质力学中的应用,Euclid空间上张量场分析、二维曲面(Riemann流形)上的张量场分析的相关知识体系要点,以及作为应用的可变形边界局部动力学有关研究的理论基础等。张量分析是我国著名力学家周培源先生常用的数学及力学分析方法,亦谨以此文表示为前辈诚挚的仰慕之情。 关键词:连续介质力学;Euclid空间;二维曲面;涡量与涡动力学 1引言 一般连续介质力学的理论体系,引入初始物理构形以及当前物理构形,对二者可再分别引入初始参数构形以及当前参数构形,物理构形与参数构形之间的关系即为一般曲线坐标系,数学上对应为有限维Euclid空间之间二个开集之间的微分同胚。 为研究边界的有限变形运动对介质运动的影响,我们对于当前物理构形引入显含时间的曲线坐标系,表现为时空空间中的微分同胚。通过构造适当的曲线坐标系可将物理空间中几何形态不规则且随时间变化的运动区域微分同胚至参数空间中的几何形态规则且不随时间变化的参数区域。如图l所示,对于研究出口边界可作有限变形运动的射流场,其当前物理构形显得极其复杂,但我们可以考虑如图所示的对应于当前物理构形的显含时间的曲线坐标系,使得当前参数构形不仅几何形态规则而且不随时间变化。进一步将连续介质运动的控制方程按曲线坐标系的局部基展开就可获得定义于参数区域上的控制方程。特别地,可基于非完整系理论系统获得控制方程在一般单位正交系(非完整系)下的分量方程,也适用于按时均分解的湍流控制方程。我们亦可将把相关方法推广至张量梯度的多点表示形式。 以上所述,一定程度上归纳了现代张量分析在现代连续介质力学中有关应用的基本思想及方法。本文将叙述Euclid空间上张量场分析、二维曲面(Riemann流形)上的张量场分析的相关知识体系要点,以及作为应用的可变形边界局部动力学有关研究的理论基础。
第二章 连续介质力学的基本定律 在第一章中,我们仅考察了连续介质运动的运动学描述,而没有考虑到引起运动和变形的因素。本章我们将引入应力等概念,并给出连续介质力学的基本定律:质量守恒定律、动量平衡定律、动量矩平衡定律、能量守恒定律及熵不等式。 2.1 应力矢量与应力张量 在物体的运动中,物体的两部分之间或物体与其外界间的力学作用是通过力来描述的。在连续介质力学中我们主要研究三种类型的力:(1)一个物体的两部分之间的接触力;(2)由外界作用于物体边界上的接触力;(3)由外界作用于物体内部点的非接触力(如重力、离心力等)。在另一方面,由于(1)(2)型的力总是通过某一接触面发生作用的,因此通常把作用于单位接触面积上的接触力称为表面力,或简称面力;由于(3)型力作用于物体整个体积内所含的物质点,因此通常把它称为体积力,或简称体力。 在连续介质力学中重要的公理之一就是关于接触力形式的柯西假设。柯西假设在运动过程中的时刻t 对于任何物质坐标X 和与之对应的接触面S 上的单位法矢量n ,表面力的存在形式为 ()n t X t t ,,= (2.101) 通常,我们规定()n t X t t ,,=指向接触面S 的外法向时为正,反之为负(见图2.1). 现在不管在X 和S 面与S'面的曲率相差多少。 为了研究物体内部的力学状态,我们把一物体用一假想平面S 截断成两部分A 和B ,如图2.3所示。此时S 面就是A 和B 相互作用的接触面,B 部分对A 部分一点的作用,便可以用A 部分截面上的表面力t n 来表征,我们称之为应力矢量。反过来,考虑A 部分对B 部分作用,按照牛顿的作用与反作用定律可得应力矢量t n -。它与t n 作用于同一平面上的同一点处,并且大小相等,方向相反。即 t t n n =- (2.102) 对于物体内部的一点P ,通过它可以有无穷多个方向的截面,而对于不同方向的截面,应力矢量也就不同,这种复杂情况只有引进应力张量的概念才能充分地加以描述。为了刻画一点的应力状态,设想在一点P 的附近任意给定一个单位法矢量为 (),cos ,cos ,cos 321ααα=n ()n e n e n e ???=321,, (2.103) 的平截面。相应地,过P 点沿活动标架作三个坐标平面。于是它们在物体内截得一个微小四面体,如图2.4所示。在这个微小四面体的每一个面上,都受有物体的其余部分给它的作用力,不妨设在ABC 上受到的作用力为t A ?,在PBC ,PCA 与PAB 上的作用力分别为-t A 11?、-t A 22?与-t A 33?,其中?A 与?A i 分别为各微小平面的面积,作用于微小四面体ABCP 上单位质量的体力为b 。 现在假设对物体的任何部分,特别是对微小四面体ABCP 而言,动量的变化率与作用的合力成正比。虽然这是个很自然且牛顿第二定律更强的新假设(因为牛顿第二定律只适用于整个物体),然而,它却不能用实验直接验证,因为不可能做内部表面接触力的直接测定,这种力的存在与大小只能由其它量的观测推知。描述一点是应力张量,描述通过一点的某一截面是应力矢量。 对于微小四面体ABCP ,柯西定律给出 t A t A t A t A b V ?????---+112233ρ
摘要:弹塑性力学在材料加工工程中的应用相当广泛,首先说明下材料加工工程包括焊接、铸造、塑性成形三个方面。我主要是简单说明下弹塑性力学在金属塑性成形方面的应用。金属的变形分为两个阶段:弹性变形阶段与塑性变形阶段,对这两个阶段的研究相应的就分为弹性力学跟塑性力学[1]。 关键词:弹性力学、塑性力学、塑性成形、有限元、屈服准则、滑移线、应力、应变 首先来简单介绍下两个学科。弹性力学也称弹性理论,主要研究弹性体在外力作用或温度变化等外界因素下所产生的应力、应变和位移,从而解决结构或机械设计中所提出的强度和刚度问题。在研究对象上,弹性力学同材料力学和结构力学之间有一定的分工[2]。材料力学基本上只研究杆状构件;结构力学主要是在材料力学的基础上研究杆状构件所组成的结构,即所谓杆件系统;而弹性力学研究包括杆状构件在内的各种形状的弹性体。 弹性力学是固体力学的重要分支,广泛应用于建筑、机械、化工、航天等工程领域。弹性体是变形体的一种,它的特征为:在外力作用下物体变形,当外力不超过某一限度时,除去外力后物体即恢复原状。绝对弹性体是不存在的。物体在外力除去后的残余变形很小时,一般就把它当作弹性体处理。 首先来简单介绍下弹性力学在塑性成形方面的应用。弹性力学一般来解决两个方面的问题,一个是平面问题,一个是空间问题。而平面问题的解决包括平面问题的直角坐标解答、平面问题的极坐标解答、平面问题的有限单元法解答。应用弹性力学来解决塑性成形方面的应力、应变方面的问题,恰当的应力大小、应变程度就有金属的不同工艺性能。分析各种结构物或其构件在弹性阶段的应力和位移,校核它们是否具有所需的强度跟刚度,并寻求或改进它们的计算方法。空间问题解决的是运用平衡微分方程来分析物体内任一点的应力状态、最大与最小的应力等问题[3]。 有限元法在塑性成形方向的应用有这重要的作用,我简单说下有限元法在板料冲压方面的应用。在冲压板料成形加工中,钣金件展开计算非常重要。求得钣金件的展开毛坯,是分析钣金件变形程度、设计工艺以及拟定工艺规程的前提。合理的毛坯形状和尺寸,可以明显改善冲压过程中板料变形不均匀的现象,充分发挥金属的成形性能。在钣金件的展开方法中,基于全量理论的有限元逆算法只
一、引论 连续介质力学研究物体的宏观力学微观粒子性质.在宏观现象中,物体变化的最小特征尺度远大于原子的尺度,虽然物理上物体是物质点的集合,质量连续性假设对物休的宏观力学过程的研究却是合理的,在连续介质力学中可以对物体进行无限的分割,也就是说,可以用场的观点来描述物体的内部变化和作用过程. 质量连续性假设要求物体连续地充满它所占据的空间,即可以用三维欧氏空间的一个开集表示物体的客观存在、指示其位置.开集中的一点表征占据该位置点的一个微小介质团,这样的介质团我们称之为物体单元,开集中所有点表征的物体单元组成了物体.若要用严格的数学理性推演连续介质力学,必须知道物体单元在数学上的确切涵义,即要回答: 表征物体单元的点是开集还是闭集?若是闭集,则物体单元表现为数学上离散的点,物体是连续点的集合,可以用构形(物体在空间所占的区域)表示;若是开集,则物体单元表现为数学上点的无穷小邻域,物体是作为拓扑基的所有点邻域的并集,可以用微分流形(容许拓扑结构改变的物体表示空间)表示. 从逻辑上看,目前的连续介质力学是从经典质点力学类推得出的,它一方面把物体看作连续的质点系,物体单元具有离散特征,一方面又以场的观点看待物体的内部变化和受力,物体单元变化特征要求是连续的.在质量连续性假设下,物体单元虽然宏观意义上可以看作无穷小,但总还是有尺度内涵的,即具有连续性适用的典型尺度,而经典力学中的质点却没有尺度内涵,德冈辰雄指出,“连续介质无论怎样分割也不会成为质点,质点无论怎样连续也不是连续介质”.我们知道,经典力学中的质点在数学上表现为三维欧氏家间中的一点(闭集),把表征物体单元的数学上的点看作闭集,无异于沿用质点力学的观点,抹杀连续介质与质点系的区别,这样导出的连续介质力学(简称为质点观点的连续介质力学)是质点观点和场观点的大杂烩,这样的一种结合虽然使连续介质力学在其发展过程中可以同时借鉴经典力学和场论的一些成果,却妨碍了连续介质力学的现代发展,比如运用场论的现代发展—规范理论于连续介质时就显得不伦不类.实际上,质点观点在赋予物体变化连续性的同!讨,对物体的表示空间强加了过分的约束.限制了场的观点的发挥,使连续介质力学在描述物体复杂宏观力学过程时困难重重.为了使连续介质力学摆脱质点观点的限制,.采用与现代场论一致的基本观点,物体单元用数学上的开集表示是必须的,这时连续性可以用邻域而不是距离定义从而与拓扑学的概念一致,称之为拓扑观点.我们知道,拓扑学是现代微分几何的概念基础,现代微分几何是规范场论的数学基础,因此,拓扑观点的连续介质力学是连续介质的纯粹的场理论,它可以容许物体空间拓扑结构的改变,能够刻划物休的复杂变化过程.可见,物体单元的开集表示与场的现代观点是同气共枝的,由此导出的理论保证了数学概念上的连贯、逻辑上的统一,并且能接纳耗散结构作为物体复杂变化的物理基础. 二、流动与变形 物体的流动由物沐单元的运动组合而成,物体的变形由物件单元的变形组合而成.物体单元不同于质点:物体单元的开集表达隐含着单元具有尺度内涵,作为开集的点不仅有平移特征,还有方向特征和尺度特征,从而可以独立地体现介质的变形和转动.物体单元的这些特征预示着单元的变形和单元的运动是两个不同的变化过程,物体单元的变形表现为点(及其邻域)的特征的改变,包括尺度的改变和方向的改变,物体单元的运动则表现为点(及其邻域)的平移(空问位置的改变)和转动(方向的改变),可见,单元的变形与其空间位置无关,单元的运动与其尺度特征无关.与此不同,作为闭集的点不具备尺度特征和方向特征,不能独立地体现介质的变形和转动,介质的变形是通过介质点之间距离及相对方位的改变体现的,介质的转动也是通过不同介质点之间的方位关系体现的,这就客观上对物体表示空间提出了要求,难以刻划复杂的变形过程,而单元的运动由于缺乏方向性,对物休单元具有曲线运动的流运过程就无法准确把握.
第一章绪论 研究连续介质宏观力学性状的分支学科。宏观力学性状是指在三维欧氏空间和均匀流逝时间下受牛顿力学支配的物质性状。连续介质力学对物质的结构不作任何假设。它与物质结构理论并不矛盾,而是相辅相成的。物质结构理论研究特殊结构的物质性状,而连续介质力学则研究具有不同结构的许多物质的共同性状。连续介质力学的主要目的在于建立各种物质的力学模型和把各种物质的本构关系用数学形式确定下来,并在给定的初始条件和边界条件下求出问题的解答。 如果一个物体的质量、动量、能量密度在数学意义上存在,这个物质就是一个物质连续统(连续介质)。这样一个物质连续统的力学就是连续介质力学(附加限制条件:只要始终保持含有足够多的粒子,而不至于使极限值不存在或者发生突跃)。它通常包括下述基本内容:①变形几何学,研究连续介质变形的几何性质,确定变形所引起物体各部分空间位臵和方向的变化以及各邻近点相互距离的变化,这里包括诸如运动,构形、变形梯度、应变张量、变形的基本定理、极分解定理等重要概念。 ②运动学,主要研究连续介质力学中各种量的时间率,这里包括诸如速度梯度,变形速率和旋转速率,里夫林-埃里克森张量等重要概念。③基本方程,根据适用于所有物质的守恒定律建立的方程,例如,热力连续介质力学中包括连续性方程、运动方程、能量方程、熵不等式等。④本构关系。⑤特殊理论,例如弹性理论、粘性流体理论、塑性理论、粘弹性理论、热弹性固体理论、热粘性流体理论等。⑥问题的求解。根据发展过程和研究内容,客观上连续介质力学已分为古典连续介质力学和近代连续介质力学。 1.1基本假设 连续介质力学的最基本假设是“连续介质假设”:即认为真实的流体和固体可以近似看作连续的,充满全空间的介质组成,物质的宏观性质依然受牛顿力学的支配。这一假设忽略物质的具体微观结构(对固体和液体微观结构研究属于凝聚态物理学的范畴),而用一组偏微分方程来表达宏观物理量(如质量,数度,压力等)。这些方程包括描述介质性质的方程(constitutive equations)和基本的