
2017年广东省广州市番禺区高考数学一模试卷(文科)
一、选择题(共12小题,每小题5分,满分60分)
1.设集合S={x|x<﹣5或x>5},T={x|﹣7<x<3},则S∩T=()
A.{x|﹣7<x<﹣5}B.{x|3<x<5}C.{x|﹣5<x<3}D.{{x|﹣7<x<5}
2.在区间[﹣1,m]上随机选取一个数x,若x≤1的概率为,则实数m的值为()
A.2 B.3 C.4 D.5
3.设f(x)=,则f(f(2))的值为()
A.0 B.1 C.2 D.3
4.已知双曲线﹣=1的左、右焦点分别为F1、F2,且F2为抛物线y2=2px的焦点,设P为两曲线的一个公共点,则△PF1F2的面积为()
A.18 B.18C.36 D.36
5.若实数x、y满足,则z=2x﹣y的最大值为()
A.B.C.1 D.2
6.已知命题p:?x∈R,x2﹣2xsinθ+1≥0;命题q:?α,β∈R,sin(α+β)≤sinα+sinβ,则下列命题中的真命题为()
A.(¬p)∧q B.¬(p∧q)C.(¬p)∨q D.p∧(¬q)
7.若函数f(x)为区间D上的凸函数,则对于D上的任意n个值x1、x2、…、
x n,总有f(x1)+f(x2)+…+f(x n)≤nf(),现已知函数f(x)=sinx在[0,]上是凸函数,则在锐角△ABC中,sinA+sinB+sinC的最大值为()
A.B.C.D.
8.三棱柱ABC﹣A1B1C1的侧棱垂直于底面,且AB⊥BC,AB=BC=AA1=2,若该三棱柱的所有顶点都在同一球面上,则该球的表面积为()
A.48πB.32πC.12πD.8π
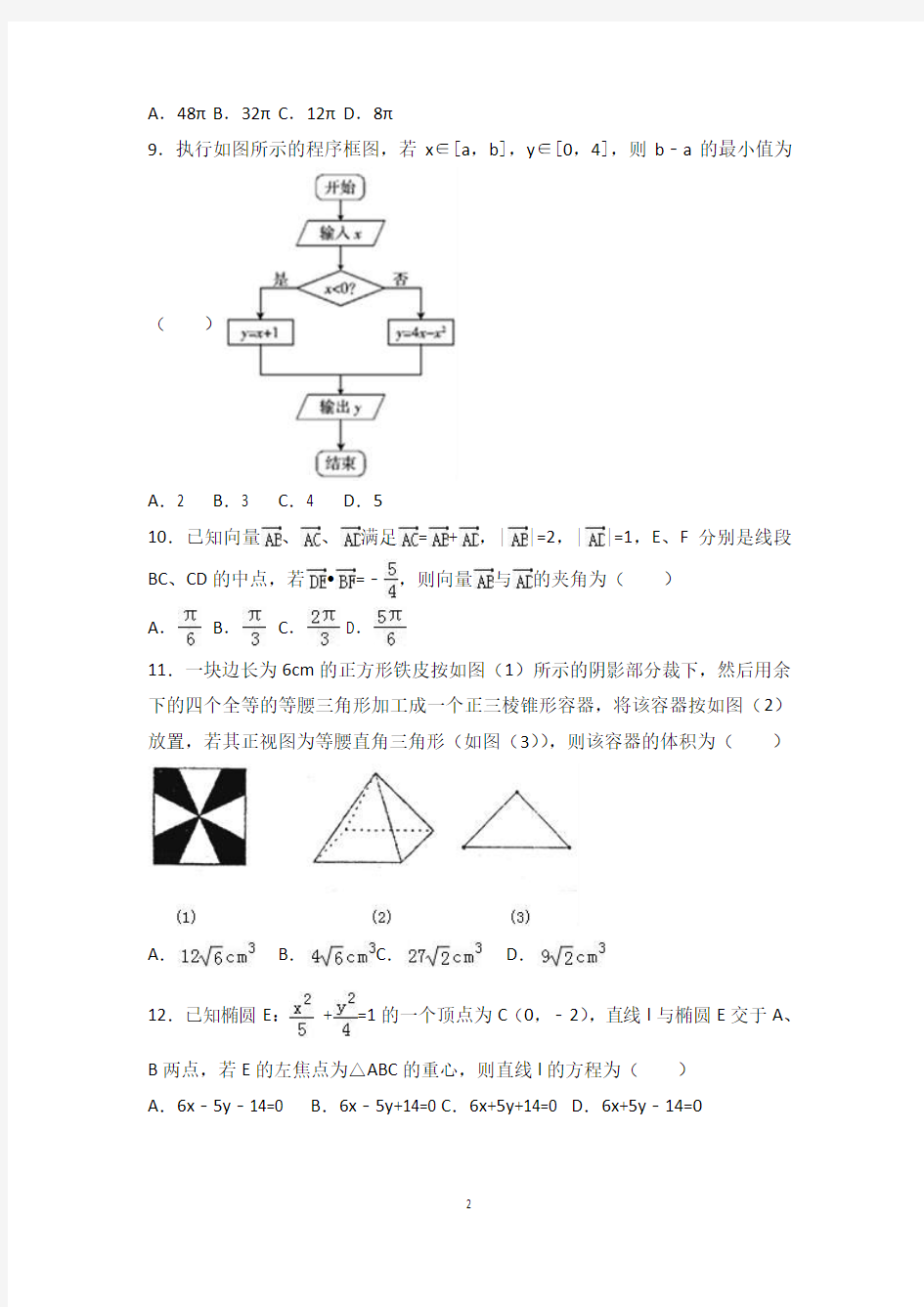
9.执行如图所示的程序框图,若x∈[a,b],y∈[0,4],则b﹣a的最小值为
()
A.2 B.3 C.4 D.5
10.已知向量、、满足=+,||=2,||=1,E、F分别是线段
BC、CD的中点,若?=﹣,则向量与的夹角为()
A.B.C. D.
11.一块边长为6cm的正方形铁皮按如图(1)所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正三棱锥形容器,将该容器按如图(2)放置,若其正视图为等腰直角三角形(如图(3)),则该容器的体积为()
A.B.C.D.
12.已知椭圆E: +=1的一个顶点为C(0,﹣2),直线l与椭圆E交于A、
B两点,若E的左焦点为△ABC的重心,则直线l的方程为()
A.6x﹣5y﹣14=0 B.6x﹣5y+14=0 C.6x+5y+14=0 D.6x+5y﹣14=0
二、填空题(共4小题,每小题5分,满分20分)
13.若复数a+i是纯虚数,则实数a=.
14.曲线y=sinx+1在点(0,1)处的切线方程为.
15.已知f(x)是定义在R上的奇函数,f(x)满足f(x+2)=﹣f(x),当0≤x ≤1时,f(x)=x,则f(37.5)等于.
16.函数f(x)=sinωx+cosωx+1(ω>0)的最小正周期为π,当x∈[m,n]时,f(x)至少有5个零点,则n﹣m的最小值为.
三、解答题(共6小题,满分70分)
17.在△ABC中,内角A、B、C所对的边分别是a、b、c,已知A=60°,b=5,c=4.(1)求a;
(2)求sinBsinC的值.
18.设等差数列{a n}的公差为d,且2a1=d,2a n=a2n﹣1.
(1)求数列{a n}的通项公式;
(2)设b n=,求数列{b n}的前n项和S n.
19.某市为了解各校(同学)课程的教学效果,组织全市各学校高二年级全体学生参加了国学知识水平测试,测试成绩从高到低依次分为A、B、C、D四个等级,随机调阅了甲、乙两所学校各60名学生的成绩,得到如图所示分布图:
(Ⅰ)试确定图中实数a与b的值;
(Ⅱ)若将等级A、B、C、D依次按照90分、80分、60分、50分转换成分数,试分别估计两校学生国学成绩的均值;
(Ⅲ)从两校获得A等级的同学中按比例抽取5人参加集训,集训后由于成绩相当,决定从中随机选2人代表本市参加省级比赛,求两人来自同一学校的概率.20.如图,三棱锥P﹣ABC中,PA=PC,底面ABC为正三角形.
(Ⅰ)证明:AC⊥PB;
(Ⅱ)若平面PAC⊥平面ABC,AB=2,PA⊥PC,求三棱锥P﹣ABC的体积.
21.已知圆C:(x﹣6)2+y2=20,直线l:y=kx与圆C交于不同的两点A、B.(Ⅰ)求实数k的取值范围;
(Ⅱ)若=2,求直线l的方程.
22.已知函数f(x)=alnx+x2﹣x,其中a∈R.
(Ⅰ)若a<0,讨论f(x)的单调性;
(Ⅱ)当x≥1时,f(x)≥0恒成立,求a的取值范围.
2017年广东省广州市番禺区高考数学一模试卷(文科)
参考答案与试题解+析
一、选择题(共12小题,每小题5分,满分60分)
1.设集合S={x|x<﹣5或x>5},T={x|﹣7<x<3},则S∩T=()A.{x|﹣7<x<﹣5}B.{x|3<x<5}C.{x|﹣5<x<3}D.{{x|﹣7<x<5}【考点】交集及其运算.
【分析】利用交集定义和不等式性质求解.
【解答】解:∵集合S={x|x<﹣5或x>5},T={x|﹣7<x<3},
∴S∩T={x|﹣7<x<﹣5}.
故选:A.
2.在区间[﹣1,m]上随机选取一个数x,若x≤1的概率为,则实数m的值为()
A.2 B.3 C.4 D.5
【考点】几何概型.
【分析】利用几何概型的公式,利用区间长度的比值得到关于m 的等式解之.
【解答】解:由题意x≤1的概率为,则,解得m=4;
故选C.
3.设f(x)=,则f(f(2))的值为()
A.0 B.1 C.2 D.3
【考点】分段函数的解+析式求法及其图象的作法.
【分析】考查对分段函数的理解程度,f(2)=log3(22﹣1)=1,所以f(f(2))=f(1)=2e1﹣1=2.
【解答】解:f(f(2))=f(log3(22﹣1))=f(1)=2e1﹣1=2,故选C.
4.已知双曲线﹣=1的左、右焦点分别为F1、F2,且F2为抛物线y2=2px的焦点,设P为两曲线的一个公共点,则△PF1F2的面积为()
A.18 B.18C.36 D.36
【考点】双曲线的简单性质.
【分析】求出P的坐标,即可求出△PF1F2的面积.
【解答】解:由题意,=6,p=12,
双曲线方程与抛物线方程联立,可得P(9,6),
∴△PF1F2的面积为=36,
故选D.
5.若实数x、y满足,则z=2x﹣y的最大值为()
A.B.C.1 D.2
【考点】简单线性规划.
【分析】作出可行域,变形目标函数,平移直线y=2x可得结论.
【解答】解:作出约束条件,所对应的可行域(如图△ABO),
变形目标函数可得y=2x﹣z,平移直线y=2x可知当直线经过点A时,
直线的截距最小,z取最大值,由可得,A(,)
代值计算可得z=2x﹣y的最大值为1,
故选:C.
6.已知命题p:?x∈R,x2﹣2xsinθ+1≥0;命题q:?α,β∈R,sin(α+β)≤sinα+sinβ,则下列命题中的真命题为()
A.(¬p)∧q B.¬(p∧q)C.(¬p)∨q D.p∧(¬q)
【考点】复合命题的真假.
【分析】分别判断出p,q的真假,从而判断出复合命题的真假即可.
【解答】解:关于命题p:?x∈R,x2﹣2xsinθ+1≥0,△=4sin2θ﹣4≤0,故p是真命题,
关于命题q:?α,β∈R,sin(α+β)≤sinα+sinβ,是真命题,
∴(¬p)∨q是真命题,
故选:C.
7.若函数f (x )为区间D 上的凸函数,则对于D 上的任意n 个值x 1、x 2、…、
x n ,总有f (x 1)+f (x 2)+…+f (x n )≤nf (
),现已知函数f (x )
=sinx 在[0,]上是凸函数,则在锐角△ABC 中,sinA +sinB +sinC 的最大值为( )
A .
B .
C .
D .
【考点】三角函数的化简求值.
【分析】利用凸函数对于D 上的任意n 个值x 1、x 2、…、x n ,总有f (x 1)+f (x 2)
+…+f (x n )≤nf (),将函数f (x )=sinx 在[0,
],
sinA +sinB +sinC
,得到所求.
【解答】解:由已知凸函数的性质得到sinA +sinB +sinC =3sin
=
;
所以在锐角△ABC 中,sinA +sinB +sinC 的最大值为;
故选D .
8.三棱柱ABC ﹣A 1B 1C 1的侧棱垂直于底面,且AB ⊥BC ,AB=BC=AA 1=2,若该三棱柱的所有顶点都在同一球面上,则该球的表面积为( ) A .48π B .32π C .12π D .8π 【考点】球的体积和表面积.
【分析】以AB ,BC ,AA 1为棱构造一个正方体,则该三棱柱的所有顶点都在该正方体的外接球上,由此能求出该球的表面积.
【解答】解:∵三棱柱ABC ﹣A 1B 1C 1的侧棱垂直于底面,且AB ⊥BC ,
AB=BC=AA 1=2, ∴以AB ,BC ,AA 1为棱构造一个正方体,
则该三棱柱的所有顶点都在该正方体的外接球上,
该球的半径R=
=
,
∴该球的表面积为S=4πR 2=4π×3=12π. 故选:C .
9.执行如图所示的程序框图,若x∈[a,b],y∈[0,4],则b﹣a的最小值为
()
A.2 B.3 C.4 D.5
【考点】程序框图.
【分析】写出分段函数,利用x∈[a,b],y∈[0,4],即可b﹣a的最小值.
【解答】解:由题意,y=,
x∈[a,b],y∈[0,4],则b﹣a的最小值为2,此时区间为[0,2]或[2,4],故选A.
10.已知向量、、满足=+,||=2,||=1,E、F分别是线段
BC、CD的中点,若?=﹣,则向量与的夹角为()
A.B.C. D.
【考点】平面向量数量积的运算.
【分析】由题意画出图形,结合?求得<,>的值,即可求出向量与的夹角.
【解答】解:如图所示,
?=(﹣)?(﹣)=?﹣﹣=﹣;
由||=||=2,||=||=1,
可得?=1,
∴cos<,>=,
∴<,>=,
即向量与的夹角为.
故选:B.
11.一块边长为6cm的正方形铁皮按如图(1)所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正三棱锥形容器,将该容器按如图(2)放置,若其正视图为等腰直角三角形(如图(3)),则该容器的体积为()
A.B.C.D.
【考点】棱柱、棱锥、棱台的体积.
【分析】推导出PM+PN=6,且PM=PN,MN=3,PM=3,设MN中点为O,则PO⊥平面ABCD,由此能求出该容器的体积.
【解答】解:如图(2),△PMN是该四棱锥的正视图,
由图(1)知:PM+PN=6,且PM=PN,
由△PMN为等腰直角三角形,知MN=3,PM=3,
设MN中点为O,则PO⊥平面ABCD,∴PO=,
∴该容器的体积为==9.
故选:D.
12.已知椭圆E: +=1的一个顶点为C(0,﹣2),直线l与椭圆E交于A、
B两点,若E的左焦点为△ABC的重心,则直线l的方程为()
A.6x﹣5y﹣14=0 B.6x﹣5y+14=0 C.6x+5y+14=0 D.6x+5y﹣14=0
【考点】椭圆的简单性质.
【分析】先由椭圆左焦点F1恰为△ABC的重心,得相交弦AB的中点坐标,再由点A、B在椭圆上,利用点差法,将中点坐标代入即可的直线l的斜率,最后由直线方程的点斜式写出直线方程即可.
【解答】解:设A(x1,y1),B(x2,y2),椭圆+=1的左焦点为(﹣1,0),∵点C(0,﹣2),且椭圆左焦点F1恰为△ABC的重心
∴=﹣1,=0
∴x1+x2=﹣3,y1+y2=2 ①
∵,,
∴两式相减得: +=0
将①代入得:=,即直线l的斜率为k==,
∵直线l 过AB中点(﹣,1)
∴直线l的方程为y﹣1=(x+)
故答案为6x﹣5y+14=0,
故选B.
二、填空题(共4小题,每小题5分,满分20分)
13.若复数a+i是纯虚数,则实数a=0.
【考点】复数代数形式的乘除运算.
【分析】利用纯虚数的定义即可得出.
【解答】解:∵复数a+i是纯虚数,则实数a=0.
故答案为:0.
14.曲线y=sinx+1在点(0,1)处的切线方程为x﹣y+1=0.
【考点】利用导数研究曲线上某点切线方程.
【分析】先对函数y=sinx+1进行求导,再根据导数的几何意义求出曲线y=sinx+1在点x=0处的切线斜率,由点斜式方程进而可得到切线方程.
【解答】解:∵y′=cosx,
∴切线的斜率k=y′|x=0=1,
∴切线方程为y﹣1=x﹣0,
即x﹣y+1=0.
故答案为:x﹣y+1=0.
15.已知f(x)是定义在R上的奇函数,f(x)满足f(x+2)=﹣f(x),当0≤x ≤1时,f(x)=x,则f(37.5)等于﹣0.5.
【考点】抽象函数及其应用.
【分析】根据题意,由f(x+2)=﹣f(x)可得f(x+4)=﹣f(x+2)=f(x),即函数f(x)的周期为4,即有f(37.5)=f(1.5),结合题意可得f(1.5)=f[2+(﹣0.5)]=﹣f(﹣0.5),结合函数的奇偶性可得f(0.5)=﹣f(﹣0.5),进而结合函数在0≤x≤1上的解+析式可得f(0.5)的值,综合即可得答案.
【解答】解:根据题意,由于f(x+2)=﹣f(x),则有f(x+4)=﹣f(x+2)=f (x),即函数f(x)的周期为4,
则有f(37.5)=f(1.5+4×9)=f(1.5),
又由f(x+2)=﹣f(x),则有f(1.5)=f[2+(﹣0.5)]=﹣f(﹣0.5),
又由函数为奇函数,则f(0.5)=﹣f(﹣0.5),
又由当0≤x≤1时,f(x)=x,则f(0.5)=0.5;
则有f(37.5)=f(1.5)=﹣f(﹣0.5)=f(0.5)=0.5,
故f(37.5)=0.5;
故答案为:0.5.
16.函数f(x)=sinωx+cosωx+1(ω>0)的最小正周期为π,当x∈[m,n]时,f(x)至少有5个零点,则n﹣m的最小值为2π.
【考点】三角函数中的恒等变换应用;正弦函数的图象.
【分析】将函数化简为f(x)=2sin(2ωx+)+1.的最小正周期为π,可得f
(x)=2sin(2x+)+1.可知在y轴左侧的第一个零点为,右侧的第一个
零点为,x∈[m,n]时,f(x)至少有5个零点,可得n﹣m的最小值.
【解答】解:函数f(x)=sinωx+cosωx+1(ω>0)
化简可得:f(x)=2sin(2ωx+)+1.
∵最小正周期为π,即T=π,
∴,可得ω=1.
∴f(x)=2sin(2x+)+1.
根据正弦函数的图象及性质可知:函数f(x)的y轴左侧的第一个零点为,
右侧的第一个零点为,x∈[m,n]时,f(x)至少有5个零点,不妨设m=,则n=.
此时n﹣m可得最小值为2π.
故答案为2π.
三、解答题(共6小题,满分70分)
17.在△ABC中,内角A、B、C所对的边分别是a、b、c,已知A=60°,b=5,c=4.
(1)求a;
(2)求sinBsinC的值.
【考点】余弦定理;正弦定理.
【分析】(1)由题意和余弦定理列出式子,即可求出a的值;
(2)由条件和正弦定理求出sinB和sinC的值,代入式子求出答案.【解答】解:(1)因为A=60°,b=5,c=4,
所以由余弦定理得,a2=b2+c2﹣2bccosA
=25+16﹣=21,
则a=;
(2)由正弦定理得,==,
所以sinB==,sinC==
所以sinBsinC=×=.
18.设等差数列{a n}的公差为d,且2a1=d,2a n=a2n﹣1.
(1)求数列{a n}的通项公式;
(2)设b n=,求数列{b n}的前n项和S n.
【考点】数列递推式;数列的求和.
【分析】(1)利用递推关系、等差数列的通项公式即可得出.
(2)利用“错位相减法”与等比数列的求和公式即可得出.
【解答】解:(1)∵等差数列{a n}的公差为d,2a n=a2n﹣1.
取n=1,则2a1=a2﹣1=a1+d﹣1,与2a1=d联立,解得d=2,a1=1.
∴a n=1+2(n﹣1)=2n﹣1.
(2)b n===,
∴数列{b n}的前n项和S n=+…+,
=+…++,
∴=+…+﹣=﹣,
∴S n=2﹣.
19.某市为了解各校(同学)课程的教学效果,组织全市各学校高二年级全体学生参加了国学知识水平测试,测试成绩从高到低依次分为A、B、C、D四个等级,随机调阅了甲、乙两所学校各60名学生的成绩,得到如图所示分布图:
(Ⅰ)试确定图中实数a与b的值;
(Ⅱ)若将等级A、B、C、D依次按照90分、80分、60分、50分转换成分数,试分别估计两校学生国学成绩的均值;
(Ⅲ)从两校获得A等级的同学中按比例抽取5人参加集训,集训后由于成绩相当,决定从中随机选2人代表本市参加省级比赛,求两人来自同一学校的概率.【考点】列举法计算基本事件数及事件发生的概率.
【分析】(Ⅰ)由甲校样本频数分布条形图能求出a,由乙校样本频率分布条形图能求出b.
(Ⅱ)由样本数据能求出甲校的平均值和乙校的平均值.
(Ⅲ)由样本数据可知集训的5人中甲校抽2人,分别记作E,F,乙校抽3人,分别记作M,N,Q,从5人中任选2人,利用列举法能求出两人来自同一学校的概率.
【解答】解:(Ⅰ)∵测试成绩从高到低依次分为A、B、C、D四个等级,
随机调阅了甲、乙两所学校各60名学生的成绩,
∴由甲校样本频数分布条形图知:
6+a+33+6=60,解得a=15,
由乙校样本频率分布条形图得:0.15+b+0.2+0.15=1,解得b=0.5.
(Ⅱ)由数据可得甲校的平均值为==67,
乙校的平均值为=90×0.15+80×0.5+60×0.2+50×0.15=73.
(Ⅲ)由样本数据可知集训的5人中甲校抽2人,分别记作E,F,乙校抽3人,分别记作M,N,Q,
从5人中任选2人,一共有10个基本事件,分别为:
EF,EM,EN,EQ,FM<FN,FQ,MN,MQ,NQ,
其中2 人来自同一学校包含中EF,MN<MQ<NQ,
∴两人来自同一学校的概率p=.
20.如图,三棱锥P﹣ABC中,PA=PC,底面ABC为正三角形.
(Ⅰ)证明:AC⊥PB;
(Ⅱ)若平面PAC⊥平面ABC,AB=2,PA⊥PC,求三棱锥P﹣ABC的体积.
【考点】棱柱、棱锥、棱台的体积;空间中直线与直线之间的位置关系.
【分析】(Ⅰ)取AC中点O,连接PO,BO,由等腰三角形的性质可得PO⊥AC,BO⊥AC,再由线面垂直的判定可得AC⊥平面POB,则AC⊥PB;
(Ⅱ)由面面垂直的性质可得PO⊥平面ABC,再由已知求出三角形ABC的面积,即PO的长度,代入棱锥体积公式求得三棱锥P﹣ABC的体积.
【解答】(Ⅰ)证明:如图,
取AC中点O,连接PO,BO,
∵PA=PC,∴PO⊥AC,
又∵底面ABC为正三角形,∴BO⊥AC,
∵PO∩OB=O,∴AC⊥平面POB,则AC⊥PB;
(Ⅱ)解:∵平面PAC⊥平面ABC,且平面PAC∩平面ABC=AC,
PO⊥AC,∴PO⊥平面ABC,
又AB=2,PA⊥PC,可得PO=1,且.
∴.
21.已知圆C:(x﹣6)2+y2=20,直线l:y=kx与圆C交于不同的两点A、B.(Ⅰ)求实数k的取值范围;
(Ⅱ)若=2,求直线l的方程.
【考点】直线与圆的位置关系.
【分析】(Ⅰ)根据题意可得圆心C(6,0)到直线l:y=kx的距离小于半径,由此求得k的范围.
(Ⅱ)把直线l:y=kx代入圆C,化简后利用韦达定理,再根据=2,可得x2=2x1,从而求得k的值,可得直线l的方程.
【解答】解:(Ⅰ)由题意可得,圆心C(6,0)到直线l:y=kx的距离小于半径
,
即<,求得﹣<k<.
(Ⅱ)把直线l:y=kx代入圆C:(x﹣6)2+y2=20,化简可得(1+k2)x2﹣12x+16=0,
∴x1+x2=,x1?x2=.
若=2,则x2=2x1,则x1=,x2=,∴则x1?x2=?=,∴k=±1,
故直线l:y=±x.
22.已知函数f(x)=alnx+x2﹣x,其中a∈R.
(Ⅰ)若a<0,讨论f(x)的单调性;
(Ⅱ)当x≥1时,f(x)≥0恒成立,求a的取值范围.
【考点】利用导数求闭区间上函数的最值;利用导数研究函数的单调性.
【分析】(I)令f′(x)=0求出f(x)的极值点,结合f(x)的定义域得出f′(x)的符号变换情况,从而得出f(x)的单调性;
(II)对a进行讨论,判断f(x)在[1,+∞)上的单调性,得出f(x)在[1,+∞)上的最小值f min(x),即可得出结论.
【解答】解:(I)f(x)的定义域为(0,+∞),
f′(x)==,
令f′(x)=0得2x2﹣x+a=0,
解得x1=,x2=,
∵a<0,∴x1<0,x2>0,
∴当0<x<时,f′(x)<0,当x>时,f′(x)>0,
∴f(x)在(0,)上单调递减,在(,+∞)上单调递增.(II)若a=0时,f(x)=x2﹣x,
∴f(x)在[1,+∞)上单调递增,∴f min(x)=f(1)=0,符合题意.
若a<0,由(I)可知f(x)在(0,)上单调递减,在(,+∞)上单调递增,
当≤1即﹣1≤a<0时,f(x)在[1,+∞)上单调递增,
∴f min(x)=f(1)=0,符合题意,
当>1即a<﹣1时,f(x)在[1,)上单调递减,在[,+∞)上单调递增,
∴f min(x)=f()<f(1)=0,不符合题意.
若a>0,令f′(x)=0得2x2﹣x+a=0,
∴当△=1﹣8a≤0即a时,f′(x)≥0恒成立,∴f(x)在[1,+∞)上单调递增,
∴f min(x)=f(1)=0,符合题意.
若0,则2x2﹣x+a=0有两正实数解,x1=,x2=,
∴f(x)在(0,)上单调递增,在(,)上单调递
减,在(,+∞)上单调递增,
∵<1,∴f(x)在[1,+∞)上单调递增,
∴f min(x)=f(1)=0,符合题意,
综上,a的取值范围是[﹣1,+∞).
2017年4月3日