
八年级上册三角形解答题专题练习(word 版
一、八年级数学三角形解答题压轴题(难)
1.如图1,直线MN 与直线AB 、CD 分别交于点E 、F ,1∠与2∠互补.
(1)试判断直线AB 与直线CD 的位置关系,并说明理由.
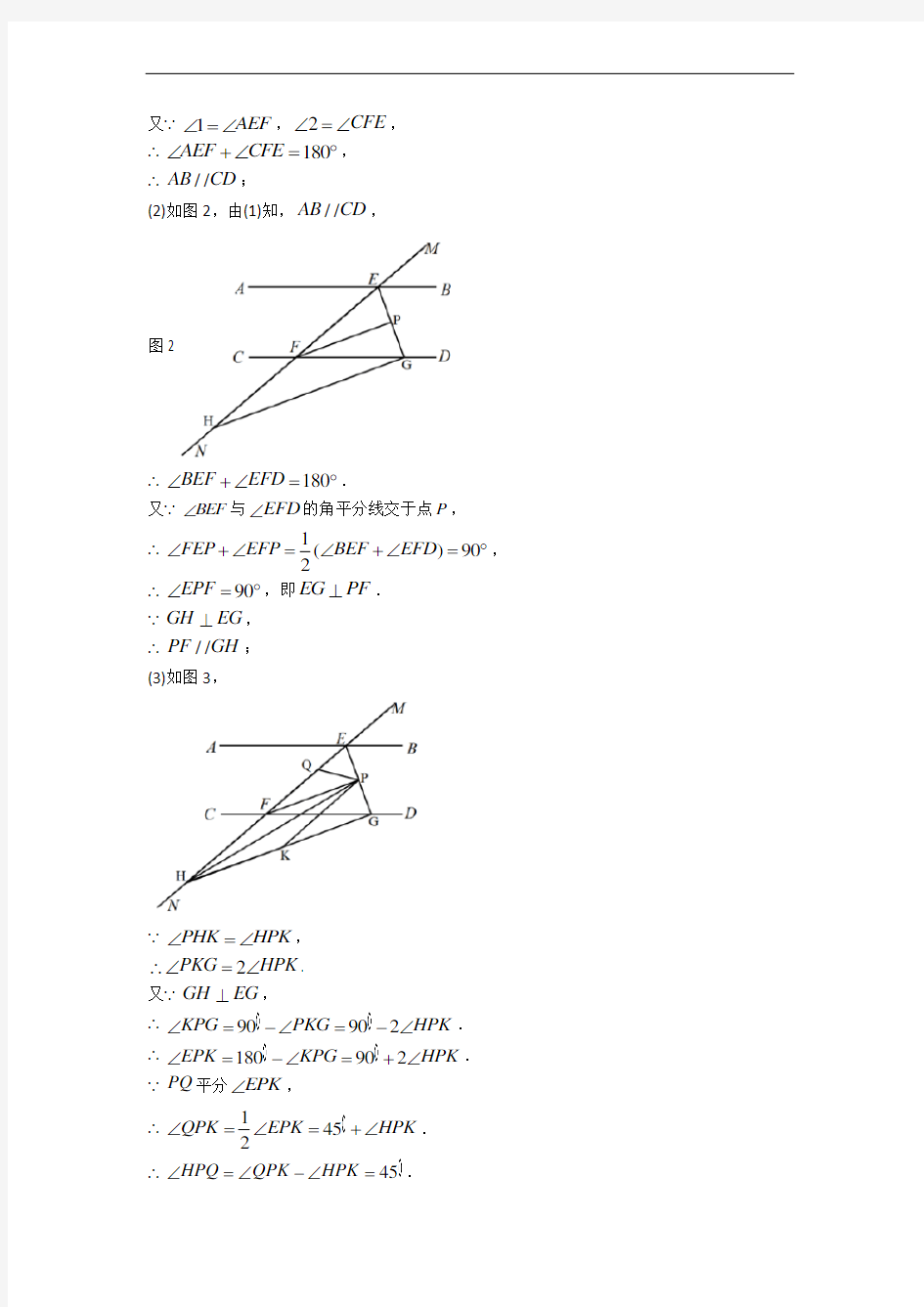
(2)如图2,BEF ∠与EFD ∠的角平分线交于点P ,EP 与CD 交于点G ,点H 是MN 上一点,且GH EG ⊥,求证://PF GH .
(3)如图3,在(2)的条件下,连接PH ,K 是GH 上一点使PHK HPK ∠=∠,作PQ 平分
EPK ∠,求HPQ ∠的度数.
【答案】(1)AB//CD ,理由见解析;(2)证明见解析;(3)45HPQ ∠=. 【解析】 【分析】
(1)利用对顶角相等、等量代换可以推知同旁内角∠AEF 、∠CFE 互补,即可证明; (2)利用(1)中平行线的性质、角平分线的性质、三角形内角和定理可得∠EPF=90°,即EG ⊥PF ,再结合GH ⊥EG ,即可证明;
(3)利用三角形外角定理、三角形内角和定理求得∠A=90°-∠3=90°-2∠2;然后由邻补角的定义、角平分线的定义推知∠QPK=-1
2
∠EPK=45°+∠2,最后根据角与角间的和差关系即可求解. 【详解】 (1)//AB CD , 理由如下:如图1,
图1
∵1∠与2∠互补, ∴12180∠+∠=?,
又∵1AEF ∠=∠,2CFE ∠=∠, ∴180AEF CFE ∠+∠=?, ∴//AB CD ;
(2)如图2,由(1)知,//AB CD ,
图2
∴180BEF EFD ∠+∠=?.
又∵BEF ∠与EFD ∠的角平分线交于点P , ∴1
(2
)90FEP EFP BEF EFD ∠+∠=
∠+∠=?, ∴90EPF ∠=?,即EG PF ⊥. ∵GH EG ⊥, ∴//PF GH ; (3)如图3,
∵PHK HPK ∠=∠,
2PKG HPK ∴∠=∠. 又∵GH EG ⊥,
∴90902KPG PKG HPK ∠=-∠=-∠. ∴180902EPK KPG HPK ∠=-∠=+∠. ∵PQ 平分EPK ∠, ∴1
452
QPK EPK HPK ∠=
∠=+∠. ∴45HPQ QPK HPK ∠=∠-∠=.
【点睛】
本题主要考查了平行线的判定与性质、角平分线的性质、三角形内角和定理等知识.解题过程关注中“数形结合”思想是解答本题的关键.
2.已知在四边形ABCD中,∠A=∠C=90°.
(1)∠ABC+∠ADC=°;
(2)如图①,若DE平分∠ADC,BF平分∠ABC的外角,请写出DE与BF的位置关系,并证明;
(3)如图②,若BE,DE分别四等分∠ABC、∠ADC的外角(即∠CDE=1
4
∠CDN,∠CBE
=1
4
∠CBM),试求∠E的度数.
【答案】(1)180°;(2)DE⊥BF;(3)450
【解析】
【分析】
(1)根据四边形内角和等于360°列式计算即可得解;
(2)延长DE交BF于G,根据角平分线的定义可得∠CDE=1
2
∠ADC,∠CBF=
1
2
∠CBM,
然后求出∠CDE=∠CBF,再利用三角形的内角和定理求出∠BGE=∠C=90°,最后根据垂直的定义证明即可;
(3)先求出∠CDE+∠CBE,然后延长DC交BE于H,再根据三角形的一个外角等于与它不相邻的两个内角的和求解即可.
【详解】
(1)解:∵∠A=∠C=90°,
∴∠ABC+∠ADC=360°-90°×2=180°;
故答案为180°;
(2)解:延长DE交BF于G,
∵DE平分∠ADC,BF平分∠CBM,
∴∠CDE=1
2
∠ADC,∠CBF=
1
2
∠CBM,
又∵∠CBM=180°-∠ABC=180°-(180°-∠ADC)=∠ADC,∴∠CDE=∠CBF,
又∵∠BED=∠CDE+∠C=∠CBF+∠BGE,
∴∠BGE=∠C=90°,
∴DG⊥BF,
即DE⊥BF;
(3)解:由(1)得:∠CDN+∠CBM=180°,∵BE、DE分别四等分∠ABC、∠ADC的外角,
∴∠CDE+∠CBE=1
4
×180°=45°,
延长DC交BE于H,
由三角形的外角性质得,∠BHD=∠CDE+∠E,∠BCD=∠BHD+∠CBE,
∴∠BCD=∠CBE+∠CDE+∠E,
∴∠E=90°-45°=45°
【点睛】
本题考查了三角形的内角和定理,四边形的内角和定理,角平分线的定义,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质是解题的关键,要注意整体思想的利用.
3.在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.如,三个内角分别为120°,40°,20°的三角形是“灵动三角形”.
如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°< ∠OAC < 90°).
(1)∠ABO的度数为°,△AOB(填“是”或“不是”灵动三角形);
(2)若∠BAC=60°,求证:△AOC为“灵动三角形”;
(3)当△ABC为“灵动三角形”时,求∠OAC的度数.
【答案】(1)30°;(2)详见解析;(3)∠OAC=80°或52.5°或30°.
【解析】
【分析】
(1)根据垂直的定义、三角形内角和定理求出∠ABO的度数,根据“智慧三角形”的概念判
断;
(2)根据“智慧三角形”的概念证明即可;
(3)分点C在线段OB和线段OB的延长线上两种情况,根据“智慧三角形”的定义计算.【详解】
(1)答案为:30°;是;
(2)∵AB⊥OM
∴∠B AO=90°
∵∠BAC=60°
∴∠OAC=∠B AO-∠BAC=30°
∵∠MON=60°
∴∠ACO=180°-∠OAC-∠MON=90°
∴∠ACO=3∠OAC,
∴△AOC为“灵动三角形”;
(3)设∠OAC= x°则∠BAC=90-x, ∠ACB=60+x ,∠ABC=30°
∵△ABC为“智慧三角形”,
Ⅰ、当∠ABC=3∠BAC时,°,
∴30=3(90-x),∴x=80
Ⅱ、当∠ABC=3∠ACB时,
∴30=3(60+x)∴x= -50 (舍去)
∴此种情况不存在,
Ⅲ、当∠BCA=3∠BAC时,
∴60+x=3(90-x),
∴x=52.5°,
Ⅳ、当∠BCA=3∠ABC时,
∴60+x=90°,
∴x=30°,
Ⅴ、当∠BAC=3∠ABC时,
∴90-x=90°,
∴x=0°(舍去)
Ⅵ、当∠BAC=3∠ACB时,
∴90-x=3(60+x),
∴x= -22.5(舍去),
∴此种情况不存在,
∴综上所述:∠OAC=80°或52.5°或30°。
【点睛】
考查的是三角形内角和定理、“智慧三角形”的概念,用分类讨论的思想解决问题是解本题的关键.
4.(1)如图1.在△ABC中,∠B=60°,∠DAC和∠ACE的角平分线交于点O,则
∠O = °,
(2)如图2,若∠B =α,其他条件与(1)相同,请用含α的代数式表示∠O 的大小; (3)如图3,若∠B =α,11
,PAC DAC PCA E n n
AC ∠=∠∠=∠,则∠P = (用含α的代数式表示).
【答案】(1)∠O =60°;(2)90°-12α;(3)11(1)180P n n
α∠=-?- 【解析】 【分析】
(1)由题意利用角平分线的性质和三角形内角和为180°进行分析求解;
(2)根据题意设∠BAC=β,∠ACB=γ,则α+β+γ=180°,利用角平分线性质和外角定义找等量关系,用含α的代数式表示∠O 的大小;
(3)利用(2)的条件可知n=2时,∠P=
1
11-1802
2
α?
?-(),再将2替换成n 即可分析求解. 【详解】
解:(1)因为∠DAC 和∠ACE 的角平分线交于点O ,且∠B=60°, 所以18060120OAC OCA οοο∠+∠=-=, 有∠O=180120οο-=60°.
(2)设∠BAC=β,∠ACB=γ,则α+β+γ=180° ∵∠ACE 是△ABC 的外角, ∴∠ACE=∠B+∠BAC=α+β ∵CO 平分∠ACE
11
()22
ACO ACE αβ∴∠=
∠=+ 同理可得:1
()2
CAO αγ∠=
+ ∵∠O+∠ACO+∠CAO=180°,
∴11
180180()()22
O ACO CAO αβαγ?
?
∠=-∠-∠=-
+-+ 1180()2αβαγ?=-+++111
180()1809090222
αβααα????=-++=--=-;
(3)∵∠B=α,
11
,
PAC DAC PCA E
n n
AC
∠=∠∠=∠,
由(2)可知n=2时,有∠P=
1
18090
2
α
??
--=
11
1-180
22
α
?
?-
(),将2替换成n即可,
∴11
(1)180
P
n n α
∠=-?-.
【点睛】
本题考查用代数式表示角,熟练掌握并综合利用角平分线定义和三角形内角和为180°以及等量替换技巧与数形结合思维分析是解题的关键.
5.(1)如图1,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
①写出图中一对全等的三角形,并写出它们的所有对应角;
②设AED
∠的度数为x,∠ADE的度数为y,那么∠1,∠2的度数分别是多少?(用含有x或y的代数式表示)
③∠A与∠1、∠2之间有一种数量关系始终保持不变,请找出这个规律.
(2)如图2,把△ABC纸片沿DE折叠,当点A落在四边形BCDE外部时,∠A与∠1、∠2的数量关系是否发生变化?如果发生变化,求出∠A与∠1、∠2的数量关系;如果不发生变化,请说明理由.
【答案】(1)①△EAD≌△EA′D,其中∠EAD=∠EA′D,∠AED=∠A′ED,∠ADE=∠A′DE;
②∠1=180°?2x,∠2=180°?2y;③∠A=1
2
(∠1+∠2);(2)变化,∠A=
1
2
(∠2-∠1),
见详解
【解析】
【分析】
(1)①根据翻折方法可得△ADE≌△A′DE;
②根据翻折方法可得∠AEA′=2x,∠ADA′=2y,再根据平角定义可得∠1=180°-2x,∠2=180°-2y;
③首先由∠1=180°-2x,2=180°-2y,可得x=90-1
2
∠1,y=90-
1
2
∠2,再根据三角形内角
和定理可得∠A=180°-x-y,再利用等量代换可得∠A=1
2
(∠1+∠2);
(2)根据折叠的性质和三角形内角和定理解答即可.【详解】
(1)①根据翻折的性质知△EAD ≌△EA ′D ,
其中∠EAD =∠EA ′D ,∠AED =∠A ′ED ,∠ADE =∠A ′DE ; ②)∵∠AED=x,∠ADE=y, ∴∠AEA′=2x,∠ADA′=2y, ∴∠1=180°-2x ,∠2=180°-2y ; ③∠A=
1
2
(∠1+∠2); ∵∠1=180°-2x ,∠2=180°-2y , ∴x=90-
12∠1,y=90-1
2
∠2, ∴∠A=180°-x-y=190-(90-
12∠1)-(90-12∠2)=1
2
(∠1+∠2). (2))∵△A′DE 是△ADE 沿DE 折叠得到, ∴∠A′=∠A,
又∵∠AEA′=180°-∠2,∠3=∠A′+∠1, ∴∠A+∠AEA′+∠3=180°,
即∠A+180°-∠2+∠A′+∠1=180°, 整理得,2∠A=∠2-∠1.
∴∠A=
1
2(∠2-∠1). 【点睛】
此题主要考查了翻折变换,关键是掌握折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
6.如图①,在△ABC 中,CD 、CE 分别是△ABC 的高和角平分线,∠BAC =α,∠B =β(α>β).
(1)若α=70°,β=40°,求∠DCE 的度数;
(2)试用α、β的代数式表示∠DCE 的度数(直接写出结果);
(3)如图②,若CE 是△ABC 外角∠ACF 的平分线,交BA 延长线于点E ,且α﹣β=30°,求∠DCE 的度数.
【答案】(1)15°;(2)DCE 2
αβ
-∠=;(3)75°.
【解析】 【分析】
(1)三角形的内角和是180°,已知∠BAC 与∠ABC 的度数,则可求出∠BAC 的度数,然后
根据角平分线的性质求出∠BCE ,再利用三角形的一个外角等于和它不相邻的两个内角的和求出∠DEC 的度数,进而求出∠DCE 的度数; (2)∠DCE =
2
αβ
- .
(3)作∠ACB 的内角平分线CE′,根据角平分线的性质求出∠ECE′=∠ACE+∠ACE′=12∠ACB+1
2
∠ACF=90°,进而求出∠DCE 的度数. 【详解】
解:(1)因为∠ACB =180°﹣(∠BAC+∠B )=180°﹣(70°+40°)=70°, 又因为CE 是∠ACB 的平分线,
所以1
352
ACE ACB ∠=
∠=?. 因为CD 是高线, 所以∠ADC =90°,
所以∠ACD =90°﹣∠BAC =20°,
所以∠DCE =∠ACE ﹣∠ACD =35°﹣20°=15°. (2)DCE 2
αβ
-∠=
.
(3)如图,作∠ACB 的内角平分线CE′, 则152
DCE αβ
-'=
=?∠.
因为CE 是∠ACB 的外角平分线,
所以∠ECE′=∠ACE+∠ACE′=11+22ACB ACF ∠∠=1
(+)2
ACB ACF ∠∠=90°, 所以∠DCE =90°﹣∠DCE′=90°﹣15°=75°. 即∠DCE 的度数为75°.
【点睛】
本题考查三角形外角的性质及三角形的内角和定理,解答的关键是沟通外角和内角的关系.解决(3),作辅助线是关键.
7.Rt △ABC 中,∠C=90°,点D 、E 分别是△ABC 边AC 、BC 上的点,点P 是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P 在线段AB 上,如图(1)所示,且∠α=50°,则∠1+∠2= °;
(2)若点P 在边AB 上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为: ;
(3)若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.
(4)若点P运动到△ABC形外,如图(4)所示,则∠α、∠1、∠2之间的关系为:.【答案】(1)140°;(2)∠1+∠2=90°+α;(3)∠1=90°+∠2+α,理由见解
析;(4)∠2=90°+∠1﹣α.
【解析】
试题分析:(1)根据四边形内角和定理以及邻补角的定义,得出∠1+∠2=∠C+∠α,进而得出即可;
(2)利用(1)中所求的结论得出∠α、∠1、∠2之间的关系即可;
(3)利用三角外角的性质,得出∠1=∠C+∠2+α=90°+∠2+α;
(4)利用三角形内角和定理以及邻补角的性质可得出∠α、∠1、∠2之间的关系.
试题分析:(1)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+∠α+∠CDP+∠CEP=360°,∴∠1+∠2=∠C+∠α,
∵∠C=90°,∠α=50°,
∴∠1+∠2=140°,
故答案为140;
(2)由(1)得∠α+∠C=∠1+∠2,
∴∠1+∠2=90°+∠α.
故答案为∠1+∠2=90°+∠α.
(3)∠1=90°+∠2+∠α.理由如下:如图③,
设DP与BE的交点为M,
∵∠2+∠α=∠DME,∠DME+∠C=∠1,
∴∠1=∠C+∠2+∠α=90°+∠2+∠α.
(4)如图④,
设PE与AC的交点为F,
∵∠PFD=∠EFC,
∴180°-∠PFD=180°-∠EFC,
∴∠α+180°-∠1=∠C+180°-∠2,
∴∠2=90°+∠1-∠α.
故答案为∠2=90°+∠1-∠α
点睛:本题考查了三角形内角和定理和外角的性质、对顶角相等的性质,熟练掌握三角形外角的性质是解决问题的关键.
8.我校快乐走班数学兴趣小组开展了一次活动,过程如下:设∠BAC=θ(0°<θ<90°)小棒依次摆放在两射线之间,并使小棒两端分别落在两射线上.
活动一:如图甲所示,从点A1开始,依次向右摆放小棒,使小棒与小棒在端点处互相垂直,A1A2为第1根小棒.
数学思考:
(1)小棒能无限摆下去吗?答:.(填“能“或“不能”)
(2)设AA1=A1A2=A2A3=1.则θ=度;
活动二:如图乙所示,从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第1根小棒,且A1A2=AA1.
数学思考:
(3)若只能摆放5根小棒,求θ的范围.
【答案】(1)能.(2)θ=22.5;(3) 15°≤θ<18°.
【解析】
【分析】
(1)根据已知条件:小棒两端能分别落在两射线上进行判断即可;
(2)根据等腰三角形的性质和三角形的外角性质即得结果;
(3)根据等腰三角形的性质和三角形的内角和定理可得关于θ的不等式组,解不等式组即得结果.
【详解】
(1)∵根据已知条件∠BAC=θ(0°<θ<90°)小棒两端能分别落在两射线上,
∴小棒能继续摆下去;
(2)∵A1A2=A2A3,A1A2⊥A2A3,
∴∠A2A1A3=45°,
∴∠AA2A1+∠θ=45°,
∵∠AA2A1=∠θ,
∴∠θ=22.5°;
(3)如图乙,∵A2A1=A2A3,∴∠A2A3A1=∠A2A1A3=2θ°,
∵A2A3=A4A3,∴∠A3A2A4=∠A3A2A4=3θ°,
∵A4A3=A4A5,∴∠A4A3A5=∠A4A5A3=4θ°,
根据三角形内角和定理和等腰三角形的性质,可得6θ?90°,5θ<90°,
∴15°?θ<18°.
【点睛】
本题考查了等腰三角形的性质、三角形内角和定理和三角形的外角性质,根据题意找出规律并结合等腰三角形的性质是解题的关键.
9.等边△ABC边长为6,P为BC上一点,含30°、60°的直角三角板60°角的顶点落在点P上,使三角板绕P点旋转。
(1)如图1,当P为BC的三等分点,且PE⊥AB时,判断△EPF的形状;并说明理由;(2)在(1)问的条件下,FE、PB的延长线交于点G,如图2,求△EGB的面积.
【答案】(1)△EPF 是等边三角形,理由见解析;(2)S △GBE =3. 【解析】
试题分析:(1)要证三角形EPF 是等边三角形,已知∠EPF=60°,只需要证PE=PF 即可,可通过证△PBE 和△PFC 全等来得出结论,是证明全等,则需要证明FP ⊥BC 和BE=PC ;
(2)由(1)不难得出∠CFG=90°,那么在△CFG 中,有∠C 的度数,可以根据CF 的长求出GC 的长,从而求出GB 的长,下面的关键就是求GB 边上的高,过E 作EH ⊥BC ,那么EH 就是所求的高,在直角△BEP 中,有BP 的长,有∠ABC 的度数,可以求出BE 、EP 的长,再根据三角形面积的不同表示方法求出EH 的长,即可求出△GBE 的面积; 试题解析:(1)△EPF 是等边三角形,理由如下: ∵PE⊥AB,∠B=60°,因此Rt△PEB 中,BE=
12BP=1
3
BC=PC ,∴∠BPE=30°,∵∠EPF=60°,∴FP⊥BC,∵∠B=∠C=60°,BE=PC ,∠PEB=∠FPC=90°,∴△BEP≌△CPF,∴EP=PF,∵∠EPF=60°,∴△EPF 是等边三角形. (2)过E 作EH⊥BC 于H ,由(1)可知:FP⊥BC,FC=BP=
23BC=4,BE=CP=1
3
BC=2,在三角形FCP 中,∠PFC=90°-∠C=30°,∵∠PFE=60°,∴∠GFC=90°,Rt△FGC 中,∠C=60°,CF=4,∴GC=2CF=8,∴GB=GC -BC=2,Rt△BEP 中∠EBP=60°,BP=4,∴PE=23,BE=2,∴EH=BE?PE÷BP=3,∴S △GBE =
1
2
BG?EH=3. 点睛:本题主要考查了全等三角形的判定和等边三角形的性质,熟练掌握全靠三角形的判定方法和等边三角形的性质是解题的关键.
10.如图 (1)所示,AB ,CD 是两条线段,M 是AB 的中点,连接AD ,MD ,BC ,BD , MC ,AC ,S △DMC ,S △DAC 和S △DBC 分别表示△DMC ,△DAC ,△DBC 的面积,当AB ∥CD 时,有S △DMC =
2
DAC
DBC
S
S +.
(1)如图 (2)所示,当图6-9(1)中AB 与CD 不平行时,S △DMC =2
DBC
DAC
S
S +是否仍然成立?请
说明理由;
(2)如图 (3)所示,当图6-9(1)中AB 与CD 相交于点O 时,S △DMC 与S △DAC ,S △DBC 有什么样的数量关系?试说明你的结论.
【答案】(1) S △DMC =2
DAC
DBC
S
S +仍成立,理由见解析; (2)S △DMC =
2
DBC
DAC
S
S -,理由见
解析. 【解析】 【分析】
(1)先看题中给出的条件为何成立,由于三角形ADC ,DMC ,DBC 都是同底,而由于AB ∥DC ,因此高相等,就能得出题中给出的结论,那么本题也要用高来求解,过A ,M ,B 分别作BC 的垂线AE ,MN ,BF ,AE ∥MN ∥BF ,由于M 是AB 中点,因此MN 是梯形AEFB 的中位线,因此MN=
1
2
(AE+BF ),三个三角形同底因此结论①是成立的. (2)本题可以利用AM=MB ,让这两条边作底边来求解,三角形ADB 中,小三角形的AB 边上的高都相等,那么三角形ADM 和DBM 的面积就相等(等底同高),因此三角形OAD ,OMD 的和就等于三角形BMD 的面积,同理三角形AOC 和OMC 的面积和等于三角形CMB 的面积.根据这些等量关系即可得出题中三个三角形的面积关系. 【详解】
(1)当AB 与CD 不平行时,S △DMC =
2
DAC
DBC
S
S +仍成立.分别过点A ,M ,B 作CD 的垂线
AE ,MN ,BF ,垂足分别为E ,N ,F.∵M 为AB 的中点,∴MN =
12(AE+BF),∴S △DAC +S △DBC =12DC·AE+12DC·BF =12
DC·(AE+BF)= 12
DC·2MN=DC·MN=2S △DMC .∴S △DMC =2
DAC
DBC
S S +;
(2)S △DMC =
2
DBC
DAC
S
S -.理由:∵M 是AB 的中点,∴S △ADM =S △BDM ,S △ACM =S △BCM ,而
S △DBC =S △BDM +S △BCM +S △DMC ,① S △DAC =S △ADM +S △ACM -S △DMC ,②∴①-②得S △DBC -S △DAC =2S △DMC ,故S △DMC =
2
DBC
DAC
S
S -.
【点睛】
本题考查了三角形中位线和梯形,解题的关键是掌握三角形中位线定理和梯形的概念.