
四边形几何证明精选
一、解答题
1.已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时旋转,它的两边分别交
CB,DC(或它们的延长线)于点M,N.当∠MAB绕点A旋转到BM=DN时(如图1),易证BM+DN=MN.
(1)当∠MAN旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量
关系?写出猜想,并加以证明.
(2)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的
数量关系?请写出你的猜想,并加以证明.
2.如图,矩形ABCD中,AB>AD,把矩形沿对角线AC
所在直线折叠,使点B落在点E处,AE交CD于点F,
连接DE.
(1)求证:△ADE≌△CED;
(2)求证:△DEF是等腰三角形.
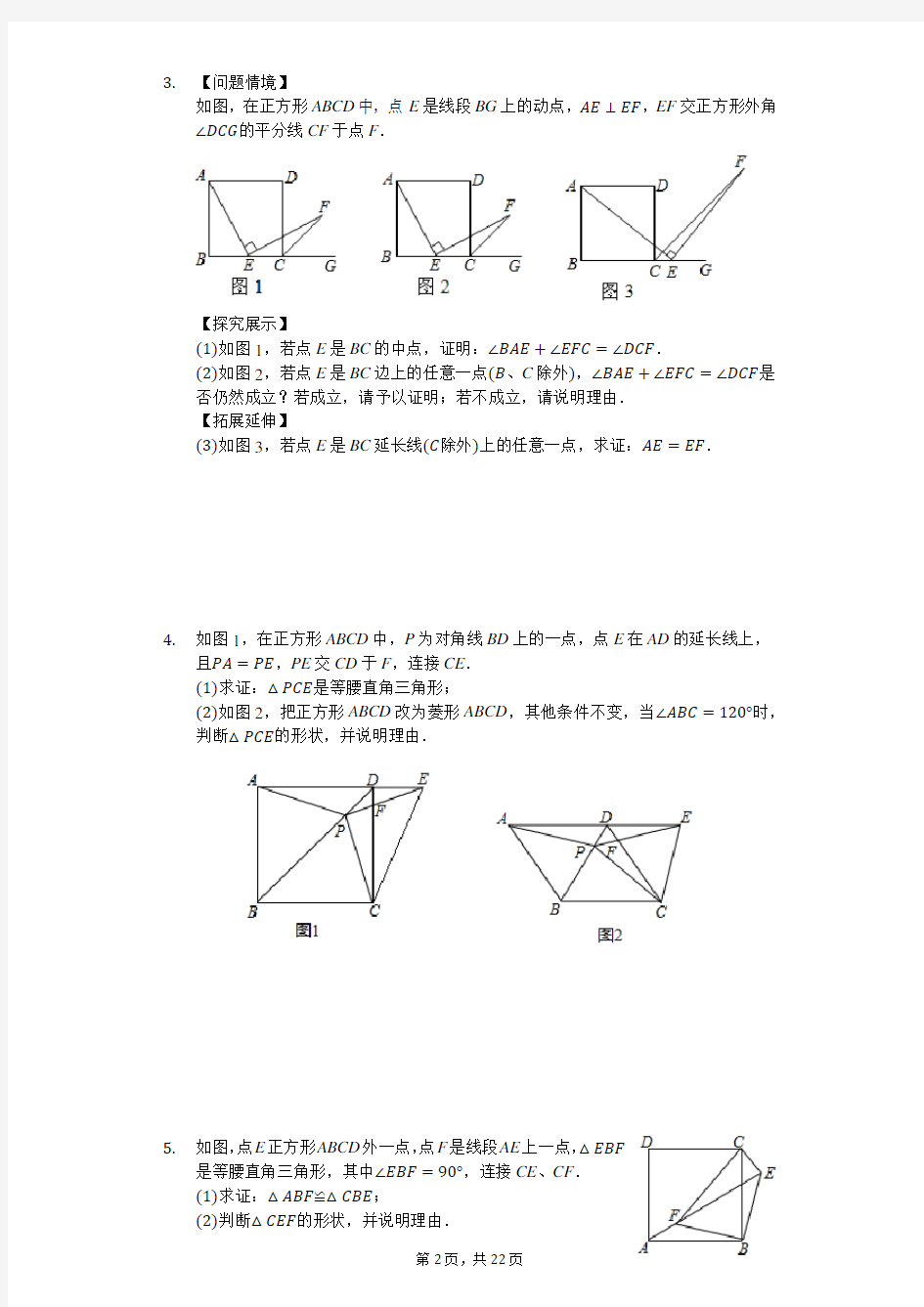
3.【问题情境】
如图,在正方形ABCD中,点E是线段BG上的动点,AE⊥EF,EF交正方形外角∠DCG的平分线CF于点F.
【探究展示】
(1)如图1,若点E是BC的中点,证明:∠BAE+∠EFC=∠DCF.
(2)如图2,若点E是BC边上的任意一点(B、C除外),∠BAE+∠EFC=∠DCF是
否仍然成立?若成立,请予以证明;若不成立,请说明理由.
【拓展延伸】
(3)如图3,若点E是BC延长线(C除外)上的任意一点,求证:AE=EF.
4.如图1,在正方形ABCD中,P为对角线BD上的一点,点E在AD的延长线上,
且PA=PE,PE交CD于F,连接CE.
(1)求证:△PCE是等腰直角三角形;
(2)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,
判断△PCE的形状,并说明理由.
5.如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF
是等腰直角三角形,其中∠EBF=90°,连接CE、CF.
(1)求证:△ABF≌△CBE;
6.如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),
以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.
(1)猜想图1中线段BG、线段DE的长度关系及所在直线的位置关系,不必证明;
(2)将图1中的正方形CEFG绕着点C按顺时针方向旋转任意角度α,得到如图2
情形.请你通过观察、测量等方法判断(1)中得到的结论是否仍然成立,并证明你的判断.
7.如图,在正方形ABCD中,点E是边AD上任意一点,BE
的垂直平分线FG交对角AC于点F.求证:
(1)BF=DF;
(2)BF⊥FE.
8.如图所示,E、F分别为平行四边形ABCD边AB、CD
的中点,AG//DB交CB的延长线于点G.
(1)求证:DE//BF;
(2)若∠G=90°,判断四边形DEBF的形状,并说明理
由.
9.如图,把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′(此时,点B′
落在对角线AC上,点A′落在CD的延长线上),A′B′交AD于点E,连接AA′、CE.求证:(1)△ADA′≌△CDE;
(2)直线CE是线段AA′的垂直平分线.
10.如图,在?ABCD中,已知E为BC的中点,连接AE并延长交DC的延长线于点F,
连接BF.
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.
11.如图,△ABC中,AB=AC,AD是∠BAC的角平分线,
点O为AB的中点,连接DO并延长到点E,使OE=OD,
连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,
并说明理由.
12.已知:如图,在四边形ABCD中,点G在边BC的延长线上,CE平分∠BCD,CF
平分∠GCD,EF//BC交CD于点O.
(1)求证:OE=OF;
(2)若点O为CD的中点,求证:四边形DECF是矩形.
13.如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,
AB上的中点,连接DE并延长至点F,使EF=2DE,连
接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理
由.
14.如图1,四边形ABCD是正方形,点G是BC边上任意一点.DE⊥AG于点E,BF//DE
且交AG于点F.
(1)求证:AE=BF;
(2)如图2,如果点G是BC延长线上一点,其余条件不变,则线段AF、BF、EF
有什么数量关系?请证明出你的结论.
15.如图,在△ABC中,∠ABC=90°,点D为AC的中点,过点C作CE⊥BD于点E,
过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
(1)证明:四边形BDFG是菱形;
(2)若AC=10,CF=6,求线段AG的长度.
16.已知正方形ABCD中,对角线AC、BD相交于O.
①如图1,若E是AC上的点,过A作AG⊥BE于G,AG、BD交于F,求证:OE=OF
②如图2,若点E在AC的延长线上,AG⊥EB交EB的延长线于G,AG延长DB
延长线于点F,其它条件不变,OE=OF还成立吗?
17.如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、
DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请
说明理由.
18.如图,EF是平行四边ABCD的对角线BD的垂直平分线,EF与边AD,BC分别交于
点E,F.
(1)求证:四边形BFDE是菱形;
(2)若ED=5,BD=8,求菱形BFDE的面积.
19.如图,已知平行四边形ABCD,过A作AM⊥BC于M,
交BD于E,过C作CN⊥AD于F,连接AF、CE.
(1)求证:四边形AECF为平行四边形;
(2)当四边形AECF为菱形,M点为BC的中点时,求
∠CBD的度数.
20.如图,在矩形ABCD中,E为AB边上一点,EC平分∠DEB,F为CE的中点,连
接AF,BF,过点E作EH//BC分别交AF,CD于G,H两点.
(1)求证:DE=DC;
(2)求证:AF⊥BF;
答案和解析
1.【答案】解:(1)BM +DN =MN 成立.
证明:如图,把△ADN 绕点A 顺时针旋转90°,
得到△ABE ,则可证得E 、B 、M 三点共线(图形画正确).
∴∠EAM =90°?∠NAM =90°?45°=45°,
又∵∠NAM =45°,
∴在△AEM 与△ANM 中,
{AE =AN ∠EAM =∠NAM AM =AM
,
∴△AEM≌△ANM(SAS),
∴ME =MN ,
∵ME =BE +BM =DN +BM ,
∴DN +BM =MN ;
(2)DN ?BM =MN .
在线段DN 上截取DQ =BM ,
在△ADQ 与△ABM 中,
∵{AD =AB
∠ADQ =∠ABM DQ =MB
,
∴△ADQ≌△ABM(SAS),
∴∠DAQ =∠BAM ,
∴∠QAN =∠MAN .
在△AMN 和△AQN 中,
{AQ =AM ∠QAN =∠MAN AN =AN
,
∴△AMN≌△AQN(SAS),
∴MN =QN ,
∴DN ?BM =MN .
【解析】(1)结论:BM +DN =MN 成立,证得B 、
E 、M 三点共线即可得到△AEM≌△ANM ,从而证得ME =MN .
(2)结论:DN ?BM =MN.首先证明△ADQ≌△ABM ,得DQ =BM ,再证明△AMN≌△AQN(SAS),得MN =QN ,
本题考查正方形的性质、旋转变换等知识,解题的关键是学会利用旋转法添加辅助线,构造全等三角形解决问题,属于中考常考题型.
2.【答案】证明:(1)∵四边形ABCD 是矩形,
∴AD =BC ,AB =CD .
由折叠的性质可得:BC =CE ,AB =AE ,
∴AD =CE ,AE =CD .
在△ADE 和△CED 中,{AD =CE
AE =CD ,
∴△ADE≌△CED(SSS).
(2)由(1)得△ADE≌△CED,
∴∠DEA=∠EDC,即∠DEF=∠EDF,
∴EF=DF,
∴△DEF是等腰三角形.
【解析】(1)根据矩形的性质可得出AD=BC、AB=CD,结合折叠的性质可得出AD= CE、AE=CD,进而即可证出△ADE≌△CED(SSS);
(2)根据全等三角形的性质可得出∠DEF=∠EDF,利用等边对等角可得出EF=DF,由此即可证出△DEF是等腰三角形.
本题考查了全等三角形的判定与性质、翻折变换以及矩形的性质,解题的关键是:(1)根据矩形的性质结合折叠的性质找出AD=CE、AE=CD;(2)利用全等三角形的性质找出∠DEF=∠EDF.
3.【答案】(1)证明:取AB的中点M,连结EM,如图1:
∵M是AB的中点,E是BC的中点,
∴在正方形ABCD中,AM=EC,
∵CF是∠DCG的平分线,
∴∠ECF=90°+45°=135°,
∵BM=BE,∴∠BME=45°,
∴∠AME=∠ECF=135°,
∵∠BEA+∠CEF=90°,∠MAE+∠BEA=90°,
∴∠MAE=∠CEF,
在△AME与△ECF中,
{∠MAE=∠CEF AM=EC
∠AME=∠ECF
,
∴△AME≌△ECF(ASA),
∴∠BAE+∠EFC=∠FCG=∠DCF;
(2)证明:取AB上的任意一点M,使得AM=EC,连结EM,如图2:
∵AE⊥EF,AB⊥BC,
∴∠BAE+∠BEA=90°,∠BEA+∠CEF=90°,
∴∠MAE=∠CEF,
∵AM=EC,
∴在正方形ABCD中,BM=BE,
∴∠AME=∠ECF=135°,
{∠MAE=∠CEF AM=EC
∠AME=∠ECF
,
∴△AME≌△ECF(ASA),
∴∠BAE+∠EFC=∠FCG=∠DCF;
(3)证明:取BA延长线上的一点N使得AN=CE,如图3:
∵AN=CE,AB⊥BC,
∴∠ANE=45°,
∴∠ECF=∠ANE=45°,
∵AD//BE,
∴∠DAE=∠BEA,
∵NA⊥AD,AE⊥EF,
∴∠NAE=∠CEF,
在△ANE与△ECF中,
{∠NAE=∠CEF
AN=CE
∠ANE=∠ECF
,
∴△ANE≌△ECF(ASA),
∴AE=EF.
【解析】(1)取AB的中点M,连结EM,根据正方形的性质和全等三角形的判定证明即可;
(2)在AB上取一点M,使AM=EC,连接EM,根据已知条件利用ASA判定△AME≌△ECF,利用全等三角形的性质证明即可.
(3)在BA的延长线上取一点N,使AN=CE,连接NE,根据已知利用ASA判定△ANE≌△ECF,利用全等三角形的性质证明即可.
此题主要考查全等三角形的判定和性质,关键是熟练掌握正方形的性质,角平分线的性质及全等三角形的判定方法.
4.【答案】(1)证明:如图1中,
∵四边形ABCD是正方形,
∴AD=DC,∠ADB=∠CDB=45°,∠ADC=90°,
在△PDA和△PDC中,
{PD=PD
∠PDA=∠PDC DA=DC
,
∴△PDA≌△PDC,
∴PA=PC,∠3=∠1,
∵PA=PE,
∴∠2=∠3,
∴∠1=∠2,
∵∠EDF=90°,∠DFE=∠PFC,
∴∠FPC=∠EDF=90°,
∴△PEC是等腰直角三角形.
(2)解:如图2中,结论:△PCE是等边三角形.
理由:∵四边形ABCD是菱形,
∴AD=DC,∠ADB=∠CDB,∠ADC=∠ABC=120°,在△PDA和△PDC中,
{PD=PD
∠PDA=∠PDC DA=DC
,
∴△PDA≌△PDC,
∴PA=PC,∠3=∠1,
∵PA=PE,
∴∠2=∠3,PA=PE=PC,
∴∠1=∠2,
∵∠DFE=∠PFC,
∴∠EPC=∠EDC,
∵∠ADC=120°,
∴∠EDC=60°,
∴∠EPC=60°,
∵PE=PC,
∴△PEC是等边三角形.
【解析】本题考查正方形的性质、菱形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.
(1)由△PDA≌△PDC,推出PA=PC,∠3=∠1,由PA=PE,推出∠2=∠3,推出∠1=∠2,由∠EDF=90°,∠DFE=∠PFC,推出∠FPC=∠EDF=90°,推出△PEC是等腰直角三角形;
(2)由△PDA≌△PDC,推出PA=PC,∠3=∠1,由PA=PE,推出∠2=∠3,PA=PE= PC,推出∠1=∠2,由∠DFE=∠PFC,推出∠EPC=∠EDC,由∠ADC=120°,推出
∠EDC=60°,推出∠EPC=60°,由PE=PC,即可证明△PEC是等边三角形.
5.【答案】(1)证明:∵四边形ABCD是正方形,
∵△EBF是等腰直角三角形,其中∠EBF=90°,∴BE=BF,
∴∠ABC?∠CBF=∠EBF?∠CBF,
∴∠ABF=∠CBE.
在△ABF和△CBE中,有{AB=CB
∠ABF=∠CBE BF=BE
,
∴△ABF≌△CBE(SAS).
(2)解:△CEF是直角三角形.理由如下:
∵△EBF是等腰直角三角形,
∴∠BFE=∠FEB=45°,
∴∠AFB=180°?∠BFE=135°,
又∵△ABF≌△CBE,
∴∠CEB=∠AFB=135°,
∴∠CEF=∠CEB?∠FEB=135°?45°=90°,
∴△CEF是直角三角形.
【解析】(1)由四边形ABCD是正方形可得出AB=CB,∠ABC=90°,再由△EBF是等腰直角三角形可得出BE=BF,通过角的计算可得出∠ABF=∠CBE,利用全等三角形的判定定理SAS即可证出△ABF≌△CBE;
(2)根据△EBF是等腰直角三角形可得出∠BFE=∠FEB,通过角的计算可得出∠AFB= 135°,再根据全等三角形的性质可得出∠CEB=∠AFB=135°,通过角的计算即可得出∠CEF=90°,从而得出△CEF是直角三角形.
本题考查了正方形的性质.全等三角形的判定及性质、等腰直角三角形的性质以及角的计算,解题的关键是:(1)根据判定定理SAS证明△ABF≌△CBE;(2)通过角的计算得出∠CEF=90°.本题属于中档题,难度不大,解决该题型题目时,通过正方形和等腰三角形的性质找出相等的边,再通过角的计算找出相等的角,以此来证明两三角形全等是关键.
6.【答案】解:(1)延长BG交DE于点H,
在△BCG与△DCE中,
{BC=DC
∠BCG=∠DCE
CG=CE
,
∴△BCG≌△DCE(SAS),
∴∠GBC=∠EDC,BG=DE,
∵∠BGC=∠DGH,
∴∠DHB=∠BCG=90°,
∴BG⊥DE;
(2)BG=DE,BG⊥DE仍然成立
如图2,∠BCD+∠DCG=∠ECG+∠DCG,即∠BCG=∠DCE,
在△BCG与△DCE中,
{
BC=DC
∠BCG=∠DCE CG=CE
,
∴△BCG≌△DCE(SAS),
∵∠BHC=∠DHG,
∴∠BCD=∠DOB=90°,
即BG⊥DE
【解析】(1)延长BG交DE于点H,易证△BCG≌△DCE,所以∠GBC=∠EDC,BG=DE,所以∠DHB=90°;
(2)易证△BCG≌△DCE,所以∠GBC=∠EDC,BG=DE,所以∠BCD=90°.
本题主要考查正方形,涉及正方形的性质,旋转的性质,全等三角形的判定与性质,综合程度较高,需要学生根据所学知识灵活解答.
7.【答案】证明:如图所示:
(1)∵四边形ABCD是正方形,
∴AB=AD,∠BAF=∠DAF=45°,∠BAE=90°,
在△BAF和△DAF中,
{AB=AD?∠BAF=∠DAF?AF=AF?
,
∴△BAF≌△DAF(SAS),
∴BF=DF;
(2)∵BE的垂直平分线FG交对角AC于点F,
∴BF=EF,
∵BF=DF,
∴EF=DF,
∴∠FDE=∠FED,
∵△BAF≌△DAF,
∴∠ABF=∠FDE,
∴∠ABF=∠FED,
∵∠FED+∠FEA=180°,
∴∠ABF+∠FEA=180°,
∴∠BAE+∠BFE=180°,
∴∠BFE=90°,
∴BF⊥FE.
【解析】(1)由正方形的性质得出AB=AD,∠BAF=∠DAF=45°,由SAS证明△BAF≌△DAF,得出对应边相等即可;
(2)由线段垂直平分线的性质得出BF=EF,证出EF=DF,得出∠FDE=∠FED,再由全等三角形的性质证出∠ABF=∠FED,由邻补角关系得出∠FED+∠FEA=180°,证出∠ABF+∠FEA=180°,由四边形内角和得出∠BAE+∠BFE=180°,求出∠BFE= 90°即可.
本题考查了正方形的性质、全等三角形的判定与性质、等腰三角形的判定与性质、四边形内角和定理等知识;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.8.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AB//CD,AB=CD.
∵点E、F分别是AB、CD的中点,
∴BE=1
2AB,DF=1
2
CD.
∴BE=DF,BE//DF,
∴四边形DFBE是平行四边形,
(2)解:四边形DEBF 是菱形;理由如下:
∵∠G =90°,AG//BD ,AD//BG ,
∴四边形AGBD 是矩形,
∴∠ADB =90°,
在Rt △ADB 中
∵E 为AB 的中点,
∴AE =BE =DE ,
∵四边形DFBE 是平行四边形,
∴四边形DEBF 是菱形.
【解析】(1)根据已知条件证明BE =DF ,BE//DF ,从而得出四边形DFBE 是平行四边形,即可证明DE//BF ,
(2)先证明DE =BE ,再根据邻边相等的平行四边形是菱形,从而得出结论.
本题主要考查了平行四边形的性质、菱形的判定,直角三角形的性质:在直角三角形中斜边中线等于斜边一半,比较综合,难度适中.
9.【答案】证明:(1)∵四边形ABCD 是正方形,
∴AD =CD ,∠ADC =90°,
∴∠A′DE =90°,
根据旋转的方法可得:∠EA′D =45°,
∴∠A′ED =45°,
∴A′D =ED ,
在△AA′D 和△CED 中{AD =CD
∠ADA′=∠CDE A′D =ED
,
∴△ADA′≌△CDE(SAS);
(2)由正方形的性质及旋转,得
CD =CB′,∠CB′E =∠CDE =90°,又CE =CE ,
∴Rt △CEB′≌Rt △CED
∴∠B′CE =∠DCE ,
∵AC =A′C
∴直线CE 是线段AA′的垂直平分线.
【解析】(1)根据正方形的性质可得AD =CD ,∠ADC =90°,∠EA′D =45°,则∠A′DE =90°,再计算出∠A′ED =45°,根据等角对等边可得A′D =ED ,即可利用SAS 证明△ADA′≌△CDE ;
(2)首先由AC =A′C ,可得点C 在AA′的垂直平分线上;再证明△AEB′≌△A′ED ,可得AE =A′E ,进而得到点E 也在AA′的垂直平分线上,再根据两点确定一条直线可得直线CE 是线段AA′的垂直平分线.
此题主要考查了正方形的性质,以及旋转的性质,关键是熟练掌握正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;找准旋转后相等的线段.
10.【答案】(1)证明:∵四边形ABCD 是平行四
边形,
∴AB//DF ,
∴∠BAF =∠CFA .
∵E 为BC 的中点,
在△AEB和△FEC中,
{∠BAE=∠CFA ∠AEB=∠FEC BE=EC
,
∴△AEB≌△FEC(AAS)
∴AB=CF;
(2)解:当BC=AF时,四边形ABFC是矩形,
理由:∵AB=CF,AB‖CF,
∴四边形ABFC是平行四边形,
∵BC=AF,
∴四边形ABFC是矩形.
【解析】此题主要考查了平行四边形的性质以及全等三角形的判定与性质等知识,正确得出△AEB≌△FEC(AAS)是解题关键.
(1)利用平行四边形的性质得出∠BAF=∠CFA,进而得出△AEB≌△FEC(AAS),求出答案;
(2)首先得出四边形ABFC是平行四边形,进而得出答案.
11.【答案】(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,
∴四边形AEBD是平行四边形,
∵AB=AC,AD是∠BAC的角平分线,
∴AD⊥BC,
∴∠ADB=90°,
∴平行四边形AEBD是矩形;
(2)当∠BAC=90°时,
理由:∵∠BAC=90°,AB=AC,AD是∠BAC的角平分线,
∴AD=BD=CD,
∵由(1)得四边形AEBD是矩形,
∴矩形AEBD是正方形.
【解析】(1)利用平行四边形的判定首先得出四边形AEBD是平行四边形,进而由等腰三角形的性质得出∠ADB=90°,即可得出答案;
(2)利用等腰直角三角形的性质得出AD=BD=CD,进而利用正方形的判定得出即可.此题主要考查了正方形的判定以及矩形的判定和等腰直角三角形的性质等知识,熟练掌握正方形和矩形的判定是解题关键.
12.【答案】证明:(1)∵CE平分∠BCD、CF平分∠GCD,
∴∠BCE=∠DCE,∠DCF=∠GCF,
∵EF//BC,
∴∠BCE=∠FEC,∠EFC=∠GCF,
∴∠DCE=∠FEC,∠EFC=∠DCF,
∴OE=OC,OF=OC,
∴OE=OF;
(2)∵点O为CD的中点,
∴OD=OC,
又OE=OF,
∵CE平分∠BCD、CF平分∠GCD,
∴∠DCE=1
2∠BCD,∠DCF=1
2
∠DCG,
,
即∠ECF=90°,
∴四边形DECF是矩形.
【解析】本题利用了角平分线的定义、平行线的性质、等角对等边、等量代换、平行四边形的判定、矩形的判定.
(1)由于CE平分∠BCD,那么∠DCE=∠BCE,而EF//BC,于是∠FEC=∠BCE,等量代换∠FEC=∠DCE,那么OE=OC,同理OC=OF,等量代换有OE=OF;
(2)由于O是CD中点,故OD=OC,而OE=OF,那么易证四边形DECF是平行四边形,又CE、CF是∠BCD、∠DCG的角平分线,∠BCD+∠DCG=180°那么易得∠ECF=90°,从而可证四边形DECF是矩形.
13.【答案】(1)证明:∵点D,E分别是边BC,AB上的中点,
∴DE//AC,AC=2DE,
∵EF=2DE,
∴EF//AC,EF=AC,
∴四边形ACEF是平行四边形,
∴AF=CE;
(2)解:当∠B=30°时,四边形ACEF是菱形;理由如下:
∵∠ACB=90°,∠B=30°,
∴∠BAC=60°,AC=1
2
AB=AE,
∴△AEC是等边三角形,
∴AC=CE,
又∵四边形ACEF是平行四边形,
∴四边形ACEF是菱形.
【解析】(1)由三角形中位线定理得出DE//AC,AC=2DE,求出EF//AC,EF=AC,得出四边形ACEF是平行四边形,即可得出AF=CE;
(2)由直角三角形的性质得出∠BAC=60°,AC=1
2
AB=AE,证出△AEC是等边三角形,得出AC=CE,即可得出结论.
本题考查了平行四边形的判定与性质、菱形的判定、三角形中位线定理、直角三角形斜边上的中线性质、等边三角形的判定与性质;熟练掌握平行四边形的判定与性质,证明三角形是等边三角形是解决问题的关键.
14.【答案】(1)证明:∵四边形ABCD是正方形,BF⊥AG,DE⊥AG,
∴DA=AB,∠BAF+∠DAE=∠DAE+∠ADE=90°,
∴∠BAF=∠ADE,
在△ABF和△DAE中,{∠BAF=∠ADE
∠AFB=∠DEA=90°DA=AB
,
∴△ABF≌△DAE(AAS),∴BF=AE,
(2)AF+EF=BF;
∴DA=AB,∠BAF+∠DAE=∠DAE+∠ADE=90°,∴∠BAF=∠ADE,
在△ABF和△DAE中,{∠BAF=∠ADE
∠AFB=∠DEA=90°DA=AB
,
∴△ABF≌△DAE(AAS),
∴BF=AE,AF=DE,
∴AF+EF=BF.
【解析】(1)根据正方形的四条边都相等可得DA=AB,再根据同角的余角相等求出
∠BAF=∠ADE,然后利用“角角边”证明△ABF和△DAE全等,再根据全等三角形对应边相等可得BF=AE,AF=DE,然后根据图形列式整理即可得证;
(2)根据题意作出图形,然后根据(1)的结论可得BF=AE,AF=DE,然后结合图形写出结论即可.
本题考查了正方形的性质,全等三角形的判定与性质,勾股定理的应用,熟记正方形的四条边都相等,每一个角都是直角,然后求出三角形全等是解题的关键.
15.【答案】(1)证明:∵AG//BD,BD=FG,
∴四边形BGFD是平行四边形,
∵CE⊥BD
∴CE⊥AG,
又∵BD为AC的中线,
∴BD=DF=1
2
AC,
∴四边形BDFG是菱形;
(2)解:∵四边形BDFG是菱形,∠ABC=90°,点D为AC的中点,
∴GF=DF=1
2
AC=5,
∵CF⊥AG,
∴AF=√AC2?CF2=√102?62=8,
∴AG=AF+GF=8+5=13.
【解析】(1)首先可判断四边形BDFG是平行四边形,再由直角三角形斜边中线等于斜边一半,可得BD=FD,则可判断四边形BDFG是菱形;
(2)由菱形的性质求得GF=DF=1
2
AC=5,由勾股定理得AF的长,继而求得AG的长.本题主要考查了菱形的判定与性质、直角三角形斜边的中线的性质以及勾股定理,注意掌握数形结合思想是解答此题的关键.
16.【答案】①证明:∵四边形ABCD是正方形,
∴OA=OB,AC⊥BD,
∴∠BOE=∠AOF=90°,
∴∠OEB+∠OBE=90°,
∵AG⊥BE,
∴∠AGE=90°,
∴∠OEB+∠OAF=90°,
∴∠OBE=∠OAF,
在△BOE和△AOF中,
{∠BOE=∠AOF?OB=OA?∠OBE=∠OAF?
,
∴△BOE≌△AOF(ASA),∴OE=OF;
②解:OE=OF还成立;理由如下:
∵四边形ABCD是正方形,∴OA=OB,AC⊥BD,∴∠BOE=∠AOF=90°,∴∠OEB+∠OBE=90°,∵AG⊥BE,
∴∠AGE=90°,
∴∠OEB+∠OAF=90°,∴∠OBE=∠OAF,
在△BOE和△AOF中,
{∠BOE=∠AOF?OB=OA?∠OBE=∠OAF?
,
∴△BOE≌△AOF(ASA),
∴OE=OF.
【解析】本题考查了正方形的性质、全等三角形的判定与性质有关知识.
①由正方形的性质得出OA=OB,AC⊥BD,得出∠BOE=∠AOF=90°,由角的互余关系得出∠OBE=∠OAF,由ASA证明△BOE≌△AOF,得出对应边相等即可;
②由正方形的性质得出OA=OB,AC⊥BD,得出∠BOE=∠AOF=90°,由角的互余关系得出∠OBE=∠OAF,由ASA证明△BOE≌△AOF,得出对应边相等即可.
17.【答案】证明:(1)∵四边形ABCD是矩形,
∴AB//DC、AD//BC,
∴∠ABD=∠CDB,
∵BE平分∠ABD、DF平分∠BDC,
∴∠EBD=1
2∠ABD,∠FDB=1
2
∠BDC,
∴∠EBD=∠FDB,
∴BE//DF,
又∵AD//BC,
∴四边形BEDF是平行四边形;
(2)当∠ABE=30°时,四边形BEDF是菱形,
∵BE平分∠ABD,
∴∠ABD=2∠ABE=60°,∠EBD=∠ABE=30°,∵四边形ABCD是矩形,
∴∠A=90°,
∴∠EDB=90°?∠ABD=30°,
∴∠EDB=∠EBD=30°,
∴EB=ED,
∴四边形BEDF是菱形.
【解析】(1)由矩形可得∠ABD=∠CDB,结合BE平分∠ABD、DF平分∠BDC得∠EBD=∠FDB,即可知BE//DF,根据AD//BC即可得证;
(2)当∠ABE=30°时,四边形BEDF是菱形,由角平分线知∠ABD=2∠ABE=60°、∠EBD=∠ABE=30°,结合∠A=90°可得∠EDB=∠EBD=30°,即EB=ED,即可得证.
本题主要考查矩形的性质、平行四边形、菱形,熟练掌握矩形的性质、平行四边形的判定与菱形的判定是解题的关键.
18.【答案】(1)证明:∵EF垂直平分BD,
∴OB=OD,
∵四边形ABCD为平行四边形,
∴AD//BC,
∴∠EDO=∠FBO,∠DOE=∠BOF,
∴△DOE≌△BOF(ASA),
∴OE=OF,
∴四边形AFCE为菱形;
(2)解:∵BD=8,
∴OD=4且ED=5,
∴EO=3,
∴S
菱形BFDE =1
2
BD×EF=EO·BD=3×8=24.
【解析】本题主要考查平行四边形的性质、垂直平分线的性质,全等三角形的判定与性质以及菱形的判定与性质.
(1)先证明△DOE≌△BOF,得出OE=OF,再根据EF垂直平分BD,可得出四边形BFDE 为菱形;
(2)根据勾股定理可得出OE的长,根据菱形的面积求解即可.
19.【答案】(1)证明∵四边形ABCD是平行四边形(已知),
∴BC//AD(平行四边形的对边相互平行),
∴∠ADE=∠CBD,AD=BC
又∵AM丄BC(已知),
∴AM⊥AD;
∵CN丄AD(已知),
∴AM//CN,
∴AE//CF;
在△ADE和△CBF中,
科组长签名:
知识点 一.正确理解定义 (1)定义:两组对边分别平行的四边形是平行四边形.定义中的“两组对边平行”是它的特征,抓住了这一特征,记忆理解也就不困难了.平行四边形的定义揭示了图形的最本质的属性,它既是平行四边形的一条性质,又是一个判定方法.同学们要在理解的基础上熟记定义. (2”表示平行四边形,例如:平行四边形ABCD ABCD,读作“平行四边形ABCD”. 2.熟练掌握性质 平行四边形的有关性质和判定都是从边、角、对角对称性四个方面的特征进行简述的. (1)角:平行四边形的邻角互补,对角相等; (2)边:平行四边形两组对边分别平行且相等; (3)对角线:平行四边形的对角线互相平分; (4)对称性:平行四边形是中心对称图形,对角线的交点是对称中心; (5)面积:①S =底×高=ah;②平行四边形的对角线将四边形分成4个面积相等的三角形. 3.学会判别方法 (1)平行四边形的判别方法 ①定义:两组对边分别平行的四边形是平行四边形②方法1:两组对角分别相等的四边形是平行四边形 ③方法2:两组对边分别相等的四边形是平行四边形④方法3:对角线互相平分的四边形是平行四边形 ⑤方法4:一组平行且相等的四边形是平行四边形 (2)平行四边形的判别方法的选择
二、.几种特殊四边形的有关概念 (1)矩形:有一个角是直角的平行四边形是矩形,它是研究矩形的基础,它既可以看作是矩形的性质,也可以看作是矩形的判定方法,对于这个定义,要注意把握:(1)平行四边形;(2)一个角是直角,两者缺一不可. (2)菱形:有一组邻边相等的平行四边形是菱形,它是研究菱形的基础,它既可以看作是菱形的性质,也可以看作是菱形的判定方法,对于这个定义,要注意把握:(1)平行四边形;(2)一组邻边相等,两者缺一不可. (3)正方形:一组邻边相等的矩形叫做正方形,它是最特殊的平行四边形,它既是平行四边形,还是菱形,也是矩形,它兼有这三者的特征,是一种非常完美的图形. (4)梯形:一组对边平行而另一组对边不平行的四边形叫做梯形,对于这个定义,要注意把握:(1)一组对边平行;(2)一组对边不平行,同时要注意和平行四边形定义的区别,还要注意腰、底、高等概念以及梯形的分类等问题. (5)等腰梯形:是一种特殊的梯形,它是两腰相等的梯形,特殊梯形还有直角梯形. 2.几种特殊四边形的有关性质 (1)矩形:(1)边:对边平行且相等;(2)角:对角相等、邻角互补;(3)对角线:对角线互相平分且相等;(4)对称性:既是轴对称图形又是中心对称图形. (2)菱形:(1)边:四条边都相等;(2)角:对角相等、邻角互补;(3)对角线:对角线互相垂直平分且每条对角线平分每组对角;(4)对称性:既是轴对称图形又是中心对称图形.(3)正方形:(1)边:四条边都相等;(2)角:四角相等;(3)对角线:对角线互相垂直平分且相等,对角线与边的夹角为450;(4)对称性:既是轴对称图形又是中心对称图形. (4)等腰梯形:(1)边:上下底不相等,两腰相等;(2)角:对角互补;(3)对角线:对角线相等;(4)对称性:是轴对称图形不是中心对称图形. 3.几种特殊四边形的判定方法 (1)矩形的判定:满足下列条件之一的四边形是矩形 (1)有一个角是直角的平行四边形;(2)对角线相等的平行四边形;(3)四个角都相等 (2)菱形的判定:满足下列条件之一的四边形是矩形 (1)有一组邻边相等的平行四边形;(2)对角线互相垂直的平行四边形;(3)四条边都相等. (3)正方形的判定:满足下列条件之一的四边形是正方形. (1)有一个角是直角的菱形;(2)有一组邻边相等的矩形;(3)对角线相等的菱形; (4)对角线互相垂直的矩形.
1 / 1 初二数学平行四边形压轴:几何证明题 1.在四边形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点,顺次连接EF 、FG 、GH 、HE . (1)请判断四边形EFGH 的形状,并给予证明; (2)试探究当满足什么条件时,使四边形EFGH 是菱形,并说明理由。 2.如图,在直角三角形ABC 中,∠ACB=90°,AC=BC=10,将△ABC 绕点B 沿顺时针方向旋转90°得到△A 1BC 1. (1)线段A 1C 1的长度是 ,∠CBA 1的度数是 . (2)连接CC 1,求证:四边形CBA 1C 1是平行四边形. 3. 如图,矩形ABCD 中,点P 是线段AD 上一动点,O 为BD 的中点, PO 的延长线交BC 于Q. (1)求证:OP=OQ ; (2)若AD=8厘米,AB=6厘米,P 从点A 出发,以1厘米/秒的速度向D 运动(不与D 重合).设点P 运动时间为t 秒,请用t 表示PD 的长;并求t 为何值时,四边形PBQD 是菱形. 4.已知:如图,在□ABCD 中,AE 是BC 边上的高,将△ABE 沿BC 方向平移,使点E 与点C 重合,得△GFC. ⑴求证:BE =DG ; ⑵若∠B =60?,当AB 与BC 满足什么数量关系时,四边形ABFG 是菱形?证明你的结论. 5. 如图,在四边形ABCD 中,AD ∥BC ,E 为CD 的中点,连结AE 、BE ,BE ⊥AE ,延长AE 交BC 的延长线于点F . 求证:(1)FC =AD ; (2)AB =BC +AD . 6.如图,在△ABC 中,AB=AC ,D 是BC 的中点,连结AD ,在AD 的延长线上取一点E ,连结BE ,CE. (1)求证:△ABE ≌△ACE (2)当AE 与AD 满足什么数量关系时,四边形ABEC 是菱形?并说明理由. B F C G D H B A 1 C 1A C A D G C B F E A Q C D P B O A B E D A D E F C B
几何证明提高题 1、如图,在△ABC 中,BD 、CE 分别是AC 、AB 上的高。G 、F 分别是BC 、DE 的中点,试证明FG ⊥DE 。 2、如图,在四边形ABCD 中,AB=AD ,CB=CD ,E 是CD 上一点,BE 交AC 于F ,连接DF . (1)若AB ∥CD ,试证明四边形ABCD 是菱形; (2)在(2)的条件下,试确定E 点的位置,使得∠EFD=∠BCD ,并说明理由. 3、已知:如图平行四边形ABCD ,DE ⊥AC ,AM ⊥BD ,BN ⊥AC ,CF ⊥BD 求证:MN ∥EF 4、已知:如图菱形ABCD ,E 是BC 上一点,AE 、BD 交于F ,若AE=AB ,∠DAE=2∠BAE 求证:BE=AF A B E
5、已知:如图正方形ABCD ,P 、Q 分别是BC 、DC 上的点,若∠1=∠2 求证:PB+QD=PA 6、已知:如图正方形ABCD ,AC 、BD 交于点O ,E 、F 分别是BC 、OD 的中点 求证:AF ⊥EF 7、已知:如图,,AB=BC ,D 、E 分别是AB 、BC 上一点,DM AE ⊥交AC 于M , BN AE ⊥交AC 于N ,若BD BE =求证:MN NC =。 8、已知:如图,//AB CD ,AE ED =,BF FC =,//EM AF 交DC 于M , 求证:FM AE =。 21C A P F O A D
10、已知:如图,⊿ABC 中,E 、F 分别是AB 、BC 中点,M 、N 是AC 上两点,EM 、FN 交于D ,若AM=MN=NC ,求证:四边形ABCD 是平行四边形。 11、已知:如图,12∠=∠,3AB AC =,BE AD ⊥,求证:AD DE =。 12、已知:如图,//AB CD ,090D ∠=,BE EC DC ==,求证:3AEC BAE ∠=∠。 13、已知:如图,AD BC ⊥,2B C ∠=∠,BE EC =,求证:1 2 DE AB = 。
八年级四边形几何证明提 高题经典 Revised by BLUE on the afternoon of December 12,2020.
几何证明提高题 1、如图,在四边形ABCD 中,AB=AD ,CB=CD ,E 是CD 上一点,BE 交AC 于F ,连接DF . (1)若AB ∥CD ,试证明四边形ABCD 是菱形; (2)在(2)的条件下,试确定E 点的位置,使得∠EFD=∠BCD ,并说明理由. 2、已知:如图平行四边形ABCD ,DE ⊥AC ,AM ⊥BD ,BN ⊥AC ,CF ⊥BD 求证:MN ∥EF 3、已知:如图菱形ABCD ,E 是BC 上一点,AE 、BD 交于 F ,若AE=AB ,∠DAE=2∠BAE 求证:BE=AF 4、已知:如图正方形ABCD ,P 、Q 分别是BC 、DC 上的点,若∠1=∠2 求证:PB+QD=PA 5、已知:如图正方形ABCD ,AC 、BD 交于点O ,E 、F 分别是BC 、OD 的中点 求证:AF ⊥EF 6已知:如图,//AB CD ,AE ED =,BF FC =,//EM AF 交DC 于M ,求证:FM AE =。 7、已知:如图,⊿ABC 中,E 、F 分别是AB 、BC 中点,M 、N 是AC 上两点, EM 、FN 交于D ,若AM=MN=N C ,求证:四 边形ABCD 是 平行四 边形。 8、已知:如图,12∠=∠,3AB AC =,BE AD ⊥,求证:AD DE =。 9、已知:如图,//AB CD ,090D ∠=, BE EC DC ==,求证:3AEC BAE ∠=∠。 10、已知:如图,AD BC ⊥,2B C ∠=∠,BE EC =,求证: 1 2 DE AB =。 11、已知:如图,AB DC =, AE DE =,BF FC =,FE 交BA 、CD 的延长线于G 、H ,求证:12∠=∠。 12、已知:如图,//AB CD , 090ADC ∠=,BE EC =,求证: 2AED EDC ∠=∠。 13、已知:如图,正方形ABCD 中,E 是DC 上一点,DF ⊥AE 交BC 于F 求证:OE ⊥OF 14、如图,分别以△ABC 的 三边为 边长, 在BC 的同侧作等边三角形 ABD ,等边三角形BCE ,等边三角形ACF ,连接DE ,EF 。求证:四边形ADEF 是平行四边形。 15、如图,点G 是正方形ABCD 对角线CA 的延长线上任意一点,以线段AG 为边作一个正方形AEFG ,线段EB 和GD 相交于点H . (1)求证:EB=GD ; (2)判断EB 与GD 的位置关系,并说明理由; (3)若AB=2,AG=2,求EB 的长. O F E D C B A F D A
1、如图,在四边形ABCD 中,AB=AD ,CB=CD ,E 是CD 上一点,BE 交AC 于F ,连接DF . (1)若AB ∥CD ,试证明四边形ABCD 是菱形; (2)在(2)的条件下,试确定E 点的位置,使得∠EFD=∠BCD ,并说明理由. 2、已知:如图平行四边形ABCD ,DE ⊥AC ,AM ⊥BD ,BN ⊥AC ,CF ⊥BD 求证:MN ∥EF 3、已知:如图菱形ABCD ,E 是BC 上一点,AE 、BD 交于F ,若AE=AB ,∠DAE=2∠BAE 求证:BE=AF 4、已知:如图正方形ABCD ,P 、Q 分别是BC 、DC 上的点,若∠1=∠2 求证:PB+QD=PA 5、已知:如图正方形ABCD ,AC 、BD 交于点O ,E 、F 分别是BC 、OD 的中点 求证:AF ⊥EF 6已知:如图,//AB CD ,AE ED =,BF FC =,//EM AF 交DC 于M ,求证:FM AE =。 7、已知:如图,⊿ABC 中,E 、F 分别是AB 、BC 中点,M 、N 是AC 上两点,EM 、FN 交于D ,若AM=MN=NC ,求证:四边形ABCD 是平行四边形。 8、已知:如图,12∠=∠,3AB AC =,BE AD ⊥,求证:AD DE =。 9、已知:如图,//AB CD ,090D ∠=,BE EC DC ==,求证:3AEC BAE ∠=∠。 10、已知:如图,AD BC ⊥,2B C ∠=∠,BE EC =,求证:1 2 DE AB = 。 11、已知:如图,AB DC =,AE DE =,BF FC =,FE 交BA 、CD 的延长线于G 、H ,求证:12∠=∠。 12、已知:如图,//AB CD ,090ADC ∠=,BE EC =,求证:2AED EDC ∠=∠。 13、已知:如图,正方形ABCD 中,E 是DC 上一点,DF ⊥AE 交BC 于F 求证:OE ⊥OF 14、如图,分别以△ABC 的三边为边长,在BC 的同侧作等边三角形ABD ,等边三角形BCE ,等边三角形ACF ,连接DE ,EF 。求证:四边形ADEF 是平行四边形。
初二数学平行四边形压轴:几何证明题 1.在四边形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点,顺次连接EF 、FG 、GH 、HE . (1)请判断四边形EFGH 的形状,并给予证明; (2)试探究当满足什么条件时,使四边形EFGH 是菱形,并说明理由。 2.如图,在直角三角形ABC 中,∠ACB=90°,AC=BC=10,将△ABC 绕点B 沿顺时针方向旋转90°得到△A 1BC 1. (1)线段A 1C 1的长度是 ,∠CBA 1的度数是 . (2)连接CC 1,求证:四边形CBA 1C 1是平行四边形. 3. 如图,矩形ABCD 中,点P 是线段AD 上一动点,O 为BD 的中点, PO 的延长线交BC 于Q. (1)求证:OP=OQ ; (2)若AD=8厘米,AB=6厘米,P 从点A 出发,以1厘米/秒的速度向D 运动(不与D 重合).设点P 运动时间为t 秒,请用t 表示PD 的长;并求t 为何值时,四边形PBQD 是菱形. 4.已知:如图,在□ABCD 中,AE 是BC 边上的高,将△ABE 沿BC 方向平移,使点E 与点C 重合,得△GFC. ⑴求证:BE =DG ; ⑵若∠B =60?,当AB 与BC 满足什么数量关系时,四边形ABFG 是菱形?证明你的结论. 5. 如图,在四边形ABCD 中,AD ∥BC ,E 为CD 的中点,连结AE 、BE ,BE ⊥AE ,延长AE 交BC 的延长线于点F . 求证:(1)FC =AD ; (2)AB =BC +AD . B F C G D H B A 1 C 1 A C A G C B F E P A D E C B
中考几何证明题四边形专题练习 一、知识考点归纳: 1.平行四边形判定定理:(1)一组对边平行且相等的四边形是平行四边形;(2)两组对边 分别相等的四边形是平行四边形;(3)有两组对边分别平行的四边形是平行四边形;(4)对角线互相平分的四边形是平行四边形. 2. 矩形、正方形:(正方形具有矩形和菱形的一切性质) 判定定理:(1)三个角是直角的四边形是矩形; (2)有一个角是直角的平行四边形是矩形。(3)对角线相等的平行四边形是矩形; 3. 菱形判定定理:(1)四边相等的四边形是菱形;(2)有一组邻边相等的平行四边形是菱形;(3)对角线互相垂直且平分的四边形是菱形;(4)对角线互相垂直的平行四边形是菱形. 二、中考真题专题训练 1.(2014乐山,第19题9分)如图,在△ABC中,AB=AC,四边形ADEF是菱形,求证:BE=CE. 2.(2014年广西钦州,第20题7分)如图,在正方形ABCD中,E、F分别是AB、BC上的点,且AE=BF.求证:CE=DF. 3. (2014乐山,第21题10分)如图,在梯形ABCD中,AD∥BC,∠ADC=90°,∠B=30°,CE⊥AB,垂足为点E.若AD=1,AB=2,求CE的长. 4.(2014青岛,第21题8分)已知:如图,ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.(1)求证:△AOD≌△EOC;
(2)连接AC,DE,当∠B=∠AEB=45°时,四边形ACED是正方形请说明理由. 5.(2014四川广安,第19题6分)如图,在正方形ABCD中,P是对角线AC上的一点,连接BP、DP,延长BC到E,使PB=PE.求证:∠PDC=∠PE C. 6.(2014海南,第23题13分)如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD,BC于点E,F,作BH⊥AF于点H,分别交AC,CD于点G,P,连接GE,GF. (1)求证:△OAE≌△OBG; (2)试问:四边形BFGE是否为菱形若是,请证明;若不是,请说明理由; 7.(2014宁夏,第22题6分)在平行四边形ABCD中,将△ABC沿AC对折,使点B落在B′处,A B′和CD相交于点O.求证:OA=O C. 8.(10分)(2013·莱芜)如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连接DE. (1)证明:DE∥CB;
四边形几何证明精选 一、解答题 1.已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时旋转,它的两边分别交 CB,DC(或它们的延长线)于点M,N.当∠MAB绕点A旋转到BM=DN时(如图1),易证BM+DN=MN. (1)当∠MAN旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量 关系?写出猜想,并加以证明. (2)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的 数量关系?请写出你的猜想,并加以证明. 2.如图,矩形ABCD中,AB>AD,把矩形沿对角线AC 所在直线折叠,使点B落在点E处,AE交CD于点F, 连接DE. (1)求证:△ADE≌△CED; (2)求证:△DEF是等腰三角形.
3.【问题情境】 如图,在正方形ABCD中,点E是线段BG上的动点,AE⊥EF,EF交正方形外角∠DCG的平分线CF于点F. 【探究展示】 (1)如图1,若点E是BC的中点,证明:∠BAE+∠EFC=∠DCF. (2)如图2,若点E是BC边上的任意一点(B、C除外),∠BAE+∠EFC=∠DCF是 否仍然成立?若成立,请予以证明;若不成立,请说明理由. 【拓展延伸】 (3)如图3,若点E是BC延长线(C除外)上的任意一点,求证:AE=EF. 4.如图1,在正方形ABCD中,P为对角线BD上的一点,点E在AD的延长线上, 且PA=PE,PE交CD于F,连接CE. (1)求证:△PCE是等腰直角三角形; (2)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时, 判断△PCE的形状,并说明理由. 5.如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF 是等腰直角三角形,其中∠EBF=90°,连接CE、CF. (1)求证:△ABF≌△CBE;
1.如图,在平行四边形ABCD中,过点D作DE⊥BC交BC于点E,且DE=AD,F为DC上一点,且AD=FD,连接AF与DE交于点G。 (1)若∠C=60°,AB=2,求GF的长; (2)过点A作AH⊥AD,且AH=CE,求证:AB=DG+AH. A
2.如图,在平行四边形ABCD 中,∠ACB =45°,点E 在对角线AC 上,BE 的延长线交CD 于点F ,交AD 的延长线于点G 。 (1)若BE =10 ,EC =2,求△BCE 的面积; (2)若∠ABE =2∠EBC ,且AB =BE ,求证:EC =DG 。 图2 图1 B
3.在平行四边形ABCD 中,点E 是AD 边上点,连接BE 。 (1)如图1,若BE 平分∠ABC ,BC =8,ED =3,求平行四边形ABCD 的周长。 (2)如图2,点F 是平行四边形ABCD 外一点,FB =CD ,连接BF 、CF ,CF 与BE 相交于点G 。若∠FBE +∠ABC =180°,点G 是CF 的中点,求证:2BG +ED =BC . 图2 图1 B
4.如图,在平行四边形ABCD 中,对角线BD ⊥AD ,E 为CD 上一点,连接AE 交BD 于F ,G 为AF 的中点,连接DG 。 (1)如图1,若DG =DF =1,BF =3,求CD 的长; (2)如图2,连接BE ,且BE =AD ,∠AEB =90°,M 、N 分别为DG 、BD 上的点,且DM =BN ,H 为AB 的中点,连接HM 、HN ,求证:∠MHN =∠AFB 。 图2 图1 A A
5.已知在□ABCD 中,AB ⊥AC ,点E 是AC 上一点,连接BE ,延长BE 交AD 于点F ,BE =CE 。 (1)如图1,当∠AEB =60°,EF =2时,求□ABCD 的面积; (2)如图2,点G 是过点E 且与BF 垂直的直线上一点,连接GF 、GC 、FC ,当GF =GC 时,求证:AB =2EG 。 图2 图1 B B
初二数学平行四边形:几何证明题 1.在四边形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点,顺次连接EF 、FG 、GH 、HE . (1)请判断四边形EFGH 的形状,并给予证明; (2)试探究当满足什么条件时,使四边形EFGH 是菱形,并说明理由。 2.如图,在直角三角形ABC 中,∠ACB=90°,AC=BC=10,将△ABC 绕点B 沿顺时针方向旋转90°得到△A 1BC 1 . (1)线段A 1C 1的长度是 ,∠CBA 1的度数是 . (2)连接CC 1,求证:四边形CBA 1C 1是平行四边形. 3. 如图,矩形ABCD 中,点P 是线段AD 上一动点,O 为BD 的中点, PO 的延长线交BC 于Q. (1)求证:OP=OQ ; (2)若AD=8厘米,AB=6厘米,P 从点A 出发,以1厘米/秒的速度向D 运动(不与D 重合).设点P 运动时间为t 秒, 请用t 表示PD 的长;并求t 为何值时,四边形PBQD 是菱形. 4.已知:如图,在□ABCD 中,AE 是BC 边上的高,将△ABE 沿BC 方向平移,使点E 与点C 重合,得△GFC. ⑴求证:BE?DG ; A B E F C G D H B A 1 C 1 A C A Q C D B
⑵若∠B?60?,当AB 与BC 满足什么数量关系时,四边形ABFG 是菱形证明你的结论. 5. 如图,在四边形ABCD 中,AD ∥BC ,E 为CD 的中点,连结AE 、BE ,BE ⊥AE ,延长AE 交BC 的延长线于点F . 求证:(1)FC =AD ; (2)AB =BC +AD . 6.如图,在△ABC 中,AB=AC ,D 是BC 的中点,连结AD ,在AD 的延长线上取一点E ,连结BE ,CE. (1)求证:△ABE ≌△ACE (2)当AE 与AD 满足什么数量关系时,四边形ABEC 是菱形并说明理由. A D G C B F E A B E D C A D E F C B
可编辑 几何证明(一)---- 对角互补 方法点拨:已知中有公共端点的两条线段相等,利用互补及平角可得另一对角相等,再通过添加辅助线得到全等的的三个条件解决问题。 补例(2013聊城)如图,四边形ABCD 中,∠A=∠BCD=90°,BC=CD ,CE⊥AD,垂足为E , 求证:AE=CE . 例:如图,△ABC 是等腰直角三角形,AB=AC ,P 是△ABC 外一点,且PB ⊥PC 试判断PA 、PB 、PC 的关系,并加以证明 变式一: 如图,△ABC 是等腰三角形,AB=AC ,∠BAC=120°,P 是△ABC 外一点, 且∠BPC=60°,试判断PA 、PB 、PC 的关系,并加以证明 变式二: 如图,△ABC 是等腰三角形,AB=AC ,∠BAC=α,P 是△ABC 外一点, 且∠BAC +∠BPC=180°,试判断PA 、PB 、PC 的关系,并加以证明(用含α的式子 表示 变式三 如图,△ABC 是等腰直角三角形,AB=BC ,P 是△ABC 外一点,且∠BPC=135°, 试判断PA 、PB 、PC 的关系,并加以证明 A B P C A B P C A B C P A B P C
可编辑 变式四 如图,△ABC 是直角三角形,∠ABC=90°,∠BAC=α,P 是△ABC 外一点, 且∠BAC +∠BPC=180°, 试判断PA 、PB 、PC 的关系,并加以证明(用含α的式子 链接中考 1.已知:如图13,在ABC △中,,AB AC BAC α=∠=( 不大于90o ),点P 为ABC △外一 点,且o 1902 APC α∠=+,连接BP . (1)当o 60α=时,APC ∠= o ;,,PA PB PC 这三条线段满足的数量关系是 ; (2)如图14,当 o 60α=时,探究,,PA PB PC 三条线段之间的数量关系,并证明; (3)用含α的式子表示,,PA PB PC 三条线段之间的数量关系,并证明. 图13 图14 2、链接中考:2013甘井子一模25题。 如图①,在△ABC 和△ADE 中,AC=AB,AE=AD,∠BAC=∠DAE=m,CE,DB 交于点F ,连接AF. (1) 如图②,当m=90°时,猜想BD,CE 的关系,并证明你的结论; (2) 在(1)的条件下,猜想线段AF,BF,CF 数量关系,并证明你的结论; (3) 直接写出AF,BF,CF 数量关系(用含m 的三角函数表示) 图① 图② 3、 .在□ABCD 中,E 是AD 上一点,AE =AB ,过点E 作直线EF ,在EF 上取一点G ,使得∠EGB =∠EAB , 连接AG .如图当EF 与CD 相交时,且∠EAB =90°,请求出线段EG 、AG 、BG 之间的数量关系,并证明你的结论. A B P C D C B E P C B A P C B A 90°
绝密★启用前 初中数学组卷 试卷副标题 考试范围:xxx ;考试时间:100分钟;命题人:xxx 注意事项: 1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上 第Ⅰ卷(选择题) 请点击修改第I 卷的文字说明 一.解答题(共29小题) 1.(2017秋?农安县期末)在△ABC 中,AD 平分∠BAC ,BD ⊥AD ,垂足为D ,过D 作DE ∥AC ,交AB 于E ,若AB=5,求线段DE 的长. 2.(2017秋?濮阳期末)如图,在△ABC 中,AB=AC ,∠A=36°,AC 的垂直平分线交AB 于E ,D 为垂足,连接EC . (1)求∠ECD 的度数; (2)若CE=5,求BC 的长.
试卷第2页,总10页 3.(2018春?巴州区期末)等腰三角形一腰上的中线把这个三角形的周长分成12cm 和21cm 两部分,求这个等腰三角形的底边长. 4.(2017秋?潮南区期末)如图,在等边△ABC 中,D 、E 分别在边BC 、AC 上,且DE ∥AB ,过点E 作EF ⊥DE 交BC 的延长线于点F . (1)求∠F 的度数; (2)若CD=2cm ,求DF 的长. 5.(2017秋?盐湖区期末)如图,已知点A 、C 分别在∠GBE 的边BG 、BE 上,且AB=AC ,AD ∥BE ,∠GBE 的平分线与AD 交于点D ,连接CD . (1)求证:①AB=AD ;②CD 平分∠ACE . (2)猜想∠BDC 与∠BAC 之间有何数量关系?并对你的猜想加以证明. 6.(2017秋?路南区期末)如图,在△ABC 中,AB=AC ,D 为BC 上一点,∠B=30°,连接AD . (1)若∠BAD=45°,求证:△ACD 为等腰三角形; (2)若△ACD 为直角三角形,求∠BAD 的度数.
九年级数学几何证明综合之四边形拔高练习 试卷简介:本测试卷中题目是卢老师九年级秋季班第一讲课堂实录测试题,包含一道探究题. 学习建议:本测试卷中包含一道类比探究题,本题主要考查对正方形的判定,等腰直角三角形的性质,菱形的判定和性质,全等三角形的性质和判定,平行线的性质等知识点的理解和掌握,综合运用性质进行推理是解此题的关键,所以学生要加深对各种图形性质的理解. 一、探究题(共1道,每道100分) 1.(2011浙江)以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连结这四个点,得四边形EFGH. (1)如图1,当四边形ABCD为正方形时,我们发现四边形EFGH是正方形;如图2,当四边形ABCD为矩形时,请判断:四边形EFGH的形状(不要求证明); (2)如图3,当四边形ABCD为一般平行四边形时,设∠ADC=α(0°<α<90°), ①试用含α的代数式表示∠HAE; ②求证:HE=HG; ③四边形EFGH是什么四边形?并说明理由. 答案:(1)答:四边形EFGH的形状是正方形. (2)解:①∠HAE=90°+α, 在平行四边形ABCD中AB∥CD, ∴∠BAD=180°-∠ADC=180°-α, ∵△HAD和△EAB是等腰直角三角形, ∴∠HAD=∠EAB=45°, ∴∠HAE=360°-∠HAD-∠EAB-∠BAD=360°-45°-45°-(180°-α)=90°+α, 答:用含α的代数式表示∠HAE是90°+α. ②证明:∵△AEB和△DGC是等腰直角三角形, ∴AE= AB,DG= CD,在平行四边形ABCD中,AB=CD,∴AE=DG,∵△HAD 和△GDC是等腰直角三角形,∴∠HDA=∠CDG=45°,∴∠HDG=∠HDA+∠ADC+∠CDG=90°+α=∠HAE,∵△HAD是等腰直角三角形,∴HA=HD,∴△HAE≌△HDG,∴HE=HG.③答:四边形EFGH是正方形,理由是:由②同理可得:GH=GF,FG=FE,∵HE=HG,∴GH=GF=EF=HE,∴四边形EFGH是菱形,∵△HAE≌△HDG,∴∠DHG=∠AHE,∵∠AHD=∠AHG+∠DHG=90°,
几何证明(与四边形有关) 【复习要点】 1、平行四边形: 性质: 判定: 2、矩形: 性质: 判定: 3、菱形: 性质: 判定: 4、正方形: 性质: 判定: 5、等腰梯形: 性质: 判定: 6、直角梯形: 性质: 判定: 【中考精炼】 1、在 □ABCD 中,E 、F 分别是AB 、CD 上的点,且AE =CF 求证:BF ∥DE 。 2、菱形ABCD 的对角线交于O 点,DE ∥AC ,CE ∥BD , 求证:四边形OCED 是矩形。 3、等腰△ABC 中,AB =AC ,D为BC 上的一动点,DE ∥AC ,DF ∥AB ,则DE +DF 是否随D 点变化而变化?若不变化请证明。 A D F E B C A D E C B O A B D C E F
P O y C (4,3) Q B (14,3)) A (14,0) x 4、如图,梯形ABCD 中,AD =18cm ,BC =21cm ,点P 从点A 开始沿AD 边向D 以1m/s 的速度移动,点Q 从C 点开始沿CB 边向B 以2m/s 的速度移动,如果P 、Q 分别从A 、C 同时出发,设移动时间为t 秒,求: (1)t 为何时,四边形ABQP 为矩形? (2)t 为何时,四边形PQCD 为等腰梯形? 5、如图,梯形ABCD 中,AD ∥BC ,M 、N 、P 、Q 分别为AD 、BC 、BD 、AC 的中 点。求证:MN 和PQ 互相平分。 6、如图,梯形OABC 中,O 为直角坐标系的原点,A 、B 、C 的坐标分别为(14,0)、(14,3)、(4,3)。点P 、Q 同时从原点出发,分别作匀速运动,点P 沿OA 以每秒1个单位向终点A 运动,点Q 沿OC 、CB 以每秒2个单位向终点B 运动。当这两点中有一点到达自己的终点时,另一点也停止运动。 (1)设从出发起运动了x 秒,且x ﹥2.5时,Q 点 的坐标; (2)当x 等于多少时,四边形OPQC 为平行四边形? (3)四边形OPQC 能否成为等腰梯形?说明理由。 (4)设四边形OPQC 的面积为y,求出当 x ﹥2.5时 y 与x 的函数关系式;并求出y 的最大值; 7、等腰梯形ABCD 中,AB =15,AD =20,∠C =30o. M 、N 同时以相同速度分别从点A 、点D 开始在AB 、AD (包括端点)上运动. (1)设ND 为x ,用x 表示出点N 到AB 的距离,并写出x 的取值范围. (2)设t=10-x,用t 表示△AMN 的面积. (3)求△AMN 的面积的最大值,并判断取最大值时△AMN 的形状. A P D B Q C N M Q P D C B A
高中数学选修4-1《几何证明选讲》 ----知识点总结 1、平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那 么在其他直线上截得的线段也相等。 推理1:经过三角形一边的中点与另一边平行的直线必平分第三边。 推理2:经过梯形一腰的中点,且与底边平行的直线平分另一腰。平分线分线段成比例定理 2、平分线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例。 推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例。 3、相似三角形的判定: 定义:对应角相等,对应边成比例的两个三角形叫做相似三角形。相似三角形对 应边的比值叫做相似比(或相似系数)。 由于从定义出发判断两个三角形是否相似,需考虑6个元素,即三组对应角是否分别相等,三组对应边是否分别成比例,显然比较麻烦。所以我们曾经给出过如下几个判定两个三角形: 4、相似的简单方法: (1)两角对应相等,两三角形相似; (2)两边对应成比例且夹角相等,两三角形相似; (3)三边对应成比例,两三角形相似。 5、预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与三角形相似。 6、判定定理1:对于任意两个三角形,如果一个三角形的两个角与另一个三角 形的两个角对应相等,那么这两个三角形相似。简述为:两角对应相等,两三角形相似。 7、判定定理2:对于任意两个三角形,如果一个三角形的两边和另一个三角 形的两边对应成比例,并且夹角相等,那么这两个三角形相似。简述为:两边对应成比例且夹角相等,两三角形相似。 8、判定定理3:对于任意两个三角形,如果一个三角形的三条边和另一个三
几何证明题的技巧 1)证明线段相等,角相等的题,通常找到线段所在图形,证明全等 2)隐藏条件:比如特殊图形的性质自己要清楚,有些时候几何题做不出来就是因为没有利用好隐藏条件 3)辅助线起到关键作用 4)几何证明步骤:依据—结论—定理切记勿忽略细微条件 5)遇到面积问题,辅助线通常做高,遇到圆,多为做半径,切线 6)个别题型做辅助线: 1 通过连结,延长,作垂直,作平行线等添加辅助线的方法,构造全等三角形。 2遇到有中点条件时,常常延长中线(即倍长中线),或以中点为旋转中心,使分散的条件汇集起来。 3遇到求边之间的和,差,倍数关系时,通常采用截长补短的方法,求角度之间的关系时,也一样。 要掌握初中数学几何证明题技巧,熟练运用和记忆如下原理是关键。 下面归类一下,多做练习,熟能生巧,遇到几何证明题能想到采用哪一类型原理来解决问题。 一、证明两线段相等 1.两全等三角形中对应边相等。 2.同一三角形中等角对等边。 3.等腰三角形顶角的平分线或底边的高平分底边。 4.平行四边形的对边或对角线被交点分成的两段相等。 5.直角三角形斜边的中点到三顶点距离相等。 6.线段垂直平分线上任意一点到线段两段距离相等。 7.角平分线上任一点到角的两边距离相等。 8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等。 *9.同圆(或等圆)中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。 *10.圆外一点引圆的两条切线的切线长相等或圆内垂直于直径的弦被直径分成的两段相等。 11.两前项(或两后项)相等的比例式中的两后项(或两前项)相等。
*12.两圆的内(外)公切线的长相等。 13.等于同一线段的两条线段相等。 二、证明两个角相等 1.两全等三角形的对应角相等。 2.同一三角形中等边对等角。 3.等腰三角形中,底边上的中线(或高)平分顶角。 4.两条平行线的同位角、内错角或平行四边形的对角相等。 5.同角(或等角)的余角(或补角)相等。 *6.同圆(或圆)中,等弦(或弧)所对的圆心角相等,圆周角相等,弦切角等于它所夹的弧对的圆周角。 *7.圆外一点引圆的两条切线,圆心和这一点的连线平分两条切线的夹角。 8.相似三角形的对应角相等。 *9.圆的内接四边形的外角等于内对角。 10.等于同一角的两个角相等。 三、证明两条直线互相垂直 1.等腰三角形的顶角平分线或底边的中线垂直于底边。 2.三角形中一边的中线若等于这边一半,则这一边所对的角是直角。 3.在一个三角形中,若有两个角互余,则第三个角是直角。 4.邻补角的平分线互相垂直。 5.一条直线垂直于平行线中的一条,则必垂直于另一条。 6.两条直线相交成直角则两直线垂直。 7.利用到一线段两端的距离相等的点在线段的垂直平分线上。 8.利用勾股定理的逆定理。 9.利用菱形的对角线互相垂直。 *10.在圆中平分弦(或弧)的直径垂直于弦。 *11.利用半圆上的圆周角是直角。 四、证明两直线平行 1.垂直于同一直线的各直线平行。 2.同位角相等,内错角相等或同旁内角互补的两直线平行。 3.平行四边形的对边平行。
第一讲:如何做几何证明题 【知识梳理】 1、几何证明是平面几何中的一个重要问题,它对培养学生逻辑思维能力有着很大作用。几何证明有两种基本类型:一是平面图形的数量关系;二是有关平面图形的位置关系。这两类问题常常可以相互转化,如证明平行关系可转化为证明角等或角互补的问题。 2、掌握分析、证明几何问题的常用方法: (1)综合法(由因导果),从已知条件出发,通过有关定义、定理、公理的应用,逐步向前推进,直到问题的解决; (2)分析法(执果索因)从命题的结论考虑,推敲使其成立需要具备的条件,然后再把所需的条件看成要证的结论继续推敲,如此逐步往上逆求,直到已知事实为止; (3)两头凑法:将分析与综合法合并使用,比较起来,分析法利于思考,综合法易于表达,因此,在实际思考问题时,可合并使用,灵活处理,以利于缩短题设与结论的距离,最后达到证明目的。 3、掌握构造基本图形的方法:复杂的图形都是由基本图形组成的,因此要善于将复杂图形分解成基本图形。在更多时候需要构造基本图形,在构造基本图形时往往需要添加辅助线,以达到集中条件、转化问题的目的。 【例题精讲】 【专题一】证明线段相等或角相等 两条线段或两个角相等是平面几何证明中最基本也是最重要的一种相等关系。很多其它问题最后都可化归为此类问题来证。证明两条线段或两角相等最常用的方法是利用全等三角形的性质,其它如线段中垂线的性质、角平分线的性质、等腰三角形的判定与性质等也经常用到。 【例1】已知:如图所示,?A B C 中,∠=?===C AC BC AD DB AE CF 90,,,。 求证:DE =DF F E D C B A
【巩固】如图所示,已知?A B C 为等边三角形,延长BC 到D ,延长BA 到E ,并且使AE =BD ,连结CE 、DE 。 求证:EC =ED 【例2】已知:如图所示,AB =CD ,AD =BC ,AE =CF 。 求证:∠E =∠F 【专题二】证明直线平行或垂直 在两条直线的位置关系中,平行与垂直是两种特殊的位置。证两直线平行,可用同位角、内错角或同旁内角的关系来证,也可通过边对应成比例、三角形中位线定理证明。证两条直线垂直,可转化为证一个角等于90°,或利用两个锐角互余,或等腰三角形“三线合一”来证。 【例3】如图所示,设BP 、CQ 是?A B C 的内角平分线,AH 、AK 分别为A 到BP 、CQ 的垂线。 求证:KH ∥BC A C E D F B A B D C E A B Q P H C K
每日一练--几何证明 班级:姓名: 1.如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.(1)若AB∥CD,试证明四边形ABCD是菱形; (2)在(2)的条件下,试确定E点的位置,使得∠EFD=∠BCD,并说明理由. 2.如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD 翻折,使点A落在BC边上的点F处. (1)直接写出点E、F的坐标; (2)在x轴、y轴上是否分别存在点M、N,使得四边形MNFE的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.
3.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H. (1)求证:EB=GD; (2)判断EB与GD的位置关系,并说明理由; (3)若AB=2,AG=2,求EB的长. 4.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF. (1)BD与CD之间有什么数量关系,并说明理由; (2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由. 5.D,E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB,AC的中点.O是△ABC所在平面上的动点,连接OB,OC,点G,F分别是OB,OC的中点,顺次连接点D,G,F, E. (1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形; (2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?(请直接写出答案,不用证明)
专题27 几何证明综合复习(判定四边形形状- 矩形) 教学重难点 1.培养学生通过探索和证明,发展推理意识和能力 2.通过证明举例的学习和实践,懂得演绎推理的一般规则,并掌握规范表达的格式;了解证明之前进行分析的基本思路; 3.体会用“分析综合法”探求解题思路; 4.学习添置辅助线的基本方法,会添置常见的辅助线; 5.会用文字语言、图形语言、符号语言三种数学语言进行证明说理。 【说明】:本部分为知识点方法总结性梳理,目的在于让学生能从题目条件和所证明结论,去寻找证明思路,用时大概 5-8 分钟左右。 【知识点、方法总结】:中考几何题证明思路总结 几何证明题重点考察的是学生的逻辑思维能力,能通过严密的" 因为"、"所以 " 逻辑将条件一步步转化 为所要证明的结论。这类题目出法相当灵活,不像代数计算类题目容易总结出固定题型的固定解法,而更看重的是对重要模型的总结、常见思路的总结。所以本文对中考中最常出现的若干结论做了一个较为全面的思路总结。 一、证明两线段相等 1.两全等三角形中对应边相等。 2.同一三角形中等角对等边。 3.等腰三角形顶角的平分线或底边的高平分底边。 4.平行四边形的对边或对角线被交点分成的两段相等。 5.直角三角形斜边的中点到三顶点距离相等。 6.线段垂直平分线上任意一点到线段两段距离相等。 7.角平分线上任一点到角的两边距离相等。 8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等。 9.同圆(或等圆)中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。
10.两前项(或两后项)相等的比例式中的两后项(或两前项)相等。 、证明两角相等 1.两全等三角形的对应角相等。 2.同一三角形中等边对等角。 3.等腰三角形中,底边上的中线(或高)平分顶角。 4.两条平行线的同位角、内错角或平行四边形的对角相等。 5.同角(或等角)的余角(或补角)相等。 6.同圆(或圆)中,等弦(或弧)所对的圆心角相等; 7.相似三角形的对应角相等; 8.等于同一角的两个角相等。 三、证明两直线平行 1.垂直于同一直线的各直线平行。 2.同位角相等,内错角相等或同旁内角互补的两直线平行。 3.平行四边形的对边平行。 4.三角形的中位线平行于第三边。 5.梯形的中位线平行于两底。 6.平行于同一直线的两直线平行。 7.一条直线截三角形的两边(或延长线)所得的线段对应成比例,则这条直线平行于第三边。 四、证明两直线互相垂直 1.等腰三角形的顶角平分线或底边的中线垂直于底边。 2.三角形中一边的中线若等于这边一半,则这一边所对的角是直角。 3.在一个三角形中,若有两个角互余,则第三个角是直角。 4.邻补角的平分线互相垂直。 5.一条直线垂直于平行线中的一条,则必垂直于另一条。 6.两条直线相交成直角则两直线垂直。