
导数习题题型十七:含参数导数问题的分类讨论问题
含参数导数问题的分类讨论问题
1.求导后,导函数的解析式含有参数,导函数为零有实根(或导函数的分子能分解因式), 导函数为零的实根中有参数也落在定义域内,但不知这些实根的大小关系,从而引起讨论。
★已知函数ax x a x x f 2)2(2
131)(23++-=(a>0),求函数的单调区间
)2)((2)2()(--=++-='x a x a x a x x f ★★例1 已知函数x a x
a
x x f ln )2(2)(+--
=(a>0)求函数的单调区间 2
2
2)
)(2(2)2()(x a x x x a x a x x f --=++-=' ★★★例3已知函数()()22
21
1
ax a f x x R x -+=∈+,其中a R ∈。 (Ⅰ)当1a =时,求曲线()y f x =在点()()
2,2f 处的切线方程; (Ⅱ)当0a ≠时,求函数()f x 的单调区间与极值。
解:(Ⅰ)当1a =时,曲线()y f x =在点()()
2,2f 处的切线方程为032256=-+y x 。
(Ⅱ)由于0a ≠,所以()()
1
2)1(222+-+='x x a x f ,由
()'0f x =,得121
,x x a a
=-=。这两个实根都在定
()()()()()()
2
2
'
2222
122122111a x a x a x x ax a a f x x x ?
?--+ ?+--+??==++义域R 内,但不知它们之间 的大小。因此,需对参数a 的取值分0a >和0a <两种情况进行讨论。 (1)当0a >时,则12x x <。易得()f x 在区间1,a ?
?
-∞-
???
,(),a +∞内为减函数, 在区间1,a a ??
-
???
为增函数。故函数()f x 在11x a =-处取得极小值
21f a a ??
-=- ???
; 函数()f x 在2x a =处取得极大值()1f a =。
(1) 当0a <时,则12x x >。易得()f x 在区间),(a -∞,),1
(+∞-a
内为增函数,在区间
)1,(a a -为减函数。故函数()f x 在11
x a
=-处取得极小值
21f a a ??
-=- ???
;函数
()f x 在
2x a =处取得极大值()1f a =。
以上三点即为含参数导数问题的三个基本讨论点,在求解有关含参数的导数问题时,可按上述三点
的顺序对参数进行讨论。因此,对含参数的导数问题的讨论,还是有一定的规律可循的。当然,在具体解题中,可能要讨论其中的两点或三点,这时的讨论就更复杂一些了,需要灵活把握。
★★★(区间确定零点不确定的典例)
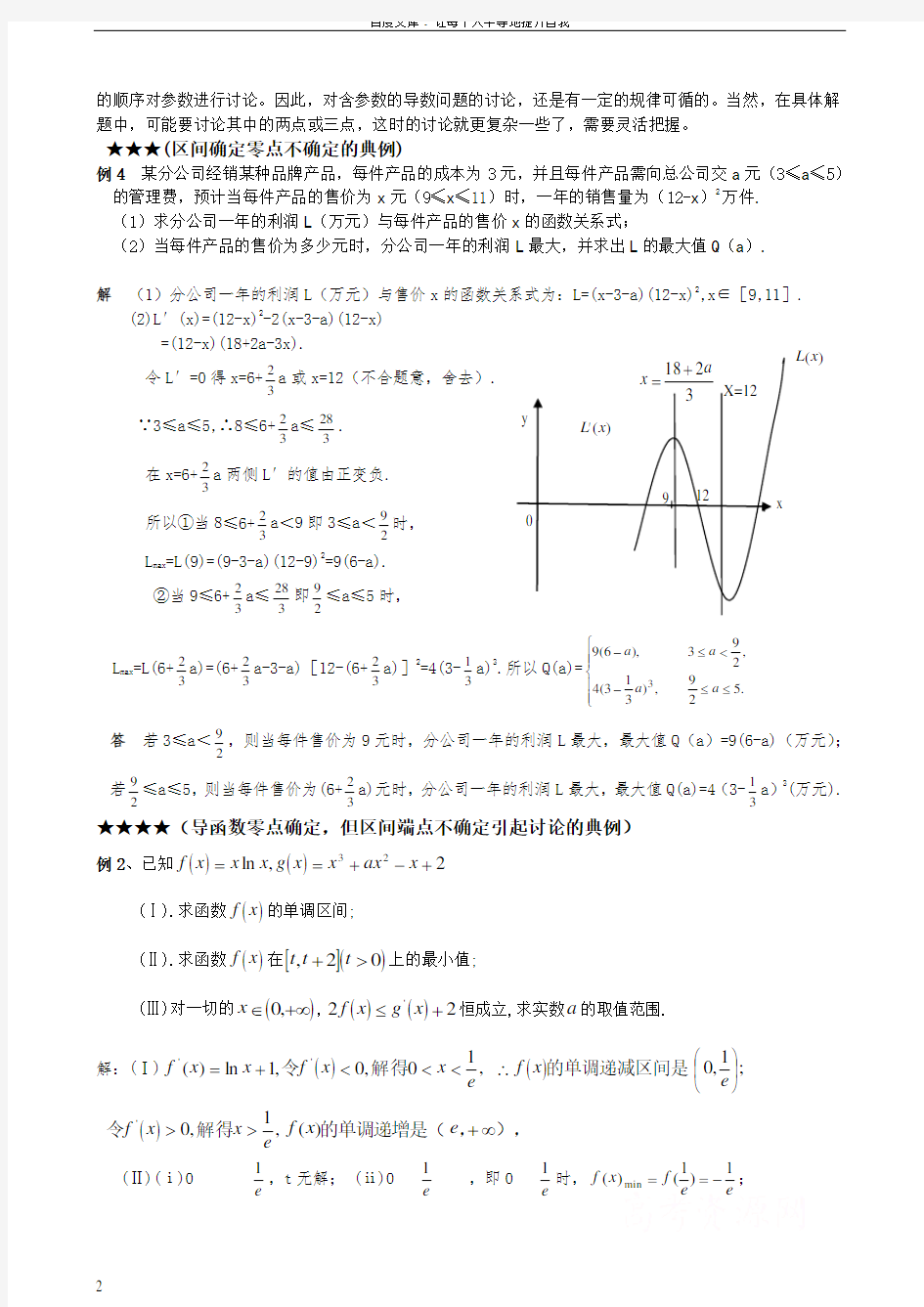
例4 某分公司经销某种品牌产品,每件产品的成本为3元,并且每件产品需向总公司交a 元(3≤a ≤5)
的管理费,预计当每件产品的售价为x 元(9≤x ≤11)时,一年的销售量为(12-x )2
万件. (1)求分公司一年的利润L (万元)与每件产品的售价x 的函数关系式;
(2)当每件产品的售价为多少元时,分公司一年的利润L 最大,并求出L 的最大值Q (a ).
解 (1)分公司一年的利润L (万元)与售价x 的函数关系式为:L=(x-3-a)(12-x)2
,x ∈[9,11].
(2)L ′(x)=(12-x)2
-2(x-3-a)(12-x) =(12-x)(18+2a-3x).
令L ′=0得x=6+32
a 或x=12(不合题意,舍去). ∵3≤a ≤5,∴8≤6+3
2a ≤
3
28. 在x=6+3
2
a 两侧L ′的值由正变负.
所以①当8≤6+32a <9即3≤a <2
9
时,
L max =L(9)=(9-3-a)(12-9)2
=9(6-a). ②当9≤6+3
2a ≤
328即2
9
≤a ≤5时, L max =L(6+32a)=(6+32a-3-a)[12-(6+32a)]2=4(3-31a)3.所以Q(a)=???
?
??
?
≤≤-<
≤-.52
9
,
)313(4,2
9
3),6(93a a a a
答 若3≤a <2
9,则当每件售价为9元时,分公司一年的利润L 最大,最大值Q (a )=9(6-a)(万元);若2
9≤a ≤5,则当每件售价为(6+3
2a)元时,分公司一年的利润L 最大,最大值Q(a)=4(3-3
1a )3
(万元).
★★★★(导函数零点确定,但区间端点不确定引起讨论的典例)
例2、已知()()2,ln 2
3
+-+==x ax x x g x x x f
(Ⅰ).求函数()x f 的单调区间;
(Ⅱ).求函数()x f 在[]()02,>+t t t 上的最小值;
(Ⅲ)对一切的()+∞∈,0x ,()()22'+≤x g x f 恒成立,求实数a 的取值范围. 解:(Ⅰ)(),10,0,1ln )('
'
e
x x f
x x f <<<+=解得令 ();1,0??
?
?
?∴e x f 的单调递减区间是
(),1
,0'e x x f >>解得令),,
的单调递增是(∞+e x f )(
(Ⅱ)(ⅰ)0 e 1,t 无解; (ⅱ)0 1 时,e e f x f 1)1()(min -==; )(x L y x 12 9 )(x L ' X=12 3218a x += (ⅲ) e 12+<≤t t ,即e t 1 ≥时,单调递增在]2,[)(+t t x f ,tlnt )t ()(min ==f x f ……9分 e t e t x f 1 10tlnt e 1-)(min ≥< (Ⅲ)由题意:2123ln 22 +-+≤ax x x x 在()+∞∈,0x 上恒成立,即123ln 22++≤ax x x x 可得x x x a 2123ln -- ≥(分离参数),设()x x x x h 21 23ln - -=, 则()()()2 2' 213121231x x x x x x h +-- =+-=……12分 令()0'=x h ,得3 1 ,1-==x x (舍) 当10< ∴当1=x 时,()x h 取得最大值, ()x h max =-2……13分.2-≥∴a . 二.求导后,导函数为零有实根(或导函数的分子能分解因式),但不知导函数为零的实根是否落在定义域内,从而引起讨论。(用导数解决函数问题若求导后研究函数的导数问题时能 转化为研究二次函数问题时,二次项的系数含参数按系数大于零、等于零、小于零分类;再按在二次项的系数不等于零时对判别式按△>0、△=0、△<0;在△>0时,求导函数的零点再根据零点是否在在定义域内进行套论,若零点含参数在对零点之间的大小进行讨论。) ★1 已知函数 x a x x a x f )1(2 13 )(23-+-=,求函数的单调区间 )1)(1()1()(2a ax x a x ax x f +--=-+-=' ★★例2 已知函数2 2 ln )1()(x a x a x f ++=(a>0),求函数的单调区间 x a ax x x a x ax x f ) 1)(1()1()(2+--= -+-= ' ★★★例3 已知a 是实数,函数( ))f x x a =- (Ⅰ)求函数()f x 的单调区间; (Ⅱ)设()g a 为()f x 在区间[]0,2上的最小值。 (i )写出()g a 的表达式; (ii )求a 的取值范围,使得()62g a -≤≤-。 解:(Ⅰ)函数的定义域为[)0,+∞,( ))' 30a x f x x ? ?- ? ===>,由'()0f x = 得3 a x = 。考虑3a 是否落在导函数'()f x 的定义域()0,+∞内,需对参数a 的取值分0a ≤及0a >两 种情况进行讨论。 (1) 当0a ≤时,则' ()0f x >在()0,+∞上恒成立,所以()f x 的单调递增区间为[)0,+∞。 (2) 当0a >时,由' ()0f x >,得3a x > ;由' ()0f x <,得03 a x <<。 因此,当0a >时,()f x 的单调递减区间为0,3a ??????,()f x 的单调递增区间为,3 a ??+∞???? 。 (Ⅱ)(i )由第(Ⅰ)问的结论可知: (1) 当0a ≤时,()f x 在[)0,+∞上单调递增,从而()f x 在[]0,2上单调递增,所以 ()()00g a f ==。 (2) 当0a >时,()f x 在0,3a ??????上单调递减,在,3a ??+∞???? 上单调递增,所以: ② 当 ()0,23a ∈,即06a <<时,()f x 在0,3a ??????上单调递减,在,23a ?? ???? 上单调递增, 所以( )3a g a f ?? == ? ?? 932a a -=。 ③ 当 [)2,3 a ∈+∞,即6a ≥时,()f x 在[]0,2上单调递减,所以()( ))22g a f a =-。 综上所述,( ))0,06 2,~6a g a a a a ?≤? ?=< ,由62-≤≤-解得36a ≤<; ④ 若6a ≥ ,由)622a -≤-≤- 解得62a ≤≤+。 综上所述,a 的取值范围为32a ≤≤+ 三.求导后,因导函数为零是否有实根(或导函数的分子能否分解因式)不确定,而引起的讨论。 ★例1已知函数x ax x f +=22 1)( 求函数的单调区间 1)(+='ax x f ★★例2已知函数ax x x f -=ln )(求函数的单调区间 a x x f -= '1 )( x ax x f 1)(+-=' ★★★例3 设k R ∈ ,函数1 ,11(),()(),1x x f x F x f x kx x R x ? -==-∈??≥? , 试讨论函数()F x 的单调性。 解:∵1 ,11(),()(),1x x f x F x f x kx x R x ? -==-∈??≥? ()( )2 2 11,11,1,11()(),'(),11k x x kx x x x F x f x kx F x kx x x ?--?? 。 考虑导函数'()0F x =是否有实根,从而需要对参数k 的取值进行讨论。 (一)若1x <,则() () 2 2 11'()1k x F x x --= -。由于当0k ≤时,'()0F x =无实根,而当0k >时, '()0F x =有实根, 因此,对参数k 分0k ≤和0k >两种情况讨论。 (1) 当0k ≤时,'()0F x ≥在(,1)-∞上恒成立,所以函数()F x 在(,1)-∞上为增函数; (2) 当0k >时,() ( ) () 2 2 21111'()11k x x k x F x x x ??????---+???? --??????= =--。 由'()0F x = ,得121,1x x ?? == ? ? ,因为0k >,所以121x x <<。 由'()0F x > ,得11x <<;由'()0F x < ,得1x <-。 因此,当0k >时,函数()F x 在(,1-∞ 上为减函数,在(1上为增函数。 (二)若1x > ,则'()F x =。由于当0k ≥时,'()0F x =无实根,而当0k <时, '()0F x =有实根,因此,对参数k 分0k ≥和0k <两种情况讨论。 (1) 当0k ≥时,'()0F x <在[)1,+∞上恒成立,所以函数()F x 在[)1,+∞上为减函数; (2) 当0k < 时,1'()k F x ?-?==。 由'()0F x >,得2114x k >+ ;由'()0 F x <,得2 1 114x k <<+。 因此,当0k <时,函数()F x 在211,14k ? ?+????上为减函数,在211,4k ?? ++∞???? 上为增函数。 综上所述: (1) 当0k >时,函数()F x 在(,1-∞ 上为减函数,在(1上为增函数,在[)1,+∞上为减函数。 (2) 当0k =时,函数()F x 在(,1)-∞上为增函数,在[)1,+∞上为减函数。 (3) 当0k <时,函数()F x 在(,1)-∞上为增函数,在211,14k ??+ ????上为减函数,在211,4k ?? ++∞???? 上为增函数。 ★★★★ 19.设a >0,讨论函数f (x )=lnx+a (1-a )x 2 -2(1-a )x 的单调性。 解:函数()f x 的定义域为(0,).+∞22(1)2(1)1(),a a x a x f x x ---+'= 当2 12(1)10a a x ≠--+=时,方程2a(1-a)x 的判别式112(1).3a a ???=-- ??? ①当1 0,0,()3 a f x '<< ?>时有两个零点, 1211 0,22x x a a ≠ ->=+ (1) 且当12120,()0,()(0,)(,)x x x x f x f x x x '<<>>+∞或时在与内为增函数; 当1212,()0,()(,)x x x f x f x x x '<<<时在内为减函数; ②当 1 1,0,()0,()(0,)3 a f x f x '≤ ③当1 1,()0(0),()(0,)a f x x f x x '==>>+∞时在内为增函数; ④当 1>a 时0>?,)1(2)1)(13(211a a a a a x ----= ) 1(2)1)(13(211a a a a a x ---+= 由2222 2 )1(4)1)(13(41)1(2)13)(1(21a a a a a a a a a a ----=??? ? ??----??? ??)1(4134122a a a a --+=)1(41312a a a a --+-=0)1(422<-=a a a )1(2)1)(13(211a a a a a x ----= >0 ) 1(2)1)(13(211a a a a a x ---+=<0 所以在定义域(0,+∞)内有唯一零点1x , 且当110,()0,()(0,)x x f x f x x '<<>时在内为增函数;当1x x >时,1()0,()(,)f x f x x '<+∞在内为减函数。 ()f x 的单调区间如下表: ( 其 中 1211 22x x a a = =+ ) 因函数的零点的个数不确定而引起的讨论。 例.已知函数f(x)=1n x ,g(x)= a x +2 2 1(a 为常数),若直线l 与y=f(x)和y=g(x)的图象都相切,且l 与y=f(x)的图象相切于定点P (1,f (1)). (1)求直线l 的方程及a 的值; (2)当k∈R 时,讨论关于x 的方程f(x 2 +1)-g(x)=k 的实数解的个数. 解:(1)∵f′(x)= x 1 ,∴f(1)=1 ∴k 1=1,又切点为P (1,f (1),即(1,0)∴l 的解析式为y=x-1, y=x-1 ∵l 与y=g(x)相切, 由 y= a x +2 2 1,消去y 得x 2-2x+2a+2=0,∴△=(-2)2-4(2a+2)=0,得a=-21 (2)令h (x )=f(x 22 +1)2 1212+-x 1 03a << 113 a ≤≤ 1a > 1(0,)x 12(,)x x 2(,)x +∞ (0,)+∞ 1(0,)x 1(,)x +∞ ∵h′(x)= 212x x +-x=-2 1) 1)(1(x x x x ++-,则 ) (101x h ,x x '<<-<时或-1<x <0或x >1时, 故x=±1时,h (x )取极大值1n2, x=0时,h (x )取极小值 2 1 。 因此当 k∈(1n2,+∞),原方程一解;当k=1n2时,原方程有两解;当2 1 <k <1n2时,原方程有四解;当k= 21时,原方程有三解;当k <2 1 时,原方程有两解 5.求参数的范围时由于不能分离出参数而引起的对参数进行的讨论 例1:(此为不能分离出参数a 的例题)已知322 ()69f x x ax a x =-+(a ∈R ).当0a > 时,若对 []0,3x ?∈有()4f x ≤恒成立,求实数a 的取值范围. 解:因为f(x)=x 3-6ax 2+9a 2x ,x 3-6ax 2+9a 2x-4≤0 所以f'(x)=3x 2-12ax+9a 2 =(3x-3a )(x -3a), 在()a ,∞-上()x f '>0()x f 是增函数,在()a a 3,上()x f '<0()x f 是减函数,在()+∞,3a 上()x f '>0()x f 是增 函数。所以函数在x=a 时,()()a f x f =极大,所以函数在x=a 时,()()a f x f 3=极小 因对[]0,3x ?∈有()4f x ≤恒成立, 求实数a 的取值范围.极值点 指定区间端点位置关系不确定引起讨论。讨论如下: ∵a>0 ①当两个极值点都在指定区间[]3,0内时。即0<3a ≤3,也就是0 在()a ,0上()x f '>0()x f 是增函数,在()a a 3,上()x f '<0()x f 是减函数,在(),3a 上()x f '>0()x f 是增函数。所以函数在x=a 时,()()a f x f =极大,所以函数在x=a 时,()()a f x f 3=极小 ()()(){} 3,max max f a f x f = ()()(){}a f f x f 3,0min min = []0,3x ?∈有()4f x ≤恒成立, 等价于()()?????≤-≤-≤<0430410f a f a ? ?? ??≤-+-≤-+-≤<0427542704961 02333a a a a a a 解得??? ? ????? +≤≤-≤≤<93219321110a a a 即0 ②当两个极值点有一个在指定区间[]3,0内时。即03时,也就是10时为什么分为0 在()a ,0上()x f '>0()x f 是增函数,在](3,a 上()x f '<0()x f 是减函数, 所以函数在x=a 时,()()a f x f =极大, ()()a f x f =max ()()(){}3,0min min f f x f = []0,3x ?∈有()4f x ≤恒成立,等价于()?? ?≤-≤<0 431a f a 解得93