指数分布应用 ()

指数分布相关问题一. 在概率论中有一种分布是指数分布，其概率密度函数为

f(x)=λe^(-λ) x>0

(0 x<=0 )

这种分布具有无记忆性，和寿命分布类似。举个例子来说就是，一个人已经活了20岁和他还能再活20岁这两件事是没有关系的。因此指数分布也被戏称为“永远年轻”。另外正态分布也用到了指数函数，只不过表达式比较复杂，这在高中数学中也有涉及到。

二. 在复变函数中，也经常用到指数形式表示一个负数。比如说1+i=根号2*e^(πi/4)

这是根据著名的欧拉公式得到的：cosa+isina=e^(ai),当然复指数与实数范围内的指数有很多不同的地方，在复变函数中还会学深入的学到。

复指数在信号的频谱分析中还有很重要的应用，要研究一个周期信号的还有那些频率分量就要把它展开成若干个复指数函数的线性组合，这个过程叫傅里叶分解，是法国数学家、物理学家傅里叶（Fourier）发现的。学习电信类的相关专业会对信号的分析有一个系统的学习。

幂函数最重要的应用就是级数。不严谨的说，就是把一个函数展开成无穷项等比数列求和的形式，只不过每项都是关于x的幂函数，利用这个幂级数，可以把任意一个函数表示成多项式，方便近似计算。另外，刚才提到的傅里叶分解也就是把一个周期函数（信号）展开成傅里叶级数。如果函数是非周期的（即周期无限大）这个过程就叫做傅里叶变换。

指数分布的应用:

一. 许多电子产品的寿命分布一般服从指数分布。有的系统的寿命分布也可用指数分布来近似。它在可靠性研究中是最常用的一种分布形式。指数分布是伽玛分布和威布尔分布的特殊情况，产品的失效是偶然失效时，其寿命服从指数分布。

指数分布可以看作当威布尔分布中的形状系数等于1的特殊分布，指数分布的失效率是与时间t无关的常数，所以分布函数简单。

二. 在电子元器件的可靠性研究中，指数分布应用广泛，在日本的工业标准和美国军用标准中，半导体器件的抽验方案都是采用指数分布。此外，指数分布还用来描述大型复杂系统（如计算机）的故障间隔时间的失效分布。但是，由于指数分布具有缺乏“记忆”的特性．因而限制了它在机械可靠性研究中的应用，所谓缺乏“记忆”，是指某种产品或零件经过一段时间t0的工作后,仍然如同新的产品一样,不影响以后的工作寿命值，或者说，经过一段时间t0的工作之后，该产品的寿命分布与原来还未工作时的寿命分布相同，显然，指数分布的这种特性，与机械零件的疲劳、磨损、腐蚀、蠕变等损伤过程的实际情况是完全矛盾的，它违背了产品损伤累积和老化这一过程。所以，指数分布不能作为机械零件功能参数的分布形式。

指数分布虽然不能作为机械零件功能参数的分布规律，但是，它可以近似地作为高可靠性的复杂部件、机器或系统的失效分布模型，特别是在部件或机器的整机试验中得到广泛的应用。

三. 排队论，也称随机服务系统理论。排队是在日常生活中经常遇到的现象，在医院中，目前要求服务的数量通常都超过服务机构的容量。对服务系统进行定量分析，综合平衡患者与服机构的设置，以期提高服务质量。

一、资料来源与方法

(一)根据我院超声科的调查，应用排队论的理论和方法评价与优化该服务系统。超声科有3台B超仪，机构形式是单队——多服务台的情形，服务时间是随机的，服务时间的分布假定平稳，即分布的参数不受时间的影响。调查内容是单位时间内到达的患者数与服务时间。

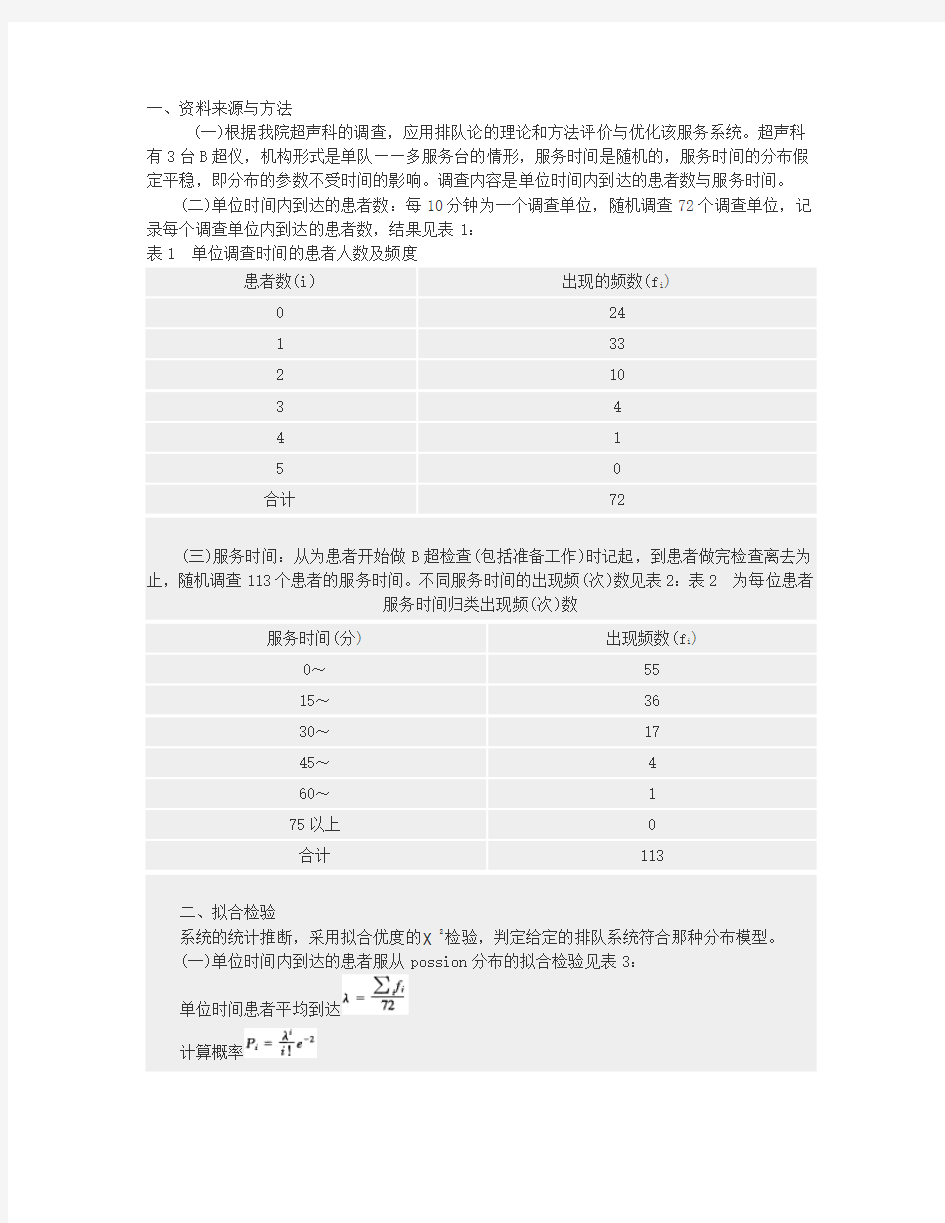
(二)单位时间内到达的患者数：每10分钟为一个调查单位，随机调查72个调查单位，记录每个调查单位内到达的患者数，结果见表1：

表1 单位调查时间的患者人数及频度

单位时间内到达的患者服从possion

单位时间患者平均到达

计算概率

计算理论频数

值

每次检查平均服务时间

式中x i′为组中值

计算概率：

计算理论频数

值

型，应用其计算公式得各项指标：λ=0.0958；μ=0.0523；C=3。

服务强度：

空闲概率：

等待检查的平均患者人数：

系统中平均逗留患者数：

患者平均等待时间： 患者平均逗留时间：

系统满员率：

患者到达后必须等待的概率，也称超员率(即系统中患者数已有3人，各服务台没有空闲

时)：

四、结论与系统最优化

(一)根据以上结果知，该服务机构平均利用率61%，空闲概率14%，满员率14%，说明仪器的充分利用与2、4、5台B 超仪的情形(见表5)相比最好的，患者平均等待时间6分钟，在B 超室平均逗留25分钟，有50%以上患者到达后需等待，系统较为忙碌，难以保证服务质量，特别是系统发生意外(如某台设备故障)时，需长时间排队(见表5)。将设备增加至5台，各项指标虽有明显改善，但设备利用率仅36.6%，显然造成一定浪费。综上所述，4台B 超仪是该系统

的最优选择。 表5 不同服务台数下各台的运行值

一、旬天气情况

气温：八月中旬平均气温百色市南北山区及南丹、金秀等地24.4～26.5℃，贺州、柳州、贵港三市全部，桂林、南宁两市大部、百色、河池两市局部及防港、梧州等地28.6～31.0℃，我区其余地区为26.6～28.5℃；与常年同期相比，崇左、玉林两市局部及北海等地正常到偏低0.5℃，其余大部地区偏高0.1～3.4℃，其中桂林大部、柳州、河池两市局部及象州等地偏高2.0℃以上。旬极端最高气温全区30.0～37.2℃，大部地区出现在11日、15日或19日，局部出现在13～14日或16日。

降雨：八月中旬降雨量北海、防城港、钦州、崇左四市大部，河池、百色、贺州、梧州、玉林五市局部及永福、来宾、贵港等地为50～202.4毫米，其中北海、合浦、东兴、防城、防城港、贵港、钦州等站旬降雨量超过100毫米，我区其余地区0.1～49.9毫米；与常年同期相比，崇左、防城港、河池三市局部及永福、来宾、钟山、梧州、贵港、北海等地正常到偏多6成，其中钟山、贵港两地旬降雨量偏多6成以上，我区其余地区偏少1～10成。旬降雨日数我区桂东北大部地区为3～4天，其余大部地区为6～8天；与常年同期相比，大部地区正常到偏少2天。

日照：八月中旬日照时数全区37～105小时，与常年同期相比，全区大部偏多2～3成。

二、监测结论

根据2010年8月中旬的MODIS卫星数据制作本旬归一化植被指数（NDVI）遥感监测图像（见图1）。本旬归一化植被指数值主要分布在33～68（放大100倍，以下同）范围内，空间分布特征：NDVI值在45～56之间的区域占全区面积最大，其次为33～44之间的区域。在各类地物中，林区NDVI值最高，一般大于57，裸地和城镇用地的NDVI值较低，一般在33以下。受云影响，甘蔗产区的植被指数无法监测。本旬我区各市归一化植被指数（NDVI）分段统计结果见表1。

表1 2010年8月中旬广西各市归一化植被指数（NDVI）分段面积统计表

*注：面积单位均为平方千米，百分比为该面积占广西国土总面积的百分比。

三、监测图像及说明

本次监测利用了广西壮族自治区气象减灾研究所DVBS系统接收的2010年8月中旬的MODIS卫星数据，数据经一系列预处理、分析，NDVI最大值合成并放大100倍，得到本旬广西NDVI遥感监测图像（见图1）。

图1 2010年8月中旬广西归一化植被指数（NDVI）

标准正态分布表

标准正态分布表 集团文件发布号：（9816-UATWW-MWUB-WUNN-INNUL-DQQTY-

标准正态分布表

4432198653 1.80.964 1 0.964 8 0.965 6 0.966 4 0.967 2 0.967 8 0.968 6 0.969 3 0.970 0.970 6 1.90.971 3 0.971 9 0.972 6 0.973 2 0.973 8 0.974 4 0.975 0.975 6 0.976 2 0.976 7 20.977 2 0.977 8 0.978 3 0.978 8 0.979 3 0.979 8 0.980 3 0.980 8 0.981 2 0.981 7 2.10.982 1 0.982 6 0.983 0.983 4 0.983 8 0.984 2 0.984 6 0.985 0.985 4 0.985 7 2.20.986 1 0.986 4 0.986 8 0.987 1 0.987 4 0.987 8 0.988 1 0.988 4 0.988 7 0.989 2.30.989 3 0.989 6 0.989 8 0.990 1 0.990 4 0.990 6 0.990 9 0.991 1 0.991 3 0.991 6 2.40.991 8 0.992 0.992 2 0.992 5 0.992 7 0.992 9 0.993 1 0.993 2 0.993 4 0.993 6 2.50.993 8 0.994 0.994 1 0.994 3 0.994 5 0.994 6 0.994 8 0.994 9 0.995 1 0.995 2 2.60.995 3 0.995 5 0.995 6 0.995 7 0.995 9 0.996 0.996 1 0.996 2 0.996 3 0.996 4 2.70.996 5 0.996 6 0.996 7 0.996 8 0.996 9 0.997 0.997 1 0.997 2 0.997 3 0.997 4 2.80.997 4 0.997 5 0.997 6 0.997 7 0.997 7 0.997 8 0.997 9 0.997 9 0.998 0.998 1 2.90.998 1 0.998 2 0.998 2 0.998 3 0.998 4 0.998 4 0.998 5 0.998 5 0.998 6 0.998 6 x00.10.20.30.40.50.60.70.80.9 30.998 7 0.999 0.999 3 0.999 5 0.999 7 0.999 8 0.999 8 0.999 9 0.999 9 1.000 正态分布概率表 Φ（ u ） =

t分布和标准规定正态分布

数理统计实验 t分布与标准正态分布 院（系）: 班级: 成员:

成员: 成员: 指导老师: 日期:

目录 t分布与标准正态分布的关系 (1) 一、实验目的 (1) 二、实验原理 (1) 三、实验内容及步骤 (1) 四、实验器材 (6) 五、实验结果分析 (6) 六、实验结论 (6)

t分布与标准正态分布的关系 一、实验目的 正态分布是统计中一种很重要的理论分布，是许多统计方法的理论基础。正态分布有两个参数，μ和σ，决定了正态分布的本质。为了应用和计算方便，常将一般的正态变量X通过μ变换[(X-μ)/σ]转化成标准正态变量μ，以使原来各种形态的正态分布都转换为μ=0，σ=1的标准正态分布，亦称μ分布。对于标准正态分布来说，μ是数据整体的平均值，σ是整体的标准差。但实际操作过程中，人们往往难以获得μ和σ。因此人们只能通过样本对这两个参数做出估计，用样本平均值和样本标准差代替整体的平均值和标准差，从而得出了t分布。另外从图像的层面说，正态分布的位置和形态只与μ和σ有关，而t分布不只与样本平均值和样本标准差有关，还与自由度相关。通过实验了解t分布与标准正态分布之间的关系。 二、实验原理 运用EXCEL软件验证t分布与标准正态分布的关系，绘制相应的统计图表进行分析。 三、实验内容及步骤 1.打开Excel文件，将“t分布与标准正态分布N（0，1）”合并并居中，黑体，20字号，红色；

2.选中文件,选项,自定义功能区,加载开发工具.在开发工具中插入滚动条,调节滚动条大小； 3.设置A2单元格格式,数字自定义区”!n=#,##0;[红 色]￥-#,##0”.然后左对齐,设置为红色；

几种重要的概率分布

1、均匀分布（uniform） 定义：设连续型 随机变量X的分布函数为F(x)=(x-a)/(b-a),a≤x≤b 则称随机变量X服从[a,b]上的均匀分布,记为X~U[a,b]. 若[x1,x2]是[a,b]的任一子区间,则P{x1≤x≤x2}=(x2-x1)/(b-a) 这表明X落在[a,b]的子区间内的概率只与子区间长度有关,而与子区间位置无关,因此X落在[a,b]的长度相等的子区间内的可能性是相等的,所谓的均匀指的就是这种等可能性. 在实际问题中,当我们无法区分在区间[a,b]内取值的随机变量X取不同值的可能性有何不同时,我们就可以假定X服从[a,b]上的均匀分布 若随机变量X的密度函数为 则称随机变量X服从区间[a,b]上的均匀分布。记作X~U(a,b). 均匀分布的分布函数为

图像如下图所示： 均匀分布的数学期望E(X)=1/(2*(b+a))，方差为D(X)=1/(12*(b-a)2)。 2、正态分布 如果连续型随机变量X的密度函数为

其中，-∞

3.F分布 F分布定义为: 设X、Y为两个独立的随机变量，X服从自由度为k1的>2分布，Y服从自由度为k2的>2 分布，这2 个独立的>2分布被各自的自由度除以后的比率这一统计量的分布。即：上式F服从第一自由度为k1，第二自由度为k2的F分布 F分布的性质 1、它是一种非对称分布； 2、它有两个自由度，即n1 -1和n2-1，相应的分布记为F（n1 –1，n2-1），n1 –1通常称为分子自由度，n2-1通常称为分母自由度； 3、F分布是一个以自由度n1 –1和n2-1为参数的分布族，不同的自由度决定了F 分布的形状。 4、F分布的倒数性质：Fα,df1,df2=1/F1-α,df1,df2 密度函数表达式

常用连续型分布性质汇总及其关系

常用连续型分布性质汇总及其关系 1. 常用分布 1．1 正态分布 （1）若X 的密度函数和分布函数分别为 ()( )()22 222(), . ,. x t x p x x F x e dt x μσμσ-- -- -∞ = -∞<<+∞= -∞<<+∞ 则称X 服从正态分布，记作()2~,,X N μσ，其中参数,0.μσ-∞<<+∞> （2）背景：一个变量若是由大量微小的、独立的随机因素的叠加结果，则此变量一定是正态变量。测量误差就是由量具零点偏差、测量环境的影响、测量技术的影响、测量人员的心理影响等等随机因素叠加而成的，所以测量误差常认为服从正态分布。 （3）关于参数,μσ： μ是正态分布的的数学期望，即()E X μ=，称μ为正态分布的位置参 数。μ为正态分布的对称中心，在μ的左侧和()p x 下的面积为0.5；在 μ的右侧和()p x 下的面积也是0.5，所以μ也是正态分布的中位数。 2σ是正态分布的方差，即2().Var X σ=σ是正态分布的标准差，σ愈小，正态分布愈集中，σ愈大，正态分布愈分散。σ又称为是正态分布的的尺度参数。 （4）称0,1μσ==时的正态分布(0,1)N 为标准正态分布。记U 为标准正 态分布变量，()u ?和()u Φ为标准正态分布的密度函数和分布函数。 ()u ?和()u φ满足：

()()()(); 1. u u u u ??-=Φ-=-Φ （5）标准化变换： 若()2~,,X N μσ则()~0,1.X U N μ σ -= （6）若()2~,,X N μσ则对任意实数a 与b ，有 ()( ),()1( ),()( )( ),b P X b a P a X b a P a X b μ σ μ σμ μ σ σ -≤=Φ-<=-Φ--<≤=Φ-Φ 0.6826,1,()()()0.9545,2,.0.9973, 3.k P X k k k k k μσ=?? -<=Φ-Φ-==??=? （7）特征函数 22 ()exp{}.2 t t i t σ?μ=-（标准正态分布2()exp{}2t t ?=-） 1.2.均匀分布 （1）若X 的密度函数和分布函数分别为 1 ().0 a x b P x b a else ?<

讲连续型随机变量分布及随机变量的函数的分布

第七讲 连续型随机变量（续）及 随机变量的函数的分布 3. 三种重要的连续型随机变量 （1）均匀分布 设连续型随机变量X 具有概率密度 )5.4(,, 0,,1 )(??? ??<<-=其它b x a a b x f 则称X 在区间(a,b)上服从均匀分布, 记为X~U(a,b). X 的分布函数为 )6.4(. , 1,, ,,0)(???? ???≥<≤--<=b x b x a a b a x a x x F （2）指数分布 设连续型随机变量X 的概率密度为 )7.4(, , 0,0,e 1)(/?????>=-其它x x f x θ θ 其中θ>0为常数, 则称X 服从参数为θ的指数分布. 容易得到X 的分布函数为 )8.4(. , 0,0,1)(/?? ?>-=-其它x e x F x θ 如X 服从指数分布, 则任给s,t>0, 有 第二章 随机变量及其分布 §4 连续型随机变量 及其概率密度 O x f (x )1 2 3 123=1/3=1=2

P{X>s+t | X > s}=P{X > t} (4.9) 事实上 }. {e e e )(1)(1}{}{} {)} (){(}|{//)(t X P s F t s F s X P t s X P s X P s X t s X P s X t s X P t s t s >===-+-=>+>= >>?+>=>+>--+-θ θθ 性质(4.9)称为无记忆性. 指数分布在可靠性理论和排队论中有广泛的运用. （3）正态分布 设连续型随机变量X 的概率密度为 ) 10.4(,,e 21)(2 22)(∞<<-∞= -- x x f x σμσ π其中μ,σ(σ>0)为常数, 则称X 服从参数为 μ,σ的正态分布或高斯(Gauss)分布, 记为 X~N(μ,2σ). 显然f(x)≥0, 下面来证明 1d )(=? +∞ ∞ -x x f 令t x =-σμ/)(, 得到 dx e dx e t x 2 2)(22 22121- ∞ +∞ --- ∞ +∞ -? ? = π σ πσμ . 1d 21d 21 ) 11.4(π 2d d e ,, d d ,d e 2 2)(20 2 22 /)(2 2 /2 2 22 222== ====? ??? ? ? ?∞ ∞ -- ∞ ∞ ---∞ - +∞∞-+∞ ∞ -+-∞∞ --x e x e r r I u t e I t I t x r u t t π σ πθσ μπ 于是 得转换为极坐标则有记f(x)具有的性质: f (x )的图形: O x f (x ) =5 =5 0.266 0.3990.798 x O f (x ) 1.5 1 0.5

标准正态分布表

标准正态分布表 x 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0 0.500 0 0.504 0 0.508 0 0.512 0 0.516 0 0.519 9 0.523 9 0.527 9 0.531 9 0.535 9 0.1 0.539 8 0.543 8 0.547 8 0.551 7 0.555 7 0.559 6 0.563 6 0.567 5 0.571 4 0.575 3 0.2 0.579 3 0.583 2 0.587 1 0.591 0 0.594 8 0.598 7 0.602 6 0.606 4 0.610 3 0.614 1 0.3 0.617 9 0.621 7 0.625 5 0.629 3 0.633 1 0.636 8 0.640 4 0.644 3 0.648 0 0.651 7 0.4 0.655 4 0.659 1 0.662 8 0.666 4 0.670 0 0.673 6 0.677 2 0.680 8 0.684 4 0.687 9 0.5 0.691 5 0.695 0 0.698 5 0.701 9 0.705 4 0.708 8 0.712 3 0.715 7 0.719 0 0.722 4 0.6 0.725 7 0.729 1 0.732 4 0.735 7 0.738 9 0.742 2 0.745 4 0.748 6 0.751 7 0.754 9 0.7 0.758 0 0.761 1 0.764 2 0.767 3 0.770 3 0.773 4 0.776 4 0.779 4 0.782 3 0.785 2 0.8 0.788 1 0.791 0 0.793 9 0.796 7 0.799 5 0.802 3 0.805 1 0.807 8 0.810 6 0.813 3 0.9 0.815 9 0.818 6 0.821 2 0.823 8 0.826 4 0.828 9 0.835 5 0.834 0 0.836 5 0.838 9 1 0.841 3 0.843 8 0.846 1 0.848 5 0.850 8 0.853 1 0.855 4 0.857 7 0.859 9 0.86 2 1 1.1 0.864 3 0.866 5 0.868 6 0.870 8 0.872 9 0.87 4 9 0.877 0 0.879 0 0.881 0 0.883 0 1.2 0.884 9 0.886 9 0.888 8 0.890 7 0.892 5 0.894 4 0.89 6 2 0.898 0 0.899 7 0.901 5 1.3 0.903 2 0.904 9 0.906 6 0.90 8 2 0.90 9 9 0.911 5 0.913 1 0.914 7 0.916 2 0.917 7 1.4 0.919 2 0.920 7 0.922 2 0.923 6 0.925 1 0.926 5 0.927 9 0.929 2 0.930 6 0.931 9 1.5 0.933 2 0.934 5 0.935 7 0.937 0 0.938 2 0.939 4 0.940 6 0.941 8 0.943 0 0.944 1 1.6 0.945 2 0.946 3 0.947 4 0.948 4 0.949 5 0.950 5 0.951 5 0.952 5 0.953 5 0.953 5 1.7 0.955 4 0.956 4 0.957 3 0.958 2 0.959 1 0.959 9 0.960 8 0.961 6 0.962 5 0.963 3 1.8 0.964 1 0.964 8 0.965 6 0.966 4 0.967 2 0.967 8 0.968 6 0.969 3 0.970 0 0.970 6 1.9 0.971 3 0.971 9 0.972 6 0.973 2 0.973 8 0.974 4 0.975 0 0.975 6 0.976 2 0.976 7 2 0.977 2 0.977 8 0.978 3 0.978 8 0.979 3 0.979 8 0.980 3 0.980 8 0.981 2 0.981 7 2.1 0.982 1 0.982 6 0.983 0 0.983 4 0.983 8 0.984 2 0.984 6 0.98 5 0 0.985 4 0.985 7 2.2 0.98 6 1 0.986 4 0.986 8 0.98 7 1 0.987 4 0.987 8 0.988 1 0.988 4 0.988 7 0.98 9 0 2.3 0.989 3 0.989 6 0.989 8 0.990 1 0.990 4 0.990 6 0.990 9 0.991 1 0.991 3 0.991 6 2.4 0.991 8 0.992 0 0.992 2 0.992 5 0.992 7 0.992 9 0.993 1 0.993 2 0.993 4 0.993 6 2.5 0.993 8 0.994 0 0.994 1 0.994 3 0.994 5 0.994 6 0.994 8 0.994 9 0.995 1 0.995 2 2.6 0.995 3 0.995 5 0.995 6 0.995 7 0.995 9 0.996 0 0.996 1 0.996 2 0.996 3 0.996 4 2.7 0.996 5 0.996 6 0.996 7 0.996 8 0.996 9 0.997 0 0.997 1 0.997 2 0.997 3 0.997 4 2.8 0.997 4 0.997 5 0.997 6 0.997 7 0.997 7 0.997 8 0.997 9 0.997 9 0.998 0 0.998 1 2.9 0.998 1 0.998 2 0.998 2 0.998 3 0.998 4 0.998 4 0.998 5 0.998 5 0.998 6 0.998 6 x 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 3 0.998 7 0.999 0 0.999 3 0.999 5 0.999 7 0.999 8 0.999 8 0.999 9 0.999 9 1.000 0

正态分布讲解(含标准表)

2．4正态分布 复习引入： 总体密度曲线:样本容量越大，所分组数越多，各组的频率就越接近于总体在相应各组取值的概率．设想样本容量无限增大，分组的组距无限缩小，那么频率分布直方图就会无限接近于一条光滑曲线,这条曲线叫做总体密度曲线． 总体密度曲线 b 单位 O 频率/组距 a 它反映了总体在各个范围内取值的概率．根据这条曲线，可求出总体在区间(a，b)内取值的概率等于总体密度曲线，直线x=a，x=b及x轴所围图形的面积． 观察总体密度曲线的形状，它具有“两头低，中间高，左右对称”的特征，具有这种特征的总体密度曲线一般可用下面函数的图象来表示或近似表示： 2 2 () 2 , 1 (),(,) 2 x x e x μ σ μσ ? πσ - - =∈-∞+∞ 式中的实数μ、)0 (> σ σ是参数，分别表示总体的平均数与标准差，, ()x μσ ? 的图象为正态分布密度曲线,简称正态曲线． 讲解新课：

一般地，如果对于任何实数a b <，随机变量X 满足 ,()()b a P a X B x dx μσ?<≤=?, 则称 X 的分布为正态分布（normal distribution ) ．正态分布完全由参数μ和σ确定，因此正态分布常记作),(2 σ μN ．如果随机变量 X 服从正态分布，则记为X ～),(2σμN . 经验表明，一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和，它就服从或近似服从正态分布．例如，高尔顿板试验中，小球在下落过程中要与众多小木块发生碰撞，每次碰撞的结果使得小球随机地向左或向右下落，因此小球第1次与高尔顿板底部接触时的坐标 X 是众多随机碰撞的结果，所以它近似服从正态分布．在现实生活中，很多随机变量都服从或近似地服从正态分布．例如长度测量误差；某一地区同年龄人群的身高、体重、肺活量等；一定条件下生长的小麦的株高、穗长、单位面积产量等；正常生产条件下各种产品的质量指标（如零件的尺寸、纤维的纤度、电容器的电容量、电子管的使用寿命等）；某地每年七月份的平均气温、平均湿度、降雨量等；一般都服从正态分布．因此，正态分布广泛存在于自然现象、生产和生活实际之中．正态分布在概率和统计中占有重要的地位． 说明:1参数μ是反映随机变量取值的平均水平的特征数，可以用样本均值去佑计；σ是衡量随机变量总体波动大小的特征数，可以用样本标准差去估计． 2.早在 1733 年，法国数学家棣莫弗就用n ！的近似公式得到了正态分布．之后，德国数学家高斯在研究测量误差时从另一个角度导出了它，并研究了它的性质，因此，人们也称正态分布为高斯分布． 2．正态分布),(2 σ μN ）是由均值μ和标准差σ唯一决定的分布 通过固定其中一个值，讨论均值与标准差对于正态曲线的影响

几种常用连续型随机变量

几种常用的连续型随机变量 给出一个新概念：广义概率密度函数。 设连续型随机变量ξ的概率密度函数为φ(x ), 那么任何与之成正比的函数f (x )∝φ(x ), 都叫做ξ的广义概率密度函数, 或者说, 一个函数f (x )是ξ的广义概率密度函数, 说明存在着一实数a , 使得 φ(x )=af (x ) (1) 而知道了广义概率密度函数, ξ的概率密度函数就可以根据性质1)(=?+∞ ∞ -dx x ?, 求出 将(1)式代入得: 1)()(??+∞ ∞ -+∞ ∞ -==dx x af dx x ? 则?∞+∞ -= dx x f a )(1 因此, 知道了广义概率密度函数就等于知道了一般的概率密度函数, 我们只需关心函数的形状就可以了解概率密度的性质了. 因此也不必关于那个常数是什么. 4.4 指数分布 指数分布的概率密度函数为 ?? ?>=-其它 )(x e x x λλ? 它的图形如下图所示: 它的期望和方差如下计算: () λ λ λ?ξλλλλλ1 1 )(0 =- =+-=-= = = ∞ +-∞+-∞ +-+∞ -+∞ -+∞ ∞ -????x x x x x e dx e xe e xd dx e x dx x x E

() 2 20 202 2 2 2 2 2)(|λξλ λ?ξλλλλ= = +-=-= = = ????∞+-∞+-+∞ -+∞ -+∞∞ -E dx xe e x e d x dx e x dx x x E x x x x 2 2 2 221 1 2 )(λ λ λ ξξξ= - = -=E E D 指数分布常用来作为各种"寿命"分布的近似. 4.5 Γ-分布 如果一个随机变量ξ只取正值, 且在正半轴的广义概率密度函数的形式是x 的某次方x k 乘上指数函数e -λx , 即 ?? ?>->>=-其它 ) 0,1(0)(λλk x e x x f x k 那么就称ξ服从Γ-分布了. 上式中之所以要求k >-1, λ>0, 是因为广义积分 ?? +∞ -+∞ ∞ -= )(dx e x dx x f x k λ 只有在这种条件下才收敛. 此外, 传统上为了方便起见, 用另一个常数r =k +1, 因此广义概率密度函数写为 ?? ?>>>=--其它 ) 0,0(0)(1λλr x e x x f x r 而真实的概率密度函数φ(x )=af (x ), 可以给出常数a 由下式计算: ?∞ +--= 11 dx e x a x r λ 这样, 计算的关键就是要计算广义积分 ?+∞ --0 1dx e x x r λ, 作代换t =λx , 则x =t /λ, dx =dt /λ, 则???+∞ --+∞ --+∞ --= ? ?? ? ?=0 101 011 1 dt e t dt e t dx e x t r r t r x r λ λ λλ, 问题就转成怎样计算广义积分? +∞ --0 1dt e t t r , 这个积分有一个参数r >0, 在r 为一些特定 的参数时, 如当r =1时, 上面的广义积分还是可以计算的, 但是当r 为任意的正实数时, 此广 义积分就没有一般的公式, 一般的原函数表达式. 在这种情况下数学家常用的办法就是定义一个新的函数. 比如说, 在中学学的三角函数就无法用一个加减乘除的公式表示, 因此就发明了sin , cos 这样的记号来代表三角函数. 同样, 上面的广义积分的取值只依赖于参数r , 每给定一个r 值就有一个积分值与之对应, 因此也可以定义一个函数, 叫Γ-函数, 定义为

指数族和几何分布

指数族和几何分布 关于指数族和广义线性模型的相关知识，详情请点击。 以φ为参数的指数分布为： ,...2,1)1();(1=-=-y y p y ，φφφ （1）证明指数分布是指数族分布。 ) 1log ))1exp((log()log )1log()1exp(()1();(1φφφφφφ φφ-+?-=+--=-=-y y y p y 于是， )1log()1log()(, )() 1(),1(log 1)(η ηφφ ηφφηe e a y y T e y b -=--==-=?-==， （2）使用具有几何反应变量的广义线性模型，执行回归，可得 典型反应函数为： η φ ηηηe y E y T E g -====11 1] ;[] );([)( （3）给定一组训练集},...,2,1);,{()()(m i y x i i =，令一个样本的log 似然性为);|()()(θi i x y p ，下面我们求解随机梯度上升的更新规则。先写出

)1log(11 log 1log ))1log )1g(log(exp(lo );|(log )()() ()()()()()()()()()()()(-+=--=--=---==--i T i T i T i T x i i T x i i T x x i i T i i i e y x e y x e e y x y x y p l θθθθθθθφφφθθ， )(θl 关于j θ求导，得到 ) ( )()()()()( )()())1(1 ()1() 1()()()()()(i j x i x i j i i j x i j x i i j j x e y e x y x e x e y x l i T i T i T i T θθθθθ---- =--?+=??-- 所以梯度上升更新规则为 )()()11(:)(i j x i j j x e y i T θαθθ-- +=。

几种常见的分布知识讲解

一、常见数据类型 在正式的解释分布之前，我们先来看一看平时遇到的数据。数据可大致分为离散型数据和连续型数据。 离散型数据 离散型数据顾名思义就是只取几个特定的值。例如：当你掷骰子的时候，结果只有1,2,3,4,5,6，不会出现类似1.5,2.5。 连续型数据 在一个给定的范围内，连续型数据可以取任意值。这个范围可以是有限的或者是无穷的。例如：一个人的体重或者身高，可以取值54kg,54.4kg,54.33333kg等等都没有问题。 下面就开始介绍分布的类型。 二、分布类型 伯努利分布（Bernoulli Distribution） 首先从最简单的分布开始，伯努利分布实际上是一个听起来最容易理解的分布。伯努利分布一次实验有两个可能的结果，比如1代表success及0代表failure。随机变量X X一个取值为1并代表成功，成功概率为p p，一个取值为0表示失败，失败概率为q q或者说1?p1?p。 这里，概率分布函数为p x(1?p)1?x px(1?p)1?x，其中x∈(0,1)x∈(0,1)，我们也可以写成如下形式： P(x)={1?p，p，x=0x=1P(x)={1?p，x=0p，x=1 成功和失败的概率没必要相同，也就是没必要都是0.5，但是这俩概率加和应该为1，比如可以是下面的图：

这个图就是p(success)=0.15，p(failure)=0.85p(success)=0.15，p(failure) =0.85。 下面说一下随机变量的期望，一个分布的期望就是这个分布的均值。服从伯努利分布的随机变量X X的期望值就是： E(X)=1?p+0?(1?p)=p E(X)=1?p+0?(1?p)=p 服从伯努利分布的随机变量的方差是： V(X)=E(X2)?[E(X)]2=p?p2=p(1?p)V(X)=E(X2)?[E(X)]2=p?p2=p(1?p) 还有许多伯努利分布的例子，比如说明天是否会下雨，今天会不会去健身，明天乒乓球比赛是不是会赢。 均匀分布（Uniform Distribution） 当你掷骰子的时候，结果出现1到6中的任何一个，而任何一个结果出现的概率都是相同的，这就是均匀分布最原始的雏形。你可能看出来了，与伯努利分布不同的是，这n n个出现的结果的概率都是相同的。 一个随机变量X X为均匀分布是指密度函数如下： f(x)=1b?a?∞

连续型随机变量的分布与例题讲解

连续型随机变量的分布 （一）连续型随机变量及其概率密度函数 1.定义：对于随机变量X 的分布函数 F(X) ，若存在非负函数f(x), 使对于 任意的实数 x，有F ( x)x f(x) 称为 X f (t)dt ，则称X为连续性随机变量， 的概率密度函数，简称概率密度。 注： F(x)表示曲线下x 左边的面积，曲线下的整个面积为1。 2 .密度函数f(x) 的性质：注： f( x)不是概率。 1) f( x)≥ 0 + f ( x) dx = 1 2) ò-x 2 3)P{x 1 < X ? x 2 }òx1 f (x) dx = F (x 2 ) - F (x 1 ) 特别地，连续型随机变量在某一点的概率为零，即 P{ X = x} = 0. （但 { X=x} 并不一定是不可能事件） 因此P(a≤X ≤ b)= P(a< X

几种常见的分布

一、常见数据类型数据可大致分为离散我们先来看一看平时遇到的 数据。在正式的解释分布之前，型数据和连续型数据。离散型数据结果只当你掷骰子的时候，离散型数据顾名思义就是只取几个特定的值。例如：。1,2,3,4,5,6，不会出现类似1.5,2.5有连续型数据这个范围可以是有限的或 者是连续型数据可以取任意值。在一个给定的范围内，等 54kg,54.4kg,54.33333kg无穷的。例如：一个人的体重或者身高，可以取值等都没有问题。下面就开始介绍分布的类型。二、分布类型）Bernoulli Distribution伯努利分布（首先从最简单的分布开始，伯努利分布实际上是一个听起来最容易理解的分布。。代表0failure1代表success及伯努利分布一次实验有两个可能的结果，比如pX表示失，一个取值为1并代表成功，成功概率为0随机变量pX一个取值为pq1?或者说1?p。败，失败概率为q(0,1)∈xp(1?p)，我们(0,1)x这里，概率分布函数为px(1?p)1?x，其中∈xx1?也可以写成如下形式：x=0x=1pP(x)={1?p x=1 ，，，x=0p，P(x)={1?p，但是这俩概率加和应该0.5成功和失败的概率没必要相同，也就是没必要都是，比如可以是下面的图：为 1. p(failure)=0.85p(success)=0.15p(failure)这个图就是p(success)=0.15，，

=0.85。服从伯努利下面说一下随机变量的期望，一个分布的期望就是这个分布的均值。X X分布的随机变量的期望值就是： p)=p?(1?E(X)=1?p+0?(1?p)=pE(X)=1?p+0服从伯努利分布的随机变量的方差 是：p)(1?=p?p=pV(X)=E(X)?[E(X)] V(X)=E(X2)?[E(X)]2=p?p2=p(1?p)222明天今天会不会去健身，还有许多伯努利分布的例子，比如说明天是否会下雨，乒乓 球比赛是不是会赢。）均匀分布（Uniform Distribution而任何一个结果出现的概率中的任何一个，1到6当你掷骰子的时候，结果出现与伯努利 分布不都是相同的，这就是均匀分布最原始的雏形。你可能看出来了，n n个出现的结果的概率都是相同的。同的是，这X X为均匀分布是指密度函数如下：一个随机变量<∞≤b?f(x)=1ba?∞(a+b)2V(X)= Variance->V(X)=(b?a)21212?a)(b2b=0a=0，所以对于标准

标准正态分布表

标准正态分布表 标准正态分布表怎么看 将未知量Z对应的列上的数与行所对应的数字结合查表定位 例如要查Z=1.96的标准正态分布表 首先在Z下面对应的数找到1.9 然后在Z右边的行中找到6 这两个数所对应的值为0.9750 即为所查的值 有谁知道，为什么标准正态分布表x的右边和下边都有值啊，难道一个x可以有两个值，看表是怎么看啊 那是一个精度问题，例如当x=0.12,那么应该先在x下方找到0.1，再在右边找到0.02，那么这两个同时对应的那个数就应该是你所要的！ 标准正态分布的x值算出来介于两个之间,取哪一个。概论值如果介于两个间,取更大的还是更近的啊 精度要求不是很高的话，在正中取中间值，靠一边取更近的，四舍五入。 精度要求高的话用插值函数，比如在两点间作一次函数逼近。 为什么u0.025等于1.96？标准正态分布表查不到这个结果啊。u0.05是多少？u0.1是多少？ 因为P{Z<1.96}=1-0.025=0.975 u0.05=1.645 因为P{Z<1.645}=1-0.05 u0.1类似 统计学中，标准正态分布表中Z值代表意义 Z值只是一个临界值，他是标准化的结果，本身没有意义，有意义的在于在标准正态分布模型中它代表的概率值。通过查表便可以知道。 标准正态分布 期望值μ=0，即曲线图象对称轴为Y轴，标准差σ=1条件下的正态分布，记为N(0，1)。 标准正态分布又称为u分布，是以0为均数、以1为标准差的正态分布，记为N（0，1）。 标准正态分布的密度函数为：

标准正态分布曲线下面积分布规律是：在-1.96～+1.96范围内曲线下的面积等于0.9500，在-2.58～+2.58范围内曲线下面积为0.9900。统计学家还制定了一张统计用表（自由度为∞时），借助该表就可以估计出某些特殊u1和u2值范围内的曲线下面积。

连续型随机变量的分布与例题讲解

连续型随机变量的分布 (一)连续型随机变量及其概率密度函数 1.定义：对于随机变量X的分布函数F(X),若存在非负函数f(x),使 对于任意的实数x,有F(W(M，则称X为连续性随机变量，f(x)称 为X的概率密度函数，简称概率密度。 注：尺劝表示曲线下x左边的面积，曲线下的整个面积为 lo 2 .密度函数f(x)的性质：注：不是概率。 1)??f(x)M0?? 2)? j f(x)dx = \ 3)P{x, < X < x2} = ~f(x)(/x =F(x2) -F(Xj) 特别地，连续型随机变量在某一点的概率为零，即 P{X = x} = 0.(但{脸力并不一定是不可能事件) 因此PQWXWb)二P(a

注：iv)与离散型随机变量不同,

易知 ； (3) P(|X|<. 解⑴ P(XW 二①二 (2) P(X> =1- P(XW =1-①= (3) P(|X|< =P0有 P///-h/2/r s

指数分布族

指数族 3.1指数分布族 对于每个感兴趣的分布都可能获得属性（例如均值、方差和极大似然估计量稍后正确的定义）。然而，这可能是麻烦的，代数学是沉闷的并且我们无法看到重点。反而，我们考虑到这是一个包含几个我们总所周知分布的“伞形”分布族，我们将对这样的分布得到一个均值和方差的一般式（在这个课程中，当我们考虑到这是一个广义线性模型时就将会是很有用的）。用这些结果去表达极大似然估计就是充分统计量的函数，由此是最佳无偏估计量（在完整的假设下）。换句话说，对于这个分布族的最大似然估计量（在之前我们已经遇到很多次）的确是最佳参数据计量（在最小方差方面）。 假设随机变量变量有概率分布，并且可以写成如下形式 如果的分布（离散随机变量的概率分布函数和连续随机变量的概率密度函数）可以写成上面的形式，则称属于指数族分布。大量的众所周知的概率分布都属于这个分布族。因此通过理解指数组的性质，我们可以得到大量分布函数的总结。 例 3.1.1（a）指数分布，因此概率密度函数可以写成 因此， （b）二项分布可以被写成 因此 应该提到的是当是一个向量的维度大于1时，可以简单的概括指数族。假设是一个维向量。 P属于指数族，当分布族满足 此时(线性无关)， 3.1.1 自然指数分布族

若我们让（），并且是一个可逆函数（因此空间包含和呈一对一对应关系），然后我们重写3.1得 此时，当时成为自然指数分布族。 现在通过转换,我们给出自然指数族形式的例子。 （1）指数分布已经是自然指数分布族形式。 （2）关于二项分布，我们让，因为是可逆的，这产生了对数分布当 因此我们感兴趣的已经转变，我们经常配合一个(后来的模型过程中),和转换回获得的估计量。 自然指数族的一些性质 我们现在讨论自然指数族的一些有趣的属性。 引理3.1.1设随机变量服从自然指数族分布。的矩生成函数是 而且, 证明：设足够小使是个分布，则矩母函数为 因为（），同时我们回忆到 和.因此 （ 因此最终结果, 备注 3.1.1自然指数族的均值和方差使获得极大似然估计量变得非常简单。我

正态分布概率公式(部分)

Generated by Foxit PDF Creator ? Foxit Software https://www.doczj.com/doc/5e3594568.html, For evaluation only.
图 62正态分布概率密度函数的曲线 正态曲线可用方程式表示。 n 当 →∞时，可由二项分布概率函数方程推导出正态 分布曲线的方程：
fx= （61 ） () .6
式中： x—所研究的变数； fx —某一定值 x出现的函数值，一般称为概率 () 密度函数 （由于间断性分布已转变成连续性分布，因而我们只能计算变量落在某 一区间的概率， 不能计算变量取某一值， 即某一点时的概率， 所以用 “概率密度” 一词以与概率相区分），相当于曲线 x值的纵轴高度； p—常数，等于 31 .4 19……； e— 常数，等于 2788……； μ 为总体参数，是所研究总体 5 .12 的平均数， 不同的正态总体具有不同的 μ ， 但对某一定总体的 μ 是一个常数； δ 也为总体参数， 表示所研究总体的标准差， 不同的正态总体具有不同的 δ ， 但对某一定总体的 δ 是一个常数。 上述公式表示随机变数 x的分布叫作正态分布， 记作 N μ ,δ2 )， “具 ( 读作 2 平均数为 μ，方差为 δ 的正态分布”。正态分布概率密度函数的曲线叫正态 曲线，形状见图 62。 （二）正态分布的特性
1、正态分布曲线是以 x μ 为对称轴，向左右两侧作对称分布。因 =
的
数值无论正负， 只要其绝对值相等， 代入公式 61 ） （ .6 所得的 fx 是相等的， () 即在平均数 μ 的左方或右方，只要距离相等，其 fx 就相等，因此其分布是 () 对称的。在正态分布下，算术平均数、中位数、众数三者合一位于 μ 点上。

常用连续型概率分布

常用连续型概率分布 概率密度函数图及R语言实现 作者：张丹(@Conan_Z) Email: bsspirit@https://www.doczj.com/doc/5e3594568.html, Website: http://www.fens.me 日期：2012-11-26

正态分布 n=100 x <- seq(-5,5,length.out=n) plot(x,dnorm(x,0,1),col="red",xlim=c(-5,5),ylim=c(0,1),type='l', xaxs="i", yaxs="i",ylab='density',xlab='', main="The Normal Density Distribution") lines(x,dnorm(x,0,0.5),col="green") lines(x,dnorm(x,0,2),col="blue") lines(x,dnorm(x,-2,1),col="orange") legend("topright",legend=paste("m=",c(0,0,0,-2)," sd=", c(1,0.5,2,1)), lwd=1, col=c("red", "green","blue","orange"))

指数分步 n=100 x<-seq(-1,2,length.out=n) plot(x,dexp(x,0.5),col="red",xlim=c(0,2),ylim=c(0,5),type='l', xaxs="i", yaxs="i",ylab='density',xlab='', main="The Exponential Density Distribution") lines(x,dexp(x,1),col="green") lines(x,dexp(x,2),col="blue") lines(x,dexp(x,5),col="orange") legend("topright",legend=paste("rate=",c(.5, 1, 2,5)), lwd=1, col=c("red", "green","blue","orange"))