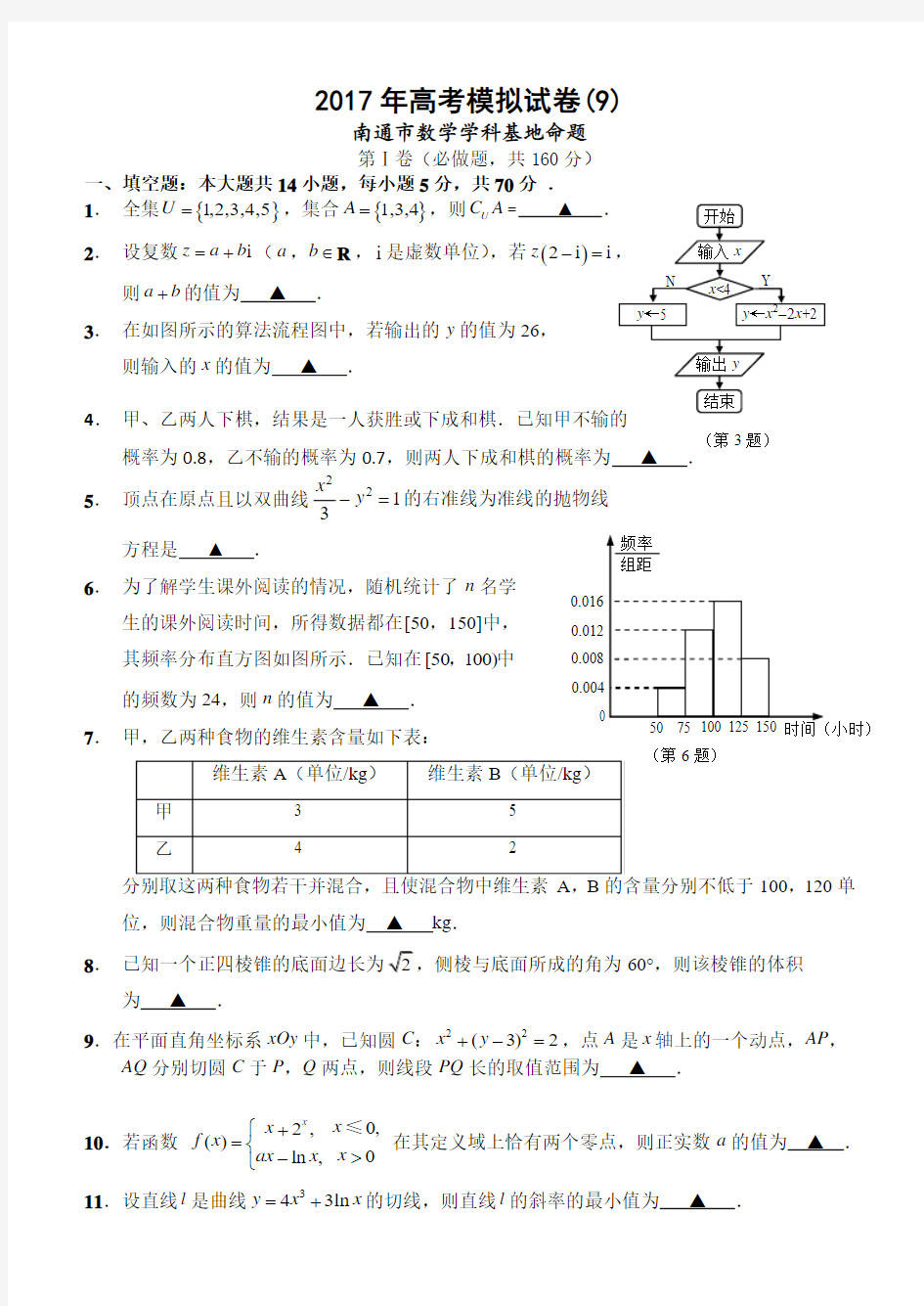

(第3题)
(第6题)
2017年高考模拟试卷(9)
南通市数学学科基地命题
第Ⅰ卷(必做题,共160分)
一、填空题:本大题共14小题,每小题5分,共70分 .
1. 全集{}1,2,3,4,5U =,集合{}1,3,4A =,则U C A = ▲ .2. 设复数i z a b =+(a b ∈,R ,i 是虚数单位),若()2i i z -=则a b +的值为 ▲ .
3. 在如图所示的算法流程图中,若输出的y 的值为26,
则输入的x 的值为 ▲ .
4. 概率为0.8,乙不输的概率为0.7,则两人下成和棋的概率为 ▲ .
5. 顶点在原点且以双曲线13
22
=-y x 的右准线为准线的抛物线 方程是 ▲ .
6. 为了解学生课外阅读的情况,随机统计了n 名学
生的课外阅读时间,所得数据都在[50,150]中, 其频率分布直方图如图所示.已知在[50 100),
中 的频数为24,则n 的值为 ▲
. 7. 甲,乙两种食物的维生素含量如下表:
100,120单位,则混合物重量的最小值为 ▲ kg .
8. 60°,则该棱锥的体积
为 ▲ .
9.在平面直角坐标系xOy 中,已知圆C :22(3)2x y +-=,点A 是x 轴上的一个动点,AP ,
AQ 分别切圆C 于P ,Q 两点,则线段PQ 长的取值范围为 ▲ . 10.若函数 0,
2,()0ln ,≤x x x f x x ax x ?+=?>-?
在其定义域上恰有两个零点,则正实数a 的值为 ▲ .
12.扇形AOB 中,弦1AB =,C 为劣弧
AB 上的动点,AB 与OC 交于点P ,则OP BP ?
的最小值是 ▲ .
13.在平面直角坐标系xOy 中,已知(cos sin )A αα,
,(cos sin )B ββ,
是直线y =上的两点,则tan()αβ+的值为 ▲ .
14.已知函数3()2f x x a a =--+-有且仅有三个零点,且它们成等差数列,则实数a 的
取值集合为 ▲ .
二、解答题:本大题共6小题,共90分. 15.(本小题满分14分)
已知tan α=2,cos β=- 72
10
,且α,β∈(0,π), (1)求cos2α的值; (2)求2α-β的值. 16.(本小题满分14分)
如图,在四棱锥P ABCD -中,△ACD 是正三角形,BD 垂直平分AC ,垂足为M ,
ABC ∠=120° ,=1PA AB =,2PD =,N 为PD 的中点.
(1)求证:AD ⊥平面PAB ; (2)求证:CN ∥平面PAB .
17. (本小题满分14分)
在平面直角坐标系xOy 中,已知A B ,分别是椭圆2
2
221(0)y
x a b a b
+=>>的上、下顶点,
点()
102M ,为线段AO
的中点,AB =.
(1)求椭圆的方程;
(2)设(2)N t ,(0t ≠),直线NA ,NB 分别
交椭圆于点P Q ,,直线NA ,NB ,PQ 的斜率分别为1k ,2k ,3k . ① 求证:P M Q ,,三点共线; D
(第16题)
P
A
P
B
P
C
M N
18.(本小题满分16分)
如图,一个角形海湾AOB ,∠AOB =2θ(常数θ为锐角).拟用长度为l (l 为常数)的围网围成一个养殖区,有以下两种方案可供选择: 方案一:如图1,围成扇形养殖区OPQ ,其中⌒
PQ =l ; 方案二:如图2,围成三角形养殖区OCD ,其中CD =l ;
(1)求方案一中养殖区的面积S 1 ;
(2)求证:方案二中养殖区的最大面积S 2=l 2
4tan θ
;
(3)为使养殖区的面积最大,应选择何种方案?并说明理由.
19.(本小题满分16分)
已知数列{}n a 的首项为2,前n 项的和为n S ,且111241n n n a a S +-=-(*n ∈N ).
(1)求2a 的值; (2)设1n
n n n
a b a a +=
-,求数列{}n b 的通项公式;
(3)若m p r a a a ,,(*m p r ∈,,N ,m p r <<,)成等比数列,试比较2p 与
mr 的大小,并证明.
20.(本小题满分16分)
已知函数2
()ln )x
f x e a x b x
=+
+(,其中,a b R ∈. 2.71828e =是自然对数的底数. (1)若曲线()y f x =在1x =处的切线方程为(1)y e x =-.求实数,a b 的值;
(2)① 若2a =-时,函数()y f x =既有极大值,又有极小值,求实数b 的取值范围; ② 若2a =,2b ≥-.若()f x kx ≥对一切正实数x 恒成立,求实数k 的最大值
l
l
A
O
B
A
O
B
图1
Q P
A
O
B
C D 图2
(第18题)
2θ
2θ
2θ
1O
2O A
B
P
Q
D
C
第II 卷(附加题,共40分)
21.【选做题】本题包括A, B,C,D 四小题,每小题10分,请选定其中两小题,并在相应的答题.......区域内作答.....
. A ,(选修4-1;几何证明选讲)
如图,1O ,2O 交于两点P Q ,,直线AB 过点P ,与1O ,2O 分别交于点A B ,,
直线CD 过点Q ,与1O ,2O 分别交于点C D ,. 求证:AC ∥BD . B .(选修4-2:矩阵与变换)
若二阶矩阵M 满足:12583446M ????
= ? ?????
. (1)求二阶矩阵M ;
(2)若曲线2
2
:221C x xy y ++=在矩阵M 所对应的变换作用下得到曲线C '
,求曲线C '
的方程.
C .(选修4-4:坐标系与参数方程)
已知点(1)P αα-(其中[
)0,2)απ∈,点P 的轨迹记为曲线1C ,以坐标原点 为极点,x 轴的正半轴为极轴建立极坐标系,点Q 在曲线21:)
4
C ρπ
θ=
+
上. (1)求曲线1C 的极坐标方程和曲线2C 的直角坐标方程;
(2)当0,02ρθπ≥≤<时,求曲线1C 与曲线2C 的公共点的极坐标. D .(选修4-5:不等式选讲)
已知实数0x >,0y >,0z >,证明:1239()()2462
y
x z x y z ++++≥.
【选做题】第22题、23题,每题10分,共计20分.
22.已知正六棱锥S ABCDEF -的底面边长为2,高为1.现从该棱锥的7个顶点中随机
选取3个点构成三角形,设随机变量X 表示所得三角形的面积.
(1)求概率(P X 的值;
(2)求X 的分布列,并求其数学期望()E X .
23.已知数列{a n }满足:a 1=1,对任意的n ∈N *,都有a n +1=(1+
1n 2
+n
)a n +12n .
(1)求证:当n ≥2时,a n ≥2;
(2)利用“?x >0,ln(1+x )<x ”,证明:a n <2e 34
(其中e 是自然对数的底数).
2017年高考模拟试卷(9)参考答案
南通市数学学科基地命题
一、填空题
1. {}2,5.
2. 15.
3.-
4. 4. 0.
5. 5. 26y x =-.
6. 60.
7. 30. 线性规划或待定系数法,设甲、乙混货物分别为x ,y 克,由题意3x+4y 100
5x+2y 120≥??≥?,
设x+y=34)(52)x y x y λ
μ+++(,解得,31==1414
λμ,,即可. 8.
. 9.
[3. 设CA=x,则
PQ=2CPcos PQ ≤<. 10. 1e . 易知函数()f x 在(],0-∞上有一个零点,所以由题意得方程ln 0ax x -= 在()0+∞,上恰有一解,即ln x a =在()0+∞,上恰有一解. 令ln ()x g x x =,2 1ln ()0x g x x -'==,得e x =,当()0,e x ∈时,()g x 单调递增,当()e ,+x ∈∞时,()g x 单调递减,所以()1e e a g ==. 11.9. 223331212922k x x x x x =+ =++≥,也可以求导. 12. 1 16-.设弦AB 中点为M ,则()OP BP OM MP BP MP BP ?=+?=? , 若MP BP ,同向,则0OP BP ?> ;若MP BP ,反向,则0OP BP ?< , 故OP BP ? 的最小值在MP BP ,反向时取得, 此时1||||2MP BP += ,2||||1||||()216 MP BP OP BP MP BP +?=-?-=- ≥, 当且仅当 1||||4 MP BP == 时取等号,即OP BP ? 的最小值是116-. 13 . (方法一)由题意,得sin sin ααββ?=+??=+?? 所以αβ, 是方程sin x x 即方程( ) πsin 3x -5ππ()26k k αβ +=+∈Z ,所以tan()αβ+= (方法二)同上,αβ, sin 0x x -的两根. 设()sin f x x x - ()cos f x x x '=-. 令()0f x '= ,得0tan x =,所以02x αβ+=,所以 (方法三)直线210x y +-=交单位圆于A B ,两点, 过O 作OH AB ⊥,垂足为H ,易知OH = 因为OC 60COH ∠=?,即1502 αβ +=?, 所以tan()tan300αβ+=?= 14.9?-??? .32()322x x a x f x x a x a x ?--?=??--+- ,≥,,, 当x a ≥时,320x x --=,得11x =-,23x =, 结合图形知, ① 当1a <-时,313x -, ,成等差数列,则35x =-,代入3220x a --+-=得,9a =-; ② 当13a -≤≤时,方程3220x a x --+-=,即22(1)30x a x +-+=的根为34x x , , 则343x x =,且3432x x +=,解得4x ,又342(1)x x a +=-,所以a . ③ 当3a >时,显然不符合. 所以a 的取值集合95?-??? . 二?解答题:本大题共6小题,共90分. 15. (1)因为tan α=2,所以 sin α cos α =2,即sin α=2cos α. 又sin 2α+cos 2α=1,所以5cos 2α=1,即cos 2α=1 5. 所以 cos2α=2cos 2α-1=-3 5 . (2)由α∈(0,π),且tan α=2>1,得α∈(π4,π2),所以2α∈(π 2,π). 由题知cos2α=-35,所以sin2α=4 5. 又因为β∈(0,π),cos β=-7210∈(-1,0),所以β∈(π 2 ,π), 所以sin β= 210,且2α-β∈(-π2,π 2 ). 因为sin(2α-β)=sin2αcos β-cos2αsin β=45×(-7210)-(-35)×210=-2 2, 所以2α-β=-π 4 . 16.(1)因为BD 垂直平分AC ,所以BA BC =, 在△ABC 中,因为120ABC ∠=?, 所以30BAC ∠=?. 因为△ACD 是正三角形,所以60DAC ∠=?, 所以90BAD ∠=?,即AD AB ⊥. 因为=1AB ,120ABC ∠ =?,所以AD AC == 又因为1PA =,2PD =,由222PA AD PD +=, 知90PAD ∠=?,即AD AP ⊥. 因为AB AP ?,平面PAB ,AB AP A = , 所以AD ⊥平面PAB . (2)(方法一)取AD 的中点H ,连结CH ,NH . 因为N 为PD 的中点,所以HN ∥PA , 因为PA ?平面PAB ,HN ?平面PAB , 所以HN ∥平面PAB . 由△ACD 是正三角形,H 为AD 的中点, 所以CH AD ⊥. 由(1)知,BA AD ⊥,所以CH ∥BA , 因为BA ?平面PAB ,CH ?平面PAB , H P A B C D M N 因为CH HN ?,平面CNH ,CH HN H = , 所以平面CNH ∥平面PAB . 因为CN ?平面CNH , 所以CN ∥平面PAB . (方法二)取PA 的中点S , 过C 作CT ∥AD 交AB 的延长线于T ,连结ST ,SN . 因为N 为PD 的中点,所以SN ∥AD ,且12 SN AD =, 因为CT ∥AD ,所以CT ∥SN . 由(1)知,AB AD ⊥,所以CT AT ⊥, 在直角△ CBT 中,1BC =,60CBT ∠=? , 得CT = 由(1)知,AD 12CT AD =, 所以CT SN =. 所以四边形SNCT 是平行四边形, 所以CN ∥TS . 因为TS ?平面PAB ,CN ?平面PAB , 所以CN ∥平面PAB . 17.(1)由题意知,124()2b b =-=, 解得a =1b =, 所以椭圆的方程为2 212x y +=. (2)① 由(2)N t ,,(01)A , ,(01)B -,,则 直线NA 的方程为11y x t =+, 直线NB 的方程为31y x t =-. P A B C D M N T S 由221122y x t x y ?=+???+=?,得,222422.2t x t t y t ?=-?+?-?=+? , ,故() 2224222t t t t P -- ++,. 由223122y x t x y ?=-???+=?,得,22 2121818.18t x t t y t ?=?+?-?=+? , ,故() 222 12181818t t t t Q -++,. 所以直线PM 的斜率22 2 2162482 PM t t t k t t t ---+== -+, 直线QM 的斜率222 181261812818 QM t t t k t t t ---+==+, 所以PM QM k k =,故P M Q ,,三点共线. ② 由①知,11k t =,213k t =,2 368t k t -=. 所以2 1323122 463182t k k k k k k t t t -+-=?-=-, 所以132312k k k k k k +-为定值12 -. 18.(1)设OP =r ,则l =r ·2θ,即r =l 2θ ,所以 S 1=12lr =l 24θ,θ∈(0,π 2 ). (2)设OC =a ,OD =b .由余弦定理,得l 2=a 2+b 2-2ab cos2θ,所以 l 2≥2ab -2ab cos2θ. 所以 ab ≤l 2 2(1-cos2θ),当且仅当a =b 时“=”成立. 所以S △OCD =12ab sin2θ≤l 2sin2θ4(1-cos2θ)=l 24tan θ ,即S 2=l 2 4tan θ. (3)1S 2-1S 1=4l 2(tan θ-θ),θ∈(0,π 2 ),. 令f (θ)=tan θ-θ,则f '(θ)=(sin θcos θ)'-1=sin 2θ cos 2θ . 当θ∈[0,π2)时,f '(θ)>0,所以f (θ)在区间[0,π 2 )上单调增. 所以,当θ∈(0,π2)时,总有f (θ)>f (0)=0,即1S 2-1 S 1 >0,即S 1>S 2. 19. (1)易得2143 a =. (2)由111241n n n a a S +-=-,得11241 n n n n n a a a a S ++-=-, 所以1 1241n n n n n a a S a a ++-= -①. 所以12 121 241n n n n n a a S +++++-= ②, 由②-①,得12112112n n n n n n n n n a a a a a a a a a +++++++= ---. 因为10n a +≠,所以22112n n n n n n a a a a a a ++++= - --. 所以121112n n n n n n a a a a a a +++++ -=--,即12111n n n n n n a a a a a a ++++-=--, 即11n n b b +-=,所以数列{}n b 是公差为1的等差数列. 因为1 1213a b = =,所以数列{}n b 的通项公式为14n b n =-. (3)由(2)知, 114n n n a n a a +=--,所以114311 414 n n a n a n n ++=+=--, 所以1n n a a +=,所以数列41n a n ?? ??-?? 是常数列. 由 1 2a =,所以2(41)3n a n =-. (方法一)由m p r a a a ,,(m p r <<)成等比数列, 则41m -,41p -,41r -成等比数列,所以2(41)(41)(41)p m r -=--, 所以2168164()0p p mr m r --++=,即2424()0p p mr m r --++=(*). (途径一)(* )式即为2424()4p p mr m r mr -=-+<-, 所以2211(2))22p -< ,即11222p -<, 所以p <2p mr <. (途径二)(*)式即为24241 p p r m r -+=-. 2222 所以2p mr <. (方法二)由m p r a a a ,,(m p r <<)成等比数列, 则41m -,41p -,41r -成等比数列, 记4m α=,4p β=,4r γ=(1αβγ<<<), 则有1α-,1β-,1γ-成等比数列, 所以2(1)(1)(1)βαγ-=--,即22()ββαγαγ-=-+. 若2βαγ=,即2p mr =时,则2αγβ+=,所以αβγ==,矛盾; 若2βαγ>,则22()0βαγβαγ-+=->,所以1()12βαγ>+>, 所以[][]2221(2)()()()()()024 αγ ββαγαγαγαγαγαγ+---+>-+--+=->, 矛盾. 所以2βαγ<,即2p mr <. 20. (1) 由题意知曲线()y f x =过点(1,0),且'(1)e f =; 又因为2 22'()ln e x a f x a x b x x +=- + +? ? ?? ? , 则有(1)e(2)0,'(1)e()e, f b f a b =+==+=?? ?解得3,2a b ==-. (2) ①当2a =-时,函数()y f x =的导函数2 2'()e 2ln 0x f x x b x =-- +=?? ?? ? , 若'()0f x =时,得2 22ln b x x =+, 设2 2 ()2ln g x x x =+ (0)x > . 由233 2424 '()x g x x x x -=-=0=,得x =1ln 2g =+. 当0x << 时,'()0g x <,函数()y g x =在区间() 上为减函数,()(1ln 2,)g x ∈++∞1ln 2b >+()b g x =x 2x 12()x x <. 此时,函数()y f x =既有极大值,又有极小值. ②由题意2e ln x a x b x kx + +??≥ ?? ? 对一切正实数x 恒成立,取1x =得(2)e k b ≤+. 下证2e ln e (2)x a x b x b x + +??≥+ ?? ? 对一切正实数x 恒成立. 首先,证明e e x x ≥. 设函数()e e x u x x =-,则'()e e x u x =-,当1x >时,'()0u x >; 当1x <时,'()0u x <;得e e (1)0x x u -=≥,即e e x x ≥,当且仅当都在1x =处取到等号. 再证1ln 1x x + ≥. 设1()ln 1v x x x =+ -,则21'()x v x x -= ,当1x >时,'()0v x >; 当1x <时,'()0v x <;得()(1)0v x v =≥,即1ln 1x x +≥, 当且仅当都在1x =处取到等号. 由上可得2e ln (2)e x a x b x b x + +??≥+ ?? ? ,所以min ()(2)e f x b x ?? =+ ???, 即实数k 的最大值为(2)e b +. 数学Ⅱ(附加题) 21. A. 连结PQ , 因为四边形ACQP 是1O 的内接四边形, 所以A PQD ∠=∠, 又在2O 中,PBD PQD ∠=∠,所以A PBD ∠=∠, 所以AC ∥BD . B .(1) 设1234A ?? = ??? ,则12234A = =-, 1213122A --?? ?∴= ? -?? , 21582131461122M -?????? ?∴== ? ? ?-???? ?? . (2)11112x x x x x M M y y y y y -'''-????????????=∴== ? ? ? ? ???'''-???????????? , 即,2, x x y y x y ''=-??''=-+? 代入22 221x xy y ++=可得 () ()()()2 2 22221x y x y x y x y ''''''''-+--++-+=,即22451x x y y ''''-+=, 故曲线C '的方程为2 2 451x xy y -+=. C. (1)曲线1C :22(1)2x y ++=,极坐标方程为22cos 10ρθ+-= 曲线2C 的直角坐标方程为1y x =-; (2) 曲线1C 与曲线2C 的公共点的坐标为(0,1)-,极坐标为3(1,)2 π . D. 因为0x >,0y >,0z >, 所以123x y z ++, 2463y x z ++, 所以1239()()y x z ++++≥. 当且仅当::1:2:3x y z =时,等号成立. 22.(1)从7个顶点中随机选取3个点构成三角形, 共有3 7=35C 种取法.其中X ABF , 这类三角形共有6个. 因此(3 7 6 6 35 P X C == = . (2)由题意,X 2 , 其中X ABF ,这类三角形共有6个; 其中2X =的三角形有两类,如△P AD (3个),△P AB (6个),共有9个; 其中X PBD ,这类三角形共有6个; 其中X =CDF ,这类三角形共有12个; 其中X =BDF ,这类三角形共有2个. 因此(635P X = ,()9235 P X ==, (6 35P X = ,(12 35P X ==,(235 P X ==. 所以随机变量X 的概率分布列为: 所求数学期望 ()E X 69612223535353535+?+++. 23. (1)①当n =2时,a 2=2,不等式成立. ②假设当n =k (k ≥2)时不等式成立,即a k ≥2,则当n =k +1时,a k +1=(1+1k (k +1))a k +1 2k >2. 所以,当n =k +1时,不等式也成立. 根据①,②可知,对所有n ≥2,a n ≥2成立. (2)当n ≥2时,由递推公式及(1)的结论有a n +1=(1+1n 2+n )a n +12n ≤(1+1n 2+n +1 2 n +1)a n (n ≥2). 两边取对数,并利用已知不等式ln(1+x )<x ,得 ln a n +1≤ln(1+1n 2+n +12n +1)+ln a n <ln a n +1n 2+n +1 2n +1, 故 ln a n +1-ln a n <1n 2+n +1 2 n +1(n ≥2), 求和可得ln a n -ln a 2<12?3+1 3?4+…+1 (n -1)n +123+12 4+…+1 2n =(12-13)+(13-14)+…+(1n -1-1n )+12 3·1-12n -2 1-12=12-1n +122-12n <3 4. 由(1)知,a 2=2,故有ln a n 2<3 4,即a n <2e 34(n ≥2), 而a 1=1<2e 34,所以对任意正整数n ,有a n <2e 3 4.