
构造全等三角形之截长补短
【笔记】
截长补短法作辅助线,适合于证明线段的和、差、倍、分等类的题目(例:EF=DE+BF,CD=2CE)截长:在长边上截取一条与某一短边相同的线段,再证剩下的线段与另一短边相等。
补短:通过延长短边或旋转等方式使两短边拼合到一起。
【例1】如下图所示,△ABC中,∠C=2∠B,∠1=∠2,求证:AB=AC+CD.
【例2】如图,AB∥CD,CE,BE分别平分∠BCD和∠CBA,点E在AD上.求证:BC=AB+CD.
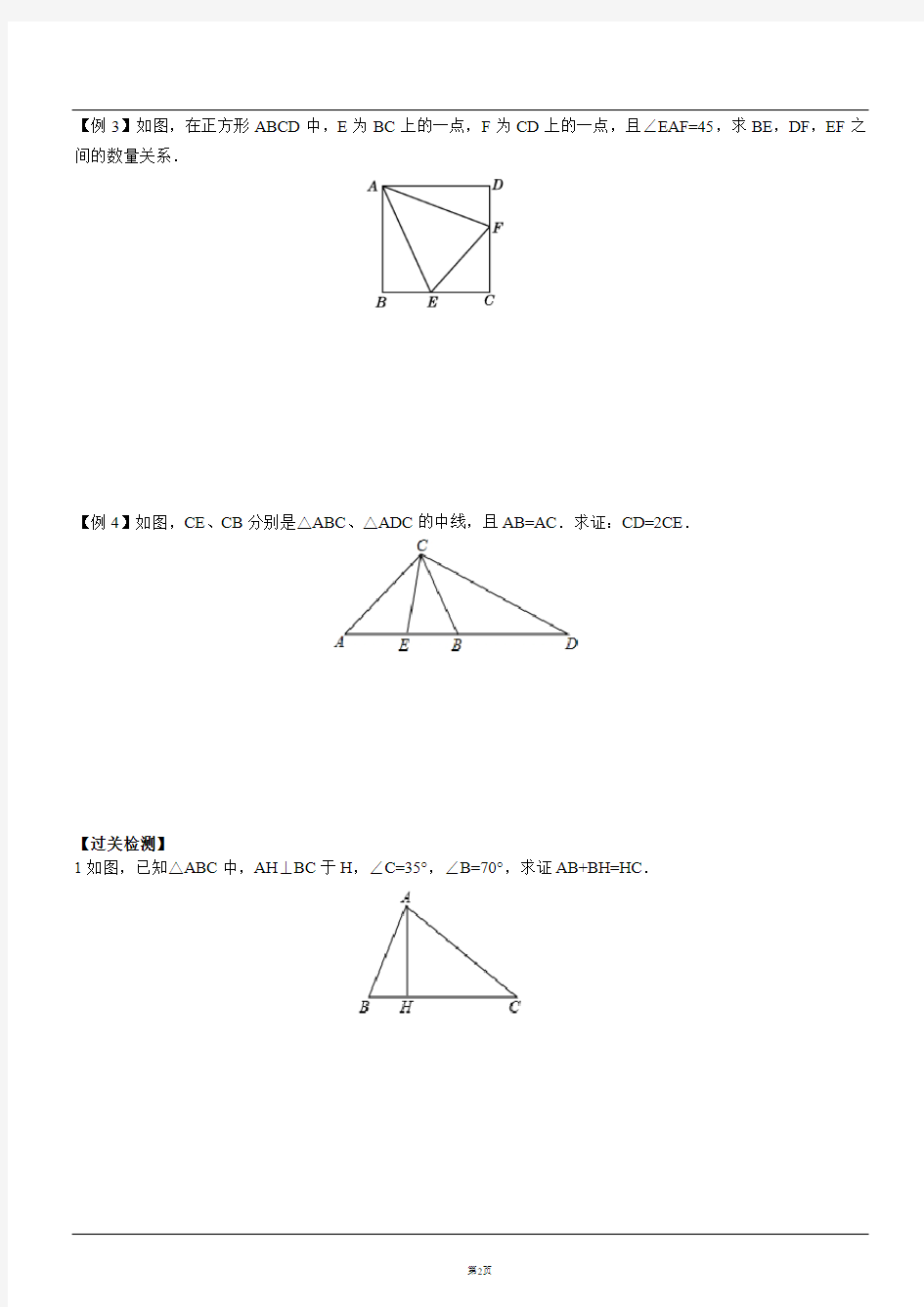
【例3】如图,在正方形ABCD中,E为BC上的一点,F为CD上的一点,且∠EAF=45,求BE,DF,EF之间的数量关系.
【例4】如图,CE、CB分别是△ABC、△ADC的中线,且AB=AC.求证:CD=2CE.
【过关检测】
1如图,已知△ABC中,AH⊥BC于H,∠C=35°,∠B=70°,求证AB+BH=HC.
2.在△ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交BC于点P,BQ平分∠ABC交AC于点Q,且AP 与BQ相交于点O.求证:AB+BP=BQ+AQ.
3.如图,△ABC是正三角形,△BDC是等腰三角形,BD=CD,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC边于M、N两点,连接MN.探究BM、MN、NC之间的关系,并说明理由.
4.已知,AD是△ABC的中线,AE⊥AB,AE=AB,AF⊥AC,AF=AC,连结EF.试猜想线段AD与EF的关系,并证明.
【出门测】
1.如图,已知△ABC 中,∠A =90°,AB =AC ,BE 平分∠ABC ,CE ⊥BD 于E ,求证:CE =
BD .
2.如图,已知正方形ABCD 中,E 为BC 边上任意一点,AF 平分∠DAE .求证:AE -BE =DF .
3.已知,如图3-1,∠1=∠2,P 为BN 上一点,且PD ⊥BC 于点D ,AB +BC =2BD .求证:∠BAP +∠BCP =180°
4.如图,已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,连接BE 并延长交AC 于点F ,AF=EF ,求证:AC=BE .
1
2
A
B
C
D
P
1
2
N
全等三角形辅助线之截长补短与倍长中线 一.填空题(共1小题) 1.(2015秋?宿迁校级月考)如图,在Rt△ABC中,∠C=90°,AD平分∠BAC 交BC于D.若BD:DC=3:2,点D到AB的距离为6,则BC的长是.二.解答题(共10小题) 2.(2010秋?涵江区期末)如图所示,在Rt△ABC中,∠C=90°,BC=AC,AD平分∠BAC交BC于D,求证:AB=AC+CD. 3.如图,AD是△ABC中BC边上的中线,求证:AD<(AB+AC).4.(2013秋?藁城市校级期末)在△ABC中,∠ACB=90°,AC=BC,直线,MN 经过点C,且AD⊥MN于点D,BE⊥MN于点E. (1)当直线MN绕点C旋转到如图1的位置时,求证:DE=AD+BE; (2)当直线MN绕点C旋转到如图2的位置时,求证:DE=AD﹣BE; (3)当直线MN绕点C旋转到如图3的位置时,线段DE、AD、BE之间又有什么样的数量关系请你直接写出这个数量关系,不要证明. 5.已知△ABC中,∠A=60°,BD,CE分别平分∠ABC和∠ACB,BD、CE交于点O,试判断BE,CD,BC的数量关系,并说明理由. 6.(2012秋?西城区校级期中)已知:如图,△ABC中,点D,E分别在AB,AC边上,F是CD中点,连BF交AC于点E,∠ABE+∠CEB=180°,判断BD与CE 的数量关系,并证明你的结论. 7.(2010秋?丰台区期末)已知:如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC,点D是△ABC内的一点,且AD=AC,若∠DAC=30°,试探究BD与CD的数量关系并加以证明. 8.已知点M是等边△ABD中边AB上任意一点(不与A、B重合),作∠DMN=60°,交∠DBA外角平分线于点N. (1)求证:DM=MN; (2)若点M在AB的延长线上,其余条件不变,结论“DM=MN”是否依然成立请你画出图形并证明你的结论. 9.(2015春?闵行区期末)如图所示,在正方形ABCD中,M是CD的中点,E 是CD上一点,且∠BAE=2∠DAM.求证:AE=BC+CE. 10.已知:如图,ABCD是正方形,∠FAD=∠FAE.求证:BE+DF=AE.11.(2010秋?巢湖期中)如图,CE、CB分别是△ABC、△ADC的中线,且AB=AC.求证:CD=2CE.
名师堂 校区地址: 南充 市顺庆区吉隆街 咨询电话: 2244028优学小班——提分更快、针对更强、时效更高 构造全等三角形种常用方法 在证明两个三角形全等时,选择三角形全等的五种方法(“SSS ”,“SAS ”,“ASA ”,“AAS ”,“HL ”)中,至少有一组相等的边,因此在应用时要养成先找边的习惯。如果选择找到了一组对应边,再找第二组条件,若找到一组对应边则再找这两边的夹角用“SAS ”或再找第三组对应边用“SSS ”;若找到一组角则需找另一组角(可能用“ASA ”或“AAS ”)或夹这个角的另一组对应边用“SAS ”;若是判定两个直角三角形全等则优先考虑“HL ”。上述可归纳为: () ()() ()S SSS S A SAS S S SAS A A AAS ASA ??? ????????? ?用用用用或 搞清了全等三角形的证题思路后,还要注意一些较难的一些证明问题,只要构造合适的全等三角形,把条件相对集中起来,再进行等量代换,就可以化难为易了.下面举例说明几种常见的构造方法,供同学们参考. 1.截长补短法 例1.如图(1)已知:正方形ABCD 中,∠BAC 的平分线交BC 于E , 求证:AB+BE=AC . 解法(一)(补短法或补全法)延长AB 至F 使AF=AC , 由已知△AEF ≌△AEC ,∴∠F=∠ACE=45o, ∴BF=BE ,∴AB+BE=AB+BF=AF=AC . 解法(二)(截长法或分割法)在AC 上截取AG=AB ,由已知 △ ABE ≌△AGE ,∴EG=BE, ∠AGE=∠ABE,∵∠ACE=45o, ∴CG=EG, ∴AB+BE=AG+CG=AC . 2.平行线法(或平移法) 若题设中含有中点可以试过中点作平行线或中位线,对Rt △,有时可作出斜边的中线. 例2.△ABC 中,∠BAC=60°,∠C=40°AP 平分∠BAC 交BC 于P ,BQ 平分∠ABC 交AC 于Q , 求证:AB+BP=BQ+AQ . 证明:如图(1),过O 作OD ∥BC 交AB 于D ,∴∠ADO=∠ABC =180°-60°-40°=80°,又∵∠AQO=∠C+∠QBC=80°, ∴∠ADO=∠AQO ,又∵∠DAO=∠QAO ,OA=AO , ∴△ADO ≌△AQO ,∴OD=OQ ,AD=AQ ,又∵OD ∥BP , ∴∠PBO=∠DOB ,又∵∠PBO=∠DBO ,∴∠DBO=∠DOB , ∴BD=OD ,∴AB+BP=AD+DB+BP =AQ+OQ+BO=AQ+BQ . A B C P Q D O D
全等三角形——截长补短法 一、知识梳理: 截长补短法 截长补短法是几何证明题中十分重要的方法。通常来证明几条线段的数量关系。 截长法: (1)过某一点作长边的垂线 (2)在长边上截取一条与某一短边相同的线段,再证剩下的线段与另一短边相等. 补短法 (1)延长短边。 (2)通过旋转等方式使两短边拼合到一起。…… 二、典型例题: 例1、如图,在ABC ?中,60BAC ∠=?,AD 是BAC ∠的平分线,且AC AB BD =+,求ABC ∠的度数. 及时练习: 如图所示,在Rt △ABC 中,∠C=90°,BC=AC ,AD 平分∠BAC 交BC 于D ,求证:AB=AC+CD . 例2、已知ABC ?中,60A ∠ =,BD 、CE 分别平分ABC ∠和.ACB ∠,BD 、CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明. D O E C B A
M D C B A P C B A 及时练习: 如图,已知在ABC 内,0 60BAC ∠=,0 40C ∠=,P ,Q 分别在BC ,CA 上,并且AP , BQ 分别是BAC ∠,ABC ∠的角平分线。求证:BQ+AQ=AB+BP 例3、如图.已知正方形ABCD 中,M 为CD 的中点,E 为MC 上一点,且∠BAE =2∠DAM . 求证:AE =BC +CE . 及时练习: 如图,AD ⊥AB ,CB ⊥AB ,DM =CM =a ,AD =h ,CB =k , ∠AMD =75°,∠BMC =45°,则AB 的长为 ( ) A . a B . k C . 2 k h + D . h 例4、以ABC ?的AB 、AC 为边向三角形外作等边ABD ?、ACE ?,连结CD 、BE 相交于点O . 求证:OA 平分DOE ∠.
B C 专题 中点问题(一)中线倍长构造全等2018.10.17 学习目标:会用倍长中线构造全等的办法去解决三角形中存在有中线的数学问题。 一、练前谈话 几何证明中,当发现条件不够时,通常会想到通过作辅助线来构造条件,我们八年级上册的数学学习中,常规辅助线的作法有连线段、作平行线、作垂线、截长补短……还有一条非常重要的辅助线作法,那就是“倍长中线法”,这也是中考几何题中常用的一种方法。 二、认识体会 1.如图,AD 为△ABC 的中线,延长AD 至E ,使DE=AD ,连CE , 求证:AB=CE ,且AB//CE 。 小结:本题中倍长了三角形的中线,从而构造了全等三角形,通过证全等得出对应角相等,再利用平行线的判定定理证平行。 三、小试牛刀 2.如图,△ABC 中,D 为BC 中点。 (1)求证:AB+AC >2AD ; (2)若AB=5,AC=3,求AD 的取值范围。 D B C
小结:本题通过倍长中线构造了三角形全等,从而把几条线段转换在同一个三角形中进行比较。 四、再接再厉 3.如图,在△ABC 中,点O 为BC 中点,点M 为AB 上一点,ON ⊥OM 交AC 于N 。 求证:BM+CN >MN 。 五、激流勇进 4.如图,AD 是△ABC 的中线,点E 在BC 的延长线上,CE=AB ,∠BAC=∠BCA , 求证:AE=2AD 。 O B C D E C
六、斩将夺关 5.如图,AB=AE ,AB ⊥AE ,AD=AC ,AD ⊥AC ,点M 为BC 的中点,求证: DE=2AM 。 【方法归纳】将中点处的线段倍长,构造SAS 全等三角形。 七、今夜无眠(课外作业) 6、如图1,在等腰Rt△ACB 中,∠ACB=90°,AC=BC ;在等腰Rt△DCE 中,∠DCE=90°,CD=CE ;点D 、E 分别在边BC 、AC 上,连接AD 、BE ,点N 是线段BE 的中点,连接CN 与AD 交于点G . (1)求证:CN⊥AD. (2)把等腰Rt△DCE 绕点C 转至如图2位置,点N 是线段BE 的中点,延长NC 交AD 于点H ,请问(2)中的结论还成立吗?若成立,请给出证明;若不成立,请说明理由. 【温馨提示】将中点处的线段倍长,构造SAS 全等三角形,还能形成平行线。 D E
手拉手模型 要点一:手拉手模型 特点:由两个等顶角的等腰三角形所组成,并且顶角的 顶点为公共顶点 结论:(1)△ABD ≌△AEC (2)∠α+∠BOC=180° (3)OA平分∠BOC 变形: 例1.如图在直线ABC的同一侧作两个等边三角形ABD ?,连结AE与CD,?与BCE 证明 (1)DBC ? ? ABE? (2)AE与DC之间的夹角为? 60 (3)BH平分AHC ∠ 变式精练1:如图两个等边三角形ABD ?,连结 ?与BCE AE与CD, 证明(1)DBC ? ABE? ? (2)AE与DC之间的夹角为? 60
(3)AE 与DC 的交点设为H ,BH 平分AHC ∠ 变式精练2:如图两个等边三角形ABD ?与BCE ?,连结AE 与CD , 证明(1)DBC ABE ??? (2)AE 与DC 之间的夹角为?60 (3)AE 与DC 的交点设为H ,BH 平分AHC ∠ 例2:如图,两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H 问:(1)CDE ADG ???是否成立 (2)AG 是否与CE 相等 (3)AG 与CE 之间的夹角为多少度 (4)HD 是否平分AHE ∠ 例3:如图两个等腰直角三角形ADC 与EDG ,连结CE AG ,,二者相交于点H 问:(1)CDE ADG ???是否成立 (2)AG 是否与CE 相等 (3)AG 与CE 之间的夹角为多少度 (4)HD 是否平分AHE ∠ 例4:两个等腰三角形ABD ?与BCE ?,其中 BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD ,
D C B A E D F C B A 全等三角形作辅助线经典例题 常见辅助线的作法有以下几种: 1)遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”. 2)遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全 等变换中的“旋转”. 3)遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中 的“对折”,所考知识点常常是角平分线的性质定理或逆定理. 4)过图形上某一点作特定的平分线,构造全等三角形,利用的思维模式是全等变换中的“平移”或“翻 转折叠”;(遇垂线及角平分线时延长垂线段,构造等腰三角形) 5)截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是 之与特定线段相等,再利用三角形全等的有关性质加以说明.这种作法,适合于证明线段的和、差、倍、分等类的题目. 特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解答. 一、倍长中线(线段)造全等 1:已知,如图△ABC中,AB=5,AC=3,则中线AD的取值范围是_________. 2:如图,△ABC中,E、F分别在AB、AC上,DE⊥DF,D是中点,试比较BE+CF与EF的大小. 3:如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AD平分∠BAE. E D C B A 中考应用: 以ABC ?的两边AB、AC为腰分别向外作等腰Rt ABD ?和等腰Rt ACE ?,90, BAD CAE ∠=∠=? 连接DE,M、N分别是BC、DE的中点.探究:AM与DE的位置关系及数量关系.(1)如图①当ABC ?为直角三角形时,AM与DE的位置关系是,线段AM与DE的数量关系是; (2)将图①中的等腰Rt ABD ?绕点A沿逆时针方向旋转?θ(0<θ<90)后,如图②所示,(1)
角平分线、倍长中线、构造全等提高 1.如图所示,在△ABC 中,∠A =90°,BD 平分∠ABC ,AD =2cm ,则点D 到BC 的距离为________cm . 2.如图,在△ABC 中,∠C =900,BC =40,AD 是∠BAC 的平分线交BC 于D ,且DC ∶DB =3∶5,则点D 到AB 的距离是. 3.如图,已知BD 是∠ABC 的内角平分线,CD 是∠ACB 的外角平分线,由D 出发,作点D 到BC 、 AC 和AB 的垂线DE 、DF 和DG ,垂足分别为E 、F 、G ,则DE 、DF 、DG 的关系是. 4.AD 是△BAC 的角平分线,自D 向AB 、AC 两边作垂线,垂足为E 、F ,那么下列结论中错误的是 A .DE =DF B .AE =AF C .B D =CD D .∠AD E =∠ADF 5.如图,已知AB ∥CD ,O 为∠A 、∠C 的角平分线的交点,OE ⊥AC 于E ,且OE =2,则两平行线间AB 、CD 的距离等于. 6.到三角形三条边的距离都相等的点是这个三角形的( ) A .三条中线的交点 B .三条高的交点 C .三条边的垂直平分线的交点 D .三条角平分线的交点 【例题】 1. 如图,已知AC ∥BD 、EA 、EB 分别平分∠CAB 和△DBA ,CD 过点E ,则AB 与AC +BD ?相等 吗.请说明理由. 2.在△ABC 中,∠B =60°,∠A ,∠C 的角平分线AE ,CF 相交于点O , (1)如图1,若AB =BC ,求证:OE =OF ; (2)如图2,若AB ≠BC ,试判断线段OE 与OF 是否相等,并说明理由 D C A B E 3题图 D C B A
八年级数学全等三角形辅助线添加之截长补短 (全等三角形)拔高练习 试卷简介:本讲测试题共两个大题,第一题是证明题,共7个小题,每小题10分;第二题解答题,2个小题,每小题15分。 学习建议:本讲内容是三角形全等的判定——辅助线添加之截长补短,其中通过截长补短来添加辅助线是重点,也是难点。希望同学们能学会熟练通过截长补短来做辅助线,进而构造出全等的三角形。 一、解答题(共1道,每道20分) 1.如图,已知点C是∠MAN的平分线上一点,CE⊥AB于E,B、D分别在AM、AN上,且AE=(AD+AB).问:∠1和∠2有何关系? 答案: 解:∠1+∠2=180° 证明:过点C作CF⊥AN于点F,由于AC平分∠NAM,所以CF=CE,则在Rt△ACF和Rt△ACE 中 ∴△ACF≌△ACE(HL),∴AF=AE,由于2AE=AD+AB,所以AB-AE=AF-AD ∴DF=BE,在△CFD和△CEB中所以△CFD≌△CEB(SAS),∴∠2=∠FDC,又∠1+∠FDC=180°,∴∠1+∠2=180°。 解题思路:见到角平分线就要想到作垂直,找到全等关系是解决此类问题的关键 易错点:找到三角形全等的所有条件
试题难度:四颗星知识点:三角形 二、证明题(共8道,每道10分) 1.如图,已知△ABC中,∠A=90°,AB=AC,BE平分∠ABC,CE⊥BD于E,求证:CE=BD. 答案: 延长CE交BA的延长线于点H,由BE平分ABC,BE CE,得CE=EH=CH。 又1+H=90°,,2+H=90° 1= 2 在△ACH和△ABD中 HAC=DAB=90° AC=AB 1= 2 △ACH≌△ABD(ASA) CH=BD CE=CH=BD 解题思路: 根据题意,要证明CE=BD,延长CE与BA,由题意的垂直平分线可得CE的两倍长CH,只需证明CH=BD即可,很显然有全等可以证明出结论 易错点:不能正确利用题中已知条件BF平分∠ABC,CE⊥BD于E,做出辅助线,进而解答。试题难度:三颗星知识点:全等三角形的判定与性质 2. 如图,已知正方形ABCD中,E为BC边上任意一点,AF平分∠DAE.求证:AE-BE=DF.
全等三角形的构造方法 全等三角形是初中数学中的重要内容之一,是今后学习其他内容的基础。判断三角形全等公理有SAS、ASA、AAS、SSS和HL,如果能够直接证明三角形的全等的,直接根据相应的公理就可以证明,但是如果给出的条件不全,就需要根据已知的条件结合相应的公理来进行分析,先推导出所缺的条件然后再证明。一些较难的一些证明问题要构造合适的全等三角形,把条件相对集中起来,再进行等量代换,就可以化难为易了。 构造方法有: 1.截长补短法。 2.平行线法(或平移法):若题设中含有中点可以试过中点作平行线或中位线,对Rt△,有时可作出斜边的中线。 3.旋转法:对题目中出现有一个公共端点的相等线段时,可试用旋转方法构造全等三角形。 4.倍长中线法:题中条件若有中线,可延长一倍,以构造全等三角形,从而将分散条件集中在一个三角形内。 5.翻折法:若题设中含有垂线、角的平分线等条件的,可以试用轴对称性质,沿轴翻转图形来构造全等三角形。下面举例说明几种常见的构造方法,供同学们参考. 1.截长补短法(通常用来证明线段和差相等) “截长法”即把结论中最大的线段根据已知条件分成两段,使其中一段与较短线段相等,然后证明余下的线段与另一条线段相等的方法. “补短法”为把两条线段中的一条接长成为一条长线段,然后证明接成 的线段与较长的线段相等,或是把一条较短的线段加长,使它等于较长 的一段,然后证明加长的那部分与另一较短的线段相等.
例1.如图所示,在Rt△ABC中,∠C=90°,BC=AC,AD平分∠BAC 交BC于D,求证:AB=AC+CD. 例2 已知:如图,AB=AC,E为AB上一点,F是AC延长线上一点,且BE=CF,EF 交BC于点D.求证:DE=DF. (2)已知:如图,AB=AC,E为AB上一点,F是AC延长线上一点,且,EF交BC 于点D,且D为EF的中点. 求证:BE=CF.
巧添辅助线——倍长中线 【夯实基础】 例:ABC ?中,AD 就是BAC ∠的平分线,且BD=CD,求证AB=AC 方法1:作D E ⊥AB 于E,作D F ⊥AC 于F,证明二次全等 方法2:辅助线同上,利用面积 方法3:倍长中线AD 【方法精讲】常用辅助线添加方法——倍长中线 △ABC 中 方式1: 延长AD 到E, AD 就是BC 边中线 使DE=AD, 连接BE 方式2:间接倍长 作CF ⊥AD 于延长MD 到N, 作BE ⊥AD 的延长线于使DN=MD, 连接BE 连接CD 【经典例题】 例1:△ABC 中,AB=5,AC=3,求中线AD 的取值范围 提示:画出图形,倍长中线AD,利用三角形两边之与大于第三边 例2:已知在△ABC 中,AB=AC,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F,且DF=EF,求证:BD=CE 方法1:过D 作DG ∥AE 交BC 于G,证明ΔDGF ≌ΔCEF 方法2:过E 作EG ∥AB 交BC 的延长线于G,证明ΔEFG ≌ΔDFB 方法3:过D 作DG ⊥BC 于G,过E 作EH ⊥BC 的延长线于H 证明ΔBDG ≌ΔECH
例3:已知在△ABC 中,AD 就是BC 边上的中线,E 就是AD 上一点,且BE=AC,延长BE 交AC 于F,求 证:AF=EF 提示:倍长AD 至G ,连接BG,证明ΔBDG ≌ΔCDA 三角形BEG 就是等腰三角形 例4:已知:如图,在ABC ?中,AC AB ≠,D 、E 在BC 上,且DE=EC,过D 作BA DF //交AE 于点F,DF=AC 、 求证:AE 平分BAC ∠ 提示: 方法1:倍长AE 至G,连结DG 方法2:倍长FE 至H,连结CH 例5:已知CD=AB,∠BDA=∠BAD,AE 就是△ABD 的中线,求证:∠C=∠BAE 提示:倍长AE 至F,连结DF 证明ΔABE ≌ΔFDE(SAS) 进而证明ΔADF ≌ΔADC(SAS) 【融会贯通】 1、在四边形ABCD 中,AB ∥DC,E 为BC 边的中点,∠BAE=∠EAF,AF 与DC 的延长线相交于点F 。试探究线段AB 与AF 、CF 之间的数量关系,并证明您的结论 提示:延长AE 、DF 交于G 证明AB=GC 、AF=GF 所以AB=AF+FC B 第 1 题图 A B F D E C
A D B C E 图2-1 截长补短法 人教八年级上册课本中,在全等三角形部分介绍了角的平分线的性质,这一性质在许多问题里都有着广泛的应用.而“截长补短法”又是解决这一类问题的一种特殊方法,在无法进行直接证明的情形下,利用此种方法常可使思路豁然开朗.请看几例. 例1. 已知,如图1-1,在四边形ABCD 中,BC >AB ,AD =DC ,BD 平分∠ABC . 求证:∠BAD +∠BCD =180°. 分析:因为平角等于180°,因而应考虑把两个不在一起的通过全等转化成为平角,图中缺少全等的三角形,因而解题的关键在于构造直角三角形,可通过“截长补短法”来实现. 证明:过点D 作DE 垂直BA 的延长线于点E ,作DF ⊥BC 于点F ,如图1-2 ∵BD 平分∠ABC ,∴DE =DF , 在Rt △ADE 与Rt △CDF 中, ?? ?==CD AD DF DE ∴Rt △ADE ≌Rt △CDF (HL ),∴∠DAE =∠DCF . 又∠BAD +∠DAE =180°,∴∠BAD +∠DCF =180°, 即∠BAD +∠BCD =180° 例2. 如图2-1,AD ∥BC ,点E 在线段AB 上,∠ADE =∠CDE ,∠DCE =∠ECB . 求证:CD =AD +BC . 分析:结论是CD =AD +BC ,可考虑用“截长补短法”中的“截长”,即在CD 上截取CF =CB ,只要再证DF =DA 即可,这就转化为证明两线段相等的问题,从而达到简化问题的目的. 证明:在CD 上截取CF =BC ,如图2-2 在△FCE 与△BCE 中, ?? ? ??=∠=∠=CE CE BCE FCE CB CF ∴△FCE ≌△BCE (SAS ),∴∠2=∠1. A B C D 图1-1 F E D C B A 图1-2 A D B C E F 1 234 图2-2
初中数学全等专题倍长中线法 1.如图,在△ABC中,AC=5,中线AD=7,则AB边的取值范围是( ) A.2<AB<12 B.4<AB<12 C.9<AB<19 D.10<AB<19 答案:C 解题思路:延长AD至E,使DE=AD,连接CE,可先证明△ABD≌△ECD,则AB=CE,在△ACE中,根据三角形的三边关系,得AE-AC<CE<AE+AC,即9<CE<19.则9<AB<19.故选C. 2.如图,已知CB、CD分别是钝角△AEC和锐角△ABC的中线,且AC=AB,给出下列结论:①AE=2AC;②CE=2CD;③∠ACD=∠BCE;④CB平分∠DCE,则以上结论正确的是() A.①②④ B.①③④ C.①②③ D.①②③④ 答案:A 解题思路:①正确,延长CD至点F,使得DF=CD,连接AF,可先证明△ADF≌△BDC,再证明△ACF≌△BEC,由这两个三角形全等可以得知②、④正确。由△ACF≌△BEC,得∠ACD=∠E,若要∠ACD=∠BCE,则需∠E=∠BCE,则需BC=BE,显然不成立,故③选项错误 3.如图,点E是BC的中点,∠BAE=∠CDE,延长DE到点F使得EF=DE,连接BF,则下列说法正确的是() ①BF∥CD ②△BFE≌△CDE ③AB=BF ④△ABE为等腰三角形 A.①②③ B.②③④ C.①③④ D.①②③④ 答案:A 解题思路:可以先证明△BEF≌△CED,可以得到②正确,进而得到∠F=∠D,BF∥CD,①正确,又∵∠BAE=∠CDE=∠F,∴AB=BF,③正确。④不正确。 4.如图,在正方形ABCD中,E为AB边的中点,G、F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为()
1 2 截长补短 截长补短”是几何证明题中十分重要的方法, 通常用来证明几条线段的数量关系, 即若 题目条件或结论中含有 a b c ”的条件,需要添加辅助线时可以考虑 截长补短”的方法。 另外的较短线段。 补短法: ①延长较短线段中的一条,使延长出来的线段等于另外的较短线段,然后证明两线段之和等 于较长线段。即延长a ,得到b ,证:a b ①延长较短线段中的一条, 使延长后的线段等于较长线段, 一条较短线段。 即延长a ,得到c ,证:b c-a 。 例1.已知:如图,在 △ ABC 中,△仁△Z, △ B=2AC .求证: 1.补短法: 证明:如图,延长 AB 到E ,使BE=BD ,连接DE . △ △ABD 是 △BDE 的一个外角 △ △ABDME + △BDE ABE=BD △ △EMBDE △ △ABD=2 △E △ △ABD=2 △C △ △EMC 在 AADE 和 AADC 中 △ △ADE △△ADC (AAS )截长法:在较长的线段上截取一条线段等于较短线段, 再设法证明较长线段的剩余线段等于 然后证明延长出来的部分等于另 AC=AB+BD . AD AD
1 2 证明:如图,在 CD 上截取CF=CB . △CE 平分△CBD 在△CFE 和 △CBE 中 △AE=AC △AC=AB + BE=AB + BD 2.截长法: 证明:如图,在 AC 上截取AF=AB ,连接DF . 在△ABD 和△AFD 中 AB AF AD AD △ △ABD △△AFD ( SAS ) △ ABMAFD , BD=FD △ △B=2 △C △ △AFD =2 △C △ △AFD 是^DFC 的一个外角 △ △AFD me + 舉DC △ AFDCmC ADF=FC ABD=FC △AC=AF+FC=AB+BD 例2.如图,在四边形 ABCD 中,△ A=AB=90,点 E 为AB 边上一点,且 DE 平分△ ADC , CE 平分△ BCD .求证:CD=AD+BC . CF CB CE CE
倍长中线构造全等三角 形 -CAL-FENGHAI.-(YICAI)-Company One1
巧添辅助线——倍长中线 【夯实基础】 例:ABC ?中,AD是BAC ∠的平分线,且BD=CD,求证AB=AC 方法1:作DE⊥AB于E,作DF⊥AC于F,证明二次全等方法2:辅助线同上,利用面积 方法3:倍长中线AD 【方法精讲】常用辅助线添加方法——倍长中线 △ABC中 AD到E, AD是BC边中线, 连接BE 方式2 ⊥AD于F, AD的延长线于 连接 【经典例题】 例1:△ABC中,AB=5,AC=3,求中线AD的取值范围 提示:画出图形,倍长中线AD,利用三角形两边之和大于第三边 例2:已知在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE 方法1:过D作DG∥AE交BC于G,证明ΔDGF≌ΔCEF 方法2:过E作EG∥AB交BC的延长线于G,证明ΔEFG 方法3:过D作DG⊥BC于G,过E作EH⊥BC 证明ΔBDG≌ΔECH 2
3 例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交 AC 于F ,求证:AF=EF 提示:倍长AD 至G ,连接BG ,证明ΔBDG ≌ΔCDA 三角形BEG 是等腰三角形 例4:已知:如图,在ABC ?中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC. 求证:AE 平分BAC ∠ 提示: 方法1:倍长AE 至G ,连结DG 方法2:倍长FE 至H ,连结CH 例5:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAE 提示:倍长AE 至F ,连结DF 证明ΔABE ≌ΔFDE (SAS ) 进而证明ΔADF ≌ΔADC (SAS ) 【融会贯通】 1、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。试探究线段AB 与AF 、CF 之间的数量关系,并证明你的结论 提示:延长AE 、DF 交于G 证明AB=GC 、AF=GF 所以AB=AF+FC B 第 1 题图 A B F D E C
倍长中线法 知识网络详解: 中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线. 所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法. 倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用SAS 证全等(对顶角) 倍长中线最重要的一点,延长中线一倍,完成SAS 全等三角形模型的构造。 【方法精讲】常用辅助线添加方法——倍长中线 △ABC 中 方式1: 延长AD 到E , AD 是BC 边中线 使DE=AD , 连接BE 方式2:间接倍长 作CF ⊥AD 于F , 延长MD 到N , 作BE ⊥AD 的延长线于E 使DN=MD , 连接BE 连接CN 经典例题讲解: 例1:△ABC 中,AB=5,AC=3,求中线AD 的取值范围 D A B C E D A B C F E D C B A N D C B A M
例2:已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE 过D 作DG//AC 例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF 例4:已知:如图,在ABC ?中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC. 求证:AE 平分BAC ∠ F E D A B C F E C A B D A B F D E C
例题1 如图所示,在Rt△ABC中,∠C=90°,BC=AC,AD平分∠BAC交BC于D,求证:AB=AC+CD. 考点:全等三角形的判定与性质. 专题:证明题. 分析:利用已知条件,求得∠B=∠E,∠2=∠1,AD=AD,得出△ABD≌△AED(AAS),∴AE=AB.∵AE=AC+CE=AC+CD,∴AB=AC+CD. 解答:证法一:如答图所示,延长AC,到E使CE=CD,连接DE. ∵∠ACB=90°,AC=BC,CE=CD, ∴∠B=∠CAB=45°,∠E=∠CDE=45°, ∴∠B=∠E. ∵AD平分∠BAC, ∴∠1=∠2 在△ABD和△AED中, ∠B=∠E,∠2=∠1,AD=AD, ∴△ABD≌△AED(AAS). ∴AE=AB. ∵AE=AC+CE=AC+CD, ∴AB=AC+CD. 证法二:如答图所示,在AB上 截取AE=AC,连接DE, ∵AD平分∠BAC, ∴∠1=∠2. 在△ACD和△AED中, AC=AE,∠1=∠2,AD=AD, ∴△ACD≌△AED(SAS). ∴∠AED=∠C=90,CD=ED, 又∵AC=BC,
∴∠B=45°. ∴∠EDB=∠B=45°. ∴DE=BE, ∴CD=BE. ∵AB=AE+BE, ∴AB=AC+CD. 点评:本题考查了全等三角形的判定和性质;通过SAS的条件证明三角形全等,利用三角形全等得出的结论来求得三角形各边之间的关系. 例题2 图,AD是△ABC中BC边上的中线,求证:AD<(AB+AC). 考点:全等三角形的判定与性质;三角形三边关系. 专题:计算题. 分析:可延长AD到E,使AD=DE,连BE,则△ACD≌△EBD得BE=AC,进而在△ABE中利用三角形三边关系,证之. 解答:证明:如图延长AD至E,使AD=DE,连接BE. ∵BD=DC,AD=DE,∠ADC=∠EDB ∴△ACD≌△EBD∴AC=BE 在△ABE中,AE<AB+BE,即2AD<AB+AC∴AD<(AB+AC) 点评:本题主要考查全等三角形的判定及性质以及三角形的三边关系问题,能够熟练掌握.
构造全等三角形的基本方法 第一种:倍长中线法(利用中点、中线构造) 例题1、如图,△ABC中,AD是中线,AB=4,AC=6,AD的范围是.2】
第二种:利用角平分线 角平分线常见的辅助线作法: 例题2、已知在△ABC中,∠B=2∠C,∠A的平分线AD交BC边于点D.求证:AC=AB+BD. 3】 【例1】
例题3、BE是角平分线,AD垂直BE于D,求证:∠2=∠1+∠C 第三种:截长补短法(通常用来证明线段和差相等) “截长法”即把结论中最大的线段根据已知条件分成两段,使其中一段与较短线段相等,然后证明余下的线段与另一条线段相等的方法.“补短法”为把两条线段中的一条接长成为一条长线段,然后证明接成的线段与较长的线段相等,或是把一条较短的线段加长,使它等于较长的一段,然后证明加长的那部分与另一较短的线段相等. 例题5:如图(1)已知:正方形ABCD中,∠BAC的平分线交BC于E, 求证:AB+BE=AC. 例题6、AB//CD,BE,CE是角平分线,求证:BC=AB+CD
第四种:旋转 对题目中出现有一个公共端点的相等线段时,可试用旋转方法构造全等三角形 例3、如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=6,PB=2,PC=4,求∠BPC的度数. 例4、如图,正方形ABCD中,DE=3,BF=1,∠EAF=45°,则EF= .
例5、如图所示,两个边长都为2的正方形ABCD和OPQR,如果O点正好是正方形ABCD的中心,而正方形OPQR可以绕O点旋转,那么它们重叠部分的面积为 第五种:平行线法 例7、如图,△ABC中,AB=AC。E是AB上异于A、B的任意一点,延长AC到D,使CD=BE,连接DE交BC于F。求证:EF=FD。
D C B A 全等三角形——截长补短法 一、知识梳理: 截长补短法 截长补短法是几何证明题中十分重要的方法。通常来证明几条线段的数量关系。 截长法: (1)过某一点作长边的垂线 (2)在长边上截取一条与某一短边相同的线段,再证剩下的线段与另一短边相等. 补短法 (1)延长短边。 (2)通过旋转等方式使两短边拼合到一起。…… 二、典型例题: 例1、如图,在ABC ?中,60BAC ∠=?,AD 是BAC ∠的平分线,且AC AB BD =+,求ABC ∠的度数. 及时练习: 如图所示,在Rt △ABC 中,∠C=90°,BC=AC ,AD 平分∠BAC 交BC 于D ,求证:AB=AC+CD . 例2、已知ABC ?中,60A ∠=,BD 、CE 分别平分ABC ∠和.ACB ∠,BD 、CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明.
N E B M A D M D C B A D O E C B A 及时练习: 如图,点M 为正三角形ABD 的边AB 所在直线上的任意一点(点B 除外),作60DMN ∠=?,射线MN 与DBA ∠外角的平分线交于点N ,DM 与MN 有怎样的数量关系? 例3、如图.已知正方形ABCD 中,M 为CD 的中点,E 为MC 上一点,且∠BAE =2∠DAM . 求证:AE =BC +CE . 及时练习: 如图,AD ⊥AB ,CB ⊥AB ,DM =CM =a ,AD =h ,CB =k , ∠AMD =75°,∠BMC =45°,则AB 的长为 ( ) A . a B . k C . 2 k h + D . h 例4、以ABC ?的AB 、AC 为边向三角形外作等边ABD ?、ACE ?,连结CD 、BE 相交于点O . 求证:OA 平分DOE ∠.
全等三角形专题 ——截长补短 角的平分线具有其特有的性质,这一性质在许多问题里都有着广泛的应用,而“截长补短法”又是解决这一类问题的一种特殊的方法,利用此种方法常可使思路豁然开朗。 1、 如图, AD BC //,点E 在线段AB 上,ADE CDE ∠=∠,DCE ECB ∠=∠, 求证:CD=AD+BC 2、已知如图,1=2∠∠,P 为BN 上一点,且PD BC ⊥于点D,且0 180 BAP BCP ∠+∠=, 求证:AB+BC=2BD 2、 已知,如图在ABC 中,2 C B ∠ = ∠,12∠=∠, 求证:AB=AC+CD 4、已知ABC 中,0 60A ∠=,BD ,CE 分别评分ABC ∠和ACB ∠,BD,CE 交于点O ,试判断BE,CD,BC 的数量关系,并加以证明。 5、如图所示,ABC 是边长为1的等边三角形,BDC 是顶角为0 120的等腰三角形,以D 为顶点的一个 060的MDN ∠,点M ,N 分别在AB,AC 上,求AMN 的周长。 6、如图,在ABC 中,0 60BAC ∠=,AD 是BAC ∠的平分线,且AC=AB+BD,求ABC ∠的度数。 7、已知如图,ABCD 是正方形,FAD FAE ∠=,求证:BE+DF=AF 8、在ABC 中,2B C ∠=∠,且AD BC ⊥于D ,求证:CD=AB+BD
全等三角形在中考中必考题型 1、已知,在中ABC ,0C=90∠,AC=BC ,直线l绕点A旋转,过点B,C分别向直线l做垂线,垂足 分别是点D、点E。 (1)如图1,求证:BD+CE=AE; (2)当直线l绕点A顺时针转到如图2,则BD、CE 、AE 之间满足的数量关系 是 2、已知ABCD ,连接AC,AC=AB,E为线段BC上的一动点,F为直线DC上一动点,且EAF B ∠=∠。 (1)如图(1) ,当060B ∠=时,求证:CE+CF=CA 。 3、已知ABC ,有一个以P 为顶点的角,且1 2 APE ACD ∠=∠,将此角的顶点放在边BC 上,角的一边始 终经过点A ,另一边与ACB ∠的外角的平分线交于点E 。 (1)如图1,当ABC 三角形为等边三角形时,求证:CP+CE=CA 。 4、在中Rt ABC 中,090ACB ∠=,AC=BC ,点P 为BC 所在直线上一点,分别过点B 、C 作直线AP 的垂线,垂足分别为点D ,X 。 (1)当点P 在线段BC 上时,如图1,求证:2AD BD CE -= (2)当点P 在CB 的反向延长线上时,如图2,线段AD 、BD 、CE 三者之间满足的数量关系是 B
倍长中线模型,全等三角形搭桥,难题分析讲解三角形是初中数学里最基本的几何图形,而其边上,又是很常见的条件。当涉及三角形问题时,常采用延长中线一倍的办法,即倍长中线法,实现角和线段的转化,以此来作辅助线解题。好处是通过此法构造全等三角形继而得到平行,也可以证明三角形全等,可将分散的条件集中在一个三角形内解题,常常出奇制胜,化腐朽为神奇。且看模型,和模型产生的基本结论. 倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用SAS证全等(其中有对顶角相等)
例1:△ABC 中,AB=5,AC=3,求中线AD 的取值范围。 分析:延长AD 至E ,使ED=AD ,连接 BE ,见模型1, 可证△ABD 与△ECD 全等,把AB 边转移到EC 上了, 再看△AEC ,用第三边大于两边之差小于两边之和可解。 【归纳总结】 1. 三角形的三边关系是求线段范围的常用方法. 2. 出现中线时,常考虑倍长中线构造全等三角形,实现线段的转化. 例 2:已知在△ABC 中,AD 是 BC 边上的中线, E 是 AD 上的一点,且BE=AC ,延长BE 交AC 于F , 求证:AF=EF 延长ED 至G ,使GD=ED ,利用SAS 可证△BED 与△CGD 全等,把BE 转移到GC 上,∠G=∠1,由已知 BE=AC ,得到GC=AC ,由等腰三角形性质可知∠G=∠3, 通过∠G 传递,得到∠2=∠3,得证AF=EF 例3:已知:如图,在△ABC 中,AB ≠AC ,D 、E 在BC 上,且DE=EC ,过D 作DF//BA 交AE 于点F ,DE=AC ,求证:AE 平分∠BAC 证明:如图,延长FE 到G ,使EG=EF ,连接CG . 在△DEF 和△CEG 中, ∵ ,∴△DEF ≌△CEG . ∴DF=GC ,∠DFE=∠G .∵DF ∥AB ,∴∠DFE=∠BAE . ∵DF=AC ,∴GC=AC .∴∠G=∠CAE .∴∠BAE=∠CAE . 即AE 平分∠BAC ?? ???==FG FE CEG =∠DEF ∠EC ED
全等三角形作辅助线经典例题 常见辅助线的作法有以下几种: 1) 遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折” ? 2) 遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全 等变换中的“旋转” ? 3) 遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中 的“对折”,所考知识点常常是角平分线的性质定理或逆定理. 4) 过图形上某一点作特定的平分线,构造全等三角形,利用的思维模式是全等变换中的“平移”或“翻 转折叠”;(遇垂线及角平分线时延长垂线段,构造等腰三角形) 5) 截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是 之与特定线段相等,再利用三角形全等的有关性质加以说明?这种作法,适合于证明线段的和、差、倍、分等类的题目. 特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解答. 一、倍长中线(线段)造全等 1:已知,如图△ ABC中,AB=5,AC=3,则中线AD的取值范围是 _______________ . 2 :如图,△ ABC中,E、F分别在AB、AC 上, DE丄DF,D是中点,试比较BE+CF 与EF的大小. 3 :如图,△ ABC中,BD=DC=AC ,E是DC的中点,求证:AD平分/ BAE. 中考应用: ABC的两边AB、AC为腰分别向外作等腰Rt ABD和等腰Rt ACE BAD CAE 90,连接DE,M、N分别是BC、DE的中点?探究:AM与DE的位 置关系及数量关系. (1 )如图① 当ABC为直角三角形时,AM与DE的位置关系 是________________ ,线段AM与DE的数量关系是________________ ; (2 )将图①中的等腰Rt ABD绕点A沿逆时针方向旋转(0< <90)后,如图②所示,(1 )