
No .1 线性规划
1、某织带厂生产A 、B 两种纱线和C 、D 两种纱带,纱带由专门纱线加工而
工厂有供纺纱的总工时7200h ,织带的总工时1200h 。 (1) 列出线性规划模型,以便确定产品的数量使总利润最大;
(2) 如果组织这次生产具有一次性的投入20万元,模型有什么变化?对模型
的解是否有影响?
解:(1)设A 的产量为x 1,B 的产量为x 2,C 的产量为x 3,D 的产量为x 4,则
有线性规划模型如下:
max f (x )=(168-42)x 1 +(140-28)x 2 +(1050-350)x 3 +(406-140)x 4
=126 x 1 +112 x 2 +700 x 3 +266 x 4
s.t. ??
?
??=≥≤+≤+++4,3,2,1 ,012005.02 720041023434321i x x x x x x x i
(2)如果组织这次生产有一次性的投入20万元,由于与产品的生产量无关,
故上述模型只需要在目标函数中减去一个常数20万,因此可知对模型的解没有影响。 2、将下列线性规划化为极大化的标准形式
解:将约束条件中的第一行的右端项变为正值,并添加松弛变量x 4,在第二行添加人工变量x 5,将第三行约束的绝对值号打开,变为两个不等式,分别添加松弛变量x 6, x 7,并令x x x 333
='-'',则有
max[-f (x )]= {-2 x 1 -3 x 2 -5('-''x x 33)+0 x 4 -M x 5+0 x 6 +0 x 7} s.t. 0,,,,,,,13
55719 13 55719
16 9976 5 765433217
3321633
215332143321≥'''=+''+'-+-=+''-'+-=+''+'-+-=+''-'+--??
??
?
????
x x x x x x x x x x x x x x x x x x x x x x x x x x x x ??????
?±≥≤+-=-+--≥-+++=不限
3213213213213
21 ,0,13|5719|169765
..532)(min x x x x x x x x x x x x t s x x x x f
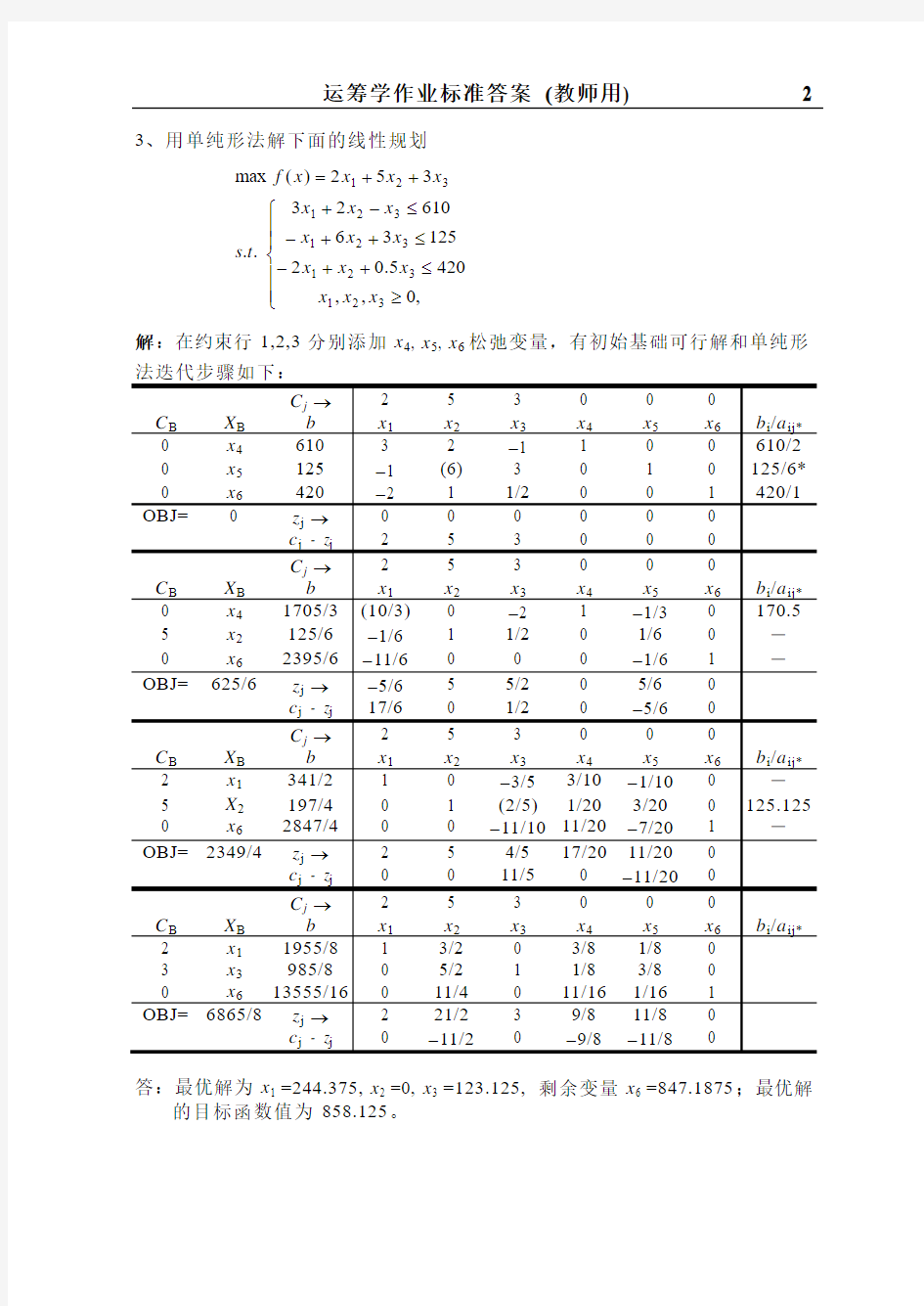
3、用单纯形法解下面的线性规划
???
???
?≥≤++-≤++-≤-+++= ,0,,4205.021********* ..352)(max 321321321321321x x x x x x x x x x x x t s x x x x f 解:在约束行1,2,3分别添加x 4, x 5, x 6松弛变量,有初始基础可行解和单纯形
答:最优解为x 1 =244.375, x 2 =0, x 3 =123.125, 剩余变量x 6 =847.1875;最优解
的目标函数值为858.125。
No .2 两阶段法和大M 法 解:将原问题变为第一阶段的标准型
???
??≥=+-+=+-+--?+?=0,,,,,75
3802 ..00)(max 6
54321642153216
521x x x x x x x x x x x x x x t s x x x x x f
答:最优解为x 1 =14,x 2 =33,目标函数值为254。 2、用大M 法解下面问题,并讨论问题的解
1、用两阶段法解下面问题:
???
??≥≥+≥++=0,75
3802 ..64)(min 2
121212
1x x x x x x t s x x x f
???
???
?≥≥++≤++-≤++++= ,0,,52151565935 ..121510)(max 321321321321321x x x x x x x x x x x x t s x x x x f
解:第1、2行约束条件添加x 4, x 5松弛变量,第3行添加x 6剩余变量和x 7
答:最后单纯形表中检验数都小于等于0,已满足最优解判定条件,但人工变量x 7仍未迭代出去,可知原问题无可行解(无解)。 No .3 线性规划的对偶问题
解:对偶问题为
?????
????
±≥≤=+-≥++-≥+≤+++=不限
321313213121321,0,00 53 2 2..645)(min y y y y y y y y y y y y t s y y y y g
1、写出下列线性规划问题的对偶问题:
(1) ??????
?±≥≤=++≤+≥+-+-+=不限
43214323143213
21 ,0,,06 4 2 5 ..532)(max x x x x x x x x x x x x x t s x x x x f
?
?
?
???
????
?≤≥±-≥-≤≥≤-≥≤0
,0,12 8 4 14 2 6321332211x x x x x x x x x 不限 令改写后约束条件每行对应的对偶变量为y 1,...,y 6,则有对偶规划如下:
??????
?≥≤≥+-≤+=+--++-=0
,, ,0,,8 3
4 ..12841426)(max 642531654321654321y y y y y y y y y y y y t s y y y y y y y g
第二种解法:将原问题的约束条件该写为
并令,12 ,4 ,2332211
+='-='+='x x x x x x 则原问题改写为下左式,并有对偶问题如下式,
???????≤≤-≤≤++=0
,,834
.4108)(max 321321321y y y y y y t s y y y y g
2、写出下问题的对偶问题,解对偶问题,并证明原问题无可行解
解:对偶问题为 约束条件标准化为
??
?
??≥-≥+--≥-+-=0,,324..)(min 321321313
21y y y y y y y y t s y y y y g ?????≥=-+-=++-0,,,,3 + 2 4 54321532143
1y y y y y y y y y y y y
(2)
??
?
??-≤≤-≤≤≤≤-+-=8
1214
462 ..834)(min 3213
21x x x t s x x x x f
解:原问题的约束条件可改写为右式
??
?
??≤+≤≤-≤≤+≤4
12010406203
21x x x
???????≥'''≤'≤'≤'-'+'-'='0,,4108.116834)(min 321
3
2
1
321x x x x x x t s x x x x f
??????
?≥≤+--≤-≤+--=
,0, 121
1 ..34)(max 212122121x x x x x x x t s x x x f
入变量
答:迭代到第三步,x1为入变量,但主列中技术系数全为负值,故对偶问题有可行解但解无界,由弱对偶定理推论可知,原问题无可行解。
3、用对偶单纯形法求下面问题
???
??≥≥+≥++=0
,75
3802 ..64)(min 21212121x x x x x x t s x x x f
答:最优解为x 1 =14,x 2 =33,目标函数值为254。 No .4 线性规划的灵敏度分析
原问题为max 型,x 4,x 5为松驰变量,x 6为剩余变量,回答下列问题: (1)资源1、2、3的边际值各是多少?(x 4,x 5是资源1、2的松驰变量,x 6是
资源3的剩余变量)
(2)求C 1, C 2 和C 3的灵敏度范围; (3)求?b 1,?b 2的灵敏度范围。 解:(1) q 1 =11, q 2 =0, q 3 = -1。 (2) x 1 , x 2 为基变量,故
[]max /,/,/max ,.,---?????
?≤?---≤?-≤≤+∞?≤≤+∞
61311231131816533181111???C C C C
max /min /,/..-??????≤≤----?????
??-≤≤?-≤≤61311
131231815
105222??C C C 9 x 3 为非基变量,故
-∞≤≤?-∞≤≤?C C 33610
(3) 5.16 3/123,3/42min 3/24max 11≤?≤-????
???----≤?≤??????-b b 同理有 -≤≤+∞22?b No .5 运输问题
1、分别用西北角法、最低费用法和运费差额法,求下面运输问题(见表)的初
始可行解,并计算其目标函数。(可不写步骤)
2、以上题中最低费用法所得的解为初始基础可性解,用表上作业法(踏石法)
求出最优解。(要求列出每一步的运费矩阵和基础可行解矩阵)
OBJ =955 ?
(15) 4
-7 10 -7 -6 -3 5 6 9
6 4 11
OBJ =1415 OBJ =850
4
4 5 209 2 13 10 14 6
答:x 13=5, x 14=15, x 24=30, x 32=15, x 33
=25,
x 41=25, x 43=5, x 45=30, OBJ=850。
No .6 指派问题
1、有4个工人。要指派他们分别完成4项工作。每人做各项工作所消耗的时
?标?
∨4 ∨8 ∨5 ?∨1
2637划线过程(发现有4条直线) 找到最优解
答:容易看出,共有四个最优解:①甲→B ,乙→D ,丙→A ,丁→C ; ②甲→D ,乙→B ,丙→A ,丁→C ;③甲→B ,乙→D ,丙→C ,丁→A ;④甲→D ,乙→B ,丙→C ,丁→A ;OBJ=10。
OBJ =850
*
*
*
第二个最优解:OBJ =10
2、学生A 、B 、C 、D 的各门成绩如下表,现将此4名学生派去参加各门课的单项竞赛。竞赛同时举行,每人只能参加一项。若以他们的成绩为选派依解:变换效率矩阵为适用于min 化问题,用96减去上面矩阵中所有元素值,
∨3 ∨1 ?变? 2
5
3 1 ∨2 ∨4
No .7 动态规划
1、某公司有9个推销员在全国三个不同市场里推销货物,这三个市场里推销员人数与收益的关系如下表,做出各市场推销人员数的分配方案,使总收益最大。
解:令分配到各地区的推销员人数为决策变量x k ,k =1,2,3代表第1、2、3地区;令各地区可供分配的推销员人数为状态变量s k 。最先分配给第1地区,
第一个最优解:OBJ =10
然后第2、第3地区,则 s 1=9。
状态转移公式为:s k +1 = s k -x k ; 目标函数为:f d x i i 313==∑m ax ()
第1阶段:第3地区, s 3 有0~9种可能,由收益表第3行可知d (x 3)
答:第1地区分配2名推销员,第2 地区不分配人员,第3地区分配7名推销员,总收益为218。
2、设某工厂要在一台机器上生产两种产品,机器的总运转时间为5小时。生产这两种产品的任何一件都需占用机器一小时。设两种产品的售价与产品产量成线性关系,分别为(12-x 1)和(13-2x 2)。这里x 1和x 2分别为两种产品的产量。假设两种产品的生产费用分别是4x 1和3x 2,问如何安排两种产品的生产量使该机器在5小时内获利最大。(要求用连续变量的动态规划方法求解) 解:设可用机时为状态s i ,先分配产品1机时,故有状态转移方程
s k +1 = s k -x k (i =1,2)
边界值 s 1 =5, s 3=0
目标函数为:}3)213(4)12max{(2221112x x x x x x f --+--=*
)}210()8max{(2
22211x x x x -+-=
由边界条件s 3 = s 2 -x 2 =0,得 x 2 = s 2,因此有
2
2222221210210)(s s x x s f -=-=* 则动态规划总效果的递推方程为
)}
210()
8{(0
max )}
()8{(0
max )(2
222111212
11112s s x x x s f x x x x f -
+-
>=+->=**
由状态方程 s 2 = s 1 -x 1 =5-x 1,代入上式得
}318{0
max }
)5(2)5(10)8{(0max )(2
1112112
11112x x x x x x x x x f ->=---+->=*
令 df x dx x 21111860()/=-=,解得 x 1 =3。因此,
27933182=?-?=*f
答:最优策略为第1种产品生产3件,第二种产品生产2件,5小时内最大利润为27元。 No .8 最短路问题
1、求下图中v 1到所有点的最短路径及其长度。(要求最短路用双线在图中标出,保留图中的标记值)
解:最短路及其长度如图中粗线和节点上永久标记所示,
2、将上图看作无向图,写出边权邻接矩阵,用Prim 算法求最大生成树,并画出该树图。
解:由图可得邻接矩阵,由Prim 算法的最大生成树如下图,
3
v 7
答:最大生成树的权值为39。
11
√1 √3 √2 √6 √4 √5 √7 √8
No .9 网络流问题
1、求下面网络s 到t 的最大流和最小截,从给定的可行流开始标号法。(要求每得到一个可行流后,即每次增广之后,重新画一个图,标上增广后的可行流,再进行标号法) 解:
v 3
5t
(s ,2)
+
v 3
5
t
(s
答:最大流为15,最小割截为
V s v V v v v v t ==(,),(,,,,)31245
No .10 随机服务系统:输入过程
1、对一服务系统进行观察,总观察时间为102.7分钟,到达系统的累计人数
为40人,顾客累计的排队等待时间为44.8分钟,顾客累计的服务时间为79.6分钟,求
(1)系统中平均排队长度; (2)平均同时接受服务的人数。
解:总观察时间为T =102.7分钟,累计到达人数40,故
λt = 40/T =0.3895人/分钟
由题意可知 T W T T W T W q W W h W q q h h ====4484079640.,/;
.,/
由little 公式,L W W W L L d t d t q h q h ==+=+λλ(),
v 3
5
(s ,9)
(3,4)
(s
v 3
5(s (s ,5)
(2,3)
v t
(s
(1) L W T T q t q W q ==λ/=44.8/102.7=0.436 (2) L W T T h t h W h ==λ/=79.6/102.7=0.775
答:平均排队队长0.436人,平均同时接受服务的人数为0.775人。
2、某选举站对甲、乙二人进行选举,选票中只能选其中一人才有效。假设投
票的人流服从泊松分布,投甲票的人的到达率为λ1 =4人/小时,投乙票的人的到达率为λ2 =2人/小时;再假设所有投票人的票都是有效的,而选举结果的统计是在一个与选民不见面的屋里与投票过程同时进行的。问选举开始后半小时统计结果为: (1)甲得三票,乙得1票的概率; (2)总票数为5的概率; (3)甲得全票的概率。
解:(1)假设投甲、乙票的人流不相关,则有
P
甲
3(1/2)P
乙
1(1/2)=
2/122/143
12/12!
3)2/14(?-?-??
?e e !
=0.066;
(2) 1008.0025.2!
5)2/16()2/1(32/165
5==?=
-?-e e P ;
(3) 甲得全票的事件为投乙票的人一个未来而投甲票的人至少来一个,即
P 乙0(1-P 甲0)=318.0)135.01(368.0)1(21=-?=---e e 。 No .11 随机服务系统:标准服务系统
1、某自动交换台有4条外线,打外线的呼叫强度为2次/分钟,为泊松流,
平均通话时长为2分钟。当4条外线全忙时,用户呼叫将遇忙音。假设用户遇忙音后立即停止呼叫。问 (1)用户拨外线遇忙的概率为多大? (2)一小时内损失的话务量为多少?
(3)外线的利用率为多少?(4)过负荷为100%时,外线的利用率为多少? 解:已知损失制系统,n =4,λ=2次/分钟,h =2分钟,ρ = 4erl , (1) 遇忙的概率为B =p 4 =0.31;
(2) 一小时内损失的话务量=ρ B =1.24erl ; (3) 外线利用率为 ηρ=-=()/.1069B n 。
(4) 过负荷100%时,外线利用率为 η=-=8105746408508(.)/.。
2、某车间机器发生故障为一泊松流,平均4台/小时。车间只有一名维修工,
平均7分钟处理一台故障。若为该维修工增加一特殊工具可使平均故障处理时间降到5分钟,但这一特殊工具的使用费用为5元/分钟。机器故障停工每台每分钟损失5元,问购置这台特殊工具是否合适?
解:该系统可认为是M/M/1无限源等待制,已知 λ=4台/小时,h 17=分钟,
h 25=分钟;h 1、h 2分别为增加特殊工具前后修复一台机器故障的平均用时。
先求增加特殊工具前后每台机器的平均故障停机历时(等待时间+维修时间),由单服务员等待系统的平均队长公式有:
L L d d 111122221460740875105=
-=-=-==-=-=ρρλμλρρλ
μλ
/.,. 由Little 公式得,
W L d d 1 =1/λ=0.875/4=0.21875(小时)=13.125分钟,
W L d d 2 2=/λ=0. 5/4=0.125(小时)=7.5分钟,
则不引入特殊工具时每台故障的总费用为 C 1=5?W d1=65.625元; 而引入特殊工具时每台故障的总费用为 C 2=5?W h +5?W d2=62. 5元; 答:购置特殊工具是合适的。
3、有M/M/n :∞/∞/FIFO(先到先服务)系统,输入业务量为ρ,求
当n =1, 2 , 3时的等待概率D ,和平均逗留队长L d 的公式。 解:由爱尔兰等待公式 D n n n j n n n n j
n j n =
-?? ?
?
?+-?? ??
?=-∑
ρρρρρ!!!1
1
, 和L D n d =+
-?
?
?
?
?ρρ1有 n =1时,D =ρ,L d =
ρρ
1-;
n =2时,D =ρρ22+,L d =442ρ
ρ
-; n =3时,D =
ρρρ32
64++,L d =
1861862323
ρρρρρρ+-+--。
No .12 随机服务系统:特殊服务系统
1、下面是四个点间的双向业务量矩阵{f ij }和距离矩阵{d ij }
{d ij }
1 2 3 4 所谓双向业务量f ij ,它表示i 呼叫j
的业务量与j 呼叫i 的业务量之和,因此有f ij =f ji 。根据双向业务量所得的网路是无向网路,各点间的电路群都是双向电路,可同时为电路两端的用户呼叫服务。假设每条电路单位长度的费用为1单位,汇接局的交换机每条电路接口费用为1单位。
{f ij }
1 2 3 4
(1)根据业务量矩阵求最佳的骨干线路网,并求骨干线路各点间线束容量(电路数),要求各线束的呼损小于0.01,并计算全网费用。
(2)若在不存在骨干电路的点对间开设独立的直达电路群,计算此时网路中各点对间的线束容量及全网费用,仍要求各线束的呼损小于0.01。 (3)若在不存在骨干电路的点对间开设高效直达电路群,其呼损小于0.3,计算此时网路中各点对间的线束容量及全网费用,要求骨干线束的呼损小于0.01。
解:
(1)由流量矩阵{f ij }可得最大生成树如下图,显然节点1为汇接局,该树为星形结构,即为骨干电路,点间路由表如下矩阵所示。
1 2 3 4
由路由表可计算骨干电路上的双向业务流
量:
F 12=f 12+f 23+f 24=5+2+0=7erl, F 13=f 13+f 23+f 43=6+2=1.5=9.5erl, F 14=f 14+f 24+
f 34=4+0+1.5=5.5erl
该网路结构是完全的汇接制,骨干电路仍是全利用度的,根据B<0.01的服务等级要求,查爱尔兰损失表可得
n 12=14, n 13=17, n 14=12,
由此可计算出全网费用为 C
1 =2(14+17+12)=86。
(2) 若在节点(2-3)和(3-4)间开独立的直达电路,网路如下图,只有节点(2-4)间需转接,但f 24=0,故该网中没有转接业务量。
查表结果 (F ij , n ij ) 标于图上。由此可计算出全网费用为
C 2 =2 (11+13+10)+(7+6)=81。
(3) 若在节点(2-3)和(3-4)间开高效直达电路,网路
结构仍如上图,但骨干电路(1-2), (1-3), (1-4)上存在节点(2-3)和(3-4)间的溢流,由此它是一个部分利用度系统,需要利用Wilkinson 等效流理论来作计算。首先计算高效电路,因为它们是全利用度的,由B<0.3,查表得
n 23=3, n 34=3
求(2,3)和(3,4)的溢出话务量,有
E i or E A E A A A
n A A
i i w w w w w 331
3
31312112232419
021202030226331930
21932204211181911191923
05916
()/!
/!
.,().....().,()().=
=
==+
---=?==-+
++-=
+==∑ (.),
1 σ
同理有
E i A E i i w w 3313
23121515315
0562541875
013431515020150201510201515310201515027278
(.)./!./!...,.(.).,.(..
..
).=
=
==?==-+
++-==∑
σ
下面求(1-2),(1-3),(1-4)上的等效流和所需电路数, ①骨干电路(1,2) n 12上的业务流为
A A f f w w w w 122 12
121121204215542105916555916
=+=+==+=+=..,
..σσ
等效流为
A A A q A A n A q A w w w w w w w w w =+-?? ????==-+==--=σσσσ 12
2 122 12 122 12 12 122 12 12 31568898110845103114
.,/.,/. 查表E n N ()(5.).,+=68898001 得n +N =12,故 N =12-0.3114=11.6886,取
N =12,即 n 12=12。 ②骨干电路(1,4) n 14上的业务流为
A A f f w w w w 142 22
14214140201544201502728442728
=+=+==+=+=..,
..σσ
等效流为
A A A q A A n A q A w w w w w w w w w =+-?? ????==-+==--=σσσσ 14
2 142 14 142 14 12 142 14 14 314324541108084101482
.,/.,/. 查表E n N ()(.).,+=432454001 得n +N =10,取
N =10,即 n 14=10。 ③骨干电路(1,3),(有两个溢流) n 13上的业务流为
A A A f f w w w w w w 132 12 22
131213130421020156662250591602728668644
=++=+++==++=++=...,
...σσσ
等效流为
A A A q A A n A q A w w w w w w w w w =+-?? ????==-+==--=σσσσ 13
2 132 1
3 13
2 1
3 13 132 13 13 3169780110869441040335
.,/.,/. 查表E n N ()(.).,+=69780001 得n +N =14,取
N =14,即 n 13=14。
所得网路配置入右图,骨干电路上标的是(A w ,σw 2)及电路数。全网费用为
C 3 =2(12+14+10)+(3+3)=78
答:经比较设置高效电路的网路配置最优。 No .13 存储论
1、某工厂每年需某种原料1000kg ,一次定购费为200元,定购量Q 与单价
k 的关系为
0 ≤ Q < 500kg , k 1 =2元/kg 500 ≤ Q < 1000kg , k 2 =1.5元/kg 1000 ≤ Q ,
k 3 =1.2元/kg
已知原料存储费也与Q 有关
0 ≤ Q < 500kg , C s1 =2元/kg.年 500 ≤ Q < 1000kg , C s2 =1.5元/kg.年 1000kg ≤ Q ,
C s3 =1.2元/kg.年
求最佳订货量Q m ,并求该订货量下的全年总费用C (Q m )。 解:已知D =1000公斤/年,C d =200元,C s 如题意; (1) 用公式Q DC C d s
02=
先求Q 01, Q 02, Q 03,
Q 0121000200
220054472=??==. < 500公斤,(落入该批量价区间) Q 022*******
1520025825164=??=?=... < 1000公斤, (落入该批量价区间)
Q 0321000200
1220028867557735=
??=?=.
.. < 1000公斤, (落在该批量价区间外)
(2) 计费各方案年费用C i ,因为Q01, Q02都落入各自适用批量价区间,故
C Q k
D 1011210002002894421000289443()..=???+=+?=元
C Q k
D 202221000200157746151000227460()....=
???+=+?=元
而按第三批量段购买,最少购买1000公斤,故
C M C M DC M k
D s d 3333
11205121000100020010001210002000()../.=
+
+=??+?+?=元
答:最佳订货量为每次1000公斤,全年总费用(含购料费)为2000元。
习题课1
1、某工厂生产用2单位A 和1单位B 混合而成的成品出售,市场无限制。A 和B 可以在该工厂的3个车间中的任何车间生产,生产每单位的A 和B 在
试建立使成品数量最大的线性规划模型。 解:设车间1生产x 1A 单位A 、生产x 1B 单位B ;
设车间2生产x 2A 单位A 、生产x 2B 单位B ; 设车间3生产x 3A 单位A 、生产x 3B 单位B ; 则有生产安排最优化的模型如下:
????
?
????=≥++≥++≤+≤+≤+++=3,2,1,0,)(2100
5.15.112021002.
.)(max 321321332211321i x x x x x x x x x x x x x x t s x x x x f iB iA B B B A A A B A B A B A B
B B 这是一个可分解的线性规划,这类问题就容易出现退化现象。
2、某饮料工厂按照一定的配方将A 、B 、C 三种原料配成三种饮料出售。配方规定了这三种饮料中A 和C 的极限成分,具体见下表,
饮料甲、乙、丙分别由不同比例的A 、B 、C 调兑而成,设调兑后不同成分的体积不变,求最大收益的生产方案。
解:设x 1A 为饮料甲中A 的总含量 (升),设x 2A 为饮料乙中A 的总含量 (升)
设x 1B 为饮料甲中B 的总含量 (升),设x 2B 为饮料乙中B 的总含量 (升) 设x 1C 为饮料甲中C 的总含量 (升),设x 2C 为饮料乙中C 的总含量 (升) 设x 3A 为饮料丙中A 的总含量 (升), 设x 3B 为饮料丙中B 的总含量 (升) 设x 3C 为饮料丙中C 的总含量 (升)
运筹学A卷) 一、单项选择题(从下列各题四个备选答案中选出一个正确答案,答案选错或未选者,该题不得分。每小题1分,共10分) 1.线性规划具有唯一最优解就是指 A.最优表中存在常数项为零 B.最优表中非基变量检验数全部非零 C.最优表中存在非基变量的检验数为零 D.可行解集合有界 2.设线性规划的约束条件为 则基本可行解为 A.(0, 0, 4, 3) B.(3, 4, 0, 0) C.(2, 0, 1, 0) D.(3, 0, 4, 0) 3.则 A.无可行解 B.有唯一最优解medn C.有多重最优解 D.有无界解 4.互为对偶的两个线性规划, 对任意可行解X 与Y,存在关系 A.Z > W B.Z = W C.Z≥W D.Z≤W 5.有6 个产地4个销地的平衡运输问题模型具有特征 A.有10个变量24个约束
B.有24个变量10个约束 C.有24个变量9个约束 D.有9个基变量10个非基变量 6、下例错误的说法就是 A.标准型的目标函数就是求最大值 B.标准型的目标函数就是求最小值 C.标准型的常数项非正 D.标准型的变量一定要非负 7、m+n-1个变量构成一组基变量的充要条件就是 A.m+n-1个变量恰好构成一个闭回路 B.m+n-1个变量不包含任何闭回路 C.m+n-1个变量中部分变量构成一个闭回路 D.m+n-1个变量对应的系数列向量线性相关 8.互为对偶的两个线性规划问题的解存在关系 A.原问题无可行解,对偶问题也无可行解 B.对偶问题有可行解,原问题可能无可行解 C.若最优解存在,则最优解相同 D.一个问题无可行解,则另一个问题具有无界解 9、有m个产地n个销地的平衡运输问题模型具有特征 A.有mn个变量m+n个约束…m+n-1个基变量 B.有m+n个变量mn个约束 C.有mn个变量m+n-1约束 D.有m+n-1个基变量,mn-m-n-1个非基变量 10.要求不超过第一目标值、恰好完成第二目标值,目标函数就是
《运筹学》期末考试试卷(A) 学院 班级 姓名 学号 考生注意∶ 1.本试题共 七 题,共 3 页,请考生认真检查; 一、某炼油厂生产三种牌号的汽油,70#,80#和85#汽油。每种汽油有不同的辛烷值和含硫量的质量要求并由三种原料油调和而成。每种原料也有不同的质量指标。每种原料每日可用 数量、质量指标和生产成本见表1,每种汽油的质量要求和销售价格见表2。问该炼油厂如何安排生产才能使其利润最大?假定在调和中辛烷值和含硫量指标都符合线性相加关系。试建立数学模型。(25分) 二、用对偶单纯形法求解下列线性规划问题:(25分) ? ???? ??0 ,,9645252max 32132323212 1≥≥+≤+=+++=x x x x x x x x x x x x z
三、已知某运输问题的产销平衡表与单位运价表如下表所示,B 2地区需要的115单位必须满足,试确定最优调拨方案。(20分) 四、从甲, 乙, 丙, 丁, 戊五人中挑选四人去完成四项工作,已知每人完成各项工作的时间如下表所示。规定每项工作只能由一个人去单独完成,每个人最多承担一项工作,假定甲必须保证分配到工作,丁因某种原因不同意承担第四项工作。在满足上述条件下,如何分配工作, 五、求V 1到各点的最短路及最短路径。(20分) v 1 v 2 v 3 v 6 v 4 v 7 v 5 911 10 11 11 11 108 4 六、某公司有资金4百万元向A ,B ,C 三个项目追加投资,各个项目可以有不同的投资额(以百万元为单位),相应的效益值如下表。问怎样分派资金,使总效益值最大,试用动态规划方法求解。(25分)
二、计算题(60分) 1、已知线性规划(20分) MaxZ=3X1+4X2 X1+X2≤5 2X1+4X2≤12 3X1+2X2≤8 X1,X2≥0 其最优解为: 基变量X1X2X3X4X5 X33/2 0 0 1 -1/8 -1/4 X25/2 0 1 0 3/8 -1/4 X1 1 1 0 0 -1/4 1/2 σj 0 0 0 -3/4 -1/2 1)写出该线性规划的对偶问题。 2)若C2从4变成5,最优解是否会发生改变,为什么? 3)若b2的量从12上升到15,最优解是否会发生变化,为什么? 4)如果增加一种产品X6,其P6=(2,3,1)T,C6=4该产品是否应该投产?为什么?解: 1)对偶问题为 Minw=5y1+12y2+8y3 y1+2y2+3y3≥3 y1+4y2+2y3≥4 y1,y2≥0 2)当C2从4变成5时, σ4=-9/8 σ5=-1/4 由于非基变量的检验数仍然都是小于0的,所以最优解不变。 3)当若b2的量从12上升到15 X=9/8 29/8 1/4 由于基变量的值仍然都是大于0的,所以最优解的基变量不会发生变化。 4)如果增加一种新的产品,则 P6’=(11/8,7/8,-1/4)T σ6=3/8>0 所以对最优解有影响,该种产品应该生产 2、已知运输问题的调运和运价表如下,求最优调运方案和最小总费用。(共15分)。 B1B2B3产量销地 产地 A1 5 9 2 15 A2 3 1 7 11 A3 6 2 8 20 销量18 12 16 解:初始解为
计算检验数 由于存在非基变量的检验数小于0,所以不是最优解,需调整 调整为: 重新计算检验数 所有的检验数都大于等于0,所以得到最优解 3、某公司要把4个有关能源工程项目承包给4个互不相关的外商投标者,规定每个承包商只能且必须承包一个项目,试在总费用最小的条件下确定各个项目的承包者,总费用为多少?各承包商对工程的报价如表2所示: (15分) 项目 投标者 A B C D 甲 15 18 21 24 乙 19 23 22 18 丙 26 17 16 19 丁 19 21 23 17 答最优解为: X= 0 1 0 0 1 0 0 0 0 0 1 0 0 0 0 1 总费用为50 4. 考虑如下线性规划问题(24分) B 1 B 2 B 3 产量/t A 1 15 15 A 2 11 11 A 3 18 1 1 20 销量/t 18 12 16 B 1 B 2 B 3 产量/t A 1 5 13 0 15 A 2 -2 0 0 11 A 3 0 0 20 销量/t 18 12 16 B 1 B 2 B 3 产量/t A 1 15 15 A 2 11 11 A 3 7 12 1 20 销量/t 18 12 16 B 1 B 2 B 3 产量/t A 1 5 13 0 15 A 2 0 2 2 11 A 3 0 0 0 20 销量/t 18 12 16
·No .1 线性规划 1、某织带厂生产A 、B 两种纱线和C 、D 两种纱带,纱带由专门纱线加工而 工厂有供纺纱的总工时7200h ,织带的总工时1200h 。 (1) 列出线性规划模型,以便确定产品的数量使总利润最大; (2) 如果组织这次生产具有一次性的投入20万元,模型有什么变化?对模型 的解是否有影响? 解:(1)设A 的产量为x 1,B 的产量为x 2,C 的产量为x 3,D 的产量为x 4,则 有线性规划模型如下: max f (x )=(168-42)x 1 +(140-28)x 2 +(1050-350)x 3 +(406-140)x 4 =126 x 1 +112 x 2 +700 x 3 +266 x 4 s.t. ?? ? ??=≥≤+≤+++4,3,2,1 ,012005.02 720041023434321i x x x x x x x i (2)如果组织这次生产有一次性的投入20万元,由于与产品的生产量无关, 故上述模型只需要在目标函数中减去一个常数20万,因此可知对模型的解没有影响。 2、将下列线性规划化为极大化的标准形式 解:将约束条件中的第一行的右端项变为正值, 并添加松弛变量x 4,在第二行添加人工变量x 5,将第三行约束的绝对值号打开,变为两个不等式,分别添加松弛变量x 6, x 7,并令x x x 333='-'',则有 max[-f (x )]= {-2 x 1 -3 x 2 -5('-''x x 33 )+0 x 4 -M x 5+0 x 6 +0 x 7} s.t. 0,,,,,,,13 55719 13 55719 16 9976 5 7654332173321633 215332143321≥'''=+''+'-+-=+''-'+-=+''+'-+-=+''-'+--?? ?? ? ???? x x x x x x x x x x x x x x x x x x x x x x x x x x x x ?????? ?±≥≤+-=-+--≥-+++=不限3213213213213 21 ,0,13|5719|169765 ..532)(m in x x x x x x x x x x x x t s x x x x f
第一章线性规划1、 由图可得:最优解为 2、用图解法求解线性规划: Min z=2x1+x2 ? ? ? ? ? ? ? ≥ ≤ ≤ ≥ + ≤ + - 10 5 8 24 4 2 1 2 1 2 1 x x x x x x 解: 由图可得:最优解x=1.6,y=6.4
Max z=5x 1+6x 2 ? ?? ??≥≤+-≥-0 ,23222212 121x x x x x x 解: 由图可得:最优解Max z=5x 1+6x 2, Max z= + ∞
Maxz = 2x 1 +x 2 ????? ? ?≥≤+≤+≤0,5242261552121211x x x x x x x 由图可得:最大值?????==+35121x x x , 所以?????==2 3 21x x max Z = 8.
12 12125.max 2328416412 0,1,2maxZ .j Z x x x x x x x j =+?+≤? ≤?? ≤??≥=?如图所示,在(4,2)这一点达到最大值为2 6将线性规划模型化成标准形式: Min z=x 1-2x 2+3x 3 ????? ??≥≥-=++-≥+-≤++无约束 321 321321321,0,05232 7x x x x x x x x x x x x 解:令Z ’=-Z,引进松弛变量x 4≥0,引入剩余变量x 5≥0,并令x 3=x 3’-x 3’’,其中x 3’≥ 0,x 3’’≥0 Max z ’=-x 1+2x 2-3x 3’+3x 3’’ ????? ? ?≥≥≥≥≥≥-=++-=--+-=+-++0 ,0,0'',0',0,05 232 '''7'''543321 3215332143321x x x x x x x x x x x x x x x x x x x
3)若问题中 x2 列的系数变为(3,2)T,问最优解是否有变化; 4)c2 由 1 变为 2,是否影响最优解,如有影响,将新的解求出。 Cj CB 0 0 Cj-Zj 0 4 Cj-Zj 3 4 Cj-Zj 最优解为 X1=1/3,X3=7/5,Z=33/5 2对偶问题为Minw=9y1+8y2 6y1+3y2≥3 3y1+4y2≥1 5y1+5y2≥4 y1,y2≥0 对偶问题最优解为 y1=1/5,y2=3/5 3 若问题中 x2 列的系数变为(3,2)T 则P2’=(1/3,1/5σ2=-4/5<0 所以对最优解没有影响 4)c2 由 1 变为2 σ2=-1<0 所以对最优解没有影响 7. 求如图所示的网络的最大流和最小截集(割集,每弧旁的数字是(cij , fij )。(10 分) V1 (9,5 (4,4 V3 (6,3 T 3 XB X4 X5 b 9 8 X1 6 3 3 X4 X3 1 8/5 3 3/5 3/5 X1 X3 1/3 7/5 1 0 0 1 X2 3 4 1 -1 4/5 -11/5 -1/3 1 - 2 4 X 3 5 5 4 0 1 0 0 1 0 0 X4 1 0 0 1 0 0 1/3 -1/ 5 -1/5 0 X5 0 1 0 -1 1/5 -4/5 -1/3 2/5 -3/5 VS (3,1 (3,0 (4,1 Vt (5,3 V2 解: (5,4 (7,5 V4 V1 (9,7 (4,4 V3 (6,4 (3,2 Vs (5,4 (4,0 Vt (7,7 6/9 V2 最大流=11 (5,5 V4 8. 某厂Ⅰ、Ⅱ、Ⅲ三种产品分别经过 A、B、C 三种设备加工。已知生产单位各种产品所需的设备台时,设备的现有加工能力及每件产品的预期利润见表:ⅠⅡⅢ设备能力(台.h A 1 1 1 100 B 10 4 5 600 C 2 2 6 300 单
(一)线性规划建模与求解 B.样题:活力公司准备在5小时内生产甲、乙两种产品。甲、乙两种产品每生产1 单位分别消耗2小时、1小时。又根据市场需求信息,乙产品的产量应该至少是甲产品产量的3倍。已知甲、乙两种产品每销售1单位的利润分别为3百元和1百元。请问:在5小时内,甲、乙两种产品各生产多少单位,才能够使得总销售利润最大? 要求:1、建立该问题的线性规划模型。 2、用图解法求出最优解和最大销售利润值,并写出解的判断依据。如果不存在最优解,也请说明理由。 解:1、(1)设定决策变量: 设甲、乙两种产品分别生产x 1 、x 2 单位 。 (2)目标函数: max z=2 x 1+x 2 (3)约束条件如下:1221 12 25..3,0+≤??≥??≥?x x s t x x x x 2、该问题中约束条件、目标函数、可行域和顶点见图1所示,其中可行域用阴影部分标记,不等式约束条件及变量约束要标出成立的方向,目标函数只须画出其中一条等值线, 结论:本题解的情形是: 无穷多最优解 ,理由: 目标函数等值线z=2 x 1 +x 2 与 约束条件2 x 1+x 2≤5的边界平行 。甲、乙两种产品的最优产量分别为 (5,0)或(1,3)单位;最大销售利润值等于 5 百元。 (二)图论问题的建模与求解样题 A.正考样题(最短路问题的建模与求解,清华运筹学教材编写组第三版267-268页例 13)某企业使用一台设备,每年年初,企业都要做出决定,如果继续使用旧的,要付维修费;若购买一台新设备,要付购买费。但是变卖旧设备可以获得残值收入,连续使用1年、2年、3年、4年以上卖掉的设备残值分别为8万元、6万元、3万元和0万元。试制定一个5年的更新计划,使总支出最少。已知设备在各年的购买费与维修费如表2所示。要求:(1)建立某种图论模型;(2)求出最少总支出金额。
参考书 1.《运筹学》(科学版精品课程立体化教材·管理学系列)(第2版),张伯生等编著,科学出版社,2012年; 2.《数据、模型与决策》(第13版),戴维·R·安德森/丹尼斯·J·斯威尼编著,于淼译,机械出版社,2012年; 3、《运筹学》(新体系经济管理系列教材),李成标,刘新卫主编,清华大学出版社,2012年; 4.《运筹学——优化模型与算法》,(美)拉丁(Rardin,R.L.) 著,电子工业出版社,2007年 5.《Introduction to Operations Research》(第6 版)(外原版经典教材), F. S. Hillier and G. J. Lieberman 著,McGraw-Hill 出版社; 6. 《运筹学》,党耀国,李帮义等编著,科学出版社,2009年; 7. 《物流运筹学》,刘蓉主编,电子工业出版社,2012年; 8. 《运筹学导论》(第9版)(美国麦格劳-希尔教育出版公司工商管理最新教材(英文版)),(美)希利尔,(美)利伯曼著,清华大学出版社,2010年; 9. 《运筹学》(第4版)(面向21世纪课程教材(信息管理与信息系统专业教材系列),《运筹学》教材编写组编,清华大学出版社,2012年; 10.《运筹学:应用与解决方法》(第4版)(美国商学院原版教材精选系列),(美)温斯顿著,清华大学出版社,2011年; 11.《管理运筹学》(高等学校经济与工商管理系列教材),茹少峰,申卯兴编著,清华大学出版社,2008年; 12.《运筹学》(第3版),刁在筠等编,高等教育出版社,2007年;
13.《实用运筹学:模型、方法与计算》,韩中庚主编,清华大学出版社,2007年; 14.《运筹学》(现代信息管理与信息系统系列教材),李红艳,范君晖主编,清华大学出版社,2012 年; 15.《管理运筹学:管理科学方法》(21世纪管理科学与工程系列教材),谢家平著,中国人民大学出版社,2010年; 16.《运筹学与实验》,薛毅,耿美英编著,电子工业出版社,2008年; 17.《实用运筹学——上机实验指导及习题解答》,叶向编,中国人民大学出版社,2007年; 18.《应用运筹学》(第二版),曹勇,周晓光,李宗元编著,经济管理出版社,2008年; 19.《运筹学导论》(第8版),(美)希利尔(Hillier,F.S.),(美)利伯曼(Lieberman,G.J.)著,胡运权等译,清华大学出版社,2007年; 20.《经济管理运筹学习题集》,王玉梅,孙在东,张志耀编著,中国标准出版社,2012年; 21.《运筹学习题集》(第4版),胡运权主编,清华大学出版社,2010年; 22.《运筹学解题指导》,周华任主编,清华大学出版社,2006年; 23.《运筹学概率模型应用范例与解法》(第4版),(美)温斯顿(Winston,W.L.)著,李乃文等译,清华大学出版社,2006年; 24.《运筹学学习辅导与习题解析》(第3版),戎晓霞,宿洁,刘桂真编,高等教育出版社,2009年; 25.《管理运筹学习题集》(普通高等学校管理科学与工程类学科核心课程教材辅
运筹学课后习题答案__林齐宁版本__北邮出版社运筹学作业标准答案 (教师用) ?No.1 线性规划 1 1、某织带厂生产A、B两种纱线和C、D两种纱带,纱带由专门纱线加工而成。这四种产品的产值、成本、加工工时等资料列表如下: 工厂有供纺纱的总工时7200h,织带的总工时1200h。 (1) 列出线性规划模型,以便确定产品的数量使总利润最大; (2) 如果组织这次生产具有一次性的投入20万元,模型有什么变化,对模型 的解是否有影响, 解:(1)设A的产量为x1,B的产量为x2,C的产量为x3,D的产量为x4,则有线性规划模型如下: =126 x1 +112 x2 +700 x3 +266 x4 (2)如果组织这次生产有一次性的投入20万元,由于与产品的生产量无关, 故上述模型只需要在目标函数中减去一个常数20万,因此可知对模型的解没有影响。 2、将下列线性规划化为极大化的标准形式 解:将约束条件中的第一行的右端项变为正值,并添加松弛变量x4,在第二行添加人工变量x5,
将第三行约束的绝对值号打开,变为两个不等式, 分别添加松弛变量x6, x7,并令,则 不限 有 12337 运筹学作业标准答案 (教师用) 3、用单纯形法解下面的线性规划
2 解:在约束行1,2,3分别添加x4, x5, x6松弛变量,有初始基础可行解和单纯形法迭代步骤如下: 答:最优解为x1 =244.375, x2 =0, x3 =123.125, 剩余变量x6 =847.1875;最优解 的目标函数值为858.125。 运筹学作业标准答案 (教师用) No.2 两阶段法和大M法 1、用两阶段法解下面问题: 3 解:将原问题变为第一阶段的标准型 第二阶段 答:最优解为x1 =14,x2 =33,目标函数值为254。
第14章对策论基础 14.1 复习笔记 1.对策行为和对策论 对策行为:具有竞争或对抗性质的行为称为对策行为。 对策论:亦称竞赛论或博弈论,是研究具有斗争或竞争性质现象的数学理论和方法。 2.对策行为的三个基本要素 局中人:一局对策中,有权决定自己行动方案的对策参加者,称为局中人。通常用表 I 示局中人的集合,一般要求一个对策中至少要有两个局中人。 策略集:一局对策中,可供局中人选择的一个实际可行的完整的行动方案称为一个策略。参加对策的每一局中人,都有自己的策略集。一般,每一局中人的策略集中至少应包括两个策略。 赢得函数(支付函数):在一局对策中,各局中人选定的策略形成的策略组称为一个局势。对任一局势,局中人可以得到一个赢得值。显然,是局势的函数,称为第个局中人的赢得函数。 3.对策的分类 (1)根据局中人的个数,分为二人对策和多人对策;
(2)根据各局中人的赢得函数的代数和是否为零,分为零和对策与非零和对策; (3)根据各局中人间是否允许合作,分为合作对策和非合作对策; (4)根据局中人的策略集中的策略个数,分为有限对策和无限对策。 此外,还有许多其他的分类方式。例如根据策略的选择是否与时间有关,可分为静态对策和动态对策;根据对策模型的数学特征,可分为矩阵对策、连续对策、微分对策、阵地对策、凸对策、随机对策等。 4.矩阵对策的数学模型 对策的局中人,每个局中人都只有有限个策略可供选择。在任一局势下,两个局中人的赢得之和总是等于零,即双方的利益是激烈对抗的。 在矩阵对策中,一般用Ⅰ、Ⅱ分别表示两个局中人,并设局中人Ⅰ有m个纯策略,局中人Ⅱ有n个纯策略,则局中人Ⅰ、Ⅱ的策略集分别为 对任一纯局势,记局中人Ⅰ的赢得值为,并称 为局中人Ⅰ的赢得矩阵(或为局中人Ⅱ的支付矩阵)。 5.矩阵对策的定义、定理 定义1 设为矩阵对策。其中 ,,
第一章 线性规划及单纯形法 1.用X j (j=1.2…5)分别代表5中饲料的采购数,线性规划模型: 12345123412341234min 0.20.70.40.30.8.3267000.50.2300.20.8100 (1,2,3,4,5,6)0 j z x x x x x st x x x x x x x x x x x x x x x x j =+++++++≥+++≥+++≥=≥555 +18 +2 0.5+2 2.解:设123456x x x x x x x 表示在第i 个时期初开始工作的护士人数,z 表示所需的总人数,则 123456 161223344556min .607060502030 (1,2.3.4.5.6)0i z x x x x x x st x x x x x x x x x x x x x i =++++++≥+≥+≥+≥+≥+≥=≥ 3.解:设用i=1,2,3分别表示商品A ,B ,C ,j=1,2,3分别代表前,中,后舱,Xij 表示装于j 舱的i 种商品的数量,Z 表示总运费收入则: 111213212223313233111213212223313233112131122232132333112131max 1000()700()600() .6001000800105740010575400105715008652000z x x x x x x x x x st x x x x x x x x x x x x x x x x x x x x x =++++++++++≤++≤++≤++≤++≤++≤++≤ 122232132333112131122232132333 122232112131 132333865300086515008650.15 8658650.15 8658650.1 8650(1,2.3.1,2,3)ij x x x x x x x x x x x x x x x x x x x x x x x x x i j ++≤++≤++≤++++≤++++≤++≥== 5. (1)
第3章 运输问题 3.1 判断表3-l 和表3-2中给出的调运方案能否作为用表上作业法求解时的初始解?为什么? 表3-1 表3-2 解:表3-l 中有5个基格,而要作为初始解,应有m+n-l=3+4-1=6个基格,所以表3-l 给出的调运方案不能作为表上作业法的初始解; 表3-2中,有10个数基格,而理论上只应有m+n-l=9个,多出了一个,所以表3-2给出的调运方案不能作为表上作业法的初始解。 3.2 表3-3和表3-4中,分别给出两个运输问题的产销平衡表和单位运价表,试用伏格尔(Vogel)法直接给出近似最优解。 表3-3 表3-4
解:(1)第一步:在表3-3中分别求各行和各列的最小运价和次小运价的差额,并分别填入该表的最右列和最下行,如表3-5所示。 表3-5 第二步:从行差额或列差额中选出最大者,选择它所在行或列中的最小元素。在表3-5中,第3列是最大差额所在列。第3列中最小元素为1,可确定产地2的产品优先供应销地3的需要,得表3-6。同时将运价表中的第3列数字划去,如表3-7所示。 表3-6 表3-7
第三步:对表3-7中未划去的元素再分别计算出各行、各列的最小运价和次小运价的差额,并填入该表的最右列和最下行。重复第一、二步,直到给出初始解为止,初始解如表3-8所示。 表3-8 (2)第一步:在表3-4中分别计算各行和各列的最小运价和次小运价的差额,并分别填入该表的最右列和最下行,如表3-9所示。 表3-9 第二步:从行或列差额中选出最大者,选择它所在行或列中的最小元素。在表3-9中第3列是最大差额所在列。第3列中最小元素为3,可确定产地1的产品优先供应销地3的需要。同时将运价表中的第1行数字划去,如表3-10所示。 表3-10
运筹学例题及解答 一、市场对I、II两种产品的需求量为:产品I在1-4月每月需10000件,5-9月每月需30000件,10-12月每月需100000件;产品II在3-9月每月需15000件,其它月份每月需50000件。某厂生产这两种产品成本为:产品I在1-5月内生产每件5元,6-12月内生产每件4.50元;产品II在1-5月内生产每件8元,6-12月内生产每件7元。该厂每月生产两种产品能力总和应不超过120000件。产品I容积每件0.2立方米,产品II容积每件0.4立方米,而该厂仓库容积为15000立方米,要求:(a)说明上述问题无可行解;(b)若该厂仓库不足时,可从外厂借。若占用本厂每月每平方米库容需1元,而租用外厂仓库时上述费用增加为1.5元,试问在满足市场需求情况下,该厂应如何安排生产,使总的生产加库存费用为最少。 解:(a) 10-12月份需求总计:100000X3+50000X3=450000件,这三个月最多生产120000X3=360000件,所以10月初需要(450000-360000=90000件)的库存,超过该厂最大库存容量,所以无解。 ? ?(b)考虑到生产成本,库存费用和生产费用和生产能力,该厂10-12月份需求的不足只需在7-9月份生产出来库存就行, 则设xi第i个月生产的产品1的数量,yi第i个月生产的产品2 的数量,zi,wi分别为第i个月末1,2的库存数s1i,s2i分别
为用于第i+1个月库存的原有及租借的仓库容量m3,可建立模型: Lingo 程序为 MODEL: sets: row/1..16/:; !这里n 为控制参数; col/1..7/:; AZ(row,col):b,x; endsets 1211 127777778 7887898998910910109101110111110111211min (4.57)( 1.5) 30000150003000015000300001500030000150003000015000.i i i i i i z x y s s x z y w x z z y w w x z z y w w x z z y w w x z z y w w st x z ===+++-=→-=+-=→+-=+-=→+-=+-=→+-=+-=→+-=+∑∑1211121100005000 120000(712)0.20.415000(712)0i i i i i i i y w x z i z w s s s i ?????????=→+=??+≤≤≤?+=+??≤≤≤???变量都大于等于
运筹学部分课后习题解答P47 1.1 用图解法求解线性规划问题 a) 12 12 12 12 min z=23 466 ..424 ,0 x x x x s t x x x x + +≥ ? ? +≥ ? ?≥ ? 解:由图1可知,该问题的可行域为凸集MABCN,且可知线段BA上的点都为 最优解,即该问题有无穷多最优解,这时的最优值为 min 3 z=2303 2 ?+?= P47 1.3 用图解法和单纯形法求解线性规划问题 a) 12 12 12 12 max z=10x5x 349 ..528 ,0 x x s t x x x x + +≤ ? ? +≤ ? ?≥ ? 解:由图1可知,该问题的可行域为凸集OABCO,且可知B点为最优值点, 即 1 12 122 1 349 3 528 2 x x x x x x = ? += ?? ? ?? +== ?? ? ,即最优解为* 3 1, 2 T x ?? = ? ?? 这时的最优值为 max 335 z=1015 22 ?+?=
单纯形法: 原问题化成标准型为 121231241234 max z=10x 5x 349 ..528,,,0x x x s t x x x x x x x +++=?? ++=??≥? j c → 10 5 B C B X b 1x 2x 3x 4x 0 3x 9 3 4 1 0 0 4x 8 [5] 2 0 1 j j C Z - 10 5 0 0 0 3x 21/5 0 [14/5] 1 -3/5 10 1x 8/5 1 2/5 0 1/5 j j C Z - 1 0 - 2 5 2x 3/2 0 1 5/14 -3/14 10 1x 1 1 0 -1/7 2/7 j j C Z - -5/14 -25/14
《物流运筹学》教案 课程名称:物流运筹学 适用专业:物流管理 规定学时:32学时,2学分 开课学期:三年级上学期 任课教师:王金红 《物流运筹学》教案 一、课程说明 《物流运筹学》运筹学是经管类专业本、专科生的主干课、学位课。通过本书学习要求学生掌握线性规划、整数规划、目标规划、图与网络分析、动态规划、存储论、排队论、决策论、博弈论的基本理论及方法,通过案例分析,要求学生学会建模的方法,能用各类模型的建立解决在经济管理中出现的各类问题。 二、教学内容 《物流运筹学》是物流管理专业的专业方向课程,教材涵盖了线性规划、整数规划、目标规划、图与网络分析、动态规划、存储论、排队论、决策论、博弈论的基本理论及方法,讨论了目标规划、图与网络分析在物流中的主要应用领域,探讨了利用线性规划、整数规划、目标规划、图与网络分析、动态规划、存储论、排队论、决策论、博弈论的基本理论及方法解决物流活动中的问题,并对物流运输路线安排、物资调配等专题进行了剖析。 三、本课程的教案主要包括下列教学活动形式
1、本章的教学目标及基本要求 2、本章各节教学内容 3、教学重点与难点 4、本章教学内容的深化和拓宽 5、本章教学方式(手段)及教学过程中应注意的问题 6、本章的主要参考书目 7、本章的思考题和习题 8、教学进程 四、课程教学的基本要求 本课程的教学环节包括:课堂讲授、习题课、课外作业。通过本课程各个教学环节的教学,重点培养学生的学习能力、分析问题解决问题的能力。 (一)课堂讲授 主要教学方法:主要采用教师课堂讲授为主,增加讨论课和习题课,调动学生学习的主观能动性。 (二)习题 习题是本课程的重要教学环节,通过习题巩固讲授过的基本理论知识,培养学生自学能力和分析问题解决问题的能力。 习题课:安排每章后。
线性规划习 题 一 1.1试述LP 模型的要素、组成部分及特征。判断下述模型是否LP 模型并简述理由。(式中x,y 为变量;θ为参数;a,b,c,d,e 为常数。) (1)max z=2x 1-x 2-3x 3 s.t.123123123121 35824350,0 x x x x x x x x x x x ++=??-+≤??-+≥??≥≤? (2)min z= 1 n k k kx =∏ s.t. 1 ,1,2...,0,1,2...,n ik k i k k a x b i m x k m =?≥=???≥=?∑ (3)min z= 1 1 n n i i j j i j a x b y ==+∑∑ s.t. ,1,2,...,,1,2,...i i j j i i ij x c i m y d j n x y e ?≤=? ≤=?? +≥? (4)max z= 1 n j j j c x =∑ s.t. 1 ,1,2,...,0,1,2,...n ij j i i j j a x b d i m x j n θ=?≤+=???≥=?∑ 1.2试建立下列问题的数学模型: (1)设备配购问题 某农场要购买一批拖拉机以完成每年三季的工作量:春种330公顷,夏管130公顷,秋收470公顷。可供选择的拖拉机型号、单台投资额及工作能力如下表所示。 问配购哪几种拖拉机各几台,才能完成上述每年工作量且使总投资最小? (2)物资调运问题
甲乙两煤矿供给A,B,C三个城市的用煤。各矿产量和各市需求如下表所示: 各矿与各市之间的运输价格如下表示: 问应如何调运,才能既满足城市用煤需求,又使运输的总费用最少? (3)食谱问题 某疗养院营养师要为某类病人拟订本周菜单。可供选择的蔬菜及其费用和所含营养成分的数量,以及这类病人每周所需各种养分的最低数量如下表所示: 另外为了口味的需求,规定一周内所用的卷心菜不多于2份,其它蔬菜不多于4份。若病人每周需14份蔬菜,问选用每种蔬菜各多少份? (4)下料问题 某钢筋车间要用一批长度为10米的钢筋下料制作长度为三米的钢筋90根和长度为四米的钢筋60根,问怎样下料最省? 用图解法求解下列LP问题: (1)min z=6x1+4x2 s.t. 12 12 12 21 34 1.5 0,0 x x x x x x +≥ ? ? +≥ ? ?≥≥ ? (2) max z=2.5x1+x2 s.t. 12 12 12 3515 5210 0,0 x x x x x x +≤? ? +≤? ?≥≥?
答案课后习题运筹学基础] [2002年版新教材 P5 导论第一章区别决策中的定性分析和定量分析,试举例。、1.——经验或单凭个人的判断就可解决时,定性方法定性(如果或者是如此重要而复杂,以致需要全面分析定量——对需要解决的问题没有经验时;用计量过时,或者发生的问题可能是重复的和简单的,涉及到大量的金钱或复杂的变量组)程可以节约企业的领导时间时,对这类情况就要使用这种方法。。举例:免了吧。。?、. 构成运筹学的科学方法论的六个步骤是哪些2观察待决策问题所处的环境;. 分析和定义待决策的问题;. 拟定模型;. 选择输入资料;. ;.提出解并验证它的合理性(注意敏感度试验)实施最优解;. :3、.运筹学定义其目的是通过定量把复杂功能关系表示成数学 模型,利用计划方法和有关许多学科的要求,分析为决策和揭露新问题提供数量根据P25 预测第二章作业 为了对商品的价格作出较正确的预测,为什么必须做到定量与定性预测的结合?即使. 1、在定量预测法诸如加权移动平均数法、指数平滑预测法中,关于权数以及平滑系数的确定,?是否也带有定性的成分使决策者能够做到心中有数。但单靠定量)定量预测常常为决策提供了坚实的基础,(1答:调查有些因素难以预料。预测有时会导致偏差,因为市场千变万化,影响价格的因素很多,所以还需要定原始数据不一定充分,所用的模型也往往过于简化,研究也会有相对局限性,)加权移(2性预测,在缺少数据或社会经济环境发生剧烈变化时,就只能用定性预测了。动平均数法中权数的确定有定性的成分;指数平滑预测中的平滑系数的确定有定性的成分。 ,试用指数平滑法,取平滑5 个年度的大米销售量的实际值(见下表)2.、某地区积累了4181.96年度的大米销售量(第一个年度的预测值,根据专家估计为= 0.9,预测第系数α千公斤) 年度 1 2 3 4 5 大米销售量实际值 (千公斤)5202 5079 3937 4453 3979 。 答: F6=a*x5+a(1-a)*x4+a(1-a)~2*x3+a(1-a)~3*x2+a(1-a)~4*F1 F6=0.9*3979+0.9*0.1*4453+0.9*0.01*3937+0.9*0.001*5079+0.9*0.0001*4181.9
《运筹学》期末考试试卷(A) 学院班级姓名学号 考生注意∶ 1.本试题共七题,共 3 页,请考生认真检查; 一、某炼油厂生产三种牌号的汽油,70#,80#和85#汽油。每种汽油有不同的辛烷值和含硫量的质量要求并由三种原料油调和而成。每种原料也有不同的质量指标。每种原料每日可用数量、质量指标和生产成本见表1,每种汽油的质量要求和销售价格见表2。问该炼油厂如何安排生产才能使其利润最大?假定在调和中辛烷值和含硫量指标都符合线性相加关系。试建立数学模型。(25分) 二、用对偶单纯形法求解下列线性规划问题:(25分)
????? ??0 ,,9645252max 32132323212 1≥≥+≤+=+++=x x x x x x x x x x x x z 三、已知某运输问题的产销平衡表与单位运价表如下表所示,B 2地区需要的115单位必 四、从甲, 乙, 丙, 丁, 戊五人中挑选四人去完成四项工作,已知每人完成各项工作的时间如下表所示。规定每项工作只能由一个人去单独完成,每个人最多承担一项工作,假定甲必须保证分配到工作,丁因某种原因不同意承担第四项工作。在满足上述条件下,如何分配工作,使完成四项工作总的花费时间最少。(20分) 五、求V 1到各点的最短路及最短路径。(20分)
v 1 v 2 v 3 v 6 v 4 v 7 v 5 911 10 11 11 11 10 8 4 六、某公司有资金4百万元向A ,B ,C 三个项目追加投资,各个项目可以有不同的投资额(以百万元为单位),相应的效益值如下表。问怎样分派资金,使总效益值最大,试用动态规划方法求解。(25分) 七、用单纯形法解线性规划问题,如何判断下列问题:(15分) 1. 无可行解; 2. 有多重解; 3. 有无界解。 试卷(A)参考答案 一、 解:设代表第i 种原料混入第j 种产品中的数量,其中i=1,2,3;j=1,2,3;则
《管理运筹学》(第二版)课后习题参考答案 第1章线性规划(复习思考题) 1.什么是线性规划?线性规划的三要素是什么? 答:线性规划(Lin ear Programmi ng, LP )是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。 建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。 2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误? 答:(1)唯一最优解:只有一个最优点; (2)多重最优解:无穷多个最优解; (3)无界解:可行域无界,目标值无限增大; (4)没有可行解:线性规划问题的可行域是空集。 当无界解和没有可行解时,可能是建模时有错。 3.什么是线性规划的标准型?松弛变量和剩余变量的管理含义是什么? 答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项b i 0, 决策变量满足非负性。 如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“2型约束的左边取值大于右边规划值,出现剩余量。 4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。 答:可行解:满足约束条件AX b,X 0的解,称为可行解。 基可行解:满足非负性约束的基解,称为基可行解 可行基:对应于基可行解的基,称为可行基。 最优解:使目标函数最优的可行解,称为最优解。 最优基:最优解对应的基矩阵,称为最优基。 它们的相互关系如右图所示:
运筹学习题库 数学建模题(5) 1、某厂生产甲、乙两种产品,这两种产品均需要A 、B 、C 三种资源,每种产品的资源消耗量及单位产品销售后所能获得的利润值以及这三种资源的储备如下表所示: 试建立使得该厂能获得最大利润的生产计划的线性规划模型,不求解。 解:设甲、乙产品的生产数量应为x1、x2,则x1、x2≥0,设z 是产品售后的总利润,则 max z =70x 1+120x 2 s.t. ????? ??≥≤+≤ +≤+0 300103200643604921212121x x x x x x x x , 2建立使利润最大的生产计划的数学模型,不求解。 解:设甲、乙两种产品的生产数量为x 1、x 2, 设z 为产品售后总利润,则max z = 4x 1+3x 2 s.t. ???????≥≤≤+≤+ ,50040005.253000222112121x x x x x x x 3、一家工厂制造甲、乙、丙三种产品,需要三种资源——技术服务、劳动力和行政管理。每种产品的资源消耗量、单位产品销售后所能获得的利润值以及这三种资源的储备量如下表所示:
建立使得该厂能获得最大利润的生产计划的线性规划模型,不求解。 解:建立线性规划数学模型: 设甲、乙、丙三种产品的生产数量应为x 1、x 2、x 3,则x 1、x 2、x 3≥0,设z 是产品售后的总利润,则 max z =10x 1+6x 2+4x 3 s.t. ???????≥≤++≤++≤++0 3006226005410100321321321321x x x x x x x x x x x x ,, 4、一个登山队员,他需要携带的物品有:食品、氧气、冰镐、绳索、帐篷、照相器材、通 信器材等。每种物品的重量合重要性系数如表所示。设登山队员可携带的最大重量为25kg,试建立队员所能携带物品最大量的线性规划模型,不求解。 解:引入0—1变量x i , x i =1表示应携带物品i ,,x i =0表示不应携带物品I ?? ?==≤++++++++++++=7 ,...,2,1,10254212625510481418152076543217654321i x x x x x x x x x x x x x x x naxz i 或 5、工厂每月生产A 、B 、C 三种产品,单件产品的原材料消耗量、设备台时的消耗量、资源根据市场需求,预测三种产品最低月需求量分别是150、260、120,最高需求量是250、310、130,试建立该问题数学模型,使每月利润最大,为求解。 解:设每月生产A 、B 、C 数量为321,,x x x 。 321121410x x x MaxZ ++= 250042.15.321≤++x x x 产 品 资 源