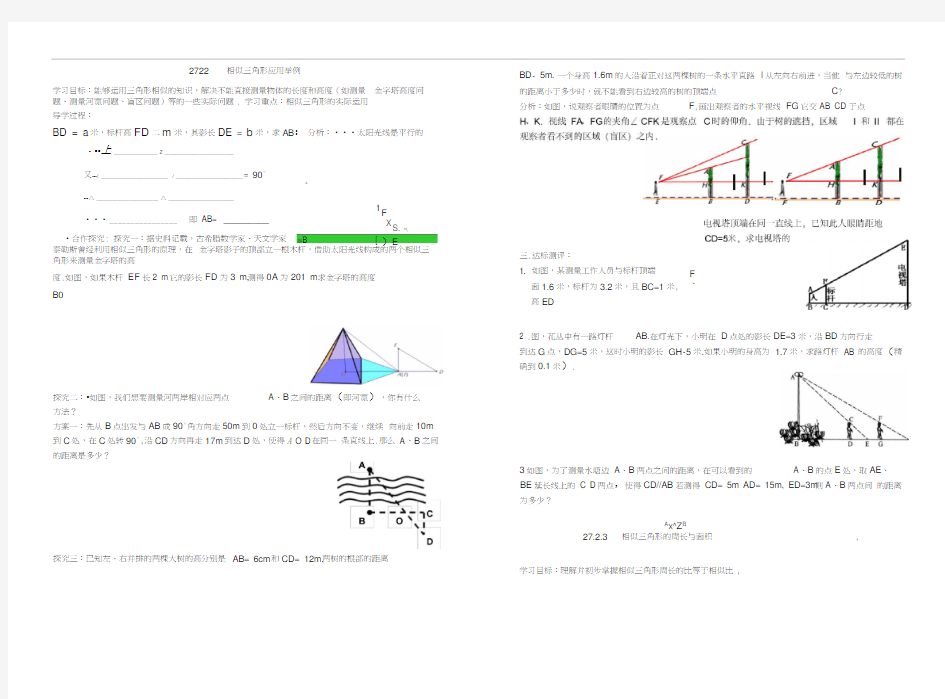
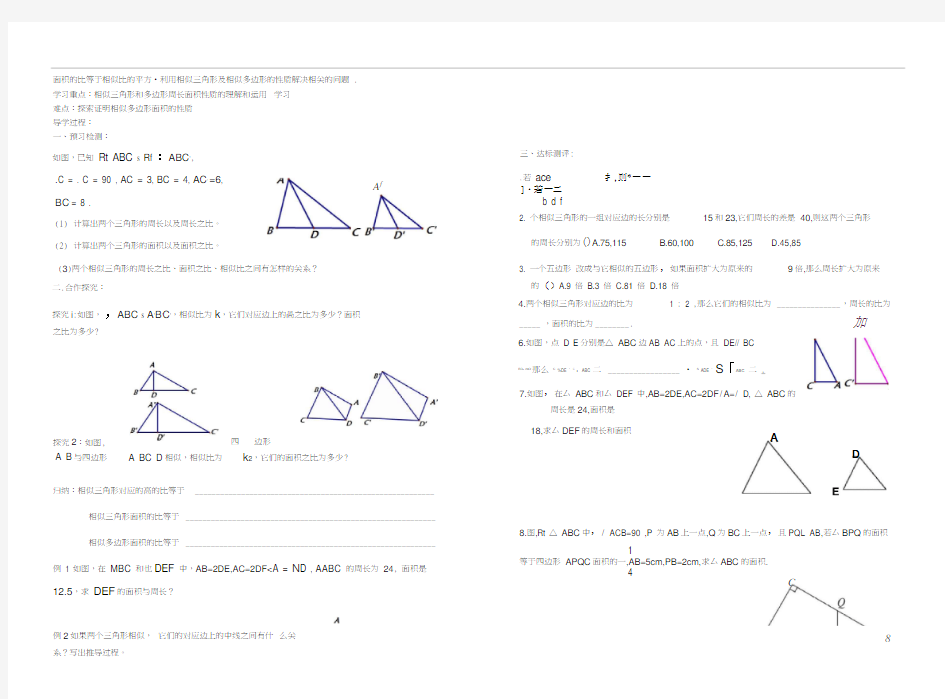
12.5,求DEF的面积与周长?
例2如果两个三角形相似,它们的对应边上的中线之间有什么关
系?写出推导过程。
4.两个相似三角形对应边的比为 1 : 2 ,那么它们的相似比为_______________ ,周长的比为
_____ ,面积的比为________ .加
6.如图,点D E分别是△ ABC边AB AC上的点,且DE// BC
BD= 2AD那么C %DE : C:ABC 二_________________ ? S ADE :
S「ABC二 .
7.如图,在厶ABC和厶DEF 中,AB=2DE,AC=2DF/A=/ D, △ ABC的
周长是24,面积是
18,求厶DEF的周长和面积
A
D
8.图,Rt △ ABC中,/ ACB=90 ,P 为AB上一点,Q为BC上一点,且PQL AB,若厶BPQ的面积
1
等于四边形APQC面积的一,AB=5cm,PB=2cm,求厶ABC的面积.
4
C
8
27.3位似-1
学习目标:了解位似图形及其有关概念,了解位似与相似的联系和区别,掌握位
似图形的性质.掌握位似图形的画法, 能够利用作位似图形的方法将一个图形 放大或缩小.
学习重点:位似图形的定义及与相似的关系 学习难点:位似图形的准确作图,动手能力的落实 一、预习检测:
图中多边形相似吗?观察下面的四个图,你发现每个图中的两个多边形各对应点 的连线有什么特征?
(1) __________________________________ 位似图形:如果两个多边形不仅 _______ ,而且对
应顶点的连线 _______________________________ ,对应
边 _______ 或 _______________________ ,那么这样的两个图形叫做位似图形,这个点叫 做 _____________ ,这时的相似比又称为 _____________ .
(2) 掌握位似图形概念,需注意:
① 位似是一种具有位置关系的相似,所以两个图形是位似图形,必定是 ___ 图形,
而相似图形不- -定是 _ ________ 图形; ② 两个位似图形的位似中心只有一个;
③ 两个位似图形可能位于位似中心的两侧,也可能位于位似中心的一侧; ④ 位似比就是相似比?利用位似图形的定义可判断两个图形是否位似.
2. 画出所给图中的位似中心.
二.达标检测:
1、 四边形ABCD 和四边形A1B1GD 是位似图形,位似中心是点 O,贝U 它们的对应点的连线
一定经过 _______________ 。
2、 四边形ABCD 和四边形AB1CD 是位似图形,点 O 是位似中心。如果 OA OA=1:3,那
么 AB: AB 1=
(3)位似图形上任意一对对应点到位似中心的距离等于 3、如果四边形 ABCD 与四边形 EFGH 是位似图形,且位似比为
a ,下列说法正确的是
(4)两个位似图形的主要特征是:每对位似对应点与位似中心共线;不经过位似中心的 对应线段平行. 二.合作探究:
探究1:如图,点0是厶ABC 外的一点,分别在射线 0A 、OB 、0C 上取一点 D 、E 、 F , 使得 _________ 。①△ ABC^A EFG ②
AC BD AB BC CD DA
a ③
a 。
EG FH
EF FG GH HE
0D 0E OF OA OB OC =3,连接 DE EF 、FD,所得△ DEF
与厶ABC 是否相似?证明你的结论。
O
F
E
4、如果正五边形 FGHM 是由正五边形ABCDEg 过位似变换得到的,若
F 列结论正确的是() A 、2DE=3MN
B 、3DE=2MN
C 、3/A=2Z F
D 、2 /A=3/F
AB: FG=2 3,贝U
1
探究2:把图中的四边形 ABCD 缩小到原来的一.
2
四、课堂检测(当堂训练)
1、如图,以O 为位似中心,将 ABC 放大为原来的两倍。
D
27.3位似-2
学习目标:掌握位似图形在直角坐标系下的点的坐标的变化规律,能利用直角坐标系下位似图
形对应点坐标变化的规律来解决问题
学习重点:用图形坐标的变化来表示图形的位似变化
学习难点:把一个图形按一定比例放大或缩小后,点的坐标的变化规律导学过程:
一、预习检测:
2.如图,△ ABC与△ A B C是位似图形,且顶点都在格点上,则位似中心的坐标是
3.如图,四边形ABCD和四边形A B' C D'位似,位似比人=2 ,四边形A ' B ' C' D'
和四边形A B〃C D'位似,位似比k2=1 ?四边形A〃B〃C〃D〃和四边形ABCD是位
在平面直角坐标系中有两点A(6,3),
把线段AB缩小
B( 6,0),以原点0为位似中心,相似比为1:3,
探究:(1)在方法一中,A'的坐标是,B'的坐标是,对应点坐标之
比是;(2)在方法
坐标之比是
二、合作探究案:
二中,A''的坐标是,B''的坐标是,对应点
如图,.'ABC三个顶点坐标分别为A 2,3 B 2,1 C 3,1,以点0为位似中心,相似
似图形吗?位似比是多少?
题图
4.如图表示厶AOB和把它缩小后得到的△ COD求△ COD和厶AOB的相似比.
比为2,将ABC放大,观察对应顶点坐标的变化,
你有什么发现?
位似变换后代B,C的对应点坐标为:
A' B' C'
归纳:在平面直角坐标系中,如果位似变换是以原点为位似中
心,相似比为k ,那么位似图形对应点的坐
标的比等于;
三、达标测评:
1.如图,在12X 12的正方形网格中,△ TAB的顶点坐标分别为
T (1, 1 )、A ( 2, 3)、B (4, 2).
(1 )以点T ( 1 , 1 )为位似中心,按比例尺TA':TA=3 : 1
在位似中心的同侧将△ TAB放大为△ TA' B',放大后点A、B的
对应点分别为A'、B'.画出厶TA' B',并写出点A'、B'的坐标;
(2)在(1)中,若C (a, b)为线段AB上任一点,写出变化后点
C的对应点C的坐标.
5.如图,△ ABC三个顶点坐标分别为A (2,—2) , B (4,—5) , C( 5,—1),以原点O 为位似中
心,将这个三角形放大为原来的2倍.
6.如图,△ ABC是格点三角形?在建立平面直角坐标系后,点B的坐标为(-1 , -1 ).
(1)把厶ABC向左平移5格后得到AA 1BG,则点B1的坐标为___________________
5 题图
6 题图
相似三角形全讲义(教师版)
相似三角形全讲义(教师版)
————————————————————————————————作者:————————————————————————————————日期:
相似三角形基本知识 知识点一:放缩与相似形 1.图形的放大或缩小,称为图形的放缩运动。 2.把形状相同的两个图形说成是相似的图形,或者就说是相似性。 注意:⑴相似图形强调图形形状相同,与它们的位置、颜色、大小无关。 ⑵相似图形不仅仅指平面图形,也包括立体图形相似的情况。 ⑶我们可以这样理解相似形:两个图形相似,其中一个图形可以看作是由另一个图形放大或缩小得到的. ⑷若两个图形形状与大小都相同,这时是相似图形的一种特例——全等形. 3.相似多边形的性质:如果两个多边形是相似形,那么这两个多边形的对应角相等,对应边的长度成比例。 注意:当两个相似的多边形是全等形时,他们的对应边的长度的比值是1. 知识点二:比例线段有关概念及性质 (1)有关概念 1、比:选用同一长度单位量得两条线段。a 、b 的长度分别是m 、n ,那么就说这两条线段 的比是a :b =m :n (或 n m b a =) 2、比的前项,比的后项:两条线段的比a :b 中。a 叫做比的前项,b 叫做比的后项。 说明:求两条线段的比时,对这两条线段要用同一单位长度。 3、比例:两个比相等的式子叫做比例,如 d c b a = 4、比例外项:在比例d c b a = (或a :b =c :d )中a 、d 叫做比例外项。 5、比例内项:在比例d c b a = (或a :b =c :d )中b 、c 叫做比例内项。 6、第四比例项:在比例d c b a = (或a :b =c :d )中,d 叫a 、b 、c 的第四比例项。 7、比例中项:如果比例中两个比例内项相等,即比例为 a b b a =(或a:b =b:c 时,我们把b 叫做a 和d 的比例中项。 8.比例线段:对于四条线段a 、b 、c 、d ,如果其中两条线段的长度的比与另两条线段的长度的比相等,即 d c b a =(或a :b= c : d ) ,那么,这四条线段叫做成比例线段,简称比例线段。(注意:在求线段比时,线段单位要统一,单位不统一应先化成同一单位)
《相似三角形的应用举例》中考真题
相似三角形的应用举例 1. (2011浙江金华,9,3分)如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为( ) A.600m B.500m C.400m D.300m 【答案】B 2. (2011浙江丽水,9,3分)如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直. 如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为( ) A.600m B.500m C.400m D.300m 【答案】B 3. (2011湖南怀化,21,10分)如图8,△ABC,是一张锐角三角形的硬纸片,AD 是边BC 上的高, B C=40cm,AD=30cm,从这张硬纸片上剪下一个长HG 是宽HE 的2倍的矩形EFGH ,使它的一边EF 在B C 上,顶点G 、H 分别在AC ,AB 上,A D 与HG 的交点为M. (1) 求证:;AM HG AD BC (2) 求这个矩形EFGH 的周长.
【答案】 (1) 解:∵四边形EFGH 为矩形 ∴EF∥GH ∴∠AHG=∠ABC 又∵∠HAG=∠BAC ∴ △AHG∽△ABC ∴ ;AM HG AD BC = (2)由(1)得 ;AM HG AD BC =设HE=x ,则HG=2x ,AM=AD-DM=AD-HE=30-x 可得40 23030x x =-,解得,x=12 , 2x=24 所以矩形EFGH 的周长为2×(12+24)=72cm. 4. (2011上海,25,14分)在Rt △ABC 中,∠ACB =90°,BC =30,AB =50.点P 是AB 边上任意一点,直线PE ⊥AB ,与边AC 或BC 相交于E .点M 在线段AP 上,点N 在线段BP 上,EM =EN ,sin ∠EMP = 1213 . (1)如图1,当点E 与点C 重合时,求CM 的长; (2)如图2,当点E 在边AC 上时,点E 不与点A 、C 重合,设AP =x ,BN =y ,求y 关于x 的函数关系式,并写出函数的定义域; (3)若△AME ∽△ENB (△AME 的顶点A 、M 、E 分别与△ENB 的顶点E 、N 、B 对应),求AP 的长. 图1 图2 备用图 【答案】(1)∵∠ACB =90°,∴AC . ∵S =12 AB CP ??=1 2 AC BC ??, ∴CP =AC BC AB ?=403050 ?=24. 在Rt△CPM 中,∵sin∠EMP =1213 , ∴1213CP CM =.
《相似三角形的应用》教案
27.2.3 相似三角形的应用(王军) 一、教学目标 1.核心素养 通过学习相似三角形的应用举例,初步形成基本的推理能力和应用意识.2.学习目标 进一步巩固相似三角形的知识,学会用相似三角形知识解决不能直接测量的物体的长度或高度等一些实际问题. 3.学习重点 运用相似的判定和性质定理解决实际问题. 4.学习难点 灵活运用三角形相似的知识解决实际问题(如何把实际问题抽象为数学问题).二、教学设计 (一)课前设计 1.预习任务 任务1 阅读教材P39-40,思考:如何测量不能到达顶部的物体的高度? 任务2 阅读教材P39-40,思考:如何测量不能直接到达的两点间的距离? 任务3 阅读教材P40-41,思考:什么是视点、视线、仰角、俯角?什么是盲区?2.预习自测 1.测量不能到达顶部的物体的高度,通常借助太阳光照射物体形成影子,根据同一时刻物高与影长______或利用相似三角形来解决. 2.求不能直接到达的两点间的距离,关键是构造___________,然后根据相似三角形的性质求出两点间的距离. 3.如图,小明测量某广场旗杆的高度,他从A走1.8m到C 处时,他头顶的影子正好与点A重合.已知小明身高1.58m, 并测得BC=7.2m,则旗杆的高度是( ) A.8m B.7.9m C.7.5m D.7.2m (二)课堂设计 1.知识回顾 1.三角形相似的判定方法:
(1)定义法:三个对应角相等,三条对应边成比例的两个三角形相似. (2)平行法:平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角形与原三角形相似; (3)判定定理1(边边边):三边对应成比例,两三角形相似; (4)判定定理2(边角边):两边对应成比例且夹角相等,两三角形相似; (5)判定定理3(角角):两角对应相等,两三角形相似; (6)直角三角形相似的判定定理(HL):斜边和一条直角边成比例的两个直角三角形相似. 2.相似三角形的性质: (1)相似三角形对应角相等、对应边成比例. (2)相似三角形对应边上的高线之比、对应边上中线之比、对应角平分线之比等于相似比. 相似三角形对应线段之比等于相似比. (3)相似三角形的周长之比等于相似比. (4)相似三角形的面积之比等于相似比的平方. 2.问题探究 问题探究一如何测量不能到达顶部的物体的高度?重点、难点知识★▲ ●活动1 探究利用三角形相似测量物高 据史料记载,古希腊数学家、天文学家泰勒斯 曾经利用相似三角形的原理,在金字塔影子的 顶部立一根木杆,借助太阳光线构成的两个相 似三角形来测量金字塔的高度. 小组合作:自学课本第39页,例题4----测量金字塔高度问题。 例:如图,如果木杆EF长2 m,它的影长FD为3m,测得OA为 201m,求金字塔的高度BO. 怎样测出OA的长?
相似三角形的综合应用(提高)
相似三角形的应用 【学习目标】 1、探索相似三角形的性质,能运用性质进行有关计算. 2、通过典型实例认识现实生活中物体的相似,能运用图形相似的知识解决一些简单的实际问题(如何把实际问题抽象为数学问题). 【知识回顾】 一、相似三角形的性质 (1)对应边的比相等,对应角相等. (2)相似三角形的周长比等于相似比. (3)相似三角形的面积比等于相似比的平方...... . (4)相似三角形的对应边上的高、中线、角平分线的比等于相似比. 二、相似三角形的应用: 1、利用三角形相似,可证明角相等;线段成比例(或等积式); 2、利用三角形相似,求线段的长等 3、利用三角形相似,可以解决一些不能直接测量的物体的长度.如求河的宽度、求建筑物的高度等. 【典型例题】 例1:如图,△ABC 是一块锐角三角形余料,边BC=120mm , 高AD=80mm , 要把它加工成矩形零件,使一边在BC 上,其余两个顶点分别在边AB 、AC 上, (1)若这个矩形是正方形,那么边长是多少? (2)若这个矩形的长是宽的2倍,则边长是多少? 【同步练习】如图,△ABC 是一块三角形余料,AB=AC=13cm ,BC=10cm ,现在要把它加工成正方形零件,使正方形的一边在△ABC 的边上,其余两个顶点分别在三角形另外两条边上.试求正方形的边长是多少? 例2:阅读以下文字并解答问题: 在“测量物体的高度” 活动中,某数学兴趣小组的4名同学选择了测量学校里的四棵树的高 A B C Q M D N P E
度.在同一时刻的阳光下,他们分别做了以下工作: 小芳:测得一根长为1米的竹竿的影长为0.8米,甲树的影长为4.08米(如图1). 小华:发现乙树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图2),墙壁上的影长为1.2米,落在地面上的影长为2.4米. 小丽:测量的丙树的影子除落在地面上外,还有一部分落在教学楼的第一级台阶上(如图3),测得此影子长为0.2米,一级台阶高为0.3米,落在地面上的影长为4.4米. 小明:测得丁树落在地面上的影长为2.4米,落在坡面上影长为3.2米(如图4).身高是1.6m 的小明站在坡面上,影子也都落坡面上,小芳测得他的影长为2m . (1)在横线上直接填写甲树的高度为 米. (2)求出乙树的高度(画出示意图). (3)请选择丙树的高度为( ) A 、6.5米 B 、5.75米 C 、6.05米 D 、7.25米 (4)你能计算出丁树的高度吗?试试看. 【同步练习】如图,有一路灯杆AB(底部B 不能直接到达),在灯光下,小明在点D 处测得自己的影长DF =3m ,沿BD 方向到达点F 处再测得自己得影长FG =4m ,如果小明得身高为1.6m ,求路灯杆AB 的高度. 图1 图2 图3 图 4
相似三角形的应用举例
27.2.2相似三角形应用举例 教学目标: 1.进一步巩固相似三角形的知识. 2.能够运用三角形相似的知识,解决不能直接测量物体的长度和高度(如测量金字塔高度问题、测量河宽问题)等的一些实际问题. 3.通过把实际问题转化成有关相似三角形的数学模型,进一步了解数学建模的思想,培养分析问题、解决问题的能力. 重点、难点 1.重点:运用三角形相似的知识计算不能直接测量物体的长度和高度. 2.难点:灵活运用三角形相似的知识解决实际问题(如何把实际问题抽象为数学问题). 一、知识链接 1、判断两三角形相似有哪些方法? 2、相似三角形有什么性质? 二、.探索新知 1、问题1:学校操场上的国旗旗杆的高度是多少?你有什么办法测量? 2、在平行光线的照射下,不同物体的物高与影长成比例 练习:(1.)一根1.5米长的标杆直立在水平地面上,它在阳光下的影长为2.1米;此时一棵水杉树的影长为10.5米,这棵水杉树高为( ) A.7.5米 B.8米 C.14.7米 D.15.75米
(2.)在某一刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的高为60 米,那么高楼的影长是多少米? 3. 世界现存规模最大的金字塔位于哪个国家,叫什么金字塔? 胡夫金字塔是埃及现存规模最大的金字塔,被喻为“世界古代七大奇观之一”.塔的4个斜面正对东南西北四个方向,塔基呈正方形,每边长约230多米.据考证,为建成大金字塔,共动用了10万人花了20年时间.原高146.59米,但由于经过几千年的风吹雨打,顶端被风化吹蚀,所以高度有所降低.在古希腊,有一位伟大的科学家叫泰勒斯.一天,希腊国王阿马西斯对他说:“听说你什么都知道,那就请你测量一下埃及金字塔的高度吧!”,这在当时条件下是个大难题,因为是很难爬到塔顶的.你知道泰勒斯是怎样测量大金字塔的高度的吗? 3、例题讲解 例3: 据史料记载,古希腊数学家、天文学家泰勒斯曾经利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成的两个相似三角形来测量金字塔的高度. 如图,如果木杆EF长2 m,它的影长FD为3 m,测得OA为201 m,求金字塔的高度BO.(思考如何测出OA的长?) 分析:根据太阳光的光线是互相平行的特点,可知在同一时刻的阳光下,竖直的两个物体的影子互相平行,从而构造相似三角形,再利用相似三角形的判定和性质,根据已知条件,求出金字塔的高度. 解: 4、课堂练习 在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为90米,那么高楼的高度是多少米? (在同一时刻物体的高度与它的影长成正比例.)
相似三角形在实际生活中的应用上课讲义
相似三角形在实际生活中的应用
相似三角形在实际生活中的应用 【知识点击】 1、如果两个图形不仅是相似图形,而且每组对应点所在的直线都经过,那么这样的两个图形就称为位似图形。此时的这个点叫做,相似比又称为. 注:位似图形作为一种特殊的相似图形,是最重要的图形之一.但相似图形未必都能够成位似关系.所谓位似图形,是指两个图形不仅是相似图形,而且___________________,此时的这个点叫做位似中心,相似比又称为_____________.位似图形具有相似图形的所有性质,利用位似的方法可以将一个多边形放大或缩小. 2、相似多边形的性质_____________________________________________________ 【重点演练】 知识点一、位似图形 例1、如图,在6×8网格图中,每个小正方形边长均为1,点O和△ABC的顶点均在小正方形的顶点. (1)以O为位似中心,在网格图中作△A′B′C′和△ABC位似,且位似比为1︰2; (2)连接(1)中的AA′,求四边形AA′C′C的周长.(结果保留根号) 例2、如图3,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10cm,OA′=20cm,则五边形ABCDE的周长与五边形A′B′C′D′E′的周长的比值是.
B′ A′ -1 x 1 O -1 1 y B A C 标准对数视力 0.1 4.0 0.12 4.1 0.15 4.2 变式训练: 1.视力表对我们来说并不陌生.如图是视力表的一部分,其中开口向上的两个“E ”之间的变换是( ) A .平移 B .旋转 C .对称 D .位似 2. 如图,正方形OEFG 和正方形ABCD 是位似形,点F 的坐标为(1,1),点C 的坐标为 (4,2),则这两个正方形位似中心的坐标是 . 3、如图,△ABC 中,A ,B 两个顶点在x 轴的上方,点C 的坐标是(-1,0).以点C 为位似中心,在x 轴的下方作△ABC 的位似图形△A ′B ′C ,并把△ABC 的边长放大到原来的2倍.设点B 的对应点B′的横坐标是a ,则点B 的横坐标是( ) A .1 2 a - B .1(1)2 a -+ C .1 (1)2 a -- D .1 (3)2 a -+ 图3 O A B C D E A ′ B ′ C ′ ′ E ′ y x A B C D F E G O
九年级数学相似三角形的应用举例
19.7相似三角形的应用 目的:利用相似三角形的性质解决实际问题. 中考基础知识 通过证明三角形相似 线段成比例()() ????方程含有未知数的等式函数求最值等问题 备考例题指导 例1.如图,P 是△ABC 的BC 边上的一个动点,且四边形ADPE 是平行四边形. (1)求证:△DBP ∽△EPC ; (2)当P 点在什么位置时,S ADPE = 1 2 S △ABC ,说明理由. 分析: (1) 证明两个三角形相似,常用方法是证明两个角对应相等,题目中有 ADPE ? 平行线?角相等,命题得证. (2)设 BP BC =x ,则CP BC =1-x , ADPE ?DP ∥AC , EP ∥AB , △BDP ∽△BAC △CPE ∽△CBA ∴ FPC ABC S S ??=(CP CB )2=(1-x )2,BDP BAC S S ??=(BP BC )2=x 2 ∴ BDP CPE ABC S S S ???+=x 2+(1-x )2 . ∵S ADPE = 12 S △ABC ,即ADPE ABC S S ?=1 2.
∴x2+(1-x)2=1 2 (转化为含x的方程) x=1 2 , ∴BP BC = 1 2 . 即P应为BC之中点. 例2.已知△ABC中,∠ACB=90°,过点C作CD⊥AB于D,且AD=m,BD=n,AC2:BC2=2: 1,又关于x的方程1 4 x2-2(n-1)x+m2-12=0的两个实数根的差的平方小于192,求m,n 为整数时,?一次函数y=mx+n的解析式. 分析:这是一个几何、代数综合题,由条件发现,建立关于m,n的方程或不等式,?求出m,n再写出一次函数. 抓条件:AC2:BC2=2:1做文章(转化到m,n上). 双直角图形?有相似形?比例式(方程) ∠ACB=90°,CD⊥AB Rt△BCD∽Rt△BAC BC2=BD·BA,同理有AC2=AD·AB, ∴ 2 2 BC AC = BD BA AD AB ?=m=2n ① 抓条件:x1+x2=8(n-1),x1x2=4(m2-12). 由(x1-x2)2<192 配方(x1+x2)2-4x1x2<192. 64(n-1)2-16(m2-12)<192, 4n2-m2-8n+4<0.② ①代入②?n>1 2 . 又由△≥0得4(n-1)2-4×1 4 (m2-12)≥0, ①代入上式得n≤2.③
相似三角形详细讲义
知识梳理 相似三角形的概念 对应角相等,对应边成比例的三角形,叫做相似三角形. 相似用符号“∽”表示,读作“相似于”. 相似三角形对应边的比叫做相似比(或相似系数). 相似三角形对应角相等,对应边成比例. 注意: ①对应性:即两个三角形相似时,通常把表示对应顶点的字母写在对应位置上,这样写比较容易 找到相似三角形的对应角和对应边. ②顺序性:相似三角形的相似比是有顺序的. ③两个三角形形状一样,但大小不一定一样. ④全等三角形是相似比为1的相似三角形.二者的区别在于全等要求对应边相等,而相似要求对 应边成比例. 相似三角形的基本定理 定理:平行于三角形一边的直线和其它两边(或两边延长线)相交,所构成的三角形与原 三角形相似. 定理的基本图形: 用数学语言表述是:
BC DE // , ADE ∽ABC . 相似三角形的等价关系 (1)反身性:对于任一ABC 有ABC ∽ABC . (2)对称性:若ABC ∽'''C B A ,则'''C B A ∽ABC . (3)传递性:若ABC ∽C B A '',且C B A ''∽C B A ,则ABC ∽C B A . 三角形相似的判定方法 1、定义法:对应角相等,对应边成比例的两个三角形相似. 2、平行法:平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角 形与原三角形相似. 3、判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两 个三角形相似.简述为:两角对应相等,两三角形相似. 4、判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹 角相等,那么这两个三角形相似.简述为:两边对应成比例且夹角相等,两三角形相似. 5、判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这 两个三角形相似.简述为:三边对应成比例,两三角形相似.(在遇到两个三角形的三边都知道的情况优先考虑,把边长分别从小到大排列,然后分别计算他们的比值是否相等来判断是否相似) 6、判定直角三角形相似的方法: (1)以上各种判定均适用. (2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似. (3)直角三角形被斜边上的高分成的两个直角三角形与原三角形相似. 直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。 公式 如图,Rt △ABC 中,∠BAC=90°,AD 是斜边BC 上的高,则有射影定理如下: (1)(AD )2=BD ·DC , (2)(AB )2=BD ·BC , (3)(AC )2=CD ·BC 。 证明:在 △BAD 与△ACD 中,∠B+∠C=90°,∠DAC+∠C=90°,∴∠B=∠DAC ,又∵∠ BDA=∠ADC=90°,∴△BAD ∽△ACD 相似,∴ AD/BD =CD/AD ,即 (AD )2=BD ·DC 。其余类似可证。 注:由上述射影定理还可以证明勾股定理。由公式(2)+(3)得: (AB )2+(AC )2=BD ·BC+CD ·BC =(BD+CD)·BC=(BC )2, 即 (AB )2+(AC )2=(BC )2。 这就是勾股定理的结论。 判断相似三角形的几条思路: 1 条件中若有平行线,可采用相似三角形的基本定理 2 条件中如果有一对等角,可再找一对等角(用判定1)或再找夹边成比例。(用判定2)3条件中若有两边对应成比例,可找夹角相等(直角可以直接得出相似)4条件中若有一对直角,可考虑在找一对等角或证明斜边,直角边对应成比例。5条件中若
《相似三角形》最全讲义(完整版).docx
相似三角形基本知识 知识点一:放缩与相似形 1?图形的放大或缩小,称为图形的放缩运动。 2.把形状相同的两个图形说成是相似的图形,或者就说是相似性。 注意:⑴相似图形强调图形形状相同,与它们的位?用、颜色、大小无关。 ⑵相似图形不仅仅指平面图形,也包括?立体图形相似的情况。 ⑶我们可以这样理解相似形:两个图形相似,其中一个图形可以看作是由另一个图形放大或缩小 得 到的. ⑷若两个图形形状与大小都相同,这时是相似图形的一种特例一一全等形. 3?相似多边形的性质:如果两个多边形是相似形,那么这两个多边形的对应角相等,对应边的长度成比例。 注意:当两个相似的多边形是全等形时,他们的对应边的长度的比值是1. 知识点二:比例线段有关概念及性质 (1)有关概念 1、比:选用同一长度单位量得两条线段。a. b的长度分別是m、n,那么就说这两条线段 a _ m 的比是a: b = m: n (或〃n) 2、比的前项,比的后项:两条线段的比a: b屮。a叫做比的前项,b叫做比的后项。 说明:求两条线段的比时,对这两条线段要用同一单位长度。 兰_ £ 3、比例:两个比相等的式子叫做比例,如芦° a _ £ 4、比例外项:在比例“ d(或a: b=c: d)中a、d叫做比例外项。 a _ c 5、比例内项:在比例〃〃(或a: b = c: d)中b、c叫做比例内项。 a _ c 6、第四比例项:在比例〃d(或a: b=c: d)中,d叫a、b、c的第四比例项。 7、比例中项:如果比例中两个比例内项相等,即比例为U(或a:b=b:c时,我们把b 叫做a和d的比例中项。 &比例线段:对于四条线段a、b、c、d,如果其中两条线段的长度的比与另两条线段的长
《相似三角形应用举例(1)》教学设计
《相似三角形应用举例(1)》教学设计 福报学校黄世辉 一、教学目标 1、进一步巩固相似三角形的判定方法和基本性质. 2、能够运用三角形相似的知识,解决不能直接测量物体的高度和宽度等实际问题. 3、通过把实际问题转化成有关相似三角形的数学模型,进一步了解数学建模的思想,培养分析问题、解决问题的能力. 二、教学重难点 重点:运用三角形相似计算不能直接测量物体的高度和宽度.难点:如何把实际问题抽象为数学问题. 三、教学过程 (一)知识回顾 1、回顾相似三角形的概念及判定方法. 2、复习“相似多边形对应角相等、对应边的比相等”性质. (二)提出问题 利用三角形的相似,如何解决一些不能直接测量的物体的长度问题?(学生小组讨论) 师生归纳:“相似三角形对应边的比相等” 四条对应边中若已知三边则可求第四边. (三)小试牛刀—测量物高
1、例题探究:(教材第48页例3)据史料记载,古希腊数学家、天文学家泰勒斯曾经利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成的两 个相似三角形来测量金字塔的高 度. 如图1,如果木杆EF 长2 m , 它的影长FD 为3 m ,测得OA 为201 m ,求金字塔的高度BO .(思考如何测出OA 的长?) 师生活动:学生小组讨论,师生共同交流,画出示意图,通过观察示意图,使学生建立起相似图形的几何直觉,并能明确表述求OA 的方法中蕴含的数学知识. 分析:根据太阳光的光线是互相平行的特点,可知在同一时刻的阳光下,竖直的两个物体的影子互相平行,从而构造相似三角形,再利用相似三角形的性质,根据已知条件,求出金字塔的高度. 解:太阳光是平行光线,即B A ∥ED, ∴∠BAO =∠EDF. 又∠AOB =∠DFE=90°, ∴△ABO ∽△DEF. ∴BO OA EF FD =, 20121343 OA EF BO FD ??===. 因此金字塔的高度为134m. 2、换式练习:(教材第50页练习1)在某一时刻,测得一根高
相似三角形完整讲义(教师版)
相似三角形基本知识 知识点一:放缩与相似形 1.图形的放大或缩小,称为图形的放缩运动。 2.把形状相同的两个图形说成是相似的图形,或者就说是相似性。 注意:⑴相似图形强调图形形状相同,与它们的位置、颜色、大小无关。 ⑵相似图形不仅仅指平面图形,也包括立体图形相似的情况。 ⑶我们可以这样理解相似形:两个图形相似,其中一个图形可以看作是由另一个图形放大或缩小得到的. ⑷若两个图形形状与大小都相同,这时是相似图形的一种特例——全等形. 3.相似多边形的性质:如果两个多边形是相似形,那么这两个多边形的对应角相等,对应边的长度成比例。 注意:当两个相似的多边形是全等形时,他们的对应边的长度的比值是1. 知识点二:比例线段有关概念及性质 (1)有关概念 1、比:选用同一长度单位量得两条线段。a 、b 的长度分别是m 、n ,那么就说这两条线段 的比是a :b =m :n (或 n m b a =) 2、比的前项,比的后项:两条线段的比a :b 中。a 叫做比的前项,b 叫做比的后项。 说明:求两条线段的比时,对这两条线段要用同一单位长度。 3、比例:两个比相等的式子叫做比例,如 d c b a = 4、比例外项:在比例d c b a = (或a :b =c :d )中a 、d 叫做比例外项。 5、比例内项:在比例d c b a = (或a :b =c :d )中b 、c 叫做比例内项。 6、第四比例项:在比例d c b a = (或a :b =c :d )中,d 叫a 、b 、c 的第四比例项。 7、比例中项:如果比例中两个比例内项相等,即比例为 a b b a =(或a:b =b:c 时,我们把b 叫做a 和d 的比例中项。 8.比例线段:对于四条线段a 、b 、c 、d ,如果其中两条线段的长度的比与另两条线段的长度的比相等,即 d c b a =(或a :b= c : d ) ,那么,这四条线段叫做成比例线段,简称比例线段。(注意:在求线段比时,线段单位要统一,单位不统一应先化成同一单位)
相似三角形与实际应用
1 / 2 初中数学优秀生特长生培训方案 相似三角形与实际应用 一, 思想、方法解读 利用相似三角形解决实际问题的方法与步骤 1、 分析题意 2、 画出图形 3、 找出两个能解决问题的两个相似三角形 4、 证明这两个三角形相似 5、 写出比例式(要包含已知条件和题中要求的未知量或相关量) 6、 由比例式解决问题或由比例式列方程解决问题 二,思想方法分类例析 (一)利用相似三角形进行测量 例1.在一次数学活动课上,李老师带领学生去测教学楼的高度,在阳光下,测得身高为1.65m 的黄丽同学BC 的影长BA 为1.1m ,与此同时,测得教学楼DE 的影长DF 为12.1m ,如图所示,请你根据已测得的数据,测出教学楼DE 的高度.(精确到0.1m) 例2.我侦察员在距敌方200米的地方发现敌人的一座建筑物,但 不知其高度又不能靠近建筑物测量,机灵的侦察员食指竖直举在右眼 前,闭上左眼,并将食指前后移动,使食指恰好将该建筑物遮住。若 此时眼睛到食指的距离约为40cm ,食指的长约为8cm,你能根据上述 条件计算出敌方建筑物的高度吗?请说出你的思路。 例3.小明想利用树影测量树高,他在某一时刻测得长为1m 的竹竿影长0.9m ,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上,如图,他先测得留在墙上的影高1.2m ,又测得地面部分的影长2.7m ,他求得的树高是多少? 例4.如图:学校旗杆附近有一斜坡.小明准备测量学校旗杆AB 的高度,他发现当斜坡正对着太阳时,旗杆AB 的影子恰好落在水 平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC =20 米,斜坡坡面上的影长CD =8米,太阳光线AD 与水平地面成30° 角,斜坡CD 与水平地面BC 成30°的角,求旗杆AB 的高度(精确到1米). (二)利用相似三角形进行方案设计 例5、如图, ABC 是一块锐角三角形余料,边BC=120毫米,高 AH=80毫米,要把它加工成正方形零件,使正方形的一边在BC 上, 其余两个顶点分别在AB 、AC 上.这个正方形零件的边长是多少? 例6、一块直角三角形木板的一条直角边AB 长为1.5m ,面 积为1.22m ,工人师傅要把它加工成一个面积最大的正方形桌 面,请甲、乙两位同学进行设计加工方案,甲的方案如图(1),乙的 A B C D
九年级数学相似三角形的性质及应用(教师版)知识点+典型例题+详细答案(吐血推荐)
相似三角形的性质及应用 【学习目标】 1、探索相似三角形的性质,能运用性质进行有关计算; 2、通过典型实例认识现实生活中物体的相似,能运用图形相似的知识解决一些简单的实际问题(如何把实际问题抽象为数学问题). 【要点梳理】 要点一、相似三角形的性质 1.相似三角形的对应角相等,对应边的比相等. 2. 相似三角形中的重要线段的比等于相似比. 相似三角形对应高,对应中线,对应角平分线的比都等于相似比. 3. 相似三角形周长的比等于相似比 ∽ ,则 由比例性质可得: 4. 相似三角形面积的比等于相似比的平方 ∽ ,则 分别作出 与 的高 和,则 211 22=1122 ABC A B C BC AD k B C k A D S k S B C A D B C A D '''''''????=='''''''''??△△ 要点诠释:相似三角形的性质是通过比例线段的性质推证出来的. 要点二、相似三角形的应用 1.测量高度 测量不能到达顶部的物体的高度,通常使用“在同一时刻物高与影长的比例相等”的原理解决. 要点诠释:测量旗杆的高度的几种方法: 平面镜测量法 影子测量法 手臂测量法 标杆测量法
2.测量距离 测量不能直接到达的两点间的距离,常构造如下两种相似三角形求解。 1.如甲图所示,通常可先测量图中的线段DC、BD、CE的距离(长度),根据相似三角形的性质,求出AB的长. 2.如乙图所示,可先测AC、DC及DE的长,再根据相似三角形的性质计算AB的长. 要点诠释: 1.比例尺:表示图上距离比实地距离缩小的程度,比例尺= 图上距离/ 实际距离; 2.太阳离我们非常遥远,因此可以把太阳光近似看成平行光线.在同一时刻,两物体影子之比等于其对应高的比; 3.视点:观察事物的着眼点(一般指观察者眼睛的位置); 4. 仰(俯)角:观察者向上(下)看时,视线与水平方向的夹角. 【典型例题】 类型一、相似三角形的性质 1. △ABC∽△DEF,若△ABC的边长分别为5cm、6cm、7cm,而4cm是△DEF中一边的长度,你能求出△DEF的另外两边的长度吗?试说明理由. 【答案】 设另两边长是xcm,ycm,且x<y. (1)当△DEF中长4cm线段与△ABC中长5cm线段是对应边时,有, 从而x=cm,y=cm. (2)当△DEF中长4cm线段与△ABC中长6cm线段是对应边时,有, 从而x=cm,y=cm. (3)当△DEF中长4cm线段与△ABC中长7cm线段是对应边时,有, 从而x=cm,y=cm. 综上所述,△DEF的另外两边的长度应是cm,cm或cm,cm 或cm,cm三种可能. 2.如图所示,已知△ABC中,AD是高,矩形EFGH内接于△ABC中,且长边FG在BC 上,矩形相邻两边的比为1:2,若BC=30cm,AD=10cm.求矩形EFGH的面积.
《相似三角形的应用》练习题1
3.5 相似三角形的应用(1) 【知能点分类训练】 知能点1 测量问题 1.在一张比例尺为1:30 ?000?的地图上,?一多边形地区的周长为70cm,?面积为340cm2,那么该地区的实际周长为______km,面积为_______km2. 2.一个三角形的三边长分别为9cm,10cm,18cm,另一个与它相似的三角形的最长边为6cm,则另两条边的边长为________. 3.某一时刻量得电线杆的影长为2.7m,而垂直于地面的1m?高的小树的影长为0.3m,则电线杆的高为________. 4.有两块相似的多边形的菜地,两较短边的比为2:3,?经测量较小的菜地面积为820m2,则另一块菜地的面积为_________. 5.AB是斜靠在墙上的梯子,梯脚B距墙是1.5m,梯子上一点C到墙的距离是1.2m,BC长为0.5m,则梯子AB的长为______m. 知能点2 设计问题 6.设离小孔M 20cm处有一支长为16cm的蜡烛AB,经小孔M成像,在小孔M后面30cm 的屏幕上所成像A′B′的长为_________cm. 7.小明打网球时要使球恰好能打过网,而且 落在离网5m的位置上,则球拍击球的高度h应为 (). A.2.7m B.1.8m C.0.9m D.6m 8.把一根长50cm的细铁丝截成两段,把每段折为一个等边三角形,两个等边三角形的高的比为3:2,则它们的边长分别为________和________. 9.比例规是一种画图工具,使用它可以把线段按一定比例伸长或缩短.如果把比例规的两脚合上,使转动点固定在所要求的刻度上,如在刻度4上,然后张开两脚,?使比例规的两脚分别放在线段a的两个端点上,这时比例规的另外两个脚的端点所代表的线段就是线 段a长的1 4 ,你知道为什么吗? 【综合应用提高】 10.在某时刻1.6m高的人的影长为2m,此时距墙2m远的大树的影子落在墙上的部分为1m,求这棵树的高度. 11.一条河的两岸可以看做平行,在河的这岸每隔4m有一棵树,?在河的对岸每隔50m
中考试题相似三角形的应用
学科:数学 专题:相似三角形的应用 主讲教师:黄炜北京四中数学教师 重难点易错点解析 在构造相似模型时,务必找准对应边. 题一 题面:如图所示,AB是斜靠在墙壁上的长梯,梯脚B距离墙角1.6m,梯上点D距离墙1.4m,BD长0.55m,则梯子长为( ) A.3.85m B.4.00m C.4.40m D.4.50m 金题精讲 题一 题面:在已知半圆内,求作内接正方形.
位似变换 满分冲刺 题一 题面:如图,小明准备测量学校旗杆AB的高度,当他发现斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,测得水平地面上的影长BC=20m,斜坡坡面上的影长CD=8m,太阳光线AD与水平地面成30°角,斜坡CD与水平地面所成的锐角为30°,求旗杆AB的高度. 相似三角形的应用 题二 题面:如图,正方形ABCD和正方形OEFG中,点A和点F的坐标分别为(3,2),(-1,-1),则两个正方形的位似中心的坐标是_________. 位似中心、平面直角坐标系
题三 题面:在已知三角形内,求作内接正方形. 相似三角形的应用 讲义参考答案 重难点易错点解析 题一 答案:C . 金题精讲 题一 答案:正方形EFGH 即为所求. 满分冲刺 题一 答案:20324 3 m .
题二 答案:位似中心的坐标是(1,0)或(-5,-2). 题三 答案:方法1:利用位似形的性质作图法(图16) 图16 作法:(1)在AB上任取一点G',作G'D'⊥BC; (2)以G'D'为边,在△ABC内作一正方形D'E'F'G'; (3)连结BF',延长交AC于F; (4)作FG∥CB,交AB于G,从F,G各作BC的垂线FE,GD,那么DEFG就是所求作的 内接正方形. 方法2:利用代数解析法作图(图17) 图17 (1)作AH(h)⊥BC(a); (2)求h+a,a,h的比例第四项x; (3)在AH上取KH=x; (4)过K作GF∥BC,交两边于G,F,从G,F各作BC的垂线GD,FE,那么DEFG就是所 求的内接正方形. 初中数学试卷 灿若寒星制作
相似三角形详细讲义
教育教学讲义 学员姓名:年级:学科教师:上课时间:辅导科目:数学课时数:2 课题相似三角形 教学目标 1 通过本章的学习,要熟悉数学中的转化思想,数形结合,分类讨论思想特殊值法。 2转化思想:利用相似性质解决问题时,经常用到转化思想,如在有关面积的问题中,往往要借助于线段的比,周长的比等进行转化,进而解决问题。 3数形结合思想:对于很多几何图形,我们都要善于观察,找出其中的隐含条件,做到数形结合,从而解决问题。 4分类讨论思想:在运用相似三角形的对应边成比例的性质时,如果题目的条件中,不能确定如何对应,则应给予讨论。 教学内容 课前检测全等三角形的概念? 知识梳理 相似三角形的概念 对应角相等,对应边成比例的三角形,叫做相似三角形. 相似用符号“∽”表示,读作“相似于”. 相似三角形对应边的比叫做相似比(或相似系数). 相似三角形对应角相等,对应边成比例. 注意: ①对应性:即两个三角形相似时,通常把表示对应顶点的字母写在对应位置上,这样写比较容易 找到相似三角形的对应角和对应边. ②顺序性:相似三角形的相似比是有顺序的. ③两个三角形形状一样,但大小不一定一样. ④全等三角形是相似比为1的相似三角形.二者的区别在于全等要求对应边相等,而相似要求对 应边成比例. 相似三角形的基本定理 定理:平行于三角形一边的直线和其它两边(或两边延长线)相交,所构成的三角形与原 三角形相似. 定理的基本图形: 用数学语言表述是:
BC DE // , ADE ?∴∽ABC ?. 相似三角形的等价关系 (1)反身性:对于任一ABC ?有ABC ?∽ABC ?. (2)对称性:若ABC ?∽'''C B A ?,则'''C B A ?∽ABC ?. (3)传递性:若ABC ?∽C B A '?'',且C B A '?''∽C B A ''''''?,则ABC ?∽C B A ''''''?. 三角形相似的判定方法 1、定义法:对应角相等,对应边成比例的两个三角形相似. 2、平行法:平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角 形与原三角形相似. 3、判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两 个三角形相似.简述为:两角对应相等,两三角形相似. 4、判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹 角相等,那么这两个三角形相似.简述为:两边对应成比例且夹角相等,两三角形相似. 5、判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这 两个三角形相似.简述为:三边对应成比例,两三角形相似.(在遇到两个三角形的三边都知道的情况优先考虑,把边长分别从小到大排列,然后分别计算他们的比值是否相等来判断是否相似) 6、判定直角三角形相似的方法: (1)以上各种判定均适用. (2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似. (3)直角三角形被斜边上的高分成的两个直角三角形与原三角形相似. 直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。 公式 如图,Rt △ABC 中,∠BAC=90°,AD 是斜边BC 上的高,则有射影定理如下: (1)(AD )2=BD ·DC , (2)(AB )2=BD ·BC , (3)(AC )2=CD ·BC 。 证明:在 △BAD 与△ACD 中,∠B+∠C=90°,∠DAC+∠C=90°,∴∠B=∠DAC ,又∵∠ BDA=∠ADC=90°,∴△BAD ∽△ACD 相似,∴ AD/BD =CD/AD ,即 (AD )2=BD ·DC 。其余类似可证。 注:由上述射影定理还可以证明勾股定理。由公式(2)+(3)得: (AB )2+(AC )2=BD ·BC+CD ·BC =(BD+CD)·BC=(BC )2, 即 (AB )2+(AC )2=(BC )2。 这就是勾股定理的结论。 判断相似三角形的几条思路: 1 条件中若有平行线,可采用相似三角形的基本定理 2 条件中如果有一对等角,可再找一对等角(用判定1)或再找夹边成比例。(用判定2)3条件中若有两边对应成比例,可找夹角相等(直角可以直接得出相似)4条件中若有一对直角,可考虑在找一对等角或证明斜边,直角边对应成比例。5条件中若
相似三角形应用举例1(含答案)
相似三角形应用举例1 新颖题 如右图,在等边△ABC 的边BC 上取点D ,使 BD DC =1 2 ,作CH ⊥AD ,H 为垂足,连结BH , 求证:∠DBH=∠DAB . 证明:过A 作AM ⊥BC 于M ,在Rt △ADM 和Rt △CDH 中, ∠ADM=?∠CDH ,?∠AMD=?∠CHD=990°, 所以△CDH ∽△ADM , 所以 AD DM CD DH =,CD=2BD ,DM=1 2BD , 所以AD DB BD DH =. 因为∠ADB=?∠BDH ,? 所以△ADB ∽△BDH , 所以∠DBH=∠DAB . 一、基础练习 1.在同一时刻,小R 量得小D 的身高是1.5m ,其影长是1m ,旗杆的影长是8m ,则旗杆高度是________m . 2.如图1,测量小玻璃管口径的量具ABC 上,AB 长为5mm ,AC 被分为50等分,如果小管口DE 正好对着量具上29份处(DE ∥AB ),那么小管口径就是________mm . (1) (2) 3.如图2,测得QS=40m ,ST=100m ,QR=60m ,则河宽PQ 约为_______m . 4.如图3,测得BD=10m ,DC=40m ,EC=30m ,则河宽AB 约为______m . (3) (4) (5) 5.如图4,测得BO=6m ,OD=3.4m ,CD=1.7m ,则旗杆AB 高约为______m . 6.如图5,测得CD=1.7m ,DE=3.4m ,BD=6m ,则旗杆AB 高约为______m . 7.将两块完全相同的等腰直角三角形的三角板摆放如图6,?假设图形中的所有的点,线都在同一平面内,则图形中相似但又不全等的三角形是________.