
第三章 空间向量与立体几何 单元测试
(时间:90分钟 满分:120分) 第Ⅰ卷(选择题,共50分)
一、选择题:本大题共10小题,每小题5分,共50分. 1.以下四组向量中,互相平行的组数为( )
①a =(2,2,1),b =(3,-2,-2);②a =(8,4,-6),b =(4,2,-3);③a =(0,-1,1),b =(0,3,-3);④a =(-3,2,0),b =(4,-3,3)
A .1组
B .2组
C .3组
D .4组
解析:∵②中a =2b ,∴a ∥b ;③中a =-1
3b , ∴a ∥b ;而①④中的向量不平行.
,
答案:B
2.在以下命题中,不正确的个数为( )
①|a |-|b |=|a +b |是a ,b 共线的充要条件;②若a ∥b ,则存在唯一的实数λ,使a =λb ;③对空间任意一点O 和不共线的三点A ,B ,C ,若OP →
=2OA →-2OB →-OC →
,则P ,A ,B ,C 四点共面;④若{a ,b ,c }为空间的一组基底,则{a +b ,b +c ,c +a }构成空间的另一组基底;⑤|(a ·b )·c |=|a |·|b |·|c |.
A .2个
B .3个
C .4个
D .5个
解析:①|a |-|b |=|a +b |?a 与b 共线,但a 与b 共线时|a |-|b |=|a +b |不一定成立,故不正确;②b 需为非零向量,故不正确;③因为2-2-1≠1,由共面向量定理知,不正确;④由基底的定义知正确;⑤由向量的数量积的性质知,不正确.
答案:C
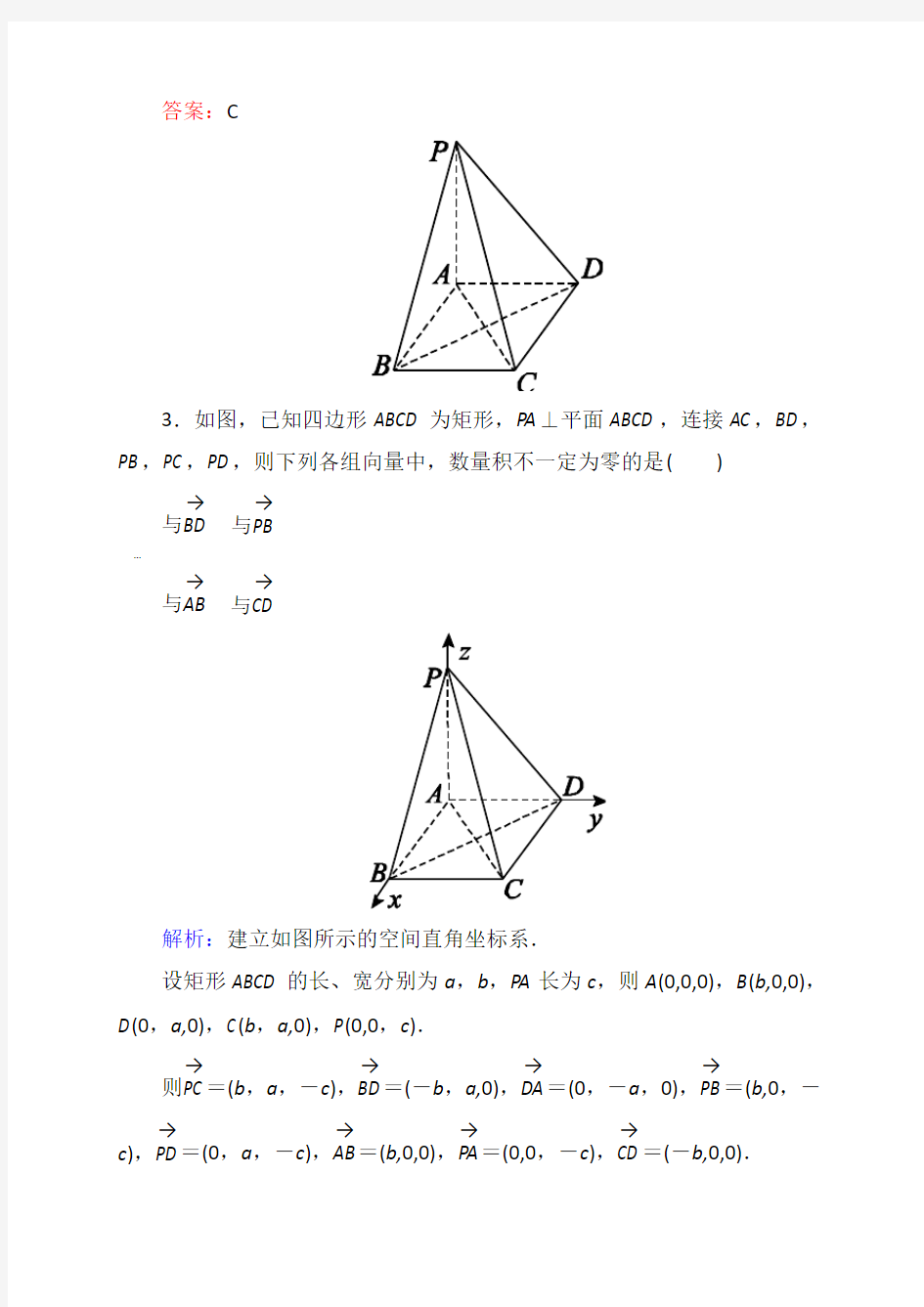
3.如图,已知四边形ABCD 为矩形,PA ⊥平面ABCD ,连接AC ,BD ,PB ,PC ,PD ,则下列各组向量中,数量积不一定为零的是( )
与BD → 与PB →
…
与AB → 与CD
→
解析:建立如图所示的空间直角坐标系.
设矩形ABCD 的长、宽分别为a ,b ,PA 长为c ,则A (0,0,0),B (b,0,0),D (0,a,0),C (b ,a,0),P (0,0,c ).
则PC →=(b ,a ,-c ),BD →=(-b ,a,0),DA →=(0,-a ,0),PB →
=(b,0,-c ),PD →=(0,a ,-c ),AB →=(b,0,0),PA →=(0,0,-c ),CD →
=(-b,0,0).
∴PC →·BD →=-b 2+a 2不一定为0. DA →·PB →=0,PD →·AB →=0,PA →·CD →=0. 答案:A
4.已知向量e 1、e 2、e 3是两两垂直的单位向量,且a =3e 1+2e 2-e 3,
b =e 1+2e 3,则(6a )·? ??
??
12b 等于( ) A .15
B .3 :
C .-3
D .5
解析:(6a )·? ??
??
12b =3a·b =3(3e 1+2e 2-e 3)·(e 1+2e 3)=9|e 1|2-6|e 3|2=3.
答案:B
5.如图,AB =AC =BD =1,AB ?面α,AC ⊥面α,BD ⊥AB ,BD 与面α成30°角,则C 、D 间的距离为( )
A .1
B .2
解析:|CD →|2=|CA →+AB →+BD →|2=|CA →|2+|AB →|2+|BD →|2
+2CA →·AB →
+2AB →·BD →+2CA →·BD →=1+1+1+0+0+2×1×1×cos120°=2.∴|CD →|= 2.
答案:C
6.已知空间三点O (0,0,0),A (-1,1,0),B (0,1,1)在直线OA 上有一点H 满足BH ⊥OA ,则点H 的坐标为( ) /
A .(-2,2,0)
B .(2,-2,0)
解析:由OA →
=(-1,1,0),且点H 在直线OA 上,可设H (-λ,λ,0),则BH →
=(-λ,λ-1,-1).
又BH ⊥OA ,∴BH →·OA →
=0, 即(-λ,λ-1,-1)·(-1,1,0)=0,
即λ+λ-1=0,解得λ=1
2,∴H ? ??
??-12,12,0.
答案:C
7.已知a =(cos α,1,sin α),b =(sin α,1,cos α),则向量a +b 与a -b 的夹角是( )
A .90°
B .60°
C .30°
D .0°
:
解析:(a +b )·(a -b )=a 2-b 2=(cos 2α+sin 2α+1)-(sin 2α+1+cos 2α)=
0,∴(a +b )⊥(a -b ).
答案:A
8.已知E 、F 分别是棱长为1的正方体ABCD -A 1B 1C 1D 1的棱BC 、CC 1的中点,则截面AEFD 1与底面ABCD 所成二面角的正弦值是( )
解析:以D 为坐标原点,以DA 、DC 、DD 1分别为x 轴、y 轴、z 轴建立
空间直角坐标系,如图.则A (1,0,0),E ? ????12,1,0,F ? ??
??
0,1,12,D 1(0,0,1),l
所以AD 1→=(-1,0,1),AE →=?
??
??
-12,1,0.
设平面AEFD 1的法向量为n =(x ,y ,z ), 则?????
n ·AD 1→=0,n·AE →=0,
????
-x +z =0,
-x
2+y =0.
∴x =2y =z .取y =1,则n =(2,1,2),而平面ABCD 的一个法向量为u =(0,0,1),∵cos 〈n ,u 〉=23,∴sin 〈n ,u 〉=5
3. /
答案:C
9.在三棱锥P -ABC 中,△ABC 为等边三角形,PA ⊥平面ABC ,且PA =AB ,则二面角A -PB -C 的平面角的正切值为( )
解析:设PA =AB =2,建立如图所示的空间直角坐标系. 则B (0,2,0),C (3,1,0),P (0,0,2), ∴BP →
=(0,-2,2), BC →
=(3,-1,0).
设n =(x ,y ,z )是平面PBC 的一个法向量.
`
则?????
BP →·n =0,BC →·n =0,
即?
??
??
-2y +2z =0,
3x -y =0.
令y =1,则x =3
3 ,z =1.
即n =? ??
??
33,1,1.
易知m =(1,0,0)是平面PAB 的一个法向量. 则cos 〈m ,n 〉=m·n |m ||n |=3
31×213=7
7.
∴正切值tan 〈m ,n 〉= 6.
答案:A
10.已知OA →=(1,2,3),OB →=(2,1,2),OP →
=(1,1,2),点Q 在直线OP 上运动,则当QA →·QB →
取得最小值时,点Q 的坐标为( )
—
解析:∵Q 在OP 上,∴可设Q (x ,x,2x ),则QA →
=(1-x,2-x,3-2x ),
QB →
=(2-x,1-x,2-2x ). ∴QA →·QB →=6x 2-16x +10, ∴x =4
3时,QA →·QB →最小,
这时Q ? ??
??43,43,83.
答案:C
第Ⅱ卷(非选择题,共70分)
二、填空题:本大题共4小题,每小题5分,共20分.
11.已知a =(3,-2,-3),b =(-1,x -1,1),且a 与b 的夹角为钝角,则x 的取值范围是__________.
解析:因为a 与b 的夹角为钝角,于是-1<cos 〈a ,b 〉<0,因此a·b <0,且a 与b 的夹角不为π,即cos 〈a ,b 〉≠-1.
"
解得x ∈? ????-2,53∪? ??
??53,+∞.
答案:? ????-2,53∪? ??
??5
3,+∞
12.如图所示,已知正四面体A-BCD中,AE=
1
4AB,CF=
1
4CD,则直线DE和BF所成的角的余弦值为__________.
解析:ED
→
=EA
→
+AD
→
=
1
4BA
→
+AD
→
,
BF
→
=BC
→
+CF
→
=BC
→
+
1
4CD
→
,
cos〈ED
→
,BF
→
〉=
ED
→
·BF
→
|ED
→
|·|BF
→
|
=
?
?
?
?
?
?
1
4BA
→
+AD
→
·
?
?
?
?
?
?
BC
→
+
1
4CD
→
?
?
?
?
?
?
1
4BA
→
+AD
→
2·
?
?
?
?
?
?
BC
→
+
1
4CD
→
2
=
4
13.
答案:
4
13
…
13.已知a=(x,2,-4),b=(-1,y,3),c=(1,-2,z),且a,b,c 两两垂直,则(x,y,z)=__________.
解析:由题意知????
?
-x +2y -12=0,x -4-4z =0,
-1-2y +3z =0,
解得x =-64,y =-26,z =-17. 答案:(-64,-26,-17)
14.已知空间四边形OABC ,如图所示,其对角线为OB 、AC ,M 、N 分别为OA 、BC 的中点,点G 在线段MN 上,且MG →=3GN →,现用基向量OA →
、OB →、OC →表示向量OG →,并设OG →=x ·OA →+y ·OB →+z ·OC →,则x 、y 、z 的和为__________.
解析:OG →=OM →+MG →=12OA →+34MN →=12OA →+34? ????
?-12OA →+OC →+12CB →=12OA →
-38OA →+34OC →+38OB →-38OC →=18OA →+38OB →+38OC →,
∴x =18,y =38,z =38. ∴x +y +z =7
8. 答案:78
^
三、解答题:本大题共4小题,满分50分.
15.(12分)已知a =(1,2,-2). (1)求与a 共线的单位向量b ;
(2)若a 与单位向量c =(0,m ,n )垂直,求m 、n 的值. 解:(1)设b =(λ,2λ,-2λ),而b 为单位向量, ∴|b |=1,即λ2+4λ2+4λ2=9λ2=1. ∴λ=±1
3.(4分)
∴b =? ????13,23,-23或b =? ????
-13,-23,23.(6分)
(2)由题意,知????? a·c =0,|c |=1,??????
1×0+2m -2n =0,m 2+n 2+02=1,
解得?????
m =2
2,n =2
2,
或?????
m =-2
2,n =-22.
(12分)
;
16.(12分)如下(左)图,在Rt △ABC 中,∠C =90°,BC =3,AC =6,D ,
E 分别为AC 、AB 上的点,且DE ∥BC ,DE =2,将△ADE 沿DE 折起到△A 1DE 的位置,使A 1C ⊥CD ,如下(右)图.
(1)求证:A1C⊥平面BCDE;
(2)若M是A1D的中点,求CM与平面A1BE所成角的大小.
解:(1)∵AC⊥BC,DE∥BC,∴DE⊥AC.
∴DE⊥A1D,DE⊥CD,∴DE⊥平面A1DC.
∴DE⊥A1C.
又∵A1C⊥CD,
∴A1C⊥平面BCDE.(4分)
—
(2)如图所示,以C为坐标原点,建立空间直角坐标系C-xyz,则A1(0,0,23),D(0,2,0),M(0,1,3),B(3,0,0),E(2,2,0).
设平面A 1BE 的法向量为n =(x ,y ,z ),则n ·A 1B →=0,n ·BE →
=0. 又A 1B →
=(3,0,-23), BE →
=(-1,2,0),
∴?
????
3x -23z =0,-x +2y =0. 令y =1,则x =2,z =3,∴n =(2,1,3). 设CM 与平面A 1BE 所成的角为θ. ∵CM →
=(0,1,3),
∴sin θ=|cos 〈n ,CM →〉|=|n ·CM →
|n |·|CM →||=48×4
=2
2. ∴CM 与平面A 1BE 所成角的大小为π
4.(12分)
^
17.(12分)如图,已知正方形ABCD 和矩形ACEF 所在的平面互相垂直,
AB =2,AF =1,M 是线段EF 的中点.
(1)求证:AM ∥平面BDE ;
(2)试在线段AC 上确定一点P ,使得PF 与CD 所成的角是60°.
解:(1)证明:如图,建立空间直角坐标系. 设AC ∩BD =N ,连接NE ,
则N ? ??
??22,2
2,0,E (0,0,1),
∴NE →=? ??
??-22,-2
2,1.
又A (2,2,0),M ? ??
??22,2
2,1,
;
∴AM →=? ??
??
-22,-22,1.
∴NE →=AM →
,且NE 与AM 不共线. ∴NE ∥AM .
又NE ?平面BDE ,AM ?平面BDE , ∴AM ∥平面BDE .(6分) (2)设P (t ,t,0)(0≤t ≤2),
则PF →=(2-t ,2-t,1),CD →
=(2,0,0). 又∵PF →与CD →
所成的角为60°.
|2-t ·2|2-t
2
+2-t 2
+1·2
=12, 解之得t =22,或t =32
2(舍去).
/
故点P 为AC 的中点.(12分)
18.(14分)如图,在圆锥PO 中,已知PO =2,⊙O 的直径AB =2,C
是AB ︵
的中点,D 为AC 的中点.
(1)证明:平面POD ⊥平面PAC ; (2)求二面角B -PA -C 的余弦值.
解: (1)证明:如图所示,以O 为坐标原点,OB ,OC ,OP 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系,则O (0,0,0),A (-1,0,0),B (1,0,0),
C (0,1,0),P (0,0,2),
D ? ??
??
-12,12,0.
设n 1=(x 1,y 1,z 1)是平面POD 的一个法向量,则由n 1·OD →=0,n 1·OP →
=0,
得?????
-12x 1+12y 1=0,2z 1=0.(4分)
∴z 1=0,x 1=y 1.
取y 1=1,得n 1=(1,1,0).
设n 2=(x 2,y 2,z 2)是平面PAC 的一个法向量,则由n 2·PA →=0,n 2·PC →=0,
得?????
-x 2-2z 2=0,y 2-2z 2=0.
∴x 2=-2z 2,y 2=2z 2, 取z 2=1,得n 2=(-2,2,1). ∵n 1·n 2=(1,1,0)·(-2,2,1)=0, ∴n 1⊥n 2.从而平面POD ⊥平面PAC .(8分) (2)∵y 轴⊥平面PAB .
∴平面PAB 的一个法向量为n 3=(0,1,0).由(1)知,平面PAC 的一个法向量为n 2=(-2,2,1).
设向量n 2和n 3的夹角为θ, 则cos θ=n 2·n 3|n 2|·|n 3|=25
=105.
由图可知,二面角B -PA -C 的平面角与θ相等,∴二面角B -PA -C 的余弦
10
值为
5.(14分)
一、选择题 1.若把空间平行于同一平面且长度相等的所有非零向量的始点放置在同一点,则这些向量的终点构成的图形是( ) A.一个圆 B.一个点 C.半圆 D.平行四边形 答案:A 2.在长方体1111ABCD A B C D -中,下列关于1AC 的表达中错误的一个是( ) A.11111AA A B A D ++ B.111AB DD D C ++ C.111AD CC D C ++ D.11111 ()2 AB CD AC ++ 答案:B 3.若,,a b c 为任意向量,∈R m ,下列等式不一定成立的是( ) A.()()a b c a b c ++=++ B.()a b c a c b c +=+··· C.()a b a b +=+m m m D.()()a b c a b c =···· 答案:D 4.若三点,,A B C 共线,P 为空间任意一点,且PA PB PC αβ+=,则αβ-的值为( ) A.1 B.1- C. 1 2 D.2- 答案:B 5.设(43)(32)a b ==,,,,,x z ,且∥a b ,则xz 等于( ) A.4- B.9 C.9- D. 649 答案:B 6.已知非零向量12e e ,不共线,如果1222122833e e e e e e =+=+=-, ,AB AC AD ,则四点,,,A B C D ( ) A.一定共圆 B.恰是空间四边形的四个顶点心 C.一定共面 D.肯定不共面 答案:C 7.如图1,空间四边形ABCD 的四条边及对 角线长都是a ,点E F G ,,分别是AB AD CD ,,
的中点,则2a 等于( ) A.2BA AC · B.2AD BD · C.2FG CA · D.2EF CB · 答案:B 8.若123123123=++=-+=+-,,a e e e b e e e c e e e ,12323d e e e =++,且x y z =++d a b c ,则,,x y z 的值分别为( ) A.51122--,, B.51122 -,, C.51122 --,, D.51122 ,, 答案:A 9.若向量(12)λ=,,a 与(212)=-, ,b 的夹角的余弦值为8 9,则λ=( ) A.2 B.2- C.2-或 255 D.2或255 - 答案:C 10.已知ABCD 为平行四边形,且(413)(251)(375)A B C --,,,,,,,,,则顶点D 的坐标为( ) A.7412??- ???,, B.(241),, C.(2141)-,, D.(5133)-,, 答案:D 11.在正方体1111ABCD A B C D -中,O 为AC BD ,的交点,则1C O 与1A D 所成角的( ) A.60° B.90° C.3arccos 3 D.3arccos 6 答案:D 12.给出下列命题: ①已知⊥a b ,则()()a b c c b a b c ++-=···; ②,,,A B M N 为空间四点,若BA BM BN ,,不构成空间的一个基底,那么A B M N ,,,共面; ③已知⊥a b ,则,a b 与任何向量都不构成空间的一个基底; ④若,a b 共线,则,a b 所在直线或者平行或者重合. 正确的结论的个数为( ) A.1 B.2 C.3 D.4 答案:C 二、填空题 13.已知(315)(123)==-,,,,,a b ,向量c 与z 轴垂直,且满足94==-,··c a c b ,则c = . 答案:2221055?? - ??? ,,
2016-2017第二学期第七章单元测试题 班级__________ 座位_________ 姓名_________ 成绩_____________ 一、选择题(每题3分,共30分) 1.下列说法错误的是( ) A. 零向量与任一非零向量平行 B. 零向量与单位向量的模不相等 C. 平行向量方向相同 D. 平行向量一定是共线向量 2.下列四式不能化简为 的是( ) A.( )+ B.( )+( ) C. + - D. - + 3.已知 =(3,4), =(5,12), 与 则夹角的余弦为( ) A. 65 63 B.65 C. 513 D. 13 4.已知 、 均为单位向量,它们的夹角为60°,那么∣ +3 ∣=( ) A. 7 B. 10 C. 13 D.4 5.点P (-2,6)关于点M(1,2)的对称点C 的坐标为( ) A.(0,-2 ) B.(0,10) C.(4,-2) D.(-4,2) 6.设 , 为不共线向量, = , =-4 - , =-5 -3 ,则下列关系式中正确的是( ) A. B. C. D. 7.与向量a=(-5,4)平行的向量是( ) A.(-5K,4K) B.( k 5-,k 4 -) C.(-10,2) D.(5K,4K) 8. 线段AB 的中点为C ,若AB =BC l ,则l =( ) A 2、 B -2、 C 2或-2、 D -2或 1 2 、 9.与向量(2,3)垂直的向量是( ) A.(-2,3 ) B.(-2,-3) C.(-3,2 ) D.(2,-3) 10.已知点M (3.-3),N (8,y ),且∣ ∣=13,则y 的值为( )
选修2-1第三章空间向量检测题(一) 时间:120分钟 总分:150分 第Ⅰ卷(选择题,共60分) 1.已知向量a =(2,-3,5)与向量b =(3,λ,15 2 )平行,则λ=( ) A.23 B.92 C .-92 D .-23 2.在长方体ABCD -A 1B 1C 1D 1中,AB →+BC →+CC 1→-D 1C 1→等于( ) A.AD 1→ B.AC 1→ C.AD → D.AB → 3.若向量a =(1,m,2),b =(2,-1,2),若cos 〈a ,b 〉=8 9,则m 的值为( ) A .2 B .-2 C .-2或2 55 D .2或-2 55 4.已知空间向量a =(1,1,0),b =(-1,0,2),则与向量a +b 方向相反的单位向量的坐标是( ) A .(0,1,2) B .(0,-1,-2) C .(0,15,2 5 ) D .(0,-15,-2 5 ) 5.已知A ,B ,C 三点不共线,对平面ABC 内任一点O ,下列条件中能确定M 与点A ,B ,C 一定共面的是( )
A.OM →=OA →+OB →+OC → B.OM →=2OA →-OB →-OC → C.OM →=OA →+12OB →+13OC → D.OM →=13OA →+13OB →+13OC → 6.如图,已知空间四边形OABC ,其对角线为OB , AC ,M ,N 分别是对边OA ,BC 的中点,点G 在线 段MN 上,且MG →=2GN →,现用基向量OA →,OB →,OC →表示向量,设OG →=xOA →+yOB →+zOC →,则x ,y ,z 的值分别是( ) A .x =13,y =13,z =13 B .x =13,y =13,z =1 6 C .x =13,y =16,z =13 D .x =16,y =13,z =1 3 7.如图所示,已知三棱锥A -BCD ,O 为△BCD 内一点,则AO →=13 (AB →+AC →+AD →)是O 为△BCD 的重心的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件 8.已知平行六面体ABCD -A 1B 1C 1D 1中,若ABCD 是边长为2的正方形, AA 1=1,∠A 1AD =∠A 1AB =60°,则BD 1的长为( ) A .3 B.7 C.13 D .9 9.如图所示,在直三棱柱ABC -A 1 B 1 C 1中,AB =BC =AA 1,∠ABC =90°,点E ,F 分别是棱AB ,BB 1的中点,则直线 EF 与BC 1所成的角是( ) A .45° B .60° C .90° D .120°
空间向量与立体几何 一、知识网络: 二.考纲要求: (1)空间向量及其运算 ① 经历向量及其运算由平面向空间推广的过程; ② 了解空间向量的概念,了解空间向量的基本定理及其意义,掌握空间向量的正交分解及其坐标表示; ③ 掌握空间向量的线性运算及其坐标表示; ④ 掌握空间向量的数量积及其坐标表示,能运用向量的数量积判断向量的共线与垂直。 (2)空间向量的应用 ① 理解直线的方向向量与平面的法向量; ② 能用向量语言表述线线、线面、面面的垂直、平行关系; ③ 能用向量方法证明有关线、面位置关系的一些定理(包括三垂线定理); ④ 能用向量方法解决线线、线面、面面的夹角的计算问题,体会向量方法在研究几何问题中的作用。 三、命题走向 本章内容主要涉及空间向量的坐标及运算、空间向量的应用。本章是立体几何的核心内容,高考对本章的考查形式为:以客观题形式考查空间向量的概念和运算,结合主观题借助空间向量求夹角和距离。 预测10年高考对本章内容的考查将侧重于向量的应用,尤其是求夹角、求距离,教材上淡化了利用空间关系找角、找距离这方面的讲解,加大了向量的应用,因此作为立体几何解答题,用向量法处
理角和距离将是主要方法,在复习时应加大这方面的训练力度。 第一课时 空间向量及其运算 一、复习目标:1.理解空间向量的概念;掌握空间向量的加法、减法和数乘; 2.了解空间向量的基本定理; 3.掌握空间向量的数量积的定义及其性质;理解空间向量的夹角的概念;掌握空间向量的数量积的概念、性质和运算律;了解空间向量的数量积的几何意义;能用向量的数量积判断向量的共线与垂直。 二、重难点:理解空间向量的概念;掌握空间向量的运算方法 三、教学方法:探析类比归纳,讲练结合 四、教学过程 (一)、谈最新考纲要求及新课标高考命题考查情况,促使积极参与。 学生阅读复资P128页,教师点评,增强目标和参与意识。 (二)、知识梳理,方法定位。(学生完成复资P128页填空题,教师准对问题讲评)。 1.空间向量的概念 向量:在空间,我们把具有大小和方向的量叫做向量。如位移、速度、力等。 相等向量:长度相等且方向相同的向量叫做相等向量。 表示方法:用有向线段表示,并且同向且等长的有向线段表示同一向量或相等的向量。 说明:①由相等向量的概念可知,一个向量在空间平移到任何位置,仍与原来的向量相等,用同向且等长的有向线段表示;②平面向量仅限于研究同一平面内的平移,而空间向量研究的是空间的平移。 2.向量运算和运算率 说明:①引导学生利用右图验证加法交换率,然后推广到首尾相接的若干向量之和;②向量加法的平行四边形法则在空间仍成立。 3.平行向量(共线向量):如果表示空间向量的有向线段所在的直线互相平行或重合,则这些向量 叫做共线向量或平行向量。a 平行于b 记作a ∥b 。 注意:当我们说a 、b 共线时,对应的有向线段所在直线可能是同一直线,也可能是平行直线;当 我们说a 、b 平行时,也具有同样的意义。 共线向量定理:对空间任意两个向量a (a ≠)、b ,a ∥b 的充要条件是存在实数λ使b =λa (1)对于确定的λ和a ,b =λa 表示空间与a 平行或共线,长度为 |λa |,当λ>0时与a 同向, 当λ<0时与a 反向的所有向量。 (3)若直线l ∥a ,l A ∈,P 为l 上任一点,O 为空间任一点,下面根据上述定理来推导的表达式。
向量法解立体几何 立体几何的计算和证明常常涉及到二大问题:一是位置关系,它主要包括线线垂直,线面垂直,线线平行,线面平行;二是度量问题,它主要包括点到线、点到面的距离,线线、线面所成角,面面所成角等。 一、基本工具 1.数量积: cos a b a b θ?= 2.射影公式:向量a 在b 上的射影为 a b b ? 3.直线0Ax By C ++=的法向量为 (),A B ,方向向量为 (),B A - 4.平面的法向量(略) 二、用向量法解空间位置关系 1.平行关系 线线平行?两线的方向向量平行 线面平行?线的方向向量与面的法向量垂直 面面平行?两面的法向量平行 2.垂直关系 线线垂直(共面与异面)?两线的方向向量垂直 线面垂直?线与面的法向量平行 面面垂直?两面的法向量垂直 三、用向量法解空间距离 1.点点距离
点()111,,P x y z 与()222,,Q x y z 的 距离为PQ =u u u r 2.点线距离 求点()00,P x y 到直线:l 0Ax By C ++=的距离: 方法:在直线上取一点(),Q x y , 则向量PQ u u u r 在法向量(),n A B =上的射影 PQ n n ?u u u r = 即为点P 到l 的距离. 3.点面距离 求点()00,P x y 到平面α的距离: 方法:在平面α上去一点(),Q x y ,得向量PQ u u u r , 计算平面α的法向量n , 计算PQ u u u r 在α上的射影,即为点P 到面α的距离. 四、用向量法解空间角 1.线线夹角(共面与异面) 线线夹角?两线的方向向量的夹角或夹角的补角 2.线面夹角 求线面夹角的步骤: ① 先求线的方向向量与面的法向量的夹角,若为锐角角即可,若为钝角,则取其补角; ②再求其余角,即是线面的夹角. 3.面面夹角(二面角) 若两面的法向量一进一出,则二面角等于两法向量的夹角;法
实用文档 《空间向量与立体几何》单元测试题3 一、选择题 1、空间四边形OABC 中,OB OC =,3 AOB AOC π ∠=∠= , 则cos <,OA BC >的值是( ) A . 21 B .22 C .-2 1 D .0 2、若A )12,5,(--x x x ,B )2,2,1(x x -+,当B A 取最小值时,x 的值等于( ) A .19 B .78- C .78 D .14 19 3、若A )1,2,1(-,B )3,2,4(,C )4,1,6(-,则△ABC 的形状是( ) A .不等边锐角三角形 B .直角三角形 C .钝角三角形 D .等边三角形 4、若向量)2,1,2(),2,,1(-==b a λ,且a 与b 的夹角余弦为9 8 ,则λ等于( ) A .2 B .2- C .2-或 552 D .2或55 2- 5、已知点(3,1,4)A --,则点A 关于x 轴对称的点的坐标为( ) A .)4,1,3(-- B .)4,1,3(--- C .)4,1,3( D .)4,1,3(--
实用文档 6、下列各组向量中不平行的是( ) A .)4,4,2(),2,2,1(--=-=b a B .)0,0,3(),0,0,1(-==d c C .)0,0,0(),0,3,2(==f e D .)40,24,16(),5,3,2(=-=h g 二、填空题 7、已知正方体1111ABCD A B C D -的棱长是1,则直线1DA 与AC 间的距离为 。 8、已知空间四边形OABC ,点,M N 分别为,OA BC 的中点,且c C O b B O a A O ===,,,用a ,b , c 表示N M ,则N M =_______________。 9、若19(0,2, )8A ,5(1,1,)8B -,5 (2,1,)8 C -是平面α内的三点,设平面α的法向量),,(z y x a = ,则=z y x ::________________。 10、若(3)a b +⊥)57(b a -,且(4)a b -⊥)57(b a -,则a 与b 的夹角为____________。 11、已知向量,3,5k r j i b k j i m a ++=-+=若//a b 则实数=m ______,=r _______。
空间向量与立体几何知识点归纳总结 一.知识要点。 1. 空间向量的概念:在空间,我们把具有大小和方向的量叫做向量。 注:(1 )向量一般用有向线段表示同向等长的有向线段表示同一或相等的向量。 (2)向量具有平移不变性 2. 空间向量的运算。 定义:与平面向量运算一样,空间向量的加法、减法与数乘运算如下(如图)。 OB OA AB a b =+=+;BA OA OB a b =-=-;()OP a R λλ=∈ 运算律:⑴加法交换律:a b b a +=+ ⑵加法结合律:)()(c b a c b a ++=++ ⑶数乘分配律:b a b a λλλ+=+)( 运算法则:三角形法则、平行四边形法则、平行六面体法则 3. 共线向量。 (1)如果表示空间向量的有向线段所在的直线平行或重合,那么这些向量也叫做共 线向量或平行向量,a 平行于b ,记作b a //。 (2)共线向量定理:空间任意两个向量a 、b (b ≠0 ),a //b 存在实数λ,使a =λb 。 (3)三点共线:A 、B 、C 三点共线<=>λ= <=>)1(=++=y x OB y OA x OC 其中 (4)与共线的单位向量为a ± 4. 共面向量 (1)定义:一般地,能平移到同一平面内的向量叫做共面向量。 说明:空间任意的两向量都是共面的。 (2)共面向量定理:如果两个向量,a b 不共线,p 与向量,a b 共面的条件是存在实数 ,x y 使p xa yb =+。 (3)四点共面:若A 、B 、C 、P 四点共面<=>y x AP += <=>)1(=++++=z y x OC z OB y OA x OP 其中 5. 空间向量基本定理:如果三个向量,,a b c 不共面,那么对空间任一向量p ,存在一 个唯一的有序实数组,,x y z ,使p xa yb zc =++。
《平面向量》单元测试卷A (含答案) 一、选择题:(本题共10小题,每小题4分,共40分) 1.下列命题中的假命题是( ) A 、A B BA -→ -→ 与的长度相等; B 、零向量与任何向量都共线; C 、只有零向量的模等于零; D 、共线的单位向量都相等。 2.||||a b a b a b → → → → → → >若是任一非零向量,是单位向量;①;②∥; ||0||1|| a a b b a → →→ → → >=±=③;④;⑤ ,其中正确的有( ) A 、①④⑤ B 、③ C 、①②③⑤ D 、②③⑤ 3.0a b c a b c a b c → → → → → → → → → → ++=设,,是任意三个平面向量,命题甲:;命题乙:把,, 首尾相接能围成一个三角形。则命题甲是命题乙的( ) A 、充分不必要条件 B 、必要不充分条件 C 、充要条件 D 、非充分也非必要条件 4.AD -→ 下列四式中不能化简为的是( ) A 、A B CD B C -→ -→ -→ ++() B 、AM MB B C C D -→ -→ -→ -→ +++()() C 、AC AB A D CB -→ -→ -→ -→ ++-()() D 、OC OA CD -→ -→ -→ -+
5.) ,则( ),(,),(设21b 42a -=-=→ → A 、共线且方向相反与→ →b a B 、共线且方向相同与→ →b a C 、不平行与→ → b a D 、是相反向量与→ → b a 6.如图1,△ABC 中,D 、E 、F 分别是边BC 、CA 和AB 的中点,G 是△ABC 中的重心,则下列各等式中不成立的是( ) A 、→-→ -=BE 3 2BG B 、→-→ -=AG 2 1DG C 、→ -→--=FG 2CG D 、→ -→ -→ -=+BC 2 1FC 3 2DA 3 1 7. )(,则锐角∥,且),(,),(设=-+=--=→→→→θθθb a 4 1 cos 1b cos 12a A 、4 π B 、 6 π C 、3 π D 、 3 6ππ或 8.) 所成的比是( 分,则所成比为分若→ -→--CB A 3AB C A 、2 3 - B 、3 C 、3 2- D 、-2 9.) 的范围是( 的夹角与,则若θ→ →→→
已知两异面直线 b a,,,,, A B a C D b ∈∈,则异面直线所成的角θ为:cos AB CD AB CD θ? = u u u r u u u r u u u r u u u r 例题 【空间向量基本定理】 例1.已知矩形ABCD,P为平面ABCD外一点,且PA⊥平面ABCD,M、N分别为PC、PD上的点,且M分成定比2,N分PD成定比1,求满足的实数x、y、z的值。 分析;结合图形,从向量出发,利用向量运算法则不断进行分解,直到全部向量都用、、表示出来,即可求出x、y、z的值。 如图所示,取PC的中点E,连接NE,则。 点评:选定空间不共面的三个向量作基向量,并用它们表示出指定的向量,是用向量解决立体几何问题的一项基本功,要结合已知和所求,观察图形,联想相关的运算法则和公式等,就近表示所需向量。再对照目标,将不符合目标要求的向量当作新的所需向量,如此继续下去,直到所有向量都符合目标要求为止,这就是向量的分解。有分解才有组合,组合是分解的表现形式。空间向量基本定理恰好说明,用空间三个不共面的向量组可以表示出空间任意一个向量,而且a,b,c的系数是惟一的。 【利用空间向量证明平行、垂直问题】 例2.如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB于点F。 (1)证明:PA方形ABCD—中,E、F分别是,的中点,求:(1)异面直线AE与CF所成角的余弦值; (2)二面角C—AE—F的余弦值的大小。
点评:(1)两条异面直线所成的角可以借助这两条直线的方向向量的夹角求得,即。 (2)直线与平面所成的角主要可以通过直线的方向向量与平面的法向量的夹角求得,即 或 (3)二面角的大小可以通过该二面角的两个面的法向量的夹角求得,它等于两法向量的夹角或其补角。 【用空间向量求距离】 例4.长方体ABCD —中,AB=4,AD=6,,M 是A 1C 1的中点,P 在线段BC 上,且|CP|=2,Q 是DD 1的中点, 求: (1)异面直线AM 与PQ 所成角的余弦值; (2)M 到直线PQ 的距离; (3)M 到平面AB 1P 的距离。 本题用纯几何方法求解有一定难度,因此考虑建立空间直角坐标系,运用向量坐标法来解决。利用向量的模和夹角求空间的线段长和两直线的夹角,在新高考试题中已多次出现,但是利用向量的数量积来求空间的线与线之间的夹角和距离,线与面、面与面之间所成的角和距离还涉及不深,随着新教材的推广使用,这一系列问题必将成为高考命题的一个新的热点。现列出几类问题的解决方法。 (1)平面的法向量的求法:设,利用n 与平面内的两个向量a ,b 垂直,其数量积为零,列出两个三元 一次方程,联立后取其一组解。 (2)线面角的求法:设n 是平面的一个法向量,AB 是平面 的斜线l 的一个方向向量,则直线与平面 所成 角为n AB n AB ??= θθsin 则 (3)二面角的求法:①AB,CD 分别是二面角 的两个面内与棱l 垂直的异面直线,则二面角的大小为
东升学校《空间向量与立体几何》单元测试题 一、选择题(本大题8小题,每小题5分,共40分) 1、若a r ,b r ,c r 是空间任意三个向量, R λ∈,下列关系式中,不成立 的是( ) A .a b b a +=+r r r r B .() a b a b λλλ+=+r r r r C .( )()a b c a b c ++=++r r r r r r D .b a λ=r r 2、给出下列命题 ①已知a b ⊥r r ,则() () a b c c b a b c ?++?-=?r r r u r r r r r ; ②A 、B 、M 、N 为空间四点,若,,BA BM BN u u u r u u u u r u u u r 不构成空间的一个基 底,则A 、B 、M 、N 共面; ③已知a b ⊥r r ,则,a b r r 与任何向量不构成空间的一个基底; ④已知{ } ,,a b c r r r 是空间的一个基底,则基向量,a b r r 可以与向量 m a c =+u r r r 构成空间另一个基底. 正确命题个数是( ) A .1 B .2 C .3 D .4 3、已知,a b r r 均为单位向量,它们的夹角为 60,那么 3a b +r r 等于 ( ) A . 7 B . 10 C .13
D .4 4、 1,2,,a b c a b ===+r r r r r 且c a ⊥r r ,则向量a b r r 与的夹角为( ) A .30 B .60 C .120 D .150 5、已知()()3,2,5,1,,1,a b x =-=-r r 且2a b ?=r r ,则 x 的值是( ) A .3 B .4 C .5 D .6 6、若直线l 的方向向量为a r ,平面α 的法向量为n r ,则能使//l α的 是( ) A .()()1,0,0,2,0,0a n ==-r r B .()()1,3,5,1,0,1a n ==r r C .()()0,2,1,1,0,1a n ==--r r D .()()1,1,3,0,3,1a n =-=r r 7、在平面直角坐标系中, (2,3),(3,2)A B --,沿x 轴把平面直角坐标 系折成120的二面角后,则线段的长度为( ) A .2 B . 11 C .32 D .4 2 8、正方体1B 1C 1D 1的棱长为1是A 1B 1中点,则E 到平面1D 1的距离是( ) A . 3 B . 22 C . 1 2
立体几何空间向量知识点总结 知识网络: 知识点拨: 1、空间向量的概念及其运算与平面向量类似,向量加、减法的平行四边形法则,三角形法则以及相关的运算律仍然成立.空间向量的数量积运算、共线向量定理、共面向量定理都是平面向量在空间中的推广,空间向量基本定理则是向量由二维到三维的推广. 2、当a 、b 为非零向量时.0a b a b ?=?⊥是数形结合的纽带之一,这是运用空间向量研究线线、线面、面面垂直的关键,通常可以与向量的运算法则、有关运算律联系来解决垂直的论证问题. 3、公式 cos ,a b a b a b ?<>= ?是应用空间向量求空间中各种角的基础,用这个公式可以求 两异面直线所成的角(但要注意两异面直线所成角与两向量的夹角在取值范围上的区别),再结合平面的法向量,可以求直线与平面所成的角和二面角等. 4、直线的方向向量与平面的法向量是用来描述空间中直线和平面的相对位置的重要概念,通过研究方向向量与法向量之间的关系,可以确定直线与直线、直线与平面、平面与平面等的位置关系以及有关的计算问题. 5、用空间向量判断空间中的位置关系的常用方法 (1)线线平行 证明两条直线平行,只需证明两条直线的方向向量是共线向量. (2)线线垂直 证明两条直线垂直,只需证明两条直线的方向向量垂直,即0a b a b ?=?⊥.
(3)线面平行 用向量证明线面平行的方法主要有: ①证明直线的方向向量与平面的法向量垂直; ②证明可在平面内找到一个向量与直线方向向量是共线向量; ③利用共面向量定理,即证明可在平面内找到两不共线向量来线性表示直线的方向向量. (4)线面垂直 用向量证明线面垂直的方法主要有: ①证明直线方向向量与平面法向量平行; ②利用线面垂直的判定定理转化为线线垂直问题. (5)面面平行 ①证明两个平面的法向量平行(即是共线向量); ②转化为线面平行、线线平行问题. (6)面面垂直 ①证明两个平面的法向量互相垂直; ②转化为线面垂直、线线垂直问题. 6、运用空间向量求空间角 (1)求两异面直线所成角 利用公式cos, a b a b a b ? <>= ? , 但务必注意两异面直线所成角θ的范围是 0, 2 π ?? ???, 故实质上应有:cos cos,a b θ=<> . (2)求线面角 求直线与平面所成角时,一种方法是先求出直线及射影直线的方向向量,通过数量积求出直线与平面所成角;另一种方法是借助平面的法向量,先求出直线方向向量与平面法向量的夹角φ,即可求出直线与平面所成的角θ,其关系是sinθ=| cosφ|. (3)求二面角 用向量法求二面角也有两种方法:一种方法是利用平面角的定义,在两个面内先求出与棱垂直的两条直线对应的方向向量,然后求出这两个方向向量的夹角,由此可求出二面角的大小;另一种方法是转化为求二面角的两个面的法向量的夹角,它与二面角的大小相等或互补. 7、运用空间向量求空间距离 空间中的各种距离一般都可以转化为求点与点、点与线、点与面的距离. (1)点与点的距离 点与点之间的距离就是这两点间线段的长度,因此也就是这两点对应向量的模. (2)点与面的距离 点面距离的求解步骤是: ①求出该平面的一个法向量; ②求出从该点出发的平面的任一条斜线段对应的向量; ③求出法向量与斜线段向量的数量积的绝对值再除以法向量的模,即得要求的点面距
一、多选题 1.在ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,ABC 的面积为S .下列 ABC 有关的结论,正确的是( ) A .cos cos 0A B +> B .若a b >,则cos2cos2A B < C .24sin sin sin S R A B C =,其中R 为ABC 外接圆的半径 D .若ABC 为非直角三角形,则tan tan tan tan tan tan A B C A B C ++= 2.在△ABC 中,a ,b ,c 是角A ,B ,C 的对边,已知A =3 π ,a =7,则以下判断正确的是( ) A .△ABC 的外接圆面积是493 π ; B .b cos C +c cos B =7; C .b +c 可能等于16; D .作A 关于BC 的对称点A ′,则|AA ′|的最大 值是 3.已知ABC ?是边长为2的等边三角形,D ,E 分别是AC 、AB 上的两点,且 AE EB =,2AD DC =,BD 与CE 交于点O ,则下列说法正确的是( ) A .1A B CE ?=- B .0OE O C += C .32 OA OB OC ++= D .ED 在BC 方向上的投影为 76 4.下列结论正确的是( ) A .已知a 是非零向量,b c ≠,若a b a c ?=?,则a ⊥(-b c ) B .向量a ,b 满足|a |=1,|b |=2,a 与b 的夹角为60°,则a 在b 上的投影向量为 12 b C .点P 在△ABC 所在的平面内,满足0PA PB PC ++=,则点P 是△ABC 的外心 D .以(1,1),(2,3),(5,﹣1),(6,1)为顶点的四边形是一个矩形 5.在ABC 中,内角A 、B 、C 所对的边分别为a 、b 、 c ,不解三角形,确定下列判断错误的是( ) A . B =60°,c =4,b =5,有两解 B .B =60°,c =4,b =3.9,有一解 C .B =60°,c =4,b =3,有一解 D .B =60°,c =4,b =2,无解 6.在ABC ?中,角A ,B ,C 所对的边分别为a ,b ,c ,且 ()()()::9:10:11a b a c b c +++=,则下列结论正确的是( ) A .sin :sin :sin 4:5:6A B C = B .AB C ?是钝角三角形
空间向量与立体几何单元测试题一、选择题 1、若a,b,c是空间任意三个向量, R λ∈,下列关系式中,不成立的是() A.a b b a +=+ B. () a b a b λλλ +=+ C.()() a b c a b c ++=++ D. b a λ = 2、给出下列命题 ①已知a b ⊥, 则 ()() a b c c b a b c ?++?-=? ; ②A、B、M、N 为空间四点,若 ,, BA BM BN 不构成空间的一个基底, 则A、B、M 、N共面; ③已知a b ⊥,则,a b与任何向量不构成空间的一个基底; ④已知{} ,, a b c 是空间的一个基底,则基向量 ,a b 可以与向量 m a c =+构成空间另一个基底. 正确命题个数是() A.1 B.2 C.3 D.4 3、已知,a b 均为单位向量,它们的夹角为60?,那么 3 a b + 等于() A 7 B 10 C 13 D.4 4、 1,2,, a b c a b ===+ 且 c a ⊥,则向量a b 与 的夹角为() A.30?B.60?C.120?D.150?5、已知 ()() 3,2,5,1,,1, a b x =-=- 且 2 a b?=,则x的值是() A.3 B.4 C.5 D .6 6、若直线l的方向向量为 a,平面α的法向量为n,则能使//lα的是( ) A ()() 1,0,0,2,0,0 a n ==- B. ()() 1,3,5,1,0,1 a n == C ()() 0,2,1,1,0,1 a n ==-- D. ()() 1,1,3,0,3,1 a n =-= 7.空间四边形OABC中,OB OC =, 3 AOB AOC π ∠=∠=,则cos<, OA BC>的值是() A. 2 1 B. 2 2 C.- 2 1 D.0 8、正方体ABCD-1 1 1 1 D C B A的棱长为1,E是 1 1 B A中点,则E到平面 1 1 D ABC的距离是() A. 3 B. 2 C. 1 2D. 3 9.若向量a与b的夹角为60°,4 = b,(2)(3)72 a b a b +-=-,则a=() A.2B.4 C.6 D.12 10.如图,A1B1C1—ABC是直三棱柱,∠BCA=90°,点D1、F1分别是A1B1、A1C1的中点,若BC=CA=CC1,则BD1与AF1所成角的余弦值是() A. 10 30 B. 2 1 C. 15 30 D. 10 15 1
一、多选题 1.在ABC 中,a ,b ,c 分别是内角A ,B ,C 2sin c A =,且 02 C << π ,4b =,则以下说法正确的是( ) A .3 C π = B .若72 c = ,则1cos 7B = C .若sin 2cos sin A B C =,则ABC 是等边三角形 D .若ABC 的面积是4 2.在ABC 中,a ,b ,c 分别为角A ,B ,C 的对边,已知 cos cos 2B b C a c =-, ABC S = △b = ) A .1cos 2 B = B .cos 2 B = C .a c += D .a c +=3.已知ABC 的面积为3,在ABC 所在的平面内有两点P ,Q ,满足20PA PC +=, 2QA QB =,记APQ 的面积为S ,则下列说法正确的是( ) A .//P B CQ B .2133 BP BA BC = + C .0PA PC ?< D .2S = 4.已知ABC ?是边长为2的等边三角形,D ,E 分别是AC 、AB 上的两点,且 AE EB =,2AD DC =,BD 与CE 交于点O ,则下列说法正确的是( ) A .1A B CE ?=- B .0OE O C += C .3 2 OA OB OC ++= D .ED 在BC 方向上的投影为 76 5.设P 是ABC 所在平面内的一点,3AB AC AP +=则( ) A .0PA PB += B .0PB PC += C .PA AB PB += D .0PA PB PC ++= 6.ABC 中,2AB =,30ACB ∠=?,则下列叙述正确的是( ) A .ABC 的外接圆的直径为4. B .若4A C =,则满足条件的ABC 有且只有1个 C .若满足条件的ABC 有且只有1个,则4AC = D .若满足条件的ABC 有两个,则24AC <<
向量法解立体几何 引言 立体几何的计算和证明常常涉及到二大问题:一是位置关系,它主要包括线线垂直,线面垂直,线线平行,线面平行;二是度量问题,它主要包括点到线、点到面的距离,线线、线面所成角,面面所成角等。教材上讲的比较多的主要是用向量证明线线、线面垂直及计算线线角,而如何用向量证明线面平行,计算点到平面的距离、线面角及面面角的例题不多,给老师对这部分内容的教学及学生解有关这部分内容的题目造成一定的困难,下面主要就这几方面问题谈一下自己的想法,起到一个抛砖引玉的作用。 一、基本工具 1.数量积: cos a b a b θ?= 2.射影公式:向量a 在b 上的射影为 a b b ? 3.直线0Ax By C ++=的法向量为 (),A B ,方向向量为 (),B A - 4.平面的法向量(略) 二、用向量法解空间位置关系 1.平行关系 线线平行?两线的方向向量平行 线面平行?线的方向向量与面的法向量垂直 面面平行?两面的法向量平行 2.垂直关系
线线垂直(共面与异面)?两线的方向向量垂直 线面垂直?线与面的法向量平行 面面垂直?两面的法向量垂直 三、用向量法解空间距离 1.点点距离 点()111,,P x y z 与()222,,Q x y z 的 距离为(PQ x =2.点线距离 求点()00,P x y 到直线:l 0Ax By C ++=的距离: 方法:在直线上取一点(),Q x y , 则向量PQ 在法向量 (),n A B =上的射影PQ n n ?= 即为点P 到l 的距离. 3.点面距离 求点()00,P x y 到平面α的距离: 方法:在平面α上去一点(),Q x y ,得向量PQ , 计算平面α的法向量n , 计算PQ 在α上的射影,即为点P 到面α的距离. 四、用向量法解空间角 1.线线夹角(共面与异面) 线线夹角?两线的方向向量的夹角或夹角的补角 2.线面夹角 求线面夹角的步骤:
& 第三章 空间向量与立体几何 单元测试 (时间:90分钟 满分:120分) 第Ⅰ卷(选择题,共50分) 一、选择题:本大题共10小题,每小题5分,共50分. 1.以下四组向量中,互相平行的组数为( ) ①a =(2,2,1),b =(3,-2,-2);②a =(8,4,-6),b =(4,2,-3);③a =(0,-1,1),b =(0,3,-3);④a =(-3,2,0),b =(4,-3,3) A .1组 B .2组 C .3组 D .4组 : 解析:∵②中a =2b ,∴a ∥b ;③中a =-1 3b , ∴a ∥b ;而①④中的向量不平行. 答案:B 2.在以下命题中,不正确的个数为( ) ①|a |-|b |=|a +b |是a ,b 共线的充要条件;②若a ∥b ,则存在唯一 的实数λ,使a =λb ;③对空间任意一点O 和不共线的三点A ,B ,C ,若OP → =2OA →-2OB →-OC → ,则P ,A ,B ,C 四点共面;④若{a ,b ,c }为空间的一组基底,则{a +b ,b +c ,c +a }构成空间的另一组基底;⑤|(a ·b )·c |=|a |·|b |·|c |. A .2个 B .3个 C .4个 D .5个 解析:①|a |-|b |=|a +b |?a 与b 共线,但a 与b 共线时|a |-|b |=|a +b |不一定成立,故不正确;②b 需为非零向量,故不正确;③因为2-2-1≠1,由共面向量定理知,不正确;④由基底的定义知正确;⑤由向
量的数量积的性质知,不正确. ! 答案:C 3.如图,已知四边形ABCD 为矩形,PA ⊥平面ABCD ,连接AC ,BD ,PB , PC ,PD ,则下列各组向量中,数量积不一定为零的是( ) 与BD → 与PB → 与AB → 与CD → 解析:建立如图所示的空间直角坐标系. 设矩形ABCD 的长、宽分别为a ,b ,PA 长为c ,则A (0,0,0),B (b,0,0), D (0,a,0),C (b ,a,0),P (0,0,c ). - 则PC →=(b ,a ,-c ),BD →=(-b ,a,0),DA →=(0,-a ,0),PB → =(b,0,
平面向量单元测试题2 一,选择题: 1,下列说法中错误得就是( ) A.零向量没有方向? B.零向量与任何向量平行 C.零向量得长度为零? D.零向量得方向就是任意得 2,下列命题正确得就是( ) A、若、都就是单位向量,则= B、若=, 则A、B、C、D四点构成平行四边形 C、若两向量、相等,则它们就是始点、终点都相同得向量 D、与就是两平行向量 3,下列命题正确得就是( ) A、若∥,且∥,则∥。 B、两个有共同起点且相等得向量,其终点可能不同。 C、向量得长度与向量得长度相等, D、若非零向量与就是共线向量,则A、B、C、D四点共线。 4,已知向量,若,=2,则 ( ) A.1B、C、 D、 5,若=(,),=(,),,且∥,则有( ) A,+=0, B,―=0, C,+=0,D, ―=0, 6,若=(,),=(,),,且⊥,则有( ) A,+=0, B,―=0, C,+=0, D, ―=0, 7,在中,若,则一定就是 ( ) A.钝角三角形? B.锐角三角形C.直角三角形 D.不能确定 8,已知向量满足,则得夹角等于( ) A. B C D 二,填空题:(5分×4=20分) 9。已知向量、满足==1,=3,则= 10,已知向量=(4,2),向量=(,3),且//,则=
11,、已知三点A(1,0),B(0,1),C(2,5),求cos∠BAC = 12,、把函数得图像按向量经过一次平移以后得到得图像, 则平移向量就是(用坐标表示) 三,解答题:(10分×6 = 60分) 13,设且在得延长线上,使,,则求点 得坐标 14,已知两向量求与所成角得大小, 15,已知向量=(6,2),=(-3,k),当k为何值时,有 (1),∥ ? (2),⊥ ? (3),与所成角θ就是钝角 ? 16,设点A(2,2),B(5,4),O为原点,点P满足=+,(t为实数); (1),当点P在x轴上时,求实数t得值; (2),四边形OABP能否就是平行四边形?若就是,求实数t得值;若否,说明理由, 17,已知向量=(3, -4), =(6, -3),=(5-m,-3-m), (1)若点A、B、C能构成三角形,求实数m应满足得条件; (2)若△ABC为直角三角形,且∠A为直角,求实数m得值. 18,已知向量 (1)求向量; (2)设向量,其中, 若,试求得取值范围、 平面向量单元测试题2答案: 一,选择题: A D C D B C C A 二,填空题: 9,2; 10,6; 11, 12, 三,解答题: 13,解法一:设分点P(x,y),∵=―2,λ=―2 ∴ (x―4,y+3)=―2(―2―x,6―y), x―4=2x+4, y+3=2y―12,∴ x=―8,y=15, ∴P(―8,15)解法二:设分点P(x,y),∵=―2,λ=―2 ∴x==―8, y==15, ∴ P(―8,15) 解法三:设分点P(x,y),∵, ∴―2=, x=―8, 6=, y=15, ∴P(―8,15) 14,解:=2, = , cos<,>=―, ∴<,>=1200, 15,解:(1),k=-1; (2), k=9; (3), k<9, k≠-1