
随机信号分析
第一章
1. 2. 3. 4. 5. 6. 7.
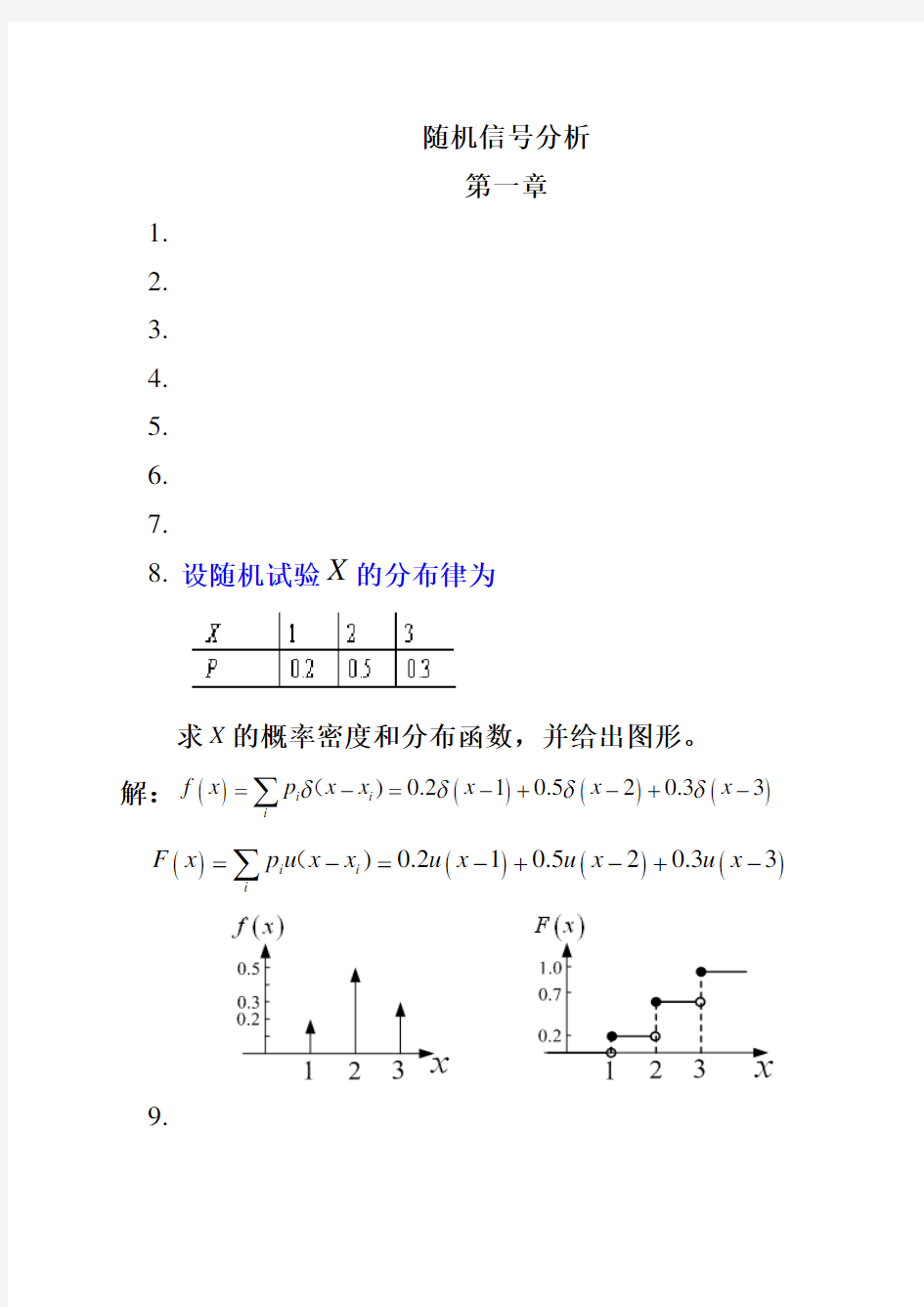
8. 设随机试验X 的分布律为
求X 的概率密度和分布函数,并给出图形。
解:()()()())0.210.520.33i i i
f x p x x x x x δ
δδδ=-=-+-+-∑( ()()()())0.210.520.33i i i
F x p u x x u x u x u x =-=-+-+-∑(
9.
10. 设随机变量X 的概率密度函数为()x
f x ae
-=,
求:(1)
系数a ;(2)其分布函数。
解:(1)由
()1f x dx ∞
-∞
=?
()
()2x
x
x f x dx ae dx a
e dx e dx a ∞
∞
∞
---∞
-∞
-∞
==+=?
??
?
所以12a =
(2)()1()2
x
x
t
F x f t dt e dt --∞
-∞=
=?
?
所以X 的分布函数为
()1,02
11,02
x
x e x F x e x -?
?-≥?? 11. 12.
13. 若随机变量X 与Y 的联合分布律为
求:(1)X 与Y 的联合分布函数与密度函数;(2)X 与Y 的边缘分布律;(3)Z XY =的分布律;(4)X 与Y 的相
关系数。 解:(1)
()()
()()()()()()
,,0.07,10.18,0.15,10.081,10.321,0.201,1ij i j i
j
F x y p u x x y y u x y u x y u x y u x y u x y u x y =--=+++-+-++-+--∑∑
()()
()()()()()(),,0.07,10.18,0.15,10.081,10.321,0.201,1ij i j i
j
f x y p x x y y x y x y x y x y x y x y δδδδδδδ=--=+++-+-++-+--∑∑
(2)X 的分布律为(i ij j
P P ?=∑)
()()00.070.180.150.4010.080.320.200.60P X P X ==++===++=
Y 的分布律为
()()()10.070.080.1500.180.320.5010.150.200.35
P Y P Y P Y =-=+===+===+=
(3)Z XY =的分布律为
()()()()()
()()()()()111,10.080001,00.400.320.72111,10.20
P Z P XY P X Y P Z P XY P X P X Y P Z P XY P X Y =-==-===-======+===+======== (4)因为
()()()00.4010.600.60
10.1500.5010.350.20E X E Y =?+?==-?+?+?=
()()10.0800.7210.200.12E XY =-?+?+?=
则
()()()()
ov ,0.120.600.200
C X Y E XY E X E Y =-=-?=
X 与Y 的相关系数0XY ρ=,可见它们无关。
14.
15. 设随机变量()~0,1X N ,()~0,1Y N 且相互独立,
U X Y V X Y =+??=-?
。 (1) 随机变量(),U V 的联合概率密度(),UV f u v ; (2) 随机变量U 与V 是否相互独立? 解:(1)随机变量(),X Y 的联合概率密度为
()()222
2
1,,,2x y XY f x y e
x y R
π
+-
=∈
由反函数 22u v x u v y +?=???-?=??, 1112211222J ==-
-
, ()()()222
4
1
,,,,4u v UV XY f u v f x y J e
u v R π
+-
=?=∈
由于,
(3)
22224
4
4
1114u v u v e
e e π
+-
--????=? ? ? ? ??
???
()()()()2
,,UV U V f u v f u f v u v R =∈
所以随机变量U 与V 相互独立。 16. 17. 18. 19.
20. 已知对随机变量X 与Y ,有1EX =,3EY =,
()4D X =,()16D Y =,0.5XY ρ=,又设 3U X Y =+,
2V X Y =-,试求EU ,EV ,()D U ,()D V 和
(,)Cov U V 。
(22
()()D U EU EU =-)
解:首先,
22
()()5EX D X EX =+=,
22()()25EY D Y EY =+=。
又因为
()(,)7XY E XY Cov X Y EX EY EX EY ρ=+?=+?=
于是
(3)36EU E X Y EX EY =+=+=
(2)25EV E X Y EX EY =-=-=-
()2
2
2
2
222
()()3()(96)()76
D U EU EU
E X Y EU E X XY Y EU =-=+-=++-=
()2
2
2
2
222()()2()(44)()52
D V EV EV
E X Y EV E X XY Y EV =-=--=-+-=
[]22()(3)(2)(352)70E UV E X Y X Y E X XY Y =+-=--=-
(,)()40Cov U V E UV EU EV =-?=-
21. 22.
23. 已知随机变量X 服从[0,]a 上的均匀分布。随机变量
Y 服从[,]X a 上的均匀分布,试求
(1) (),(0)E Y X X a ≤≤; (2) EY
解:(1)对[0,]x a ∈有,
()2a X
E Y X +=
(2)
/23
(())2
24a X
a a EY E E Y X E a ++??===
=
???
24.
25. 设太空梭飞行中,宇宙粒子进入其仪器舱的数目N 服从(参数为λ)泊松分布。进舱后每个粒子造成损坏的概率为p ,彼此独立。求:造成损坏的粒子平均数目。解:每个粒子是否造成损坏用i X 表示
1,1,2,,0i X i N
?==?
?L 造成损坏没有造成损害
,
造成损坏的粒子数
1
N
i
i Y X ==∑ ,于是
()
1
1
(|)(|)
|n
i i n
i i E Y N n E X N n E X N n =======∑∑
可合理地认为N 和i X 是独立的,于是
()1
(|)n
i i E Y N n E X np
====∑
()()()()(|)E Y E E Y N E Np pE N p λ====
27. 若随机变量X 的概率特性如下,求其相应的特征函数:
(1)X 为常数c ,即{}1P X c ==;
(2)参数为2的泊松分布; (3)(-1,1)伯努利分布:
()0.4(1)0.6(1)f x x x δδ=-++
(4)指数分布:
30
3(),
x
x e f x -≥?=??其他
解:(1)()jvX jvc jvc X v E e E e e φ????===????
, 如果c=0,则()1X v φ=。
(2)
{}
()()0
00
1()!!jv jv jvX jvk X k k
jv k jvk k k e e
v E e e P X k e e e e k k e e e λλ
λλλφλλ∞
=∞
∞--==--??===??====∑∑∑
(3)()11()0.40.60.40.6jv jvX jv jv jv
X v E e e e e e φ--??==?+?=+??
(4)3(3)003
()333jvX
jvx x
jv x
X v E e e e dx e
dx jv φ+∞
+∞
--??==?==
??-??
28. 随机变量123,,X X X 彼此独立;且特征函数分别为
123(),(),()v v v φφφ,求下列随机变量的特征函数:
(1)12X X X =+; (2)123X X X X =++; (3)12323X X X X =++; (4)1232410X X X X =+++;
解:(1)12X X X =+
12()()()jvX
X v E e v v φφφ??==??
(2)123X X X X =++
同(1),123()()()()X v v v v φφφφ= (3)12323X X X X =++
123()()(2)(3)X v v v v φφφφ=
(4)1232410X X X X =+++
10
123()(2)()(4)jv X v e v v v φφφφ=
29. 随机变量X 具有下列特征函数,求其概率密度函数、均值、均方值与方差。
(1)2424()0.20.30.20.20.1j v j v j v j v v e e e e φ--=++++;
(2)()
0.30.7jv jv
v e e
φ-=+; (3)()4/(4)v jv φ=-
;
(4)()(sin5)/(5)v v v φ=;
解:(1)1()i
k
j v x i i v p e
φ==∑
()()1
k
i i i f x p x x δ==-∑
2424()0.20.30.20.20.1j v j v j v j v v e e e e φ--=++++
()()()()()()0.20.320.240.220.14f x x x x x x δδδδδ=+-+-++++
()()()(0)/20.340.220.240.10.6E X j
φ'==?+?+-?+-?=
()()()()22
2
2
2
2
(0)
20.340.220.240.1 6.8
E X
j φ''=-=?+?+-?+-?=
()()()22 6.80.36 6.44Var X E X E X =-=-=
(2)()
11
()
0.30.7jv jv v e
e
φ??-=+
()()()0.310.71f x x x δδ=-++
()()(0)/10.310.70.4E X j φ'==?+-?=-
()()()
2
2
2
2
(0)10.310.71E X
j φ''=-=?+-?=
()()()2210.160.84Var X E X E X =-=-= (3)()4/(4)v jv φ=-
()4/(4)v jv φ-=+
利用傅里叶变换公式,可知这是指数分布,
()44()x
f x e u x -=
()4/(4)v jv φ=-
()()(0)k k k E X j φ??=-??
()2
1
(0)/4(4)
4
v E X j jv φ-='==-= ()2
3
1(0)8(4)
8
v E X
jv φ-=''=-=-= ()()2
2
111
()81616
Var X E X E X =-=-=。
(4)()
()sin /2()2
/2x t p t sa τωτωτ
ττωτ??=?=
???
sin 51sin10/2()10()51010/2v v v v v v φφ??
==??=-???? ,利用傅里叶变换公式,可知这是均匀分布,
()1
,5510
0,x f x ?-<
()0E X =, ()2
1025123Var X ==,
()()()2
2
25
3E X Var X E X =+=
。
30. 利用傅立叶变换推导均匀分布的特征函数。
解:由于()f x 是宽度为b a -,高度为1b a -,中心在2
a b
+
处的矩形函数。即()1()2b a a b f x p x b a -+?
?=- ?-?? 其傅立叶变换为
[]()2sin ()/21
()()()/2jv a b v b a F v b a e b a v b a -+??-=?-???--??
()()X v F v φ-=Q
[]
[]
()2
sin ()2()()()2()jvb jva
jv a b X v b a e e v F v e v b a jv b a φ+--=-=
=
--
31. 32.
33. 设有高斯随机变量
2
~(,)X N μσ,试利用随机变量的矩发生特性(()
()(0)k k k E X j φ??=-??
)证明: (1) EX μ= (2) 222
EX σμ=+
(3) 323
3EX μσμ=+
解:特征函数为22
()exp(2)X v j v v φμσ=-
由矩发生性质,
222
2
()(0)()()e
X
j v v v EX j j j v μσφμσμ
-='=-=--=
222222
2
2
2
2
2
2
22
()(0)()()e e
X
j v v j v v v EX j j j v μσμσφμσσσμ
--=''=-??=---?
?=+22
22333
232
22
2
23
()(0)()()e 3()e
3X
j v v j v v v EX j j j v j v μσμσφμσσμσμσμ--='''=-??=----?
?=+