
高三数学第二轮专题复习必备精品系列教案习题(4)
三角函数
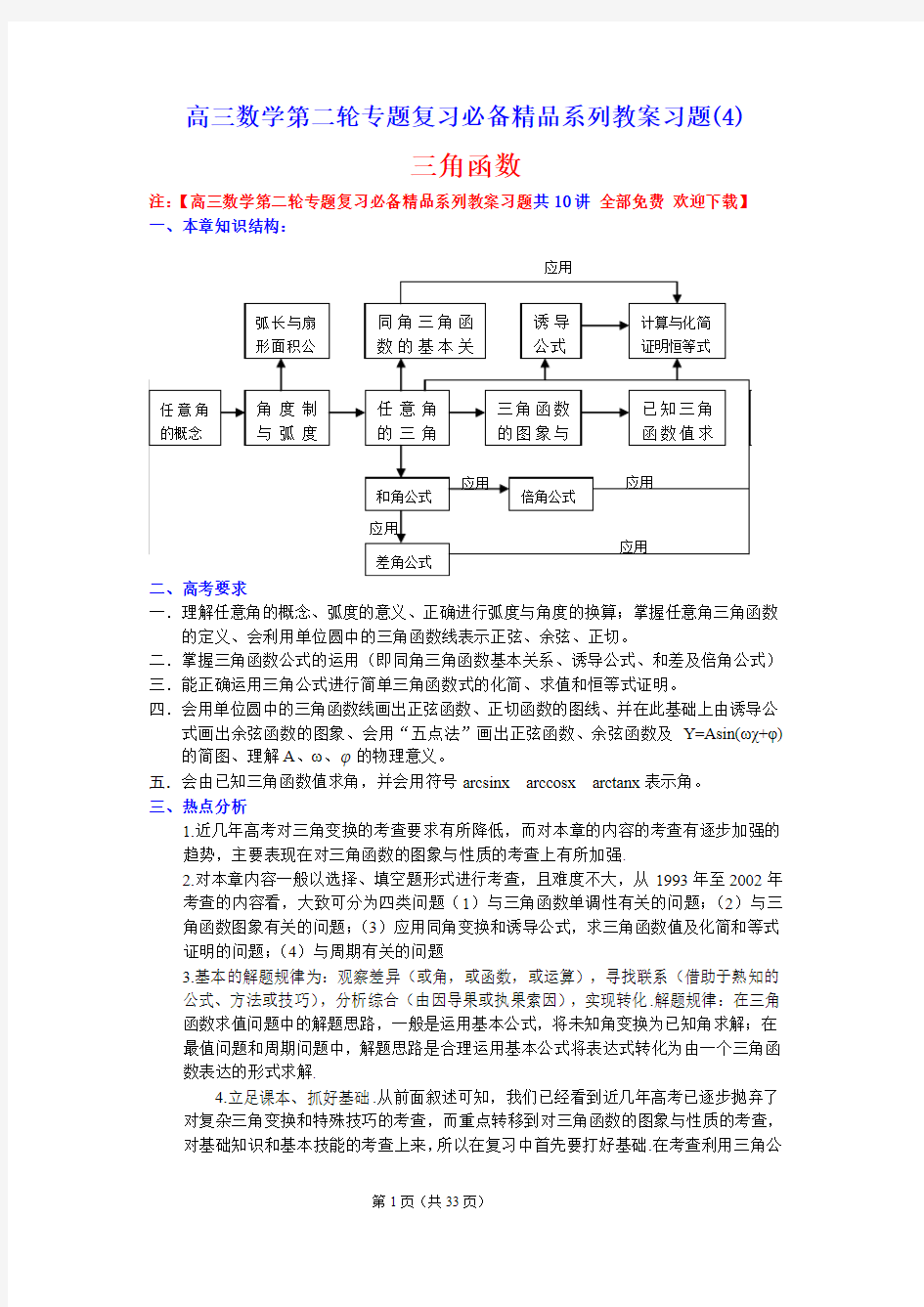
注:【高三数学第二轮专题复习必备精品系列教案习题共10讲全部免费欢迎下载】一、本章知识结构:
应用
二、高考要求
一.理解任意角的概念、弧度的意义、正确进行弧度与角度的换算;掌握任意角三角函数的定义、会利用单位圆中的三角函数线表示正弦、余弦、正切。
二.掌握三角函数公式的运用(即同角三角函数基本关系、诱导公式、和差及倍角公式)三.能正确运用三角公式进行简单三角函数式的化简、求值和恒等式证明。
四.会用单位圆中的三角函数线画出正弦函数、正切函数的图线、并在此基础上由诱导公式画出余弦函数的图象、会用“五点法”画出正弦函数、余弦函数及Y=Asin(ωχ+φ)的简图、理解A、ω、 的物理意义。
五.会由已知三角函数值求角,并会用符号arcsinx arccosx arctanx表示角。
三、热点分析
1.近几年高考对三角变换的考查要求有所降低,而对本章的内容的考查有逐步加强的
趋势,主要表现在对三角函数的图象与性质的考查上有所加强.
2.对本章内容一般以选择、填空题形式进行考查,且难度不大,从1993年至2002年
考查的内容看,大致可分为四类问题(1)与三角函数单调性有关的问题;(2)与三角函数图象有关的问题;(3)应用同角变换和诱导公式,求三角函数值及化简和等式证明的问题;(4)与周期有关的问题
3.基本的解题规律为:观察差异(或角,或函数,或运算),寻找联系(借助于熟知的
公式、方法或技巧),分析综合(由因导果或执果索因),实现转化.解题规律:在三角函数求值问题中的解题思路,一般是运用基本公式,将未知角变换为已知角求解;在最值问题和周期问题中,解题思路是合理运用基本公式将表达式转化为由一个三角函数表达的形式求解.
4.立足课本、抓好基础.从前面叙述可知,我们已经看到近几年高考已逐步抛弃了
对复杂三角变换和特殊技巧的考查,而重点转移到对三角函数的图象与性质的考查,对基础知识和基本技能的考查上来,所以在复习中首先要打好基础.在考查利用三角公
式进行恒等变形的同时,也直接考查了三角函数的性质及图象的变换,可见高考在降低对三角函数恒等变形的要求下,加强了对三角函数性质和图象的考查力度.
四、复习建议
本章内容由于公式多,且习题变换灵活等特点,建议同学们复习本章时应注意以下几点:(1)首先对现有公式自己推导一遍,通过公式推导了解它们的内在联系从而培养逻辑推理
能力。
(2)对公式要抓住其特点进行记忆。有的公式运用一些顺口溜进行记忆。
(3)三角函数是中学阶段研究的一类初等函数。故对三角函数的性质研究应结合一般函数
研究方法进行对比学习。如定义域、值域、奇偶性、周期性、图象变换等。通过与函数这一章的对比学习,加深对函数性质的理解。但又要注意其个性特点,如周期性,通过对三角函数周期性的复习,类比到一般函数的周期性,再结合函数特点的研究类比到抽象函数,形成解决问题的能力。
(4)由于三角函数是我们研究数学的一门基础工具,近几年高考往往考察知识网络交汇处
的知识,故学习本章时应注意本章知识与其它章节知识的联系。如平面向量、参数方程、换元法、解三角形等。(2003年高考应用题源于此)
5.重视数学思想方法的复习,如前所述本章试题都以选择、填空题形式出现,因
此复习中要重视选择、填空题的一些特殊解题方法,如数形结合法、代入检验法、特殊值法,待定系数法、排除法等.另外对有些具体问题还需要掌握和运用一些基本结论.
如:关于对称问题,要利用y=sinx的对称轴为x=kπ+(k∈Z),对称中心为(kπ,0),(k∈Z)等基本结论解决问题,同时还要注意对称轴与函数图象的交点的纵坐标特征.在求三角函数值的问题中,要学会用勾股数解题的方法,因为高考试题一般不能查表,给出的数都较特殊,因此主动发现和运用勾股数来解题能起到事半功倍的效果.
6.加强三角函数应用意识的训练,1999年高考理科第20题实质是一个三角问题,
由于考生对三角函数的概念认识肤浅,不能将以角为自变量的函数迅速与三角函数之间建立联系,造成思维障碍,思路受阻.实际上,三角函数是以角为自变量的函数,也是以实数为自变量的函数,它产生于生产实践,是客观实际的抽象,同时又广泛地应用于客观实际,故应培养实践第一的观点.总之,三角部分的考查保持了内容稳定,难度稳定,题量稳定,题型稳定,考查的重点是三角函数的概念、性质和图象,三角函数的求值问题以及三角变换的方法.
7.变为主线、抓好训练.变是本章的主题,在三角变换考查中,角的变换,三角函
数名的变换,三角函数次数的变换,三角函数式表达形式的变换等比比皆是,在训练中,强化变意识是关键,但题目不可太难,较特殊技巧的题目不做,立足课本,掌握课本中常见问题的解法,把课本中习题进行归类,并进行分析比较,寻找解题规律.
针对高考中题目看,还要强化变角训练,经常注意收集角间关系的观察分析方法.另外如何把一个含有不同名或不同角的三角函数式化为只含有一个三角函数关系式的训练也要加强,这也是高考的重点.同时应掌握三角函数与二次函数相结合的题目.
8.注意对三角形中问题的复习.由于教材的变动,有关三角形中的正、余弦定
理.解三角形等内容提到高中来学习,又近年加强数形结合思想的考查和对三角变换要求的降低,对三角的综合考查将向三角形中问题伸展,从1996年和1998年的高考试题就可看出,但也不可太难,只要掌握基本知识、概念,深刻理解其中基本的数量关系即可过关.
9.在复习中,应立足基本公式,在解题时,注意在条件与结论之间建立联系,在
变形过程中不断寻找差异,讲究算理,才能立足基础,发展能力,适应高考.
在本章内容中,高考试题主要反映在以下三方面:其一是考查三角函数的性质及图象
变换,尤其是三角函数的最大值与最小值、周期。多数题型为选择题或填空题;其次是三角函数式的恒等变形。如运用三角公式进行化简、求值解决简单的综合题等。除在填空题和选择题出现外,解答题的中档题也经常出现这方面内容。 另外,还要注意利用三角函数解决一些应用问题。 五、典型例题
两角和与差的三角函数
【例1】 已知3
,34π
βαππβαπ-<-<-<
+<,求βα-2的范围。 解:设βα-2=)()(βαβα-++B A ,(A 、B 为待定的系数),则 βα-2=βα)()(B A B A -++
比较系数 2
321
12????
??
?=
=????-=-=+B A B A B A ∴βα-2=)(23)(21βαβα-++ 从而可得:6
2π
βαπ<
-<-
【例2】 设},2
3
|{},,10||,35|{Z k k B Z k k k A ∈==∈≤==πββπαα,求B A 的解
的终边相同的角的集合。
解:先写出A 与B 的交,再写出终边相同的角的集合。 设B A ∈0α,则B A ∈∈00αα且;所以παπα20102
3
, 35k k ==
∴212335k k =,即2110
9
k k =,由于Z k k ∈≤11,10|| ∴10,02±=k ;因此}15,0{π±=B A
因此所有与B A 的角的终边相同的角的集合为}Z k ,2k ,2|{∈±==ππγπγγ或k
【例3】 已知 αβαβαπ
βπ
2222sin 2
1
sin sin 2sin 2sin 34
6
-
=-<
≤-,试求,的最值。 解:∵4πβ6π<≤-
∴-2
2
sin 21<
≤β,21sin 02<≤β ∴1sin 202<≤β ∵23222sin sin sin βαα=- ∴03212≤- ?<<-≤≤≤??????<--≥-1 sin 3 10sin 1sin 3 2 01sin 2sin 30sin 2sin 322 ααααααα或 ∴ 1αsin 3 2 0αsin 31<≤≤<-或 y=4 1)21(sin sin 21)sin 2sin 3(21sin 21sin 22222--=--=-αααααβ 当sin α∈[ 32,1]时函数y 递增,∴当sina=23 时 y min =92 -; 当sin α∈(31- ,0)时,函数y 递减,∴当sin α=0时,y min =2 1 ∴ 故当)sin 2 1(sin ,9 2)sin 2 1(sin 3 2sin 22min 22αβαβα--=-=时,无最大值。 【例4】 求值() ? +??+?+?10cos 110tg 60tg 110cos 40cos 2 解: ()()2 5cos 25cos 45cos 225cos 250cos 40cos 25cos 21060cos 240cos 25cos 210sin 23 10cos 21240cos 25cos 210sin 310cos 40cos 2=? ??=??+?=??-?+?=? ?? ? ? ???+?+?= ??+?+?=·原式 【例5】 已知2π<β<α<4π3,cos(α-β)=1312,sin(α+β)=-5 3 ,求sin2α的值_________. 解法一:∵ 2π<β<α<4π3,∴0<α-β<4π.π<α+β<4 π3, ∴sin(α-β)=.5 4 )βα(sin 1)βαcos(,135)βα(cos 122-=+--=+= -- ∴sin2α=sin [(α-β)+(α+β)] =sin(α-β)cos(α+β)+cos(α-β)sin(α+β) .6556)53(1312)54(135-=-?+-?= 解法二:∵sin(α-β)= 13 5,cos(α+β)=-54 , ∴sin2α+sin2β=2sin(α+β)cos(α-β)=-65 72 sin2α-sin2β=2cos(α+β)sin(α-β)=-65 40 ∴sin2α=65 56 )65406572(21-=-- 【例6】 不查表求sin 220°+cos 280°+3cos20°cos80°的值. 解法一:sin 220°+cos 280°+3sin 220°cos80° = 21 (1-cos40°)+21 (1+cos160°)+ 3sin20°cos80° =1-21cos40°+2 1 cos160°+3sin20°cos(60°+20°) =1- 21cos40°+2 1 (cos120°cos40°-sin120°sin40°) +3sin20°(cos60°cos20°-sin60°sin20°) =1-2 1cos40°-41cos40°-43sin40°+43sin40°-23sin 220° =1- 43cos40°-43(1-cos40°)= 4 1 解法二:设x =sin 220°+cos 280°+3sin20°cos80° y =cos 220°+sin 280°-3cos20°sin80°,则 x +y =1+1-3sin60°= 2 1 ,x -y =-cos40°+cos160°+3sin100° =-2sin100°sin60°+3sin100°=0 ∴x =y = 41,即x =sin 220°+cos 280°+3sin20°cos80°=4 1. 【例7】 设关于x 的函数y =2cos 2x -2a cos x -(2a +1)的最小值为f (a ),试确定满足f (a )= 2 1 的a 值,并对此时的a 值求y 的最大值. 解:由y =2(cos x -2a )2-2 2 42+-a a 及cos x ∈[-1,1]得: f (a )?? ? ????≥-<<-----≤)2( 41)22( 122) 2( 12a a a a a a ∵f (a )= 21,∴1-4a =21?a =81 ?[2,+∞) 故-22a -2a -1=2 1,解得:a =-1,此时, y =2(cos x +21)2+2 1 ,当cos x =1时,即x =2k π,k ∈Z ,y max =5. 【例8】 求值: ? +?? ??+?+?80cot 40csc 10sin 20tan 10cos 20sin 2. 解:原式的分子? ? ?+??+?=20cos 10sin 20sin 20cos 10cos 20sin 2 ??+?=20cos 10cos 20sin 2? ? +?=20cos 10cos 40sin 320cos 20cos 60sin 220cos 80sin 40sin =? ? ?=??+?= , 原式的分母= ? ? +?=??+?80sin 80cos 40cos 280sin 80cos 40sin 1 ()??+?+?=80sin 80cos 40cos 40cos ?? ?+?= 80sin 20cos 60cos 240cos 310cos 10cos 30cos 280sin 20cos 40cos =? ? ?=??+?= , 所以,原式=1. 【例9】 已知5 4 βsin αcos ,53βcos αsin =+=+,求βαsin cos 的值. 解1:令γ2 π β-= ,则原题等价于: 已知5 4 γcos αcos ,53γsin αsin =+=+,求γcos αcos 的值. 两式分别和差化积并相除得:4 3 2γαtan =+,所以 ()2572γαtan 12γαtan 1γαcos 22 =? ?? ? ? ++? ?? ??+-=+. 分别将已知两式平方并求和得:()2 1 γαcos -=-, 所以,()()()100 11γαcos γαcos 21 γcos αcos -=-++= . 解2:由54βsin αcos ,53βcos αsin =+=+平方相加得:()2 1 βαsin -=+. 上述两式平方相减得:()25 7 βαsin 2α2cos β2cos - =-+-. 将上式前两项和差化积,得:()()()25 7βαsin 2βαsin βαsin 2-=-+-+, 结合()21βαsin -=+,可解得:()25 7 βαsin -=-. 所以,()()()βαsin βαsin 21 βsin αcos --+=100 11-=. 【例10】 已知函数()x x m x f cos sin 2-=在区间?? ? ??2π,0上单调递减,试求实数m 的取值 范围. 解:已知条件实际上给出了一个在区间?? ? ? ?2π,0上恒成立的不等式. 任取∈21,x x ?? ? ??2π,0,且21x x <,则不等式()()21x f x f >恒成立, 即 >-11cos sin 2x x m 2 2 cos sin 2x x m -恒成立. 化简得()()2112sin 2cos cos x x x x m ->- 由2 π 021<< 1 221cos cos sin 2x x x x m --< 上式恒成立的条件为:()上的最小值,在区间??? ????? ? ??--<2π0cos cos sin 21221x x x x m . 由于()2 sin 2cos 22sin 2sin 22cos 2sin 4cos cos sin 2212 1 212121211 221x x x x x x x x x x x x x x x x +-= -+--=-- 2 sin 2cos 2cos 2sin 2sin 2sin 2cos 2cos 22 1212121x x x x x x x x +??? ??+=2tan 2tan 2 tan 2tan 12212 1x x x x +?? ? ? ? += 且当2π021< < 2,2021< tan ,2tan 021< t a n 2t a n 2 t a n 1212121>?? ? ? ?-??? ? ?-=?? ? ? ?+-??? ? ?+x x x x x x , 有 22 t a n 2t a n 2t a n 2t a n 122121>+? ? ? ? ? +x x x x , 故m 的取值范围为]2,(-∞. 【例11】 ,2 7,3=nC t C B A c b ABC = c a a 的对边,已知 、、分别为角、、中,△ .,2 3 3的值求的面积为又△△b a S ABC ABC += 解:∵ A+B+C=π, ① °得由° .222)2 7 (60cos 2,2760,3=-+==∴=ab b a c C tgC ②°得由 .2 3 360sin 21,233== ab S ABC ?? ???== -+④③由①、②得方程组6,4 492 2ab ab b a ,4121 )(32= ++b a 得×④③ 2 11=+b a ∴ 【例12】 在?ABC 中,a b c ,,分别是角A B C ,,的对边,设b c a 2=+,求 2 ctg 2ctg C A ·的值 解:由条件,2b a c =+,依据正弦定理,得 () ()2 cos 2sin 22cos 2sin 4sin sin sin 2sin sin 2sin 22C A C A C A C A C A C A C A R B R -+=+++=++=· 在02 sin ≠+?C A ABC 中, ∴2 cos 22cos C A C A +=- 2 sin 2sin 22cos 2cos 22sin 2sin 2cos 2cos C A C A C A C A -=+ ∴2 cos 2cos 2sin 2 sin 3C A C A = ∴ 32 sin 2sin 2cos 2cos =C A C A ; 即32C ctg 2A ctg = 三角函数的图象与性质 【例1】 试确定下列函数的定义域 ⑴1sin 1log 2-=x y ;⑵) 1cos 2lg(sin )4(--=x x x tg y π 解:⑴要使函数有意义,只须满足条件 ??? ? ?? ?? ? ≠>≥-0sin 0sin 1 01sin 1log x x x 解得:},2652|{},622|{Z k k x k x Z k k x k x ∈+<≤+∈+≤<πππππππ ⑵要使函数有意义,只须满足条件 ???????? ? ≠<≠≥-1 1-2cosx 00 1)-lg(2cosx 0 sin )4(x x tg 有意义π 解得},322|{Z k k x k x ∈+<<πππ 【例2】 求函数x x x x x x y 2sin 2cos cos 3cos sin 3sin 233++= 的最小值 解:∵sin sin cos cos 333 3 x x x x + ()()()()[]( )() [] ()()x x x x x x x x x x x x x x x x x x x x x x x x 2cos 4cos 12cos 2 1 4cos 2cos 2cos 21 4cos sin cos 2cos cos sin 21 cos 4cos 2cos sin 4cos 2cos 21 cos cos 3cos sin sin 3sin 322222222=+=+=-++=++-=+= ∴??? ? ? +=+=+= 42sin 22sin 2cos 2sin 2cos 2cos 23πx x x x x x y 当2142sin --=??? ? ? +最小值时,y x π 【例3】 已知函数f (x )=2a sin 2x -23a sin x cos x +a +b -1,(a 、b 为常数,a <0), 它的定义域为[0, 2 π ],值域为[-3,1],试求a 、b 的值。 解:f (x )=2a sin 2x -23a sin x cos x +a +b -1 =a (1-cos2x )-3a sin2x +a +b -1 =-2a sin 12)6 π2(-+++b a x ∵0≤x ≤ π2 ∴π6≤2x +π6≤π6 7 ∴1)6π 2sin(21≤≤+-x ∵a <0 ∴a ≤-2a sin ()26x +π ≤-2a ∴3a +b -1≤-2a sin ()26 x +π +2a +b -1≤b -1 ∵值域为[-3,1] ∴???-=-+=-31311b a b ∴?? ??? =-=2 34b a 【例4】 已知函数)2 ||,0,0)(sin()(π ω>?+ω=A x A x f 的图象在y 轴上的截 距为1,它在y 轴右侧的第一个最大值点和最小值点分别为(2,0x )和(2,30-π+x ). (1)求)(x f 的解析式; (2)将y =f (x )图象上所有点的横坐标缩短到原来的3 1 (纵坐标不变),然后再将所得图象 向x 轴正方向平移 3 π 个单位,得到函数y =g (x )的图象.写出函数y =g (x )的解析式并用列表作图的方法画出y =g (x )在长度为一个周期的闭区间上的图象. 解:(1)由已知,易得A =2. ππ3)3(200=-+=x x T ,解得3 1,6=∴=ωπT . 把(0,1)代入解析式)3 sin(2?+=x y ,得 1sin 2=?.又2 π ?< ,解得6 π ?= .∴)6 3 sin(2π +=x y 为所求. (2)压缩后的函数解析式为)6 sin(2π +=x y 再平移, 得) πsin(2)(+- =x x x g )πsin(2-=x 【例5】 求函数x x x y sin 23 sin 3sin 2-+-=的最值,并写出使函数y 取得最值的x 的集 合。 解:令31sin 2≤≤-=u x u ,则, ∴函数11 12-+=+-=u u u u u y ≥-=211 当且仅当u =1时,y 最小值=1 函数y 取得最小值的x 的集合? ?? ??? ∈+ =Z k k x x ,22π π 又函数[]3111,在∈-+=u u u y 是单调递增的 证明如下:1312≤≤≤u u ()( )??? ? ? ?--=-+-=--+ =-21212 112212211211 11 1u u u u u u u u u u u u u u y y ∵u u 12< ∴u u 120-< 11 01101102 121<<<<<< u u u u ,, ∴y y y y 12120-<<,即,∴[]3111 ,在∈-+=u u u y 是单调递增的 ∴当u =3时,函数3 1213 1 3=-+=最大值y 函数y 取得最大值的x 的集合? ?? ? ?? ∈-=Z k k x x ,2 ππ2 【例6】 ABC ?中,已知三内角A 、B 、C 依次成等差数列,求C A 22cos cos +的取值范围。 解:由已知得?=+?=12060C A B , 22cos 122cos 1cos cos 22C A C A +++= +()12cos 2cos 2 1 ++=C A ()()1cos cos +-+=C A C A ()C A -- =cos 2 1 1 ()()4 5 cos 211211cos 21 120120<--≤∴ ≤-<-∴?<- 即C A 22cos cos +的取值范围为?? ? ???4521, 【例7】 已知3 200π βαβα= +≥≥,且,,问当βα、分别取何值时, ()β2sin 21 2 αtan 2αcot απcos 1----= y 取最大值,并求出此最大值。 解:βα αααα2sin 21 sin cos 1sin cos 12cos 1---++= y βαα2sin 21cos sin -=·()βα2sin 2sin 21-= ()()βαβα-+=sin cos ()βαπ -=sin 3 2cos ()βα--=sin 21 32323203203 200π βαππβπαπ βαβα≤ -≤-≤≤≤≤∴= +≥≥,,,,且, 此时,由??? ????-=-=+232πβαπβα解得???????==12712π βπα 【例8】 在ΔA BC 中,求2 sin 2sin 2sin 222C B A ++的最小值.并指出取最小值时ΔA B C 的形状,并说明理由. 解:令2 sin 2sin 2sin 222 C B A y ++=2cos 12cos 12cos 1C B A -+ -+-= )cos cos (cos 2 123C B A ++-= )2sin 212cos 2cos 2(21232B C A C A -+-+-= ∵在ΔA BC 中, 2 22B C A -=+π,∴2sin 2cos B C A =+ 又12 cos ≤-C A . ∴)2sin 212sin 2(21232 B B y -+-≥ 12sin 2sin 2+-=B B 4 3)212(sin 2+-=B 当??? ????==-21 2sin 12cos B C A 时,y 取得最小值43; 由12cos =-C A 知A =C ,由212sin = B 知?=302 B ,B=60°; 故A =B=C=60°, 即y 取最小值 4 3 时,ΔA BC 的形状为等边三角形. 【例9】 已知函数f (x )=2cos x sin(x +3 π )-3sin 2x +sin x cos x (1)求函数f (x )的最小正周期; (2)求f (x )的最小值及取得最小值时相应的x 的值; (3)若当x ∈[ 12π,12 π7]时,f (x )的反函数为f -1(x ),求f -- 1(1)的值. 解:(1)f (x )=2cos x sin(x +3 π )-3sin 2x +sin x cos x =2cos x (sin x cos 3 π +cos x sin 3 π )-3sin 2x +sin x cos x =2sin x cos x +3cos2x =2sin(2x +3 π ) ∴f (x )的最小正周期T =π (2)当2x + 3π =2k π-2 π,即x =k π-12π5 (k ∈Z )时,f (x )取得最小值-2. (3)令2sin(2x +3 π )=1,又x ∈[ 2 π 7,2π], ∴2x +3π∈[3π,2π3],∴2x +3π=6 π5,则 x =4π,故f -- 1(1)=4 π. 【例10】 已知α、β为锐角,且x (α+β-2 π)>0,试证不等式f (x )=)αsin βcos ()βsin αcos ( +x x <2对一切非零实数都成立. 证明:若x >0,则α+β> 2 π , ∵α、β为锐角,∴0<2π-α<β<2π;0<2π-β<2 π, ∴0<sin( 2π -α)<sin β.0<sin(2 π-β)<sin α, ∴0<cos α<sin β,0<cos β<sin α, ∴0< βsin cos α <1,0<α βsin cos <1, ∴f (x )在(0,+∞)上单调递减,∴f (x )<f (0)=2. 若x <0,α+β< 2 π , ∵α、β为锐角,0<β< 2π-α<2π,0<α<2π-β<2π ,0<sin β<sin(2 π-α), ∴sin β<cos α,0<sin α<sin( 2π-β),∴sin α<cos β,∴βsin α cos >1, α sin βcos >1, ∵f (x )在(-∞,0)上单调递增,∴f (x )<f (0)=2,∴结论成立. 【例11】 设z 1=m +(2-m 2)i ,z 2=cos θ+(λ+sin θ)i ,其中m ,λ,θ∈R ,已知z 1=2z 2,求λ的取值范围. 解法一:∵z 1=2z 2, ∴m +(2-m 2)i =2cos θ+(2λ+2sin θ)i ,∴? ??+=-=θλθ sin 222cos 22 m m ∴λ=1-2cos 2θ-sin θ=2sin 2θ-sin θ-1=2(sin θ-41)2-8 9 . 当sin θ= 41时λ取最小值-8 9 ,当sin θ=-1时,λ取最大值2. 解法二:∵z 1=2z 2 ∴?? ???+=-=θsin 2λ22θ cos 22 m m ∴??? ???? --= =2λ22θsin 2θcos 2 m m , ∴4 )λ22(4222--+ m m =1. ∴m 4-(3-4λ)m 2+4λ2-8λ=0,设t =m 2,则0≤t ≤4, 令f (t )=t 2-(3-4λ)t +4λ2 -8λ,则?????????≥≥≤-≤≥?0 )4(0)0(42 λ4300f f 或f (0)·f (4)≤0 ∴???? ?? ??? ≤≥≤≤≤≤--≥0λ2λ2λ043λ4 5 89λ或或 ∴- 8 9 ≤λ≤0或0≤λ≤2. ∴λ的取值范围是[-8 9 ,2]. 【例12】 如右图,一滑雪运动员自h =50m 高处A 点滑至O 点,由于运动员的技巧(不计阻力),在O 点保持速率v 0不为,并以倾角θ起跳,落至B 点,令OB =L ,试问,α=30°时,L 的最大值为多少?当L 取最大值时,θ为多大? 解:由已知条件列出从O 点飞出后的运动方程: ?? ???-=-=-==20021sin 4sin cos cos gt v L h t v L S θαθα 由①②整理得:v 0cos θ= .2 1 αsin θsin ,αcos 0gt t L v t L +-= ∴v 02 +gL sin α=41g 2t 2+22t L ≥22 22412t L t g ?=gL 运动员从A 点滑至O 点,机械守恒有:mgh = 2 1 mv 02, ∴v 02 =2gh ,∴L ≤) αsin 1(2)αsin 1(20-=-g gh g v =200(m) 即L max =200(m),又4 1g 2t 2=22 2 22t L t h S =+. ∴θcos 22αcos αcos ,20?==== g L gh t v L S g L t 得cos θ=cos α,∴θ=α=30°∴L 最大值为200米,当L 最大时,起跳仰角为30° . ① ② 【例13】 如下图,某地一天从6时到14时的温度变化曲线近似满足函数: y =A sin(ωx +φ)+b ;(1)求这段时间的最大温差;(2)写出这段曲线的函数解析式. 解:(1)由图示,这段时间的最大温差是30-10=20(℃); (2)图中从6时到14时的图象是函数y =A sin(ωx +φ)+b 的半个周期的图象. ∴ ω π221? =14-6,解得ω=8π ,由图示A =21(30-10)=10,b =21(30+10)=20,这时y =10sin(8πx +φ)+20,将x =6,y =10代入上式可取φ=43π.综上所求的解析式为y =10sin(8 π x + 4 3 π)+20,x ∈[6,14]. 【例14】 已知函数()b x a x x x f ++?? ? ? ? -+?? ? ? ? +=co s 6πsin 6πsin (R b a ∈,,且均为常 数), (1)求函数()x f 的最小正周期; (2)若()x f 在区间?? ? ???-0,3π上单调递增,且恰好能够取到()x f 的最小值2,试求b a ,的值. 解:研究三角函数的性质(如周期、最值、单调性、奇偶性等)时,首先应该对所给的函数关系式进行化简,最好化为一个角(形如?+wx )、一种三角函数的形式. (1) ()b x a x x x f ++??? ?? -+??? ??+=cos 6πsin 6πsin b x a x ++=cos 6 π cos sin 2 b x a x ++=cos sin 3()b x a +++=θsin 32 (其中θ由下面的两式所确定:3 3θcos ,3 θsin 2 2 += +=a a a ) 所以,函数()x f 的最小正周期为π2. (2) 由(1)可知:()x f 的最小值为b a ++-32,所以,232=++-b a . 另外,由()x f 在区间??????-0,3π上单调递增,可知:()x f 在区间?? ? ???-0,3π上的最小值为 ??? ??-3πf ,所以,?? ? ??-3πf =232=++-b a . 解之得:2,1=-=b a 【例15】 设R x ∈,试比较()x f =x cos cos 与()x g =x sin sin 的大小关系. 解:观察所给的两个函数,它们均是两个三角函数的复合函数,因此,我们不难想到: 它们可能仍然具备三角函数的某些性质,如单调性、周期性、奇偶性等. 初步判断便可以确定:()x f 、()x g 都是周期函数,且最小正周期分别为π、π2.所以,只需考虑[]π,π-∈x 的情形. 另外,由于()x f 为偶函数,()x g 为奇函数,所以,很自然的可以联想到:能否把需考虑的x 的范围继续缩小? 事实上,当[]0,π-∈x 时,()x f >0,()x g 0≤恒成立,此时,()x f >()x g . 下面,我们只需考虑[]π,0∈x 的情形. 如果我们把()x f 看作是关于x cos 的余弦函数,把()x g 看作是关于x sin 的正弦函数,那么这两个函数既不同名,自变量也不相同,为了能进行比较,我们可以作如下恒等变换,使之成为同名函数,以期利用三角函数的单调性. ?? ? ??-=x x sin 2πcos sin sin 至此为止,可以看出:由于 x sin 2 π -和x cos 同属于余弦函数的一个单调区间,(即x sin 2π-,x cos ∈[]π,0),所以,只需比较x sin 2 π-与x cos 的大小即可. 事实上, ( x sin 2π-)—x cos =x sin 2π-—x cos =??? ? ? +-4πsin 22πx 022π>-≥ 所以,利用余弦函数在[]π,0上单调递减,可得: x sin sin 综上,()x g <()x f . 点评 本题好在充分地运用了正余弦函数的值域、周期性、奇偶性、单调性等性质, 对于训练学生思维、加深对这些性质的理解、以及学习利用函数的性质去解决问题有很大的帮助.是一道很有训练价值的好题. 六、专题练习 【两角和与差的三角函数练习1】 一、选择题 1.已知方程x 2+4ax +3a +1=0(a >1)的两根均tan α、tan β,且α,β∈ (-2 π,2π),则tan 2βα+的值是( ) A. 2 1 B.-2 C. 3 4 D. 2 1 或-2 二、填空题 2.已知sin α=53,α∈(2π,π),tan(π-β)= 21 ,则tan(α-2β)=_________. 3.设α∈(43,4ππ),β∈(0,4π),cos(α-4 π)=53,sin(43π+β)=135 ,则sin(α+ β)=_________. 三、解答题 4.不查表求值: .10cos 1) 370tan 31(100sin 130sin 2? +?+?+? 5.已知cos(4π +x )=53,(12 17π<x <47π ),求x x x tan 1sin 22sin 2-+的值. 6.已知α-β=38π,且α≠k π(k ∈Z ).求 )4β 4π(sin 42 αsin 2αcsc )απcos(12-----的最大值及最大值时的条件. 7.如右图,扇形OAB 的半径为1,中心角60°,四边形PQRS 是扇形的内接矩形,当其面积最大时,求点P 的位置,并求此最大面积. 8.已知cos α+sin β=3,sin α+cos β的取值范围是D ,x ∈D ,求函数y =10 43 2log 2 1 ++x x 的最小值,并求取得最小值时x 的值. 参考答案 一、1.解析:∵a >1,tan α+tan β=-4a <0. tan α+tan β=3a +1>0,又α、β∈(- 2π,2π)∴α、β∈(-2 π,θ),则2βα+∈(-2π,0), 又tan(α+β)= 342 tan 12tan 2)tan(,34)13(14tan tan 1tan tan 2 =β+α-β +α=β+α=+--=βα-β+α又a a , 整理得2tan 2 22β αtan 32βα-+++=0.解得tan 2 βα+=-2. 答案:B 2.解析:∵sin α=5 3,α∈(2π,π),∴cos α=-54 则tan α=- 43,又tan(π-β)=21 可得tan β=-2 1, 247) 3 4()43(1) 34(43β2tan αtan 1βtan αtan )β2αtan(.34)21(1) 21 (2βtan 1βtan 2β2tan 22 2= -?-+---=?+-=--=---?= -= 答案: 24 7 3.解析:α∈( 4 π 3, 4π),α-4π∈(0, 2π),又cos(α-4π)=53. 65 56 )βαsin(. 6556 13554)1312(53)β4π3sin()4παsin()β4π3cos()4παcos()]β4π 3()4παcos[(] 2 π )β4π3()4παsin[()βαsin(. 13 12 )β4π3cos(,135)β4π3sin().π,4π3(β4π3).4π,0(β,54)4παsin(= +=?+-?-=+?-++?--=++--=-++-=+∴-=+∴=+∈+∴∈=-∴即 答案: 65 56 三、4.答案:2 75285 3)54(25 7) 4cos() 4π sin(2sin sin cos cos )cos (sin sin 2cos sin 1sin 2cos sin 2tan 1sin 22sin 5 4)4πsin(,π24π3π5,π4712π17. 25 7 )4π(2cos 2sin ,53)4πcos(:.522=-?=++=-+=- +=-+-=+∴<+<∴<<=+-=∴=+x x x x x x x x x x x x x x x x x x x x x x x 又解 2 )3π 22αsin(22)21()π322αsin(4.3π22α4π 38α24βα,π38βα2 2 βαcos 2βαsin 42)2βsin 2α (sin 2)2 βsin 2121(42αcos 2αcos 22αsin 2)2β2πcos(14 2αsin 1)αcos 1(2αsin ) 4β 4π(sin 42 αsin 2αcsc )απcos(1:.62 2 22---=--?-=∴-=-=-∴=---+=-+=--?=----+=-----= t t 令解 π≠αk (k ∈Z ),3 22322π - π≠π-α∴k (k ∈Z ) ∴当 ,2ππ23π22α-=-k 即3ππ4α+=k (k ∈Z )时,)π3 2 2αsin(-的最小值为-1. 7.解:以OA 为x 轴.O 为原点,建立平面直角坐标系,并设P 的坐标为(cos θ,sin θ),则 |PS |=sin θ.直线OB 的方程为y =3x ,直线PQ 的方程为y =sin θ.联立解之得Q (3 3 sin θ;sin θ),所以|PQ |=cos θ- 3 3 sin θ. 于是S PQRS =sin θ(cos θ-3 3 sin θ) =3 3 (3sin θcos θ-sin 2θ) =33(2 3 sin2θ-2θ2cos 1-) =33(23 sin2θ+21cos2θ-21) = 33sin(2θ+6 π)-63. ∵0<θ< 3π,∴6π<2θ+6π<65π.∴21<sin(2θ+6 π )≤1. ∴sin(2θ+ 6 π )=1时,PQRS 面积最大,且最大面积是63, 此时,θ=6 π ,点P 为的中点,P ( 21,23). 8.解:设u =sin α+cos β.则u 2+(3)2=(sin α+cos β)2+(cos α+sin β)2=2+2sin(α+β)≤ 4.∴u 2 ≤1,-1≤u ≤1.即D =[-1,1],设t =32+x ,∵-1≤x ≤1,∴1≤t ≤5.x =2 3 2-t . .2 1 ,232,2,258log 2log 82log ,0log .82,2,42. 82 24142142104325.05.05 .0min 5.0max 2-==+==-==∴>=====≤+ =+=++= ∴x x t y M M y M t t t t t t t x x M 此时时时是减函数在时即当且仅当 【两角和与差的三角函数练习2】 一、选择题 1.下列各三角函数式中,值为正数的是 ( C ) (A )sin ()- π4 (B )cos 250 (C )tg()'- 69010 (D )ctg 113 π 2.α是第四象限的角,则下列三角函数的值为正的是 ( B ) (A )sin α (B )cos α (C )tg α (D )ctg α 3.)(3 14cos π -的值为 ( B ) (A ) 21 (B )21- (C )23 (D )2 3 - 4.已知sin α=54 - ,α是第三象限角,则tg α2 = ( C ) (A )±2 (C )±12 (C )-2 (D )-12 5.若αsin =5 4 ,且α为锐角,则sin 2α的值等于 ( B ) (A ) 25 12 (B )2524 (C )2512- (D )2524- 6.若α= 20,β= 25,则)1)(1(βαtg tg ++的值为 ( B ) (A )1 (B )2 (C )12+ (D )13+ 7.已知)25 ,23(ππ∈x ,则=-x sin 1 ( C ) (A ))42sin(2π+x (B ))4 2sin(2π +-x 【高中数学】数学《三角函数与解三角形》复习资料 一、选择题 1.函数()1sin cos 1sin cos 1tan 01sin cos 1sin cos 32x x x x f x x x x x x x π+-++? ?=++<< ?+++-? ?的最小值为 ( ) A B C D 【答案】B 【解析】 【分析】 利用二倍角公式化简函数()f x ,求导数,利用导数求函数的最小值即可. 【详解】 2 2222sin 2sin cos 2cos 2sin cos 1sin cos 1sin cos 2222221sin cos 1sin cos 2cos 2sin cos 2sin 2sin cos 222222 x x x x x x x x x x x x x x x x x x x x +++-+++= ++++-++ 2sin sin cos 2cos sin cos sin cos 222222222sin cos sin 2cos sin cos 2sin sin cos 22222222x x x x x x x x x x x x x x x x x ???? ++ ? ?????=+= +=???? ++ ? ? ???? , 则()21tan 0sin 32f x x x x π? ?= +<< ?? ?, 322222 21sin 2cos 16cos cos 1()sin 3cos sin 3cos 3sin cos x x x x f x x x x x x x ' ' ' --+????=+=-+= ? ????? . 令()cos 0,1t x =∈,() 32 61g t t t =--+为减函数,且102g ??= ??? , 所以当03 x π <<时, ()1 1,02 t g t <<<,从而()'0f x <; 当 3 2 x π π << 时,()1 0,02 t g t << >,从而()'0f x >. 故( )min 33f x f π??== ??? . 故选:A 【点睛】 本题主要考查了三角函数的恒等变换,利用导数求函数的最小值,换元法,属于中档题. 2.在ABC ?中,角,,A B C 所对的边分别为,,a b c 满足,222b c a bc +-=, 齐桓晋文之事 一、导入: 在两千多年前,我国的思想领域曾经历过一个辉煌的时代,真正的做到了百花齐放,百家争鸣。以后任何一个时代,我们在思想领域的变革都没有当时那么巨大,形式都没有当时那么多样,内容都没有那么自由。这个时代是:春秋战国时期。大家能举出当时比较有代表性的派别吗?其中的儒家思想对我国文化乃至政治的影响都可以说是空前绝后的。儒家思想的代表人物是孔子和孟子,他们分别被称为“圣人”和“亚圣”。孔子大家都非常熟悉,而对他的再传弟子孟子就可能不太了解了。有谁能说说孟子的有关情况。 二、关于孟子: 1、孟子其人 孟子(前372—前289年),名轲,字子舆,战国时邹(现山东邹县东南)人。 孟子是战国时儒家学派的代表人物,曾受业于子思(孔子的孙子)的门人,30岁左右收徒讲学。44岁开始周游列国,晚年回到家乡讲学著述,直到去世。后世统治者都把他作为尊崇的偶像,到元、明时被称为“亚圣”。 2、《孟子》其书 《孟子》共七篇,分别为《梁惠王》、《公孙丑》、《滕文公》、《离娄》、《万章》、《告子》、《尽心》。各章又都分为上下两篇。作为一部语录体著作,它记录的是有关孟子重要思想的一些言论。到南宋时,朱熹把它与《礼记》中的《大学》、《中庸》两篇以及《论语》合为“四书”,把读经的传统推向更加狭窄的胡同,成为后世(如明、清两代)科举考试八股文的唯一的取材依据。 3、孟子思想 ①性本善(凡人都可以为尧舜) ②民为贵,社稷次之,君为轻(民本) ③穷则独善其身,达则兼济天下(封建时代士大夫出世进退的准则) ④富贵不能淫,贫贱不能移,威武不能屈(对国君傲然视之) ⑤劳心者治人,劳力者治于人。治于人者食于人,治人者食人,天下之通义也 [思考:为什么孟子的思想会被后世接受呢?]任何一种哲学,都会创立自己的理想世界。比起道家的小国寡民、佛家的因果报应来说,儒家的集大成思想家孟子的理想世界则诱人得多。孟子提出了一幅君民同乐、仁义并施的王道乐土和太平盛世的理想图景。这对于王者来说,自然是最好不过了,有什么比百姓归附,国力强盛更令他们满意的呢?对于老百姓来说,也是如此,有谁不乐意做太平盛世的人呢? 4、《孟子》的时代意义 当时的社会背景:①争地以战,杀人盈野;争城以战,杀人盈城 ②庖有肥肉,厩有肥马;民有饥色,野有饿莩 时代意义:孟子的思想具有着明显的进步性。其思想核心就是“民本思想”。民贵君轻,在今天看来,它至少包括重视国家利益,反对特权意识、保护人民等多方面的含义。这种社会变革时期的新观念,正符合人民的愿望,具有一定的人道主义精神,至今在我们的思想领域里有着重大影响。孟子的追求是一种对社会出路的探索,他的求真的追求精神也是值得今天我们学习的。另外,《孟子》的散文成就极高,作为文化精粹,我们当然有研究、借鉴、继承和发扬的必要。 5、“王道”和“霸道” 这是先秦时代一对相对的概念。“王道”是儒家提出的以仁义治天下的政治主张;霸道指君主凭借武力、刑法、权势等进行统治。孟子所处的时代是沿着霸道的方向前进的,凡是行法家主张,讲求耕战,富国强兵,便取得胜利。司马迁《史记?孟子荀卿列传》说:“当世之时,秦用商君,富国强兵。楚、魏用吴起,战胜弱敌。齐宣王用孙子、田忌之徒,而诸侯东面朝齐。天下方务于合纵连横,以攻伐为贤;而孟轲乃述唐虞三代之德,是以所如者不合。” 三、课文分析 齐宣王问曰:“齐桓、晋文之事,可得闻乎?”见面即问称霸的事,说明有称霸的意图。避免了平铺直叙,形成了迂回曲折、波澜起伏的论辩风格。孟子对曰:“仲尼之徒无道桓文之事者,是以后世无传焉,臣未之闻也。岔开话题,为下文宣讲“王道”铺垫。无以,则王乎?”提出并明确话题,以问“霸道”开始,转入说“王道”。 辩论技巧:掌握对方心理,进而因势利导。 孟子能掌握齐宣王问霸政的目的只是想统一天下,故立即引导他讨论可达到统一天下的方法——行王道(仁政),促使宣王有兴趣与孟子继续谈下去。“保民而王”,国家富强正合于宣王之意,故他便有更大兴趣讨论王道,保民之道了。 曰:“德何如,则可以王(wàng)矣?”语意急切,欲称霸之心昭然若揭,同时也显示了其畏难心理。曰:“保民而王,莫之能御也。”曰:“若寡人者,可以保民乎哉?”语意急切,欲称霸之心昭然若揭,同时也显示了其畏难心理。曰:“可。”曰:“何由知吾可也?”语意急切,欲称霸之心昭然若揭。曰:“臣闻之胡龁(húhé)曰:‘王坐于堂上,有牵牛而过堂下者。王见之,曰:“牛何之?”对曰:“将以衅(xìn)钟。”王曰:“舍之!吾不忍其觳觫(húsǜ),若无罪而就死地。”对曰:“然则废衅钟与?”曰:“何可废也?以羊易之。”’不识有诸?”曰:“有之。”不 高中数学三角函数基础知识点及答案 1、角的概念的推广:平面内一条射线绕着端点从一个位置旋转到另一个位置所的图形。按逆时针方向旋转所形成的角叫正角,按顺时针方向旋转所形成的角叫负角,一条射线没有作任何旋转时,称它形成一个零角。射线的起始位置称为始边,终止位置称为终边。 2、象限角的概念:在直角坐标系中,使角的顶点与原点重合,角的始边与x 轴的非负半轴重合,角的终边在第几象限,就说这个角是第几象限的角。如果角的终边在坐标轴上,就认为这个角不属于任何象限。 3. 终边相同的角的表示: (1)α终边与θ终边相同(α的终边在θ终边所在射线上)?2()k k αθπ=+∈Z , 注意:相等的角的终边一定相同,终边相同的角不一定相等.如与角 1825-的终边相同,且绝对值最小的角的度数是___,合___弧度。 弧度:一周的弧度数为2πr/r=2π,360°角=2π弧度,因此,1弧度约为57.3°,即57°17'44.806'', 1°为π/180弧度,近似值为0.01745弧度,周角为2π弧度,平角(即180°角)为π弧度, 直角为π/2弧度。(答:25-;5 36 π- ) (2)α终边与θ终边共线(α的终边在θ终边所在直线上) ?()k k αθπ=+∈Z . (3)α终边与θ终边关于x 轴对称?2()k k αθπ=-+∈Z . (4)α终边与θ终边关于y 轴对称?2()k k απθπ=-+∈Z . (5)α终边与θ终边关于原点对称?2()k k απθπ=++∈Z . (6)α终边在x 轴上的角可表示为:,k k Z απ=∈; α终边在y 轴上的角可表示为:,2k k Z παπ=+∈;α终边在坐标轴上的角可表示为:,2 k k Z π α=∈. 如α的终边与 6 π 的终边关于直线x y =对称,则α=____________。 (答:Z k k ∈+ ,3 2π π) 4、α与2α的终边关系:由“两等分各象限、一二三四”确定.如若α是第 二象限角,则2 α 是第_____象限角 (答:一、三) 5.弧长公式:||l R α=,扇形面积公式:211||22 S lR R α==,1弧度 (1rad)57.3≈. 如已知扇形AOB 的周长是6cm ,该扇形的中心角是1弧度,求该扇形的面积。 (答:22cm ) 6、任意角的三角函数的定义:设α是任意一个角,P (,)x y 是α的终边上的任意一点(异于原点),它与原点的距离是220r x y =+>,那么 s i n ,c o s y x r r αα==,()tan ,0y x x α=≠,cot x y α=(0)y ≠,sec r x α=()0x ≠, ()csc 0r y y α=≠。三角函数值只与角的大小有关,而与终边上点P 的位置无关。 三角函数专题训练 19.(本小题满分12分) 在△ABC 中角A 、B 、C 的对边分别为a b c 、、,设向量(,cos ),(,cos )//.m a B n b A m n m n ==≠u r r u r r u r r 且, (Ⅰ)若sin sin A B +=6,求A ; (Ⅱ)若ABC ?的外接圆半径为1,且,abx a b =+试确定x 的取值范围. 17.(本小题共12分) 已知函数()sin()(0,||)2f x M x M πω??=+>< 的部分图象如图所示. (I )求函数()f x 的解析式; (II )在△ABC 中,角C B A 、、的对边分别是c b a 、、若(2)cos cos ,()2 A a c B b C f -=求的取值范围. 17.(本小题满分12分)已知向量231444x x x m (sin ,),n (cos ,cos )==.记()n m x f ?= (I )若32f ()α=,求23 cos()πα-的值; (Ⅱ)在?ABC 中,角A 、B 、C 的对边分别是a 、b 、c ,且满足 ()2cos cos a c B b C -=,若13f (A )+= ,试判断?ABC 的形状. 17、海岛B 上有一座高为10米的塔,塔顶的一个观测站A ,上午11时测得一游船位于岛北偏东15°方向上,且俯角为30°的C 处,一分钟后测得该游船位于岛北偏西75°方向上,且俯角45°的D 处。(假设游船匀速行驶) (1)求该船行使的速度(单位:米/分钟)(5分) (2)又经过一段时间后,游船到达海岛B 的正西方向E 处,问此时游船距离海岛B 多远。(7分) 19.解:因为(,cos ),(,cos )//m a B n b A m n ==u r r u r r 且, 所以cos cos a A b B =,-------------------------------------------1分 由正弦定理,得sin cos sin cos A A B B =, 《齐桓晋文之事》教案 教材分析: 《齐桓晋文之事》为必修五第四单元“以天下为己任”中的首篇,是孟子晚年第二次到齐国和齐宣王的一次谈话记录。它较为系统地阐明了孟子行仁政而王天下的政治主张,充分表现出孟子文章的曲折尽情、气盛言和的特色,洋溢着一种波澜壮阔的气势美,而且在论证的过程中又富有逻辑的力量。学习时,须用心体会。 学情分析: 本文篇幅较长,说理迂回,学生理解有一定难度。但是,在单元三中学生刚学的《逍遥 游》与本文同属先秦诸子散文。晨练四中古文“桓公问治民于管子”中爱民的思想,又与 本文大有相通之处。再加上本学期学生刚在历史课文中学过孟子思想,文章中又有些有趣的譬喻,所以本文对学生来说是“熟悉的陌生人”。 教学目标: 1、学生能有效积累王、保等重点文言实词,之、以等重点文言虚词;能正确识别文中 的倒装句等特殊句式;能准确翻译“老吾老,以及人之老;幼吾幼,以及人之幼”等重要句 子。 2、学生能理解孟子的“保民而王”的仁政思想,及“制民之产”的具体措施。 3、学生能总结并鉴赏本文中孟子善于设喻、迂回曲折、层层深入的的论辩特色。 教学重点 目标 1 、2 教学难点 目标 2 、3 课时安排 2课时 第一课时 一、介绍 1、孟子其人 孟子,名轲,字子舆,战国时邹(现山东邹县东南)人,战国时儒家学派的代表人物。 曾受业于子思(孔子的孙子)的门人, 30 岁左右收徒讲学。 44 岁开始周游列国,游说诸侯,宣扬“仁政”,但是始终不受重用,然而他傲视诸侯,决不苟同,晚年回到家乡讲学着述,直 到去世。后世统治者都把他作为尊崇的偶像,到元、明时被称为“亚圣”。 2、《孟子》其书 《孟子》共七篇,分别为《梁惠王》、《公孙丑》、《滕文公》、《离娄》、《万章》、《告子》、《尽心》。各章又都分为上下两篇。作为一部语录体着作,它记录的是有关孟子重要思想的 一些言论。到南宋时,朱熹把它与《礼记》中的《大学》、《中庸》两篇以及《论语》合为“四书”。 3、孟子思想 ①性本善(凡人皆可成尧舜) ②民本思想(民为贵,社稷次之,君为轻) ③封建时代士大夫出世进退的准则(穷则独善其身,达则兼济天下) ④富贵不能淫,贫贱不能移,威武不能屈。 ⑤劳心者治人,劳力者治于人。治于人者食于人,治人者食人,天下之通义也。 《三角函数》 【知识网络】 一、任意角的概念与弧度制 1、将沿x 轴正向的射线,围绕原点旋转所形成的图形称作角. 逆时针旋转为正角,顺时针旋转为负角,不旋转为零角 2、同终边的角可表示为 {}()360k k Z ααβ? =+∈g x 轴上角:{}()180k k Z αα=∈o g y 轴上角:{}()90180k k Z αα=+∈o o g 3、第一象限角:{}()036090360k k k Z αα? ?+<<+∈o g g 第二象限角:{}()90 360180360k k k Z αα??+<<+∈o o g g 第三象限角:{}()180360270360k k k Z αα? ?+<<+∈o o g g 第四象限角: {}()270 360360360k k k Z αα??+<<+∈o o g g 4、区分第一象限角、锐角以及小于90o 的角 第一象限角:{}()0360 90360k k k Z αα? ?+<<+∈o g g 锐角: {}090αα< ,2 4 , 0π απ ≤ ≤=k ,2 345, 1παπ≤≤=k 所以 2 α 在第一、三象限 6、弧度制:弧长等于半径时,所对的圆心角为1弧度的圆心角,记作1rad . 7、角度与弧度的转化:01745.0180 1≈=?π 815730.571801'?=?≈? = π 9、弧长与面积计算公式 弧长:l R α=?;面积:211 22 S l R R α=?=?,注意:这里的α均为弧度制. 二、任意角的三角函数 1、正弦:sin y r α=;余弦cos x r α=;正切tan y x α= 其中(),x y 为角α终边上任意点坐标,r = 2、三角函数值对应表: 3、三角函数在各象限中的符号 三角函数大题压轴题练习 1.已知函数()cos(2)2sin()sin()344 f x x x x π ππ =- +-+ (Ⅰ)求函数()f x 的最小正周期和图象的对称轴方程 (Ⅱ)求函数()f x 在区间[,]122 ππ -上的值域 解:(1) ()cos(2)2sin()sin()344 f x x x x πππ =-+-+ 1cos 22(sin cos )(sin cos )2x x x x x x = ++-+ 221cos 22sin cos 2x x x x = ++- 1cos 22cos 222 x x x = +- s i n (2) 6 x π =- 2T 2 π π= =周期∴ 由2(),()6 2 23 k x k k Z x k Z π π ππ π- =+ ∈= +∈得 ∴函数图象的对称轴方程为 ()3 x k k Z π π=+ ∈ (2) 5[,],2[,]122636 x x ππ πππ ∈- ∴-∈- 因为()sin(2)6 f x x π =- 在区间[,]123ππ- 上单调递增,在区间[,]32 ππ 上单调 递减, 所以 当3 x π= 时,()f x 取最大值 1 又 1()()12 222f f π π- =- <=,当12 x π =-时,()f x 取最小值2- 所以 函数 ()f x 在区间[,]122 ππ - 上的值域为[ 2.已知函数2 π()sin sin 2f x x x x ωωω?? =+ ?? ? (0ω>)的最小正周期为π. (Ⅰ)求ω的值; (Ⅱ)求函数()f x 在区间2π03 ?????? ,上的取值范围. 解:(Ⅰ)1cos 2()22x f x x ωω-= +112cos 222 x x ωω=-+ π1sin 262x ω? ?=-+ ?? ?. 因为函数()f x 的最小正周期为π,且0ω>, 所以 2π π2ω =,解得1ω=. (Ⅱ)由(Ⅰ)得π1()sin 262 f x x ??=- + ?? ?. 因为2π03 x ≤≤, 所以ππ7π2666 x --≤≤, 所以1πsin 2126x ??- - ?? ?≤≤, 因此π130sin 2622x ? ?- + ?? ?≤≤,即()f x 的取值范围为302?????? ,. 3. 已知向量m =(sin A ,cos A ),n =1)-,m ·n =1,且A 为锐角. (Ⅰ)求角A 的大小; (Ⅱ)求函数()cos 24cos sin ()f x x A x x R =+∈的值域. 解:(Ⅰ) 由题意得3sin cos 1,m n A A =-= 1 2sin()1,sin().662 A A ππ-=-= 由A 为锐角得 ,6 6 3 A A π π π - = = (Ⅱ) 由(Ⅰ)知1 cos ,2 A = 所以2 2 1 3()cos 22sin 12sin 2sin 2(sin ).2 2 f x x x x s x =+=-+=--+ 因为x ∈R ,所以[]sin 1,1x ∈-,因此,当1sin 2x =时,f (x )有最大值3 2 . 当sin 1x =-时,()f x 有最小值-3,所以所求函数()f x 的值域是332??-???? , 齐桓晋文之事教案 题目:齐桓晋文之事教案 一、《齐桓晋文之事》学习要点 (一)简介《孟子》和孟子的生平思想及散文特点 1、关于《孟子》 《孟子》是记录战国时代思想家孟轲的思想和政治言论的书,一般认为是孟子和他的门徒合著。全书共七篇(即《梁惠王》《公孙丑》《滕文公》《离娄》《万章》《告子》《尽心》,各篇又都分上下两篇),共261章。是儒家经典之一,也是先秦诸子散文中重要作品。 2、孟子的生平思想 孟子(前372—前289),名轲,字子舆,战国时邹(今山东邹县)人。他曾受业于子思(孔子之孙)的门人,三十岁左右聚徒讲学,四十四岁开始周游列国,宣扬“仁政”“王道”,因主张不被采纳,退而讲学著述,直到去世。孟子受到尊崇,被后人称为“亚圣”,与“圣人”孔子并称为“孔孟”。 孟子继承了孔子的学说并有所发展,他主张实行仁政,抨击暴政(联系学过的课文《寡人之于国也》),提出了系统的仁政学说。他提出了“民为贵,社稷次之,君为轻”的民本思想。孟子主张人性是善的。要通过学养保持善性,在道德上具备仁、义、礼、智,能做到“舍生取义”——可以为正 义而献身。孟子有治国平天下的抱负,也有“有所不为”的操守,他提出的“穷则独善其身,达则兼善天下”,成为封建时代士人的秘世准则。孟子一身正气,决不附和权贵,他称赞“富贵不能淫(放纵),贫贱不能移,威武不能屈”的节操。 3、孟子散文特点 孟子的文章感情强烈,雄辩有力,气势磅礴。他说:我知言,我善养吾浩然之气。其为气也,至大至刚,以直养而无害,则塞乎天地之间。 孟子的文章善设机(智)巧(妙),引人入彀(诱引论敌进入预先构想的范围处在自己的掌握控制之中而驳服他);善用譬喻,生动说理。 孟子的散文对后世产生了巨大影响。 4、课文背景 课文记录孟子游历齐国时和齐宣王的一次谈话,是一篇语录体论辩文。孟子游说齐宣王放弃当时以功伐取胜的霸道,施行王道,从而集中阐述了他的仁政主张,描绘了一幅“保民而王”的社会蓝图。 《齐桓晋文之事》选自《孟子·梁惠王上》,称“齐桓晋文之事章”(261章之一)。 (二)课文内容 1、内容结构 三角函数总结及统练 一. 教学内容: 三角函数总结及统练 (一)基础知识 1. 与角α终边相同的角的集合},2{Z k k S ∈+==απβ 2. 三角函数的定义(六种)——三角函数是x 、y 、r 三个量的比值 3. 三角函数的符号——口诀:一正二弦,三切四余弦。 4. 三角函数线 正弦线MP=αsin 余弦线OM=αcos 正切线AT=αtan 5. 同角三角函数的关系 平方关系:商数关系: 倒数关系:1cot tan =?αα 1c s c s i n =?αα 1s e c c o s =?αα 口诀:凑一拆一;切割化弦;化异为同。 6. 诱导公式——口诀:奇变偶不变,符号看象限。 α απ+k 2 α- απ- απ+ απ-2 α π -2 α π +2 正弦 αsin αsin - αsin αsin - αsin - αcos αcos 余弦 αcos αcos αcos - αcos - αcos αsin αsin - 正切 αtan αtan - αtan - αtan αtan - αcot αcot - 余切 αcot αcot - αcot - αcot αcot - αtan αtan - 7. 两角和与差的三角函数 ?????? ? ?+-=-?-+=+?????????+?=-?-?=+?-?=-?+?=+βαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαt a n t a n 1t a n t a n )t a n (t a n t a n 1t a n t a n )t a n (s i n s i n c o s c o s )c o s (s i n s i n c o s c o s )c o s (s i n c o s c o s s i n )s i n (s i n c o s c o s s i n )s i n ( 8. 二倍角公式——代换:令αβ= ??????? -= -=-=-=?=ααααααααααα22222tan 1tan 22tan sin cos sin 211cos 22cos cos sin 22sin 降幂公式?????? ?+=-=22cos 1cos 22cos 1sin 22αααα 半角公式: 2cos 12 sin αα -± =;2cos 12cos αα+±=; αα αcos 1cos 12tan +-± = αα ααα cos 1sin sin cos 12 tan += -= 9. 三角函数的图象和性质 函数 x y sin = x y cos = x y tan = 三角函数专题复习 在三角函数复习过程中,认真研究考纲是必须做的重要工作。三角函数可以当成函数内容中的重要一支,要注意与其它知识的联系。 一、研究考题,探求规律 1. 从表中可以看出:三角函数题在试卷中所处的位置基本上是第一或第二题,本章高考重点考查基础知识,仍将以容易题及中档为主,题目的难度保持稳定,估计这种情况会继续保持下去 2. 特点:由于三角函数中,和差化积与积化和差公式的淡出,考查主体亦发生了变化。偏重化简求值,三角函数的图象和性质。考查运算和图形变换也成为了一个趋势。三角函数试题更加注重立足于课本,注重考查基本知识、基本公式及学生的运算能力和合理变形能力,对三角变换的要求有所降低。三角化简、求值、恒等式证明。图象。最值。 3、对三角函数的考查主要来自于:①课本是试题的基本来源,是高考命题的主要依据,大多数试题的产生是在课本题的基础上组合、加工和发展的结果。②历年高考题成为新高考题的借鉴,有先例可循。 二、典例剖析 例1:函数22()cos 2cos 2x f x x =-的一个单调增区间是 A .2(,)33ππ B .(,)62ππ C .(0,)3π D .(,)66 ππ- 【解析】函数22()cos 2cos 2 x f x x =-=2cos cos 1x x --,从复合函数的角度看,原函数看作2()1g t t t =--,cos t x =,对于2()1g t t t =--,当1[1,]2t ∈-时,()g t 为减函数,当1[,1]2 t ∈时,()g t 为增函数,当2(,)33x ππ∈时,cos t x =减函数,且11(,)22 t ∈-, ∴ 原函数此时是单调增,选A 【温馨提示】求复合函数的单调区间时,需掌握复合函数的性质,以及注意定义域、自变量系数的正负.求复合函数的单调区间一般思路是:①求定义域;②确定复合过程;③根据外层函数f(μ)的单调性,确定φ(x)的单调性;④写出满足φ(x)的单调性的含有x 的式子,并解出x 的范围;⑤得到原函数的单调区间(与定义域求交).求解时切勿盲目判断. 例2、已知tan 2θ=. (Ⅰ)求tan 4πθ??+ ??? 的值; (Ⅱ)求cos2θ的值. 【解析】 (Ⅰ)∵tan 2θ=, tan tan 4tan 41tan tan 4π θπθπθ+??∴+= ???- 高一数学第一次月考试题 一. 选择题(每题5分,共60分) 1.函数)6 2sin(2π +=x y 的最小正周期是( ) A .π4 B .π2 C .π D .2 π 2.0sin300=( ) A .1 2 B . 32 C .-12 D .-32 3.如图,在直角坐标系xOy 中,射线OP 交单位圆O 于点P ,若∠ AOP =θ,则点P 的坐标是( ) A .(cos θ,sin θ) B .(-cos θ,sin θ) C .(sin θ,cos θ) D .(-sin θ,cos θ) 4.如果sin α-2cos α 3sin α+5cos α =-5,那么tan α的值为( ) A .-2 B .2 D .-2316 5.函数)2 52sin(π+=x y 的图象的一条对称轴方程是( ) A .2 π-=x B .4 π-=x C .8 π = x D .4 5π= x 6.将函数y =sin(x -π 3)的图象上所有点的横坐标伸长到原来的2 倍(纵坐标不变),再将所得的图象向右平移π 3个单位,得到的图象 对应的解析式是( ) A .y =sin 1 2x B .y =sin(12x -π 2) C .y =sin(12x -π 6 ) D .y =sin(2x -π 6 ) 7.已知α是第二象限角,且4tan =-3 α,则( ) A .4sin =-5α B .4sin =5α C .3cos =5α D .4cos =-5 α 8.已知3 cos +=25πθ?? ???,且3,22 ππθ? ? ∈ ??? ,则tan θ=( ) A .43 B .-43 C .34 D .-34 9.已知函数f (x )=2sin(ωx +φ)(ω>0,|φ|< π 2 )的部分图象如 齐桓晋文之事[情感目标] 1、体悟孟子当仁不让的治世精神。 2、领会孟子耐心细致的工作态度和巧妙灵活的工作方法。 3、理解孟子的民本思想和同情广大劳动人民的深切情怀。 [认知目标] 1、学习课文中重要的实词、虚词及句式。 2、学习孟子迂回曲折的论辩方法。 3、学习比喻在文章中的运用和重要作用。 [技能目标] 1、能够理顺思路错综的文章的理路。 2、善于切分课文这样的没有明显标志的长文章。 3、能够运用简单的比喻进行论辩。 教学过程: 一、谈话导入: 简介孟子,问学生喜不喜欢读《孟子》,引入对《孟子》的介绍,学生自读165页《孟子》简介,导入课文。 相关知识补充:1、孟子与《孟子》 孟子(前372—前289年),名轲,字子舆,战国时邹(现山东邹县东南)人。 孟子是战国时儒家学派的代表人物,曾受业于子思(孔子的孙子)的门人,30岁左右收徒讲学。44岁开始周游列国,晚年回到家乡讲学著述,直到去世。后世统治者都把他作为尊崇的偶像,到元、明时被称为“亚圣”。 《孟子》共七篇,分别为《梁惠王》、《公孙丑》、《滕文公》、《离娄》、《万章》、《告子》、《尽心》。各章又都分为上下两篇。作为一部语录体著作,它记录的是有关孟子重要思想的一些言论。到南宋时,朱熹把它与《礼记》中的《大学》、《中庸》两篇以及《论语》合为“四书”,把读经的传统推向更加狭窄的胡同,成为后世(如明、清两代)科举考试八股文的唯一的取材依据。 2、《孟子》的思想和当时的社会 任何一种哲学,都会创立自己的理想世界。比起道家的小国寡民、佛家的因果报应来说,儒家的集大成思想家孟子的理想世界则诱人得多。孟子提出了一幅君民同乐、仁义并施的王道乐土和太平盛世的理想图景。这对于王者来说,自然是最好不过了,有什么比百姓归附,国力强盛更令他们满意的呢?对于老百姓来说,也是如此,有谁不乐意做太平盛世的人呢? 孟子的思想能够流传久远的原因还远不只于此。在孟子的大思想的统摄之下,孟子的“王道”思想,宣传仁政,还提出“民为贵,社稷次之,君为轻”的民本思想,这充分体现了社会的民主和文明的正当的进步趋势,反映了大多数人的愿望,顺应了时代潮流,这就使他的学说有着深厚的民众基础,容易为多数人接受;而作为统治者,既然能够“王天下”,那么,这种学说就正好可以用来作为自己统治社会的工具,所以,他们会极力推行孟子的学说。 孟子的哲学人格也与他人不同,他主张人性本善,进而十分强调个人修养,提出了“穷则独善其身,达则兼济天下”的封建士大夫的出世进退准则。这种思想当然是具有更大的麻醉作用,所以,封建时代的知识分子(当时的社会精英)总是缺乏进取精神和改革社会的意识,容易被故纸堆埋没,而封建统治者也正好以此来约束全社会。 最后,长期以来,孟子轻视体力劳动和体力劳动者的思想也在很大程度上迎合了中国的士大夫阶层,从而使他的学说得以更加久远地流传。且听听他的一些说法:“无君子莫治野人,无野人莫养君子。”“劳心者治人,劳力者治于人。治于人者食于人,治人者食人,天下之通义也。” 高中数学三角函数复习专题 一、知识点整理 1角的概念的推广: 正负,范围,象限角,坐标轴上的角; 2、角的集合的表示: ① 终边为一射线的角的集合: x|x 2k ② 终边为一直线的角的集合: xx k 3、任意角的三角函数: (1) 弧长公式:1 aR R 为圆弧的半径,a 为圆心角弧度数,1为弧长 (2) 扇形的面积公式 :S 1 -IR R 为圆弧的半径,1为弧长。 2 (3) 三角函数定义: 角 中边上任意一点P 为(x,y),设|OP| r 则: sin — ,cos r x J r tan y r=寸孑圧 x 女口:公式 cos( ) cos cos sin sin 的证明 (4)特殊角的三角函数值 ③两射线介定的区域上的角的集合: x2k ④两直线介定的区域上的角的集合: x k x k ,k Z ? k 360', k Z ,k Z = | ,k Z ; 反过来,角 的终边上到原点的距离为 r 的点P 的坐标可写为:P r cos ,r sin 4 x 4 4 sin cos tan - -si n + cos -ta n - + si n -cos -ta n + -si n -cos + tan 2 . -si n + cos -ta n 2k + + si n + cos + tan sin con tan 2 + cos + sin + cot 2 + cos -si n -cot 3 2 -cos -si n + cot 3_ 2 -cos + sin -cot 三角函数值等于 的同名三角函数值,前面 加 上一个把 看作锐角时,原三角函数值的 符 号;即:函数名不变,符号看象限 三角函数值等于 的异名三角函数值,前面 加 上一个把 看作锐角时,原三角函数值的 符号; 即:函数名改变,符号看象限: sin x 比如 cos 一 x 4 cos x cos x sin 一 (6)三角函数线:(判断正负、比较大小,解方程或不等式等) 如图,角 的终边与单位圆交于点P ,过点P 作x 轴的垂线, 垂足为M ,则 过点A(1,0)作x 轴的切线,交角终边0P 于点T ,贝U (7)同角三角函数关系式: ③ 平方关系:sin 2 a cos 2 a 1 ①倒数关系: tan acota 1 ②商数关系: tana ^ina cosa (8)诱导公试 三角函数及数列大题训练 1.设数列{}n a 满足21112,32n n n a a a -+=-= (1) 求数列{}n a 的通项公式;令n n b na =,求数列的前n 项和n S 2.等比数列{}n a 的各项均为正数,且212326231,9.a a a a a +== (1)求数列{}n a 的通项公式.(2)设 31323log log ......log ,n n b a a a =+++ 求数列1n b ?? ???? 的前项和. 3.已知,,a b c 分别为ABC ?三个内角,,A B C 的对边,cos 3sin 0a C a C b c +--= (1)求A (2)若2a =,ABC ?的面积为3;求,b c 。 4.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知a =b cos C +c sin B . (1)求B ;(2)若b =2,求△ABC 面积的最大值. 5.已知数列{}n a 满足11a =,131n n a a +=+. ⑴证明1{}2 n a +是等比数列,并求{}n a 的通项公式;(2)证明:1231112 n a a a ++<…+. 6.ABC ?的内角A 、B 、C 的对边分别为a 、b 、c ,已知cos()cos 1A C B -+=,2a c =,求C 。 7.ABC ?的内角A 、B 、C 的对边分别为,,a b c 。已知90,2A C a c b -=+= ,求C 8.如图,在△ABC 中,∠ABC =90°,AB= 3 ,BC=1,P 为△ABC 内一点,∠BPC =90° (1)若PB=1 2,求PA ;(2)若∠APB =150°,求tan ∠PBA 9.在△ABC 中,a, b, c 分别为内角A, B, C 的对边, 且2sin (2)sin (2)sin .a A a c B c b C =+++ (Ⅰ)求A 的大小;(Ⅱ)求sin sin B C +的最大值. 10.已知等差数列{a n }满足a 2=0,a 6+a 8= -10 (I )求数列{a n }的通项公式;(II )求数列? ? ????-1 2 n n a 的前n 项和。 11. 在ABC ?中,角A 、B 、C 的对边分别为a ,b ,c 。角A ,B ,C 成等差数列。 (Ⅰ)求cos B 的值;(Ⅱ)边a ,b ,c 成等比数列,求sin sin A C 的值。 12.设向量a =(3sin x ,sin x ),b =(cos x ,sin x ),x ∈π0,2 ?? ???? . (1)若|a |=|b |,求x 的值;(2)设函数f (x )=a ·b ,求f (x )的最大值. 13.在△ABC 中,内角A 、B 、C 的对边分别为a ,b ,c ,且a >c ,已知? =2,cosB=, b=3,求:(Ⅰ)a 和c 的值;(Ⅱ)cos (B ﹣C )的值. A B C P [高中语文《齐桓晋文之事》教案] 齐桓晋文之事 高中语文课文《齐桓晋文之事》是孟子文章中非常有影响的名篇,下面是小编给大家带来的高中语文《齐桓晋文之事》教案,希望对你有帮助。 高中语文《齐桓晋文之事》优秀教案 教学目标 1、体悟孟子当仁不让的治世精神。 2、理解孟子的民本思想和同情广大劳动人民的深切情怀。 3、学习孟子迂回曲折的论辩方法。 4、学习课文中重要的实词、虚词及句式。 教学方法 讲读法。 教学手段 多媒体。 教学课时 二课时 第一课时 教学过程 一、朗读课文。要求学生朗读全文二至三遍。正音。 二、熟读下列重点段,并参考注释,弄通这几段话的大意。见中学语文网中网对译。 ①“齐宣王问曰”至“可”。 ②“无伤也”至“君子远庖厨也”。 ③“挟太山以超北海”至“王请度之”。 ④“五亩之宅”至“然而不王者,未之有也”。 三、思考以下问题。 1、孟子在本文中的基本政治主张是什么? 明确: 孟子劝说齐宣王放弃霸道,施行王道,“保民而王”。在这次谈话中,孟子集中阐述了他的仁政和经济思想,描绘了一幅“保民而王”的社会蓝图。他从齐宣王有“不忍”之心说起,鼓励齐宣王发扬“仁术”,推恩百姓,以德服天下。在孟子看来,仁者无敌,得民心者得天下,“保民”是王道的基础。 2、孟子的论辩思路是怎样的?试根据文章的结构层次来说明。 明确: 本文是一篇谈话记录,齐宣王提问,孟子回答,问与答紧密相连,不容易看出层次。这里根据内容,把课文分为三部分。 第一部分,主要说齐宣王未实行王道,不是不能,而是不为。 这部分又可分为三层。 第一层,提出并明确话题,以问“霸道”开始,转入说“王道”。齐宣王一见孟子,就迫不及待地问齐桓晋文称霸的事,正说明他有称霸的企图。齐桓公、晋文公是春秋五霸中的二霸。前者九合诸侯,一匡天下;后者曾定乱扶周,破楚救宋,都是当时的霸主。因为他们的行事不是靠仁政,而是凭武力,因此被儒家称为“霸道”,与“王道”相对立。所以问齐桓、晋文之事,等于问霸道之事,这对于崇尚王道的孟子来说,无异于劈头一瓢冷水。而孟子以“臣未之闻也”一句,轻轻把话题岔开,转而谈论王道。 第二层,提出“保民而王”的中心论点,肯定齐宣王能够保民而王。在孟子看来,王天下 高三数学三角函数专题训练 1.为得到函数πcos 23y x ?? =+ ?? ? 的图像,只需将函数sin 2y x =的图像( ) A .向左平移5π12个长度单位 B .向右平移5π12 个长度单位 C .向左平移 5π6 个长度单位 D .向右平移 5π6 个长度单位 2.若动直线x a =与函数()sin f x x =和()cos g x x =的图像分别交于M N ,两点,则M N 的最大值为( ) A .1 B . 2 C . 3 D .2 3.把函数sin y x =(x R ∈)的图象上所有点向左平行移动3 π 个单位长度,再把所得图象上所有点的横坐标缩短到原来的1 2倍(纵坐标不变),得到的图 象所表示的函数是( ) A .sin(2)3 y x π =-,x R ∈ B.sin( ) 2 6 x y π =+ ,x R ∈ C.s in (2)3 y x π =+,x R ∈ D.sin(2) 3 2y x π=+ ,x R ∈ 4.设5sin 7 a π=,2cos 7 b π=,2tan 7 c π=,则( ) A.c b a << B.a c b << C.a c b << D.b a c << 5.将函数sin(2)3 y x π =+ 的图象按向量α 平移后所得的图象关于点(,0) 12 π - 中 心对称,则向量α的坐标可能为( ) A .(,0)12π - B .(,0)6 π - C .( ,0)12 π D .( ,0)6 π 6.函数2 ()sin 3sin cos f x x x x =+ 在区间 ,42ππ?? ???? 上的最大值是( ) A.1 B.13 2 + C. 3 2 D.1+ 3 7.若,5sin 2cos -=+a a 则a tan =( ) A.2 1 B. 2 C.2 1- D.2- 三角函数复习专题 一、核心知识点归纳: ★★★1、正弦函数、余弦函数和正切函数的图象与性质: sin y x = cos y x = tan y x = 图象 定义域 R R ,2x x k k ππ?? ≠+∈Z ???? 值域 []1,1- []1,1- R 最值 当22 x k π π=+ () k ∈Z 时,max 1y =; 当22 x k π π=- ()k ∈Z 时,min 1y =-. 当()2x k k π=∈Z 时, max 1y =; 当2x k ππ=+ ()k ∈Z 时,min 1y =-. 既无最大值也无最小值 周期性 2π 2π π 奇偶性 奇函数 偶函数 奇函数 单调性 在2,22 2k k π πππ? ? - + ??? ? ()k ∈Z 上是增函数;在 32,222k k ππππ??++??? ? ()k ∈Z 上是减函数. 在[]()2,2k k k πππ-∈Z 上是增函数;在 []2,2k k πππ+ ()k ∈Z 上是减函数. 在,2 2k k π πππ? ? - + ?? ? ()k ∈Z 上是增函数. 对称性 对称中心()(),0k k π∈Z 对称轴 ()2 x k k π π=+ ∈Z 对称中心 (),02k k ππ? ?+∈Z ?? ? 对称轴()x k k π=∈Z 对称中心 (),02k k π?? ∈Z ??? 无对称轴 ★★2.正、余弦定理:在ABC ?中有: 函 数 性 质 ①正弦定理: 2sin sin sin a b c R A B C ===(R 为ABC ?外接圆半径) 2sin 2sin 2sin a R A b R B c R C =??=??=? ? sin 2sin 2sin 2a A R b B R c C R ? =?? ? =?? ? =?? 注意变形应用 ②面积公式:111 sin sin sin 222 ABC S abs C ac B bc A ?= == ③余弦定理: 222222 2222cos 2cos 2cos a b c bc A b a c ac B c a b ab C ?=+-?=+-??=+-? ? 222 222222 cos 2cos 2cos 2b c a A bc a c b B ac a b c C ab ?+-=?? +-?=???+-= ?? 二、练习题 1、角α的终边过点 b b 则且(,5 3 cos ),4,--=α的值( ) A 、3 B 、-3 C 、3± D 、5 2、已知2π θπ<<,3 sin()25 πθ+=-,则tan(π-θ)的值为( ) A .34 B .43 C .34- D .4 3 - 3、2(sin cos )1y x x =--是 ( ) A .最小正周期为2π的偶函数 B .最小正周期为2π的奇函数 4、为得到函数πcos 3y x ? ?=+ ?? ?的图象,只需将函数sin y x =的图像( ) A .向左平移π 6个长度单位 B .向右平移 π 6 个长度单位 C .向左平移5π 6 个长度单位 D .向右平移 5π 6 个长度单位 5、()sin()(0,0,||)2 f x A x A ωφωφπ =+>>< 是( ) A. y = 2sin(x -4π) B. y = 2sin(x +4π) C. y = 2sin (2x -8π) D. y = 2sin (2x +8 π )高考数学压轴专题2020-2021备战高考《三角函数与解三角形》技巧及练习题附答案
齐桓晋文之事高三教案
高中数学三角函数基础知识点及答案
高三数学 三角函数专题训练(含解析)
齐桓晋文之事教案.docx
高中数学三角函数知识点归纳总结
最新上海高中数学三角函数大题压轴题练习
齐桓晋文之事教案
高考数学三角函数知识点总结及练习
2020年高考数学三角函数专题解题技巧
高中数学三角函数练习题
高三年级语文《齐桓晋文之事》教学设计
高中数学三角函数复习专题(2)
高考全国卷三角函数大题训练
[高中语文《齐桓晋文之事》教案] 齐桓晋文之事
高三数学三角函数专题训练
高考数学三角函数复习专题