数学实验3-插值与数值积分-安振华-2012011837

实验3：插值与数值积分

化学工程系分2 安振华2012011837

【实验目的】

1．掌握用MATLAB 计算拉格朗日、分段线性、三次样条三种插值的方法，改变节点的数目，以及能对三种插值结果进行初步分析；2．熟练掌握用MATLAB 及梯形公式、辛普森公式计算数值积分；3．通过实例学习用插值和数值积分解决实际问题。

【实验内容】

预备：

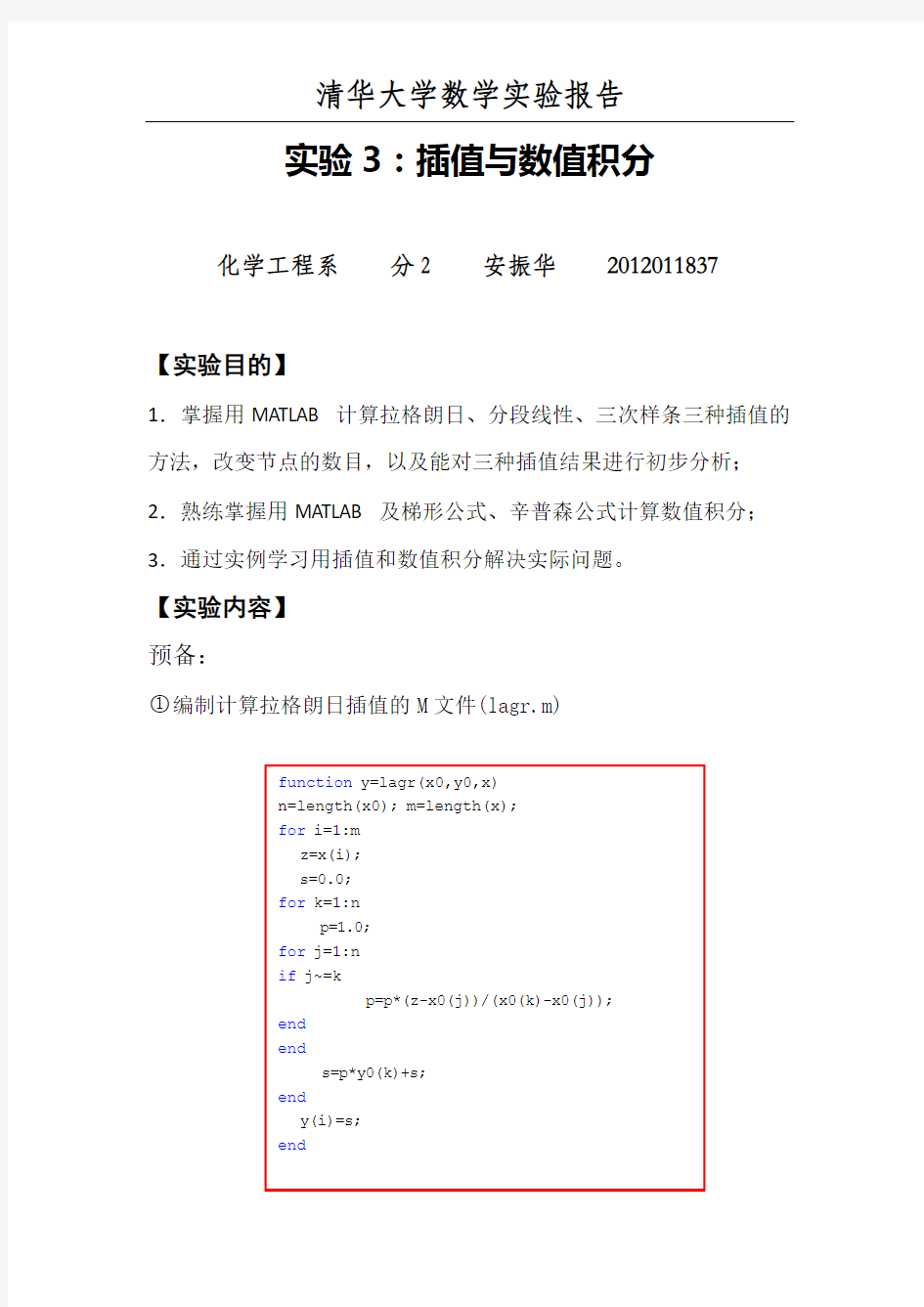
○1编制计算拉格朗日插值的M文件(lagr.m)

○2分段线性插值函数（interp.m）

【实验三：习题10】

表3.10给出的x,y数据位于机翼断面的轮廓线上，y1与y2分别对应轮廓的上下线，假设需要得到x坐标每改变0.1时的y坐标。试完成加工所需数据，画出曲线，求机翼剖面的面积。

【分析】

由于给定的数据点是有限的，要想确定更多的有效数据，就要运用插值方法。而加工断面的面积，则应通过数值积分分别求出上下轮廓线对x 轴围成的面积，然后作差求得。

【解答】

运用学习的三种插值方法逐一计算，具体如下： 1、拉格朗日多项式插值

MATLAB 程序:

运行结果：

给出机翼剖面面积 S=40.3044

051015

0.5

1

1.5

2

2.5

3

3.5

051015

-20

-15

-10

-5

5

MATLAB 程序:

运行结果：

给出机翼剖面面积 S=10.7500

051015

0.511.522.533.5

051015

0.5

1

1.5

2

2.5

3

3.5

MATLAB 程序:

运行结果：

给出机翼剖面面积 S=11.3444

整合程序，将三种差值方法集成在同一程序，可以直观地比较各自得出的结果。

051015

0.511.522.533.5

051015

0.5

1

1.5

2

2.5

3

3.5

整合后的MATLAB 程序:

运行结果：

01020

-20

-15

-10

-5

5

拉格朗日插值01020

分段线性插值

01020

0.5

1

1.5

2

2.5

3

3.5

三次样条插值

【结果分析】

由图可知拉格朗日插值法得出图形与实际不符，不予考虑，可见拉格朗日插值方法的收敛性无法得到保证；分段线性插值的大致形状与原图相近，但它得到的图线不平滑，应用到机翼这样的部件上也是无法使用的。而三次样条插值比较光滑，误差最小。

由梯形公式得到加工剖面面积为11.3444。根据梯形公式和辛普森公式的应用特点（已知被积函数的情况下应用辛普森函数更方便，而对于此处插值得到的数据则用梯形公式更方便），故此处应用梯形公式。又由于在插值之后，步长较短，因此推测梯形公式也较为准确。

综上，此问题的最佳解决方案是采用三次样条插值方法，机翼剖面的面积为11.3444。

【实验三：习题11】

图3.11是欧洲一个国家的地图，为算出它的国土面积，首先对该国地图做出如下测量：以由西向东方向为x轴，由南到北方向为y 轴，选择方便的原点，并将从最西边界点到最东边界点在x轴上的区间适当的划分为若干段，在每个分点的y方向测出南边界点和北边界点的y坐标y1和y2，得到表3.11（单位：mm）。

根据地图的比例尺我们知道18mm相当于40km，试由测量数据计算该国国土的近似面积，与它的精确值41288km2作比较。

图3.11

表3.11 地图边界点数据

【分析】

由3.10解题思路知，可以先用三种插值计算方法分别进行插值，得到图像后分析选择与实际符合最好的方案进行计算。计算时可以选择辛普森积分或梯形积分方式进行积分运算。将结果与精确值进行比较和误差分析即可

【解答】

运用学习的三种插值方法分别计算，具体如下：

MATLAB 程序:

运行结果：

050100150200

A.实际地图

050100150200

5

B.拉格朗日插值

050100150200

C.分段线性插值

050100150200

D.三次样条插值

由以上图像分析可得，拉格朗日插值所得结果与实际偏差非常大，顾舍弃该方法。选择三次样条插值或分线段性插值法分析计算。

MATLAB程序:

运行结果：

S1 = 42407

S2 =42458

【结果分析】

这两种方法得到的最终结果都很相近，和精确值41288km2虽然也有一定误差，但并不是很大，分别为2.71%和2.83%，在误差可以接受的范围内。此题中，分段线性插值法的拟合效果最好，与实际轮廓最为相符。这与通常三次样条插值最适合的案例不符，原因可能是该题有关国家边界线，很多国界线沿经纬线分布，因而并不是严格的平滑曲线。

【实验三：习题12】

在桥梁的一端每隔一段时间记录1min有几辆车过桥，得到下表的过桥车辆数量：

试估计一天通过桥梁的车流量。

【分析】

表中所给21组数据（时间x0,车辆数y0）可视为节点，每间隔1min做一个插值点。根据前两题的经验，一般情况下三次样条插值法拟合较好，误差较小故此次直接可以通过三次样条插值法进行插值，得到曲线后求算面积即是一天通过桥梁的车流量。

【解答】

通过三次样条插值法进行插值，得到曲线后利用梯形积分法求算面积即是一天通过桥梁的车流量。

MATLAB程序：

运行结果：

Q=12668 【结果分析】

作图如上图，可以看出图线光滑，拟合较好，综上所述，一天通过桥梁的车流量为：12668辆

【实验总结】

1、通过本次实验，我了解了多种插值方法，熟练掌握了拉格朗日插值法、分段线性插值法和三次样条插值法，在课下了解了牛顿、高斯的插值方法。通过实验，我学会了解决科学研究中的许多数据处理问题。

0510152025

-5

5

10

15

20

25

30

一天内车流变化曲线

2、了解了几种数值积分的方法及其原理，知道分析他们误差的方法。在实验中能够熟练运用其求不同类型数组或函数的积分。

3、综合比较三种插值方法，我觉得他们各有特点。其中分段线性插值与三次样条插值的收敛性都能保证（三次样条插值得到的图线光滑，使用比较广泛），拉格朗日插值的收敛性对有些函数无法保证，有时也会出现龙格现象，这限制了拉格朗日插值法的应用，但在一定区间内拉格朗日插值法也有它自己的优势。

定积分的方法总结

定积分的方法总结 定积分是新课标的新增内容，其中定积分的计算是重点考查的考点之一，下面例析定积分计算的几种常用方法． 一、定义法 例1、求 s i n b a x d x ? ， （b a <） 解:因为函数s i n x 在],[b a 上连续，所以函数sin x 在],[b a 上可积，采用特殊的 方法作积分和．取h = n a b -，将],[b a 等分成n 个小区间, 分点坐标依次为 ?=+<<+<+

数值积分与数值微分实验报告

实验三 数值积分与数值微分 【实验内容】 选用复合梯形公式，复合Simpson 公式，Romberg 算法高斯算法计算 （1） )5343916.1(sin 44102≈-=? I dx x I （2） )9460831.0,1)0((sin 10≈==?I f dx x x I （3） dx x e I x ?+=1024 ;（4） dx x x I ?++=1021)1ln( 【实验前的预备知识】 1、 深刻认识数值积分法的意义； 2、 明确数值积分精度与步长的关系； 3、 根据定积分的计算方法，可以考虑二重积分的计算问题。 4、 比较各种积分方法复杂度及收敛速度。 【实验方法或步骤】 1、 编制数值积分算法的程序； 2、 分别用两种算法计算同一个积分，并比较其结果； 3、 分别取不同步长n a b h /)(-=，试比较计算结果（如20,10=n 等）； 4、 给定精度要求ε，试用变步长算法，确定最佳步长。 程序： 复合梯形公式求函数f 在区间【a ，b 】上的定积分代码 function [I,step]=CombineTraprl(f,a,b,eps) if(nargin==3) eps=1.0e-4;

end n=1; h=(b-a)/2; I1=0; I2=(subs(sym(f),findsym(sym(sym(f)),a)+subs(sym(f),findsym(sym(f)),b))/h; while abs(I2-I1)>eps n=n+1; h=(b-a)/n; I1=I2; I2=0; for i=0:n-1 x=a+h*i; x1=x+h; I2=I2+(h/2)*(subs(sym(f),findsym(sym(f)),x)+subs(sym(f),findsym(sym(f)),x1)); end end I=I2;step=n; 用该方法计算)5343916.1(sin 44 102≈-=?I dx x I 的程序为 [q,s]=CombineTraprl('sqrt(4-(sinx)^2)',0,0.25,1.5343916) 得结果为q =0.4986 s =3即结果为0.4986积分区间为3个 辛普森公式求函数f 在区间【a ，b 】上的定积分代码 function [I,step]=IntSimpson(f,a,b,type,eps) %type 分别为1，2，3时分别为辛普森公式，3/8公式，复合辛普森 if(type==3&&nargin==4) eps=1.0e-4; end I=0; switch type case 1, I=((b-a)/6)*(subs(sym(f),findsym(sym(f)),a)+... 4*subs(sym(f),findsym(sym(f)),(a+b)/2)+... subs(sym(f),findsym(sym(f)),b)); step=1; case 2, I=((b-a)/8)*(subs(sym(f),findsym(sym(f)),a)+... 3*subs(sym(f),findsym(sym(f)),(2*a+b)/3)+... 3*subs(sym(f),findsym(sym(f)),(a+2*b)/3)+subs(sym(f),findsym(sym(f)),b)); step=1; case 3, n=2; h=(b-a)/2;

三次样条插值、拉格朗日插值、herminte插值

三次样条插值： function s=spline(x0,y0,y2l,y2n,x) n=length(x0); km=length(x); a(1)=-0.5; b(1)=3*(y0(2)-y0(1))/(2*(x0(2)-x0(1))); for j=1:n-1 h(j)=x0(j+1)-x0(j); end for j=2:n-1 alpha(j)=h(j-1)/(h(j-1)+h(j)); beta(j)=3*((1-alpha(j))*y0(j)-y(j-1)/h(j-1)+alpha(j)*(y0(j+1)-y0(j))/h(j)); a(j)=-alpha(j)/(2+(1-alpha(j))*a(j-1)); b(j)=(beta(j)-(1-alpha(j))*b(j-1))/(2+(1-alpha(j))*a(j-1)); end m(n)=(3*(y0(n)-y0(n-1))/h(n-1)+y2n*h(n-1)/2-b(n-1))/(2+a(n-1)); for j=(n-1):-1:1 m(j)=a(j)*m(j+1)+b(j); end for k=1:km for j=1:(n-1) if ((x(k)>x0(j))&(x(k)

七大积分总结

七大积分总结 一． 定积分 1. 定积分的定义：设函数f(x)在[a,b]上有界，在区间[a,b]中任意插入n －1个分点： a=x 0

? ??==b a b a b a du u f dt t f dx x f )()()(。 （2） 定义中区间的分法与ξi 的取法是任意的。 （3） 定义中涉及的极限过程中要求λ→0，表示对区间[a,b]无限细分的过程，随λ →0必有n →∞，反之n →∞并不能保证λ→0，定积分的实质是求某种特殊合式的极限： 例：∑?=∞→=n i n n i f dx x f 1 1 0n 1 )()(lim （此特殊合式在计算中可以作为公式使用） 2. 定积分的存在定理 定理一 若函数f(x)在区间[a,b]上连续，则f(x)在[a,b]上可积。 定理二 若函数f(x)在区间[a,b]上有界，且只有有限个间断点，则f(x)在区间上可积。 3. 定积分的几何意义 对于定义在区间[a,b]上连续函数f(x)，当f(x)≥0时，定积分 ? b a dx x f )(在几何上表示由曲线y=f(x),x=a,x=b 及x 轴所围成的曲边梯形的面积；当f(x) 小于0时，围成的曲边梯形位于x 轴下方，定积分?b a dx x f )(在几何意义上表示曲边梯形面积的负值。若f(x)在区间上既取得正值又取得负值时，定积分的几何意义是：它是介于x 轴，曲线y=f(x),x=a,x=b 之间的各部分曲边梯形的代数和。 4．定积分的性质 线性性质（性质一、性质二）

几种定积分的数值计算方法

几种定积分的数值计算方法 摘要:本文归纳了定积分近似计算中的几种常用方法,并着重分析了各种数值方法的计 算思想,结合实例,对其优劣性作了简要说明. 关键词:数值方法;矩形法;梯形法;抛物线法;类矩形;类梯形 Several Numerical Methods for Solving Definite Integrals Abstract:Several common methods for solving definite integrals are summarized in this paper. Meantime, the idea for each method is emphatically analyzed. Afterwards, a numerical example is illustrated to show that the advantages and disadvantages of these methods. Keywords:Numerical methods, Rectangle method, Trapezoidal method, Parabolic method, Class rectangle, Class trapezoid

1. 引言 在科学研究和实际生产中,经常遇到求积分的计算问题,由积分学知识可知,若函数 )(x f 在区间],[b a 连续且原函数为)(x F ,则可用牛顿-莱布尼茨公式 ?-=b a a F b F x f ) ()()( 求得积分.这个公式不论在理论上还是在解决实际问题中都起到了很大的作用. 在科学研究和实际生产中,经常遇到求积分的计算问题,由积分学知识可知,若函数)(x f 在区间],[b a 连续且原函数为)(x F ,则可用牛顿-莱布尼茨公式 ?-=b a a F b F x f ) ()()( 求得积分.这个公式不论在理论上还是在解决实际问题中都起到了很大的作用.另外,对于求导数也有一系列的求导公式和求导法则.但是,在实际问题中遇到求积分的计算,经常会有这样的情况: (1)函数)(x f 的原函数无法用初等函数给出.例如积分 dx e x ?-1 02 , ? 1 sin dx x x 等,从而无法用牛顿-莱布尼茨公式计算出积分。 (2)函数)(x f 使用表格形式或图形给出,因而无法直接用积分公式或导数公式。 (3)函数)(x f 的原函数或导数值虽然能够求出,但形式过于复杂,不便使用. 由此可见,利用原函数求积分或利用求导法则求导数有它的局限性,所以就有了求解数值积分的很多方法,目前有牛顿—柯特斯公式法,矩形法,梯形法,抛物线法,随机投点法,平均值法,高斯型求积法,龙贝格积分法,李查逊外推算法等等,本文对其中部分方法作一个比较． 2.几何意义上的数值算法 s 在几何上表示以],[b a 为底,以曲线)(x f y =为曲边的曲边梯形的面积A ,因此,计 算s 的近似值也就是A 的近似值,如图1所示.沿着积分区间],[b a ,可以把大的曲边梯形分割成许多小的曲边梯形面积之和.常采用均匀分割,假设],[b a 上等分n 的小区间 ,x 1-i h x i +=b x a x n ==,0,其中n a b h -= 表示小区间的长度. 2.1矩形法

数据分析实验报告

数据分析实验报告 文稿归稿存档编号：[KKUY-KKIO69-OTM243-OLUI129-G00I-FDQS58-

第一次试验报告 习题1.3 1建立数据集，定义变量并输入数据并保存。 2数据的描述，包括求均值、方差、中位数等统计量。 分析—描述统计—频率，选择如下： 输出： 统计量 全国居民 农村居民 城镇居民 N 有效 22 22 22 缺失 均值 1116.82 747.86 2336.41 中值 727.50 530.50 1499.50 方差 1031026.918 399673.838 4536136.444 百分位数 25 304.25 239.75 596.25 50 727.50 530.50 1499.50 75 1893.50 1197.00 4136.75 3画直方图，茎叶图，QQ 图。（全国居民） 分析—描述统计—探索，选择如下： 输出： 全国居民 Stem-and-Leaf Plot Frequency Stem & Leaf 5.00 0 . 56788 数据分析实验报告 【最新资料，WORD 文档，可编辑修改】

2.00 1 . 03 1.00 1 . 7 1.00 2 . 3 3.00 2 . 689 1.00 3 . 1 Stem width: 1000 Each leaf: 1 case(s) 分析—描述统计—QQ图，选择如下： 输出： 习题1.1 4数据正态性的检验：K—S检验，W检验数据： 取显着性水平为0.05 分析—描述统计—探索，选择如下：（1）K—S检验

结果：p=0.735 大于0.05 接受原假设，即数据来自正太总体。 （2 ）W 检验 结果：在Shapiro-Wilk 检验结果972.00 w ，p=0.174大于0.05 接受原假设，即数据来自正太总体。 习题1.5 5 多维正态数据的统计量 数据：

定积分总结

定积分讲义总结 内容一 定积分概念 一般地，设函数()f x 在区间[,]a b 上连续，用分点0121i i n a x x x x x x b -=<<<<<<<=L L 将区间[,]a b 等分成n 个小区间，每个小区间长度为x ?（b a x n -?= ），在每个小区间[]1,i i x x -上取一点()1,2,,i i n ξ=L ，作和式：1 1 ()()n n n i i i i b a S f x f n ξξ==-=?=∑∑ 如果x ?无限接近于0（亦即n →+∞）时，上述和式n S 无限趋近于常数S ，那么称该常数S 为函数()f x 在区间[,]a b 上的定积分。记为：()b a S f x dx = ? 其中()f x 成为被积函数，x 叫做积分变量，[,]a b 为积分区间，b 积分上限，a 积分下限。 说明：（1）定积分 ()b a f x dx ? 是一个常数，即n S 无限趋近的常数S （n →+∞时）称为()b a f x dx ?，而不是n S ． （2）用定义求定积分的一般方法是：①分割：n 等分区间[],a b ；②近似代替：取点[]1,i i i x x ξ-∈；③求和： 1()n i i b a f n ξ=-∑；④取极限：()1()lim n b i a n i b a f x dx f n ξ→∞=-=∑? 例1．弹簧在拉伸的过程中，力与伸长量成正比，即力()F x kx =（k 为常数，x 是伸长量），求弹簧从平衡位置拉长b 所作的功． 分析：利用“以不变代变”的思想，采用分割、近似代替、求和、取极限的方法求解． 解： 将物体用常力F 沿力的方向移动距离x ，则所作的功为W F x =?． 1．分割 在区间[]0,b 上等间隔地插入1n -个点，将区间[]0,1等分成n 个小区间： 0,b n ??????，2,b b n n ?? ????，…，()1,n b b n -?????? 记第i 个区间为()1,(1,2,,)i b i b i n n n -???=? ? ??L ，其长度为()1i b i b b x n n n -??=-= 把在分段0, b n ? ???? ?，2,b b n n ?? ????，…，()1,n b b n -?????? 上所作的功分别记作：1W ?，2W ?，…，n W ? （2）近似代替 有条件知：()()11i i b i b b W F x k n n n --???=??=?? ? ?? (1,2,,)i n =L （3）求和 ()1 1 1n n n i i i i b b W W k n n ==-=?=??∑∑ =()()22222 110121122n n kb kb kb n n n n -?? ++++-==-?? ?? ??? L

数值积分实验报告

数值分析实验报告 实验四数值积分 一、用复合辛普森和龙贝格算法计算： 复合辛普森主函数xps： function xps(a,b,eps) n=0;Sd=0; S=(f(a)+f(b))*(b-a)/2; while abs(Sd-S)>eps Sd=S; n=n+1; h=(b-a)/n; for i=1:n+1 x(i)=a+(i-1)*h; end S1=f(x(1))+f(x(n+1)); S2=0; S3=0; for i=2:n S2=S2+f(x(i)); end S2=2*S2; for i=1:n S3=S3+f((x(i)+x(i+1))/2); end S3=4*S3; S=(S1+S2+S3)*h/6; end fprintf('%.15f\n',S); 龙贝格主函数romberg2： function romberg2 (a,b,eps) %a,b为区间，eps为精度 Rd=0; R=(b-a)/2*(f(a)+f(b)); N=0; while abs(Rd-R)>eps Rd=R; N=N+1; for k=1:2 if k==1 n=N*2;

else; n=N; end h=(b-a)/n; for i=1:n+1 x(i)=a+(i-1)*h; end C=0; for i=1:n C1=7*f(x(i))+32*f(x(i)+1/4*h)+12*f(x(i)+2/4*h)+32*f(x(i)+3/4*h)+7*f(x(i+1)); C=C+C1*h/90; end if k==1 R=C*64/63; else R=R-C/63; end end end fprintf('结果为：%.15f',R); 1、建立被积函数文件f.m function y=f(x) y=exp(-x^2); 2、调用xps.m、romberg2.m求定积分. >> xps(0,0.5,0.0000001) 0.461281071728228 >>romberg2 (0,0.5,0.0000001) 结果为： 0.461281006413932

数值分析实验报告-插值、三次样条Word版

实验报告：牛顿差值多项式&三次样条 问题：在区间[-1,1]上分别取n=10、20用两组等距节点对龙格函数21()25f x x 作多项式插值及三次样条插值，对每个n 值，分别画出插值函数及()f x 的图形。 实验目的：通过编程实现牛顿插值方法和三次样条方法，加深对多项式插值的理解。应用所编程序解决实际算例。 实验要求： 1． 认真分析问题，深刻理解相关理论知识并能熟练应用； 2． 编写相关程序并进行实验； 3． 调试程序，得到最终结果； 4． 分析解释实验结果； 5． 按照要求完成实验报告。 实验原理： 详见《数值分析 第5版》第二章相关内容。 实验内容： （1）牛顿插值多项式 1.1 当n=10时： 在Matlab 下编写代码完成计算和画图。结果如下： 代码： clear all clc x1=-1:0.2:1; y1=1./(1+25.*x1.^2); n=length(x1); f=y1(:); for j=2:n for i=n:-1:j f(i)=(f(i)-f(i-1))/(x1(i)-x1(i-j+1)); end end syms F x p ; F(1)=1;p(1)=y1(1); for i=2:n F(i)=F(i-1)*(x-x1(i-1)); p(i)=f(i)*F(i); end

syms P P=sum(p); P10=vpa(expand(P),5); x0=-1:0.001:1; y0=subs(P,x,x0); y2=subs(1/(1+25*x^2),x,x0); plot(x0,y0,x0,y2) grid on xlabel('x') ylabel('y') P10即我们所求的牛顿插值多项式，其结果为：P10（x）=-220.94*x^10+494.91*x^8-9.5065e-14*x^7-381.43*x^6-8.504e-14*x^5+123.36*x^4+2.0 202e-14*x^3-16.855*x^2-6.6594e-16*x+1.0 并且这里也能得到该牛顿插值多项式的在[-1，1]上的图形，并和原函数进行对比（见Fig.1）。 Fig.1 牛顿插值多项式（n=10）函数和原函数图形 从图形中我们可以明显的观察出插值函数在两端点处发生了剧烈的波动，产生了极大的误差，即龙格现象，当n=20时，这一现象将更加明显。 1.2 当n=20时： 对n=10的代码进行修改就可以得到n=20时的代码。将“x1=-1:0.2:1;”改为“x1=-1:0.1:1;”即可。运行程序，我们得到n=20时的牛顿插值多项式，结果为：P20(x)= 260188.0*x^20 - 1.0121e6*x^18 + 2.6193e-12*x^17 + 1.6392e6*x^16 + 2.248e-11*x^15 - 1.4429e6*x^14 - 4.6331e-11*x^13 + 757299.0*x^12 + 1.7687e-11*x^11 - 245255.0*x^10 + 2.1019e-11*x^9 + 49318.0*x^8 + 3.5903e-12*x^7 - 6119.2*x^6 - 1.5935e-12*x^5 + 470.85*x^4 + 1.3597e-14*x^3 - 24.143*x^2 - 1.738e-14*x + 1.0 同样的，这里得到了该牛顿插值多项式的在[-1，1]上的图形，并和原函数进行对比（见Fig.2）。

数值分析实验指导 - 7 积分

数值分析实验指导 潘志斌 2014年3月

实验七 数值积分 数值实验综述：通过数值积分实验掌握数值积分的实现，理解各种数值积分公式的特性，并能用数值积分求解积分方程和微分方程。 基础实验 7.1 Newton-cotes 型求积公式 实验目的：学会Newton-cotes 型求积公式,并应用该算法于实际问题. 实验内容：求定积分 ? π cos xdx e x 实验要求：选择等分份数n ,用复化Simpson 求积公式求上述定积分的误差不超过810-的近似值,用MATLAB 中的内部函数int 求此定积分的准确值,与利用复化Simpson 求积公式计算的近似值进行比较。 7.2 Romberg 算法 实验目的：学会数值求积的Romberg 算法,并应用该算法于实际问题. 实验内容：求定积分 ? 1 5 .0dx x 实验要求： （1）要求程序不断加密对积分区间的等分,自动地控制Romberg 算法中的加速收敛过程,直到定积分近似值的误差不超过610-为止,输出求得的定积分近似值。 （2）可用MATLAB 中的内部函数int 求得此定积分的准确值与Romberg 算法计算的近似值进行比较。 7.3 Gauss 型求积公式 实验目的：学会Gauss 型求积公式,并应用该算法于实际问题. 实验内容：求定积分 ? -+4 42 1x dx 实验要求： （1）把Gauss 点的表格存入计算机,以Gauss-Legendre 求积公式作为本实验的例子,要求程序可以根据不同的阶数n ,自动地用n 阶Gauss-Legendre 求积

公式计算上述定积分的近似值.体会Gauss型求积公式是具有尽可能高的代数精度的数值求积公式。 （2）可用MATLAB中的内部函数int求得此定积分的准确值与Gauss型求积公式求得的值进行比较。

数值分析上机实验报告

数值分析上机实验报告

《数值分析》上机实验报告 1.用Newton 法求方程 X 7-X 4+14=0 在（0.1，1.9）中的近似根（初始近似值取为区间端点，迭代6次或误差小于0.00001）。 1.1 理论依据： 设函数在有限区间[a ，b]上二阶导数存在，且满足条件 {}α?上的惟一解在区间平方收敛于方程所生的迭代序列 迭代过程由则对任意初始近似值达到的一个中使是其中上不变号 在区间],[0)(3,2,1,0,) (') ()(],,[x |))(),((|,|,)(||)(|.4;0)(.3],[)(.20 )()(.110......b a x f x k x f x f x x x Newton b a b f a f mir b a c x f a b c f x f b a x f b f x f k k k k k k ==- ==∈≤-≠>+ 令 )9.1()9.1(0)8(4233642)(0)16(71127)(0)9.1(,0)1.0(,1428)(3 2 2 5 333647>?''<-=-=''<-=-='<>+-=f f x x x x x f x x x x x f f f x x x f 故以1.9为起点 ?? ?? ? ='- =+9.1)()(01x x f x f x x k k k k 如此一次一次的迭代，逼近x 的真实根。当前后两个的差<=ε时，就认为求出了近似的根。本程序用Newton 法求代数方程(最高次数不大于10)在（a,b ）区间的根。

1.2 C语言程序原代码： #include #include main() {double x2,f,f1; double x1=1.9; //取初值为1.9 do {x2=x1; f=pow(x2,7)-28*pow(x2,4)+14; f1=7*pow(x2,6)-4*28*pow(x2,3); x1=x2-f/f1;} while(fabs(x1-x2)>=0.00001||x1<0.1); //限制循环次数printf("计算结果：x=%f\n",x1);} 1.3 运行结果： 1.4 MATLAB上机程序 function y=Newton(f,df,x0,eps,M) d=0; for k=1:M if feval(df,x0)==0 d=2;break else x1=x0-feval(f,x0)/feval(df,x0); end e=abs(x1-x0); x0=x1; if e<=eps&&abs(feval(f,x1))<=eps d=1;break end end

插值法实验报告

实验二插值法 1、实验目的： 1、掌握直接利用拉格郎日插值多项式计算函数在已知点的函数值；观察拉格郎日插值的龙格现象。 2、了解Hermite插值法、三次样条插值法原理，结合计算公式，确定函数值。 2、实验要求: 1)认真分析题目的条件和要求，复习相关的理论知识，选择适当的解决方案和算法； 2)编写上机实验程序，作好上机前的准备工作； 3)上机调试程序，并试算各种方案，记录计算的结果（包括必要的中间结果）； 4)分析和解释计算结果； 5)按照要求书写实验报告； 3、实验内容： 1) 用拉格郎日插值公式确定函数值；对函数f(x)进行拉格郎日插值，并对f(x)与插值多项式的曲线作比较。 已知函数表：（0.56160,0.82741）、（0.56280,0.82659）、（0.56401,0.82577）、（0.56521,0.82495）用三次拉格朗日插值多项式求x=0.5635时函数近似值。 2) 求满足插值条件的插值多项式及余项 1) 4、题目：插值法 5、原理： 拉格郎日插值原理： n次拉格朗日插值多项式为：L n (x)=y l (x)+y 1 l 1 (x)+y 2 l 2 (x)+…+y n l n (x)

n=1时，称为线性插值， L 1(x)=y (x-x 1 )/(x -x 1 )+y 1 (x-x )/(x 1 -x )=y +(y 1 -x )(x-x )/(x 1 -x ) n=2时，称为二次插值或抛物线插值， L 2(x)=y (x-x 1 )(x-x 2 )/(x -x 1 )/(x -x 2 )+y 1 (x-x )(x-x 2 )/(x 1 -x )/(x 1 -x 2 )+y 2 (x -x 0)(x-x 1 )/(x 2 -x )/(x 2 -x 1 ) n=i时， Li= （X-X0）……(X-X i-1)(x-x i+1) ……(x-x n) （X-X0）……(X-X i-1)(x-x i+1) ……(x-x n) 6、设计思想： 拉格朗日插值法是根据n + 1个点x0, x1, ... x n(x0 < x1 < ... x n)的函数值f (x0), f (x1) , ... , f (x n)推出n次多項式p(x)，然后n次多項式p (x)求出任意的点x对应的函数值f (x)的算法。 7、对应程序： 1 ) 三次拉格朗日插值多项式求x=0.5635时函数近似值 #include"stdio.h" #define n 5 void main() { int i,j; float x[n],y[n]; float x1; float a=1; float b=1; float lx=0; printf("\n请输入想要求解的X：\n x="); scanf("%f",&x1); printf("请输入所有点的横纵坐标：\n"); for(i=1;i

定积分计算的总结论文

定积分计算的总结论文公司内部档案编码：[OPPTR-OPPT28-OPPTL98-OPPNN08]

定积分计算的总结 闫佳丽 摘 要：本文主要考虑定积分的计算,对一些常用的方法和技巧进行了归纳和总结.在定积分的计算中,常用的计算方法有四种：（1）定义法、（2）牛顿—莱布尼茨公式、（3）定积分的分部积分法、（4）定积分的换元积分法. 关键词：定义、牛顿—莱布尼茨公式、分部积分、换元. 1前言 17世纪后期，出现了一个崭新的数学分支—数学分析.它在数学领域中占据着主导地位.这种新数学思想的特点是非常成功地运用了无限过程的运算即极限运算.而其中的微分和积分这两个过程，则构成系统微积分的核心.并奠定了全部分析学的基础.而定积分是微积分学中的一个重要组成部分. 2正文 那么，究竟什么是定积分呢我们给定积分下一个定义：设函数()f x 在[],a b 有定义，任给[],a b 一个分法T 和一组{}k ξξ=，有积分和 1 (,)()n k k k T f x σξξ==?∑，若当()0l T →时，积分和(,)T σξ存在有限极限， 设()0()0 1 lim (,)lim ()n k k l T l T k T f x I σξξ→→==?=∑，且数I 与分法T 无关，也与k ξ在[]1,k k x x -的取法无关，即{}0,0,:(),k T l T εδδξξ?>?>?

数值分析实验报告1

实验一 误差分析 实验（病态问题） 实验目的：算法有“优”与“劣”之分，问题也有“好”与“坏”之别。对数值方法的研究而言，所谓坏问题就是问题本身对扰动敏感者，反之属于好问题。通过本实验可获得一个初步体会。 数值分析的大部分研究课题中，如线性代数方程组、矩阵特征值问题、非线性方程及方程组等都存在病态的问题。病态问题要通过研究和构造特殊的算法来解决，当然一般要付出一些代价（如耗用更多的机器时间、占用更多的存储空间等）。 问题提出：考虑一个高次的代数多项式 )1.1() ()20()2)(1()(20 1∏=-=---=k k x x x x x p 显然该多项式的全部根为1,2,…,20共计20个，且每个根都是单重的。现考虑该多项式的一个扰动 )2.1(0 )(19=+x x p ε 其中ε是一个非常小的数。这相当于是对（）中19x 的系数作一个小的扰动。我们希望比较（）和（）根的差别，从而分析方程（）的解对扰动的敏感性。 实验内容：为了实现方便，我们先介绍两个Matlab 函数：“roots ”和“poly ”。 roots(a)u = 其中若变量a 存储n+1维的向量，则该函数的输出u 为一个n 维的向量。设a 的元素依次为121,,,+n a a a ，则输出u 的各分量是多项式方程 01121=+++++-n n n n a x a x a x a 的全部根；而函数 poly(v)b =

的输出b 是一个n+1维变量，它是以n 维变量v 的各分量为根的多项式的系数。可见“roots ”和“poly ”是两个互逆的运算函数。 ;000000001.0=ess );21,1(zeros ve = ;)2(ess ve = ))20:1((ve poly roots + 上述简单的Matlab 程序便得到（）的全部根，程序中的“ess ”即是（）中的ε。 实验要求： （1）选择充分小的ess ，反复进行上述实验，记录结果的变化并分析它们。 如果扰动项的系数ε很小，我们自然感觉（）和（）的解应当相差很小。计算中你有什么出乎意料的发现表明有些解关于如此的扰动敏感性如何 （2）将方程（）中的扰动项改成18x ε或其它形式，实验中又有怎样的现象 出现 （3）（选作部分）请从理论上分析产生这一问题的根源。注意我们可以将 方程（）写成展开的形式， ) 3.1(0 ),(1920=+-= x x x p αα 同时将方程的解x 看成是系数α的函数，考察方程的某个解关于α的扰动是否敏感，与研究它关于α的导数的大小有何关系为什么你发现了什么现象，哪些根关于α的变化更敏感 思考题一：（上述实验的改进） 在上述实验中我们会发现用roots 函数求解多项式方程的精度不高，为此你可以考虑用符号函数solve 来提高解的精确度，这需要用到将多项式转换为符号多项式的函数poly2sym,函数的具体使用方法可参考Matlab 的帮助。

定积分应用方法总结(经典题型归纳).docx

精品文档 定积分复习重点 定积分的考查频率不是很高，本讲复习主要掌握定积分的概念和几何意义，使 用微积分基本定理计算定积分，使用定积分求曲边图形的面积和解决一些简单的物 理问题等． 1. 定积分的运算性质 (1) b b kf (x)dx k f (x)dx(k 为常数 ). a a (2) b b f 1 ( x)dx b 2 ( x)dx. [ f 1 ( x) f 2 ( x)]dx f a a a b c b 其中 a

(完整版)哈工大-数值分析上机实验报告

实验报告一 题目：非线性方程求解 摘要：非线性方程的解析解通常很难给出，因此线性方程的数值解法就尤为重要。本实验采用两种常见的求解方法二分法和Newton法及改进的Newton法。 前言：（目的和意义） 掌握二分法与Newton法的基本原理和应用。 数学原理： 对于一个非线性方程的数值解法很多。在此介绍两种最常见的方法：二分法和Newton法。 对于二分法，其数学实质就是说对于给定的待求解的方程f(x)，其在[a,b]上连续，f(a)f(b)<0，且f(x)在[a,b]内仅有一个实根x*，取区间中点c，若，则c恰为其根，否则根据f(a)f(c)<0是否成立判断根在区间[a,c]和[c,b]中的哪一个，从而得出新区间，仍称为[a,b]。重复运行计算，直至满足精度为止。这就是二分法的计算思想。

Newton法通常预先要给出一个猜测初值x0，然后根据其迭代公式 产生逼近解x*的迭代数列{x k}，这就是Newton法的思想。当x0接近x*时收敛很快，但是当x0选择不好时，可能会发散，因此初值的选取很重要。另外，若将该迭代公式改进为 其中r为要求的方程的根的重数，这就是改进的Newton法，当求解已知重数的方程的根时，在同种条件下其收敛速度要比Newton法快的多。 程序设计： 本实验采用Matlab的M文件编写。其中待求解的方程写成function的方式，如下 function y=f(x); y=-x*x-sin(x); 写成如上形式即可，下面给出主程序。 二分法源程序： clear %%%给定求解区间 b=1.5; a=0;

%%%误差 R=1; k=0;%迭代次数初值 while (R>5e-6) ; c=(a+b)/2; if f12(a)*f12(c)>0; a=c; else b=c; end R=b-a;%求出误差 k=k+1; end x=c%给出解 Newton法及改进的Newton法源程序：clear %%%% 输入函数 f=input('请输入需要求解函数>>','s') %%%求解f(x)的导数 df=diff(f);