
高考数学圆锥曲线知识点总结 方程的曲线:
在平面直角坐标系中,如果某曲线C(看作适合某种条件的点的集合或轨迹 )上的点与一个二元方程f(x,y)=0的实数解建立了如下的关系:(1)曲线上的点的坐标都是这个方程的解;(2)以这个方程的解为坐标的点都是曲线上的点,那么这个方程叫做曲线的方程;这条曲线叫做方程的曲线。
点与曲线的关系:若曲线C 的方程是f(x,y)=0,则点P0(x0,y0)在曲线C 上?f(x0,y 0)=0;点P0(x0,y0)不在曲线C 上?f(x0,y0)≠0。
两条曲线的交点:若曲线C1,C2的方程分别为f1(x,y)=0,f2(x,y)=0,则点P0(x0,y0)是C1,C2的交点?{0
),(0
),(002001==y x f y x f 方程组有n 个不同的实数解,两条曲线就有n 个不同的交点;方程组没有实数解,曲线就没有交点。 二、圆:
1、定义:点集{M ||OM |=r },其中定点O 为圆心,定长r 为半径.
2、方程:(1)标准方程:圆心在c(a,b),半径为r 的圆方程是(x-a)2+(y-b)2=r2 圆心在坐标原点,半径为r 的圆方程是x2+y2=r2
(2)一般方程:①当D2+E2-4F >0时,一元二次方程x2+y2+Dx+Ey+F=0叫做圆的一般方程,圆心为
)2,2(E
D --
半
径是
2422F
E D -+。配方,将方程x2+y2+Dx+Ey+F=0化为(x+
2D )2+(y+2E )2=
44F -E D 22+
②当D2+E2-4F=0时,方程表示一个点(-2D ,-2E
);
③当D2+E2-4F <0时,方程不表示任何图形.
点与圆的位置关系 已知圆心C(a,b),半径为r,点M 的坐标为(x0,y0),则|MC |<r ?点M 在圆C 内,|MC |=r ?点M 在圆C 上,|MC |>r ?点M 在圆C 内,其中|MC |=
2
020b)-(y a)-(x +。
直线和圆的位置关系:①直线和圆有相交、相切、相离三种位置关系:直线与圆相交?有两个公共点;直线与圆相切?有一个公共点;直线与圆相离?没有公共点。
②直线和圆的位置关系的判定:(i)判别式法;(ii)利用圆心C(a,b)到直线Ax+By+C=0的距离2
2
B A C
Bb Aa d +++=
与半径r 的大小关系来判定。 三、圆锥曲线的统一定义:
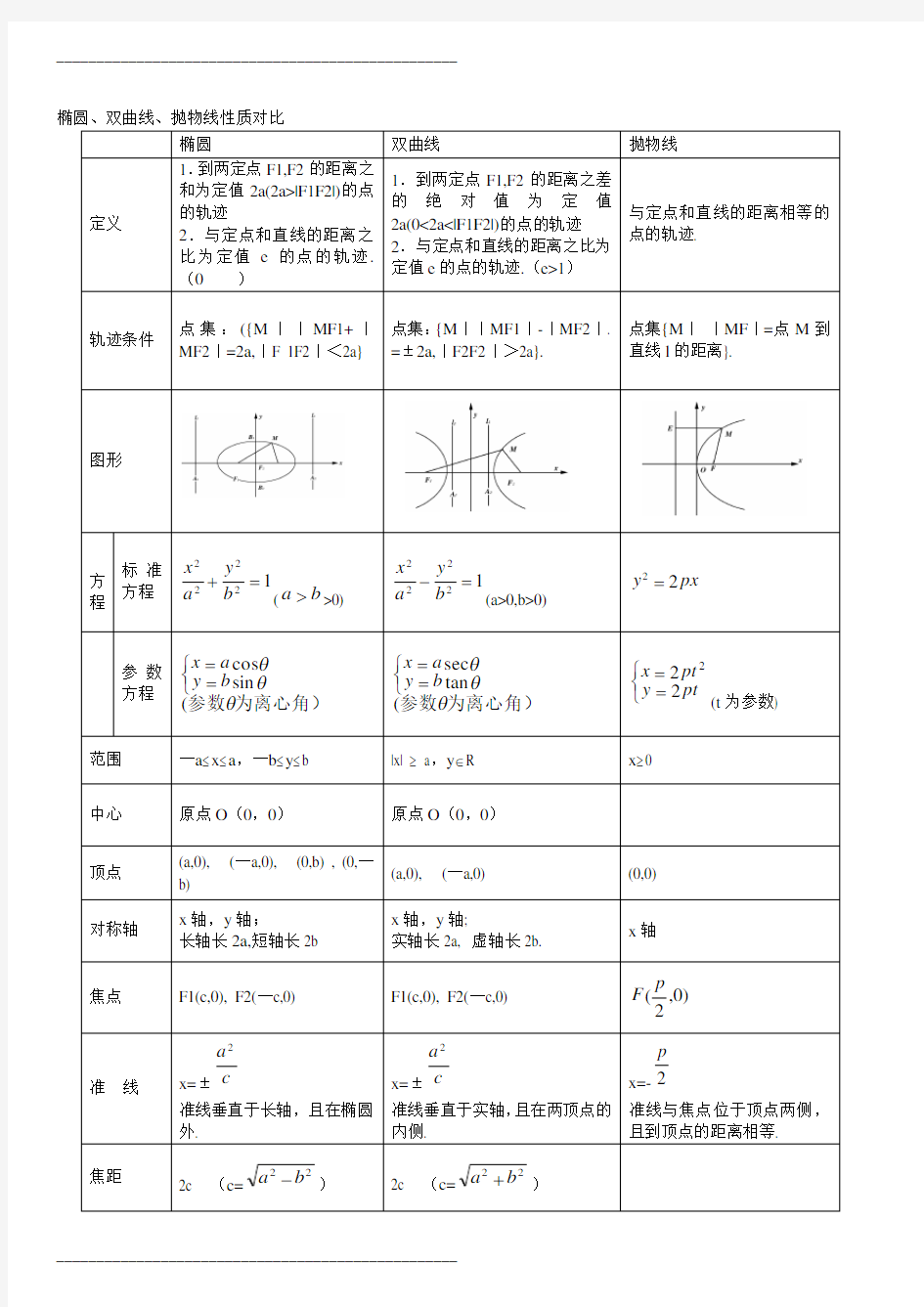
平面内的动点P(x,y)到一个定点F(c,0)的距离与到不通过这个定点的一条定直线l 的距离之 比是一个常数e(e >0),则动点的轨迹叫做圆锥曲线。其中定点F(c,0)称为焦点,定直线l 称为准线,正常数e 称为离心率。当0<e <1时,轨迹为椭圆;当e=1时,轨迹为抛物线;当e >1时,轨迹为双曲线。 四、椭圆、双曲线、抛物线:
椭圆
双曲线
抛物线
定义
1.到两定点F1,F2的距离之和为定值2a(2a>|F1F2|)的点的轨迹
2.与定点和直线的距离之比为定值e 的点的轨迹.(0 1.到两定点F1,F2的距离之差的绝对值为定值2a(0<2a<|F1F2|)的点的轨迹 2.与定点和直线的距离之比为定值e 的点的轨迹.(e>1) 与定点和直线的距离相等的点的轨迹. 轨迹条件 点集:({M ||MF1+|MF2|=2a,|F 1F2|<2a} 点集:{M ||MF1|-|MF2|. =±2a,|F2F2|>2a}. 点集{M | |MF |=点M 到直线l 的距离}. 图形 方 程 标准方程 122 22=+b y a x (b a >>0) 122 22=-b y a x (a>0,b>0) px y 22= 参数 方程 为离心角)参数θθθ(sin cos ? ??==b y a x 为离心角)参数θθθ(tan sec ? ??==b y a x ???==pt y pt x 222 (t 为参数) 范围 ─a ≤x ≤a ,─b ≤y ≤b |x| ≥ a ,y ∈R x ≥0 中心 原点O (0,0) 原点O (0,0) 顶点 (a,0), (─a,0), (0,b) , (0,─b) (a,0), (─a,0) (0,0) 对称轴 x 轴,y 轴; 长轴长2a,短轴长2b x 轴,y 轴; 实轴长2a, 虚轴长2b. x 轴 焦点 F1(c,0), F2(─c,0) F1(c,0), F2(─c,0) )0,2(p F 准 线 x=±c a 2 准线垂直于长轴,且在椭圆外. x=±c a 2 准线垂直于实轴,且在两顶点的内侧. x=-2p 准线与焦点位于顶点两侧,且到顶点的距离相等. 焦距 2c (c=22b a -) 2c (c=22b a +) ⑶等轴双曲线:双曲线2 22a y x ±=-称为等轴双曲线,其渐近线方程为x y ±=,离心率2=e . ⑷共轭双曲线:以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线,叫做已知双曲线的共轭双曲线.λ=-22 22b y a x 与 λ-=-22 2 2b y a x 互为共轭双曲线,它们具有共同的渐近线:02222=-b y a x . ⑸共渐近线的双曲线系方程:) 0(2 22 2 ≠=-λλb y a x 的渐近线方程为0=±b y a x 如果双曲线的渐近线为0=±b y a x 时,它 的双曲线方程可设为) 0(2 22 2 ≠=- λλb y a x . 【备注2】抛物线: (1)抛物线2 y =2px(p>0)的焦点坐标是(2p ,0),准线方程x=-2p ,开口向右;抛物线2 y =-2px(p>0)的焦点坐标是 (-2p ,0),准线方程x=2p ,开口向左;抛物线2 x =2py(p>0)的焦点坐标是(0,2p ),准线方程y=-2p ,开口向上; 抛物线2 x =-2py (p>0)的焦点坐标是(0,-2p ),准线方程y=2p ,开口向下. (2)抛物线2 y =2px(p>0)上的点M(x0,y0)与焦点F 的距离 20p x MF + =;抛物线2 y =-2px(p>0)上的点M(x0,y0) 与焦点F 的距离 02x p MF -= (3)设抛物线的标准方程为2 y =2px(p>0),则抛物线的焦点到其顶点的距离为2p ,顶点到准线的距离2p ,焦点到 准线的距离为p. (4)已知过抛物线2 y =2px(p>0)焦点的直线交抛物线于A 、B 两点,则线段AB 称为焦点弦,设A(x1,y1),B(x2,y2), 则弦长AB =2 1x x ++p 或 α2sin 2p AB =(α为直线AB 的倾斜角),221p y y -=,2,41221p x AF p x x +==(AF 叫做焦半径). 五、坐标的变换: (1)坐标变换:在解析几何中,把坐标系的变换(如改变坐标系原点的位置或坐标轴的方向)叫做坐标变换.实施坐标变换时,点的位置,曲线的形状、大小、位置都不改变,仅仅只改变点的坐标与曲线的方程. (2)坐标轴的平移:坐标轴的方向和长度单位不改变,只改变原点的位置,这种坐标系的变换叫做坐标轴的平移,简称移轴。 (3)坐标轴的平移公式:设平面内任意一点M ,它在原坐标系xOy 中的坐标是9x,y),在新坐标系x ′O ′y ′中 的坐标是 ),(''y x .设新坐标系的原点O ′在原坐标系xOy 中的坐标是(h,k),则 k y y h x x +=+=''或k y y h x x -=-='' 叫做平移(或移轴)公式. 点P 处的切线PT 平分△PF1F2在点P 处的外角. PT 平分△PF1F2在点P 处的外角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点. 以焦点弦PQ 为直径的圆必与对应准线相离. 以焦点半径PF1为直径的圆必与以长轴为直径的圆内切. 若000(,)P x y 在椭圆22 221x y a b +=上,则过0P 的椭圆的切线方程是00221x x y y a b +=. 若000(,)P x y 在椭圆22 221x y a b +=外,则过0P 作椭圆的两条切线切点为P1、P2,则切点弦P1P2的直线方程是 00221x x y y a b +=. 椭圆22 221x y a b += (a >b >0)的左右焦点分别为F1,F 2,点P 为椭圆上任意一点12F PF γ∠=,则椭圆的焦点角形 的面积为 122tan 2F PF S b γ ?=.