
《信息论与编码(第二版)》曹雪虹答案
第二章
2.1一个马尔可夫信源有3个符号{}1,23,u u u ,转移概率为:()11|1/2p u u =,()21|1/2p u u =,
()31|0p u u =,()12|1/3p u u =,()22|0p u u =,()32|2/3p u u =,()13|1/3p u u =,()23|2/3p u u =,()33|0p u u =,画出状态图并求出各符号稳态概率。
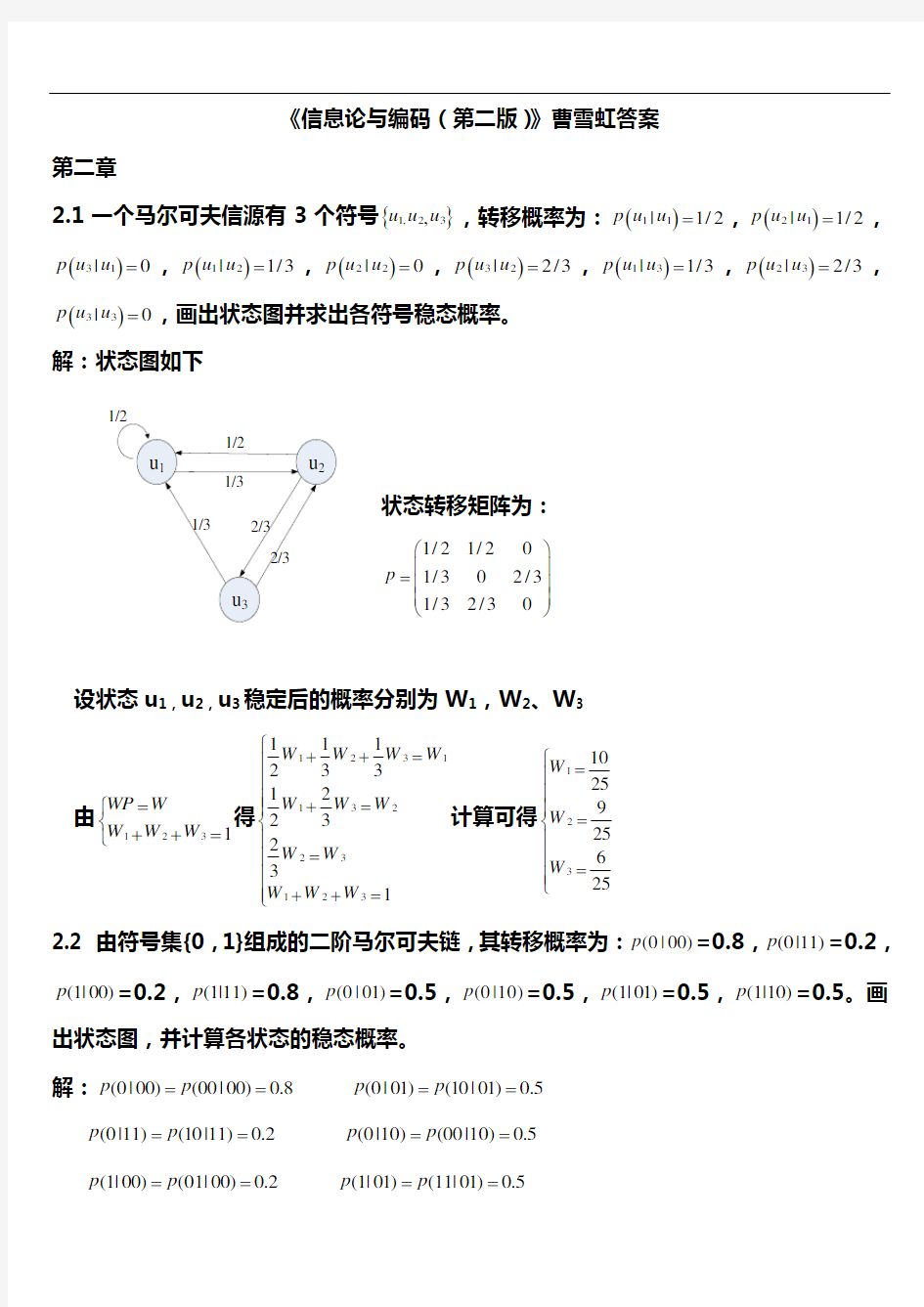
解:状态图如下
状态转移矩阵为:
1/21/2
01/302/31/32/30p ?? ?= ? ???
设状态u 1,u 2,u 3稳定后的概率分别为W 1,W 2、W 3
由1231WP W W W W =??++=?得1231132
231231
112331223231W W W W W W W W W W W W ?++=???+=???=???++=?
计算可得1231025925625W W W ?=???=
??
?=?? 2.2 由符号集{0,1}组成的二阶马尔可夫链,其转移概率为:(0|00)p =0.8,(0|11)p =0.2,
(1|00)p =0.2,(1|11)p =0.8,(0|01)p =0.5,(0|10)p =0.5,(1|01)p =0.5,(1|10)p =0.5。画
出状态图,并计算各状态的稳态概率。
解:(0|00)(00|00)0.8p p == (0|01)(10|01)0.5p p ==
(0|11)(10|11)0.2p p == (0|10)(00|10)0.5p p == (1|00)(01|00)0.2p p == (1|01)(11|01)0.5p p ==
(1|11)(11|11)0.8p p == (1|10)(01|10)0.5p p == 于是可以列出转移概率矩阵:0.80.20
0000.50.50.50.500000.20.8p ?? ?
?= ? ???
状态图为:
设各状态00,01,10,11的稳态分
布概率为W 1,W 2,W 3,W 4 有
41
1i i WP W W ==???=??∑ 得 131
132
24324412340.80.50.20.50.50.20.50.81W W W W W W W W W W W W W W W W +=??+=??+=??+=?+++=?? 计算得到123451417175
14W W W W ?
=??
?=??
?=???=
?
2.3 同时掷出两个正常的骰子,也就是各面呈现的概率都为1/6,求: (1) “3和5同时出现”这事件的自信息; (2) “两个1同时出现”这事件的自信息;
(3) 两个点数的各种组合(无序)对的熵和平均信息量; (4) 两个点数之和(即2, 3, … , 12构成的子集)的熵; (5) 两个点数中至少有一个是1的自信息量。 解:(1)
bit
x p x I x p i i i 170.418
1
log )(log )(18
1
61616161)(=-=-==
?+?= (2)
bit
x p x I x p i i i 170.536
1
log )(log )(36
1
6161)(=-=-==
?=
(3)
两个点数的排列如下: 11 12 13 14 15 16 21 22 23 24 25 26 31 32 33 34 35 36 41 42 43 44 45 46 51 52 53 54 55 56 61 62 63 64 65 66
共有21种组合:
其中11,22,33,44,55,66的概率是3616
1
61=
? 其他15个组合的概率是18
161612=?? symbol bit x p x p X H i
i i / 337.4181log 18115361log 3616)(log )()(=??? ??
?+?-=-=∑
(4)参考上面的两个点数的排列,可以得出两个点数求和的概率分布如下:
symbol bit x p x p X H X P X i
i i / 274.3 61log 61365log 365291log 912121log 1212181log 1812361log 36
12 )
(log )()(36112181111211091936586173656915121418133612)(=?
?? ??
+?+?+?+?+?-=-=??????????=?
?????∑(5)
bit x p x I x p i i i 710.136
11
log
)(log )(3611116161)(=-=-==
??=
2-4
2.5 居住某地区的女孩子有25%是大学生,在女大学生中有75%是身高160厘米以上的,而女孩子中身高160厘米以上的占总数的一半。假如我们得知“身高160厘米以上的某女孩是大学生”的消息,问获得多少信息量? 解:
设随机变量X 代表女孩子学历
X x 1(是大学生) x 2(不是大学生) P(X)
0.25
0.75
设随机变量Y 代表女孩子身高
Y y 1(身
高>160cm )
y 2(身高
<160cm )
P(Y)
0.5
0.5
已知:在女大学生中有75%是身高160厘米以上的 即:bit x y p 75.0)/(11=
求:身高160厘米以上的某女孩是大学生的信息量 即:bit y p x y p x p y x p y x I 415.15
.075
.025.0log )()/()(log
)/(log )/(11111111=?-=-=-=
2.6 掷两颗骰子,当其向上的面的小圆点之和是3时,该消息包含的信息量是多少?当小圆点之和是7时,该消息所包含的信息量又是多少? 解:
1)因圆点之和为3的概率1()(1,2)(2,1)18
p x p p =+= 该消息自信息量()log ()log18 4.170I x p x bit =-== 2)因圆点之和为7的概率
1()(1,6)(6,1)(2,5)(5,2)(3,4)(4,3)6p x p p p p p p =+++++=
该消息自信息量()log ()log6 2.585I x p x bit =-== 2.7 设有一离散无记忆信源,其概率空间为123401233/81/41/41/8X x x x x P ====????
= ?
????
? (1)求每个符号的自信息量
(2)信源发出一消息符号序列为{202 120 130 213 001 203 210 110 321 032 011 223 210},求该序列的自信息量和平均每个符号携带的信息量 解:12
2118
()log log 1.415()3
I x bit p x === 同理可以求得233()2,()2,()3I x bit I x bit I x bit ===
因为信源无记忆,所以此消息序列的信息量就等于该序列中各个符号的信息量之和 就有:123414()13()12()6()87.81I I x I x I x I x bit =+++= 平均每个符号携带的信息量为
87.81
1.9545
=bit/符号 2.8 试问四进制、八进制脉冲所含信息量是二进制脉冲的多少倍? 解:
四进制脉冲可以表示4个不同的消息,例如:{0, 1, 2, 3} 八进制脉冲可以表示8个不同的消息,例如:{0, 1, 2, 3, 4, 5, 6, 7} 二进制脉冲可以表示2个不同的消息,例如:{0, 1}
假设每个消息的发出都是等概率的,则:
四进制脉冲的平均信息量symbol bit n X H / 24log log )(1=== 八进制脉冲的平均信息量
symbol bit n X H / 38log log )(2===
二进制脉冲的平均信息量symbol bit n X H / 12log log )(0===
所以:四进制、八进制脉冲所含信息量分别是二进制脉冲信息量的2倍和3倍。 2-9 “-” 用三个脉冲 “●”用一个脉冲
(1) I(●)= I(-)= (2) H=
2-10 (2) P(黑/黑)= P(白/黑)= H(Y/黑)=
(3) P(黑/白)= P(白/白)=
H(Y/白)= (4) P(黑)= P(白)= H(Y)=
2.11 有一个可以旋转的圆盘,盘面上被均匀的分成38份,用1,…,38的数字标示,其中有两份涂绿色,18份涂红色,18份涂黑色,圆盘停转后,盘面上的指针指向某一数字和颜色。
(1)如果仅对颜色感兴趣,则计算平均不确定度 (2)如果仅对颜色和数字感兴趣,则计算平均不确定度 (3)如果颜色已知时,则计算条件熵
解:令X 表示指针指向某一数字,则X={1,2,……….,38} Y 表示指针指向某一种颜色,则Y={l 绿色,红色,黑色} Y 是X 的函数,由题意可知()()i j i p x y p x = (1)3
112381838
()()log
log 2log 1.24()3823818
j j j H Y p y p y ===+?=∑bit/符号
(2)2(,)()log 38 5.25H X Y H X ===bit/符号
(3)(|)(,)()()() 5.25 1.24 4.01H X Y H X Y H Y H X H Y =-=-=-=bit/符号
2.12 两个实验X 和Y ,X={x 1 x 2 x 3},Y={y 1 y 2 y 3},l 联合概率(),i j ij r x y r =为
1112132122233132
337/241/2401/241/41/2401/247/24r r r r r r r
r r ????
? ?= ? ? ? ?????
(1) 如果有人告诉你X 和Y 的实验结果,你得到的平均信息量是多少? (2) 如果有人告诉你Y 的实验结果,你得到的平均信息量是多少?
(3) 在已知Y 实验结果的情况下,告诉你X 的实验结果,你得到的平均信息量是多少? 解:联合概率(,)i j p x y 为 2
2221
(,)(,)log (,)
72411
2log 4log 24log 4247244
i j i j ij
H X Y p x y p x y ==?
+?+∑ =2.3bit/符号
X 概率分布 21
()3log 3 1.583
H Y =?=bit/符号
(|)(,)() 2.3 1.58H X Y H X Y H Y =-=- Y 概率分布是
=0.72bit/符号
2.13 有两个二元随机变量X 和Y ,它们的联合概率为
并定义另一随机变量Z = XY (一般乘积),试计算: (1) H(X), H(Y), H(Z), H(XZ), H(YZ)和H(XYZ);
(2) H(X/Y), H(Y/X), H(X/Z), H(Z/X), H(Y/Z), H(Z/Y), H(X/YZ), H(Y/XZ)和
H(Z/XY);
(3) I(X;Y), I(X;Z), I(Y;Z), I(X;Y/Z), I(Y;Z/X)和I(X;Z/Y)。 解: (1)
symbol
bit y p y p Y H y x p y x p y p y x p y x p y p symbol bit x p x p X H y x p y x p x p y x p y x p x p j
j j i
i i / 1)(log )()(2
1
8183)()()(21
8381)()()(/ 1)(log )()(2
1
8183)()()(21
8381)()()(22212121112212221111=-==
+=+==
+=+==-==
+=+==+=
+=∑∑
Z = XY 的概率分布如下:
symbol
bit z p Z H z z Z P Z k
k / 544.081log 8187log 87
)()(818710)(2
21=??? ??+-=-=??????????===?
?????∑
symbol
bit z x p z x p XZ H z p z x p z x p z x p z p z x p z p z x p z x p z x p z p x p z x p z x p z x p z x p x p i k k i k i / 406.181log 8183log 8321log 21
)(log )()(8
1)()()()()(8
35.087)()()()()()(5.0)()(0)()()()(2222221211112121111112121111=??? ??++-=-==
=+==-=-=+====+=∑∑
symbol
bit z y p z y p YZ H z p z y p z y p z y p z p z y p z p z y p z y p z y p z p y p z y p z y p z y p z y p y p j k
k j k j / 406.181log 8183log 8321log 21
)(log )()(8
1
)()()()()(8
35.087)()()()()()(5.0)()(0)()()()(2222221211112121111112121111=??? ??++-=-==
=+==-=-=+====+=∑∑
symbol
bit z y x p z y x p XYZ H y x p z y x p y x p z y x p z y x p z y x p y x p z y x p y x p z y x p z y x p z y x p z x p z y x p z x p z y x p z y x p y x p z y x p y x p z y x p z y x p z y x p z y x p z y x p i
j
k
k j i k j i / 811.181log 8183log 8383log 8381log 8
1
)(log )()(8
1
)()()
()()(0
)(8
3)()()()()(8
38121)()()()()()(8/1)()()()()(0
)(0)(0)(22222222222122122121121221211211111121111111211111111211111212221211=??? ??+++-=-==
==+====+=-=-==+===+===∑∑∑
(2)
symbol
bit XY H XYZ H XY Z H symbol bit XZ H XYZ H XZ Y H symbol bit YZ H XYZ H YZ X H symbol bit Y H YZ H Y Z H symbol bit Z H YZ H Z Y H symbol bit X H XZ H X Z H symbol bit Z H XZ H Z X H symbol bit X H XY H X Y H symbol bit Y H XY H Y X H symbol
bit y x p y x p XY H i j
j i j i / 0811.1811.1)()()/(/ 405.0406.1811.1)()()/(/ 405.0406.1811.1)()()/(/ 406.01406.1)()()/(/ 862.0544.0406.1)()()/(/ 406.01406.1)()()/(/ 862.0544.0406.1)()()/(/ 811.01811.1)()()/(/ 811.01811.1)()()/(/ 811.181log 8183log 8383log 8381log 81
)(log )()(2=-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==??? ??+++-==-=∑∑
(3)
symbol
bit YZ X H Y X H Y Z X I symbol bit XZ Y H X Y H X Z Y I symbol bit YZ X H Z X H Z Y X I symbol
bit Z Y H Y H Z Y I symbol bit Z X H X H Z X I symbol bit Y X H X H Y X I / 406.0405.0811.0)/()/()/;(/ 457.0405.0862.0)/()/()/;(/ 457.0405.0862.0)/()/()/;(/ 138.0862.01)/()();(/ 138.0862.01)/()();(/ 189.0811.01)/()();(=-=-==-=-==-=-==-=-==-=-==-=-=
2-14 (1)
P(ij)= P(i/j)=
(2) 方法1: = 方法2:
2-15 P(j/i)=
2.16 黑白传真机的消息元只有黑色和白色两种,即X={黑,白},一般气象图上,黑色的出现概率p(黑)=0.3,白色出现的概率p(白)=0.7。
(1)假设黑白消息视为前后无关,求信源熵H(X),并画出该信源的香农线图
(2)实际上各个元素之间是有关联的,其转移概率为:P(白|白)=0.9143,P(黑|白)=0.0857,P(白|黑)=0.2,P(黑|黑)=0.8,求这个一阶马尔可夫信源的信源熵,并画出该信源的香农线图。
(3)比较两种信源熵的大小,并说明原因。 解:(1)221010
()0.3log 0.7log 0.881337
H X =+=bit/符号 P(黑|白)=P(黑)
P(白|白)=P(白) 黑
白
0.7
0.3
0.7
0.3
P(黑|黑)=P(黑) P(白|黑)=P(白)
(2)根据题意,此一阶马尔可夫链是平稳的(P(白)=0.7不随时间变化,P(黑)=0.3不随时 间变化)
212
222
2
1
()(|)(,)log (,)
111
0.91430.7log 0.08570.7log 0.20.3log 0.91430.08570.2
10.80.3log 0.8
i j i j ij
H X H X X p x y p x y ∞===?+?+?+?∑
=0.512bit/符号
2.17 每帧电视图像可以认为是由3
105个像素组成的,所有像素均是独立变化,且每
像素又取128个不同的亮度电平,并设亮度电平是等概出现,问每帧图像含有多少信息量?若有一个广播员,在约10000个汉字中选出1000个汉字来口述此电视图像,试问广播员描述此图像所广播的信息量是多少(假设汉字字汇是等概率分布,并彼此无依赖)?若要恰当的描述此图像,广播员在口述中至少需要多少汉字? 解:1)
symbol
bit X NH X H symbol
bit n X H N
/ 101.27103)()(/ 7128log log )(6
5
22?=??===== 2)
symbol
bit X NH X H symbol bit n X H N
/ 13288288.131000)()(/ 288.1310000log log )(22=?=====
3)158037288
.13101.2)()(6
=?==
X H X H N N 2.20 给定语音信号样值X 的概率密度为1
()2
x p x e λλ-=,x -∞<<+∞,求H c (X),并证明它小于同样方差的正态变量的连续熵。 解
201()()log ()()log 21
()log ()()log 211log log ()2211
1log log ()log
()222
11
log 2log 22x
c x x x x x x
x x
H X p x p x dx p x e dx
p x dx p x x edx
e e x dx
e e x dx e x dx e xe λλλλλλλλλλλλλλλλ+∞
+∞
--∞-∞+∞
+∞
-∞-∞+∞
--∞
+∞
--∞+∞-=-=-=---=-+=-+?-+=-+???????
?0
1log log (1)212log log log
2x x dx
e x e e e λλλλλλ
+∞
-??=--+??=-+=
2
2
()0,()E X D X λ
==
,221214()log 2log ()22e H X e H X ππλλ=
==>= 2.24 连续随机变量X 和Y 的联合概率密度为:???
??≤+=其他
1
),(2222
r y x r y x p π,求H(X), H(Y),
H(XYZ)和I(X;Y)。
(提示:?-=20222log 2
sin log π
π
xdx )
解:
???
?
??????
??????
?
-+-=+
==-==--=--=--=-+-=--=---=--=-=≤≤--===----------
---202020
220
2
20
20
22220
2
20
222222
2222222222222
22222
22
2
22sin log 2
2cos 1422cos 1log 4
sin log sin 4
log sin 4
sin log sin 4
sin log sin 4)
cos (sin log sin 4cos log 4log 2log )(/ log 2
1
log log 2
1
1log 2log log )(2log log )(2
log )( 2log )( )(log )()()
( 21)()(2
2222
22
2π
π
π
π
π
ππθ
θθ
πθθπθ
θθπ
θθπ
θθθπ
θθθπθθθπθπππππππππd d r d rd d r d r r r r d r r r r x dx x r x r r dx x r r x r dx
x r x p symbol
bit e r e
r r dx
x r x p r dx
x r x p dx r
x p dx
r x r x p dx
x p x p X H r x r r x r dy r dy xy p x p r
r
r r
r
r r r r r r r
r r
r c x r x r x r x r 令其中:
e
e e d e d e d e d e d e
d d d e
r d r d d r r d d d r d r 220
2220
220
22
0220
2220
22
20
20
20
220
20
220
20
20
20
20
log 2
1
2sin log 21log 212cos log 1
log 122cos 1log 2
cos log 2
sin log cos cos sin 21
sin log 2sin sin log 2sin 12sin sin log 1
sin log 2cos 2
log 2
1
1log sin log 2cos 2
1log sin log 2cos 2
)2log 2
(2
2sin log 1
log sin log 2cos 2
sin log 2
2cos log 2
log 2
-=--=--=+-
=-=-=?
??
?
??-==
+-=-
-=-
-
+
-
=-
+
-
=
?????
?
?
??
?
??
?
??π
π
ππ
π
π
π
π
π
π
π
π
π
π
π
π
π
θπθ
θπ
θπθ
θ
πθ
θπθ
θ
θθ
θπθθθθπθ
θπθ
θθπθ
θθπθ
θθπππ
θπ
θ
θθπθθπθθπ
θπ
其中:
bit/symbol
e r e r XY H Y H X H Y X I bit/symbol r dxdy xy p r dxdy r
xy p dxdy
xy p xy p XY H bit/symbol
e r X H Y H x p y p r y r r y r dx r dx xy p y p c c c c R
R
R
c C C y r y r y r y r log log log log log 2 )()()();( log )(log 1
log
)( )(log )()( log 2
1
log )()()
()()
( 21
)()(222222222222
2222
2222
22
2-=--=-+===-=-=-===≤≤--===???????
?
---
---πππππππππ
2.25 某一无记忆信源的符号集为{0, 1},已知P(0) = 1/4,P(1) = 3/4。 (1) 求符号的平均熵;
(2) 有100个符号构成的序列,求某一特定序列(例如有m 个“0”和(100 - m )个“1”)的自信息量的表达式; (3) 计算(2)中序列的熵。 解:
(1)symbol bit x p x p X H i
i i / 811.043log 4
341log 4
1)(log )()(=??
? ??+-=-=∑
(2)
bit m x p x I x p m
i i m
m
m i 585.15.414
3
log
)(log )(4
34341)(100
100100
100100+=-=-==?
??
?????? ??=---
(3) symbol bit X H X H / 1.81811.0100)(100)(100=?== 2-26
P(i)= P(ij)= H(IJ)=
2.29 有一个一阶平稳马尔可夫链1,2,,,r X X X ,各X r 取值于集合{}1,2,3A a a a =,已知起始概率P(X r )为1231/2,1/4p p p ===,转移概率如下图所示
j i 1
2
3
1 2 3
1/2 2/3 2/3
1/4 0 1/3
1/4 1/3 0
(1) 求123(,,)X X X 的联合熵和平均符号熵 (2) 求这个链的极限平均符号熵 (3) 求012,,H H H 和它们说对应的冗余度 解:(1)
12312132,112132(,,)()(|)(|)()(|)(|)
H X X X H X H X X H X X X H X H X X H X X =++=++
1111111
()log log log 1.5/224444
H X bit =---=符号
X 1,X 2的联合概率分布为
212()()j i j i
p x p x x =∑
X 2的概率
分布为
12()i j p x x
1 2 3 1 1/4 1/8 1/8 2 1/6 0 1/12 3
1/6
1/12
1 2
3
14/24
5/24 5/24
那么
21111131131
(|)log 4log 4log 4log log3log log348862126212
H X X =++++++
=1.209bit/符号 X 2X 3的联合概率分布为
那么
32771535535
(|)log 2log 4log 4log log3log log3244883627236272
H X X =
++++++ =1.26bit/符号
123(,,) 1.5 1.209 1.26 3.969H X X X bit =++=/符号
所以平均符号熵3123 3.969
(,,) 1.3233
H X X X bit =
=/符号 (2)设a 1,a 2,a 3稳定后的概率分布分别为W1,W2,W3,转移概率距阵为11
12442
103321033
P ?? ? ?
?= ? ? ? ???
由1i WP W W =???=??∑ 得到 123132123122123311431W W W W W W W W W ?++=???+=??++=???计算得到12347314314W W W ?=??
?=??
?=??
又满足不可约性和非周期性
3
14111321
()(|)(,,)2(,,0) 1.2572441433
i i i H X W H X W H H bit ∞===
+?=∑/符号
(3)0log3 1.58H bit ==/符号 1 1.5
H bit =/符号 2 1.5 1.209
1.3552
H bit +=
=/符号 00 1.25110.211.58γη=-=-=11 1.25110.6171.5γη=-=-= 22 1.25
110.0781.355
γη=-=-=
a 1
a 3
a 21/2
2/3
1/4
1/32/31/4
2-30 (1) 求平稳概率 P(j/i)= 解方程组 得到 (2)
信源熵为:
2-31
P(j/i)= 解方程组 得到W1= , W2= , W3=
2.32 一阶马尔可夫信源的状态图如图2-13所示,信源X 的符号集为(0,1,2)。 (1)求信源平稳后的概率分布P(0),P(1),P(2) (2)求此信源的熵
(3)近似认为此信源为无记忆时,符号的概率分布为平稳分布。求近似信源的熵H(X)并与H ∞进行比较
解:根据香农线图,列出转移概率距阵1/2/2/21/2/2/21p p p P p p p p p p -??
??=-??
??-??
令状态0,1,2平稳后的概率分布分别为W1,W2,W3
3
1
1i i WP W W ==???=??∑ 得到 1231
1232123(1)2
2
(1)221p p p W W W W p p W p W W W W W W ?
-++=??
?+-+
=??++=???
计算得到131313W W W ?=??
?
=??
?=??
由齐次遍历可得
112
()(|)3(1,,)(1)log log 3221i i i p p H X W H X W H p p p p p ∞==?-=-+-∑
,()log 3 1.58/H X bit ==符号 由最大熵定理可知()H X ∞存在极大值
或者也可以通过下面的方法得出存在极大值:
()121log(1)(1)log log
1222(1)H X p p p
p p p p p p ∞???-=---+-++??=-???--?
? 112(1)22(1)
p p p =-+-- 又01p ≤≤所以
[]0,2(1)p p ∈+∞-当p=2/3时12(1)p
p =- 0 p p ∞?=->?- 2/3 ()log 02(1) H X p p p ∞?=- 一、(11’)填空题 (1)1948年,美国数学家香农发表了题为“通信的数学理论”的长篇论文,从而创立了信息论。 (2)必然事件的自信息是 0 。 (3)离散平稳无记忆信源X的N次扩展信源的熵等于离散信源X的熵的 N倍。 (4)对于离散无记忆信源,当信源熵有最大值时,满足条件为__信源符号等概分布_。 (5)若一离散无记忆信源的信源熵H(X)等于2.5,对信源进行等长的无失真二进制编码,则编码长度至少为 3 。 (6)对于香农编码、费诺编码和霍夫曼编码,编码方法惟一的是香农编码。(7)已知某线性分组码的最小汉明距离为3,那么这组码最多能检测出_2_______个码元错误,最多能纠正___1__个码元错误。 (8)设有一离散无记忆平稳信道,其信道容量为C,只要待传送的信息传输率R__小于___C(大于、小于或者等于),则存在一种编码,当输入序列长度n足够大,使译码错误概率任意小。(9)平均错误概率不仅与信道本身的统计特性有关,还与___译码规则____________和___编码方法___有关 三、(5')居住在某地区的女孩中有25%是大学生,在女大学生中有75%是身高1.6米以上的,而女孩中身高1.6米以上的占总数的一半。 假如我们得知“身高1.6米以上的某女孩是大学生”的消息,问获得多少信息量? 解:设A表示“大学生”这一事件,B表示“身高1.60以上”这一事件,则 P(A)=0.25 p(B)=0.5 p(B|A)=0.75 (2分) 故 p(A|B)=p(AB)/p(B)=p(A)p(B|A)/p(B)=0.75*0.25/0.5=0.375 (2分) I(A|B)=-log0.375=1.42bit (1分) 四、(5')证明:平均互信息量同信息熵之间满足 I(X;Y)=H(X)+H(Y)-H(XY) 证明: 第二章 信息量和熵 2.2 八元编码系统,码长为3,第一个符号用于同步,每秒1000个码字,求它的 信息速率。 解:同步信息均相同,不含信息,因此 每个码字的信息量为 2?8log =2?3=6 bit 因此,信息速率为 6?1000=6000 bit/s 2.3 掷一对无偏骰子,告诉你得到的总的点数为:(a) 7; (b) 12。问各得到多少信 息量。 解:(1) 可能的组合为 {1,6},{2,5},{3,4},{4,3},{5,2},{6,1} )(a p =366=6 1 得到的信息量 =) (1 log a p =6log =2.585 bit (2) 可能的唯一,为 {6,6} )(b p =361 得到的信息量=) (1 log b p =36log =5.17 bit 2.4 经过充分洗牌后的一副扑克(52张),问: (a) 任何一种特定的排列所给出的信息量是多少? (b) 若从中抽取13张牌,所给出的点数都不相同时得到多少信息量? 解:(a) )(a p =! 521 信息量=) (1 log a p =!52log =225.58 bit (b) ???????花色任选 种点数任意排列 13413!13 )(b p =13 52134!13A ?=1352 13 4C 信息量=1313 52 4log log -C =13.208 bit 2.9 随机掷3颗骰子,X 表示第一颗骰子的结果,Y 表示第一和第二颗骰子的 点数之和,Z 表示3颗骰子的点数之和,试求)|(Y Z H 、)|(Y X H 、 ),|(Y X Z H 、)|,(Y Z X H 、)|(X Z H 。 解:令第一第二第三颗骰子的结果分别为321,,x x x ,1x ,2x ,3x 相互独立, 则1x X =,21x x Y +=,321x x x Z ++= )|(Y Z H =)(3x H =log 6=2.585 bit )|(X Z H =)(32x x H +=)(Y H =2?( 361log 36+362log 18+363log 12+364log 9+365log 536)+36 6 log 6 =3.2744 bit )|(Y X H =)(X H -);(Y X I =)(X H -[)(Y H -)|(X Y H ] 而)|(X Y H =)(X H ,所以)|(Y X H = 2)(X H -)(Y H =1.8955 bit 或)|(Y X H =)(XY H -)(Y H =)(X H +)|(X Y H -)(Y H 而)|(X Y H =)(X H ,所以)|(Y X H =2)(X H -)(Y H =1.8955 bit ),|(Y X Z H =)|(Y Z H =)(X H =2.585 bit )|,(Y Z X H =)|(Y X H +)|(XY Z H =1.8955+2.585=4.4805 bit 2.10 设一个系统传送10个数字,0,1,…,9。奇数在传送过程中以0.5的概 率错成另外一个奇数,其余正确接收,求收到一个数字平均得到的信息量。 解: 8,6,4,2,0=i √ );(Y X I =)(Y H -)|(X Y H 因为输入等概,由信道条件可知, 1. 有一个马尔可夫信源,已知p(x 1|x 1)=2/3,p(x 2|x 1)=1/3,p(x 1|x 2)=1,p(x 2|x 2)=0,试画出该信源的香农线图,并求出信源熵。 解:该信源的香农线图为: 1/3 ○ ○ 2/3 (x 1) 1 (x 2) 在计算信源熵之前,先用转移概率求稳定状态下二个状态x 1和 x 2 的概率)(1x p 和)(2x p 立方程:)()()(1111x p x x p x p =+)()(221x p x x p =)()(2132x p x p + )()()(1122x p x x p x p =+)()(222x p x x p =)(0)(2131x p x p + )()(21x p x p +=1 得4 3 1)(=x p 4 12)(=x p 马尔可夫信源熵H = ∑∑- I J i j i j i x x p x x p x p )(log )()( 得 H=0.689bit/符号 2.设有一个无记忆信源发出符号A 和B ,已知4 341)(.)(= =B p A p 。求: ①计算该信源熵; ②设该信源改为发出二重符号序列消息的信源,采用费诺编码方法,求其平均信息传输速率; ③又设该信源改为发三重序列消息的信源,采用霍夫曼编码方法,求其平均信息传输速率。 解:①∑- =X i i x p x p X H )(log )()( =0.812 bit/符号 ②发出二重符号序列消息的信源,发出四种消息的概率分别为 用费诺编码方法 代码组 b i BB 0 1 BA 10 2 AB 110 3 AA 111 3 无记忆信源 624.1)(2)(2 ==X H X H bit/双符号 平均代码组长度 2B =1.687 bit/双符号 B X H R )(22==0.963 bit/码元时间 ③三重符号序列消息有8个,它们的概率分别为 用霍夫曼编码方法 代码组 b i BBB 64 27 0 0 1 BBA 64 9 0 )(6419 1 110 3 信息论与编码理论习题解 第二章-信息量和熵 解: 平均每个符号长为:154 4.0312.032= ?+?秒 每个符号的熵为9183.03log 3 1 23log 32=?+?比特/符号 所以信息速率为444.34 15 9183.0=?比特/秒 解: 同步信号均相同不含信息,其余认为等概, 每个码字的信息量为 3*2=6 比特; 所以信息速率为600010006=?比特/秒 解:(a)一对骰子总点数为7的概率是 36 6 所以得到的信息量为 585.2)366(log 2= 比特 (b) 一对骰子总点数为12的概率是36 1 所以得到的信息量为 17.536 1 log 2= 比特 解: (a)任一特定排列的概率为 ! 521 ,所以给出的信息量为 58.225! 521 log 2 =- 比特 (b) 从中任取13张牌,所给出的点数都不相同的概率为 1352 13 13 521344!13C A =? 所以得到的信息量为 21.134 log 1313 52 2=C 比特. 解:易证每次出现i 点的概率为 21 i ,所以 比特比特比特比特比特比特比特398.221 log 21)(807.1)6(070.2)5(392.2)4(807.2)3(392.3)2(392.4)1(6,5,4,3,2,1,21 log )(26 12=-==============-==∑ =i i X H x I x I x I x I x I x I i i i x I i 解: 可能有的排列总数为 27720! 5!4!3! 12= 没有两棵梧桐树相邻的排列数可如下图求得, Y X Y X Y X Y X Y X Y X Y X Y 图中X 表示白杨或白桦,它有???? ??37种排法,Y 表示梧桐树可以栽 种的位置,它有???? ??58种排法,所以共有???? ??58*???? ??37=1960种排法保证没有 两棵梧桐树相邻,因此若告诉你没有两棵梧桐树相邻时,得到关于树排列的信息为1960log 27720log 22-= 比特 解: X=0表示未录取,X=1表示录取; Y=0表示本市,Y=1表示外地; Z=0表示学过英语,Z=1表示未学过英语,由此得 《信息论与编码》教学大纲 一课程简介 课程编号:04254002 课程名称:信息论与编码Informatics & Coding 课程类型:基础课必修课 学时:32 学分:2 开课学期:第六学期 开课对象:通信、电子专业 先修课程:概率论与数理统计、信号与系统、随机信号原理。 参考教材:信息论与编码,陈运,周亮,陈新,电子工业出版社,2002年8月 二课程性质、目的与任务 信息论在理论上指出了建立最佳编码、最佳调制和最佳接收方法的最佳系统的理论原则,它对通信体制和通信系统的研究具有指导意义。提高信息传输的可靠性和有效性始终是通信工作所追求的目标。因此,信息论与编码是从事通信、电子系统工程的有关工程技术人员都必须掌握的基本理论知识。 内容提要:本课程包括狭义相对论和提高通信可靠性的差错控制编码理论。信息论所研究的主要问题是在通信系统设计中如何实现有效性和可靠性。 三教学基本内容与基本要求 本课程总学时为32。其中理论教学为28,实验学时为4。 主要的理论教学内容包括:离散信源和连续信源的熵、条件熵、联合熵和平均互信息量的概念及性质;峰值功率受限和平均功率受限下的最大熵定理和连续信源熵的变换;变长码的霍夫曼编码方法,熟悉编码效率和平均码长的计算;最大后验概率准则和最大似然译码准则等。 实验内容主要包括:离散无记忆信道容量的迭代算法,循环码的编译码。 四教学内容与学时分配 第3章离散信源无失真编码 第6章网络信息论 (教学要求:A—熟练掌握;B—掌握;C—了解) 五实习、实验项目及学时分配 1.离散无记忆信道容量的迭代算法2学时 要求用Matlab编写计算离散信道容量的实用程序并调试成功,加深对信道容量的理解。 2.循环码的编译码2学时 要求用Matlab编写程序,用软件完成循环码的编译码算法。 六教学方法与手段 常规教学与多媒体教学相结合。 香农信息论的基本理论探究 制作者:陈喆指导老师:杜奕 【内容摘要】:信息是自从人类出现以来就存在于这个世界上了,天地万物,飞禽走兽,以及人类的生存方式都离不开信息的产生和传播。人类每时每刻都在不停的接受信息,传播信息,以及利用信息。从原来的西汉时期的造纸,到近代西方的印刷术,以及现在的计算机,信息技术在人类历史的进程当中随着生产力的进步而发展。而信息理论的提出却远远落后于信息的出现,它是在近代才被提出来而形成一套完整的理论体系。信息论的主要基本理论包括:信息的定义和度量;各类离散信源和连续信源的信息熵;有记忆、无记忆离散和连续信道的信道容量;无失真信源编码定理。 【关键词】:平均自信息信道容量信源编码霍夫曼码 1211()()log()q q i j i j i j H X X P a a a a ===-∑∑ 此联合熵表明原来信源X 输出任意一对可能的消息的共熵,即描述信源X 输出长度为2的序列的平均不确定性,或者说所含有的信息量。可以用1122() H X X 作为二维离散平稳信源X 的信息熵的近视值。 除了平稳离散信源之外,还存在着非平稳离散信源。在非平稳离散信源中有一类特殊的信源。这种信源输出的符号序列中符号之间的依赖关系是有限的,这种关系满足我们在随机过程中讲到的马尔可夫链的性质,因此可用马尔可夫链来处理。马尔可夫信源是一种非常重要的非平稳离散信源。那么马尔可夫信源需要满足一下两个条件: (1) 某一时刻信源符号的输出只与此刻信源所出的状态有关,而与以前的状态及以前的输出符号都无关。 (2) 信源某l 时刻所处的状态由当前的输出符号和前一时刻(l -1)信源的状态唯一决定。 马尔可夫信源的输出的符号是非平稳的随机序列,它们的各维概率分布随时间的推移可能会改变。第l 时间信源输出什么符号,不但与前一(l -1)时刻信源所处的状态和所输出的符号有关,而且一直延续到与信源初始所处的状态和所输出的符号有关。一般马尔可夫信源的信息熵是其平均符号熵的极限值,它的表达式就是: 121()lim ()N N H H X H X X X N ∞∞→∞== . 二.平均互信息 信道的任务是以信号方式传输信息和存储信息的。我们知道信源输出的是携带着信息的消息。消息必须要转换成能在信道中传输或存储的信号,然后通过信道传送到收信者。并且认为噪声或干扰主要从信道中引入。信道根据用户的多少,可以分为两端信道,多端信道。 根据信道输入端和输出端的关联,可以分为无反馈信道,反馈信道。根据信道的参数与时间的关系信道可以分为固定参数信道,时变参数信道。根据输入和输出信号的统计特性可以分为离散信道,连续信道,半离散或半连续信道和波形信道。 为了能够引入平均互信息量的定义,首先要看一下单符号离散信道的数学模型,在这种信道中,输出变量和输入变量的传递概率关系: (|)(|)(|)(1,2,,;1,2,,)j i j i P y x P y b x a P b a i r j s ====== 传递概率所表达的意思是,在信道当输入符号为a ,信道的输出端收到b 的概率。 我们知道,信道输入信源X 的熵是表明接收端收到符号之前信源的平均不确定性,可以称为先验熵。如果信道中无干扰噪声,信道输出符号与输出符号一一对应,那么,接受到传送过来的符号就消除了对发送符号的先验不确定性。但是我们实际的生活中一般信道中有干扰存在,接收到输出后对发送的是什么符号仍有不确定性。表示在输出端收到输出变量Y 的符号后,对于输入端的变量X 尚存在的平均不确定性。即信道疑义度: ,1(|)()log (|)X Y H X Y P xy P x y =∑ 这个信道的疑义度是由于干扰噪声引起的。前面我们看到了输出端接收到输出符号前关于变量X 的先验熵,以及接收到输出符号后关于输入变量X 的平均不确定性,通过信道传输消除了一定的不确定性,获得了一定的信息。那么定义单符号信道的平均互信息量 (;)()(|)I X Y H X H X Y =- 信息论与编码课程论文 电子邮件安全与密码学的应用 刘畅,200900840179 山东大学威海分校机电与信息工程学院,威海 264209 摘要:本文分析了传统电子邮件系统存在的安全性问题,探讨应用密码技术采弥补这些安全漏洞,并且绍了在安全电子邮件系统中使用的密码技术。 关键词:RSA;PGB;PEM 1、概述 随着计算机技术和网络技术的迅速发展,电子邮件的应用也越来越广泛.成为网络牛活中重要的组成部分,大有取代传统邮件之势。作为一种新的信息传递技术,电子邮件以其简单、快捷、方便的优势被人们所接受和喜爱。但是也存在一些问题妨碍了它的推广。其中关键之一就是电子邮件的信息安全。由于电子邮件技术在设计之初是为了科学家之间的通信方便,所以并来考虑信息安全因素。但是髓着时代的发展。尤其是电子商务的速成长。作为其沟通手段的电子邮件的安全性问题就不得不受到高度重视。人们很自然的想到把已经成熟的密码技术商用于电子邮件系统。密码技术就是对信息进行重新编码。从而达到隐藏信息内容使非法用户无法获取真实信息内容的一种手段。本文就浅述一下密码技术安全电子邮件中的应用。 2、密码学简介 2.1、加密的历史 作为保障数据安全的一种方式,数据加密起源于公元前2000年。埃及人是最先使用特别的象形文字作为信息编码的人。随着时间推移,巴比伦,希腊等都开始使用一些方法来保护他们的书面信息。对信息进行编码曾被Julias Caesar(恺撒大帝)使用,也曾用于历次战争中,包括美国独立战争,美国内战和两次世界大战。最广为人知的编码机器是German Enigma机,在第二次世界大战中德国人利用它创建了加密信息。此后,由于Alan Turing 和Ultra计划及其他人的努力,终于对德国人的密码进行了破解。当初,计算机的研究就是为了破解德国人的密码,当时人们并没有想到计算机给今天带来的信息革命。随着计算机的发展,运算能力的增强,过去的密码都变的十分简单了。于是人们又不断地研究出了新的数据加密方式,如私有密钥算法和公有密钥算法。可以说,是计算机推动了数据加密技术的发展。 2.2、密码学的发展 密码学的发展可以分为两个阶段。第一个阶段是计算机出现之前的四千年(早在四千年前,古埃及就开始使用密码传递消息),这是传统密码学阶段,基本上靠人工对消息加密、传输和防破译。第二阶段是计算机密码学阶段,包括: ①传统方法的计算机密码学阶段。解密是加密的简单逆过程,两者所用的密钥是可以简单地互相推导的,因此无论加密密钥还是解密密钥都必须严格保密。这种方案用于集中式系统是行之有效的。 ②包括两个方向:一个方向是公用密钥密码(RSA),另一个方向是传统方法的计算机密码体制——数据加密标准(DES)。 一个马尔可夫信源有3个符号{}1,23,u u u ,转移概率为:()11|1/2p u u =,()21|1/2p u u =, ()31|0p u u =,()12|1/3p u u =,()22|0p u u =,()32|2/3p u u =,()13|1/3p u u =,()23|2/3p u u =,()33|0p u u =,画出状态图并求出各符号稳态概率。 解:状态图如下 状态转移矩阵为: 1/21/2 01/302/31/32/30p ?? ?= ? ??? 设状态u 1,u 2,u 3稳定后的概率分别为W 1,W 2、W 3 由1231WP W W W W =??++=?得1231132231231 112331223 231W W W W W W W W W W W W ?++=???+=???=???++=? 计算可得1231025925625W W W ?=??? =?? ?=?? 由符号集{0,1}组成的二阶马尔可夫链,其转移概率为:(0|00)p =,(0|11)p =,(1|00)p =, (1|11)p =,(0|01)p =,(0|10)p =,(1|01)p =,(1|10)p =。画出状态图,并计算各状态 的稳态概率。 解:(0|00)(00|00)0.8p p == (0|01)(10|01)0.5p p == (0|11)(10|11)0.2p p == (0|10)(00|10)0.5p p == (1|00)(01|00)0.2p p == (1|01)(11|01)0.5p p == (1|11)(11|11)0.8p p == (1|10)(01|10)0.5p p == 信息论与编码 1. 通信系统模型 信源—信源编码—加密—信道编码—信道—信道解码—解密—信源解码—信宿 | | | (加密密钥) 干扰源、窃听者 (解密秘钥) 信源:向通信系统提供消息的人或机器 信宿:接受消息的人或机器 信道:传递消息的通道,也是传送物理信号的设施 干扰源:整个系统中各个干扰的集中反映,表示消息在信道中传输受干扰情况 信源编码: 编码器:把信源发出的消息变换成代码组,同时压缩信源的冗余度,提高通信的有效性 (代码组 = 基带信号;无失真用于离散信源,限失真用于连续信源) 译码器:把信道译码器输出的代码组变换成信宿所需要的消息形式 基本途径:一是使各个符号尽可能互相独立,即解除相关性;二是使各个符号出现的概率尽可能相等,即概率均匀化 信道编码: 编码器:在信源编码器输出的代码组上增加监督码元,使之具有纠错或检错的能力,提高通信的可靠性 译码器:将落在纠检错范围内的错传码元检出或纠正 基本途径:增大码率或频带,即增大所需的信道容量 2. 自信息:()log ()X i i I x P x =-,或()log ()I x P x =- 表示随机事件的不确定度,或随机事件发生后给予观察者的信息量。 条件自信息://(/)log (/)X Y i j X Y i j I x y P x y =- 联合自信息:(,)log ()XY i j XY i j I x y P x y =- 3. 互信息:;(/) () (;)log log ()()()i j i j X Y i j i i j P x y P x y I x y P x P x P y == 信源的先验概率与信宿收到符号消息后计算信源各消息的后验概率的比值,表示由事件y 发生所得到的关于事件x 的信息量。 4. 信息熵:()()log ()i i i H X p x p x =-∑ 表示信源的平均不确定度,或信源输出的每个信源符号提供的平均信息量,或解除信源不确定度所需的信息量。 条件熵:,(/)()log (/)i j i j i j H X Y P x y P x y =- ∑ 联合熵:,()()log ()i j i j i j H XY P x y P x y =-∑ 5. 平均互信息:,()(;)()log ()() i j i j i j i j p x y I X Y p x y p x p y =∑ 2011-2012 信息论与编码理论1 B 卷答案 一、 单项选择题(每题3分,总计15分) 1.当底为e 时,熵的单位为( C )。 A 奈特 B 哈特 C 奈特/符号 D 哈特/符号 2.下列关系式中( B )正确。 A )();(X I Y X I ≥ B );(),(Y X I Y X H ≥ C )|()|(X Y H Y X H ≥ D );();(Y X H Y X I ≤ 3.下列( D )陈述是正确的。 A Shannon 编码是最优码 B LZ 编码是异字头码 C Huffman 编码可以不需要知道信源的分布 D 典型序列的数目不一定比非典型的多 ) 4.下列数组中( A )不满足二个字母上的Kraft 不等式。 A (1,1,1) B (2,2,2,2) C (3,3,3) D (4,4,4) 5.下列( D )是只对输出对称的。 A ????? ? ??316 12121613 1 B ????? ??2.04.04.04.02.04.04.04.02.0 C ??????? ? ??32313132 3231 D ??? ? ??2.04.04.04.02.02.0 二、填空题(每空2分,总计20分) 1.若二元离散无记忆中25.0)0(=p ,75.0)1(=p ,则当给出100比特的信源序列,其中有5个1,则其自信息为3log 52002-比特,整个序列的熵为)3log 4 3 2(1002- 比特/符号. 2.若某离散信道信道转移概率矩阵为?? ????????5.025.025.025.05.025.025.025.05.0,则其信道容量为5.13log 2-比 特/符号;转移概率矩阵为???? ? ?????25.05.025.05.025.025.025.025.05.0,则其信道容量为5.13log 2-比特/符号。 3. 两个相同的BSC 做级联信道,其信道转移矩阵分别为??? ? ??--p p p p 11 , 则级联信道的信道转移矩阵为??????+---+-22222212222221p p p p p p p p ,无穷多个级联后的矩阵为??? ???5.05.05.05.0。 4.若一个信道的输入熵为6.2)(=X H 比特/符号,输出熵为3.2)(=Y H 比特/符号, 第一章 1.通信系统的基本模型: 2.信息论研究内容:信源熵,信道容量,信息率失真函数,信源编码,信道编码,密码体制的安全性测度等等 第二章 1.自信息量:一个随机事件发生某一结果所带的信息量。 2.平均互信息量:两个离散随机事件集合X 和Y ,若其任意两件的互信息量为 I (Xi;Yj ),则其联合概率加权的统计平均值,称为两集合的平均互信息量,用I (X;Y )表示 3.熵功率:与一个连续信源具有相同熵的高斯信源的平均功率定义为熵功率。如果熵功率等于信源平均功率,表示信源没有剩余;熵功率和信源的平均功率相差越大,说明信源的剩余越大。所以信源平均功率和熵功率之差称为连续信源的剩余度。信源熵的相对率(信源效率):实际熵与最大熵的比值 信源冗余度: 0H H ∞=ηη ζ-=1 意义:针对最大熵而言,无用信息在其中所占的比例。 3.极限熵: 平均符号熵的N 取极限值,即原始信源不断发符号,符号间的统计关系延伸到无穷。 4. 5.离散信源和连续信源的最大熵定理。 离散无记忆信源,等概率分布时熵最大。 连续信源,峰值功率受限时,均匀分布的熵最大。 平均功率受限时,高斯分布的熵最大。 均值受限时,指数分布的熵最大 6.限平均功率的连续信源的最大熵功率: 称为平均符号熵。 定义:即无记忆有记忆N X H H X H N X H X NH X H X H X H N N N N N N )() ()()()()()(=≤∴≤≤ 若一个连续信源输出信号的平均功率被限定为p ,则其输出信号幅度的概率密度分布是高斯分布时,信源有最大的熵,其值为 1log 22 ep π.对于N 维连续平稳信源来说,若其输出的N 维随机序列的协方差矩阵C 被限定,则N 维随机矢量为正态分布时信源 的熵最大,也就是N 维高斯信源的熵最大,其值为1log ||log 222N C e π+ 7.离散信源的无失真定长编码定理: 离散信源无失真编码的基本原理 原理图 说明: (1) 信源发出的消息:是多符号离散信源消息,长度为L,可以用L 次扩展信 源表示为: X L =(X 1X 2……X L ) 其中,每一位X i 都取自同一个原始信源符号集合(n 种符号): X={x 1,x 2,…x n } 则最多可以对应n L 条消息。 (2)信源编码后,编成的码序列长度为k,可以用k 次扩展信宿符号表示为: Y k =(Y 1Y 2……Y k ) 称为码字/码组 其中,每一位Y i 都取自同一个原始信宿符号集合: Y={y 1,y 2,…y m } 又叫信道基本符号集合(称为码元,且是m 进制的) 则最多可编成m k 个码序列,对应m k 条消息 定长编码:信源消息编成的码字长度k 是固定的。对应的编码定理称为定长信源编码定理。 变长编码:信源消息编成的码字长度k 是可变的。 8.离散信源的最佳变长编码定理 最佳变长编码定理:若信源有n 条消息,第i 条消息出现的概率为p i ,且 p 1>=p 2>=…>=p n ,且第i 条消息对应的码长为k i ,并有k 1<=k 2<=…<=k n 信息论与编码理论习题答案全解 第二章 信息量和熵 2.2 八元编码系统,码长为3,第一个符号用于同步,每秒1000个码字,求它的 信息速率。 解:同步信息均相同,不含信息,因此 每个码字的信息量为 2?8log =2?3=6 bit 因此,信息速率为 6?1000=6000 bit/s 2.3 掷一对无偏骰子,告诉你得到的总的点数为:(a) 7; (b) 12。问各得到多少 信息量。 解:(1) 可能的组合为 {1,6},{2,5},{3,4},{4,3},{5,2},{6,1} )(a p =366=6 1 得到的信息量 =) (1 log a p =6log =2.585 bit (2) 可能的唯一,为 {6,6} )(b p =361 得到的信息量=) (1 log b p =36log =5.17 bit 2.4 经过充分洗牌后的一副扑克(52张),问: (a) 任何一种特定的排列所给出的信息量是多少? (b) 若从中抽取13张牌,所给出的点数都不相同时得到多少信息量? 解:(a) )(a p =! 521 信息量=) (1 log a p =!52log =225.58 bit (b) ???????花色任选 种点数任意排列 13413!13 )(b p =13 52134!13A ?=1352 13 4C 信息量=1313 52 4log log -C =13.208 bit 2.9 随机掷3颗骰子,X 表示第一颗骰子的结果,Y 表示第一和第二颗骰子的 点数之和,Z 表示3颗骰子的点数之和,试求)|(Y Z H 、)|(Y X H 、 ),|(Y X Z H 、)|,(Y Z X H 、)|(X Z H 。 解:令第一第二第三颗骰子的结果分别为321,,x x x ,1x ,2x ,3x 相互独立, 则1x X =,21x x Y +=,321x x x Z ++= )|(Y Z H =)(3x H =log 6=2.585 bit )|(X Z H =)(32x x H +=)(Y H =2?( 361log 36+362log 18+363log 12+364log 9+365log 536)+36 6 log 6 =3.2744 bit )|(Y X H =)(X H -);(Y X I =)(X H -[)(Y H -)|(X Y H ] 而)|(X Y H =)(X H ,所以)|(Y X H = 2)(X H -)(Y H =1.8955 bit 或)|(Y X H =)(XY H -)(Y H =)(X H +)|(X Y H -)(Y H 而)|(X Y H =)(X H ,所以)|(Y X H =2)(X H -)(Y H =1.8955 bit ),|(Y X Z H =)|(Y Z H =)(X H =2.585 bit )|,(Y Z X H =)|(Y X H +)|(XY Z H =1.8955+2.585=4.4805 bit 2.10 设一个系统传送10个数字,0,1,…,9。奇数在传送过程中以0.5的概 率错成另外一个奇数,其余正确接收,求收到一个数字平均得到的信息量。 解: 信道 X Y 9,7,5,3,1=i 8,6,4,2,0=i √Χ );(Y X I =)(Y H -)|(X Y H 因为输入等概,由信道条件可知, 信息论与编码应用报告互信息技术在数字图像配准中的应用 专业班级:电子信息工程 姓名: 学号:201 时间:2014年6月9日 指导老师: 2014年6月9日 目录 摘要: (1) Abstract: (2) 前言 (3) 1 概述 (4) 1.1 互信息与信息论 (4) 1.2 数字图像配准 (5) 1.2.1 数字图像配准的介绍 (5) 1.2.2 数字图像配准的方式 (5) 1.2.3 数字图像配准的发展 (6) 2 配准方法 (7) 2.1 变换和插值模型 (7) 2.2 特征点的提取 (8) 2.3 多元互信息 (11) 2.4 优化算法 (12) 2.4.1 编码方式 (12) 2.4.2适应度表示 (12) 2.4.3轮盘赌法和最优保存策略 (12) 3 互信息技术在图像配置中的应用 (13) 3.1 Harris角点后的CT图和PET图 (14) 3.2 配准过程及结果 (14) 4 总结 (14) 参考文献: (16) 互信息技术在数字图像配准中的应用 信息与计算科学专业 指导教师 【摘要】:医学图像配准技术已经被应用于心脏病诊断和包括脑瘤在内的各种各样的神经混乱诊断研究中。图像配准是使两幅图像上的对应点达到空间上一致的一个过程。本文介绍了一种基于最大互信息原理的图像配准技术。并针对基于最大互信息图像配准的不足,研究了基于Harris角点算子的多模态医学图像配准。在计算互信息的时候,采用部分体积插值法计算联合灰度直方图。在优化互信息函数的时候采用了改进的遗传算法将配准参数收敛到最优值附近。实验结果表明本方法具有较高的配准精度和稳定性。 【关键词】:图像配准互信息 Harris角点算子部分体积插值遗传算法 前言 互信息是信息论的一个基本概念,是两个随机变量统计相关性的测度。Woods用测试图像的条件熵作为配准的测度,用于PET 到MR 图像的配准。Collignon 、Wells[1] 等人用互信息作为多模态医学图像的配准测度。以互信息作为两幅图像的相似性测度进行配准时,如果两幅基于共同解剖结构的图像达到最佳配准时,它们对应的图像特征互信息应为最大。最大互信息法几乎可以用在任何不同模式图像的 I (X ;Y=1)= P(x/Y 1)I(x;Y 1) x P(x/Y 1)log P(x/Y 1) P(x) = P(X 0/Y 1)log P(X 0/Y 1) P(X 0) P(X 1/Y 1)log P(X 1/Y 1) P(X 1) 部分答案,仅供参考。 信息速率是指平均每秒传输的信息量点和划出现的信息量分别为log3Jog3, 2’ 一秒钟点和划出现的次数平均为 1 15 2 1 ~4 0.20.4 - 3 3 一秒钟点和划分别出现的次数平均为巴5 4 4 那么根据两者出现的次数,可以计算一秒钟其信息量平均为10 log 3 5 竺 5 4 2 4 4 2 解: ⑻骰子A和B,掷出7点有以下6种可能: A=1,B=6; A=2,B=5; A=3,B=4; A=4,B=3; A=5,B=2; A=6,B=1 概率为6/36=1/6,所以信息量 -log(1/6)=1+log3 ~ bit (b)骰子A和B,掷出12点只有1种可能: A=6,B=6 概率为1/36,所以信息量 -log(1/36)=2+log9 ~ bit 解: 出现各点数的概率和信息量: 1 点:1/21 , log21 ?bit ; 2 点:2/21 , log21-1 ?bit ; 3 点:1/7 , log7 4 点:4/21 , log21-2 5 点:5/21 , log (21/5 )~; 6 点:2/ 7 , log(7/2)? 平均信息量: (1/21) X +(2/21) X +(1/7) X +(4/21) X +(5/21) X +(2/7) 解: X=1:考生被录取;X=0考生未被录取; Y=1:考生来自本市;Y=0考生来自外地; Z=1:考生学过英语;z=o:考生未学过英语 P(X=1)=1/4, P( X=q=3/4; P( Y=1/ X=1)=1/2 ;P( Y=1/ X=0)=1/10 ;P(Z=1/ Y=1 )=1, P( Z=1/ X=0, Y=0 )=, P( Z=1/ X=1, Y=0 )=, P(Z=1/Y=0)= (a)P(X=0,Y=1)=P(Y=1/X=0)P(X=0)=, P(X=1,Y=1)= P(Y=1/X=1)P(X=1)= P(Y=1)= P(X=0,Y=1)+ P(X=1,Y=1)= P(X=0/Y=1)=P(X=0,Y=1)/P(Y=1)=, P(X=1/Y=1)=P(X=1,Y=1)/P(Y=1)= 信息论与编码课程设计报告设计题目:统计信源熵与费诺编码 专业班级电信 11 学号 学生姓名 指导教师 教师评分 2014年 3月24日 目录 一、设计任务与要求 (2) 二、设计思路 (3) 三、设计流程图 (4) 四、程序运行及结果 (5) 五、心得体会 (7) 参考文献 (7) 附录:源程序 (8) 一、设计任务与要求 要求完成两个题目,1和2选做一题,3、4和5选做一题。 1、统计信源熵 要求:统计任意文本文件中各字符(不区分大小写)数量,计算字符概率,并计算信源熵。 2、判断唯一可译码 要求:利用尾随后缀法判断任意输入的码是否为唯一可译码。 3、香农编码 要求:任意输入消息概率,利用香农编码方法进行编码,并计算信源熵和编码效率。 4、费诺编码 要求:任意输入消息概率,利用费诺编码方法进行编码,并计算信源熵和编码效率。 5、哈夫曼编码 要求:任意输入消息概率,利用哈夫曼编码方法进行编码,并计算信源熵和编码效率。 二、设计思路 此设计是将统计信源熵与费诺编码结合在一起。程序中采用模块化思想将实现某个功能的程序独立成一个模块,然后在主程序中加以调用。 H(X)表示信源输出后,每个消息(或符号)所提供的平均信息量。统计信源熵模块是程序从键盘中读取用户输入的字母(不区分大小写)或空格,并分别统计出总数N和每个字母、空格出现的次数n以及概率P(x i),然后由公式 可计算出信源熵。 费诺编码: 1、将信源发出的N个消息符号按其概率的递减次序依次排列。 2、将依次排列的信源符号依概率分成两组,使两个组的概率和近于相同, 并对各组赋予一个二进制代码符号“0”和“1”(编m进制码就分成 m组)。 3、将每一个大组的信源符号进一步再分成两组,使划分后的两个组的概率 和近于相同,并又分别赋予两组一个二进制符号“0”和“1” 4、如此重复,直至每组值只剩下一个信源符号为止 5、信源符号所对应的码符号序列即为费诺码 信息论与编码理论习题(三) 一、填空题(每空2分,共32分)。 1.在现代通信系统中,信源编码主要用于解决信息传输中的 ,信道编码主要用于解决信息传输中的 ,加密编码主要用于解决信息传输中的 2.离散信源?? ????=??????8/18/14/12/1)(4321x x x x x p X ,则信源的熵为 。 3.采用m 进制编码的码字长度为K i ,码字个数为n ,则克劳夫特不等式为 ,它是判断 的充要条件。 4.如果所有码字都配置在二进制码树的叶节点,则该码字为 。 5.齐次马尔可夫信源的一步转移概率矩阵为P ,稳态分布为W ,则W 和P 满足的方程为 。 6.设某信道输入端的熵为H(X),输出端的熵为H(Y),该信道为无噪有损信道,则该信道的容量为 。 7.某离散无记忆信源X ,其符号个数为n ,则当信源符号呈 分布情况下,信源熵取最大值 。 8.在信息处理中,随着处理级数的增加,输入消息和输出消息之间的平均互信息量趋于 。 二.选择题(共10分,每小题2分) 1、有一离散无记忆信源X ,其概率空间为? ? ????=??????125.0125.025.05.04321x x x x P X ,则其无记忆二次扩展信源的熵H(X 2)=( ) A 、1.75比特/符号; B 、3.5比特/符号; C 、9比特/符号; D 、18比特/符号。 2、信道转移矩阵为112132425363(/)(/) 000000(/)(/)000000(/)(/)P y x P y x P y x P y x P y x P y x ?????? ???? ,其中(/)j i P y x 两两不相等,则该信道为 A 、一一对应的无噪信道 B 、具有并归性能的无噪信道 C 、对称信道 D 、具有扩展性能的无噪信道 3、设信道容量为C ,下列说法正确的是:( ) A 、互信息量一定不大于C 1. 在无失真的信源中,信源输出由 H (X ) 来度量;在有失真的信源中,信源输出由 R (D ) 来度量。 2. 要使通信系统做到传输信息有效、可靠和保密,必须首先 信源 编码, 然后_____加密____编码,再______信道_____编码,最后送入信道。 3. 带限AWGN 波形信道在平均功率受限条件下信道容量的基本公式,也就是有名的香农公式是log(1)C W SNR =+;当归一化信道容量C/W 趋近于零时,也即信道完全丧失了通信能力,此时E b /N 0为 -1.6 dB ,我们将它称作香农限,是一切编码方式所能达到的理论极限。 4. 保密系统的密钥量越小,密钥熵H (K )就越 小 ,其密文中含有的关于明文的信息量I (M ;C )就越 大 。 5. 设输入符号表为X ={0,1},输出符号表为Y ={0,1}。输入信号的概率分布为p =(1/2,1/2),失真函数为d (0,0) = d (1,1) = 0,d (0,1) =2,d (1,0) = 1,则D min = 0 ,R (D min )= 1bit/symbol ,相应的编码器转移概率矩阵[p(y/x )]=1001?? ???? ;D max = 0.5 ,R (D max )= 0 ,相应的编码器转移概率矩阵[p(y/x )]=1010?? ???? 。 二、判断题 1. 可以用克劳夫特不等式作为唯一可译码存在的判据。 (√ ) 2. 线性码一定包含全零码。 (√ ) 3. 算术编码是一种无失真的分组信源编码,其基本思想是将一定精度数值作为序列的 编码,是以另外一种形式实现的最佳统计匹配编码。 (×) 4. 某一信源,不管它是否输出符号,只要这些符号具有某些概率特性,就有信息量。 (×) 5. 离散平稳有记忆信源符号序列的平均符号熵随着序列长度L 的增大而增大。 (×) 6. 限平均功率最大熵定理指出对于相关矩阵一定的随机矢量X ,当它是正态分布时具 有最大熵。 (√ ) 7. 循环码的码集中的任何一个码字的循环移位仍是码字。 (√ ) 8. 信道容量是信道中能够传输的最小信息量。 (×) 9. 香农信源编码方法在进行编码时不需要预先计算每个码字的长度。 (×) 10. 在已知收码R 的条件下找出可能性最大的发码i C 作为译码估计值,这种译码方 法叫做最佳译码。 (√ ) 三、计算题 某系统(7,4)码 )()(01201230123456c c c m m m m c c c c c c c ==c 其三位校验 位与信息位的关系为: 《信息论与编码》期末考察报告 题目JPEG编码 学生姓名蒲亚洁 学号20102334916 院系电子工程 专业通信工程 二O一三年一月八日 JPEG编码 蒲亚洁 滨江学院电子工程系通信工程专业10级3班 摘要:本文介绍了JPEG。JPEG是一种针对相片影像而广泛使用的一种失真压缩标准方法。JPEG 标准指定了一系列实现静态图像压缩编码的方法,这些方法的选择决定于具体应用的要求及性能价格比的考虑。这些方法基本上可以分为两种:一种是采用以离散余弦变换(DCT)为基础的有损压缩算法,另一种是采用以预测技术为基础的无损压缩算法。使用有损压缩算法时在压缩比为25﹕1 的情况下压缩后还原的图像与原始图像相比较非图像专家难以找到它们的区别因此得到了广泛的应用。 JPEG采取多种编码方式,包含有行程编码(Run Length Coding)和哈夫曼(Huffman)编码,有很高的压缩比。在编码前,先对数据进行分块,离散余弦变换(DCT)及量化,保留能量大的低频信号,丢弃高频信号以达到压缩。解码时,进行熵解码,反量化,反离散余弦变换(IDCT)。 关键词:有损压缩算法;无损压缩算法;失真压缩标准方法;哈夫曼编码;有损压缩;JPEG Abstract:This paper introduced JPEG.JPEG is a widely used for photo image of a standard method for compression distortion. JPEG standard specifies a series of static image compression coding method, these methods of selection determines the specific application requirements and performance信息论与编码试卷与答案
信息论与编码理论习题答案
信息论与编码课后习题答案
信息论与编码理论课后习题答案高等教育出版社
《信息论与编码》教学大纲
信息论与编码课程论文[1]
信息论与编码课程论文
信息论与编码课后答案
信息论与编码总结
信息论与编码理论1(B卷答案)
(完整版)信息论与编码概念总结
信息论与编码理论习题答案全解
信息论与编码课程论文
信息论与编码理论第二章习题答案
河南理工大学信息论与编码论文
信息论与编码理论习题(三)
信息论与编码试题集概要
信息论与编码期末论文