
第5讲 对数与对数函数
◆高考导航·顺风启程◆
[知识梳理]
1.对数的概念
如果a (a >0,a ≠1)的b 次幂等于N ,即a b =N ,那么数b 叫作以a 为底N 的对数,记作 log a N =b ,其中 a 叫作对数的底数, N 叫作真数.
2.对数的性质与运算法则 (1)对数的运算法则
如果a >0且a ≠1, M >0,N >0,那么 ①log a (MN )= log a M +log a N ; ②log a M
N = log a M -log a N ;
③log a M n = n log a M (n ∈R );
④log am M n =
n
m log a
M (m ,n ∈R ,且m ≠0) . (2)对数的性质
①a log a N = N ;②log a a N = N (a >0且a ≠1). (3)对数的重要公式
①换底公式: log b N =log a N
log a b (a ,b 均大于零且不等于1);
②log a b =1
log b a ,推广log a b ·log b c ·log c d = log a d .
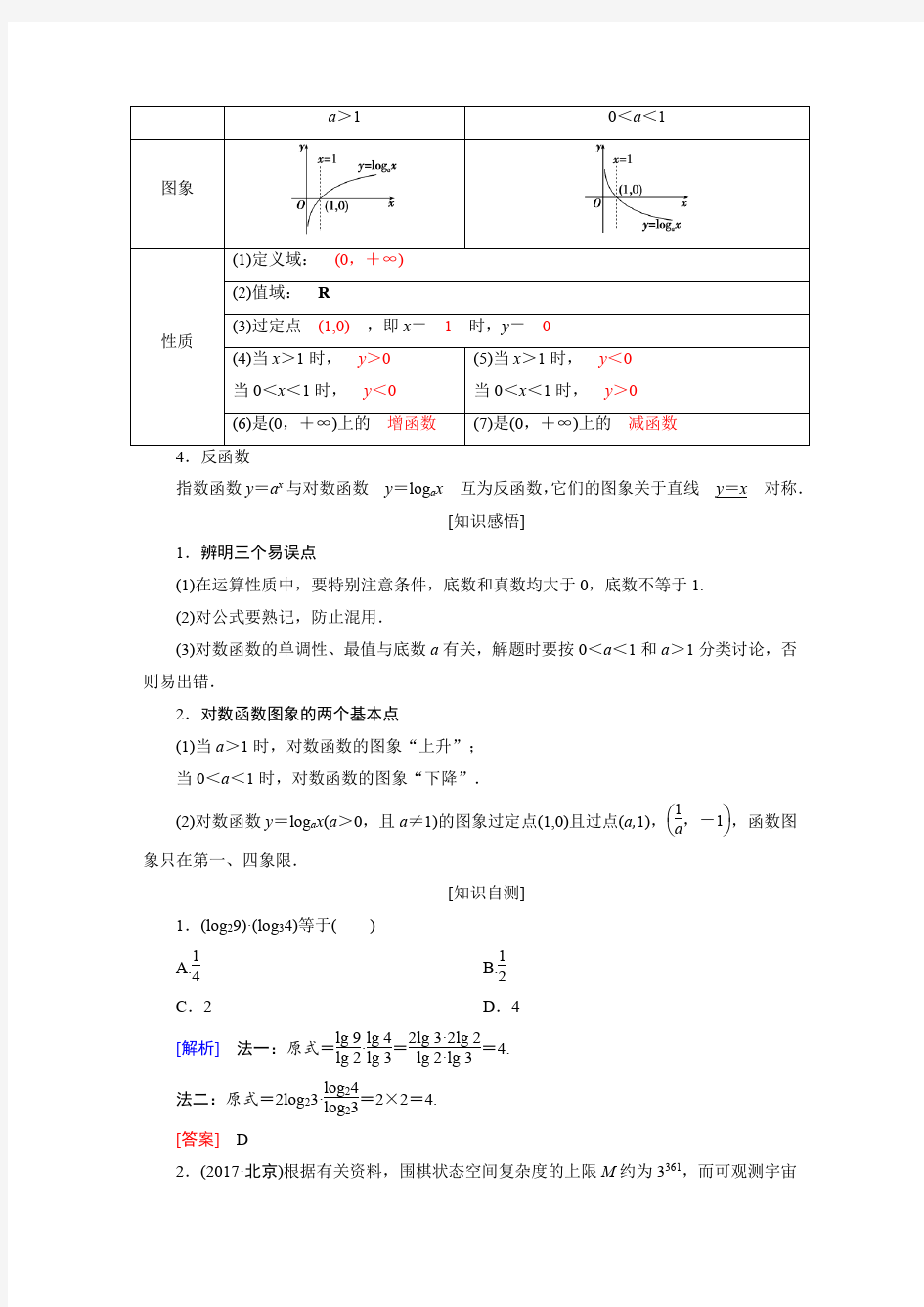
3.对数函数的图象与性质
指数函数y =a x 与对数函数 y =log a x 互为反函数,它们的图象关于直线 y =x 对称.
[知识感悟]
1.辨明三个易误点
(1)在运算性质中,要特别注意条件,底数和真数均大于0,底数不等于1. (2)对公式要熟记,防止混用.
(3)对数函数的单调性、最值与底数a 有关,解题时要按0<a <1和a >1分类讨论,否则易出错.
2.对数函数图象的两个基本点
(1)当a >1时,对数函数的图象“上升”; 当0<a <1时,对数函数的图象“下降”.
(2)对数函数y =log a x (a >0,且a ≠1)的图象过定点(1,0)且过点(a,1),????1
a ,-1,函数图象只在第一、四象限.
[知识自测]
1.(log 29)·(log 34)等于( ) A.1
4 B.1
2 C .2
D .4
[解析] 法一:原式=lg 9lg 2·lg 4lg 3=2lg 3·2lg 2
lg 2·lg 3=4.
法二:原式=2log 23·log 24
log 23=2×2=4.
[答案] D
2.(2017·北京)根据有关资料,围棋状态空间复杂度的上限M 约为3361,而可观测宇宙中普通物质的原子总数N 约为1080.则下列各数中与M
N
最接近的是( )
(参考数据:lg 3≈0.48) A .1033 B .1053 C .1073
D .1093
[解析] 设M N =x =33611080,两边取对数,lg x =lg 3361
1080=lg 3361-lg 1080=361×lg 3-80=
93.28,所以x =1093.28,即M
N
最接近1093,故选D.
[答案] D
3.(2018·成都模拟)函数y =log 0.5(4x -3)的定义域为 ________ . [解析] 由log 0.5(4x -3)≥0且4x -3>0,得3
4<x ≤1.
[答案] ????
34,1
题型一 对数的基本运 (基础保分题,自主练透)
(1)
(log 23)2-4log 23+4+log 21
3
=
( )
A .2
B .2-2log 23
C .-2
D .2log 23-2
(2)1
2lg 25+lg 2-lg 0.1-log 29×log 32的值是______. (3)已知2x =12,log 21
3
=y ,则x +y 的值为______.
(4)(2017·课标Ⅰ)设x 、y 、z 为正数,且2x =3y =5z ,则( ) A .2x <3y <5z B .5z <2x <3y C .3y <5z <2x
D .3y <2x <5z
[解析] (1)(log 23)2-4log 23+4=(log 23-2)2 =2-log 23,
又log 21
3=-log 23,两者相加即为B.
(2)原式=lg 5+lg 2+12-2=1+12-2=-1
2.
(3)∵2x =12,∴x =log 212, ∴x +y =log 212+log 21
3=log 24=2.
(4)令2x =3y =5z =k (k >1), 则x =log 2k ,y =log 3k ,z =log 5k ∴2x 3y =2lg k lg 2·lg 33lg k =lg 9lg 8>1,则2x >3y , 2x 5z =2lg k lg 2·lg 55lg k =lg 25lg 32<1, 则2x <5z ,故选D.
[答案] (1)B (2)-1
2
(3)2 (4)D
方法感悟 对数运算的一般思路
1.首先利用幂的运算把底数或真数进行变形,化成分数指数幂的形式,使幂的底数最简,然后正用对数运算性质化简合并.
2.将对数式化为同底数对数的和、差、倍数运算,然后逆用对数的运算性质,转化为同底对数真数的积、商、幂的运算.
3.a b =N ?b =log a N (a >0,且a ≠1)是解决有关指数、对数问题的有效方法,在运算中应注意互化.
【针对补偿】 1.(3+2)2log (3-
2)
5=(
)
A .1 B.1
2
C.14
D.15
[解析] 原式=(3+2)log(3-2)5 =(3+2)log(3+2)15=15.
[答案] D
2.(lg 3)2-lg 9+1(lg 27+lg 8-lg 1 000)lg 0.3·lg 1.2
= ________ .
[解析] 原式=(lg 3)2-2lg 3+1????32lg 3+3lg 2-32(lg 3-1)·(lg 3+2lg 2-1)
=(1-lg 3)·3
2
(lg 3+2lg 2-1)
(lg 3-1)·(lg 3+2lg 2-1) =-32.
[答案] -3
2
3.若log 147=a,14b =5,则用a ,b 表示log 3528= ________ . [解析] ∵14b =5,∴log 145=b ,又log 147=a , ∴log 3528=log 1428
log 1435=log 14
1427log 145+log 147=2-a a +b .
[答案]
2-a
a +b
4.设2a =5b =m ,且1a +1
b =2,则m = ________ .
[解析] ∵2a =5b =m >0,∴a =log 2m ,b =log 5m , ∴1a +1b =1log 2m +1log 5m =log m 2+log m 5=log m 10=2. ∴m 2=10,∴m =10. [答案]
10
题型二 对数函数的图象及应用(重点保分题,共同探讨)
(1)已知函数y =log a (x +c )(a ,c 为常
数,其中a >0,a ≠1)的图象如图,则下列结论成立的是( )
A .a >1,c >1
B .a >1,0<c <1
C .0<a <1,c >1
D .0<a <1,0<c <1
[解析] 由该函数的图象通过第一、二、四象限知该函数为减函数,∴0<a <1,∵图象与x 轴的交点在区间(0,1)之间,∴该函数的图象是由函数y =log a x 的图象向左平移不到1个单位后得到的,∴0<c <1.
[答案] D
(2)(2018·合肥月考)当0<x ≤1
2时,4x <log a x ,则a 的取值范围是( )
A.?
??
?0,
22 B.??
?
?
22,1
C .(1,2)
D .(2,2)
[解析] 法一:构造函数f (x )=4x 和g (x )=log a x ,当a >1时不满足条件,当0<a <1时,画出两个函数在????0,12上的图象,可知,f ????12<g ???
?1
2, 即2<log a 12,则a >22,所以a 的取值范围为????2
2,1.
法二:∵0<x ≤1
2,∴1<4x ≤2,∴log a x >4x >1,
∴0<a <1,排除选项C ,D ;取a =12,x =1
2
,
则有412=2,log 121
2=1,显然4x <log a x 不成立,排除选项A.
[答案] B
方法感悟
利用对数函数的图象可求解的两类热点问题
(1)对一些可通过平移、对称变换作出其图象的对数型函数,在求解其单调性(单调区间)、
值域(最值)、零点时,常利用数形结合思想求解.
(2)一些对数型方程、不等式问题常转化为相应的函数图象问题,利用数形结合法求解. 【针对补偿】
5.(2018·济南模拟)已知函数f (x )=log a (2x +b -1)(a >0,a ≠1)的图象如图所示,则a ,b 满足的关系是
( )
A .0<a -
1<b <1 B .0<b <a -1<1 C .0<b -
1<a <1 D .0<a -
1<b -
1<1
[解析] 由函数图象可知,f (x )在R 上递增,故a >1.函数图象与y 轴的交点坐标为(0,log a b ),由函数图象可知-1<log a b <0,解得1a <b <1.综上有0<1
a
<b <1.
[答案] A
6.(2018·成都一诊)设f (x )=|ln(x +1)|,已知f (a )=f (b )(a <b ),则( ) A .a +b >0 B .a +b >1 C .2a +b >0
D .2a +b >1
[解析] 作出函数f (x )=|ln(x +1)|的图象如图所示,
由f (a )=f (b ),得-ln(a +1)=ln(b +1),即ab +a +b =0.所以0=ab +a +b <(a +b )2
4+a
+b ,
即(a +b )(a +b +4)>0, 显然-1<a <0,b >0, ∴a +b +4>0.∴a +b >0.故选A. [答案] A
题型三 对数函数的性质及应用(高频考点题,多角突破) 考向一 求函数的定义域
1.函数f (x )=4-|x |+lg x 2-5x +6
x -3的定义域为( )
A .(2,3)
B .(2,4]
C .(2,3)∪(3,4]
D .(-1,3)∪(3,6]
[解析] 由?????
4-|x |≥0,x 2-5x +6x -3
>0,得?????
-4≤x ≤4,x >2且x ≠3,故函数定义域为(2,3)∪(3,4],故选C.
[答案] C 考向二 比较大小
2.(2017·天津)已知奇函数f (x )在R 上是增函数,g (x )=xf (x ).若a =g (-log 25.1),b =g (20.8),c =g (3),则a ,b ,c 的大小关系为( )
A .a <b <c
B .c <b <a
C .b <a <c
D .b <c <a
[解析] 因为f (x )是奇函数且在R 上是增函数,所以在x >0时,f (x )>0,从而g (x )=xf (x )是R 上的偶函数,且在[0,+∞)上是增函数,a =g (-log 2 5.1)=g (log 2 5.1),20.8<2,又4
<5.1<8,则2<log 2 5.1<3,所以即0<20.8<log 2 5.1<3,g (20.8)<g (log 2 5.1)<g (3),所以b <a <c ,故选C.
[答案] C
考向三 简单的对数不等式的解法
3.若f (x )=lg x ,g (x )=f (|x |),则g (lg x )>g (1)时,x 的取值范围是______.
[解析] 当g (lg x )>g (1)时,f (|lg x |)>f (1),由f (x )为增函数得|lg x |>1,从而lg x >1或lg x <-1,解得0<x <1
10
或x >10.
[答案] ???
?0,1
10∪(10,+∞) 考向四 由对数的单调性求参数或自变量的取值范围
4.(2018·中山模拟)已知函数f (x )=log a (8-ax )(a >0,a ≠1),若f (x )>1在区间[1,2]上恒成立,则实数a 的取值范围为______.
[解析] 当a >1时,f (x )=log a (8-ax )在[1,2]上是减函数,由f (x )>1恒成立,则f (x )min =log a (8-2a )>1,解之得1 3 . 当01恒成立,则f (x )min =log a (8-a )>1, 且8-2a >0,所以a >4,且0 ?1,8 3 方法感悟 应用对数函数性质的常见题型与求解策略: 7.(2018·山西省大同市豪洋中学四模试卷)设a =log 54,b =log 23,c =(log 0.23)2,则a ,b ,c 的大小关系为( ) A .a >b >c B .b >c >a C .a >c >b D .b >a >c [解析] ∵a =log 54∈(0,1),b =log 23>1,c =(log 0.23)2=(log 53)2<log 53<log 54,∴b >a >c .故选D. [答案] D 8.若f (x )=lg(x 2-2ax +1+a )在区间(-∞,1]上递减,则a 的取值范围为( ) A .[1,2) B .[1,2] C .[1,+∞) D .[2,+∞) [解析] 令函数g (x )=x 2-2ax +1+a =(x -a )2+1+a -a 2,对称轴为x =a ,要使函数在 (-∞,1]上递减,则有????? g (1)>0,a ≥1,即????? 2-a >0,a ≥1, 解得1≤a <2,即a ∈[1,2). [答案] A ◆牛刀小试·成功靠岸◆ 课堂达标(八) [A 基础巩固练] 1.(2018·武汉调研)若函数y =a |x |(a >0,且a ≠1)的值域为{y |y ≥1},则函数y =log a |x |的图象大致是( ) [解析] 若函数y =a |x |(a >0, 且a ≠1)的值域为{y |y ≥1},则a >1,故函数y =log a |x |的图象如图所示.故选B. [答案] B 2.已知a =2log 34.1,b =2log 32.7,c =???? 12log 30.1,则( ) A .a >b >c B .b >a >c C .a >c >b D .c >a >b [解析] c =????12log 30.1=2log 310,由于函数y =2x 在(-∞,+∞)上单调递增,且log 310>log 34.1>log 32.7故c >a >b . [答案] D 3.对于任意实数x ,符号[x ]表示不超过x 的最大整数,如:[1]=1,[1.5]=1,[-1.5]=-2,则[log 21]+[log 22]+[log 23]+[log 24]+…+[log 232]=( ) A .103 B .104 C .128 D .129 [解析] [log 21]=0,[log 22]=[log 23]=1,[log 24]=[log 25]=…=[log 27]=2,[log 28]=[log 29]=…=[log 215]=3,[log 216]=[log 217]=…=[log 231]=4,[log 232]=5,当原式=0+2×1+4×2+8×3+16×4+5=103. [答案] A 4.设f (x )=lg ? ????x -a 1-x 是奇函数,则使f (x )<0的x 的取值范围是( ) A .(-1,0) B .(0,1) C .(-∞,0) D .(-∞,0)∪(1,+∞) [解析] 由f (x )是奇函数可得a =-1, ∴f (x )=lg 1+x 1-x ,定义域为(-1,1). 由f (x )<0,可得0<1+x 1-x <1,∴-1<x <0.故选A. [答案] A 5.若实数,c 满足log a 2<log b 2<log c 2,则下列关系中不可能成立的是( ) A .a <b <c B .b <a <c C .c <b <a D .a <c <b [解析] 由log a 2<log b 2<log c 2的大小关系,可知a ,b ,c 有如下四种可能:①1<c <b <a ;②0<a <1<c <b ; ③0<b <a <1<c ;④0<c <b <a <1.对照选项可知A 中关系不可能成立. [答案] A 6.(2018·东北三校联考)设f (x )是定义在R 上的偶函数,且f (2+x )=f (2-x ),当x ∈[-2,0]时,f (x )=?? ? ?22x -1,若在区间(-2,6)内关于x 的方程f (x )-log a (x +2)=0(a >0且a ≠1)恰有4个不同的实数根,则实数a 的取值范围是( ) A.????14,1 B .(1,4) C .(1,8) D .(8,+∞) [解析] 依题意得f (x +2)=f [-(2-x )]=f (x -2),即f (x +4)=f (x ),则函数f (x )是以4为周期的函数,结合题意画出函数f (x )在x ∈(-2,6)上的图象与函数y =log a (x +2)的图象,结合图象分析可知, 要使f (x )与y =log a (x +2)的图象有4个不同的交点,则有? ???? a >1log a (6+2)<1,由此解得a >8,即a 的取值范围是(8,+∞),故选D. [答案] D 7.函数f (x )=log 2x ·log 2(2x )的最小值为 ________ . [解析] 依题意得f (x )=12log 2x ·(2+2log 2x )=(log 2x )2+log 2x =????log 2x +122-14≥-1 4,当且仅当log 2x =-12,即x =12 时等号成立,因此函数f (x )的最小值为-1 4. [答案] -1 4 8.(2018·哈尔滨模拟)已知函数f (x )=ln x 1-x ,若f (a )+f (b )=0,且0<a <b <1,则ab 的取值范围是 ________ . [解析] 由题意可知ln a 1-a +ln b 1-b =0, 即ln ????a 1-a ×b 1-b =0,从而a 1-a ×b 1-b =1, 化简得a +b =1, 故ab =a (1-a )=-a 2+a =-????a -122+1 4, 又0<a <b <1, 所以0<a <1 2, 故0<-????a -122+14<14. [答案] ??? ?0,14 9.已知函数f (x )=log a (2x -a )在区间???? 12,23上恒有f (x )>0,则实数a 的取值范围是 ________ . [解析] 当0<a <1时,函数f (x )在区间????12,23上是减函数,所以log a ????4 3-a >0,即0<4 3 -a <1, 解得13<a <43,故1 3 <a <1; 当a >1时,函数f (x )在区间????12,23上是增函数, 所以log a (1-a )>0,即1-a >1, 解得a <0,此时无解. 综上所述,实数a 的取值范围是????13,1. [答案] ????13,1 10.设f (x )=log a (1+x )+log a (3-x )(a >0,a ≠1),且f (1)=2. (1)求a 的值及f (x )的定义域; (2)求f (x )在区间????0,3 2上的最大值. [解] (1)∵f (1)=2,∴log a 4=2(a >0,a ≠1), ∴a =2. 由? ??? ? 1+x >0,3-x >0,得x ∈(-1,3), ∴函数f (x )的定义域为(-1,3). (2)f (x )=log 2(1+x )+log 2(3-x ) =log 2(1+x )(3-x )=log 2[-(x -1)2+4], ∴当x ∈(-1,1]时,f (x )是增函数; 当x ∈(1,3)时,f (x )是减函数, 函数f (x )在????0,3 2上的最大值是f (1)=log 24=2. [B 能力提升练] 1.已知函数f (x )=|lg x |.若0<a <b ,且f (a )=f (b ),则a +2b 的取值范围是( ) A .(22,+∞) B .[22,+∞) C .(3,+∞) D .[3,+∞) [解析] 函数f (x )=|lg x |的大致图象如图所示. 由题意结合图知0<a <1,b >1. ∵f (a )=|lg a |=-lg a =lg 1 a =f ( b )=|lg b |=lg b , ∴b =1a .∴a +2b =a +2a . 令g (a )=a +2 a ,则易知g (a )在(0,2)上为减函数, ∴当0<a <1时,g (a )=a +2 a >g (1)=1+2=3.故选C. [答案] C 2.(2018·黄冈模拟)若函数f (x )=log 1 2(-x 2+4x +5)在区间(3m -2,m +2)内单调递增, 则实数m 的取值范围为( ) A.????43,3 B.???? 43,2 C.????43,2 D.????43,+∞ [解析] 先保证对数有意义,即-x 2+4x +5>0, 解得-1<x <5.又可得二次函数y =-x 2+4x +5的对称轴为x =-4 2×(-1)=2,由复合 函数单调性可得函数f (x )=log 1 2 (-x 2+4x +5)的单调递增区间为(2,5), 要使函数f (x )=log 1 2(-x 2+4x +5)在区间(3m -2,m +2)内单调递增,只需 ???? ? 3m -2≥2,m +2≤5,3m -2<m +2, 解得4 3 ≤m <2.故选C. [答案] C 3.已知函数f (x )=|log 2x |,正实数m ,n 满足m <n ,且f (m )=f (n ),若f (x )在区间[m 2,n ]上的最大值为2,则n +m =______. [解析] 根据已知函数f (x )=|log 2x |的图象知,0<m <1<n ,所以0<m 2<m <1,根据函数图象易知,当x =m 2时取得最大值,所以f (m 2)=|log 2m 2|=2,又0<m <1,解得m =1 2.再 结合f (m )=f (n )求得n =2,所以n +m =5 2 . [答案] 5 2 4.已知函数f (x )=ln x 1-x ,若f (a )+f (b )=0,且0 [解析] 由题意可知ln a 1-a +ln b 1-b =0, 即ln ??? ?a 1-a ·b 1-b =0, 从而a 1-a ·b 1-b =1,化简得a +b =1, 故ab =a (1-a )=-a 2+a =-????a -122+14. 又0 2 , 故0<-????a -122+14<1 4,即ab ∈????0,14. [答案] ??? ?0,14 5.(2018·山东省枣庄十六中4月模拟试卷)已知函数f (x )=log a 1-mx x -1 (a >0,a ≠1)是奇 函数. (1)求实数m 的值; (2)判断函数f (x )在(1,+∞)上的单调性,并给出证明; (3)当x ∈(n ,a -2)时,函数f (x )的值域是(1,+∞),求实数a 与n 的值. [解] (1)∵函数f (x )=log a 1-mx x -1 (a >0,a ≠1)是奇函数. ∴f (-x )+f (x )=0解得m =-1. (2)由(1)及题设知:f (x )=log a x +1 x -1, 设t =x +1x -1=x -1+2x -1=1+2x -1, ∴当x 1>x 2>1时,t 1-t 2=2x 1-1-2x 2-1 = 2(x 2-x 1) (x 1-1)(x 2-1) ∴t 1<t 2.当a >1时,log a t 1<log a t 2,即f (x 1)<f (x 2). ∴当a >1时,f (x )在(1,+∞)上是减函数. 同理当0<a <1时,f (x )在(1,+∞)上是增函数. (3)由题设知:函数f (x )的定义域为(1,+∞)∪(-∞,-1),∴①当n <a -2≤-1时,有0<a <1.由(1)及(2)题设知:f (x )在为增函数,由其值域为(1,+∞)知????? log a 1+n n -1=1a -2=-1 (无解); ②当1≤n <a -2时,有a >3.由(1)及(2)题设知:f (x )在(n ,a -2)为减函数,由其值域为(1,+∞)知???? ? n =1log a a -1 a -3 =1得a =2+3,n =1. [C 尖子生专练] 已知函数f (x )=ln x +1 x -1 . (1)求函数f (x )的定义域,并判断函数f (x )的奇偶性; (2)对于x ∈[2,6],f (x )=ln x +1x -1>ln m (x -1)(7-x )恒成立,求实数m 的取值范围. [解] (1)由x +1 x -1>0,解得x <-1或x >1, ∴定义域为(-∞,-1)∪(1,+∞), 当x ∈(-∞,-1)∪(1,+∞)时, f(-x)=ln -x+1 -x-1 =ln x-1 x+1=-ln x+1 x-1=-f(x), ∴f(x)=ln x+1 x-1是奇函数.(2)由x∈[2,6]时, f(x)=ln x+1 x-1>ln m (x-1)(7-x) 恒成立. ∴x+1 x-1> m (x-1)(7-x) >0, ∵x∈[2,6], ∴0<m<(x+1)(7-x)在x∈[2,6]上成立. 令g(x)=(x+1)(7-x)=-(x-3)2+16,x∈[2,6], 由二次函数的性质可知x∈[2,3]时函数g(x)单调递增,x∈[3,6]时函数g(x)单调递减,x ∈[2,6]时, g(x)min=g(6)=7,∴0<m<7. 专题:对数函数知识点总结 1.对数函数的定义: 一般地,函数 x y a log =( )叫做对数函数 .定义域是 2. 对数函数的性质为 思考:函数log a y x =与函数x y a =)10(≠>a a 且的定义域、值域之间有什么关系? ___________________________________________________________________________ 对数函数的图象与指数函数的图象关于_______________对称。 一般的,函数y=a x 与y=log a x (a>0且a ≠1)互称相对应的反函数,它们的图象关于直线y=x 对称 y=f(x)存在反函数,一般将反函数记作y=f -1 (x) 如:f(x)=2x ,则f -1 (x)=log 2x,二者的定义域与值域对调,且图象关 于直线y=x 对称 函数与其反函数的定义域与值域对调,且它们的图象关于直线y=x 对称 专题应用练习 一、求下列函数的定义域 (1)0.2log (4);y x =-; (2)log 1a y x =- (0,1).a a >≠; (3)2(21)log (23)x y x x -=-++ (4)2log (43)y x =- (5) y=lg 1 1 -x (6) y=x 3log =log(5x-1)(7x-2)的定义域是________________ = )8lg(2x - 的定义域是_______________ 3.求函数2log (21)y x =+的定义域___________ 4.函数y=13 log (21)x -的定义域是 5.函数y =log 2(32-4x )的定义域是 ,值域是 . 6.函数5log (23)x y x -=-的定义域____________ 7.求函数2 log ()(0,1)a y x x a a =->≠的定义域和值域。 8.求下列函数的定义域、值域: (1)2log (3)y x =+; (2)2 2log (3)y x =-; (3)2log (47)a y x x =-+(0a >且1a ≠). 9.函数f (x )=x 1 ln (432322+--++-x x x x )定义域 10.设f(x)=lg x x -+22,则f )2 ()2(x f x +的定义域为 11.函数f(x)=)1(lo g 1 |2|2---x x 的定义域为 12.函数f(x)= 2 29)2(1x x x g --的定义域为 ; 13.函数f (x )= x 1 ln (432322+--++-x x x x )的定义域为 14 2 2 2 log log log y x =的定义域是 1. 设f (x )=lg(ax 2 -2x +a ), (1) 如果f (x )的定义域是(-∞, +∞),求a 的取值围; (2) 如果f (x )的值域是(-∞, +∞),求a 的取值围. 15.已知函数)32(log )(22 1+-=ax x x f (1)若函数的定义域为R ,数a 的取值围 (2)若函数的值域为R ,数a 的取值围 对数函数知识点及典型例题讲解 1.对数: (1) 定义:如果,那么称为,记作,其中称为对数的底,N称为真数. ①以10为底的对数称为常用对数,记作___________. ②以无理数为底的对数称为自然对数,记作_________. (2) 基本性质: ①真数N为 (负数和零无对数);②;③; ④对数恒等式:. (3) 运算性质: ① log a(MN)=___________________________; ② log a=____________________________; ③ log a M n= (n∈R). ④换底公式:log a N= (a>0,a≠1,m>0,m≠1,N>0) ⑤ . 2.对数函数: ①定义:函数称为对数函数,1) 函数的定义域为( ;2) 函数的值域为; 3) 当______时,函数为减函数,当______时为增函数; 4) 函数与函数互为反函数. ② 1) 图象经过点( ),图象在;2) 对数函数以为渐近线(当时,图象向上无限接近y轴;当时,图象向下无限接近y轴); 4) 函数y=log a x与的图象关于x轴对称. ③函数值的变化特征: ①②③①②③ 例1 计算:(1) (2)2(lg)2+lg·lg5+; (3)lg-lg+lg. 解:(1)方法一利用对数定义求值设=x,则(2+)x=2-==(2+)-1,∴x=-1.方法二利用对数的运算性质求解 = =(2+)-1=-1. (2)原式=lg(2lg+lg5)+=lg(lg2+lg5)+|lg-1| =lg+(1-lg)=1. (3)原式=(lg32-lg49)-lg8+lg245 = (5lg2-2lg7)-×+ (2lg7+lg5) =lg2-lg7-2lg2+lg7+lg5=lg2+lg5 =lg(2×5)= lg10=. 变式训练1:化简求值. (1)log2+log212-log242-1; (2)(lg2)2+lg2·lg50+lg25; (3)(log32+log92)·(log43+log83). 解:(1)原式=log2+log212-log2-log22=log2 (2)原式=lg2(lg2+lg50)+lg25=2lg2+lg25=lg100=2. (3)原式=( 例2 比较下列各组数的大小. (1)log3与log5;(2)log1.10.7与(3)已知logb<loga<logc,比较2b,2a,2c的大小关系.解:(1)∵log3<log31=0,而log5>log51=0,∴log3<log5. (2)方法一∵0<<1,<,∴0>, ∴, 即由换底公式可得log1.10.7<方法二作出y=与y=的图象. 如图所示两图象与x=相交可知log1.10.7<为减函数,且, ∴b>a>c,而y=2x是增函数,∴2b>2a>2c. 变式训练2:已知0<a<1,b>1,ab>1,则log a的大小关系是() B. C. D. 解: C 例3已知函数f(x)=log a x(a>0,a≠1),如果对于任意x∈[3,+∞)都有|f(x)|≥1成立,试求a的取值范围. 解:当a>1时,对于任意x∈[3,+∞),都有f(x)>0. 所以,|f(x)|=f(x),而f(x)=log a x在[3,+∞)上为增函数, ∴对于任意x∈[3,+∞),有f(x)≥log a3. 因此,要使|f(x)|≥1对于任意x∈[3,+∞)都成立. 只要log a3≥1=log a a即可,∴1<a≤3. 当0<a<1时,对于x∈[3,+∞),有f(x)<0, ∴|f(x)|=-f(x). ∵f(x)=log a x在[3,+∞)上为减函数, ∴-f(x)在[3,+∞)上为增函数. ∴对于任意x∈[3,+∞)都有 对数函数 (一)对数 1.对数的概念:一般地,如果N a x =)1,0(≠>a a ,那么数x 叫做以.a 为底..N 的对数,记作:N x a log =(a — 底数,N — 真数,N a log — 对数式) 说明:○1 注意底数的限制0>a ,且1≠a ; ○2 x N N a a x =?=log ; ○3 注意对数的书写格式. 两个重要对数: ○ 1 常用对数:以10为底的对数N lg ; ○ 2 自然对数:以无理数 71828.2=e 为底的对数的对数N ln . (二)对数的运算性质 如果0>a ,且1≠a ,0>M ,0>N ,那么: ○ 1 M a (log ·=)N M a log +N a log ; ○ 2 =N M a log M a log -N a log ; ○ 3 n a M log n =M a log )(R n ∈. 注意:换底公式 a b b c c a log log log = (0>a ,且1≠a ;0>c ,且1≠c ;0>b ). 利用换底公式推导下面的结论 (1)b m n b a n a m log log = ; (2)a b b a log 1log =. (二)对数函数 1、对数函数的概念:函数0(log >=a x y a ,且)1≠a 叫做对数函 数,其中x 是自变量,函数的定义域是(0,+∞). 注意:○1 对数函数的定义与指数函数类似,都是形式定义,注意辨别。如:x y 2log 2=,5 log 5x y = 都不是对数函数,而只能称 其为对数型函数. ○ 2 对数函数对底数的限制:0(>a ,且)1≠a . 对数函数·例题解析 例1.求下列函数的定义域: (1)2log x y a =; (2))4(log x y a -=; (3))9(log 2 x y a -=. 专题:对数函数知识点总结 1.对数函数的定义: 一般地,函数 x y a log =( )叫做对数函数 .定义域是 2. 对数函数的性质为 思考:函数log a y x =与函数x y a =)10(≠>a a 且的定义域、值域之间有什么关系? ___________________________________________________________________________ 对数函数的图象与指数函数的图象关于_______________对称。 | 一般的,函数y=a x 与y=log a x (a>0且a ≠1)互称相对应的反函数,它们的图象关于直线y=x 对称 y=f(x)存在反函数,一般将反函数记作y=f -1 (x) 如:f(x)=2x ,则f -1 (x)=log 2x,二者的定义域与值域对调,且图象关 于直线y=x 对称 函数与其反函数的定义域与值域对调,且它们的图象关于直线y=x 对称 专题应用练习 一、求下列函数的定义域 (1)0.2log (4);y x =-; (2 )log a y =(0,1).a a >≠; (3)2 (21)log (23)x y x x -=-++ (4 )y = ? (5) y=lg 1 1 -x (6) y=x 3log =log(5x-1)(7x-2)的定义域是________________ = )8lg(2x - 的定义域是_______________ 3.求函数2log (21)y x =+的定义域___________ 4.函数 的定义域是 5.函数y =log 2(32-4x )的定义域是 ,值域是 . 6.函数5log (23)x y x -=-的定义域____________ { 7.求函数2 log ()(0,1)a y x x a a =->≠的定义域和值域。 8.求下列函数的定义域、值域: (1)2log (3)y x =+; (2)2 2log (3)y x =-; (3)2log (47)a y x x =-+(0a >且1a ≠). 9.函数f (x )=x 1 ln (432322+--++-x x x x )定义域 10.设f(x)=lg x x -+22,则f )2 ()2(x f x +的定义域为 对数运算与对数函数复习 例1.求下列函数的定义域: (1)2log x y a =; (2))4(log x y a -=; (3))9(log 2x y a -=. 例2.比较下列各组数中两个值的大小: (1)2log 3.4,2log 8.5; (2)0.3log 1.8,0.3log 2.7; (3)log 5.1a ,log 5.9a . (4)0.91.1, 1.1log 0.9,0.7log 0.8; 例3.求下列函数的值域: (1)2log (3)y x =+;(2)22log (3)y x =-;(3)2log (47) a y x x =-+(0a >且1a ≠). 例4.(1)已知:36log ,518,9log 3018求==b a 值. 例5.判断函数2()log )f x x =的奇偶性。 对数运算与对数函数复习练习 一、选择题 1.3 log 9log 28的值是( ) A .32 B .1 C .2 3 D .2 2.函数)2(x f y =的定义域为[1,2],则函数)(log 2x f y =的定义域为( ) A .[0,1] B .[1,2] C .[2,4] D .[4,16] 3.函数2x log y 5+=(x ≥1)的值域是( ) A .R B .[2,+∞] C .[3,+∞] D .(-∞,2) 4.如果0 对数极对数函数题型总结 例题讲解 一、利用对数恒等式化简求值 1.求值: 2.求的值(a,b,c∈R+,且不等于1,N>0) 二、积、商、幂的对数 3.求值 (1)(2)lg2·lg50+(lg5)2(3)lg25+lg2·lg50+(lg2)2 4.已知3a=5b=c,,求c的值. 5.设a、b、c为正数,且满足a2+b2=c2.求证:. 6.已知:a2+b2=7ab,a>0,b>0. 求证:. 三、换底公式的运用 7.(1)已知log x y=a,用a表示; (2)已知log a x=m,log b x=n,log c x=p,求log abc x. 8.求值:(1);(2);(3). 9. 10. 11.四、对数运算法则的应用 12.9.求值 13.(1) log89·log2732 14.(2) 15.(3) 16.(4)(log2125+log425+log85)(log1258+log254+log52) 17. 18.10.求值: 19. 11.已知:log23=a,log37=b,求:log4256=? 五、函数的定义域、值域 求含有对数函数的复合函数的定义域、值域,其方法与一般函数的定义域、值域的求法类似,但要注意对数函数本身的性质(如定义域、值域及单调性)在解题中的重要作用. 12. 求下列函数的定义域. (1) y=(2) y=ln(a x-k·2x)(a>0且a11,k?R). 13.函数y=f(2x)的定义域为[-1,1],求y=f(log2x)的定义域. 六、函数图象问题 七、14.作出下列函数的图象: 八、(1) y=lgx,y=lg(-x),y=-lgx;(2) y=lg|x|;(3) y=-1+lgx. 九、 七、对数函数的单调性及其应用 利用函数的单调性可以:①比较大小;②解不等式;③判断单调性;④求单调区间;⑤求值域和最值. 15.已知则() A.B.C.D. 高一数学必修一对数及对数函数知识点总 结 数学是学习和研究现代科学技术必不可少的基本工具。以下是查字典数学网为大家整理的高一数学必修一对数及 对数函数知识点,希望可以解决您所遇到的相关问题,加油,查字典数学网一直陪伴您。 对数定义 如果a的x次方等于N(a>0,且a不等于1),那么数x叫做以a为底N的对数,记作x=logaN。其中,a叫做对数的底数,N叫做真数。 注: 1.以10为底的对数叫做常用对数,并记为lg。 2.称以无理数e(e=2.71828...)为底的对数称为自然对数,并记为ln。 3.零没有对数。 4.在实数范围内,负数无对数。在复数范围内,负数是有对数的。 对数公式 0,且a≠1)叫做对数函数,也就是说以幂(真数)为自变量,指数为因变量,底数为常量的函数,叫对数函数。/p p其中x 是自变量,函数的定义域是(0,+∞)。它实际上就是指数函数的反函数,可表示为x=ay。因此指数函数里对于a的规定, 同样适用于对数函数。/p p对数函数性质/p p align=" center="" img="" /> 定义域求解:对数函数y=logax的定义域是{x丨x>0},但如果遇到对数型复合函数的定义域的求解,除了要注意大于0以外,还应注意底数大于0且不等于1,如求函数y=logx(2x-1)的定义域,需同时满足x>0且x≠1和2x-1>0,得到x>1/2且x≠1,即其定义域为{x丨x>1/2且x≠1} 值域:实数集R,显然对数函数无界。 定点:函数图像恒过定点(1,0)。 单调性:a>1时,在定义域上为单调增函数; 奇偶性:非奇非偶函数 周期性:不是周期函数 对称性:无 最值:无 零点:x=1 注意:负数和0没有对数。 两句经典话:底真同对数正,底真异对数负。 要练说,得练听。听是说的前提,听得准确,才有条件正确模仿,才能不断地掌握高一级水平的语言。我在教学中,注意听说结合,训练幼儿听的能力,课堂上,我特别重视教师的语言,我对幼儿说话,注意声音清楚,高低起伏,抑扬有致,富有吸引力,这样能引起幼儿的注意。当我发现有的幼 对数及对数函数 1、对数的基本概念 (1)一般地,如果a (1,0≠>a a )的b 次幂等于N ,就是N a b =,那么数b 叫做以a 为底N 的对 数, 记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式 (2)常用对数:N 10log ,记作N lg ; 自然对数N e log (e =2.71828…),记作N ln . (3)指数式与对数式的关系:log x a a N x N =?=(0>a ,且1≠a ,0N >) (4)对数恒等式: 2、对数的性质 (1)负数和零没有对数,即0>N ; (2)1的对数是零,即01log =a ; (3)底的对数等于1,即1log =a a 3、对数的运算性质 (1)如果a >0,a ≠1,M >0,N >0,那么 ①N M MN a a a log log )(log +=; ②N M N M a a a log log log -=; ③M n M a n a log log = (2)换底公式: 推论:① b N N b log 1log = ; ② ; ③ 1log log =?a b b a 4、对数函数的定义: 函数 叫做对数函数,其中x 是自变量 (1)研究对数函数的图象与性质: 由于对数函数 与指数函数 互为反函数,所以 的图像和 的图像关于直线 对称。 (2)复习)10(≠>=a a a y x 且的图象和性质 ()010log >≠>=N a a N a N a ,且b N N a a b log log log = b m n b a n a m log log =a y log x =(a 0a 1)>≠且a y log x =x y a =a y log x =x y a =y x = 对数与对数函数-知识点与题型归纳 ●高考明方向 1.理解对数的概念及其运算性质,知道用换底公式能将一般 对数转化成自然对数或常用对数;了解对数在简化运算中的作用. 2.理解对数函数的概念,理解对数函数的单调性,掌握对数 函数图象通过的特殊点. 3.知道对数函数是一类重要的函数模型. 4.了解指数函数y=a x与对数函数y=log a x互为反函数 (a>0,且a≠1). ★备考知考情 通过对近几年高考试题的统计分析可以看出,本节内容在高考中属于必考内容,且占有重要的分量,主要以选择题的形式命题,也有填空题和解答题.主要考查对数运算、换底公式等.及对数函数的图象和性质.对数函数与幂、指数函数结合考查,利用单调性比较大小、解不等式是高考的热点. 一、知识梳理《名师一号》P27 注意: 知识点一对数及对数的运算性质 1.对数的概念 2 3 一般地,对于指数式a b =N ,我们把“以a 为底N 的对数b ”记作log a N ,即b =log a N (a >0,且a ≠1).其中,数a 叫做对数的底数,N 叫做真数,读作“b 等于以a 为底N 的对数”. 注意:(补充)关注定义---指对互化的依据 2.对数的性质与运算法则 (1)对数的运算法则 如果a >0且a ≠1,M >0,N >0,那么 ①log a (MN )=log a M +log a N ; ②log a M N =log a M -log a N ; ③log a M n =n log a M (n ∈R); ④log a m M n =n m log a M . (2)对数的性质 ①a log aN =N ;②log a a N =N (a >0,且a ≠1). (3)对数的重要公式 ①换底公式:log b N =log a N log a b (a ,b 均大于零且不等于1); ②log a b =1 log b a ,推广log a b ·log b c ·log c d =log a d . 注意:(补充)特殊结论:log 10,log 1a a a == 指数函数和对数函数 知识点总结 (一)指数与指数幂的运算 1.根式的概念:一般地,如果a x n =,那么x 叫做a 的n 次方根,其中n >1,且n ∈N * . 负数没有偶次方根;0的任何次方根都是0,记作00=n 。 当n 是奇数时,a a n n =,当n 是偶数时,?? ?<≥-==) 0() 0(||a a a a a a n n 2.正数的分数指数幂,规定: 0的正分数指数幂等于0,0的负分数指数幂没有意义 3.实数指数幂的运算性质),,0(R s r a ∈> (1)r a ·s r r a a += ;(2)rs s r a a =)( ;(3) s r r a a ab =)( (二)指数函数及其性质 1、指数函数的概念:一般地,函数)1,0(≠>=a a a y x 且叫做指数函数,其中x 是自 变量,函数的定义域为R . 1.对数的概念:一般地,如果N a x =)1,0(≠>a a ,那么数x 做以.a 为底..N 的对数,记作:N x a log =(a — 底数,N — 真数,N a log — 对数式) 说明: ○1 注意底数的限制0>a ,且a x N a =?log ;③注意对数的书 写格式. N a log 两个重要对数: ○ 1 常用对数:以10为底的对数N lg ; ○ 2 自然对数:以无理数Λ71828.2=e 为底的对数的对数N ln . 2、对数的运算性质:如果0>a ,且1≠a ,0>M ,0>N ,那么: ○1 M a (log ·=)N M a log +N a log ; ○ 2 =N M a log M a log -N a log ;③n a M log n =M a log )(R n ∈. 注意:换底公式a b b c c a log log log =(0>a ,且1≠a ;0>c ,且 1≠c ;0>b ) . 利用换底公式推导下面的结论 (1)b m n b a n a m log log = ; (2)a b b a log 1log =. 3、对数函数的概念:函数0(log >=a x y a ,且)1≠a 叫做对数函数,其中x 是自变量, 高考指数函数和对数函数 一.基础知识 (一)指数与指数幂的运算 1.根式的概念:一般地,如果a x n =,那么x 叫做a 的n 次方 根,其中n >1,且n ∈N * . 负数没有偶次方根;0的任何次方根都是0,记作00=n 。 当n 是奇数时,a a n n =,当n 是偶数时,? ??<≥-==)0()0(||a a a a a a n n 2.分数指数幂 正数的分数指数幂的意义,规定: )1,,,0(*>∈>=n N n m a a a n m n m )1,,,0(1 1 *>∈>= = -n N n m a a a a n m n m n m 0的正分数指数幂等于0,0的负分数指数幂没有意义 3.实数指数幂的运算性质 (1)r a ·s r r a a += ),,0(R s r a ∈>; (2)rs s r a a =)( ),,0(R s r a ∈>; (3) s r r a a ab =)( ),,0(R s r a ∈>. (二)指数函数及其性质 1、指数函数的概念:一般地,函数)1,0(≠>=a a a y x 且叫做指数函数,其中x 是自变量,函数的定义域为R . 注意:指数函数的底数的取值范围,底数不能是负数、零和1. 注意:利用函数的单调性,结合图象还可以看出: (1)在[a ,b]上,)1a 0a (a )x (f x ≠>=且值域是)] b (f ),a (f [ 或)]a (f ),b (f [; (2)若0x ≠,则1)x (f ≠;)x (f 取遍所有正数当且仅当R x ∈; (3)对于指数函数)1a 0a (a )x (f x ≠>=且,总有a )1(f =; 二、对数函数 (一)对数 1.对数的概念:一般地,如果N a x =)1,0(≠>a a ,那么数x 叫做以.a 为底..N 的对数,记作:N x a log =(a — 底数,N — 真数,N a log — 对数式) 说明:○1 注意底数的限制0>a ,且1≠a ; ○ 2 x N N a a x =?=log ; ○ 3 注意对数的书写格式. 两个重要对数: ○ 1 常用对数:以10为底的对数N lg ; ○ 2 自然对数:以无理数 71828.2=e 为底的对数的对数N ln . 指数式与对数式的互化 幂值 真数 对数 (二)对数的运算性质 如果0>a ,且1≠a ,0>M ,0>N ,那么:○1 M a (log ·=)N M a log +N a log ;○ 2 =N M a log M a log -N a log ; ○ 3 n a M log n =M a log )(R n ∈. 注意:换底公式 a b b c c a log log log = (0>a ,且1≠a ;0>c ,且1≠c ;0>b ). 利用换底公式推导下面的结论 (1)b m n b a n a m log log =;(2)a b b a log 1log =. (二)对数函数 1、对数函数的概念:函数0(log >=a x y a ,且)1≠a 叫做对 指对函数 1比较大小,是指对函数这里很爱考的一类题型,主要依靠指对函数本身的图像性质来做题,此外,对于公式的理解也很重要。常用方法有建立中间量;估算;作差法;作商法等。 1、若π2log =a ,6log 7=b ,8.0log 2=c ,则( ) A.c b a >> B.c a b >> C.b a c >> D.a c b >> 2、三个数6log ,7.0,6 7.067 .0的大小顺序是( ) A.60.70.70.7log 66<< B.60.70.70.76log 6<< C.0.760.7log 660.7<< D.60.7 0.7log 60.76<< 3、设 1.5 0.90.48 12314,8 ,2y y y -??=== ? ?? ,则( ) A.312y y y >> B.213y y y >> C.132y y y >> D.123y y y >> 4、当10<> B.a a a a a a >> C.a a a a a a >> D.a a a a a a >> 5、设 1)3 1()31(31<<>x x b a ,则下列不等式成立的是( ) A .10<<a 且1≠a ),则()f x 一定过点( ) A.无法确定 B.)3,0( C.)3,1( D.)4,2( 2、当10≠>a a 且时,函数()32-=-x a x f 必过定点( ) 3、函数0.(12>+=-a a y x 且)1≠a 的图像必经过点( ) 4、函数1)5.2(log )(-+=x x f a 恒过定点( ) 5、指数函数()x a x f =的图象经过点?? ? ??161,2,则a =( ) 6、若函数log ()a y x b =+ (0>a 且1≠a )的图象过)0,1(-和)1,0(两点,则b a ,分别为( ) A.2,2==b a B.2,2==b a C.1,2==b a D.2,2==b a 3针对指对函数图像性质的题专题:对数函数知识点总结及类型题归纳
对数函数知识点及典型例题讲解
对数函数知识点总结(供参考)
专题:对数函数知识点总结及类型题归纳
对数函数典型例题
对数极对数函数题型总结
高一数学必修一对数及对数函数知识点总结
对数及对数函数知识点总结及题型分析
对数与对数函数-知识点与题型归纳
指数函数和对数函数 知识点总结
高考学生指数与对数函数知识点小结及典型例题
高三总复习-指对数函数题型总结归纳
对数函数知识点总结