
实验二数值方法计算积分
学号:姓名:指导教师:实验目的
1、了解并掌握matlab软件的基本编程、操作方法;
2、初步了解matlab中的部分函数,熟悉循环语句的使用;
3、通过上机进一步领悟用复合梯形、复合辛普森公式,以及用龙贝格求积
方法计算积分的原理。
、用不同数值方法计算积分x In xdx=- 4 .
09
(1) 取不同的步长h.分别用复合梯形及辛普森求积计算积分,给出误差中关
于h的函数,并与积分精确值比较两个公式的精度,是否存在一个最小的h,使得精度不能再被改善?
(2) 用龙贝格求积计算完成问题(1)。
、实现实验
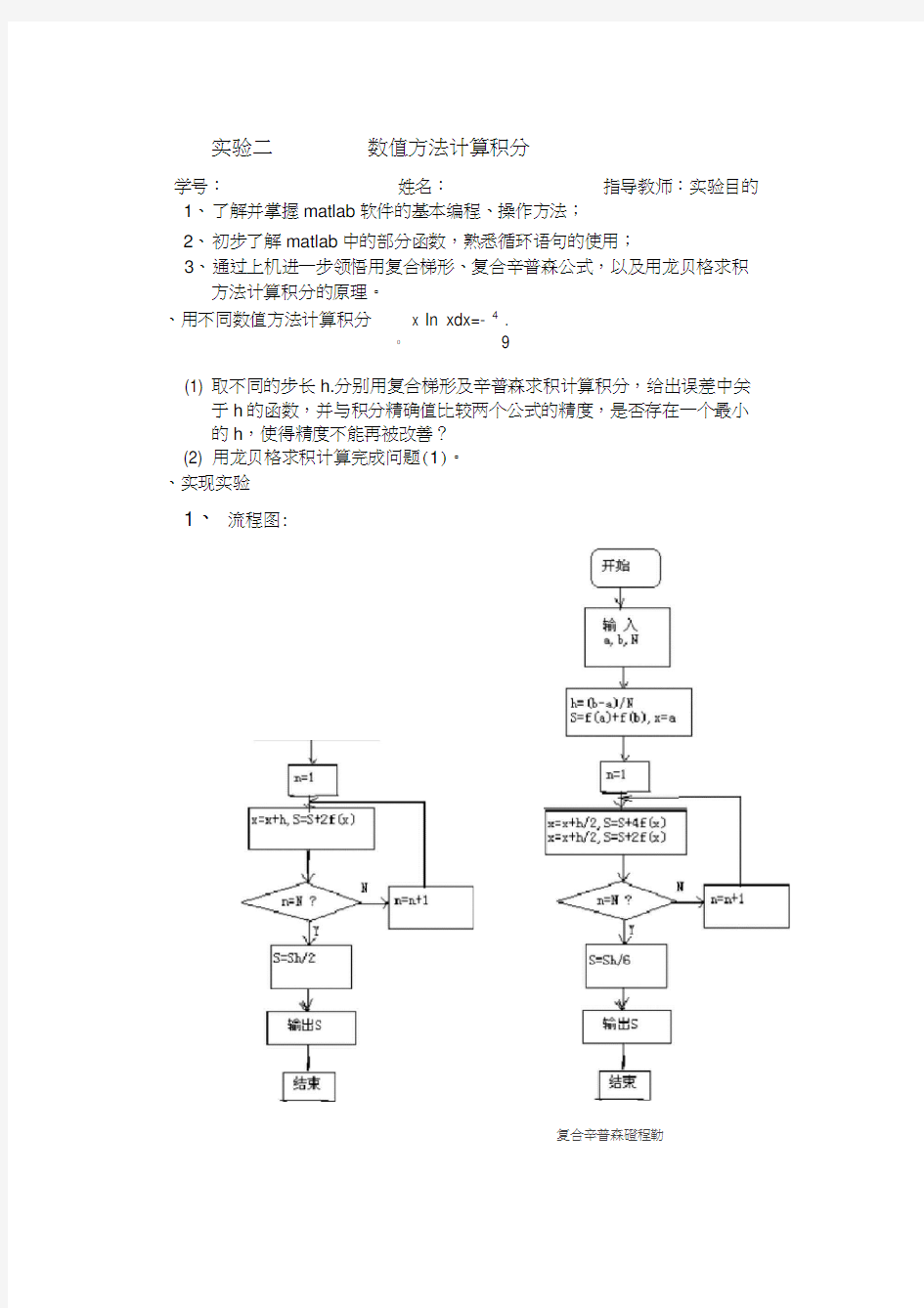
1、流程图:
复合辛普森磴程勒
下图是龙贝格算法框图:
开始
2、算法:
h n 1
(1)复合梯形公式:Tn =—[f(a) f (b) 2 f (xk)];
2 k i
h n 1 n 1
(2)复合辛普森公式:Sn=— [f(a)+f(b)+2 f (xk)] +4 f (x 1/2)];
6 k 1 k 0
以上两种算法都是将a-b之间分成多个小区间(n ),则
h=(b-a)/n, X k二a+kh, x k+1/2 =a+(k+1/2)h,利用梯形求积根据两公式便可。
⑶龙贝格算法:在指定区间内将步长依次二分的过程中运用如下公式
4 1
1、S n= —T2n- — Tn
3 3
2、Cn= — S2n—Sn
15 15
64 1
3、Rn= — C2n- — Cn从而实现算法。
63 63
3、程序设计
(1)、复合梯形法:
fun ctio n t=n atrapz(fname,a,b, n)
h=(b-a)/n;
fa=feval(f name,a);fb=feval(fname,b);f=feval(f name,a+h:h:b-h+0.001*h);
t=h*(0.5*(fa+fb)+sum (f));
(2 )、复合辛普森法:
fun ctio n t=n atrapz(fname,a,b, n)
h=(b-a)/n;
fa=feval(f name,a);fb=feval(fname,b);f1=feval(f name,a+h:h:b-h+0.001*h);
f2=feval(fname,a+h/2:h:b-h+0.001*h);
t=h/6*(fa+fb+2*sum(f1)+4*sum(f2));
(3)龙贝格法:
function [l,step]=Roberg(f,a,b,eps)
if(nargin==3)
eps=1.0e-4;
en d;
M=1;
tol=10;
k=0;
T=zeros(1,1);
h=b-a;
T(1,1)=(h/2)*(subs(sym(f),fi ndsym(sym(f)),a)+subs(sy m(f),fin dsym(sym(f)),b));
while tol>eps
k=k+1;
h=h/2;
Q=0; for i=1:M
x=a+h*(2*i-1);
Q=Q+subs(sym(f),fi ndsym(sym(f)),x); end
T(k+1,1)=T(k,1)/2+h*Q;
M=2*M;
for j=1:k
T(k+1,j+1)=T(k+1,j)+(T(k+1,j)-T(k,j))/(4Aj-1); end
tol=abs(T(k+1,j+1)-T(k,j));
end
I=T(k+1,k+1);
step=k;
4、实验结果;(1)复合梯形法
for it at long ;rtatrapz (inline C sqrt (K) . *log (x) ) f eps^ 1, 10)fl format short;
arts =
-0.41705283177947
?formai long ;natrapz(irLLirieC' sqrt(x)? *log (s)' ) j epsj L 100}, format short, ans =
-0.44311790800816
?format long ;n at trapz (inline C sqrt (x)* *log (M V) j eps,, lj 1000), format short: an呂二
-0. 44438753899716
(2)、复合辛普森法结果:
fornta/t long ; na"t rapz (inlirLe(' sq^rt (x) ■ ^log lx) epsj 1」10) j £o rmat skort ;
ams —
-0.43529789007469
?f ornLat long:; nat zapz (ml ine ( suet (x). Klog (,x) '、, eps^ 100i) f orniat short ; ars 二
-0.4441 Cl 17841567
£口mat long ;nat rapz (iixl me sqr t (x) ■ *Log (x,J' ),eps:3 1』lOOOl))£omat sherl ; ans =
-0.44443^11761418
(3) 龙贝格法结果
>>[Q J, s] =Rab^rg (* sqrt (j) *lcg(I)30. 0000001 ±1)
q 二
-0..4444
s -
9
四?总结由结果(1)、( 2)可知复合辛普森法求积分精度明显比复合梯形法求积的精度要高,且当步长取不同值时即n越大、h越小时,积分精度越高。实验结
果说明不存在一个最小的h,使得精度不能再被改善。又两个相应的关于h的误差(余项)Rn(f)=- - - h2f ( n ;Rn(f)=-b - (h/2)4f凶(n,其中n属于a 到b。可知
12 180
h愈小,余项愈小,从而积分精度越高。
数值实验课试题 本次数值实验课结课作业,请按题目要求内容写一篇文章。按题目要求 人数自由组合,每组所选题目不得相同(有特别注明的题目除外)。试题如下: 1)解线性方程组的Gauss 消去法和列主元Gauss 消去法(2人)/*张思珍,巩艳华*/ 用C 语言将不选主元和列主元Gauss 消去法编写成通用的子程序,然后用你编写的程序求解下列84阶的方程组 ???? ?????? ? ??=??????????? ????????????? ? ?1415151515768 168 168 168 1681684 8382321 x x x x x x 参考书目: 1.《计算机数值方法》,施吉林、刘淑珍、陈桂芝编 2.《数值线性代数》,徐树方、高立、张平文编 3.《数值分析简明教程》,王能超编 2)解线性方程组的平方根法(4人)/*朱春成、黄锐奇、张重威、章杰*/ 用C 语言将平方根法和改进的平方根法编写成通用的子程序,然后用你编写的程序求解对称正定方程组b Ax =,其中 (1)b 随机的选取,系数矩阵为100阶矩阵 ?????? ???? ? ? ?101 1101 1101 1101 1101110 ; (2)系数矩阵为40阶的Hilbert 矩阵,即系数矩阵A 的第i 行第j 列元素为 1 1-+= j i a ij ,向量b 的第i 个分量为∑=-+ = n j i j i b 1 1 1. 参考书目: 1.《计算机数值方法》,施吉林、刘淑珍、陈桂芝编 2.《数值线性代数》,徐树方、高立、张平文编
3.《数值分析简明教程》,王能超编 3)三对角线方程组的追赶法(3人)/*黄佳礼、唐伟、韦锡倍*/ 用C 语言将三对角线方程组的追赶法法编写成通用的子程序,然后用你编写的程序求解如下84阶三对角线方程组 ???? ?????? ? ??=??????????? ????????????? ? ?1415151515768 168 168 168 16816 84 8382321 x x x x x x 参考书目: 1.《计算机数值方法》,施吉林、刘淑珍、陈桂芝编 2.《数值分析简明教程》,王能超编 4)线性方程组的Jacobi 迭代法(3人)/*周桂宇、杨飞、李文军*/ 用C 语言将Jacobi 迭代法编写成独立的子程序,并用此求解下列方程组, 精确到小数点后5位 ???? ? ??=????? ??????? ? ?-149012 2111221 3 2 1 x x x 参考书目: 1.《计算机数值方法》,施吉林、刘淑珍、陈桂芝编 2.《数值线性代数》,徐树方、高立、张平文编 3.《数值分析简明教程》,王能超编 5)线性方程组的Gauss-Seidel 迭代法(3人)/*张玉超、范守平、周红春*/ 用C 语言将Gauss-Seidel 迭代法编写成独立的子程序,并用此求解下列方程组,精确到小数点后5位 ???? ? ??=????? ??????? ? ?--39721 1111112 3 2 1 x x x 参考书目: 1.《计算机数值方法》,施吉林、刘淑珍、陈桂芝编 2.《数值线性代数》,徐树方、高立、张平文编 3.《数值分析简明教程》,王能超编 6)解线性方程组的最速下降法法(2人)/*赵育辉、阿热孜古丽*/ 用C 语言将最速下降法编写成通用的子程序,然后用你编写的程序求解对称
勒贝格积分 将给定的函数按函数值的区域进行划分,作和、求极限而产生的积分概念,就是勒贝格积分。 概念简述 定义:设f (x) 是E ∈ L q(mE < ∞) 上的有界函数,则称f (x) ∈ L(E) ,如果对任意ε > 0,必然存在E 的分划D,使 S(D, f ) -s(D, f ) = ΣωimEi<ε, 这里S(D, f ) 及s(D, f )分别是f (x) 关于分划D 的大和及小和,ωimEi是Ei上的振幅。 它与黎曼积分的主要区别在于前者是对函数的函数值区域进行划分; 后者是对函数定义域进行划分。 对此Lebesgue自己曾经作过一个比喻,他说: 假如我欠人家一笔钱,现在要还,此时按钞票的面值的大小分类,然后 计算每一类的面额总值,再相加,这就是Lebesgue积分思想;如不按面额大小分类,而是按从钱袋取出的先后次序来计算总数,那就是Riemann积分思想。(参见:周性伟,实变函数教学的点滴体会,《高等理科教学》,2000.1) 即采取对值域作分划,相应得到对定义域的分划(每一块不一定是区间), 使得在每一块上的振幅都很小, 即按函数值的大小对定义域的点加 以归类。 积分介绍 积分是“和”的概念。即将东西加起来。所以积分早期是从面积,路 程等计算中发展起来。比如计算面积,将X轴的区间分成若干小区间,将 小区间的高度(Y值)乘以小区间的长度,然后加起来。用极限法就可以求得精确的面积。这是传统的积分概念(黎曼积分)。 勒贝格从另一个角度来考虑积分概念,导致勒贝格积分和测度概念。比如 计算面积,可以将小区间的高度(Y值)乘以对应的所有小区间的长度的和(测度),然后加起来。又比如现有硬币:25, 25,10,5,10,1,5,25。用黎曼积分来求和:25+25+10+5+10+1+5+25=106。用勒贝格积分来求和:25*3+10*2+5*2+1=106。结果是一样。但对于一些“坏”函数,结果是不一样。比如在X轴[0,1]闭区间上定义函数: Y=1,当X是无理数; Y=0,当X是有理数。 求该函数覆盖的面积。
曲线拟合的数值计算方法实验 【摘要】实际工作中,变量间未必都有线性关系,如服药后血药浓度与时间的关系;疾病疗效与疗程长短的关系;毒物剂量与致死率的关系等常呈曲线关系。曲线拟合(curve fitting)是指选择适当的曲线类型来拟合观测数据,并用拟合的曲线方程分析两变量间的关系。曲线直线化是曲线拟合的重要手段之一。对于某些非线性的资料可以通过简单的变量变换使之直线化,这样就可以按最小二乘法原理求出变换后变量的直线方程,在实际工作中常利用此直线方程绘制资料的标准工作曲线,同时根据需要可将此直线方程还原为曲线方程,实现对资料的曲线拟合。常用的曲线拟合有最小二乘法拟合、幂函数拟合、对数函数拟合、线性插值、三次样条插值、端点约束。 关键词曲线拟合、最小二乘法拟合、幂函数拟合、对数函数拟合、线性插值、三次样条插值、端点约束 一、实验目的 1.掌握曲线拟合方式及其常用函数指数函数、幂函数、对数函数的拟合。 2.掌握最小二乘法、线性插值、三次样条插值、端点约束等。 3.掌握实现曲线拟合的编程技巧。 二、实验原理 1.曲线拟合 曲线拟合是平面上离散点组所表示的坐标之间的函数关系的一种数据处理方法。用解析表达式逼近离散数据的一种方法。在科学实验或社会活动中,通过 实验或观测得到量x与y的一组数据对(X i ,Y i )(i=1,2,...m),其中各X i 是彼此不同的。人们希望用一类与数据的背景材料规律相适应的解析表达式,y=f(x,c)来反映量x与y之间的依赖关系,即在一定意义下“最佳”地逼近或 拟合已知数据。f(x,c)常称作拟合模型,式中c=(c 1,c 2 ,…c n )是一些待定参 数。当c在f中线性出现时,称为线性模型,否则称为非线性模型。有许多衡量拟合优度的标准,最常用的一种做法是选择参数c使得拟合模型与实际观测值在
实验一误差分析 实验1.1(病态问题) 实验目的:算法有“优”与“劣”之分,问题也有“好”与“坏”之别。对数值方法的研究而言,所谓坏问题就是问题本身对扰动敏感者,反之属于好问题。通过本实验可获得一个初步体会。 数值分析的大部分研究课题中,如线性代数方程组、矩阵特征值问题、非线性方程及方程组等都存在病态的问题。病态问题要通过研究和构造特殊的算法来解决,当然一般要付出一些代价(如耗用更多的机器时间、占用更多的存储空间等)。 问题提出:考虑一个高次的代数多项式 显然该多项式的全部根为1,2,…,20共计20个,且每个根都是单重的。现考虑该多项式的一个扰动 其中ε(1.1)和(1.221,,,a a 的输出b ”和“poly ε。 (1(2 (3)写成展 关于α solve 来提高解的精确度,这需要用到将多项式转换为符号多项式的函数poly2sym,函数的具体使用方法可参考Matlab 的帮助。 实验过程: 程序: a=poly(1:20); rr=roots(a); forn=2:21 n form=1:9 ess=10^(-6-m);
ve=zeros(1,21); ve(n)=ess; r=roots(a+ve); -6-m s=max(abs(r-rr)) end end 利用符号函数:(思考题一)a=poly(1:20); y=poly2sym(a); rr=solve(y) n
很容易的得出对一个多次的代数多项式的其中某一项进行很小的扰动,对其多项式的根会有一定的扰动的,所以对于这类病态问题可以借助于MATLAB来进行问题的分析。 学号:06450210 姓名:万轩 实验二插值法
本科实验报告 课程名称:计算机数值方法 实验项目:方程求根、线性方程组的直接解 法、线性方程组的迭代解法、代数插值和最 小二乘拟合多项式 实验地点:行勉楼 专业班级: ******** 学号: ********* 学生姓名: ******** 指导教师:李誌,崔冬华 2016年 4 月 8 日
y = x*x*x + 4 * x*x - 10; return y; } float Calculate(float a,float b) { c = (a + b) / 2; n++; if (GetY(c) == 0 || ((b - a) / 2) < 0.000005) { cout << c <<"为方程的解"<< endl; return 0; } if (GetY(a)*GetY(c) < 0) { return Calculate(a,c); } if (GetY(c)*GetY(b)< 0) { return Calculate(c,b); } } }; int main() { cout << "方程组为:f(x)=x^3+4x^2-10=0" << endl; float a, b; Text text; text.Getab(); a = text.a; b = text.b; text.Calculate(a, b); return 0; } 2.割线法: // 方程求根(割线法).cpp : 定义控制台应用程序的入口点。// #include "stdafx.h" #include"iostream"
心得体会 使用不同的方法,可以不同程度的求得方程的解,通过二分法计算的程序实现更加了解二分法的特点,二分法过程简单,程序容易实现,但该方法收敛比较慢一般用于求根的初始近似值,不同的方法速度不同。面对一个复杂的问题,要学会简化处理步骤,分步骤一点一点的循序处理,只有这样,才能高效的解决一个复杂问题。
实验二定积分的近似计算 一、问题背景与实验目的 利用牛顿—莱布尼兹公式虽然可以精确地计算定积分的值,但它仅适用于被积函数的原函数能用初等函数表达出来的情形.如果这点办不到或者不容易办到,这就有必要考虑近似计算的方法.在定积分的很多应用问题中,被积函数甚至没有解析表达式,可能只是一条实验记录曲线,或者是一组离散的采样值,这时只能应用近似方法去计算相应的定积分. 本实验将主要研究定积分的三种近似计算算法:矩形法、梯形法、抛物线法.对于定积分的近似数值计算,Matlab有专门函数可用. 二、相关函数(命令)及简介 1.sum(a):求数组a的和. 2.format long:长格式,即屏幕显示15位有效数字. (注:由于本实验要比较近似解法和精确求解间的误差,需要更高的精度).3.double():若输入的是字符则转化为相应的ASCII码;若输入的是整型数值则转化为相应的实型数值. 4.quad():抛物线法求数值积分. 格式:quad(fun,a,b) ,注意此处的fun是函数,并且为数值形式的,所以使用*、/、^等运算时要在其前加上小数点,即.*、./、.^等. 例:Q = quad('1./(x.^3-2*x-5)',0,2); 5.trapz():梯形法求数值积分. 格式:trapz(x,y) 其中x为带有步长的积分区间;y为数值形式的运算(相当于上面介绍的函数fun) 例:计算 0sin()d x x π ? x=0:pi/100:pi;y=sin(x); trapz(x,y) 6.dblquad():抛物线法求二重数值积分. 格式:dblquad(fun,xmin,xmax,ymin,ymax),fun可以用inline定义,也可以通过某个函数文件的句柄传递. 例1:Q1 = dblquad(inline('y*sin(x)'), pi, 2*pi, 0, pi) 顺便计算下面的Q2,通过计算,比较Q1 与Q2结果(或加上手工验算),找出积分变量x、y的上下限的函数代入方法. Q2 = dblquad(inline('y*sin(x)'), 0, pi, pi, 2*pi) 例2:Q3 = dblquad(@integrnd, pi, 2*pi, 0, pi) 这时必须存在一个函数文件integrnd.m:
实验报告 学院(系)名称: 主程序部分列选主元部分
实验结果: 一.列主元消去法 输入各个数据,最终使用列选主元法,得到结果为:x1=x2=x3=1二.高斯-赛德尔迭代法 输入各个数据,输出每一步迭代数据,最终结果为:x1=0.285716,附录(源程序及运行结果) 一.列主元高斯消去法 #include 勒贝格积分的若干简介 我们先学习了Riemann 积分(简称R 积分),从而慢慢引入到了勒贝格积分,因此我将在下文中分几部分来讲勒贝格积分。 首先介绍一下在有界函数范围内,R 积分还是存在这很大的缺陷,主要表现在以下两个方面[1]: ⑴R 积分与极限可交换的条件太严。 ⑵积分运算不完全是微分运算的逆运算。 ⑶不适宜于无界区间:黎曼积分只能用来在有界区间内对函数进行积分。 ⑷缺乏单调收敛。 鉴于R 积分的上述缺陷,人们致力于对此进行改进。1902年,法国数学家勒贝格基于可列可加的测度,成功引进了一种新的积分,即Lebesgue 积分(简称L 积分)。那么,建立L 积分的基本思路和步骤是怎么样的呢?L 积分的思路也基本与R 积分一样先分割,作积分和,取取极限。 在重新审视R 积分和曲边梯形面积的关系时,另一个建立L 积分的思路浮现出来。首先,为了避免可测函数不是有界函数,最后的积分值可能会出现∞-∞的不定情形的出现,在定义L 积分时第一步仅限于非负函数。其次,注意到非负函数围成的曲边梯形的面积,对于L 积分,可以将“可测集分割”加以取代,形成所谓“简单函数”,从而过度到L 积分“横着数”的思想。 下文将详细的介绍L 积分和R 积分的区别和联系。 关于Lebesgue 积分与Riemann 积分的定义比较 1.1勒贝格积分的定义[3]: 定义1:设)(x f 是n R E ?()∞ 重庆三峡学院数学分析课程论文 二重积分的计算方法 院系数学与统计学院 专业数学与应用数学(师范) 姓名 年级 2010级 学号 指导教师刘学飞 2014年5月 二重积分的计算方法 (重庆三峡学院数学与统计学院10级数本1班) 摘 要 :本文总结出了求二重积分的几种方法,比如用定义、公式、定理、性质求极限. 关键词 :函数极限;计算方法;洛必达法则; 四则运算 引言 二重积分的概念和计算是多元函数微积分学的重要部分,在几何、物理、力学等方面有着重 要的应用.重积分是由一元函数积分推广而来的,但与一元函数相比,计算重积分的难度除了与被 积函数有关外,还与积分区域的特点有关,计算重积分的主要思想方法是化重积分为累次积分.求 二重积分的方法很多且非常灵活,本文归纳了二重积分计算的一些常见方法和技巧. 1. 预备知识 1.1二重积分的定义 设(),f x y 是定义在可求面积的有界区域D 上的函数. J 是一个确定的数,若对任给的正数 ε,总存在某个正数δ,使对于D 的任意分割T ,当它的细度T δ<时,属于T 的所有积分和都有 ()1 ,n i i i i f J ξησ ε=?-<∑, 则称(),f x y 在D 上可积,数J 称为函数(),f x y 在D 上的二重积分,记作(),D J f x y d σ= ??, 其中(),f x y 称为二重积分的被积函数, ,x y 称为积分变量, D 称为积分区域. 1.2二重积分的若干性质 1.21若(),f x y 在区域D 上可积, k 为常数,则(),kf x y 在D 上也可积,且 (),D kf x y d σ??(),D k f x y d σ=??. 1.22 若(),f x y ,(),g x y 在D 上都可积,则()(),,f x y g x y ±在D 上也可积,且 ()()[,,]D f x y g x y d σ±??()(),,D D f x y d g x y d σσ=±????. 目录 摘要 (2) 英文摘要 (2) 1.引言 (3) 2.勒贝格积分在数学分析中的应用 (3) 2.1 在概念方面 (3) 2.2 在定理方面 (3) 3.勒贝格积分的计算 (3) 3.1可测函数与连续函数有着密切的关系 (4) 3.2连续函数与可积函数的关系 (5) 4.勒贝格积分的优越性 (6) 4.1从()R积分与()L积分对比中看()R积分 (6) 4.2应用()L积分理论可以简便解决数学分析中的某些问题 (8) 小结 (11) 致谢 (11) 参考文献………………………………………………………………… 摘要 勒贝格积分是变限积分函数中重要的一部分内容,实变函数是数学专 业开设的一门重要课程。山西财经大学的于秀兰,绍兴文理学院的倪仁兴 等对勒贝格积分函数均有所论述,其中绍兴文理学院的倪仁兴从两个不同 的角度深刻的说明了勒贝格积分应用范围之广。本文在借鉴他们的基础上,主要从三个方面对勒贝格积分进行研究。 关键词:勒贝格()L积分,实变函数,数学分析,一致收敛 Abstract Lebesgue inteqral is an important part in integral, Real Variable Function is an important course in Mathematical analysis. Lebesgue integral is discussed by Shanxi University of Yu Xiulan, Shaoxing University of Ni Renxing .In this paper,they draw on the basis of three main areas to study the Lebesgue inteqra l. Keyword:Lebesgue integral, Real Variable Function, Mathematical analysis, unanimously Convergence 1. 设?+=1 05dx x x I n n , (1) 由递推公式n I I n n 1 51+-=-,从0I 的几个近似值出发,计算20I ; 解:易得:0I =ln6-ln5=0.1823, 程序为: I=0.182; for n=1:20 I=(-5)*I+1/n; end I 输出结果为:20I = -3.0666e+010 (2) 粗糙估计20I ,用n I I n n 51 5111+- =--,计算0I ; 因为 0095.05 6 0079.01020 201 020 ≈<<≈??dx x I dx x 所以取0087.0)0095.00079.0(2 1 20=+= I 程序为:I=0.0087; for n=1:20 I=(-1/5)*I+1/(5*n); end I 0I = 0.0083 (3) 分析结果的可靠性及产生此现象的原因(重点分析原因)。 首先分析两种递推式的误差;设第一递推式中开始时的误差为000I I E '-=,递推过程的舍入误差不计。并记n n n I I E '-=,则有01)5(5E E E n n n -==-=-Λ。因为=20E 20020)5(I E >>-,所此递推式不可靠。而在第二种递推式中n n E E E )5 1(5110-==-=Λ,误差在缩小, 所以此递推式是可靠的。出现以上运行结果的主要原因是在构造递推式过程中,考虑误差是否得到控制, 即算法是否数值稳定。 2. 求方程0210=-+x e x 的近似根,要求4 1105-+?<-k k x x ,并比较计算量。 (1) 在[0,1]上用二分法; 程序:a=0;b=1.0; while abs(b-a)>5*1e-4 c=(b+a)/2; Lebesgue 积分与Riemann 积分的区别 Lebesgue 积分与Riemann 积分是非常重要的两种积分,在数学发展史上发挥过巨大的作用。Riemann 积分是近代数学的核心,lebesgue 积分是现代实变函数论的核心。 在有界函数范围内,R 积分存在以下缺陷。 1)R 积分与极限可交换的条件太严; 2)积分运算不完全是微分运算的逆运算; 3)不适宜于无界区间:R 积分只能用来在有界区间内对函数进行积分; 4)缺乏单调收敛。 1 积分的定义 1.1 L 积分的定义 定义1:设 () f x 是 () n E R mE ?<∞上的非负可测函数。定义()f x 是E 上的Lebesgue 积分()()()()sup x E h x f x E E f x dx h x dx ∈≤???? =?? ????? ?,()h x 是n R 上的非负可测简单函数,积分可以是+∞; 若()E f x dx <∞ ?,则称()f x 在E 上是Lebesgue 可积的。 设()f x 是n E R ?上的可测函数,若积分()E f x dx + ?、()E f x dx - ?中至少有一个是 有限值,则称()()()E E E f x dx f x dx f x dx + - =-???为()f x 在E 上的Lebesgue 积分;当上 式右端两个积分值结尾有限时,则称()f x 在E 上Lebesgue 可积的。 定义2:设E 是一个Lebesgue 可测集,mE <∞,()f x 是定义在E 上的Lebesgue 可测函数,又设()f x 是有界的,就是说是否存在l 及μ,使得()(),f x l μ?,在[] ,l μ 中任取一分点组D 01n l l l l μ =<< <= 记 ()() 11max k k k n D l l δ-≤≤=- ()() 1k k k E E l f x l -=≤≤ 并任取i k E ζ∈(约定当k E =Φ时,()()0i k f m E ζ=),作和 ()()() 1 n i k k S D f m E ζ==∑ 如果对任意的分法与i ζ的任意取法,当()0D δ→时,()S D 趋于有限的极限,则称 第二节 二重积分的计算法 教学目的:熟练掌握二重积分的计算方法 教学重点:利用直角坐标和极坐标计算二重积分 教学难点:化二重积分为二次积分的定限问题 教学内容: 利用二重积分的定义来计算二重积分显然是不实际的,二重积分的计算是通过两个定积分的计算(即二次积分)来实现的. 一、利用直角坐标计算二重积分 我们用几何观点来讨论二重积分的计算问题. 讨论中,我们假定 ; 假定积分区域可用不等式 表示, 其中, 在上连续. 据二重积分的几何意义可知,的值等于以为底,以曲面为顶的曲顶柱体的体积. 在区间上任意取定一个点,作平行于面的平面,这平面截曲顶柱体所得截面是一个以区间为底,曲线为曲边的曲边梯形,其面积为 一般地,过区间上任一点且平行于面的平面截曲顶柱体所得截面的面积为 利用计算平行截面面积为已知的立体之体积的方法,该曲顶柱体的体积为 从而有 (1) 上述积分叫做先对Y,后对X的二次积分,即先把看作常数,只看作的函数,对 计算从到的定积分,然后把所得的结果( 它是的函数 )再对从到计算定积分. 这个先对, 后对的二次积分也常记作 在上述讨论中,假定了,利用二重积分的几何意义,导出了二重积分的计算公式(1).但实际上,公式(1)并不受此条件限制,对一般的(在上连续),公式(1)总是成立的. 例如:计算 解: 类似地,如果积分区域可以用下述不等式 表示,且函数,在上连续,在上连续,则 (2) 显然,(2)式是先对,后对的二次积分. 二重积分化二次积分时应注意的问题 1、积分区域的形状 前面所画的两类积分区域的形状具有一个共同点: 对于I型(或II型)区域, 用平行于轴(轴 )的直线穿过区域内部,直线与区域的边界相交不多于两点. 如果积分区域不满足这一条件时,可对区域进行剖分,化归为I型(或II型)区域的并集. 2、积分限的确定 二重积分化二次积分, 确定两个定积分的限是关键.这里,我们介绍配置二 次积分限的方法 -- 几何法.画出积分区域的图形(假设的图形如下 ) 在上任取一点,过作平行于轴的直线,该直线穿过区域,与区域的边界有两个交 点与,这里的、就是将,看作常数而对积分时的下限和上限; 又因是在区间上任意取的,所以再将看作变量而对积分时,积分的下限为、上限为 . 例1计算,其中是由轴,轴和抛物线在第一象限内所围成的区域. 数值分析实验报告总结 随着电子计算机的普及与发展,科学计算已成为现代科 学的重要组成部分,因而数值计算方法的内容也愈来愈广泛和丰富。通过本学期的学习,主要掌握了一些数值方法的基本原理、具体算法,并通过编程在计算机上来实现这些算法。 算法算法是指由基本算术运算及运算顺序的规定构成的完 整的解题步骤。算法可以使用框图、算法语言、数学语言、自然语言来进行描述。具有的特征:正确性、有穷性、适用范围广、运算工作量少、使用资源少、逻辑结构简单、便于实现、计算结果可靠。 误差 计算机的计算结果通常是近似的,因此算法必有误差, 并且应能估计误差。误差是指近似值与真正值之差。绝对误差是指近似值与真正值之差或差的绝对值;相对误差:是指近似值与真正值之比或比的绝对值。误差来源见表 第三章泛函分析泛函分析概要 泛函分析是研究“函数的函数”、函数空间和它们之间 变换的一门较新的数学分支,隶属分析数学。它以各种学科 如果 a 是相容范数,且任何满足 为具体背景,在集合的基础上,把客观世界中的研究对象抽 范数 范数,是具有“长度”概念的函数。在线性代数、泛函 分析及相关的数学领域,泛函是一个函数,其为矢量空间内 的所有矢量赋予非零的正长度或大小。这里以 Cn 空间为例, Rn 空间类似。最常用的范数就是 P-范数。那么 当P 取1, 2 ,s 的时候分别是以下几种最简单的情形: 其中2-范数就是通常意义下的距离。 对于这些范数有以下不等式: 1 < n1/2 另外,若p 和q 是赫德尔共轭指标,即 1/p+1/q=1 么有赫德尔不等式: II = ||xH*y| 当p=q=2时就是柯西-许瓦兹不等式 般来讲矩阵范数除了正定性,齐次性和三角不等式之 矩阵范数通常也称为相容范数。 象为元素和空间。女口:距离空间,赋范线性空间, 内积空间。 1-范数: 1= x1 + x2 +?+ xn 2-范数: x 2=1/2 8 -范数: 8 =max oo ,那 外,还规定其必须满足相容性: 所以 实验三定积分的近似计算 一、问题背景与实验目的 利用牛顿—莱布尼兹公式虽然可以精确地计算定积分的值,但它仅适用于被积函数的原函数能用初等函数表达出来的情形.如果这点办不到或者不容易办到,这就有必要考虑近似计算的方法.在定积分的很多应用问题中,被积函数甚至没有解析表达式,可能只是一条实验记录曲线,或者是一组离散的采样值,这时只能应用近似方法去计算相应的定积分. 本实验将主要研究定积分的三种近似计算算法:矩形法、梯形法、抛物线法.对于定积分的近似数值计算,Matlab有专门函数可用. 二、相关函数(命令)及简介 1.sum(a):求数组a的和. 2.format long:长格式,即屏幕显示15位有效数字. (注:由于本实验要比较近似解法和精确求解间的误差,需要更高的精度).3.double():若输入的是字符则转化为相应的ASCII码;若输入的是整型数值则转化为相应的实型数值. 4.quad():抛物线法求数值积分. 格式:quad(fun,a,b) ,注意此处的fun是函数,并且为数值形式的,所以使用*、/、^等运算时要在其前加上小数点,即.*、./、.^等. 例:Q = quad('1./(x.^3-2*x-5)',0,2); 5.trapz():梯形法求数值积分. 格式:trapz(x,y) 其中x为带有步长的积分区间;y为数值形式的运算(相当于上面介绍的函数fun) 例:计算 0sin()d x x π? x=0:pi/100:pi;y=sin(x); trapz(x,y) 6.dblquad():抛物线法求二重数值积分. 格式:dblquad(fun,xmin,xmax,ymin,ymax),fun可以用inline定义,也可以通过某个函数文件的句柄传递. 例1:Q1 = dblquad(inline('y*sin(x)'), pi, 2*pi, 0, pi) 顺便计算下面的Q2,通过计算,比较Q1 与Q2结果(或加上手工验算),找出积分变量x、y的上下限的函数代入方法. Q2 = dblquad(inline('y*sin(x)'), 0, pi, pi, 2*pi) 例2:Q3 = dblquad(@integrnd, pi, 2*pi, 0, pi) 这时必须存在一个函数文件: function z = integrnd(x, y) z = y*sin(x); 7.fprintf(文件地址,格式,写入的变量):把数据写入指定文件.例:x = 0:.1:1; y = [x; exp(x)]; fid = fopen('','w'); %打开文件 fprintf(fid,'%6.2f %12.8f\n',y); %写入 fclose(fid) %关闭文件 8.syms 变量1 变量2 …:定义变量为符号. 9.sym('表达式'):将表达式定义为符号. 解释:Matlab中的符号运算事实上是借用了Maple的软件包,所以当在Matlab中要对符号进行运算时,必须先把要用到的变量定义为符号. 10.int(f,v,a,b):求f关于v积分,积分区间由a到b. 11.subs(f,'x',a):将a 的值赋给符号表达式f 中的x,并计算出值.若简单地使用subs(f),则将f的所有符号变量用可能的数值代入,并计算出值. 数值分析实验报告 一、 实验目的 1、会使用Sor 法求解一个线性方程组 2、熟悉matlab 语言并结合原理编程求方程组 3、改变ω的值观察实验结果 4、会分析实验结果 二、实验题目 编制Sor 迭代格式程序进行求解一个线性方程组的迭代计算情况,运行中要选用不同的松弛因子ω进行尝试 三、 实验原理 Jacobi 迭代和seidel 迭代对具体的线性方程组来说,逼近*x 的速度是固定不变的,遇到收敛很慢的情况时就显得很不实用。 Sor 法是一seidel 迭代为基础,并在迭代中引入参数ω以增加迭代选择的灵活性,具体为: ! 用seidel 迭代算出的,)()1()()1(k k J k k J x x x x x -=?++相减得到差向量与再用参数ω乘之再加上 )1()()()1()1()()()1(++++-=?+=k J k k k k k k x x x x x x x x ωωω,即的下一步迭代作为,由seidel 迭代的公式可以得到Sor 法的迭代格式为 n i x a x a b a x x k j n i j ij k j i j ij i ii k i k i ,2,1),()1()(1)1(11)()1( =--+-=∑∑+=+-=+ω ω 式中ω称为松弛因子。 四、 实验内容 用matlab 编程得到Sor 法求线性方程组的算法为: function [x,n]=SOR(A,b,x0,w,eps,M) if nargin==4 eps= ; M = 200; elseif nargin<4 error return : elseif nargin ==5 M = 200; end if(w<=0 || w>=2) error; return; end D=diag(diag(A)); %求A的对角矩阵L=-tril(A,-1); %求A的下三角阵( U=-triu(A,1); %求A的上三角阵B=inv(D-L*w)*((1-w)*D+w*U); f=w*inv((D-L*w))*b; x=B*x0+f; n=1; %迭代次数 while norm(x-x0)>=eps x0=x; x =B*x0+f; n=n+1; if(n>=M) ( 第六讲 定积分与定积分的近似计算 实验目的 1.通过本实验加深理解积分理论中分割、近似、求和、取极限的思想方法. 2.学习并掌握用matlab 求不定积分、定积分、二重积分、曲线积分的方法. 3.学习matlab 命令sum 、symsum 与int. 4. 了解定积分近似计算的矩形法、梯形法。(***) 实验内容 1. 学习matlab 命令 (1)求和命令sum 调用格式. sum(x),给出向量x 的各个元素的累加和,如果x 是矩阵,则sum(x)是一个元素为x 的每列列和的行向量. 例4.1.x=[1,2,3,4,5,6,7,8,9,10];? sum(x)? ans=55 例4.2.x=[1,2,3;4,5,6;7,8,9]? x= 1 2 3 4 5 6 7 8 9 sum(x)? ans=12 15 18 (2)求和命令symsum 调用格式. symsum(s,n), 求 ∑n s symsum(s,k,m,n),求∑=n m k s 当x 的元素很有规律,比如为表达式是)(k s 的数列时,可用symsum 求得x 的各项和,即 symsum ),1),((n k s =)()2()1(n s s s +++ symsum )()1()(),,),((n s m s m s n m k k s ++++= 例4.3.syms k n ? symsum(k,1,10)? ans=55 symsum(k^2,k,1,n)? ans=1/3*(n+1)^3-1/2*(n+1)^2+1/6*n+1/6 (3)matlab 积分命令int 调用格式 int (函数)(x f ) 计算不定积分 ?dx x f )( int (函数),(y x f ,变量名x ) 计算不定积分?dx y x f ),( int (函数b a x f ,),() 计算定积分 ?b a dx x f )( int (函数),,(y x f 变量名b a x ,,) 计算定积分 ?b a dx y x f ),( 1.计算不定积分 例4.4.计算 xdx x ln 2 ? 解:输入命令: int(x^2*log(x)) 可得结果: ans=1/3*x^3*log(x)-1/9*x^3 注意设置符号变量. 例4.5.计算下列不定积分: 1. dx x a ? -22 2. ?++dx x x 3 131 3. ?xdx x arcsin 2 解:首先建立函数向量. syms x syms a real y=[sqrt(a^2-x^2),(x-1)/(3*x-1)^(1/3),x^2*asin(x)]; 然后对y 积分可得对y 的每个分量积分的结果. int(y,x)? ans = [1/2*x*(a^2-x^2)^(1/2)+1/2*a^2*asin((1/a^2)^(1/2)*x), -1/3*(3*x-1)^(2/3)+1/15*(3*x-1)^(5/3), 1/3*x^3*asin(x)+1/9*x^2*(1-x^2)^(1/2)+2/9*(1-x^2)^(1/2)] 学院(系)名称: 附录(源程序及运行结果): 一.变步长梯形法 #include 数学实验报告 实验序号:4 日期:2012 年12 月13 日 实验名称定积分的近似计算 问题背景描述: 利用牛顿—莱布尼兹公式虽然可以精确地计算定积分的值,但它仅适用于被积函数的原函数能用初等函数表达出来的情形.如果这点办不到或者不容易办到,这就有必要考虑近似计算的方法.在定积分的很多应用问题中,被积函数甚至没有解析表达式,可能只是一条实验记录曲线,或者是一组离散的采样值,这时只能应用近似方法去计算相应的定积分. 实验目的: 本实验将主要研究定积分的三种近似计算算法:矩形法、梯形法、抛物线法。对于定积分的近似数值计算,Matlab有专门函数可用。 实验原理与数学模型: 1.矩形法 根据定积分的定义,每一个积分和都可以看作是定积分的一个近似值,即 在几何意义上,这是用一系列小矩形面积近似小曲边梯形的结果,所以把这个近似计算方法称为矩形法.不过,只有当积分区间被分割得很细时,矩形法才有一定的精确度. 针对不同的取法,计算结果会有不同。 (1)左点法:对等分区间 , 在区间上取左端点,即取。 (2)右点法:同(1)中划分区间,在区间上取右端点,即取。 (3)中点法:同(1)中划分区间,在区间上取中点,即取。2.梯形法 等分区间 , 相应函数值为(). 曲线上相应的点为() 将曲线的每一段弧用过点,的弦(线性函数)来代替,这使得每个 上的曲边梯形成为真正的梯形,其面积为 ,. 于是各个小梯形面积之和就是曲边梯形面积的近似值, , 即, 称此式为梯形公式。 3.抛物线法 将积分区间作等分,分点依次为 ,, 对应函数值为 (), 曲线上相应点为 (). 现把区间上的曲线段用通过三点,,的抛物线勒贝格积分和黎曼积分的关系和区别
二重积分的计算方法
勒贝格积分函数的研究 汤倩南
(完整版)数值计算方法上机实习题答案
Lebesgue积分与Riemann积分的区别
二重积分的计算方法
数值分析实验报告总结
matlab实验三定积分的近似计算
数值分析实验报告-Sor法分析
定积分与定积分的近似计算
数值计算方法实验3
定积分的近似计算