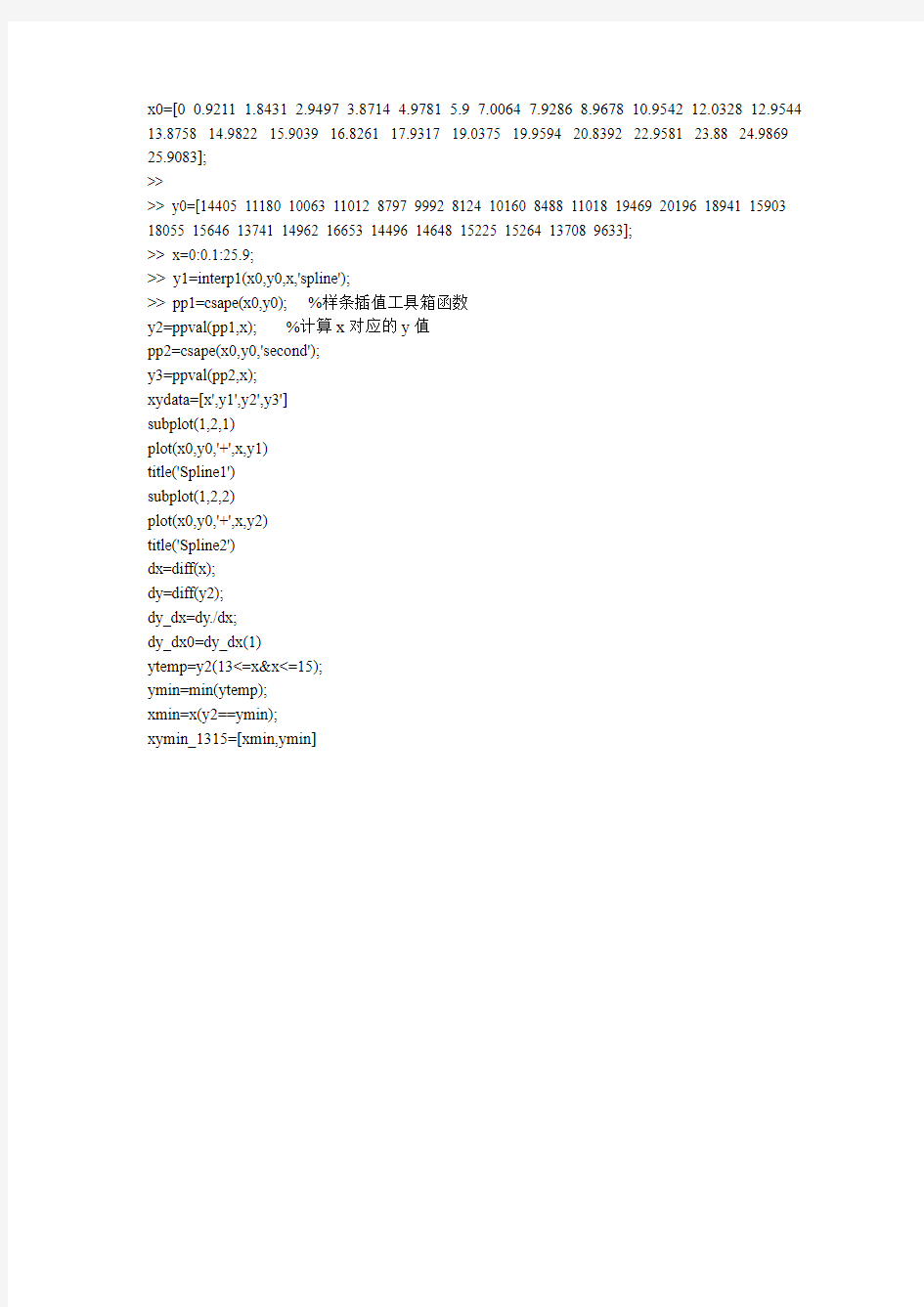
x0=[0 0.9211 1.8431 2.9497 3.8714 4.9781 5.9 7.0064 7.9286 8.9678 10.9542 12.0328 12.9544 13.8758 14.9822 15.9039 16.8261 17.9317 19.0375 19.9594 20.8392 22.9581 23.88 24.9869 25.9083];
>>
>> y0=[14405 11180 10063 11012 8797 9992 8124 10160 8488 11018 19469 20196 18941 15903 18055 15646 13741 14962 16653 14496 14648 15225 15264 13708 9633];
>> x=0:0.1:25.9;
>> y1=interp1(x0,y0,x,'spline');
>> pp1=csape(x0,y0); %样条插值工具箱函数
y2=ppval(pp1,x); %计算x对应的y值
pp2=csape(x0,y0,'second');
y3=ppval(pp2,x);
xydata=[x',y1',y2',y3']
subplot(1,2,1)
plot(x0,y0,'+',x,y1)
title('Spline1')
subplot(1,2,2)
plot(x0,y0,'+',x,y2)
title('Spline2')
dx=diff(x);
dy=diff(y2);
dy_dx=dy./dx;
dy_dx0=dy_dx(1)
ytemp=y2(13<=x&x<=15);
ymin=min(ytemp);
xmin=x(y2==ymin);
xymin_1315=[xmin,ymin]
样条插值函数及应用
摘要 样条函数具有广泛的应用,是现代函数论的一个十分活跃的分支,是计算方法的主要基础和工具之一,由于生产和科学技术向前发展的推动以及电子计算机广泛应用的需要,人们便更多地应用这个工具,也更深刻的认识了它的本质。 在实际问题中所遇到许多函数往往很复杂,有些甚至是很难找到解析表达式的。根据函数已有的数据来计算函数在一些新的点处的函数值,就是插值法所需要解决的问题。 插值法是数值逼近的重要方法之一,它是根据给定的自变量值和函数值,求取未知函数的近似值。早在一千多年前,我国科学家就在研究历法时就用到了线性插值和二次插值。而在实际问题中,有许多插值函数的曲线要求具有较高的光滑性,在整个曲线中,曲线不但不能有拐点,而且曲率也不能有突变。因此,对于插值函数必须二次连续可微且不变号 ,这就需要用到三次样条插值。 关键词三次样条函数;插值法
目录 引言 0 第一章三次样条插值 (1) 1.1 样条插值函数简介 (1) 1.2 三次样条函数应用 (2) 第二章AMCM91A 估计水塔水流量 (4) 2.1 理论分析及计算 (5) 2.2运用MATLAB软件计算 (8) 参考文献 (13)
引言 样条函数具有广泛的应用,是现代函数论的一个十分活跃的分支,是计算方法的主要基础和工具之一,由于生产和科学技术向前发展的推动以及电子计算机广泛应用的需要,人们便更多地应用这个工具,也更深刻的认识了它的本质。上世纪四十年代,在研究数据处理的问题中引出了样条函数,例如,在1946年Schoenberg将样条引入数学,即所谓的样条函数,直到五十年代,还多应用于统计数据的处理方面,从六十年代起,在航空、造船、汽车等行业中,开始大量采用样条函数。 在我国,从六十年代末开始,从船体数学放样到飞机外形设计,逐渐出现了一个使用样,逐渐出现了一个使用样条函数的热潮,并推广到数据处理的许多问题中。 在实际生活中有许多计算问题对插值函数的光滑性有较高的要求,例如飞机机翼外形、发动机进、排气口都要求有连续的二阶导数,用三次样条绘制的曲线不仅有很好的光滑度,而且当节点逐渐加密时其函数值整体上能很好地逼近被插函数,相应的导数值也收敛于被插函数的导数值,不会发生“龙格现象”。 现在国内外学者对这方面的研究也越来越重视,根据我们的需要来解决不同的问题,而且函数的形式也在不断地改进,长期以来很多学者致力于样条插值的研究,对三次样条的研究已相当成熟。
对样条函数及其插值问题的一点认识 样条函数是计算数学以及计算机辅助设计几何设计的重要工具。1946年,I. J. Schoenberg 著名的关于一元样条函数的奠定性论文“Contribution to the problem of application of equidistant data by analytic functions ”发表,建立了一元样条函数的理论基础。自此以后,关于样条函数的研究工作逐渐深入。随着电子计算机技术的不断进步,样条函数的理论以及应用研究得到迅速的发展和广泛的应用。经过数学工作者的努力,已经形成了较为系统的理论体系。 所谓(多项式)样条函数,乃指具有一定光滑性的分段(分片)多项式。一元n 次且n -1阶连续可微的样条函数具有如下的表示式: 1()()()()N n n j j j s x p x c x x x +==+--∞<<+∞∑[] 011,00,01,,...,,(1),...,(),,...,,n n n n N n N N u un u u u u x x x x x S x x x x ++++ +≥??=??
MATLAB三次样条插值之三弯矩法 首先说这个程序并不完善,为了实现通用(1,2,…,n)格式解题,以及为调用追赶法程序,没有针对节点数在三个以下的情况进行分类讨论。希望能有朋友给出更好的方法。 首先,通过函数 sanwanj得到方程的系数矩阵,即追赶法方程的四个向量参数,接下来调用 追赶法(在intersanwj函数中),得到三次样条分段函数系数因子,然后进行多项式合并得 到分段函数的解析式,程序最后部分通过判断输入值的区间自动选择对应的分段函数并计算改 点的值。附:追赶法程序 chase %%%%%%%%%%%%%% function [newv,w,newu,newd]=sanwj(x,y,x0,y0,y1a,y1b) % 三弯矩样条插值 % 将插值点分两次输入,x0 y0 单独输入 % 边值条件a的二阶导数 y1a 和b的二阶导数 y1b,这里建议将y1a和y1b换成y2a和 y2b,以便于和三转角代码相区别 n=length(x);m=length(y); if m~=n error('x or y 输入有误,再来'); end v=ones(n-1,1);u=ones(n-1,1);d=zeros(n-1,1); w=2*ones(n+1); h0=x(1)-x0; h=zeros(n-1,1); for k=1:n-1 h(k)=x(k+1)-x(k); end v(1)=h0/(h0+h(1)); u(1)=1-v(1); d(1)=6*((y(2)-y(1))/h(1)-(y(1)-y0)/h0)/(h0+h(1)); % for k=2:n-1 v(k)=h(k-1)/(h(k-1)+h(k)); u(k)=1-v(k); d(k)=6*((y(k+1)-y(k))/h(k)-(y(k)-y(k-1))/h(k-1))/(h(k-1)+h(k)); end newv=[v;1]; newu=[1;u]; d0=6*((y(1)-y0)/h0-y1a)/h0;
告: Matlab中插值函数汇总和使用说明收藏 命令1 interp1 功能一维数据插值(表格查找。该命令对数据点之间计算内插值。它找出一元函数f(x在中间点的数值。其中函数f(x由所给数据决定。x:原始数据点 Y:原始数据点 xi:插值点 Yi:插值点 格式 (1yi = interp1(x,Y,xi 返回插值向量yi,每一元素对应于参量xi,同时由向量x 与Y 的内插值决定。参量x 指定数据Y 的点。 若Y 为一矩阵,则按Y 的每列计算。yi 是阶数为length(xi*size(Y,2的输出矩阵。 (2yi = interp1(Y,xi 假定x=1:N,其中N 为向量Y 的长度,或者为矩阵Y 的行数。 (3yi = interp1(x,Y,xi,method 用指定的算法计算插值: ’nearest’:最近邻点插值,直接完成计算; ’linear’:线性插值(缺省方式,直接完成计算;
’spline’:三次样条函数插值。对于该方法,命令interp1 调用函数spline、ppval、mkpp、umkpp。这些命令生成一系列用于分段多项式操作的函 数。命令spline 用它们执行三次样条函数插值; ’pchip’:分段三次Hermite 插值。对于该方法,命令interp1 调用函数p chip,用于对向量x 与y 执行分段三次内插值。该方法保留单调性与数据的外形; ’cubic’:与’pchip’操作相同; ’v5cubic’:在MATLAB 5.0 中的三次插值。 对于超出x 范围的xi 的分量,使用方法’nearest’、’linear’、’v5cubic’的插值算法,相应地将返回NaN。对其他的方法,interp1 将对超出的分量执行外插值算法。 (4yi = interp1(x,Y,xi,method,'extrap' 对于超出x 范围的xi 中的分量将执行特殊的外插值法extrap。 (5yi = interp1(x,Y,xi,method,extrapval 确定超出x 范围的xi 中的分量的外插值extrapval,其值通常取NaN 或0。 例1 1.>>x = 0:10; y = x.*sin(x; 2.>>xx = 0:.25:10; yy = interp1(x,y,xx; 3.>>plot(x,y,'kd',xx,yy 复制代码 例2 1.>> year = 1900:10:2010;
例1 设)(x f 为定义在[0,3]上的函数,有下列函数值表: 且2.0)('0=x f ,1)('3-=x f ,试求区间[0,3]上满足上述条件的三次样条插值函数)(x s 本算法求解出的三次样条插值函数将写成三弯矩方程的形式: ) ()6()() 6()(6)(6)(211123 13 1j j j j j j j j j j j j j j j j x x h h M y x x h h M y x x h M x x h M x s -- + -- + -+ -= +++++其中,方程中的系数 j j h M 6, j j h M 61+, j j j j h h M y )6(2- , j j j j h h M y ) 6(211++- 将由Matlab 代码中的变量Coefs_1、Coefs_2、Coefs_3以及Coefs_4的值求出。 以下为Matlab 代码: %============================= % 本段代码解决作业题的例1 %============================= clear all clc % 自变量x 与因变量y ,两个边界条件的取值 IndVar = [0, 1, 2, 3]; DepVar = [0, 0.5, 2, 1.5];
LeftBoun = 0.2; RightBoun = -1; % 区间长度向量,其各元素为自变量各段的长度h = zeros(1, length(IndVar) - 1); for i = 1 : length(IndVar) - 1 h(i) = IndVar(i + 1) - IndVar(i); end % 为向量μ赋值 mu = zeros(1, length(h)); for i = 1 : length(mu) - 1 mu(i) = h(i) / (h(i) + h(i + 1)); end mu(i + 1) = 1; % 为向量λ赋值 lambda = zeros(1, length(h)); lambda(1) = 1; for i = 2 : length(lambda) lambda(i) = h(i) / (h(i - 1) + h(i));
CENTRAL SOUTH UNIVERSITY 数值分析实验报告
三次样条插值方法的应用 一、问题背景 分段低次插值函数往往具有很好的收敛性,计算过程简单,稳定性好,并且易于在在电子计算机上实现,但其光滑性较差,对于像高速飞机的机翼形线船体放样等型值线往往要求具有二阶光滑度,即有二阶连续导数,早期工程师制图时,把富有弹性的细长木条(即所谓的样条)用压铁固定在样点上,在其他地方让他自由弯曲,然后沿木条画下曲线,称为样条曲线。样条曲线实际上是由分段三次曲线并接而成,在连接点即样点上要求二阶导数连续,从数学上加以概括就得到数学样条这一概念。下面我们讨论最常用的三次样条函数及其应用。 二、数学模型 样条函数可以给出光滑的插值曲线(面),因此在数值逼近、常微分方程和偏微分方程的数值解及科学和工程的计算中起着重要的作用。 设区间[]b ,a 上给定有关划分b x x n =<<<= 10x a ,S 为[]b ,a 上满足下面条件的函数。 ● )(b a C S ,2∈; ● S 在每个子区间[]1,+i i x x 上是三次多项式。 则称S 为关于划分的三次样条函数。常用的三次样条函数的边界条件有三种类型: ● Ⅰ型 ()()n n n f x S f x S ''0'',==。 ● Ⅱ型 ()()n n n f x S f x S ''''0'''',==,其特殊情况为()()0''''==n n x S x S 。 ● Ⅲ型 ()() 3,2,1,0,0==j x S x S n j j ,此条件称为周期样条函数。 鉴于Ⅱ型三次样条插值函数在实际应用中的重要地位,在此主要对它进行详细介绍。 三、算法及流程 按照传统的编程方法,可将公式直接转换为MATLAB 可是别的语言即可;另一种是运用矩阵运算,发挥MATLAB 在矩阵运算上的优势。两种方法都可以方便地得到结果。方法二更直观,但计算系数时要特别注意。这里计算的是方法一的程序,采用的是Ⅱ型边界条件,取名为spline2.m 。 Matlab 代码如下: function s=spline2(x0,y0,y21,y2n,x) %s=spline2(x0,y0,y21,y2n,x) %x0,y0 are existed points,x are insert points,y21,y2n are the second
摘要 本文细致的讲解了三次样条插值函数的产生及在实际中解决的问题,通过MATLAB的程序编写,可以将复杂的计算省去,直接的给出了三次样条插值的结果与实际结果间的误差,验证实际结果和理论值的一致性。避免了求解方程中的不必要计算,使求解效率得到显著的提高。 关键词插值函数三次样条插值 MATLAB
1 三次样条插值函数概论 当插值节点很多时,插值多项式的次数就会很高,这不仅增大了计算量,还会影响结果的精确度.虽然可以采用上述分段插值,但是主要缺点就是个分段接头处不光滑,插值函数的导数不连续,因此想构造这样的插值:既能分段的低次插值,又能保证接头处的光滑,就产生了三次样条插值函数. 1.1定义 设函数()f x 市区间[a,b]上的二次连续可微函数,在区间[a,b]上给处一个划分。设函数()f x 是区间[a,b]上的一个划分 011...n n a x x x x b -?=<<<<= 如果函数()S x 满足条件 (1)在每个小区间1[,]k k x x +(k=1,2,….,n )上()S x 是一个部超过m 次的多项式。 (2)在节点k x (k=1,2,….,n )处具有m-1阶的连续导数。 (3)()()(0,1,2,...) j j s x f x j n == 1.2三次样条差值函数的构造 由于三次样条插值我、函数s(x)的插值节点处的二阶导数存在,因此令各节点处的二阶导数为 ' ()(0,1,...,)k s x m k n == (1.01) 根据样条插值函数的定义,三次样条插值函数是s(x)在每一个小区间)1....,1,0](,[]1-=+n k x x k k 上市不超过三次的多项式。在每一个小区间 )1....,1,0](,[]1-=+n k x x k k 上,其二阶导数为线性函数,即 '' 11 11()k k k k k k k k x x x x s x m m x x x x ++++--=+-- (1.02) 对式(1.02)积分两次,则得到 k k k k k k k k k b x x a h x x m h x x m x s +-+-++=++)(6)(6)()(3 1 3 1 (1.03)
学习报告—— 三次样条函数插值问题的讨论 班级:数学二班 学号:152111033 姓名:刘楠楠
样条函数: 由一些按照某种光滑条件分段拼接起来的多项式组成的函数;最常用的样条函数为三次样条函数,即由三次多项式组成,满足处处有二阶连续导数。 一、三次样条函数的定义: 对插值区间[,]a b 进行划分,设节点011n n a x x x x b -=<< <<=,若 函数2()[,]s x c a b ∈在每个小区间1[,]i i x x +上是三次多项式,则称其为三次样条函数。如果同时满足()()i i s x f x = (0,1,2)i n =,则称()s x 为()f x 在 [,]a b 上的三次样条函数。 二、三次样条函数的确定: 由定义可设:101212 1(),[,] (),[,]()(),[,] n n n s x x x x s x x x x s x s x x x x -∈??∈?=???∈?其中()k s x 为1[,]k k x x -上的三次 多项式,且满足11(),()k k k k k k s x y s x y --== (1,2,,k n = 由2()[,]s x C a b ∈可得:''''''()(),()(),k k k k s x s x s x s x -+-+== 有''1()(),k k k k s x s x -++= ''''1()(),(1 ,2,,1)k k k k s x s x k n -+ +==-, 已知每个()k s x 均为三次多项式,有四个待定系数,所以共有4n 个待定系数,需要4n 个方程才能求解。前面已经得到22(1)42n n n +-=-个方程,因此要唯一确定三次插值函数,还要附加2个条件,一般上,实际问题通常对样条函数在端点处的状态有要求,即所谓的边界条件。 1、第一类边界条件:给定函数在端点处的一阶导数,即 ''''00(),()n n s x f s x f == 2、第二类边界条件:给定函数在端点处的二阶导数,即
数值计算方法作业 实验4.3 三次样条差值函数 实验目的: 掌握三次样条插值函数的三弯矩方法。 实验函数: dt e x f x t ? ∞ -- = 2 221)(π 实验内容: (1) 编程实现求三次样条插值函数的算法,分别考虑不同的边界条件; (2) 计算各插值节点的弯矩值; (3) 在同一坐标系中绘制函数f(x),插值多项式,三次样条插值多项式的曲线 比较插值结果。 实验4.5 三次样条差值函数的收敛性 实验目的: 多项式插值不一定是收敛的,即插值的节点多,效果不一定好。对三次样条插值函数如何呢?理论上证明三次样条插值函数的收敛性是比较困难的,通过本实验可以证明这一理论结果。 实验内容: 按照一定的规则分别选择等距或非等距的插值节点,并不断增加插值节点的个数。 实验要求: (1) 随着节点个数的增加,比较被逼近函数和三样条插值函数的误差变化情 况,分析所得结果并与拉格朗日插值多项式比较; (2) 三次样条插值函数的思想最早产生于工业部门。作为工业应用的例子,考
虑如下例子:某汽车制造商根据三次样条插值函数设计车门曲线,其中一 算法描述: 拉格朗日插值: 错误!未找到引用源。 其中错误!未找到引用源。是拉格朗日基函数,其表达式为:() ∏ ≠=--=n i j j j i j i x x x x x l 0) ()( 牛顿插值: ) )...()(](,...,,[.... ))(0](,,[)0](,[)()(1102101210100----++--+-+=n n n x x x x x x x x x x f x x x x x x x f x x x x f x f x N 其中????? ?? ?? ?????? --=--= --= -)/(]),...,[],...,[(]...,[..],[],[],,[)()(],[01102110x x x x x f x x x f x x x f x x x x f x x f x x x f x x x f x f x x f n n n n i k j i k j k j i j i j i j i 三样条插值: 所谓三次样条插值多项式Sn(x)是一种分段函数,它在节点Xi(a 非常类似前面的三弯矩法,这里的sanzhj函数和intersanzhj作用相当于前面的sanwanj和intersanwj,追赶法程序通用,代码如下。 %%%%%%%%%%%%%%%%%%% function [newu,w,newv,d]=sanzhj(x,y,x0,y0,y1a,y1b) % 三转角样条插值 % 将插值点分两次输入,x0 y0 单独输入 % 边值条件a的一阶导数 y1a 和b的一阶导数 y1b n=length(x);m=length(y); if m~=n error('x or y 输入有误,再来'); end v=ones(n-1,1); u=ones(n-1,1); d=zeros(n-1,1); w=2*ones(n-1,1); h0=x(1)-x0; h=zeros(n-1,1); for k=1:n-1 h(k)=x(k+1)-x(k); end v(1)=h0/(h0+h(1)); u(1)=1-v(1); d(1)=3*(v(1)*(y(2)-y(1))/h(1)+u(1)*((y(1)-y0))/h0); % for k=2:n-1 v(k)=h(k-1)/(h(k-1)+h(k)); u(k)=1-v(k); d(k)=3*(v(k)*(y(k+1)-y(k))/h(k)+u(k)*(y(k)-y(k-1))/h(k-1)); end d(1)=d(1)-u(1)*y1a; d(n-1)=d(n-1)-v(n-1)*y1b; newv=v(1:n-2,:); newu=u(2:n-1,:); %%%%%%%%%%%% function intersanzhj(x,y,x0,y0,y1a,y1b) % 三转角样条插值 例:已知一组数据点,编写一程序求解三次样条插值函数满足 并针对下面一组具体实验数据 0.25 0.3 0.39 0.45 0.53 0.5000 0.5477 0.6245 0.6708 0.7280 求解,其中边界条件为. 1)三次样条插值自然边界条件源程序: function s=spline3(x,y,dy1,dyn) %x为节点,y为节点函数值,dy1,dyn分别为x=0.25,0.53处的二阶导 m=length(x);n=length(y); if m~=n error('x or y输入有误') return end h=zeros(1,n-1); h(n-1)=x(n)-x(n-1); for k=1:n-2 h(k)=x(k+1)-x(k); v(k)=h(k+1)/(h(k+1)+h(k)); u(k)=1-v(k); end g(1)=3*(y(2)-y(1))/h(1)-h(1)/2*dy1; g(n)=3*(y(n)-y(n-1))/h(n-1)+h(n-1)/2*dyn; for i=2:n-1 g(i)=3*(u(i-1)*(y(i+1)-y(i))/h(i)+v(i-1)*(y(i)-y(i-1))/h(i-1)); end for i=2:n-1; A(i,i-1)=v(i-1); A(i,i+1)=u(i-1); end A(n,n-1)=1; A(1,2)=1; A=A+2*eye(n); M=zhuigf(A,g); %调用函数,追赶法求M fprintf('三次样条(三对角)插值的函数表达式\n'); syms X; for k=1:n-1 fprintf('S%d--%d:\n',k,k+1); s(k)=(h(k)+2*(X-x(k)))./h(k).^3.*(X-x(k+1)).^2.*y(k)... +(h(k)-2*(X-x(k+1)))./h(k).^3.*(X-x(k)).^2.*y(k+1)... +(X-x(k)).*(X-x(k+1)).^2./h(k).^2*M(k)+(X-x(k+1)).*... (X-x(k)).^2./h(k).^2*M(k+1); end s=s.'; s=vpa(s,4); %画三次样条插值函数图像 for i=1:n-1 X=x(i):0.01:x(i+1); st=(h(i)+2*(X-x(i)))./(h(i)^3).*(X-x(i+1)).^2.*y(i)... +(h(i)-2.*(X-x(i+1)))./(h(i)^3).*(X-x(i)).^2.*y(i+1)... +(X-x(i)).*(X-x(i+1)).^2./h(i)^2*M(i)+(X-x(i+1)).*... (X-x(i)).^2./h(i)^2*M(i+1); plot(x,y,'o',X,st); hold on End plot(x,y); grid on %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %调用的函数: %追赶法 function M=zhuigf(A,g) n=length(A); L=eye(n); U=zeros(n); for i=1:n-1 U(i,i+1)=A(i,i+1); end U(1,1)=A(1,1); for i=2:n L(i,i-1)=A(i,i-1)/U(i-1,i-1); U(i,i)=A(i,i)-L(i,i-1)*A(i-1,i); end Y(1)=g(1); for i=2:n Y(i)=g(i)-L(i,i-1)*Y(i-1); end M(n)=Y(n)/U(n,n); for i=n-1:-1:1 M(i)=(Y(i)-A(i,i+1)*M(i+1))/U(i,i); 告: Matlab中插值函数汇总和使用说明收藏 命令1 interp1 功能一维数据插值(表格查找)。该命令对数据点之间计算内插值。它找出一元函数f(x)在中间点的数值。其中函数f(x)由所给数据决定。x:原始数据点 Y:原始数据点 xi:插值点 Yi:插值点 格式 (1)yi = interp1(x,Y,xi) 返回插值向量yi,每一元素对应于参量xi,同时由向量x 与Y 的内插值决定。参量x 指定数据Y 的点。 若Y 为一矩阵,则按Y 的每列计算。yi 是阶数为length(xi)*size(Y,2)的输出矩阵。 (2)yi = interp1(Y,xi) 假定x=1:N,其中N 为向量Y 的长度,或者为矩阵Y 的行数。 (3)yi = interp1(x,Y,xi,method) 用指定的算法计算插值: ’nearest’:最近邻点插值,直接完成计算; ’linear’:线性插值(缺省方式),直接完成计算; ’spline’:三次样条函数插值。对于该方法,命令interp1 调用函数spline、ppval、mkpp、umkpp。这些命令生成一系列用于分段多项式操作的函 数。命令spline 用它们执行三次样条函数插值; ’pchip’:分段三次Hermite 插值。对于该方法,命令interp1 调用函数p chip,用于对向量x 与y 执行分段三次内插值。该方法保留单调性与数据的外形; ’cubic’:与’pchip’操作相同; ’v5cubic’:在MATLAB 5.0 中的三次插值。 对于超出x 范围的xi 的分量,使用方法’nearest’、’linear’、’v5cubic’的插值算法,相应地将返回NaN。对其他的方法,interp1 将对超出的分量执行外插值算法。 (4)yi = interp1(x,Y,xi,method,'extrap') 对于超出x 范围的xi 中的分量将执行特殊的外插值法extrap。 (5)yi = interp1(x,Y,xi,method,extrapval) 确定超出x 范围的xi 中的分量的外插值extrapval,其值通常取NaN 或0。 例1 1.>>x = 0:10; y = x.*sin(x); 2.>>xx = 0:.25:10; yy = interp1(x,y,xx); 3.>>plot(x,y,'kd',xx,yy) 复制代码 例2 1.>> year = 1900:10:2010; 2.>> product = [75.995 91.972 105.711 12 3.203 131.669 150.697 179.323 203.212 226.505 x0=[0 0.9211 1.8431 2.9497 3.8714 4.9781 5.9 7.0064 7.9286 8.9678 10.9542 12.0328 12.9544 13.8758 14.9822 15.9039 16.8261 17.9317 19.0375 19.9594 20.8392 22.9581 23.88 24.9869 25.9083]; >> >> y0=[14405 11180 10063 11012 8797 9992 8124 10160 8488 11018 19469 20196 18941 15903 18055 15646 13741 14962 16653 14496 14648 15225 15264 13708 9633]; >> x=0:0.1:25.9; >> y1=interp1(x0,y0,x,'spline'); >> pp1=csape(x0,y0); %样条插值工具箱函数 y2=ppval(pp1,x); %计算x对应的y值 pp2=csape(x0,y0,'second'); y3=ppval(pp2,x); xydata=[x',y1',y2',y3'] subplot(1,2,1) plot(x0,y0,'+',x,y1) title('Spline1') subplot(1,2,2) plot(x0,y0,'+',x,y2) title('Spline2') dx=diff(x); dy=diff(y2); dy_dx=dy./dx; dy_dx0=dy_dx(1) ytemp=y2(13<=x&x<=15); ymin=min(ytemp); xmin=x(y2==ymin); xymin_1315=[xmin,ymin] 一.介绍 二.程序框图 开始 输入未知数X及 (xi,yi),i=0,1,…,n 计算步长H[i] 计算λ、μ、d 根据边界条件,求 解相应的方程得到 M1,…, Mn 将M代入原方程, 得到分段函数 结束 三.源码 syms h n=9;%插入节点数,可以根据题目更改 h=2/(n+1); u=0.5; v=0.5; f=inline('1/(1+25*x.^2)');%输入函数,这个也可以根据题目更改g=inline('3/h*((c-b)/h-(b-a)/h)','a','b','c','h'); for i=1:n+2 x(1)=-1; x(i+1)=x(i)+2/(n+1); y(i)=f(x(i)); end for i=1:n d(i)=g(y(i),y(i+1),y(i+2),h); end A=zeros(n,n); for i=1:n A(i,i)=2; end for i=1:n-1 A(i,i+1)=u; A(i+1,i)=v; end B=zeros(n,1); for i=1:n B(i,1)=d(i) end C=inv(A)*B for i=1:n M(i)=C(i,1); end x=(-1:h/50:1); k=1./(1+25*x.^2); cs=spline(x,k); plot(x,k,'r.'); hold on; ezplot('1/(1+25*x^2)',[-1 1]); title('三次样条插值曲线和f(x)曲线') 四.结果 系数矩阵 弯矩M 分段函数不同次幂x对应的系数 三次样条插值函数与原函数 三次样条插值C/C++程序(自己整理的) 具体推导看书<<数值分析>> code: #include freopen("threeInsert.in", "r", stdin); scanf("%d", &n); for (i = 0; i <= n; i++) scanf("%lf%lf", &x[i], &y[i]); // scanf("%lf%lf", &m[0], &m[n]); for (i = 0; i <= n - 1; i++) h[i] = x[i + 1] - x[i]; //第一种边界条件 //alph[0] = 0; alph[n] = 1; beta[0] = 2 * m[0]; beta[n] = 2 * m[n]; //第二种边界条件 alph[0] = 1; alph[n] = 0; beta[0] = 3 * (y[1] - y[0]) / h[0]; beta[n] = 3 * (y[n] - y[n - 1] / h[n - 1]); for (i = 1; i <= n - 1; i++) { alph[i] = h[i - 1] / (h[i - 1] + h[i]); beta[i] = 3 * ((1 - alph[i]) * (y[i] - y[i - 1]) / h[i - 1] + alph[i] * (y[i + 1] - y[i]) / h[i]); } a[0] = - alph[0] / 2; b[0] = beta[0] / 2; for (i = 1; i <= n; i++) { a[i] = - alph[i] / (2 + (1 - alph[i]) * a[i - 1]); b[i] = (beta[i] - (1 - alph[i]) * b[i - 1]) / (2 + (1 - alph[i]) * a[i - 1]); } m[n + 1] = 0; for (i = n; i >= 0; i--) { m[i] = a[i] * m[i + 1] + b[i]; } scanf("%lf", &xx); for (i = 0; i < n; i++) { if (xx >= x[i] && xx <= x[i + 1]) break ; } printf("%lf\n", sunc(xx, i)); 三次样条插值多项式 ——计算物理实验作业四 陈万物理学2013级 主程序: clear,clc; format rat x = [1,4,9,16,25,36,49,64]; y = [1,2,3,4,5,6,7,8]; f1 = ; fn = 1/16; [a,b,c,d,M,S] = spline(x,y,f1,fn); 子程序1: function [a,b,c,d,M,S]=spline(x,y,f1,fn) % 三次样条插值函数 % x是插值节点的横坐标 % y是插值节点的纵坐标 % u是插值点的横坐标 % f1是左端点的一阶导数 % fn是右端点的一阶导数 % a是三对角矩阵对角线下边一行 % b是三对角矩阵对角线 % c是三对角矩阵对角线上边一行 % S是插值点的纵坐标 n = length(x); h = zeros(1,n-1); deltay = zeros(1,n); miu = zeros(1,n-1); lamda = zeros(1,n-1); d = zeros(1,n-1); for j = 1:n-1 h(j) = x(j+1)-x(j); deltay(j) = y(j+1)-y(j); end % 得到h矩阵 for j = 2:n-1 sumh = h(j-1) + h(j); miu(j) = h(j-1) / sumh; lamda(j) = h(j) / sumh; d(j) = 6*( deltay(j)/h(j)-(deltay(j-1)/h(j-1)))/sumh; end % 根据第一类边界条件,作如下规定 lamda(1) = 1; d(1) = 6*(deltay(1)/h(1)-f1)/h(1); miu(1) = 1; d(n) = 6*(fn-deltay(n-1)/h(n-1))/h(n-1); 并针对下面一组具体实验数据 求解,其中边界条件为. 解:Matlab计算程序为: clear clc x=[0.25 0.3 0.39 0.45 0.53] y=[0.5000 0.5477 0.6245 0.6708 0.7280] n=length(x); for i=1:n-1 h(i)=x(i+1)-x(i); end for i=1:n-2 k(i)=h(i+1)/(h(i)+h(i+1)); u(i)=h(i)/(h(i)+h(i+1)); end for i=1:n-2 gl(i)=3*(u(i)*(y(i+2)-y(i+1))/h(i+1)+k(i)*(y(i+1)-y(i))/h(i)); end g0=3*(y(2)-y(1))/h(1); g00=3*(y(n)-y(n-1))/h(n-1); g=[g0 gl g00]; g=transpose(g) k1=[k 1]; u1=[1 u]; Q=2*eye(5)+diag(u1,1)+diag(k1,-1) m=transpose(Q\g) syms X; for i=1:n-1 p1(i)=(1+2*(X-x(i))/h(i))*((X-x(i+1))/h(i))^2*y(i); p2(i)=(1-2*(X-x(i+1))/h(i))*((X-x(i))/h(i))^2*y(i+1); p3(i)=(X-x(i))*((X-x(i+1))/h(i))^2*m(i); p4(i)=(X-x(i+1))*((X-x(i))/h(i))^2*m(i+1); p(i)=p1(i)+p2(i)+p3(i)+p4(i); p(i)=simple(p(i)); end s1=p(1) s2=p(2) s3=p(3) s4=p(4) for k=1:4 数值分析作业-三次样 条插值 数值计算方法作业 实验4.3 三次样条差值函数 实验目的: 掌握三次样条插值函数的三弯矩方法。 实验函数: dt e x f x t ? ∞ -- =2 221)(π 求f(0.13)和f(0.36)的近似值 实验内容: (1) 编程实现求三次样条插值函数的算法,分别考虑不同的边界条件; (2) 计算各插值节点的弯矩值; (3) 在同一坐标系中绘制函数f(x),插值多项式,三次样条插值多项式的曲 线比较插值结果。 实验4.5 三次样条差值函数的收敛性 实验目的: 多项式插值不一定是收敛的,即插值的节点多,效果不一定好。对三次样条插值函数如何呢?理论上证明三次样条插值函数的收敛性是比较困难的,通过本实验可以证明这一理论结果。 实验内容: 按照一定的规则分别选择等距或非等距的插值节点,并不断增加插值节点的个数。 实验要求: (1) 随着节点个数的增加,比较被逼近函数和三样条插值函数的误差变化情 况,分析所得结果并与拉格朗日插值多项式比较; (2) 三次样条插值函数的思想最早产生于工业部门。作为工业应用的例子, 考虑如下例子:某汽车制造商根据三次样条插值函数设计车门曲线,其中一段数据如下: k x 0 1 2 3 4 5 6 7 8 9 10 k y 0.0 0.79 1.53 2.19 2.71 3.03 3.27 2.89 3.06 3.19 3.29 k y ' 0.8 0.2 算法描述: 拉格朗日插值: 其中 是拉格朗日基函数,其表达式为:() ∏ ≠=--=n i j j j i j i x x x x x l 0 ) ()( 牛顿插值: ) )...()(](,...,,[.... ))(0](,,[)0](,[)()(1102101210100----++--+-+=n n n x x x x x x x x x x f x x x x x x x f x x x x f x f x NMATLAB三次样条插值之三转角法
三次样条插值自然边界条件
Matlab中插值函数汇总和使用说明
三次样条插值函数matlab程序绝不坑爹
三次样条插值函数
三次样条插值的C程序(很全啊)
三次样条插值多项式matlab
三次样条插值函数的Matlab代码
数值分析作业-三次样条插值教学提纲