
1.5.1函数y=Asin(ωx+φ)的图象(-)
一、教学目标
1. 能够将sin y x =的图象通过平移、伸缩等变换得到y=Asin(ωx+φ)的图象;
2. 能够正确理解参数,,A ω?对函数y=Asin(ωx+φ)的图象的影响;
3. 会用“五点法”画函数y=Asin(ωx+φ)的简图 二、教学过程
(一)课前任务:
请学生利用“五点法”在同一直角坐标系中画出sin y x =,1
sin 2,sin 2
y x y x ==三者的图象;(课堂中用投影仪投影) (二)新课讲授
例1画出函数y=2sinx x ∈R ;y=
2
1
sinx x ∈R 的图象(简图) 解:画简图,我们用“五点法”
∵这两个函数都是周期函数,且周期为2π ∴我们先画它们在[0,2π]上的简图列表:
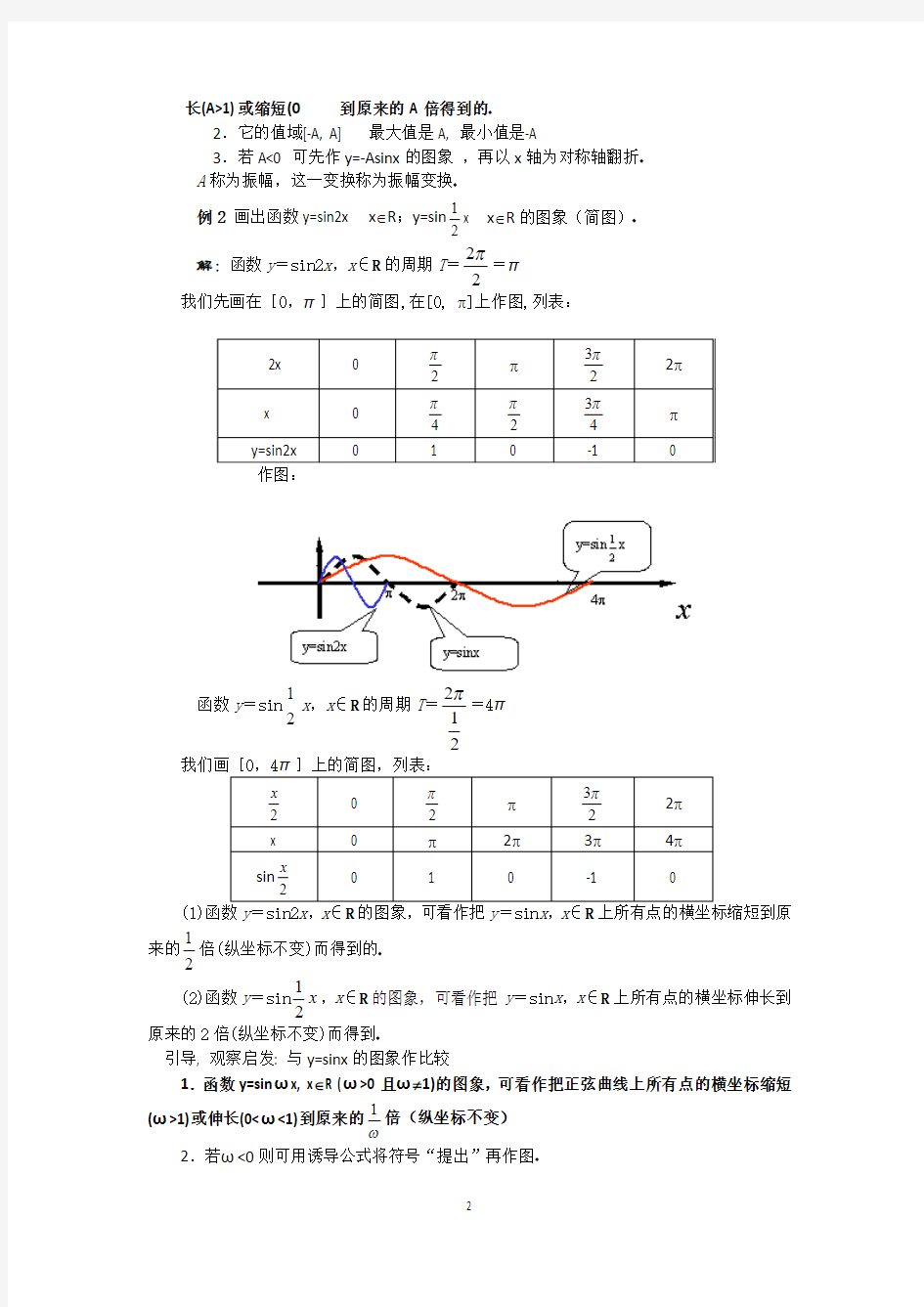
作图:
(1)y =2sin x ,x ∈R 的值域是[-2,2]
图象可看作把y =sin x ,x ∈R 上所有点的纵坐标伸长到原来的2倍而得(横坐标不变)
(2)y =
21sin x ,x ∈R 的值域是[-21,2
1] 图象可看作把y =sin x ,x ∈R 上所有点的纵坐标缩短到原来的
2
1
倍而得(横坐标不变) 引导,观察,启发:与y=sinx 的图象作比较,结论:
1.y=Asinx ,x ∈R(A>0且A ≠1)的图象可以看作把正数曲线上的所有点的纵坐标伸
长(A>1)或缩短(0 2.它的值域[-A, A] 最大值是A, 最小值是-A 3.若A<0 可先作y=-Asinx 的图象 ,再以x 轴为对称轴翻折 A 称为振幅,这一变换称为振幅变换 例2 画出函数y=sin2x x ∈R ;y=sin 2 1 x x ∈R 的图象(简图) 解:函数y =sin2x ,x ∈R 的周期T = 2 2π =π 我们先画在[0,π]上的简图,在[0, π]上作图,列表: 函数y =sin 2 1x ,x ∈R 的周期T =2 12π=4π 我们画[0,4π]上的简图,列表: (1)函数=sin2,∈R 的图象,可看作把=sin ,∈R 上所有点的横坐标缩短到原来的 2 1 倍(纵坐标不变)而得到的 (2)函数y =sin x 2 1 ,x ∈R 的图象,可看作把y =sin x ,x ∈R 上所有点的横坐标伸长到 原来的2倍(纵坐标不变)而得到 引导, 观察启发: 与y=sinx 的图象作比较 1.函数y=sin ωx, x ∈R (ω>0且ω≠1)的图象,可看作把正弦曲线上所有点的横坐标缩短 (ω>1)或伸长(0<ω<1)到原来的 ω 1 倍(纵坐标不变) 2.若ω<0则可用诱导公式将符号“提出”再作图 ω决定了函数的周期,这一变换称为周期变换 牛刀小试:sin()3y x π=+ 的图象经过如何变换可得到sin(2)3 y x π =+的图象? 解析: sin()3y x π=+1 2???????→横坐标缩短为原来的倍纵坐标不变 sin(2)3 y x π=+ 令30,,,,2322x ππ+=πππ 如:,33x t x t ππ +==- 令320,,,,2322x ππ+=πππ 如:12,2,()3323 x t x t x t πππ +==-=- 例3 在同一直角坐标系中画出函数y =sin(x +3π),x ∈R ,y =sin(x -4 π ),x ∈R 的简图解:列表 描点画图: 引导,观察,启发: (1)函数y =sin(x +3π),x ∈R 的图象可看作把正弦曲线上所有的点向左平行移动3 π 个单位长度而得到 (2)函数y =sin(x - 4π),x ∈R 的图象可看作把正弦曲线上所有点向右平行移动4 π 个单位长度而得到 一般地,函数y =sin(x +?),x ∈R(其中?≠0)的图象,可以看作把正弦曲线上所有点向左(当?>0时)或向右(当?<0时)平行移动|?|个单位长度而得到 (用平移法注意讲清 方向:“加左”“减右”) y =sin(x +?)与y =sin x 的图象只是在平面直角坐标系中的相对位置不一样,这一变换称为相位变换 牛刀小试:sin 2y x =的图象经过怎么样的变换可得到sin(2)3 y x π =+ 的图象? 解析:sin 2y x =6 π ??????? →向左平移个单位长度 sin(2)3 y x π =+ sin(2)=sin[2(x+)]36y x ππ=+ 令320,,,,222x π=πππ 如:2,2t x t x == 令320,,,,2322x ππ+=πππ 如: 12,2,3326 x t x t x t πππ +==-=-, (三)例题讲解 例1利用变换作图法画出函数1 2sin 3 6y x π??=- ???的简图 法一: 先平移,再伸缩 sin y x =36 1 sin sin 636y x y x π ππ???????????→=-???????→=- ? ????? 向右平移个单位长度 横坐标伸长为原来的倍纵坐标不变 2???????→纵坐标伸长为原来的倍 横坐标不变 12sin 3 6y x π??=- ??? 法二:先伸缩,再平移 sin y x =32 11sin sin[()]332 y x y x π π??????? →=???????→=-向右平移个单位长度横坐标伸长为原来的倍 纵坐标不变 2???????→纵坐标伸长为原来的倍 横坐标不变 12sin 36y x π??=- ??? 课堂练习:P 55 第2题 思考:sin y x =的图象经过如何变换可得1 2cos 2 4y x π??=+ ???的图象? 课堂小结: 课后作业: P58 2(3)用两种方法画出图象 第7讲 函数的图象 一、选择题 1.为了得到函数y =2x -2的图象,可以把函数y =2x 图象上所有的点( ) A.向右平行移动2个单位长度 B.向右平行移动1个单位长度 C.向左平行移动2个单位长度 D.向左平行移动1个单位长度 解析 因为y =2x -2=2(x -1),所以只需将函数y =2x 的图象上所有的点向右平移1个单位长度即可得到y =2(x -1)=2x -2的图象. 答案 B 2.小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间后,为了赶时间加快速度行驶,与以上事件吻合得最好的图象是( ) 解析 小明匀速运动时,所得图象为一条直线,且距离学校越来越近,排除 A.因交通堵塞停留了一段时间,与学校的距离不变,排除D.后来为了赶时间加快速度行驶,排除 B.故选 C. 答案 C 3.(2015·浙江卷)函数f (x )=? ?? ??x -1x cos x (-π≤x ≤π且x ≠0)的图象可能为( ) 解析 (1)因为f (-x )=? ????-x +1x cos(-x )=-? ?? ??x -1x cos x =-f (x ),-π≤x ≤π且x ≠0,所以函数f (x )为奇函数,排除A ,B.当x =π时,f (x )=? ?? ??π-1πcos π<0,排除C ,故选D. 答案 D 4.(2017·桂林一调)函数y =(x 3-x )2|x |的图象大致是( ) 解析 由于函数y =(x 3-x )2|x |为奇函数,故它的图象关于原点对称.当0 近五年高考函数图像题汇总 1(2020全国卷1理5)某校一个课外学习小组为研究某作物种子的发芽率y 和温度x (单位:°C )的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(,)(1,2,,20)i i x y i =得到下面的散点图: 由此散点图,在10°C 至40°C 之间,下面四个回归方程类型中最适宜作为发芽率y 和温度x 的回归方程类型 的是( ) A. y a bx =+ B. 2y a bx =+ C. e x y a b =+ D. ln y a b x =+ 2(2020天津卷理3)函数241x y x = +的图象大致为( ) A . B. C. D. 3(2020江苏卷理4)函数y =x cos x +sin x 在区间[–π,+π]的图象大致为( ) A. B. C. D. 4.(2019全国Ⅰ理5)函数f (x )=2sin cos ++x x x x 在[,]-ππ的图像大致为 A . B . C . D . 5.(2019全国Ⅲ理7)函数3 222 x x x y -=+在[]6,6-的图像大致为 A . B . C . D . 6.(2019浙江6)在同一直角坐标系中,函数y =1x a ,y =log a (x +12),(a >0且a ≠1)的图像可能是 A. B. C. D. 7.(2018全国卷Ⅱ)函数2()--=x x e e f x x 的图像大致为 8.(2018全国卷Ⅲ)函数42 2y x x =-++的图像大致为 9.(2018浙江)函数||2sin 2x y x =的图象可能是 A . B . C . D . 10.(2016全国I) 函数2|| 2x y x e =-在[–2,2]的图像大致为 A . B . C . D . 几种特殊函数的图象及应用 函数学习中,除了二次函数、指数函数、对数函数、三角函数等常见函数外,还有一类分式函 数、绝对值函数也常常出现.这类函数问题,虽说借助于导数等工具也能解决,但如果能够掌握这 类函数的基本图象特征,便能起到事半功倍的效果.本文介绍四个最常见的函数模型及其图象特征, 并在实际问题中借助于换元、分离变量等手段将函数表达式转化为这几个函数模型之一,根据函数 图象,迅速找到解决问题的切入点和解题思路. 先了解这四个基本函数: ①函数y = 1 (图1);②函数y = x + 1 (图2); xx 从函数的图象很容易看出函数的对称性、单调性、值域等性质,下面看它们各自的应用. c 1 1 一、形如y =a + c (c 0)的函数可利用函数y = 1 (或y = - 1 )的性质.当c 0时,函 x -b x x cc 数y =a +c 的图象可看成由函数y = c 的图象左右、上下平移得到,在区间(-,b )、(b ,+)上 x -b x cc 分别递减;当c 0时,函数y = a + c 的图象可看成由函数y = c 的图象左右、上下平移得到, x -b x 在区间(- ,b )、(b ,+)上分别递增. 例1 函数 f (x )= lg kx -1(k 0)在 10,+ )上单调递增,求实数k 的取值范围. x -1 kx - 1 kx - 1 解析:令f (x )=lg t ,t = kx -1 ,由复合函数单调性及题意可得:t = kx -1 需满足两个条件:① x - 1 x - 1 t 在 x 10,+ )上单调递增;②t 0在 x 10,+ )上恒成立. kx - 1 k - 1 考虑t = = k + (x 1) x - 1 x - 1 当 k = 1 时, f (x ) = 0 不合题意,舍去; 当k 1时,t 在(- ,1),(1,+)上均递减,不合题意,舍去; 当0 k 1时,t 在(-,1),(1,+ )上均递增, t 也在 10,+ )上递增,且当x =10时, 图 4 ). 第7讲 函数的图象 [考纲解读] 1.掌握基本初等函数的图象特征,能熟练地运用基本初等函数的图象解决问题. 2.掌握作函数图象的常用方法:①描点法;②平移法;③对称法.(重点) 3.能运用函数图象理解和研究函数的性质、解决方程解的个数或与不等式相关的问题.(难点) [考向预测] 从近三年高考情况来看,本讲一直是高考中的热点.预测2021年高考将会考查:①已知函数解析式识别函数的图象;②利用函数图象求函数零点的个数、解不等式或求参数的取值范围.题型以客观题为主,在解答题中也会用到数形结合的思想进行求解. 1.利用描点法作函数图象的流程 2.变换法作图 (1)平移变换 提醒:对于平移,往往容易出错,在实际判断中可熟记口诀:左加右减,上加下减. (2)对称变换 ①y =f (x )――→关于x 轴对称y =□03 -f (x ); ②y =f (x )――→关于y 轴对称y =□04f (-x ); ③y =f (x )――→关于原点对称y =□05 -f (-x ); ④y =a x (a >0且a ≠1)―――――――→关于直线y =x 对称 y =□06log a x (a >0且a ≠1). (3)翻折变换 ①y =f (x )―――――――――→保留x 轴上方图象 将x 轴下方图象翻折上去 y =□07|f (x )|; ②y =f (x ) ―――――――――→保留y 轴右边图象,并作其 关于y 轴对称的图象 y =□ 08f (|x |). (4)伸缩变换 y =□09f (ax ); ②y =f (x )―――――――――――――――――→a >1,纵坐标伸长为原来的a 倍,横坐标不变 0 高三复习专题函数的图 像含答案 HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】 专题四函数的图像、函数与方程 一、基本初等函数 1.五种幂函数的性质 2. 3. 考点一:知式选图 1.【2017课标1,文8】函数sin21cos x y x = -的部分图像大致为 A . B . C . D . 2.【2017课标3,文7】函数2 sin 1x y x x =++ 的部分图像大致为( ) A B C D 3.(2016·浙江,3,易)函数y =sin x 2的图象是( ) 解.D [考向1]y =sin x 2为偶函数,排除A ,C.当x =π时,y =sin x 2=0,据此可排除B ,故选D. 4.(2016·课标Ⅰ,9,中)函数y =2x 2-e |x |在[-2,2]的图象大致为( ) 5.(2014·浙江,8,易)在同一直角坐标系中,函数f (x )=x a (x ≥0),g (x )=log a x 的图象可能是( ) A B C D 5.D [考向1]方法一:分a >1,0<a <1两种情形讨论. 当a >1时,y =x a 与y =log a x 均为增函数,但y =x a 递增较快,排除C ; 当0<a <1时,y =x a 为增函数,y =log a x 为减函数,排除A ,由于y =x a 递增较慢,所 以选D. 6.(2012·湖北,6,中)已知定义在区间[0,2]上的函数y =f (x )的图象如图所示,则y =-f (2-x )的图象为( ) (排除法):当x =1时,y =-f (1)=-1,排除A ,C ;当x =2时,y =-f (0)=0,排除D.故选B. 7.(2015·浙江,5)函数f (x )=? ????x -1x cos x (-π≤x ≤π且x ≠0)的图象可能为( ) 8.(2013·山东,9)函数y =x cos x +sin x 的图象大致为( ) 解.D [考向1]y =sin x 2为偶函数,排除A ,C.当x =π时,y =sin x 2=0,据此可排除B ,故选D. 9. (2016·山东省实验中学模拟,3)函数f (x )= sin x ln (x +2) 的图象可能是( ) 解.A [考向1]由题意知???x +2>0, ln (x +2)≠0,∴x >-2且x ≠-1,故排除B ,D. 由f (1)=sin 1 ln 3>0,可排除C ,故选A. 10.函数y =? ?? ?? 12|x +1|的大致图象为( ) 解析:选B 该函数图象可以看作偶函数y =? ?? ?? 12|x |的图象向左平移1个单位得 到的. 11.函数y =log 2|x | x 的大致图象是( ) A B C D 解析:选C 由于log 2|-x |-x =-log 2|x |x ,所以函数y =log 2|x | x 是奇函数,其图象 关于原点对称.当x >0时,对函数求导可知函数图象先增后减,结合选项可知选C. 12.【2017课标1,文9】已知函数()ln ln(2)f x x x =+-,则 高中数学常见函数图像1. 2.对数函数: 3.幂函数: 定义形如αx y=(x∈R)的函数称为幂函数,其中x是自变量,α是常数. 图像 性质过定点:所有的幂函数在(0,) +∞都有定义,并且图象都通过点(1,1).单调性:如果0 α>,则幂函数的图象过原点,并且在[0,) +∞上为增函数.如果0 α<,则幂函数的图象在(0,) +∞上为减函数,在第一象限内,图象无限接近x轴与y轴. 函数 sin y x = cos y x = tan y x = 图象 定义域 R R ,2x x k k ππ??≠+∈Z ???? 值域 []1,1- []1,1- R 最值 当 22 x k π π=+ () k ∈Z 时, max 1y =; 当22 x k π π=- ()k ∈Z 时,min 1y =-. 当()2x k k π =∈Z 时, max 1y =; 当2x k π π=+ ()k ∈Z 时,min 1y =-. 既无最大值也无最小值 周期性 2π 2π π 奇偶性 奇函数 偶函数 奇函数 单调性 在 2,222k k ππππ? ?-+???? ()k ∈Z 上是增函数;在 32,222k k π πππ??++???? ()k ∈Z 上是减函数. 在[]() 2,2k k k πππ-∈Z 上 是 增 函 数 ; 在 []2,2k k πππ+ ()k ∈Z 上是减函数. 在,2 2k k π ππ π? ? - + ?? ? ()k ∈Z 上是增函数. 对称性 对称中心 ()(),0k k π∈Z 对称轴 ()2 x k k π π=+ ∈Z 对称中心 (),02k k ππ??+∈Z ?? ? 对称轴()x k k π =∈Z 对称中心(),02k k π?? ∈Z ??? 无对称轴 函数的定义: 在一个变化过程中,如果有两个变量x 与y ,并且对于x 的每一个确定的值,y 都有 _______________确定的值与其对应,x 是___________量,y 是x 的函数。 函数三种表示方法:_____________________、__________________、_______________。 画函数图象的步骤:_____________________、__________________、_______________。 1.若式子 有意义,则x 的取值范围是 . 2.函数1 1 y x = -中,自变量x 的取值范围是 . 3在实数范围内有意义,那么x 的取值范围是 . 4.函数1 2 y x = -中,自变量x 的取值范围是 . 5.在函数y =x 的取值范围是 . 6.函数y x 的取值范围是 A.1 x B. 1x < C. x ≤1 D. x ≥1 7. 下图中,不是函数图象的是 A B C D 8.小明从家到学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车沿着公路匀速行驶一段时间后到达学校,小明从家到学校行驶路程s (m )与时间t (min )的大致图象是( ) A . B . C . D . 9.如图是某一天北京与上海的气温T (单位:C ?)随时间t (单位:时)变化的图象.根据图中信息,下列说法错误..的是 A .12时北京与上海的气温相同 B .从8时到11时,北京比上海的气温高 C .从4时到14时,北京、上海两地的气温 逐渐升高 D .这一天中上海气温达到4C ?的时间大约在上午10时 10.德国心理学家艾宾浩斯(H.Ebbinghaus )研究发现,遗忘在学习之后立即开始,遗忘是有规律的.他用无意义音节作记忆材料,用节省法计算保持和遗忘的数量.通过测试,他得到了一些数据,根据这些数据绘制出一条曲线,即著名的艾宾浩斯记忆遗忘曲线,如图.该曲线对人类记忆认知研究产生了重大影响.小梅观察曲线,得出以下四个结论: ①记忆保持量是时间的函数 ②遗忘的进程是不均匀的,最初遗忘速度快,以后逐渐减慢 ③学习后1小时,记忆保持量大约为40% ④遗忘曲线揭示出的规律提示我们学习后要及时复习 其中错误的结论是 A .① B .② C .③ D .④ 11.某洗衣机在洗涤衣服时经历了注水、清洗、排水三个连续过程(工作前洗衣机内无水),在这三个过程中洗衣机内水量y (升)与时间x (分)之间的函数关系对应的图象大致为( ) 12.如图1所示,四边形ABCD 为正方形,对角线AC ,BD 相交于点O ,动点P 在正方形的 边和对角线上匀速运动. 如果点P 运动的时间为x ,点P 与点A 的距离为y ,且表示 y 与x 的函数关系的图象大致如图2所示,那么点P 的运动路线可能为 图1 图2 O B C D A 第7讲 函数的图象及其应用 基础巩固题组 (建议用时:40分钟) 一、填空题 1.把函数f (x )=(x -2)2+2的图象向左平移1个单位长度,再向上平移1个单位长度,所得图象对应的函数解析式是________. 解析 把函数f (x )=(x -2)2+2的图象向左平移1个单位长度,得y =[(x +1)-2]2+2=(x -1)2+2,再向上平移1个单位长度,得y =(x -1)2+2+1=(x -1)2+3. 答案 y =(x -1)2+3 2.函数f (x )=x +1 x 的图象的对称中心为________. 解析 f (x )=x +1x =1+1 x ,故f (x )的对称中心为(0,1). 答案 (0,1) 3.已知f (x )=? ???? 13x ,若f (x )的图象关于直线x =1对称的图象对应的函数为g (x ), 则g (x )的表达式为________. 解析 在函数g (x )的图象上任取一点(x ,y ),这一点关于x =1的对称点为(x 0,y 0),则??? x 0=2-x , y 0=y . ∴y =? ???? 132-x =3x -2. 答案 g (x )=3x -2 4.函数y =(x -1)3+1的图象的对称中心是________. 解析 y =x 3的图象的对称中心是(0,0),将y =x 3的图象向上平移1个单位,再向右平移1个单位,即得y =(x -1)3+1的图象,所以对称中心为(1,1). 答案 (1,1) 5. 设奇函数f (x )的定义域为[-5,5].若当x ∈[0,5]时,f (x )的图象如图,则不等式f (x )<0的解集是________. 解析 利用函数f (x )的图象关于原点对称.∴f (x )<0的解集为(-2,0)∪(2,5). 答案 (-2,0)∪(2,5) 6.若函数f (x )在区间[-2,3]上是增函数,则函数f (x +5)的单调递增区间是________. 解析 ∵f (x +5)的图象是f (x )的图象向左平移5个单位得到的. ∴f (x +5)的递增区间就是[-2,3]向左平移5个单位得到的区间[-7,-2] 答案 [-7,-2] 7.若方程|ax |=x +a (a >0)有两个解,则a 的取值范围是________. 解析 画出y =|ax |与y =x +a 的图象,如图.只需a >1. 答案 (1,+∞) 8.(2013·泰州模拟)已知函数f (x )=??? log 2x (x >0),2x (x ≤0),且关于x 的方程f (x )-a =0有 两个实根,则实数a 的范围是________. 解析 当x ≤0时,0<2x ≤1,所以由图象可知要使方程f (x )-a =0有两个实 第7 讲函数的图象 最新考纲 1.理解点的坐标与函数图象的关系; 2.会利用平移、对称、伸缩变换,由一个函数图象得到另一个函数的图象; 3. 会运用函数图象理解和研究函数的性质,解决方程解的个数与不等式的解的问题. 知识梳理 1.函数图象的作法 (1) 描点法作图:通过列表、描点、连线三个步骤,画出函数图象.用描点法在选点时往往选取特殊点,有时也可利用函数的性质( 如单调性、奇偶性、周期性) 画出图象. (2) 图象变换法作图:一个函数的图象经过适当的变换,得到另一个与之有关的函数图象,在高考中要求学生掌握三种变换(平移变换、伸缩变换、对称变换) . 2.函数图象间的变换 (1) 平移变换 对于平移,往往容易出错,在实际判断中可熟记口诀:左加右减,上加下减. (2) 对称变换 (3) 伸缩变换 断自测 精彩PPT 展示 图象相同.(X) ⑵ 函数y = f (x )与y = — f (x )的图象关于原点对称.(X) ⑶ 若函数y = f (x )满足f (1 + x ) = f (1 — x ),则函数f (x )的图象关于直线 x = 1对 称.(V) y =f (x ) 各点横坐标变纵坐标不变 a a a > 0 倍y = f (ax ). 横坐标不变 i A y = f (x ) 各点纵坐标变为原来苗 A > 0 倍 y = Af (x ). 判 断正误 括号内打 或 “x”) (1)当x € (0 ,+s )时,函数 y = | f (x )| 与 y = f (| x |)的 ⑷若函数y = f(x)满足f(x—1) = f(x + 1),则函数f(x)的图象关于直线x= 1对称. ( X) (5)将函数y = f( —x)的图象向右平移1个单位得到函数y= f ( —x—1)的图象.(X) 2. (2014 ?浙江卷)在同一直角坐标系中,函数f (x) = x a(x>0), g( x) = log a x的图象可 能是( ) 解析■/ a>0,且1,二f (x) = x a在(0 ,+s)上单调递增,二排除A;当0v a v 1 或a> 1时,B, C中f(x)与g(x)的图象矛盾,故选D. 答案D 3. (2014 ?山东卷)已知函数y = log a(x+ c)( a, c为常数,其中a> 0, a* 1)的图象如 图,则下列结论成立的是( ) 函数图象B1 .函数y = a| x | (a > 1)的图象是( ) B() B3.当a>1时,函数y=log a x和y=(1-a)x的图象只可能是() A4.已知y=f(x)与y=g(x)的图象如图所示 则函数F(x)=f(x)·g(x)的图象可以是(A) B5.函数(1) || x xa y a x =>的图像大致形状是()D A B C D D 7.函数x x y cos -=的部分图象是( ) A 8.若函数f(x)=x 2+b x +c 的图象的顶点在第四象限,则函数f /(x)的图象是 ( ) A 9.一给定函数) (x f y =的图象在下列图中,并且对任意)1,0 (1∈a ,由关系式) (1n n a f a =+得到的数列}{n a 满足)(* 1N n a a n n ∈>+,则该函数的图象是 ( ) A B C D C 10.函数y=kx+k 与y=x k 在同一坐标系是的大致图象是( ) A D C A 12. 当a >1时,在同一坐标系中,函数y =a - x 与y =log a x 的图像( ) B 13. 函数1 1 1--=x y 的图象是( ) D 14.函数b x a x f -=)(的图象如图,其中a 、b 为常数,则下列结论正确的是 ( ) A .0,1<>b a B .0,1>>b a C .0,10>< 函数的概念与图象5 单调性 [知识要点] 1.会判断简单函数的单调性(1)直接法 (2)图象法 2.会用定义证明简单函数的单调性:(取值,作差,变形,定号,判断) 3.函数的单调性与单调区间的联系与区别 [简单练习] 1.画出下列函数图象,并写出单调区间: ⑴ ⑵ 2.(1)判断在(0,+∞)上是增函数还是减函数。 (2)判断在( —∞,0)上是增函数还是减函数。 3.证明在定义域上是减函数。 4.下列函数中,在(0,2)上为增函数的是( ) A.y= B. y=2x-1 C. y=1-x D.y= 5.讨论函数的单调性。 6.函数y= -1的单调 递 区间为 。 7.已知f(x)在区间[a,c]上单调递减,在区间[c,d]上单调递增,则f(x)在[a,d] 上最小值为 。 22+-=x y )0(1 ≠=x x y 1)(2-=x x f x x x f 2)(2+-=x x f -=)(x 12)12(-x 3x y =x 1 8.填表已知函数f(x),的定义域是F ,函数g(x)的定义域是G ,且对于任意的,,试根据下表中所给的条件,用“增函数”、“减函数”、“不能确定”填空。 [巩固提高] 1.已知f (x )=(2kx+1x+1在(-,+)上是减函数,则( ) A.k > B.k < C.k >- D. k <- 2.在区间(0,+∞)上不是增函数的是 ( ) A.y=2x+1 B.y=3 +1 C.y= D. y=3+x +1 3.若函数f (x )=+2(a-1)x+2在区间(-,4)上为增函数,则实数a 的 取值范围是 ( ) A.a -3 B.a -3 C.a 3 D.a 3 4.如果函数f (x )是实数集R 上的增函数,a 是实数,则 ( ) A.f ()>f (a+1) B.f (a )< f (3a ) C.f (+a )>f () D.f (-1)<f () 5. 若f(x)是R 上的增函数,对于实数a,b,若a+b >0,则有 ( ) A. f(a)+ f(b) >f(-a)+ f(-b) B.f(a)+ f(b) <f(-a)+ f(-b) C. f(a)- f(b) >f(-a)- f(-b) D.f(a)- f(b) <f(-a)-f(-b) 6.函数y=的单调减区间为 。 7.函数y=+的增区间为 减区间为 。 G x ∈F x g ∈)(∞∞21212121 2x x 2 2x 2x ∞≤≥≤≥2a 2a 2a 2a 2a 11 +x 1+x x -2 一、幂函数图像的分布规律 幂函数图像的分布规律可用“一全有、二一偶、三一奇、四全无”来说明。 1.“一全有”:指所有幂函数的图像在第一象限都出现, 分布情况如图1所示,其特点如下:①抓住三条特征 线:直线x=1,y=x ,y=1把幂函数的图像分为三个区 域,这三个区域对应着幂函数y=x α在α<0,0<α<1, α>1时的图像;②第一象限内幂函数y=x α图像的区 域分布情况为:在直线x=1的右边,α越大,图像越高,越趋向于直线x=1;在直线x=1的右边,α越小,其图像越低,越趋向于x 轴。 2.“二一偶”:指当幂函数为偶函数时,其图像关于y 轴对称,即幂函数的图像出现在第一、第二象限。 3.“三一奇”:指当幂函数为奇函数时,其图像关于原点对称,即幂函数的图像出现在第一、第三象限。 4.“四必无”:指由定义,知幂函数的图像不可能出现在第四象限。 二、幂函数图像的应用 1.识别图像 例1.图2中 的曲线是幂函数y=x α在第一象限的图像,已知α取±2,±12四个值,则其相应于曲线C 1,C 2,C 3,C 4的α依次为( ) A.-2,-12,12,2 B.2,12,-12,-2 C.- 12,-2,2,12 D.2,12,-2,-12 解:根据幂函数的图像特点,立即可以断定相应于曲线C 1,C 2,C 3,C 4的α值排序是由大到小,故选B 。 2.用于判断方程的个数 例2.方程x 2=2x 的根的个数为( ) A.1 B.2 C.3 D. 解:令f(x)=x2,g(x)=2x,在同一坐标平面内作出这两个函数的图象,如图三所示,由图可知,交点有三个,所以方程x2=2x的根的个数为3,故选C。 函数图像练习题 1、小华同学接到通知,她的作文通过了《我的中国梦》征文选拔,需尽快上交该作文的电子文稿.接到通知后,小 华立即在电脑上打字录入这篇文 章,录入一段时间后因事暂停,过 了一会儿,小华继续录入并加快了 录入速度,直至录入完成.设从录 入文稿开始所经过的时间为x,录入字数为y,下面能反映y与x的函数关系的大致图象是() 2、某人匀速跑步到公 园,在公园里某处停留 了一段时间,再沿原路 匀速步行回家,此人离 家的距离与时间 的关系的大致图象是 ( ) 3、如图,扇形OAB动点P从点A出发,沿线段B0、0A匀速运动到点A,则0P的长度y与运动时间t之间的函数图象大致是() 4、某人进行登山活动,从山脚到山顶,休息一会儿又沿原路返回。若用横轴表示时间t,纵轴表示与山脚距离h,那么反映全程h与t 的关系的图是() 5.甲、乙两人在一次赛跑中,路程s(米)与所用时间t(秒)的关系如图所示,则下列说法正确的是()A.甲比乙先出发B.乙比甲跑的路程多 C.甲先到达终点 D.甲、乙两人的速度相同 6.“龟兔赛跑”讲述了这样一个故事:“领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,当醒来时,发现乌龟快到达终点了,于是,急忙追赶,但为时已晚,乌 龟还是先到达了终点.……”用 s1,s2分别表示乌龟和兔子的行程, t为时间,则下列图象中与故事情 节相吻合的图象是() 7.如图是古代计时器----“漏壶”的示意图在壶内盛一定量的水,水从壶下的小孔漏出,壶壁内画出刻度,人们根据壶中水面的位置计算时间。用x表示时间,y表示壶底到水面的高度,下面的哪个图象适合表示一小段时 间内y与x的函数关系 8、如图所示的曲线,哪个表示y 是x的函数() 9.如图所示,一枝蜡烛上细 下粗,设这枝蜡烛点燃后剩下 的长度为h,点燃时间为t,则能大 致刻画出h与t之间函数关系的图象是() 高中数学常见函数图像 1.指数函数: 定义 函数 (0x y a a =>且1)a ≠叫做指数函数 图象 1a > 01a << 定义域 R 值域 (0,)+∞ 过定点 图象过定点(0,1),即当0x =时,1y =. 奇偶性 非奇非偶 单调性 在R 上是增函数 在R 上是减函数 2.对数函数: 定义 函数 log (0a y x a =>且1)a ≠叫做对数函数 图象 1a > 01a << 定义域 (0,)+∞ 值域 R 过定点 图象过定点(1,0),即当1x =时,0y =. 奇偶性 非奇非偶 单调性 在(0,)+∞上是增函数 在(0,)+∞上是减函数 x a y =x y (0,1) O 1 y =x a y =x y (0,1) O 1 y =x y O (1,0) 1 x =log a y x =x y O (1,0) 1 x =log a y x = 3.幂函数: 定义形如αx y=(x∈R)的函数称为幂函数,其中x是自变量,α是常数. 图像 性质过定点:所有的幂函数在(0,) +∞都有定义,并且图象都通过点(1,1).单调性:如果0 α>,则幂函数的图象过原点,并且在[0,) +∞上为增函数.如果0 α<,则幂函数的图象在(0,) +∞上为减函数,在第一象限内,图象无限接近x轴与y轴. 4. 函数 sin y x = cos y x = tan y x = 图象 定义域 R R ,2x x k k ππ??≠+∈Z ???? 值域 []1,1- []1,1- R 最值 当 22 x k π π=+ () k ∈Z 时, max 1y =; 当22 x k π π=- ()k ∈Z 时,min 1y =-. 当()2x k k π =∈Z 时, max 1y =; 当2x k ππ=+ ()k ∈Z 时,min 1y =-. 既无最大值也无最小值 周期性 2π 2π π 奇偶性 奇函数 偶函数 奇函数 单调性 在 2,222k k ππππ? ?-+???? ()k ∈Z 上是增函数;在 32,222k k π πππ? ?++??? ? ()k ∈Z 上是减函数. 在[]() 2,2k k k πππ-∈Z 上 是 增 函 数 ; 在 []2,2k k πππ+ ()k ∈Z 上是减函数. 在,2 2k k π ππ π? ? - + ?? ? ()k ∈Z 上是增函数. 对称性 对称中心 ()(),0k k π∈Z 对称轴 ()2 x k k π π=+ ∈Z 对称中心 (),02k k ππ??+∈Z ?? ? 对称轴()x k k π =∈Z 对称中心(),02k k π?? ∈Z ??? 无对称轴 一个十分重要的函数的图象与性质应用 新课标高一数学在“基本不等式 ab b a ≥+2”一节课中已经隐含了函数x x y 1 +=的图象、性质与重要的应用,是高考要求范围内的一个重要的基础知识.那么在高三第一轮复习 课中,对于重点中学或基础比较好一点学校的同学而言,我们务必要系统介绍学习 x b ax y + =(ab ≠0)的图象、性质与应用. 2.1 定理:函数x b ax y +=(ab ≠0)表示的图象是以y=ax 和x=0(y 轴) 的直线为渐近线的双曲线. 首先,我们根据渐近线的意义可以理解:ax 的值与x b 的值比较,当x 很大很大的时候, x b 的值几乎可以忽略不计,起决定作用的是ax 的值;当x 的值很小很小,几乎为0的时候,ax 的值几乎可以忽略不计,起决定作用的是x b 的值.从而,函数x b ax y +=(ab ≠0)表示 的图象是以y=ax 和x=0(y 轴)的直线为渐近线的曲线.另外我们可以发现这个函数是奇 函数,它的图象应该关于原点成中心对称. 由于函数形式比较抽象,系数都是字母,因此要证明曲线是双曲线是很麻烦的,我们通过一个例题来说明这一结论. 例1.若函数x x y 3 233+= 是双曲线,求实半轴a ,虚半轴b ,半焦距c ,渐近线及其焦点,并验证双曲 线的定义. 分析:画图,曲线如右所示;由此可知它的渐近线应该是x y 3 3 = 和x=0两条直线;由此,两条渐近线的夹角的平分线y=3x 就是实轴了,得出顶点为A (3,3),A 1(-3,-3); ∴ a=OA =32, 由渐近线与实轴的夹角是30o,则有a b =tan30o, 得b=2 , c=22b a +=4, ∴ F 1(2,32)F 2(-2,-32).为了验证函数的图象是双曲线,在曲线上任意取一点P (x, x x 3233+)满足3421=-PF PF 即可; [课时作业·巩固练习] 实战演练 夯基提能 [A 组 基础保分练] 1.设x ∈R ,定义符号函数sgn(x )=???? ? 1,x >0,0,x =0, -1,x <0,则函数f (x )=|x |sgn(x )的图象大致是 ( ) 解析:由符号函数解析式和绝对值运算,可得f (x )=x ,选C. 答案:C 2.(2020·东北三校一模)函数f (x )=|x |+a x (其中a ∈R )的图象不可能是( ) 解析:当a =0时,f (x )=|x |,则其图象为A ;当x ∈(0,+∞)时,f (x )=x +a x ,f ′(x )=1 -a x 2=x 2 -a x 2,若a >0,函数f (x )在(0,a )上单调递减,在(a ,+∞)上单调递增,选项B 满足;若a <0,函数f (x )在(0,+∞)上单调递增,选项D 满足,而选项C 中的图象都不满足,故选C. 答案:C 3.已知二次函数f (x )的图象如图所示,则函数g (x )=f (x )·e x 的图象为( ) 解析:由图象知,当x <-1或x >1时,g (x )>0;当-1<x <1时,g (x )<0,由选项可知选A. 答案:A 4.(2020·辽宁大连测试)下列函数f (x )的图象中,满足f ???? 14>f (3)>f (2)的只可能是( ) 解析:因为f ????14>f (3)>f (2),所以函数f (x )有增有减,排除A ,B.在C 中,f ????14<f (0)=1,f (3)>f (0),即f ????14<f (3),排除C ,故选D. 答案:D 5.已知函数y =f (1-x )的图象如图所示,则y =f (1+x )的图象为( ) 解析:因为y =f (1-x )的图象过点(1,a ),故f (0)=a .所以y =f (1+x )的图象过点(-1,a ),选B. 答案:B 6.函数f (x )=5 x -x 的图象大致为( ) 第21课 对数(2) 1.D 2. 3 3.52 4.1222 m n -+ 5.(1) 1a - (2) 1(1)2 a b ++ 6. 313pq pq + 7. 32- 8. (1) 2 (2) 原式 266[log 2log 2=+?6(log 31)]+6(2log 2)÷ 266[log 2log 2=+?6(2log 2)]-6(2log 2)÷ 1= 9 .3- 第22课 对数(3) 1.A 2.C 3.1 4.a 5 .m = 6.原式=(log 25+log 255)5log 22log 33?=2log 525log 2 152? =2log 5log 215252?=2log 5log 4552?=4 5. 7.原式7744log 8log 64log 6log 3616 4947=+=+3664100=+= 8.32a b a +- 9.lg543lg3lg 2=+,lg 632lg3lg 7,=+ lg842lg 2lg3lg7=++ ∴lg 23lg 32lg 3lg 72lg 2lg 3lg 7a b c +=??+=??++=? ∴33lg 27a b c -+= 10.证明:∵346x y z t ===, ∴ 6 lg lg 4lg lg 3lg lg t z t y t x ===,,, ∴y t t t t x z 21lg 24lg lg 2lg lg 3lg lg 6lg 11===-=- 第23课 对数函数(1) 1.D 2.C 3.B 4.A 5.C 6.]2,1( 7.(,2.5),(,5)-∞-∞ 8.4 (0,)(1,)5+∞ 9.定义域(0,1),值域: 当1a >时,为(,2log 2)a -∞-,当01a <<时,为(2log 2,)a -+∞ 10.(2,2)- 第24课 对数函数(2) 1.A 2.B 3.155 或 4.(1,-+∞) 5.(1,2] 6.(1)定义域(-1,3);值域[2,)-+∞ ( 2 [3,1]-- 7.略 8.1 24log 3 9.(1)x x x f a -+=33log )(,-3 上节课知识检测 一、基本内容 1.利用描点法作函数图像 其基本步骤是列表、描点、连线,具体为: 2、会画基本函数图像(一次(两点想x 取0,,y 取0(或X 取1))、反比例(三点(x 取1/2、1,2)对称轴、对称中心)、二次(对称轴\顶点\开口)、幂(四点x 取0,1/2,1,2对称)、指数(三点x 取-1,0,1)、对数(三点Y-1,0,1)、对勾(两部分相等时X 值点)、三角(x 取五点;对称轴、对称中心)) 3.掌握画图像的基本方法:(1)描点法(2)图像变换法.平移、伸缩、翻折 (3)讨论分段法 (1)平移变换: y =f (x ) ――――――――――→a >0,右移a 个单位a <0,左移|a |个单位 y =f (x -a ); y =f (x ) ―――――――――→b >0,上移b 个单位b <0,下移|b |个单位 y =f (x )+b . (2)伸缩变换: y =f (x ) 1 011 1ωωωω <<>????????→,伸原的倍 ,短原的 长为来缩为来 y =f (ωx ); y =f (x ) ――――――――――――→A >1,伸为原来的A 倍0 第7讲 函数图像 一、选择题 1.函数=ln 1 |2x -3| 的大致图像为(如图所示) ( ). 解析 y =-ln|2x -3|=????? -ln (2x -3),x >3 2, -ln (3-2x ),x <3 2, 故当x >32时,函数为减函数,当x <3 2时,函数为增函数. 答案 A 2.由方程x |x |+y |y |=1确定的函数y =f (x )在(-∞,+∞)上是( ). A .增函数 B .减函数 C .先增后减 D .先减后增 解析 ①当x ≥0且y ≥0时,x 2+y 2=1,②当x >0且y <0时,x 2-y 2=1, ③当x <0且y >0时,y 2-x 2=1, ④当x <0且y <0时,无意义. 由以上讨论作图如上图,易知是减函数. 答案 B 3.已知函数f (x )=? ????1e x -tan x ? ????-π 2 A .大于1 B .大于0 C .小于0 D .不大于0 解析 分别作出函数y =? ????1e x 与y =tan x 在区间? ???? -π2,π2上的图象,得到 0第7讲函数的图象 (1)
近五年高考函数图像题汇总
几种特殊函数的图象及应用
2021高考数学一轮复习第7讲函数的图象学案含解析.doc
高三复习专题函数的图像含答案完整版
高中数学常见函数图像
函数的定义及图象
2015高考数学(理)一轮题组训练:2-7函数的图象及其应用
高考数学总复习第二章函数概念与基本初等函数第7讲函数的图象
高中数学函数图象高考题
函数的概念与图像4单调性
赏析幂函数的图象特征及应用
函数图像练习题
高中数学常见函数图像
双曲线函数的图像与性质及应用
第二章 第七节 函数的图象
《函数的概念与图象》参考答案
函数图像变换及应用
高中数学大一轮复习讲义(文科)第7讲函数图像