
习题一
1 设总体X 的样本容量5=n ,写出在下列4种情况下样本的联合概率分布. 1)),1(~p B X ; 2))(~λP X ; 3)],[~b a U X ; 4))1,(~μN X .
解 设总体的样本为12345,,,,X X X X X , 1)对总体~(1,)X B p ,
11223344555
11
1
55(1)
(,,,,)()(1)(1)i i
n
x x i i i i x x P X x X x X x X x X x P X x p p p p -==-========-=-∏∏
其中:5
1
15i
i x x ==∑
2)对总体~()X P λ
11223344555
1
1
555
1
(,,,,)()!
!
i
x
n
i i i i i x
i i P X x X x X x X x X x P X x e x e x λ
λ
λλ-==-==========
∏∏
∏
其中:5
1
15i
i x x ==∑
3)对总体~(,)X U a b
55
1151
1
,,1,...,5 (,,)()0i i i i a x b i f x x f x b a ==?≤≤=?==-???
∏∏
L ,其他
4)对总体~(,1) X N μ
()()
()2
55
55/2
22
1511
1
1 (,,)()=2exp 2i x i i i i i f x x f x x μπμ--
-===??==-- ???
∑∏L
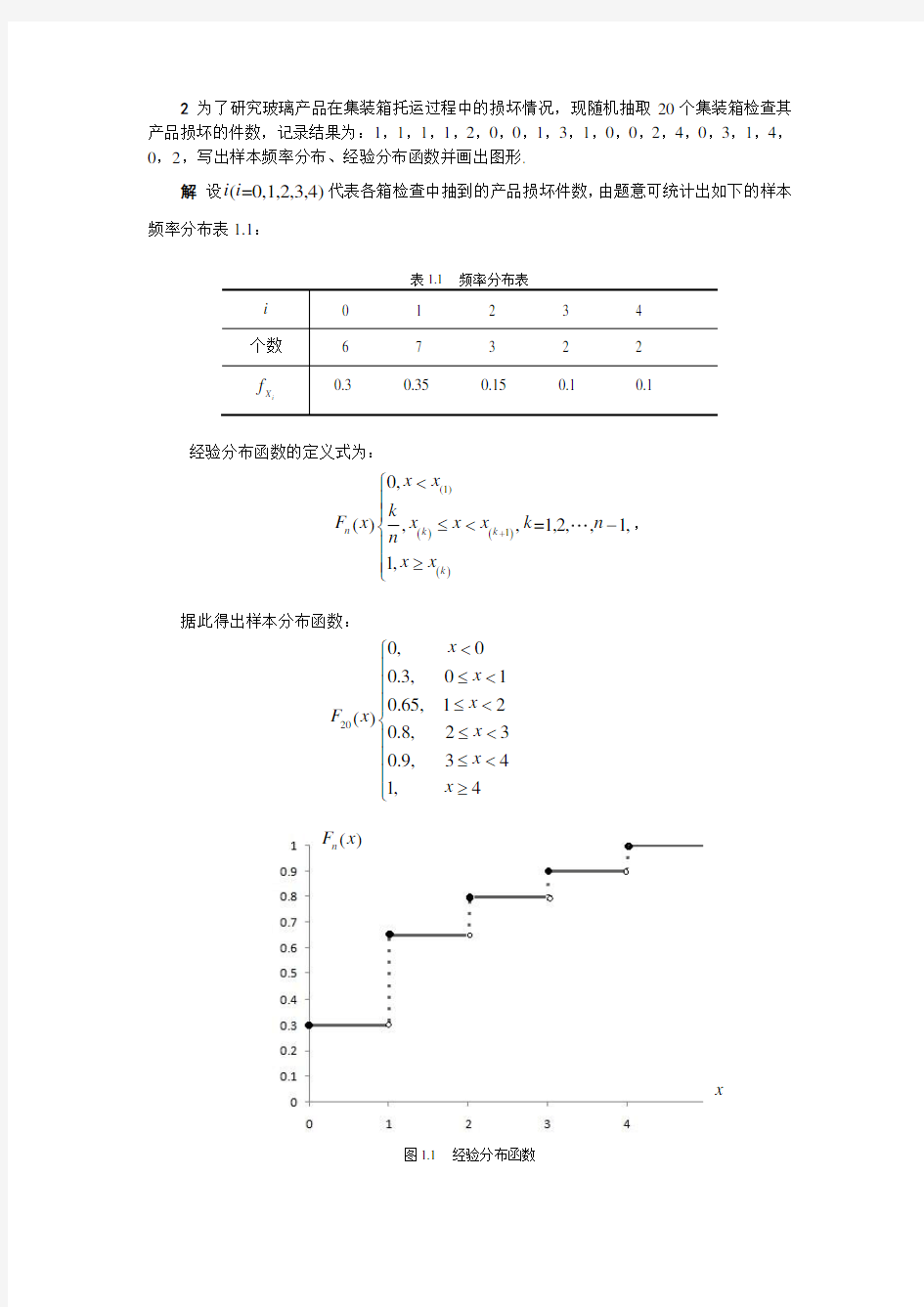
2 为了研究玻璃产品在集装箱托运过程中的损坏情况,现随机抽取20个集装箱检查其产品损坏的件数,记录结果为:1,1,1,1,2,0,0,1,3,1,0,0,2,4,0,3,1,4,0,2,写出样本频率分布、经验分布函数并画出图形.
解 设(=0,1,2,3,4)i i 代表各箱检查中抽到的产品损坏件数,由题意可统计出如下的样本频率分布表1.1:
经验分布函数的定义式为:
()()()
(1)10,(),,=1,2,,1,1,n k k k x x k
F x x x x k n n x x +
据此得出样本分布函数:
200,00.3,010.65,12()0.8,
230.9,341,4x x x F x x x x
?≤
≤
≥?
图1.1 经验分布函数
x
()
n F x
3 某地区测量了95位男性成年人身高,得数据(单位:cm)如下:
试画出身高直方图,它是否近似服从某个正态分布密度函数的图形.
解
图1.2 数据直方图
它近似服从均值为172,方差为5.64的正态分布,即(172,5.64)N .
4 设总体X 的方差为4,均值为μ,现抽取容量为100的样本,试确定常数k ,使得满足9.0)(=<-k X P μ.
解 ()
- 5P X k P k μ?
?<=
()()
555 P k X k μ=-<-<
因k 较大,由中心极限定理(0,1)
X N : ()
()()
-55P X k k k μ<≈Φ-Φ-
(5)(1(5))
k k =Φ--Φ
()2510.9k =Φ-=
所以:()50.95
k Φ=
查表得:5 1.65k =,0.33k ∴=.
5 从总体2
~(52,6.3)X N 中抽取容量为36的样本,求样本均值落在50.8到53.8之间的概率.
解 (
)50.853.8 1.1429 1.7143X P X P ??<<=-<
< ???
(0,1)X U N =
Q
()()
50.853.8 1.1429 1.7143(1.7143)( 1.14290.9564(10.8729)0.8293
P X P U ∴<<=-<<=Φ-Φ-=--=)
6 从总体~(20,3)X N 中分别抽取容量为10与15的两个独立的样本,求它们的均值之差的绝对值大于0.3的概率.
解 设两个独立的样本分别为:110,,X X K 与115,,Y Y K ,其对应的样本均值为:X 和Y . 由题意知:X 和Y 相互独立,且:
3~(20,)10X N ,3~(20,)15Y N
(0.3)1(0.3)P X Y P X Y ->=--≤
1P =-
~(0,0.5)~(0,1)(0.3)22(0.4243)0.6744
X Y N X Y
N P X Y -->=-Φ=Q
7 设110,,X X K 是总体~(0,4)X N 的样本,试确定C ,使得10
2
1
()0.05i i P X C =>=∑.
解 因~(0,4)i X N ,则
~(0,1)2
i
X N ,且各样本相互独立,则有: 10
12
2~(10)2i i X χ=??
???∑
所以:10
1022
1
1
(
)()144
i
i
i i C
P X
C P X ==>=>
∑∑
1021
110.0544i i c P X =??
=-≤= ???∑
1021
10.9544i i c P X =??
≤= ???∑
查卡方分位数表:c/4=18.31,则c=73.24.
8 设总体X 具有连续的分布函数()X F x ,1,,n X X K 是来自总体X 的样本,且i EX μ=,
定义随机变量:
1,
,1,2,,0,
i i i X Y i n X μμ
>==≤??
?L
试确定统计量∑=n
i i Y 1的分布.
解 由已知条件得:~(1,)i Y B p ,其中1()X p F μ=-.
因为i X 互相独立,所以i Y 也互相独立,再根据二项分布的可加性,有
1
~(,)n
i
i Y
B n p =∑,1()X p F μ=-.
9 设1,,n X X K 是来自总体X 的样本,试求2,,EX DX ES 。假设总体的分布为: 1)~(,);X B N p 2) ~();X P λ 3) ~[,];X U a b 4) ~(,1);X N μ 解 1) EX EX Np ==
(1)
DX Np p DX n n
-=
=
2(1)ES DX Np p ==-
2) EX EX λ==
DX DX n n
λ=
=
2ES DX λ==
3) 2
a b
EX EX +==
()2
12b a DX DX n n
-== ()2
2
12
b a ES
DX -==
4) EX EX μ==
1DX DX n n
=
= 21ES DX == 10 设1,,n X X K 为总体2~(,)X N μσ的样本,求
21()n i i E X X =??-????∑与21()n i i D X X =??-????
∑。 解
()2
22
12
(1)(1)(1)(1)n i i E X X E n S n ES n DX n σ=??-=-=-????????
=-=-∑ ()2224
21(1)(1)n i i n S D X X D n S D σσ=??-????-=-=??????????
∑ 又因为
2
2
2
(1)~(1)n S n χσ--,所以:()24
12(1)n i i D X X n σ=??-=-????
∑
11 设1,,n X X K 来自正态总体(0,1)N ,定义:121
1
||,||n
i
i Y X Y X n
===
∑,计算12,EY EY .
解 由题意知~(0,1/)X N n
,令:Y =,则~(0,1)Y N
()E Y X
22
||y y e
dy +∞
-
=
?22
0y ye
dy +∞
-
=
?
t e dt +∞-=
(1)=
=
1((||))E Y E X ==
211
11(||(||))()n n
i i i i E Y E X E X n n E X ===??=== ???∑∑12 设1,,n X X K 是总体~(,4)X N μ的样本,X 为样本均值,试问样本容量n 应分别取多大,才能使以下各式成立:
1)2
||0.1E X μ-≤;2)||0.1E X μ-≤;3)(||1)0.95P X μ-≤=。 解 1)
4~(,4)
~(,)X N X N n μμ∴Q
~(0,1)X U N =
2
E X μ
-2
4X E n =
24X X D E n ??=
+????
()4
100.1n
=
+≤ 所以:40n ≥
2)
~(0,1)X U N =
()E E U
=2
2
u u du +∞
--∞
=?
2
20
2u du +∞
-==?
所以:0.1E X μ-=
≤ 计算可得:225n ≥
3)
()
()111P X P X μμ-≤=-≤-≤
P ?=≤≤ ??
22??=Φ-Φ- ????
210.952??=Φ-≥ ? ???
查表可得:
0.975 1.96,15.362
u n ≥=≥ ,而n 取整数,16n ∴≥. 13 设1(,,)n X X K 和1(,,)n Y Y K 是两个样本,且有关系式:1()i i Y X a b
=-(,a b 均为常数,
0b ≠)
,试求两样本均值X 和Y 之间的关系,两样本方差2X S 和2
Y S 之间的关系. 解 因:()111
n i i Y X a n b
==-∑
111n i i X na b n =??
=- ???
∑ ()1
X a b
=
- 所以:()1
EY EX a b
=
- 即:
()
()()()2
2
21
12
221111111111=
1n
n Y
i i i i n
i X i S Y Y X a X a n n b b X X S n b b
===??=-=---??--??
??-=??-??∑∑∑
14 设15,,X X K 是总体~(0,1)X N 的样本.
1) 试确定常数11,c d ,使得2221121345()()~()c X X d X X X n χ++++,并求出n ; 2) 试确定常数2c ,使得222212345()/()~(,)c X X X X X F m n +++,并求出m 和n . 解 1)因:12~(0,2)X X N +,345~(0,3)X X X N ++
~(0,1)N
~(0,1)N 且两式相互独立
故:2
2
2
~(2)χ+
可得:112
c =
,11
3d =,2n =.
2) 因:222
1
2
~(2)X X χ+,
()2
3452~(1)3
X X X χ++,
所以:
()()
221
22
3452
~(2,1)3
X
X F X X X +++,
可得:23
,2,12
c m n =
==. 15 设(),(,)p p t n F m n 分别是t 分布和F 分布的p 分位数,求证
21/21[()](1,)p p t n F n --=.
证明 设1(1,)p F n α-=
,
则:()1(1P F p P p α≤=-?≤
≤=
-
((12(2(12
P T P T p P T p p P T ?≤-≤=-?≤=-?≤=
-
12
()p t
n -
=
故:2
112
()(1,)p p t
n F n α--==.
16 设21,X X 是来自总体)1,0(~N X 的一个样本,求常数c ,使:
1.0)()()(2212212
21=???
? ??>-+++c X X X X X X P .
解 易知12~(0,2)X X
N +~(0,1)N ; 同理12~(0,2)X X N
-~(0,1)N 又因:1212(,)0Cov X X X X +-=,所以12X X +与12X X -相互独立.
221212222
121212()(1)()()()()X X c X X P c P c X X X X X X ????+-+>=> ? ?++--????
2122
12()()1X X c P X X c ??
+=> ?--??
20.11c P c ???=>=- ? ?
??
所以:
0.9(1,1=39.91c
F c
=-) 计算得:c = 0.976.
17 设121,,,,n n X X X X +K 为总体2~(,)X N μσ的容量1n +的样本,2
,X S 为样本
1(,,)n X X K 的样本均值和样本方差,求证:
1
)~(1)T t n -;
2)211~(0,)n n X X N n
σ++-;
3)2
11~(0,
)n X X N n
σ--.
解 1)因:1()0n E X X +-=,2
11()n n D X X n
σ++-=
所以:2
11~(0,
)n n X
X N n σ++-
~(0,1)X N 又:
222
1
~(1)n S n χσ
--
X 2
21n S σ-相互独立
=~(1)t n -
2) 由1)可得:2
11~(0,
)n n X X
N n
σ++- 3) 因:1()0E X X -=,2
11()n D X X n
σ--=
所以:2
11~(0,
)n X X N n
σ-- 18 设1,,n X X K 为总体2~(,)X N μσ的样本,X 为样本均值,求n ,使得
(||0.25)0.95P X μσ-≤≥.
解
(
)
~(0,1)
0.25X U N X P X P μσ=
?∴-≤=-≤ ?Q
(210.95=Φ-≥
所以:(0.975Φ≥
查表可得:0.975 1.96u =,即62n ≥. 19 设1,,n X X K 为总体~[,]X U a b 的样本,试求: 1)(1)X 的密度函数; 2)()n X 的密度函数; 解 因:~[,]X U a b , 所以X 的密度函数为:
1
,[,]()0,[,]
x a b f x b a
x a b ?∈?
=-????, 0,(),1,x a x a F x a x b b a x b ≤?
?-?=<≤?-?
>??
由定理:1
(1)()(1())
()n f x n F x f x -=-
11
(
),[,]0,[,]n b x n x a b b a b a
x a b --?∈?=--????
1
()()(())
()n n f x n F x f x -=
11
(
),[,]0,[,]n x a n x a b b a b a
x a b --?∈?=--????
20 设15,,X X K 为总体~(12,4)X N 的样本,试求: 1)(1)(10)P X <; 2)(5)(15)P X < 解
~(12,4)12
~(0,1)2
i X N X N -∴
Q ()()(1)(1)10110P X P X <=-≥
()5
1110i
i P X
==-
≥∏
()()5
1
1110i i P X ==--≤∏
5
1121112i i X P =?-?
??=--≤- ? ????
?∏
51(1(1))=--Φ- 51(1)0.5785=-Φ=
()()5
(5)11515i i P X P X =<=<∏
51
12 1.52i i X P =-??
=< ???∏
55(1.5)0.93320.7077=Φ==
21 设11(,,,,,)m m m n X X X X ++K K 为总体2~(0,)X N σ的一个样本,试确定下列统计量的分布:
1
)1m
i
X Y =
; 2)2
122
1
m
i
i m n
i
i m n X Y m X =+=+=
∑∑;3)2
12
212311??
? ??+???
??=∑∑++==n m m i i m i i X n X m Y σσ
解 1)因为:
21
~(0,)m
i
i X
N m σ=∑
~(0,1)m
i X
N ∑,
2
22
1
~()
m n
i i m X n χσ
+=+∑
m
i X
∑与
2
2
1
m n
i i m X σ
+=+∑
相互独立,由抽样定理可得:
1~()m
i
m
i
X
X Y t n =
∑ 2)因为:
22
2
1
1
~()m
i
i X
m χσ
=∑,
222
1
1
~()
m n i i m X n χσ
+=+∑
且
22
1
1
m
i
i X
σ=∑与
221
1
m n
i i m X σ+=+∑
相互独立,
所以:
222
112
221
1
1=
~(,)1
m
m
i
i i i m n
m n
i i i m i m n X
X m F m n m X X n
σσ==++=+=+∑∑∑∑
3)因为:
2
1
~(0,)m
i
i X
N m σ=∑,
21
~(0,)m n i i m X N n σ+=+∑
所以:
2
21
2
()
~(1)m
i i X m χσ=∑,
2
212
()~(1)
m n
i i m X n χσ+=+∑
且
2
1
2
()
m
i i X m σ
=∑与
2
1
2
()m n
i i m X n σ
+=+∑相互独立,
由卡方分布可加性得:2
2
2
22
111~(2)m m n i i i i m n X X m n χσσ+==+????+ ? ?????
∑∑. 22 设总体X 服从正态分布),(2
σμN ,样本n X X X ,,,21Λ来自总体X ,2
S 是样本方
差,问样本容量n 取多大能满足95.067.32)1(22=???
?
??≤-σS n P ?
解 由抽样分布定理:
222
1
~(1)n S n χσ--,22
1
(
32.67)0.95n P S σ-≤=,
查表可得:n 121-=,n 22=.
23 从两个正态总体中分别抽取容量为20和15的两独立的样本,设总体方差相等,
22
21
,S S 分别为两样本方差,求?
??
?
??>39.22221S S P . 解 设12=20=15n n ,分别为两样本的容量,2σ为总体方差,由题意,
22222
2111222222
2(1)19(1)14=~(19)=~(14)n S S n S S χχσσσσ
--, 又因22
21,S S 分别为两独立的样本方差:2
12
2
12
22
2
2
1919=~(19,14)1414
S S F S S σσ 所以:221122222.391 2.3910.950.05S S P P S S ????
>=-≤=-= ? ?????
.
24 设总体),(~2
σμN X ,抽取容量为20的样本2021,,,X X X Λ,求概率
1)????
??
??≤-≤
∑=57.37)(85.102
20
1
2
σμi i X P ;
2)????
?
?
?
?≤-≤
∑=58.38)(65.112
20
1
2
σi i
X X
P .
解 1)因
~(0,1)i X N μ
σ
-,且各样本间相互独立,所以:
()
20
2
2
20
221
2
1~(20)i
i i i X X μμχχσσ==--??== ???
∑∑ 故:()210.8537.570.990.050.94P χ≤≤=-=
2)因:
()
20
2
2
21
2
2
19~(19)i
i X
X S χσ
σ
=-=
∑, 所以:
221911.6538.580.9950.10.895.S P σ??
≤≤=-= ???
25 设总体),80(~2
σN X ,从中抽取一容量为25的样本,试在下列两种情况下
)380(>-X P 的值:
1) 已知20=σ;
2) σ未知,但已知样本标准差2674.7=S . 解 1)
()
22
~(80,)80~(80,
)~(0,1),~(24)255
80380320/54X N X X X N N t S X P X P σσ-∴??
- ?
->=> ???
Q 314P U ?
?=-≤ ???12(0.75)1=-Φ+
220.77340.4532=-?=
2)()
80803 2.0647.2674/5X P X P ??
- ?->=> ???
()1 2.064120.97510.05P T =-≤=-?+=
26 设1,,n X X K 为总体2~(,)X N μσ的样本,2,X S 为样本均值和样本方差,当20n =时,求:
1)();4.472
P X σμ<+
2)2
2
2
(||);2
P S σ
σ-<
3)确定C ,使()0.90S P C X μ
>=-.
解 1)
2~(,)
~(0,)1 4.4724.472X N N X X P X P μσμμσσ??-?
?<+=< ? ?
????
Q
10.8413X P ??
=<=???
2)2222222
22
2P S P S σσσσσ????-<=-<-< ? ?????
222322P S σσ??=<< ???
221322S P σ??
=<< ???
2
2199.528.5S P σ??=<< ?
??
其中2
2
22
19=
~(19)S χχσ
,则
()2222
2
2199.528.529.528.50.950.050.9
S P S P P σσσχ????-<=<< ? ?????=<<=-= 3)
1== ? ?-?????
其中,(19)X T t ,则
0.9S P c P T X μ???>== ? -????
所以:
0.9(19)=1.328t =,计算得: 3.3676c =. 27 设总体X 的均值μ与方差2σ存在,若n X X X ,,,21Λ为它的一个样本,X 是样本均值,试证明对j i ≠,相关系数1
1),(--=--n X X X X r j i . 证明
cov(,)(,)i j X X X X r X X X X ----=
2
1()()i j n D X X D X X n
σ--=-=
21
ov(,)()i j i j i j C X X X X E X X X X X X X X n
σ--=---=-
所以:1
(,)1
i j r X X X X n --=--.
28. 设总体2~(,)X N μσ,从该总体中抽取简单随机样本)1(,,,221≥n X X X n Λ,X 是
它的样本均值,求统计量∑=+-+=
n
i i n i
X X X
T 1
2)2(的数学期望.
解 因2~(,)X N μσ,)1(,,,221≥n X X X n Λ为该总体的简单随机样本,令
i i n i Y X X +=+,则有2~(2,2)i Y N μσ
可得:1
12n
i i Y Y X n ===∑
()2
2
21
1
(2)(1)n
n
i n i i Y i i T X X X Y Y n S +===+-=-=-∑∑
22(1)2(1)Y ET n ES n σ=-=-
习题二
1 设总体的分布密度为:
(1),01
(;)0,
x x f x ααα+<<=???其它
1(,,)n X X L 为其样本,求参数α的矩估计量1?α和极大似然估计量2?α .现测得样本观测值
为:0.1,0.2,0.9,0.8,0.7,0.7,求参数α的估计值 .
解 计算其最大似然估计:
()()
11
1
11
(,)11ln (,)ln(1)ln n
n
n
n i i i i n
n i
i L x x x x L x x n x α
α
αααααα===??=+=+??=++∏∏∑K K
11
21
ln (,)ln 01?10.2112
ln n n i i n i
i d n L x x x d n x ααααα====+=+=--=∑∑K
其矩估计为:
()1 3.40.10.20.90.80.70.766
X =
+++++= 3077
.0121?,212)1()1(11
01
21
=--==++=++=+=?++X X X x dx x EX αααααααα
所以:12112??,11ln n
i
i X n X X αα=??
?- ?==-+-
? ??
?
∑, 12??0.3077,0.2112αα≈≈.
2 设总体X 服从区间[0, θ]上的均匀分布,即~[0,]X U θ,1(,,)n X X L 为其样本, 1)求参数θ的矩估计量1?θ和极大似然估计量2?θ;
2)现测得一组样本观测值:1.3,0.6,1.7,2.2,0.3,1.1,试分别用矩法和极大似然法求总体均值、总体方差的估计值. 解 1)矩估计量:
11
??,2 2.42
EX X X θθ=
=== 最大似然估计量:
11
11
1
(,)ln (,)0
n
n n
i n L x x n
L x x θθ
θθθ
===
=-
=∏
K K
无解 .此时,依定义可得:2
1?max i i n
X θ≤≤=
2)矩法:211??1.2,0.4722
12
EX DX θθ=
==
=
极大似然估计:222??1.1,0.40332
12
EX DX θθ====.
3 设1,...,n X X 是来自总体X 的样本,试分别求总体未知参数的矩估计量与极大似然估计量 .已知总体X 的分布密度为:
1),0(;),
00,
x
e
x f x x λλλλ->=>≤??
?未知
2)(;),
0,1,2,,0!
x
f x e x x λ
λ
λλ-=
=>L 未知
3)1,(;,)0
a x
b f x a b a b b a
≤≤=<-??
???,
其它
未知
4) 2
,0(;)0
x
x f x θθθ-<≤<+∞=??
?,
其它
θ未知
5)()/1,(;,),
00,
x e x f x x αβ
ααβββα
--≥=>
6)1
,0(;,),
,00,
x
x f x x αααβαβαββα
-≤≤=>
7
)2
2
2,0
(;),
00,0
x x f x x θ
θθ-
>=>≤??
未知
8)
22
(;)(1)(1)
,2,3,,01x f x x x θθθθ
-=--=< 解 1) 矩法估计:1 1 1?,EX X X λλ=== 最大似然估计: 1111 1 (,),ln (,)ln n i i i n n x x n n n i i i L x x e e L x x n x λ λλλλλλλ=--==∑===-∑∏K K 2 1 1 1 ?ln 0,n i n i i i d n n L x d X x λλλ===-=== ∑∑. 2) ~()X P λ 矩估计: 1 ?,EX X X λλ=== 最大似然估计: 11 (,),ln ln i x nx n n n i i i i L x x e e L n nx x x x λ λ λλλλλ--====-+-∑∏ ∏K 2 ?ln 0,d nx L n X d λλλ =-+==. 3) 矩估计:()2 ,212 b a a b EX DX -+== 联立方程: ( )2 *221?2 ?a X b X a b X b a M ?=- ?→+?=???-?=???=+?? 最大似然估计: 11 1 (,)(;)() n n i n i L x x f x b a θθ== = -∏ K ,ln ln()L n b a =-- ln 0d L n da b a ==-,无解,当1?min i i n a X ≤≤=时,使得似然函数最大, 依照定义,1?min i i n a X ≤≤=,同理可得1?max i i n a X ≤≤=. 4) 矩估计: ln EX dx x x θ θ+∞ +∞= =? ,不存在 最大似然估计: 12 2 1 11 (,),ln ln 2ln n n n n i i i i i L x x L n x x x θ θθ θ=====-∑∏ ∏K ln 0n L αθ ?==?,无解;依照定义,(1) ?X θ=. 5) 矩估计: ()/0 ()(1)(2)x t x EX e dx t e dt αβ ααβαββ +∞ +∞ ---= = +=Γ+Γ?? X αβ=+= 2 222 ()(1)2(2)(3)t EX t e dt αβααββ+∞ -= +=Γ+Γ+Γ? 22222 2122()i M X n ααββαββ=++=++== ∑ 2 2 2 22* 2111 ??i M X X X M n X βαβ=-=-==-=∑ 一、填空题(本题15分,每题3分) 1、总体得容量分别为10,15得两独立样本均值差________; 2、设为取自总体得一个样本,若已知,则=________; 3、设总体,若与均未知,为样本容量,总体均值得置信水平为得置信区间为,则得值为________; 4、设为取自总体得一个样本,对于给定得显著性水平,已知关于检验得拒绝域为2≤,则相应得备择假设为________; 5、设总体,已知,在显著性水平0、05下,检验假设,,拒绝域就是________。 1、; 2、0、01; 3、; 4、; 5、。 二、选择题(本题15分,每题3分) 1、设就是取自总体得一个样本,就是未知参数,以下函数就是统计量得为( )。 (A ) (B ) (C ) (D ) 2、设为取自总体得样本,为样本均值,,则服从自由度为得分布得统计量为( )。 (A ) (B ) (C ) (D ) 3、设就是来自总体得样本,存在, , 则( )。 (A )就是得矩估计 (B )就是得极大似然估计 (C )就是得无偏估计与相合估计 (D )作为得估计其优良性与分布有关 4、设总体相互独立,样本容量分别为,样本方差分别为,在显著性水平下,检验得拒绝域为( )。 (A ) (B ) (C ) (D ) 5、设总体,已知,未知,就是来自总体得样本观察值,已知得置信水平为0、95得置信区间为(4、71,5、69),则取显著性水平时,检验假设得结果就是( )。 (A )不能确定 (B )接受 (C )拒绝 (D )条件不足无法检验 1、B ; 2、D ; 3、C ; 4、A ; 5、B 、 三、(本题14分) 设随机变量X 得概率密度为:,其中未知 参数,就是来自得样本,求(1)得矩估计;(2)得极大似然估计。 解:(1) θθθ322)()(022 ===??∞+∞-x d x x d x f x X E , 令,得为参数得矩估计量。 (2)似然函数为:),,2,1(,022),(1212n i x x x x L i n i i n n n i i i Λ=<<==∏∏==θθθθ, , 而就是得单调减少函数,所以得极大似然估计量为。 第三章 假设检验 课后作业参考答案 3.1 某电器元件平均电阻值一直保持2.64Ω,今测得采用新工艺生产36个元件的平均电阻值为2.61Ω。假设在正常条件下,电阻值服从正态分布,而且新工艺不改变电阻值的标准偏差。已知改变工艺前的标准差为0.06Ω,问新工艺对产品的电阻值是否有显著影响?(01.0=α) 解:(1)提出假设64.2:64.2:10≠=μμH H , (2)构造统计量36 /06.064 .261.2/u 00 -=-= -= n X σμ (3)否定域???? ??>=???? ??>?? ??? ??<=--21212 αααu u u u u u V (4)给定显著性水平01.0=α时,临界值575.2575.22 12 =-=- α αu u , (5) 2 αu u <,落入否定域,故拒绝原假设,认为新工艺对电阻值有显著性影响。 3.2 一种元件,要求其使用寿命不低于1000(小时),现在从一批这种元件中随机抽取25件, 测得其寿命平均值为950(小时)。已知这种元件寿命服从标准差100σ=(小时)的正态分 布,试在显著水平0.05下确定这批元件是否合格。 解: {}01001:1000, H :1000 X 950 100 n=25 10002.5 V=u 0.05H x u αμμσμα-≥<====->=提出假设:构造统计量:此问题情形属于u 检验,故用统计量:此题中:代入上式得: 拒绝域: 本题中:0.950.950 u 1.64u 0.0u H =>∴即,拒绝原假设认为在置信水平5下这批元件不合格。 3.3某厂生产的某种钢索的断裂强度服从正态分布( )2 ,σ μN ,其中()2 /40cm kg =σ。现从 一批这种钢索的容量为9的一个子样测得断裂强度平均值为X ,与以往正常生产时的μ相比,X 较μ大20(2 /cm kg )。设总体方差不变,问在01.0=α下能否认为这批钢索质量显著提高? 解: (1)提出假设0100::μμμμ>=H H , (2)构造统计量5.13 /4020 /u 00 == -= n X σμ (3)否定域{}α->=1u u V (4)给定显著性水平01.0=α时,临界值33.21=-αu (5) α-<1u u ,在否定域之外,故接受原假设,认为这批钢索质量没有显著提高。 3.4某批矿砂的五个样品中镍含量经测定为(%): 3.25 3.27 3.24 3.26 3.24 设测定值服从正态分布,问在0.01α=下能否接受假设,这批矿砂的镍含量为3.25? 解: 010110 2: 3.25 H :t X 3.252, S=0.0117, n=5 0.3419 H x μμμμσ==≠==提出假设:构造统计量:本题属于未知的情形,可用检验,即取检验统计量为:本题中,代入上式得:否定域为:1-20.99512 0 V=t>t (1)0.01,(4) 4.6041, 3.25n t t t H ααα- ??-?? ?? ==<∴本题中,接受认为这批矿砂的镍含量为。 ---------------------------------------- 说明:本试卷总计100分,全试卷共 5 页,完成答卷时间2小时。 ---------------------------------------- 一、填空题(本大题共8小题,每题4分,共32分) 1、随机事件A 、B 互不相容,且A =B ;则()P A = 2、已知,10/1)/(,5/1)(,5/2)(===B A P B P A P 则=+)(B A P 3、同时掷三枚均匀硬币,则恰有两枚正面向上的概率为 。 4、若随机变量)2.0,20(~B X ,则X 的最可能值是 。 5、若n X X X ,...,,21为来自泊松分布)(λP 的一个样本,2,S X 分别为样本均值和样本方差,则 =)(X E ,=)(2S E 。 6、样本0,5,10,-3样本均数为 ,样本方差为 。 7、2σ已知时检验假设0100:;:μμμμ≠=H H ,应构造统计量为 ,拒绝域为 。 8、考查4个3水平的因子A,B,C,D 及其交互作用A ×B 与A ×C ,则做正交实验设计时,可选用的行数最少的正交表为 。 二、单项选择题(本大题共8小题,每题4分,共32分) 1、设随机事件A 、B 互不相容,且()0,()0,P A P B >>则下列结论只有( ) 成立。 A 、A 、 B 是对立事件; B 、A 、B 互不相容; C 、A 、B 不独立; D 、 A 、 B 相互独立。 2、射击三次,事件i A 表示第i 次命中目标(i =1,2,3),下列说法正确的是( )。 A 、321A A A 表示三次都没击中目标; B 、313221A A A A A A ++表示恰有两次击中目标; C 、313221A A A A A A ++表示至多一次没击中目标;D 、321A A A 表示至少有一次没击中目标。 3、随机变量),(~2σμN X ,则随着σ的减小,)|(|σμ<-X P 应( )。 A 、单调增大; B 、单调减少; C 、保持不变; D 、增减不能确定 第五章作业题解 5.1 已知正常男性成人每毫升的血液中含白细胞平均数是7300, 标准差是700. 使用切比雪 夫不等式估计正常男性成人每毫升血液中含白细胞数在5200到9400之间的概率. 解:设每毫升血液中含白细胞数为,依题意得,7300)(==X E μ,700)(==X Var σ 由切比雪夫不等式,得 )2100|7300(|)94005200(<-=< 概率论和数理统计真题讲解 (一)单项选择题(本大题共10小题,每小题2分,共20分) 在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。错选、多选或未选均无分。 1.设随机事件A与B互不相容,且P(A)>0,P(B)>0,则() A.P(B|A)=0 B.P(A|B)>0 C.P(A|B)=P(A) D.P(AB)=P(A)P(B) 『正确答案』分析:本题考察事件互不相容、相互独立及条件概率。 解析:A:,因为A与B互不相容,,P(AB)=0,正确; 显然,B,C不正确;D:A与B相互独立。 故选择A。 提示:① 注意区别两个概念:事件互不相容与事件相互独立; ② 条件概率的计算公式:P(A)>0时,。 2.设随机变量X~N(1,4),F(x)为X的分布函数,Φ(x)为标准正态分布函数,则F(3)=() A.Φ(0.5) B.Φ(0.75) C.Φ(1) D.Φ(3) 『正确答案』分析:本题考察正态分布的标准化。 解析:, 故选择C。 提示:正态分布的标准化是非常重要的方法,必须熟练掌握。 3.设随机变量X的概率密度为f(x)=则P{0≤X≤}=() 『正确答案』分析:本题考察由一维随机变量概率密度求事件概率的方法。第33页 解析:, 故选择A。 提示:概率题目经常用到“积分的区间可加性”计算积分的方法。 4.设随机变量X的概率密度为f(x)=则常数c=() A.-3 B.-1 C.- D.1 『正确答案』分析:本题考察概率密度的性质。 解析:1=,所以c=-1, 故选择B。 提示:概率密度的性质: 1.f(x)≥0; 4.在f(x)的连续点x,有F′(X)=f(x);F(x)是分布函数。课本第38页 5.设下列函数的定义域均为(-∞,+∞),则其中可作为概率密度的是() A.f(x)=-e-x B. f(x)=e-x C. f(x)= D.f(x)= 『正确答案』分析:本题考察概率密度的判定方法。 解析:① 非负性:A不正确;② 验证:B:发散; C:,正确;D:显然不正确。 故选择C。 提示:判定方法:若f(x)≥0,且满足,则f(x)是某个随机变量的概率密度。 6.设二维随机变量(X,Y)~N(μ1,μ2,),则Y ~() 『正确答案』分析:本题考察二维正态分布的表示方法。 解析:显然,选择D。 《数理统计》例题 1.设总体X 的概率密度函数为: 2 2 1)(ββ x e x f -= )0(>β 试用矩法和极大似然法估计其中的未知参数β。 解:(1)矩法 由于EX 为0, πβββββ βββββββ2 00 2 2 2 22 2 1][) ()2 (2) ()2(21 2)(2 2 2 2 2 2 2 2 2 2 = +-=- =- - ===???? ?∞ +-∞+- ∞ +- - ∞ +- ∞ ++∞ ∞ -dx e xe e d x x d xe dx e x dx x f x EX x x x x x πβ2 222 1= -=X E EX DX 令2S DX =得:S π β2 ?= (2)极大似然法 ∑= ==- =- ∏ n i i i x n n i x e e L 1 2 22 2 1 11 1 β ββ β ∑=- -=n i i x n L 1 22 1 ln ln ββ 2 31 ln 2n i i d L n x d βββ==-+∑ 令0ln =β d L d 得∑==n i i x n 1 2 2?β 2. 设总体X 的概率密度函数为: ?? ???<≥--=αα βαββαφx x x x ,0),/)(exp(1 ),;( 其中β>0,现从总体X 中抽取一组样本,其观测值为(2.21,2.23,2.25,2.16,2.14,2.25,2.22,2.12,2.05,2.13)。试分别用矩法和极大似然法估计其未知参数βα和。 解:(1)矩法 经统计得:063.0,176.2==S X β αβαβ φα β α α β ααβ α β α α β α α +=-=+-=-===∞ +-- ∞ +-- ∞ +-- -- ∞ +-- ∞ +∞ +∞-?? ? ?x x x x x e dx e xe e xd dx e x dx x x EX ][) (1 )( ) (222][) (1 222 22 2βαβαβαβ β α α αβ α β α α β α α ++=+=+-=-==--∞ +∞ +-- --∞ +-- ∞ +?? ?EX dx e x e x e d x dx e x EX x x x x 222)(β=-=EX EX DX 令???==2S DX X EX 即???==+2 2S X ββα 故063.0?,116.2?===-=S S X βα (2)极大似然法 ) (1 1 1),;(αβ β α β β βα---- == =∏X n n X n i e e x L i )(ln ln αβ β-- -=X n n L )(ln ,0ln 2αβ βββα-+-=??>=??X n n L n L 因为lnL 是L 的增函数,又12,,,n X X X α≥L 所以05.2?)1(==X α 数理统计考试试卷 一、填空题(本题15分,每题3分) 1、总体得容量分别为10,15得两独立样本均值差________; 2、设为取自总体得一个样本,若已知,则=________; 3、设总体,若与均未知,为样本容量,总体均值得置信水平为得置信区间为,则得值为________; 4、设为取自总体得一个样本,对于给定得显著性水平,已知关于检验得拒绝域为2≤,则相应得 备择假设为________; 5、设总体,已知,在显著性水平0、05下,检验假设,,拒绝域就是________。 1、; 2、0、01; 3、; 4、; 5、。 二、选择题(本题15分,每题3分) 1、设就是取自总体得一个样本,就是未知参数,以下函数就是统计量得为( )。 (A) (B) (C) (D) 2、设为取自总体得样本,为样本均值,,则服从自由度为得分布得统计量为( )。 (A) (B) (C) (D) 3、设就是来自总体得样本,存在, , 则( )。 (A)就是得矩估计(B)就是得极大似然估计 (C)就是得无偏估计与相合估计(D)作为得估计其优良性与分布有关 4、设总体相互独立,样本容量分别为,样本方差分别为,在显著性水平下,检验得拒绝域为( )。 (A) (B) (C) (D) 5、设总体,已知,未知,就是来自总体得样本观察值,已知得置信水平为0、95得置信区间为(4、71,5、69),则取显著性水平时,检验假设得结果就是( )。 (A)不能确定(B)接受(C)拒绝(D)条件不足无法检验 1、B; 2、D; 3、C; 4、A; 5、B、 三、(本题14分) 设随机变量X得概率密度为:,其中未知 参数,就是来自得样本,求(1)得矩估计;(2)得极大似然估计。 解:(1) , 令,得为参数得矩估计量。 (2)似然函数为:, 而就是得单调减少函数,所以得极大似然估计量为。 四、(本题14分)设总体,且就是样本观察值,样本方差, ) 数理统计 一、填空题 1、设n X X X ,,21为母体X 的一个子样,如果),,(21n X X X g , 则称),,(21n X X X g 为统计量。不含任何未知参数 2、设母体σσμ),,(~2 N X 已知,则在求均值μ的区间估计时,使用的随机变量为 n X σ μ - 3、设母体X 服从修正方差为1的正态分布,根据来自母体的容量为100的子样,测得子样均值为5,则X 的数学期望的置信水平为95%的置信区间为 。 025.010 1 5u ?± ; 4、假设检验的统计思想是 。 小概率事件在一次试验中不会发生 5、某产品以往废品率不高于5%,今抽取一个子样检验这批产品废品率是否高于5%, 此问题的原假设为 。 0H :05.0≤p 6、某地区的年降雨量),(~2 σμN X ,现对其年降雨量连续进行5次观察,得数据为: (单位:mm) 587 672 701 640 650 ,则2 σ的矩估计值为 。 ~ 7、设两个相互独立的子样2121,,,X X X 与51,,Y Y 分别取自正态母体)2,1(2 N 与 )1,2(N , 2 *2 2*1,S S 分别是两个子样的方差,令2*2222*121)(,S b a aS +==χχ,已知)4(~),20(~22 2221χχχχ,则__________,==b a 。 用 )1(~)1(22 2 *--n S n χσ,1,5-==b a 8、假设随机变量)(~n t X ,则 21 X 服从分布 。)1,(n F 9、假设随机变量),10(~t X 已知05.0)(2 =≤λX P ,则____=λ 。 用),1(~2 n F X 得),1(95.0n F =λ 10、设子样1621,,,X X X 来自标准正态分布母体)1,0(N , X 为子样均值,而 01.0)(=>λX P , 则____=λ 01.04)1,0(~1z N n X =?λ 11、假设子样1621,,,X X X 来自正态母体),(2 σμN ,令∑∑==-=16 11 10 1 43i i i i X X Y ,则Y 的 分布 )170,10(2 σμN % 12、设子样1021,,,X X X 来自标准正态分布母体)1,0(N ,X 与2 S 分别是子样均值和子 样方差,令2*2 10S X Y =,若已知01.0)(=≥λY P ,则____=λ 。)9,1(01.0F =λ 13、如果,?1θ2?θ都是母体未知参数θ的估计量,称1?θ比2?θ有效,则满足 。 )?()?(2 1θθD D < 14、假设子样n X X X ,,,21 来自正态母体),(2σμN ,∑-=+-=1 1 2 12 )(?n i i i X X C σ 是2σ的一个无偏估计量,则_______=C 。 ) 1(21 -n 15、假设子样921,,,X X X 来自正态母体)81.0,(μN ,测得子样均值5=x ,则μ的置信度是95.0的置信区间为 。025.03 9 .05u ?± 16、假设子样10021,,,X X X 来自正态母体),(2 σμN ,μ与2 σ未知,测得子样均值 5=x ,子样方差12=s ,则μ的置信度是95.0的置信区间为 。 025.0025.0025.0)99(),99(10 1 5z t t ≈?± 17、假设子样n X X X ,,,21 来自正态母体),(2 σμN , μ与2σ未知,计算得 一.选择题(18分,每题3分) 1. 如果 1)()(>+B P A P ,则 事件A 与B 必定 ( ) )(A 独立; )(B 不独立; )(C 相容; )(D 不相容. 2. 已知人的血型为 O 、A 、B 、AB 的概率分别是; ;;。现任选4人,则4人血 型全不相同的概率为: ( ) )(A ; )(B 40024.0; )(C 0. 24; )(D 224.0. 3. 设~),(Y X ???<+=., 0, 1,/1),(22他其y x y x f π 则X 与Y 为 ( ) )(A 独立同分布的随机变量; )(B 独立不同分布的随机变量; )(C 不独立同分布的随机变量; )(D 不独立也不同分布的随机变量. 4. 某人射击直到中靶为止,已知每次射击中靶的概率为. 则射击次数的数 学期望与方差分别为 ( ) 、 )(A 4934与; )(B 16934与; )(C 4941与; (D) 9434与. 5. 设321,,X X X 是取自N (,)μ1的样本,以下μ的四个估计量中最有效的是( ) )(A 32112110351?X X X ++=μ ; )(B 32129 4 9231?X X X ++=μ ; )(C 321321 6131?X X X ++=μ ; )(D 32141254131?X X X ++=μ. 6. 检验假设222201:10,:10H H σσ≤>时,取统计量)(~10 )(22 2 12n X i n i χμχ-= ∑=,其 拒域为(1.0=α) ( ) )(A )(21.02n χχ≤;)(B )(21.02n χχ≥;)(C )(205.02n χχ≤;)(D )(2 05.02n χχ≥. 二. 填空题(15分,每题3分) 1. 已知事件A ,B 有概率4.0)(=A P ,5.0)(=B P ,条件概率3.0)|(=A B P ,则 =?)(B A P . 2. 设随机变量X 的分布律为??? ? ??-+c b a 4.01.02.043 21 ,则常数c b a ,,应满足的条件 ) 为 . 3. 已知二维随机变量),(Y X 的联合分布函数为),(y x F ,试用),(y x F 表示概率 习 题 一 1.下列随机试验各包含几个基本事件? (1)将有记号b a ,的两只球随机放入编号为Ⅰ,Ⅱ,Ⅲ 的盒子里(每个盒子可容纳两个球) 解:用乘法原理,三个盒子编号为Ⅰ,Ⅱ,Ⅲ看作不动物,。两个球看作是可动物,一个 一个地放入盒中;a 球可放入的任一个,其放法有 313=C 种,b 球也可放入三个盒子的 任一个,其放法有313=C 种,由乘法原理知:这件事共有的方法数为11339C C ?=种。 (2)观察三粒不同种子的发芽情况。 解:用乘法原理,三粒种子,每一粒种子按发芽与否是两种不同情况(方法)。三粒种子发芽共有81 21212=??C C C 种不同情况。 (3)从五人中任选两名参加某项活动。 解:从五人中任选两名参加某项活动,可不考虑任选的两人的次序, 所以此试验的基本事件个数 1025==C n 。 (4)某人参加一次考试,观察得分(按百分制定分)情况。 解:此随机试验是把从0到100 任一种分看作一个基本事件,101=∴n 。 (5)将c b a ,,三只球装入三只盒子中,使每只盒子各装一只球。 解:可用乘法原理:三只盒子视为不动物,可编号Ⅰ,Ⅱ,Ⅲ,三只球可视为可动物,一 个一个放入盒子内(按要求)。a 球可放入三个盒子中的任一个有313=C 种方法。b 球因 为试验要求每只盒子只装一个球,所以a 球放入的盒子不能再放入b 球,b 球只能放入其余(无a 球 的盒子)两个中任一个,其放法有21 2=C 个。c 只能放入剩下的空盒中,其放法只有一个。三个球任放入三个盒中保证每个盒只有一个球,完成这件事共有方法为 611213=??C C 种。 2. 事件A 表示“五件产品中至少有一件不合格品”,事件B 表示“五件产品都是合格品”,则,A B AB U 各表示什么事件?B A 、之间有什么关系? 解: 设k A =“五件中有k 件是不合格品” =B “五件都是合格品”。此随机试验E 的样 本空间可以写成:{}12345,,,,,S A A A A A B = 而 12345A A A A A A =U U U U ,A B S ∴=U φ=AB ,A 与B 是互为对立事件。 3. 随机抽验三件产品,设A 表示“三件中至少有一件是废品”,设B 表示“三件中至少有两件是废品”,C 表示“三件都是正品”,问 ,,,,A B C A B AC U 各表示什么事件? 创作编号: GB8878185555334563BT9125XW 创作者: 凤呜大王* 模拟试题一 一、 填空题(每空3分,共45分) 1、已知P(A) = 0.92, P(B) = 0.93, P(B|A ) = 0.85, 则P(A|B ) = 。 P( A ∪B) = 。 3、一间宿舍内住有6个同学,求他们之中恰好有4个人的生日在同一个月份的概率: ;没有任何人的生日在同一个月份的概率 ; 4、已知随机变量X 的密度函数为:, ()1/4, 020,2 x Ae x x x x ?? 8、设总体~(0,)0X U θθ>为未知参数,12,,,n X X X 为其样本, 1 1n i i X X n ==∑为样本均值,则θ的矩估计量为: 。 9、设样本129,, ,X X X 来自正态总体(,1.44)N a ,计算得样本观察值10x =, 求参数a 的置信度为95%的置信区间: ; 二、 计算题(35分) 1、 (12分)设连续型随机变量X 的密度函数为: 1, 02()2 0, x x x ??≤≤?=???其它 求:1){|21|2}P X -<;2)2 Y X =的密度函数()Y y ?;3)(21)E X -; 2、(12分)设随机变量(X,Y)的密度函数为 1/4, ||,02,(,)0, y x x x y ?<<?? 《概率论与数理统计》期末考试试题(A) 专业、班级: 姓名: 学号: 十二总成绩 、单项选择题(每题3分共18分) 1. D 2 . A 3 . B 4 . A 5 . (1) (2)设随机变量X其概率分布为X -1 0 1 2 P 则 P{X 1.5}() (A) (B) 1 (C) 0 (D) 设事件A与A同时发生必导致事件A发生,则下列结论正确的是( (A) P (A) P(A I A2) (B) P(A) P(A i) P(A2) (C) P(A) P(A1 A2) (D) P(A) P(A i) P(A2) 设随机变量X~N( 3, 1), Y ?N(2, 1),且X 与Y相互独 7,贝y z~(). (A) N(0, 5); (B) N(0, 3); (C) N(0, 46); (D) N(0, 54). (5)设 X1X2, 未知,贝U( n (A) X i2 i 1 ,X n为正态总体N(, )是一个统计量。 (B) (C) X (D) (6)设样本X i,X2, 为H o: (A)U (C) 2)的一个简单随机样本,其中2, ,X n来自总体X ~ N( 0( 0已知) (n 1)S2 2 二、填空题(每空3分 xe x 1. P(B) 2. f(x) 0 (1) 如果P(A) 0, P(B) H1 : (B) (D) 共15分) 0, P(A B) 设随机变量X的分布函数为 F(x) 则X的密度函数f(x) 3e P(A) n (X i ) i 1 2), 2未知。统计假设 则所用统计量为( 3 . 1 4. 则P(BA) 0, 1 (1 x)e x, x 0, 0. n (X i 1 P(X 设总体X和丫相互独立,且都服从N(0,1) , X1,X2, 样本,丫1,丫2, Y9是来自总体丫的样本,则统计量 服从分布(要求给出自由度)。t(9 ) 2) )2 X9是来自总体X的 X1 U肩 2(1)未知函数u 的导数最高阶为2,u ``,u `,u 均为一次,所以它是二阶线性方程。 (2) 为y 最高阶导数为1,而y 2为二次,故它是一阶非线性常微分方程。 (3) 果y 是未知函数,它是一阶线性方程;如果将x 看着未知函数,它是一阶非线 性方程。 3. 提示:所满足的方程为y ``-2 y `+y=0 4. 直接代入方程,并计算Jacobi 行列式。 5.方程变形为dy=2xdx=d(x 2),故y= x 2+C 6. 微分方程求解时,都与一定的积分运算相联系。因此,把求解一个微分方程的过程称为一个微分方程。微分方程的解又称为(一个)积分。 7. 把微分方程的通解用初等函数或通过它们的积分来表达的方法。注意如果通解能归结为初等函数的积分表达,但这个积分如果不能用初等函数表示出来,我们也认为求解了这个微分方程,因为这个式子里没有未知函数的导数或微分。 8. y `=f(x,y)主要特征是f(x,y)能分解为两个因式的乘积,其中一个因式仅含有x,另一因式仅含y ,而方程p(x,y)dx+q(x,y)dy=0是可分离变量方程的主要特征,就像f(x,y)一样,p,q 分别都能分解成两个因式和乘积。 9 (1) 积分得x=-cosx+c (2) 将方程变形为x 2 y 2 dy=(y-1)dx 或1-y y 2=2x dx ,当xy ≠0,y ≠1时积分得 22x +y+ln 1-y +x 1=c (3)方程变形为 y dy +1=x x sin cos dx,当y ≠-1,sinx ≠0时积分得 y=Csinx-1 (4)方程变形为 exp(y)dy=exp(2x)dx,积分得 exp(y)= 2 1 exp(2x)+C (5)当y ≠±1时,求得通积分ln 1 1 +-y y =x+c (6)方程化为 x 2 ydx=(1- y 2 )(1+x 2 )dx 或2 2 1x x +dx=y y 21-dy,积分得 x -arctgx -ln y + 2 1y 2 =C 学习好资料 第一套试卷及参考答案 一、选择题 ( 40 分) 1、根据某医院对急性白血病患者构成调查所获得的资料应绘制 ( B ) A 条图B 百分 条图或圆图C 线图D 直方图 2、均数和标准差可全面描述D 资料的特征 A 所有分布形式E负偏态分布C正偏态分布D正态分布和近似正态分布 3、要评价某市一名5岁男孩的身高是否偏高或偏矮,其统计方法是( A ) A 用该市五岁男孩的身高的95%或99%正常值范围来评价 B 用身高差别的假设检 验来评价 C 用身高均数的95%或99%的可信区间来评价 D 不能作评价 4、比较身高与体重两组数据变异大小宜采用( A ) A 变异系数 B 方差 C 标准差 D 四分位间距 5、产生均数有抽样误差的根本原因是( A ) A. 个体差异 B. 群体差异 C. 样本均数不同 D. 总体均数不同 6、男性吸烟率是女性的10 倍,该指标为( A ) (A)相对比(B)构成比(C)定基比(D )率 7、统计推断的内容为( D ) A.用样本指标估计相应的总体指标 B.检验统计上的“检验假设” C. A和B均不是 D. A和B均是 8、两样本均数比较用t 检验,其目的是检验( C ) A两样本均数是否不同B两总体均数是否不同 C 两个总体均数是否相同 D 两个样本均数是否相同 9、有两个独立随机的样本,样本含量分别为n i和住,在进行成组设计资料的t 检 验时,自由度是( D ) (A) n i+ n2 (B) n i+ n2 - C) n1+ n2 +1 D) n1+ n2 -2 10、标准误反映( A ) A 抽样误差的大小 B 总体参数的波动大小 C 重复实验准确度的高低 D 数据的离散程度 11、最小二乘法是指各实测点到回归直线的(C) A垂直距离的平方和最小E垂直距离最小 C纵向距离的平方和最小D纵向距离最小 12、对含有两个随机变量的同一批资料, 既作直线回归分析, 又作直线相关分析。 令对相关系数检验的t值为t r,对回归系数检验的t值为t b, 二者之间具有什么关系?( C) A t r >t b B t r 考试时间 120 分钟 班级 姓名 学号 一. 填空题(每题3分,共24分) 1.设 A 、B 为随机事件,P (A)=0.5,P(B)=0.6, P(B A)=0.8.则P(B )A U . 2. 三人独立的破译一个密码,他们能译出密码的概率分别为1/5、1/4、1/3,此密码能被译出的概率是= . 3. 设随机变量2 (,)X μσN :,X Y e =,则Y 的分布密度函数为 . 4. 设随机变量2(,)X μσN :,且二次方程2 40y y X ++=无实根的概率等于, 则μ= . 5. 设()16,()25D X D Y ==, 0.3 X Y ρ=,则 ()D X Y += . 6. 掷硬币n 次,正面出现次数的数学期望为 . 7. 某型号螺丝钉的重量是相互独立同分布的随机变量,其期望是1两,标准差是两. 则100个该型号螺丝钉重量不超过斤的概率近似为 (答案用标准正态分布函数表示). 8. 设125,,X X X L 是来自总体(0,1)X N :的简单随机样本,统计量 12()/~()C X X t n +,则常数C = ,自由度n = . 二 计算题 1.(10分)设袋中有m 只正品硬币,n 只次品硬币(次品硬币的两面均有国徽),从袋中任取一只硬币,将它投掷r 次,已知每次都得到国徽.问这只硬币是正品的概率是多少? 2.(10分)设顾客在某银行窗口等待服务的时间(以分计)X 服从指数分布,其概率密度函数为 /5 (1/5)0 ()0 x e x f x -?>=? ?其它 某顾客在窗口等待服务,若超过10分钟,他就离开. 他一个月到银行5次.以Y 表示一个月内他未等到服务而离开窗口的次数,写出Y 的分布律,并求{1}P Y ≥. 3.(10分)设二维随机变量(,)X Y 在边长为a 的正方形内服从均匀分布,该正方形的对角线为坐标轴,求: (1) 求随机变量X ,Y 的边缘概率密度; (2) 求条件概率密度|(|)X Y f x y . . 4.(10分)某型号电子管寿命(以小时计)近似地服从 2(160,20)N 分布,随机的选取四只,求其中没有一只寿 命小于180小时的概率(答案用标准正态分布函数表示). 厦门大学统计学考研868概率论与数理统计考试重难点、名校真题答案与考试真题 《概率论与数理统计教程》考试重难点与名校真题答案(茆诗松第二版)由群贤厦大考研网依托多年丰富的教学辅导经验,组织教学研发团队与厦门大学优秀研究生合作整理。全书内容紧凑权威细致,编排结构科学合理,为参加2019厦门大学考研同学量身定做的必备专业课资料。 《概率论与数理统计教程》考试重难点与名校真题答案全书编排根据厦门大学考研参考书目: 《概率论与数理统计教程》(茆诗松第二版) 本资料旨在帮助报考厦门大学考研的同学通过厦大教材章节框架分解、配套的课后/经典习题讲解及相关985、211名校考研真题与解答,为考生梳理指定教材的各章节内容,深入理解核心重难点知识,把握考试要求与考题命题特征。 通过研读演练本书,达到把握教材重点知识点、适应多样化的专业课考研命题方式、提高备考针对性、提升复习效率与答题技巧的目的。同时,透过测试演练,以便查缺补漏,为初试高分奠定坚实基础。 适用院系: 统计系:071400统计学(理学) 王亚南经济研究院:统计学(理学) 适用科目: 868概率论与数理统计 内容详情 本书包括以下几个部分内容: Part 1 - 考试重难点与笔记: 通过总结和梳理《概率论与数理统计教程》(茆诗松第二版)各章节复习和考试的重难点,建构教材宏观思维及核心知识框架,浓缩精华内容,令考生对各章节内容考察情况一目了然,从而明确复习方向,提高复习效率。该部分通过归纳各章节要点及复习注意事项,令考生提前预知章节内容,并指导考生把握各章节复习的侧重点。 Part 2 - 教材配套课后/经典习题与解答 针对教材《概率论与数理统计教程》(茆诗松第二版)课后/经典习题配备详细解读,以供考生加深对教材基本知识点的理解掌握,做到对厦大考研核心考点及参考书目内在重难点内容的深度领会与运用。 概率论与数理统计 答案 一.1.(D )、2.(D )、3.(A )、4.(C )、5.(C ) 二.1.0.85、2. n =5、3. 2 ()E ξ=29、4. 0.94、5. 3/4 三.把4个球随机放入5个盒子中共有54=625种等可能结果--------------3分 (1)A={4个球全在一个盒子里}共有5种等可能结果,故 P (A )=5/625=1/125------------------------------------------------------5 分 (2) 5个盒子中选一个放两个球,再选两个各放一球有 302415=C C 种方法----------------------------------------------------7 分 4个球中取2个放在一个盒子里,其他2个各放在一个盒子里有12种方法 因此,B={恰有一个盒子有2个球}共有4×3=360种等可能结果.故 125 72625360)(== B P --------------------------------------------------10分 四.解:(1) ?? ∞∞-==+=3 04ln 1,4ln 1)(A A dx x A dx x f ---------------------3分 (2)? ==+=<10 212ln 1)1(A dx x A P ξ-------------------------------6分 (3)3 300()()[ln(1)]1Ax E xf x dx dx A x x x ξ∞-∞= ==-++?? 13(3ln 4)1ln 4ln 4 =-=-------------------------------------10分 五.解:(1)ξ的边缘分布为 ??? ? ??29.032.039.02 1 0--------------------------------2分 η的边缘分布为 ??? ? ??28.034.023.015.05 4 2 1---------------------------4分 因)1()0(05.0)1,0(==≠===ηξηξP P P ,故ξ与η不相互独立-------5分 (2)ξη?的分布列为 第一学期成人本科 数理统计学试题 一、选择题(每题1分,共30分) 1、样本是总体中:(D) A、任意一部分 B、典型部分 C、有意义的部分 D、有代表性的部分 E、有价值的部分 2、参数是指:(C) A、参与个体数 B、研究个体数 C、总体的统计指标 D、样本的总和 E、样本的统计指标 3、抽样的目的是:(E) A、研究样本统计量 B、研究总体统计量 C、研究典型案例 D、研究误差 E、样本推断总体参数 4、脉搏数(次/分)是:(B) A、观察单位 B、数值变量 C、名义变量D.等级变量E.研究个体 5、疗效是:(D) A、观察单位 B、数值变量 C、名义变量 D、等级变量 E、研究个体 6、抽签的方法属于(D) A、分层抽样 B、系统抽样 C、整群抽样 D、单纯随机抽样 E、二级抽样 7、统计工作的步骤正确的是(C) A、收集资料、设计、整理资料、分析资料 B、收集资料、整理资料、设计、统计推断 C、设计、收集资料、整理资料、分析资料 D、收集资料、整理资料、核对、分析资料 E、搜集资料、整理资料、分析资料、进行推断 8、实验设计中要求严格遵守四个基本原则,其目的是为了:(D) A、便于统计处理 B、严格控制随机误差的影响 C、便于进行试验 D、减少和抵消非实验因素的干扰 E、以上都不对 9、对照组不给予任何处理,属(E) A、相互对照 B、标准对照 C、实验对照 D、自身对照 E、空白对照 10、统计学常将P≤0.05或P≤0.01的事件称(D) A、必然事件 B、不可能事件 C、随机事件 D、小概率事件 E、偶然事件 11、医学统计的研究内容是(E) A、研究样本 B、研究个体 C、研究变量之间的相关关系 D、研究总体 E、研究资料或信息的收集.整理和分析 12、统计中所说的总体是指:(A) A、根据研究目的确定的同质的研究对象的全体 B、随意想象的研究对象的全体 C、根据地区划分的研究对象的全体 D、根据时间划分的研究对象的全体 E、根据人群划分的研究对象的全体 13、概率P=0,则表示(B) A、某事件必然发生 B、某事件必然不发生 C、某事件发生的可能性很小 D、某事件发生的可能性很大 E、以上均不对 14、总体应该由(D) A、研究对象组成 B、研究变量组成 C、研究目的而定 D、同质个体组成 E、个体组成 15、在统计学中,参数的含义是(D) 概率论与数理统计B 一.单项选择题(每小题3分,共15分) 1.设事件A 和B 的概率为12 () ,()23 P A P B == 则()P AB 可能为() (A) 0; (B) 1; (C) 0.6; (D) 1/6 2. 从1、2、3、4、5 这五个数字中等可能地、有放回地接连抽取两个数字,则这两个数字不相同的概率为() (A) 12 ; (B) 225; (C) 425 ; (D)以上都不对 3.投掷两个均匀的骰子,已知点数之和是偶数,则点数之和为6的概率为( ) (A) 518; (B) 13; (C) 1 2 ; (D)以上都不对 4.某一随机变量的分布函数为()3x x a be F x e += +,(a=0,b=1)则F (0)的值为( ) (A) 0.1; (B) 0.5; (C) 0.25; (D)以上都不对 5.一口袋中有3个红球和2个白球,某人从该口袋中随机摸出一球,摸得红球得5分,摸得白球得2分,则他所得分数的数学期望为( ) (A) 2.5; (B) 3.5; (C) 3.8; (D)以上都不对 二.填空题(每小题3分,共15分) 1.设A 、B 是相互独立的随机事件,P (A )=0.5, P (B )=0.7, 则()P A B = . 2.设随机变量~(,), ()3, () 1.2B n p E D ξ ξξ==,则n =______. 3.随机变量ξ的期望为() 5E ξ=,标准差为()2σξ=,则2()E ξ=_______. 4.甲、乙两射手射击一个目标,他们射中目标的概率分别是0.7和0.8.先由甲射击,若甲未射中再由乙射击。设两人的射击是相互独立的,则目标被射中的概率为_________. 5.设连续型随机变量ξ的概率分布密度为 2 ()22 a f x x x = ++,a 为常数,则P (ξ≥0)=_______. 三.(本题10分)将4个球随机地放在5个盒子里,求下列事件的概率 (1) 4个球全在一个盒子里; (2) 恰有一个盒子有2个球. 四.(本题10分) 设随机变量ξ的分布密度为 , 03()10, x<0x>3 A x f x x ?? =+???当≤≤当或 (1) 求常数A ; (2) 求P (ξ<1); (3) 求ξ的数学期望. 五.(本题10分) 设二维随机变量(ξ,η)的联合分布是数理统计试题及答案
《应用数理统计》吴翊李永乐第三章 假设检验课后作业参考答案
《数理统计》试卷及答案
概率论与数理统计学1至7章课后标准答案
概率论与数理统计(经管类)复习试题及答案
硕士生《数理统计》例题及答案
数理统计试题及答案
数理统计课后答案
概率论与数理统计试题及答案
概率论与数理统计-朱开永--同济大学出版社习题一答案
概率论与数理统计期末考试题及答案
概率论与数理统计期末考试试题及答案
数理统计考研复试题库及答案
医药数理统计习题及答案汇编
概率论与数理统计试题及答案
厦门大学统计学考研868概率论与数理统计考试重难点名校真题答案与考试真题
概率论与数理统计试卷及答案
数理统计学试题 答案
概率论与数理统计试题及答案2[1]