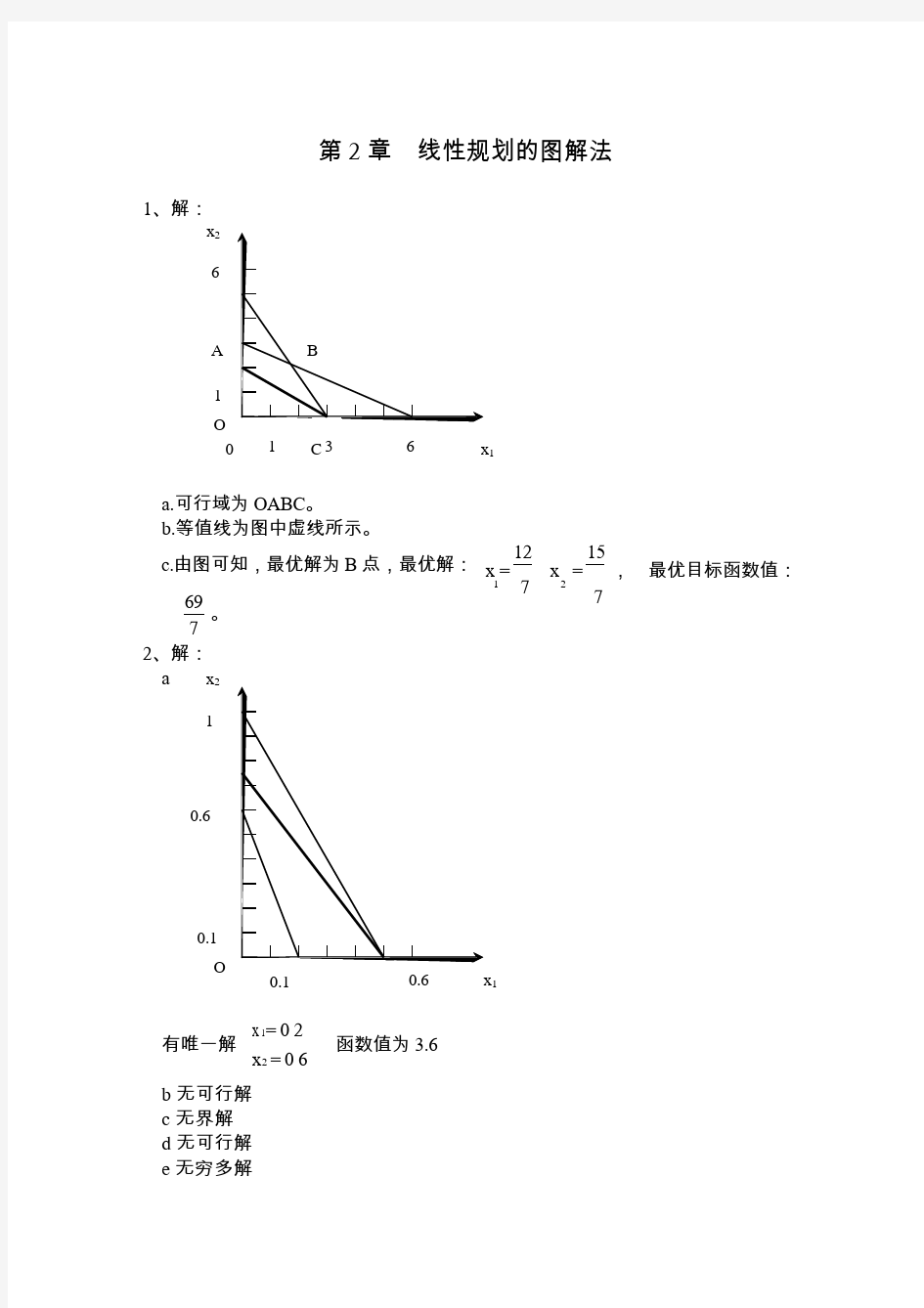

第 2 章 线性规划的图解法
a.可行域为 OABC 。
b.等值线为图中虚线所示。
c.由图可知,最优解为 B 点,最优解: 12
15
x =
x = , 最优目标函数值: 69 7 1
。 7 2
7
有唯一解
1 x
2 = 0 6
函数值为 3.6
b 无可行解
c 无界解
d 无可行解
e 无穷多解
x 1 = f 有唯一解
x2 =
3、解:
a 标准形式:
max 20
3
8
3
f =
92
函数值为
3
3x 1 + 2 x 2 + 0s 1 + 0 s2 + 0s 3
b 标准形式:
max f 9 x 1 + 2 x 2 + s 1 = 30
3 x 1 + 2 x 2 + s 2 = 13
2 x 1 + 2 x 2 + s
3 = 9
x 1 , x 2 , s 1 , s 2 , s 3 ≥ 0 = ?4 x ? 6 x ? 0s ? 0s
c 标准形式:
1 3 1 2
3 x 1 ?x 2 ?s 1 = 6
x 1 + 2 x 2 + s 2 = 10
7 x 1 ? 6 x2 = 4
x 1 , x 2 , s 1, s 2 ≥ 0
' ' ''
max f = ?x + 2x ? 2x ? 0s ? 0s
1
? 3 x 1
+
'
2 2 1 2
'
5 x2 ? 5 x 2 + s 1 = 70
'
2x1 ? 5x2 + 5x2 = 50
' '
3x1 + 2
' '
x 1 , x
4 、解:
x 2 ? 2 x 2 ?s 2 = 30 2 , x 2, s 1, s 2 ≥ 0
标准形式:max z = 10 x + 5 x + 0s + 0 s
1 2 1 2
3x + 4x + s = 9
1 2 1
5x + 2x + s = 8
1 2 2
x , x , s , s ≥ 0
1 2 1 2
s = 2, s = 0
1 2
5 、解:
标准形式:min f = 11x + 8 x + 0s + 0s + 0s
1 2 1 2 3
10x + 2x ?s = 20
1 2 1
3x + 3x ?s = 18
1 2 2
4x + 9x ?s = 36
1 2 3
x , x , s , s , s ≥ 0
1 2 1 2 3
s = 0, s = 0, s = 13
1 2 3
6 、解:
b 1 ≤ c1≤3
c 2 ≤ c2 ≤ 6
x 1 = 6
d e x2 = 4
x 1∈[ 4 , 8 ] x 2 = 16 ? 2 x 1
f 变化。原斜率从
7、解:
模型:
2
?变为? 1 3
max z = 500x + 400x
1 2
2x 1 ≤ 300
3x 2 ≤ 540
2x + 2x ≤ 440
1 2
1.2x +1.5x ≤ 300
1 2
x1, x2 ≥ 0
a x1 = 150 x2 = 70 即目标函数最优值是103000
b 2,4有剩余,分别是 330,15。均为松弛变量
c 50, 0 ,200, 0 额外利润 250
d 在 [0 ,500] 变化,最优解不变。
e 在 400到正无穷变化,最优解不变。
f 不
变
8 、解:
a 模型:min f = 8x + 3x
a b
50x + 100x ≤ 1200000
a b
5x + 4x ≥ 60000
a b
100x b ≥ 300000
x a , x b ≥ 0
基金 a,b分别为 4000,10000。
回报率:60000
b 模型变为:max z = 5x + 4x
a b
50x + 100x ≤ 1200000
a b
100x b ≥ 300000
x a , x b ≥ 0
推导出:x1 = 18000 x2 = 3000
故基金 a投资 90万,基金 b投资 30万。
第 3章线性规划问题的计算机求解
1、解:
a x1 = 150 x2 = 70 目标函数最优值 103000
b 1,3使用完2,4没用完0,330,0,15
c 50,0,200,0
含义: 1车间每增加 1工时,总利润增加 50元
3车间每增加 1工时,总利润增加 200元
2、4车间每增加 1工时,总利润不增加。
d 3车间,因为增加的利润最大
e 在 400到正无穷的范围内变化,最优产品的组合不变
f 不变因为在 [0 ,500] 的范围内
g 所谓的上限和下限值指当约束条件的右边值在给定范围内变化时,约束条
件 1的右边值在 [200,440] 变化,对偶价格仍为 50(同理解释其他约束条件)
h 100×50=5000 对偶价格不变
i 能
j 不发生变化允许增加的百分比与允许减少的百分比之和没有超出 100%
k 发生变化
2、解:
a 4000 10000 62000
b 约束条件 1:总投资额增加 1个单位,风险系数则降低 0.057
约束条件 2:年回报额增加 1个单位,风险系数升高 2.167
c 约束条件 1的松弛变量是 0,约束条件 2的剩余变量是 0
约束条件 3为大于等于,故其剩余变量为 700000
d 当c 不变时,c 在 3.75到正无穷的范围内变化,最优解不变
2 1
当c 不变时,c 在负无穷到 6.4的范围内变化,最优解不变
1 2
e 约束条件 1的右边值在 [780000 ,1500000]变化,对偶价格仍为0.057(其他
同理)
f 不能,理由见百分之一百法则二
3 、解:
a 18000 3000 102000 153000
b 总投资额的松弛变量为 0 基金 b的投资额的剩余变量为 0
c 总投资额每增加 1个单位,回报额增加 0.1
基金 b的投资额每增加 1个单位,回报额下降 0.06
d c 不变时,c 在负无穷到 10的范围内变化,其最优解不变
1 2
c 不变时,c 在 2到正无穷的范围内变化,其最优解不变
2 1
e 约束条件1的右边值在300000到正无穷的范围内变化,对偶价格仍为0.1 约束条件 2的右边值在 0到 1200000的范围内变化,对偶价格仍为-0.06
f 600000
900000
300000
+ = 100% 故对偶价格不变
900000
4、解:
a x1 = 8 5 x2 = 1 5 x3 = 0 x4 = 1 最优目标函数 18.5
b 约束条件 2和 3 对偶价格为 2和 3.5
c 选择约束条件 3,最优目标函数值 22
d 在负无穷到 5.5的范围内变化,其最优解不变,但此时最优目标函数值变化
e 在0到正无穷的范围内变化,其最优解不变,但此时最优目标函数值变化
5、解:
a 约束条件 2的右边值增加 1个单位,目标函数值将增加 3.622
b x2 产品的利润提高到 0.703,才有可能大于零或生产
c 根据百分之一百法则判定,最优解不变
d 因为
15
30 ? 9 189
65
+ > 100 % 根据百分之一百法则二,我们不能判定
111 25 ? 15
其对偶价格是否有变化
第 4章线性规划在工商管理中的应用
1、解:为了用最少的原材料得到 10台锅炉,需要混合使用 14种下料方案
设按 14种方案下料的原材料的根数分别为 x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,则可列出下面的数学模型:
min f=x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12+x13+x14
s.t.2x1+x2+x3+x4≥ 80
x2+3x5+2x6+2x7+x8+x9+x10≥350
x3+x6+2x8+x9+3x11+x12+x13≥420
x4+x7+x9+2x10+x12+2x13+3x14 ≥ 10
x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14≥ 0 用
管理运筹学软件我们可以求得此问题的解为:
x1=40,x2=0,x3=0,x4=0,x5=116.667,x6=0,x7=0,x8=0,x9
=0,x10=0,x11=140,x12=0,x13=0,x14=3.333
最优值为 300。
2、解:从上午 11时到下午 10时分成 11个班次,设 x i表示第 i班次安排的临时
工的人数,则可列出下面的数学模型:
min f=16(x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11)
s.t.x1+1 ≥ 9
x1+x2+1 ≥ 9
x1+x2+x3+2 ≥ 9
x1+x2+x3+x4+2 ≥ 3
x 2+x 3+x 4+x 5+1 ≥ 3 x 3+x 4+x 5+x 6+2 ≥ 3 x 4+x 5+x 6+x 7+1 ≥ 6 x 5+x 6+x 7+x 8+2 ≥ 12 x 6+x 7+x 8+x 9+2 ≥ 12 x 7+x 8+x 9+x 10+1 ≥ 7 x 8+x 9+x 10+x 11+1 ≥ 7
x 1,x 2,x 3,x 4,x 5,x 6,x 7,x 8,x 9,x 10,x 11≥ 0 用管理运筹学软件我们可以求得此问题的解为:
x 1=8,x 2=0,x 3=1,x 4=1,x 5=0,x 6=4,x 7=0,x 8=6,x 9=0, x 10=0,x 11=0 最优值为 320。
a 、 在满足对职工需求的条件下,在 10 时安排 8 个临时工,12 时新安排 1 个临时工,13 时新安排 1 个临时工,15 时新安排 4 个临时工,17 时新 安排 6 个临时工可使临时工的总成本最小。
b 、 这时付给临时工的工资总额为 80 元,一共需要安排 20 个临时工的班 次。
约束
松弛/剩余变量 对偶价格
1
0 -4 2 0 0 3 2 0 4 9 0 5 0 -4 6 5 0 7 0 0 8 0 0 9 0 -4 10 0 0 11
根据剩余变量的数字分析可知,可以让 11 时安排的 8 个人工作 3 小时,13 时安排的 1 个人工作 3 小时,可使得总成本更小。
C 、设在 11:00-12:00 这段时间内有 x 个班是 4 小时, y 个班是 3 小时;
设在 12:00-13:00 这段时间内有 1 x 个班是 4 小时, y 1
个班是 3 小时;其他时
段也类似。
则:由题意可得如下式子:
11
11
min z = 16 x + 12
2
2
y
∑
i = 1
1
∑
i = 1
1
S.T
x + y +1 ≥ 9
1 1
x + y + x + y +1 ≥ 9
1 1
2 2
x + y + x + y + x + y +1+1 ≥ 9
1 1
2 2
3 3
x + x + y + x + y + x + y +1+1 ≥ 3
1 2 2 3 3 4 4
x + x + y + x + y + x + y +1 ≥ 3
2 3 3 4 4 5 5
x + x + y + x + y + x + y +1+1 ≥ 3
3 4 4 5 5 6 6
x + x + y + x + y + x + y +1 ≥ 6
4 5 5 6 6 7 7
x + x + y + x + y + x + y +1+1 ≥ 12
5 6 6 7 7 8 8
x + x + y + x + y + x + y +1+1 ≥ 12
6 7 7 8 8 9 9
x + x + y + x + y + x + y +1 ≥ 7
7 8 8 9 9 10 10
x + x + y + x + y + x + y +1 ≥ 7
8 9 9 10 10 11 11
x i ≥ 0, y i ≥ 0 i=1,2,…,11
稍微变形后,用管理运筹学软件求解可得:总成本最小为 264元。
安排如下:y1=8(即在此时间段安排 8个 3小时的班),y3=1,y5=1,y7=4,x8=6 这样能比第一问节省:320-264=56元。
3、解:设生产A、B、C三种产品的数量分别为x1,x2,x3,则可列出下面的
数学模型:
max z=10 x1+12 x2+14 x2
s.t. x1+1.5x2+4x3 ≤ 2000
2x1+1.2x2+x3≤ 1000
x1 ≤ 200
x2 ≤ 250
x3 ≤ 100
x1,x2,x3≥ 0
用管理运筹学软件我们可以求得此问题的解为:
x1=200,x2=250,x3=100
最优值为 6400。
a、在资源数量及市场容量允许的条件下,生产A 200件,B 250件,C 100
件,可使生产获利最多。
b、A、B、C的市场容量的对偶价格分别为 10元,12元,14元。材料、台
时的对偶价格均为 0。说明 A的市场容量增加一件就可使总利润增加 10
元,B的市场容量增加一件就可使总利润增加 12元,C的市场容量增加
一件就可使总利润增加 14元。但增加一千克的材料或增加一个台时数都
不能使总利润增加。如果要开拓市场应当首先开拓 C产品的市场,如果
要增加资源,则应在 975到正无穷上增加材料数量,在 800到正无穷上
增加机器台时数。
4、解:设白天调查的有孩子的家庭的户数为 x11,白天调查的无孩子的家庭的户
数为 x12,晚上调查的有孩子的家庭的户数为 x21,晚上调查的无孩子的家庭的户数为 x22,则可建立下面的数学模型:
min f=25x11+20x12+30x21+24x22
s.t.x11+x12+x21+x22≥ 2000
x11+x12=x21+x22
x11+x21≥ 700
x12+x22≥ 450
x11, x12, x21, x22 ≥ 0
用管理运筹学软件我们可以求得此问题的解为:
x11=700,x12=300,x21=0,x22=1000
最优值为 47500。
a、白天调查的有孩子的家庭的户数为 700户,白天调查的无孩子的家庭的户
数为 300户,晚上调查的有孩子的家庭的户数为 0,晚上调查的无孩子的
家庭的户数为 1000户,可使总调查费用最小。
b、白天调查的有孩子的家庭的费用在 20-26元之间,总调查费用不会变化;
白天调查的无孩子的家庭的费用在 19-25元之间,总调查费用不会变化;
晚上调查的有孩子的家庭的费用在 29-无穷之间,总调查费用不会变化;
晚上调查的无孩子的家庭的费用在-20-25元之间,总调查费用不会变
化。
c、调查的总户数在 1400-无穷之间,总调查费用不会变化;
有孩子家庭的最少调查数在 0-1000之间,总调查费用不会变化;
无孩子家庭的最少调查数在负无穷-1300之间,总调查费用不会变化。5、解:设第i个月签订的合同打算租用j个月的面积为x ij,则需要建立下面的
数学模型:
min f=2800(x11+x21+x31+x41)+4500(x12+x22+x32)+6000(x13+x23)+7300 x14
s.t.x11+x12+x13+x14≥ 15
x12+x13+x14+x21+x22+x23≥10
x13+x14+x22+x23+x31+x32≥20
x14+x23+x32+x41≥ 12
x ij≥ 0,i,j=1,2,3,4
用管理运筹学软件我们可以求得此问题的解为:
x11=5,x12=0,x13=10,x14=0,x21=0,x22=0,x23=0,x31=10,x32
=0,x41=0
最优值为 102000。
即:在一月份租用 500平方米一个月,租用 1000平方米三个月;在三月份租用 1000平方米一个月,可使所付的租借费最小。
6、解:设 x ij表示第 i种类型的鸡需要第 j种饲料的量,可建立下面的数学模型:
max z=9(x11+x12+x13)+7(x21+x22+x23)+8(x31+x32+x33)-5.5
(x11+x21+x31)-4(x12+x22+x32)-5(x13+x23+x33)
s.t.x11≥ 0.5(x11+x12+x13)
x12 ≤ 0.2(x11+x12+x13)
x21 ≥0.3(x21+x22+x23)
x23 ≤ 0.3(x21+x22+x23)
x33 ≥ 0.5(x31+x32+x33)
x11+x21+x31≤ 30
x12+x22+x32≤ 30
x13+x23+x33≤30
x ij ≥ 0,i,j=1,2,3
用管理运筹学软件我们可以求得此问题的解为:
x11=30,x12=10,x13=10,x21=0,x22=0,x23=0,x31=0,x32
=20,x33=20
最优值为 365。
即:生产雏鸡饲料 50吨,不生产蛋鸡饲料,生产肉鸡饲料 40吨。
7、
设 X i——第 i个月生产的产品 I数量
Y i——第 i个月生产的产品 II数量
Z i,W i分别为第 i个月末产品 I、II库存数
S1i,S2i分别为用于第(i+1)个月库存的自有及租借的仓库容积(立方米)。则可建立如下模型:
5 12 12
min z = ∑
(5 x i + 8 y
i )
i = 1
s.t.
X1-10000=Z1
X2+Z1-10000=Z2
X3+Z2-10000=Z3
X4+Z3-10000=Z4
X5+Z4-30000=Z5
X6+Z5-30000=Z6
X7+Z6-30000=Z7
X8+Z7-30000=Z8
X9+Z8-30000=Z9
X10+Z9-100000=Z10 X11+Z10-100000=Z11 X12+Z11-100000=Z12 Y1-50000=W1
Y2+W1-50000=W2
Y3+W2-15000=W3
Y4+W3-15000=W4
Y5+W4-15000=W5
Y6+W5-15000=W6
Y7+W6-15000=W7
Y8+W7-15000=W8 + ∑(4 5 x i + 7 y i ) + ∑( s 1 i + 1 5s 2i )
i = 6 i = 1
Y9+W8-15000=W9
Y10+W9-50000=W10
Y11+W10-50000=W11
Y12+W11-50000=W12
S1i≤15000 1≤i≤12
X i+Y i≤120000 1≤i≤12
0.2Z i+0.4W i=S1i+S2i 1≤i≤12
X i≥0, Y i≥0, Z i≥0, W i≥0, S1i≥0, S2i≥0
用管理运筹学软件我们可以求得此问题的解为:最
优值= 4910500
X1=10000, X2=10000, X3=10000, X4=10000, X5=30000, X6=30000, X7=30000,
X8=45000, X9=105000, X10=70000, X11=70000, X12=70000;
Y1= 50000, Y2=50000, Y3=15000, Y4=15000, Y5=15000,
Y6=15000,Y7=15000,Y8=15000,Y9=15000,Y10=50000,Y11=50000,Y12=50000;
Z8=15000, Z9=90000, Z10 =60000, Z1=30000;
S18=3000,S19=15000,S110=12000,S111=6000;
S28=3000;
其余变量都等于 0
8、解:设第 i个车间生产第 j种型号产品的数量为 x ij,可建立下面的数学模型:
max z=25(x11+x21+x31+x41+x51)+20(x12+x32+x42+x52)+17(x13
+x23+x43+x53)+11(x14+x24+x44)
s.t. x11+x21+x31+x41+x51≤ 1400
x12+x32+x42+x52≥ 300
x12+x32+x42+x52≤800
x13+x23+x43+x53≤8000
x14+x24+x44 ≥ 700
5x11+7x12+6x13+5x14≤ 18000
6x21+3x23+3x24≤ 15000
4x31+3x32≤ 14000
3x41+2x42+4x43+2x44≤12000
2x51+4x52+5x53≤ 10000
x ij ≥ 0,i=1,2,3,4,5 j=1,2,3,4
用管理运筹学软件我们可以求得此问题的解为:
x11=0,x12=0,x13=1000,x14=2400,x21=0,x23=5000,x24=0,x31
=1400,x32=800,x41=0,x42=0,x43=0,x44=6000,x51=0,x52=0,
x53=2000
最优值为 279400
9、解:设第一个月正常生产 x1,加班生产 x2,库存 x3;第二个月正常生产 x4,
加班生产 x5,库存 x6;第三个月正常生产 x7,加班生产 x8,库存 x9;第
四个月正常生产 x10,加班生产 x11,可建立下面的数学模型:
min f = 200(x1+x4+x7+x10)+300(x2+x5+x8+x11)+60(x3+x6
+x9)
s.t.
x1≤4000
x4≤4000
x7≤4000
x10≤4000
x3≤1000
x6≤1000
x9≤1000
x2≤1000
x5≤1000
x8≤1000
x11≤1000
x1+ x2- x3=4500
x3+ x4+ x5- x6=3000
x6+ x7+ x8- x9=5500
x9+ x10+ x11=4500
x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11≥0
计算结果是:
min f= 3710000元
x1=4000吨,x2=500吨,x3=0吨,x4=4000吨,x5=0吨,
x6=1000吨,x7=4000吨,x8=500吨,x9=0吨,x10=4000吨,x11=500吨。
第 5章单纯形法
1、解:表中 a、c、e、f是可行解,a、b、f是基本解,a、f是基本可行解。
2、解:a、该线性规划的标准型为:
max 5 x1+9 x2
s.t.0.5 x1+x2+s1=8
x1+x2-s2=10
0.25x1+0.5x2-s3=6
x1,x2,s1,s2,s3≥0.
b、有两个变量的值取零,因为有三个基变量、两个非基变量,非基变量
取零。
c、(4,6,0,0,-2)
d、(0,10,-2,0,-1)
e、不是。因为基本可行解要求基变量的值全部非负。
3
b、线性规划模型为:
max 6 x1+30 x2+25 x3
s.t.3 x1+x2+s1 = 40
2 x1+x3+s2= 50
2 x1+x2-x3+s3=20
x1,x2,x3,s1,s2,s3≥0
c、初始解的基为(s1,s2,s3),初始解为(0,0,0,40,50,20),
对应的目标函数值为 0。
d、第一次迭代时,入基变量是 x2,出基变量为 s3。
4、解:最优解为(2.25,0),最优值为 9。
1
5、解:a、最优解为(2,5,4),最优值为84。
b、最优解为(0,0,4),最优值为-4。
6、解:a、有无界解
b、最优解为(0.714,2.143,0),最优值为-2.144。
7、解:a、无可行解
b、最优解为(4,4),最优值为 28。
c、
有无界解
d、最优解为(4,0,0),最优值为 8。
第 6 章
单纯形法的灵敏度分析与对偶
1
a.c1≤24
b.c2≥6
c.c s2≤8
2
a. c1≥-0.5
b. -2≤c3≤0
c. c s2≤0.5
3
a. b1≥150
b. 0≤b2≤83.333
c. 0≤b3≤150
4
a. b1≥-4
b. 0≤b2≤300
c. b3≥4
5
a. 利润变动范围 c1≤3,故当 c1=2 时最优解不变
b. 根据材料的对偶价格为 1判断,此做法不利
c. 0≤b2≤45
d. 最优解不变,故不需要修改生产计划
e. 此时生产计划不需要修改,因为新的产品计算的检验数为-12 小于零,对原生
产计划没有影响。
6
均为唯一最优解,根据从计算机输出的结果看出,如果松弛或剩余变量为零且对应的对偶价格也为零,或者存在取值为零的决策变量并且其相差值也为零时,可知此线性规划有无穷多组解。
7
a. min f= 10y1+20y2.
s.t. y1+y2≥2,
y1+5y2≥1,
y1+y2≥1,
y1, y2≥0.
b. max z= 100 y1+200 y2.
s.t. 1/2 y1+4 y2≤4,
2 y1+6 y2≤4,
2 y1+
3 y2≤2,
y1, y2≥0.
8.
a. min f= -10 y1+50 y2+20 y3-20 y4. s.t. -2 y1+3 y2+ y3- y2≥1,
3 y1+ y2 ≥2,
- y1+ y2+ y3- y2 =5,
y1, y2, y2≥0, y3没有非负限制。
b. max z= 6 y1-3 y2+2 y3-2 y4.
s.t. y1- y2- y3+ y4≤1,
2 y1+ y2+ y3- y4=3,
-3 y1+2 y2- y3+ y4≤2,
y1, y2, y4≥0, y3没有非负限制9. 对偶单纯形为
max z=4 y1-8 y2+2 y3
s.t y1- y2≤1,
- y1- y2+ y3≤2,
y1-2 y2- y3≤3,
y1, y2, y3≥0
目标函数最优值为: 10
最优解: x1=6, x2=2, x3=0
第 7章运输问题
1.
最优解如下
**
起至销点
发点 1 2 3 4
----- ----- ----- -----
1 0 250 0 50
2 400 0 0 0
3 0 0 350 150 此运输问题的成本或收益为: 19800
此问题的另外的解如下:
起至销点
发点 1 2 3 4
----- ----- ----- -----
1 0 250 50 0
2 400 0 0 0
3 0 0 300 200 此运输问题的成本或收益为: 19800
(2)如果 2分厂产量提高到 600,则为产销不平衡问题
最优解如下
**
起至销点
发点 1 2 3 4
----- ----- ----- -----
1 0 250 0 0
2 400 0 0 200
3 0 0 350 0
此运输问题的成本或收益为: 19050
注释:总供应量多出总需求量200
第 1个产地剩余50
第 3个产地剩余150
(3)销地甲的需求提高后,也变为产销不平衡问题
最优解如下
**
起至销点
发点 1 2 3 4
----- ----- ----- -----
1 50 250 0 0
2 400 0 0 0
3 0 0 350 150
此运输问题的成本或收益为: 19600
注释:总需求量多出总供应量150
第 1个销地未被满足,缺少100
第 4个销地未被满足,缺少50
最优解如下
**
起至销点
发点 1 2 3 4 5 6 7 8 ----- ----- ----- ----- ----- ----- ----- -----
1 0 0 100 0 0 200 0 0
2 0 0 0 0 350 0 0 150
3 0 50 0 100 0 0 250 0
4 0 100 0 0 0 0 0 0
5 150 0 50 0 0 0 0 0 此运输问题的成本或收益为: 1.050013E+07
最优解如下
**
起至销点
发点 1 2 3 4
----- ----- ----- -----
1 2 0 0 0
2 1 1 1 0
3 0 0 0 3
4 0 4 0 0
5 0 0 0 2
6 0 0 2 0
7 0 0 3 0 此运输问题的成本或收益为: 8465
此问题的另外的解如下:
起至销点
发点 1 2 3 4
----- ----- ----- -----
1 2 0 0 0
2 1 2 0 0
3 0 0 0 3
4 0 3 1 0
5 0 0 0 2
6 0 0 2 0
7 0 0 3 0 此运输问题的成本或收益为: 8465
《管理运筹学》课程教学大纲 课程编号:182002 英文名:Management Operations 课程类别:专业基础课 适用专业:信息管理与信息系统、物流管理、财务管理等 前置课:微积分、线性代数、概率统计、统计学、管理学原理 后置课:生产运作管理、管理系统工程、企业战略管理等 学分:4学分 课时:72课时 一、课程教学目标及学生应达到的能力 本课程是工商管理和信息管理与信息系统的专业基础课,通过本课程教学,使学生掌握“运筹学”各主要分支的基本概念、数学模型及其求解方法,掌握运筹学整体优化的思想和若干定量分析的优化技术。因此,开设运筹学课程的目的是使学生能够运用运筹学理论把实际问题构建成数学模型,选择适当的优化方法,求出最优解或满意解全过程的训练,提高学生分析和解决实际问题的能力,也为进一步学习后继课程打下坚实的基础。 二、课程教学内容与基本要求 (一)运筹学概论(2学时) 1.主要内容: 运筹学的产生、发展及应用;运筹学的主要分支。 2.基本要求 了解运筹学的产生、发展及最新发展动向和成果;了解本学科的研究内容、特点及研究方法。3.自学内容:线性代数 4.课外实践:无 (二)线性规划与单纯形法(14学时) 1.主要内容: 线性规划问题及其数学模型、线性规划问题的图解法、线性规划的基本概念和基本定理、单纯形法。 2.基本要求 (1)初步掌握建立线性规划模型方法 (2)掌握线性规划模型特征;如何化线性规划模型为标准型 (3)掌握两个变量线性规划问题的图解法 (4)了解线性规划理论依据---几个基本定理、求解线性规划问题基本思路 (5)了解引入工人变量目的 (6)牢固掌握大M法和两阶段法求解过程、判别什么情况下无解 3.自学内容:矩阵论 4.课外实践:无 (三)对偶理论与灵敏度分析(10学时) 1.主要内容: 改进单纯形法、线性对偶规划对偶问题的经济学解释——影子价格、对偶单纯形法、灵敏度分析与参数线性规划
《管理运筹学》(第二版)课后习题参考答案 第1章线性规划(复习思考题) 1.什么是线性规划?线性规划的三要素是什么? 答:线性规划(Linear Programming,LP)是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。 建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。 2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误? 答:(1)唯一最优解:只有一个最优点; (2)多重最优解:无穷多个最优解; (3)无界解:可行域无界,目标值无限增大; (4)没有可行解:线性规划问题的可行域是空集。 当无界解和没有可行解时,可能是建模时有错。 3.什么是线性规划的标准型?松弛变量和剩余变量的管理含义是什么? 答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项 ,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。 4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。 答:可行解:满足约束条件的解,称为可行解。 基可行解:满足非负性约束的基解,称为基可行解。 可行基:对应于基可行解的基,称为可行基。 最优解:使目标函数最优的可行解,称为最优解。 最优基:最优解对应的基矩阵,称为最优基。 它们的相互关系如右图所示: 5.用表格单纯形法求解如下线性规划。 s.t. 解:标准化
四 川 大 学 网 络 教 育 学 院 模 拟 试 题( A ) 《管理运筹学》 一、 单选题(每题2分,共20分。) 1.目标函数取极小(minZ )的线性规划问题可以转化为目标函数取极大的线性规 划问题求解,原问题的目标函数值等于( C )。 A. maxZ B. max(-Z) C. –max(-Z) D.-maxZ 2. 下列说法中正确的是( B )。 A.基本解一定是可行解 B.基本可行解的每个分量一定非负 C.若B 是基,则B 一定是可逆D.非基变量的系数列向量一定是线性相关的 3.在线性规划模型中,没有非负约束的变量称为 ( D ) 多余变量 B .松弛变量 C .人工变量 D .自由变量 4. 当满足最优解,且检验数为零的变量的个数大于基变量的个数时,可求得( A )。 A.多重解 B.无解 C.正则解 D.退化解 5.对偶单纯型法与标准单纯型法的主要区别是每次迭代的基变量都满足最优检验但不完全满足 ( D )。 A .等式约束 B .“≤”型约束 C .“≥”约束 D .非负约束 6. 原问题的第i个约束方程是“=”型,则对偶问题的变量i y 是( B )。 A.多余变量 B.自由变量 C.松弛变量 D.非负变量 7.在运输方案中出现退化现象,是指数字格的数目( C )。 A.等于m+n B.大于m+n-1 C.小于m+n-1 D.等于m+n-1 8. 树T的任意两个顶点间恰好有一条( B )。 A.边 B.初等链 C.欧拉圈 D.回路 9.若G 中不存在流f 增流链,则f 为G 的 ( B )。 A .最小流 B .最大流 C .最小费用流 D .无法确定 10.对偶单纯型法与标准单纯型法的主要区别是每次迭代的基变量都满足最优检验但不完全满足( D ) A.等式约束 B.“≤”型约束 C.“≥”型约束 D.非负约束 二、多项选择题(每小题4分,共20分) 1.化一般规划模型为标准型时,可能引入的变量有 ( ) A .松弛变量 B .剩余变量 C .非负变量 D .非正变量 E .自由变量 2.图解法求解线性规划问题的主要过程有 ( ) A .画出可行域 B .求出顶点坐标 C .求最优目标值 D .选基本解 E .选最优解 3.表上作业法中确定换出变量的过程有 ( ) A .判断检验数是否都非负 B .选最大检验数 C .确定换出变量 D .选最小检验数 E .确定换入变量 4.求解约束条件为“≥”型的线性规划、构造基本矩阵时,可用的变量有 ( ) A .人工变量 B .松弛变量 C. 负变量 D .剩余变量 E .稳态 变量 5.线性规划问题的主要特征有 ( ) A .目标是线性的 B .约束是线性的 C .求目标最大值 D .求目标最小值 E .非线性 三、 计算题(共60分) 1. 下列线性规划问题化为标准型。(10分)
软件结果分析题 max z=500x1+400x2; 约束条件:2x1≤300, 3x2≤540, 2x1+2x2≤440, +≤300, x1,x2≥0. 使用“管理运筹学”软件,得到的计算机解如图3-5)所示 根据图3-5回答下面的问题: (1)最优解即最优产品组合是什么此时最大目标函数值即最大利润为多少? (2)(2) 哪些车间的加工工时数已使用完哪些车间的加工工时数还没用完其松弛变量即没用完的加工工时数为多少? (3)(3) 四个车间的加工工时的对偶价格各为多少请对此对偶价格的含义予以说明. (4)(4) 如果请你在这四个车间中选择一个车间进行加班生产,你会选择哪个车间为什么? (5)(5) 目标函数中x1的系数c1,即每单位产品Ⅰ的利润值,在什么范围内变化时,最优产品的组合
不变? (6) (6) 目标函数中x2的系数c2,即每单位产品Ⅱ的利润值,从400元提高为490元时,最优产品组 合变化了没有为什么? (7) (7) 请解释约束条件中的常数项的上限与下限. (8) (8) 第1车间的加工工时数从300增加到400时,总利润能增加多少这时最优产品的组合变化了 没有? (9) (9) 第3车间的加工工时数从440增加到480时,从图3-5中我们能否求得总利润增加的数量为什 么? (10) (10) 当每单位产品Ⅰ的利润从500元降至475元,而每单位产品Ⅱ的利润从400元升至450元时, 其最优产品组合(即最优解)是否发生变化请用百分之一百法则进行判断. (11) (11) 当第1车间的加工工时数从300增加到350,而第3车间的加工工时数从440降到380时, 用百分之一百法则能否判断原来的对偶价格是否发生变化如不发生变化,请求出其最大利润. .解: (1) 1501=x ,702=x 。目标函数最优值103000。 (2) 1,3车间的加工工时已使用完;2,4车间的加工工时没用完;没用完的加工工时数为 2车间330小时,4车间15小时. (3) 50,0,200,0 含义:1车间每增加1工时,总利润增加50元;3车间每增加1工时,总利润增加200元;2车间与4车间每增加一个工时,总利润不增加。 (4) 3车间,因为增加的利润最大。 (5) 在400到正无穷的范围内变化,最优产品的组合不变。 (6) 不变 因为在[]500,0的范围内。 (7) 所谓的上限和下限值指当约束条件的右边值在给定范围内变化时,约束条件1的右边值 在[]440,200变化,对偶价格仍为50(同理解释其它约束条件)。 (8) 总利润增加了100×50=5000,最优产品组合不变。 (9) 不能,因为对偶价格发生变化。 (10) 不发生变化,因为允许增加的百分比与允许减少的百分比之和 2550100%100100 +≤ (11) 不发生变化,因为允许增加的百分比与允许减少的百分比之和%1001406014050≤+,其最大利润为103000+50×50-60×200=93500元。
第一章 思考题、主要概念及内容 1、了解运筹学的分支,运筹学产生的背景、研究的内容和意义。 2、了解运筹学在工商管理中的应用。 3、体会管理运筹学使用相应的计算机软件,注重学以致用的原则。 第二章 思考题、主要概念及内容 图解法、图解法的灵敏度分析 复习题 1. 考虑下面的线性规划问题: max z=2x1+3x2; 约束条件: x1+2x2≤6, 5x1+3x2≤15, x1,x2≥0. (1) 画出其可行域. (2) 当z=6时,画出等值线2x1+3x2=6. (3) 用图解法求出其最优解以及最优目标函数值. 2. 用图解法求解下列线性规划问题,并指出哪个问题具有惟一最优解、无穷多最优解、无界解或无可行解. (1) min f=6x1+4x2; 约束条件: 2x1+x2≥1, 3x1+4x2≥3, x1,x2≥0. (2) max z=4x1+8x2; 约束条件: 2x1+2x2≤10, -x1+x2≥8, x1,x2≥0. (3) max z=3x1-2x2; 约束条件: x1+x2≤1, 2x1+2x2≥4, x1,x2≥0. (4) max z=3x1+9x2; 约束条件:
-x1+x2≤4, x2≤6, 2x1-5x2≤0, x1,x2≥0 3. 将下述线性规划问题化成标准形式: (1) max f=3x1+2x2; 约束条件: 9x1+2x2≤30, 3x1+2x2≤13, 2x1+2x2≤9, x1,x2≥0. (2) min f=4x1+6x2; 约束条件: 3x1-x2≥6, x1+2x2≤10, 7x1-6x2=4, x1,x2≥0. (3) min f=-x1-2x2; 约束条件: 3x1+5x2≤70, -2x1-5x2=50, -3x1+2x2≥30, x1≤0,-∞≤x2≤∞. (提示:可以令x′1=-x1,这样可得x′1≥0.同样可以令x′2-x″2=x2,其中x′2,x″2≥0.可见当x′2≥x″2时,x2≥0;当x′2≤x″2时,x2≤0,即-∞≤x2≤∞.这样原线性规划问题可以化为含有决策变量x′1,x′2,x″2的线性规划问题,这里决策变量x′1,x′2,x″2≥0.) 4. 考虑下面的线性规划问题: min f=11x1+8x2; 约束条件: 10x1+2x2≥20, 3x1+3x2≥18, 4x1+9x2≥36, x1,x2≥0. (1) 用图解法求解. (2) 写出此线性规划问题的标准形式. (3) 求出此线性规划问题的三个剩余变量的值. 5. 考虑下面的线性规划问题: max f=2x1+3x2; 约束条件: x1+x2≤10, 2x1+x2≥4,
管理运筹学实验报告 班级: __________________________ 姓名: __________________________ 学号: __________________________ 学期: __________________________ 中国矿业大学管理学院 2009年3月1日
实验题目线性规划建模应用 一、实验目的 1、了解线性规划问题在Excel屮如何建、丫,主要是数据单兀格、输岀单元格、可 变单元格和冃标单元格定义以及规划求解宏定义应川设置。 2、熟练寧握Excel规划求解宏定义模块便川。 3、掌拥LINDO软件在线性规划求解中的应用 二、实验内容 某医院院周会上正在研究制定一昼夜护士值班安排计划。在会议上,护理部主任提交了-份全院24小时各时段内需要在岗护士的数量报告,见下表。 如果按照每人每天两小班轮换.中间间隔休息时间8小时.这样安排岗位不但会造成人员冗余,同时护理人员上下班不是很方便。由丁?医院护理匸作的特殊性,又要求尽量保证护理人员T?作的连续性.报终确定毎名护士连续丁作两个小班次,即24小时内-个大班*小时,即连续上满两个小班。为了合理的压缩编制,医务部提出一个合理化建议:允许不同护士的人班之间可以合理相互重叠小班,即分成八组轮班开展全人的护理值班(每一人小班时段实际上山两个交替的大班的前段和后段共同庫担)o 现在人力部门而临的问题是:如何合理安排岗位.才能满足值班的需要? 」E在会议结束Z1W,护理部又提出一个问题:冃前全院在编的正式护I:只冇5() 人.匸资定额为10元/小时;如果人力部门提供的定编超过5()人,那么必须以
管理运筹学第二版课后 习题参考答案 Document number【980KGB-6898YT-769T8CB-246UT-18GG08】
《管理运筹学》(第二版)课后习题参考答案 第1章 线性规划(复习思考题) 1.什么是线性规划线性规划的三要素是什么 答:线性规划(Linear Programming ,LP )是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。 建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。 2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误 答:(1)唯一最优解:只有一个最优点; (2)多重最优解:无穷多个最优解; (3)无界解:可行域无界,目标值无限增大; (4)没有可行解:线性规划问题的可行域是空集。 当无界解和没有可行解时,可能是建模时有错。 3.什么是线性规划的标准型松弛变量和剩余变量的管理含义是什么 答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项0 i b ,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。 4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。 答:可行解:满足约束条件0≥=X b AX ,的解,称为可行解。 基可行解:满足非负性约束的基解,称为基可行解。 可行基:对应于基可行解的基,称为可行基。 最优解:使目标函数最优的可行解,称为最优解。 最优基:最优解对应的基矩阵,称为最优基。 它们的相互关系如右图所示: 5.用表格单纯形法求解如下线性规划。 . ??? ??≥≤++≤++0,,862383 21321321x x x x x x x x x 解:标准化 32124max x x x Z ++= . ?? ? ??≥=+++=+++0,,,,862385432153 214 321x x x x x x x x x x x x x 列出单纯形表
管理运筹学试题(A) 一.单项选择(将唯一正确答案前面的字母填入题后的括号里。正确得1分,选错、多选或不选得0分。共15分) 1.在线性规划模型中,没有非负约束的变量称为() A.多余变量B.松弛变量C.自由变量D.人工变量 正确答案:A: B: C: D: 2.约束条件为AX=b,X≥0的线性规划问题的可行解集是()A.补集B.凸集C.交集D.凹集 正确答案:A: B: C: D: 3.线性规划问题若有最优解,则一定可以在可行域的()上达到。A.内点B.外点C.极点D.几何点 正确答案:A: B: C: D: 4.对偶问题的对偶是() A.基本问题B.解的问题C.其它问题D.原问题 正确答案:A: B: C: D: 5.若原问题是一标准型,则对偶问题的最优解值就等于原问题最优表中松弛变量的() A.值B.个数C.机会费用D.检验数 正确答案:A: B: C: D: 6.若运输问题已求得最优解,此时所求出的检验数一定是全部()A.大于或等于零B.大于零C.小于零D.小于或等于零 正确答案:A: B: C: D: 7.设V是一个有n个顶点的非空集合,V={v1,v2,……,vn},E是一个有m条边的集合,E={e1,e2,……em},E中任意一条边e是V 的一个无序元素对[u,v],(u≠v),则称V和E这两个集合组成了一个() A.有向树B.有向图C.完备图D.无向图 正确答案:A: B: C: D: 8.若开链Q中顶点都不相同,则称Q为()
A.基本链B.初等链C.简单链D.饱和链 正确答案:A: B: C: D: 9.若图G 中没有平行边,则称图G为() A.简单图B.完备图C.基本图D.欧拉图 正确答案:A: B: C: D: 10.在统筹图中,关键工序的总时差一定() A.大于零B.小于零C.等于零D.无法确定 正确答案:A: B: C: D: 11.若Q为f饱和链,则链中至少有一条后向边为f () A.正边B.零边C.邻边D.对边 正确答案:A: B: C: D: 12.若f 是G的一个流,K为G的一个割,且Valf=CapK,则K一定是() A.最小割B.最大割C.最小流D.最大流 正确答案:A: B: C: D: 13.对max型整数规划,若最优非整数解对应的目标函数值为Zc,最优整数解对应的目标值为Zd,那么一定有( ) A.Zc ∈Zd B.Zc =Zd C.Zc ≤Zd D.Zc ≥Zd 正确答案:A: B: C: D: 14.若原问题中xI为自由变量,那么对偶问题中的第i个约束一定为()A.等式约束B.“≤”型约束C.“≥”约束D.无法确定 正确答案:A: B: C: D: 15.若f*为满足下列条件的流:Valf*=max{Valf |f为G的一个流},则称f*为G的() A.最小值B.最大值C.最大流D.最小流 正确答案:A: B: C: D:
管理运筹学教学创新的重要性作者:徐辉单位:广东商学院工商管理学院 1引言 古朴的运筹学思想可以追溯到古代先秦时期。我们运筹学的先驱从《史记》“运筹于帷幄之中,决胜于千里之外”一语中摘取“运筹”两字作为这门学科的名称,既显示其军事起源,也表明其朴素的思想早已出现在几千年前的中国。但世上公认的运筹学学科起源于二次世界大战期间,英、美等国的军事部门为战争需要而成立的一些研究小组的活动。其热点是集中多个学科领域的科研人员,对某一特定问题进行全面、系统的分析,提出提高某武器系统效率的操作方法和执行策略。第二次世界大战结束后,运筹学的研究方法在理论上得到全面发展。作为一种重要的管理决策分析工具,运筹学的应用领域也从军事部门迅速向工商、管理和工业部门转移。运筹学是研究各种广义资源的运用、筹划以及相关决策等问题的近代新兴学科。在我国已有五十多年历史,其目的是根据问题的需求,通过数学的分析和运算,做出综合性的、合理的优化安排,以便更有效地发展有限资源的效益。“运筹学”名称最早于1938年出现在英国,当时称之为“OperationalResearch”,1942年美国开始从事这项研究工作,称之为“OperationsResearch”。运筹学的发展、运筹学在各领域的广泛应用、运筹学的定量分析对于解决实际问题的思路及其特点,适合当今社会发展对高级管理决策人才的迫切需要。本课程是工商管理类专业重要的专业基础课,也是一门实践性
和应用型很强的学科。21世纪,科技进步与社会发展提出了培养信息社会高素质人才的要求,高等教育改革不断深化,《管理运筹学》课程教学面临新的挑战,必须重新对课程原有的教学体系和教学方法进行全面的审视和思考。 2工商管理专业《管理运筹学》课程教学中存在的问题 当前的工商管理专业《管理运筹学》课程教学主要存在以下问题:一是教学目的不明确,教学方式单一。多数讲授《管理运筹学》课程的教师是学数学出身,缺乏必要的工程技术和管理知识,使得目前《管理运筹学》教学普遍存在着偏重教学理论与解题技巧的传授,将《管理运筹学》当作一门纯数学学科进行教学。这与工商管理专业培养要求相脱节,学生在学习过程中感受不到《管理运筹学》在管理中的应用。在教学方式上,也一直延用传统单一的传授方式,当学生运用所学知识去分析和解决实际问题时,显得茫然无措,无从下手。 二是学生学习兴趣不浓厚。《管理运筹学》研究问题的基本手段是建立数学模型,并较多地运用各种教学工具。学习《管理运筹学》课程,需要有良好的数学基础;其前期必修课程包括微积分、线性代数、概率论、概率论与数理统计。可以说《管理运筹学》是软科学中“硬度”较大的一门学科,兼有逻辑的数学和数学的逻辑的性质。工商管理类专业的学生绝大多数是文科生源,不少学生害怕数学。比如线性规划的单纯形法及对偶理论,要想完全领会其原理,需要大量运用线性代数的工具进行推理,因而非常抽象。在课时总体压缩的背景下,教师要在较短时间内讲授完抽象数学原理的推导,学生听不懂只好放
管理运筹学 ——管理科学方法谢家平 第一章 第一章 1. 建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。决策变量(Decision Variable)是决策问题待 定的量值,取值一般为非负;约束条件(Constraint Conditions)是指决策变量取值时受到的各种资源条件的限制, 保障决策方案的可行性;目标函数(Objective Function)是决策者希望实现的目标,为决策变量的线性函数表达式, 有的目标要实现极大值,有的则要求极小值。 2.(1)设立决策变量; (2)确定极值化的单一线性目标函数; (3)线性的约束条件:考虑到能力制约,保证能力需求量不能突破有效供给量; (4)非负约束。 3.(1)唯一最优解:只有一个最优点 (2)多重最优解:无穷多个最优解 (3)无界解:可行域无界,目标值无限增大 (4)没有可行解:线性规划问题的可行域是空集 无界解和没有可行解时,可能是建模时有错。 4. 线性规划的标准形式为:目标函数极大化,约束条件为等式,右端常数项bi≥0 , 决策变量满足非负性。 如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。 5. 可行解:满足约束条件AX =b,X≥0的解,称为可行解。 基可行解:满足非负性约束的基解,称为基可行解。 可行基:对应于基可行解的基,称为可行基。 最优解:使目标函数最优的可行解,称为最优解。 最优基:最优解对应的基矩阵,称为最优基。 6. 计算步骤: 第一步,确定初始基可行解。 第二步,最优性检验与解的判别。 第三步,进行基变换。 第四步,进行函数迭代。 判断方式: 唯一最优解:所有非基变量的检验数为负数,即σj< 0 无穷多最优解:若所有非基变量的检验数σj≤ 0 ,且存在某个非基变量xNk 的检验数σk= 0 ,让其进基,目标函数
习 题 1 1 用图解法求解下列线性规划问题,并指出问题具有唯一最优解、无穷最优解、无界解还是无可行解。 ??? ??≥≥+≥++=0 x x 42x 4x 66x 4x 3x 2x minz )a (21 212121, ?? ? ??≥≥+≤++=0 x ,x 124x 3x 2 x 2x 2x 3x maxz )b (2121212 1 ?? ? ??≤≤≤≤≤++=8 x 310x 5120 10x 6x x x maxz )c (21 212 1 ?? ? ??≥≤+-≥-+=0 x ,x 23x 2x 2x 2x 6x 5x maxz )d (21212121 答案: (a)唯一解3*,)5.0,75.0(*==z X T ); (b)无可行解; (c)唯一解16*,) 6,10(*==z X T ); (d)无界解) 2 用单纯形法求解下列线性规划问题。 ?????≥ ≤+≤++=0 x ,x 82x 5x 9 4x 3x 5x 10x maxz )a (21 212121 ?????? ? ≥≤+≤+≤+=0 x , x 5x x 242x 6x 15 5x x 2x maxz )b (21212 122 1 答案: (a)唯一解5.17*,) 5.1,1(*==z X T ),对偶问题5.17*,)786.1,357.0(*==w Y T ; (b)唯一解5.8*,) 5.1,5.3(*==z X T ) ,5.8*,)5.0,25.0,0(*==w Y T 3 用大M 法和两阶段法求解下列线性规划问题,并指出属于哪一类解。 ???????≥≥-≥+-≥+++-=0 x x x 0x 2x 2x 2x 6 x x x 2x x 2x maxz )a (3 ,2, 132 31321 321 ?????≥≥+≥++++=0 x , x ,x 62x 3x 82x 4x x x 3x 2x minz )b (3 21 21321321 答案: (a)无界解;(b)唯一解8*,) 0,8.1,8.0(*==z X T ),对偶问题8*,)0,1(*==w Y T 4已知线性规划问题的初始单纯形表(如表1-54所示)和用单纯形法迭代后得到的表(如表1-55所示)如下,试求括弧中未知数a ~l 的值。 表1-54 初始单纯形表
管理运筹学复习题 一、基本概念(判断和填空题) 1.可行解集S中的点x是极点,当且仅当x是基可行解。(T) 2.产地数与销地数相等的运输问题是产销平衡运输问题。(F) 3.基本解中取值不为零的变量一定是基变量。(F) 4.当一个线性规划问题无可行解时,它的对偶问题的解为无界解。(F) 5.任何线性规划问题存在并具有唯一的对偶问题。(T) 6.线性规划问题的最优值可以在极点上达到。(T) 7.影子价格是一种绝对值。(T) 8.线性规划问题的每一个基本可行解对应可行域上的一个顶点。(F) 9.线性规划的变量个数与其对偶问题的约束条件个数是相等的。(T) 10.线性规划问题的可行解一定是基本解。(T) 11.若线性规划存在最优解,它一定在可行域的某个顶点得到。(F) 12.影子价格无法定量反映资源在企业内部的紧缺程度。(T) 13.如果原问题有最优解,那么对偶问题也有最优解,但二者目标函数值不一定相等。 (T) 14.影子价格的大小客观反映地反映了各种不同的资源在系统内的稀缺程度。(T) 15.若线性规划问题有最优解,则最优解一定在可行域的(极点)找到。 16.线性规划问题解得到可能的结果有(唯一最优解)(无穷多最优解)(无界解)(无 可行解)。 17.最小元素法的基本思路以(单位运价最低者优先)为原则,安排初始的调运方案。 18.在线性规划问题求解过程中,如果在大M法的最优单纯形表的基变量中仍含有(人 工变量),那么该线性规划就不存在可行解。 二、选择题 1.如果某个基本可行解所对应的检验向量所有分量小于等于0,规划问题有()。 A.唯一最优解 B.无界解 C.无可行解 D.无穷多最优解 2.原问题的第i个约束方程是“=”型,则对偶问题的变量是()。 A.多余变量 B.自由变量 C.松弛变量 D.非负变量 3.对于线性规划问题,下列说法正确的是()。 A.线性规划问题没有可行解 B.在图解法上,线性规划问题的可行解区域都是在“凸”区域 C.线性规划问题如有最优解,则最优解可在可行解区域顶点上到达 D.上述说法都正确 4.线性规划问题中,如果在约束条件中没有单位矩阵作为初始可行基,我们通常用增 加()的方法来产生初始可行基。 A.多余变量 B.自由变量
清华第三版 运筹学 答案[键入文字] [键入文字] [键入文字] 运筹学教程 1. 某饲养场饲养动物出售,设每头动物每天至少需700g 蛋白质、30g 矿物质、100mg 维生素。现有五种饲料可供选用,各种饲料每kg 营养成分含量及单价如表1所示。 表1 要求确定既满足动物生长的营养需要,又使费用最省的选用饲料的方案。 解:设总费用为Z 。i=1,2,3,4,5代表5种饲料。i x 表示满足动物生长的营养需要时,第i 种饲料所需的数量。则有: ????? ? ?=≥≥++++≥++++≥++++++++=5,4,3,2,1,01008.022.05.0305.022.05.07008623..8.03.04.07.02.0min 54321543215432154321i x x x x x x x x x x x x x x x x t s x x x x x Z i 2. 某医院护士值班班次、每班工作时间及各班所需护士数如表2所示。每班护士值班 开始时间向病房报道,试决定: (1) 若护士上班后连续工作8h ,该医院最少需要多少名护士,以满足轮班需要; (2) 若除22:00上班的护士连续工作8h 外(取消第6班),其他班次护士由医院 排定上1~4班的其中两个班,则该医院又需要多少名护士满足轮班需要。 表2
6 2:00~6:00 30 解:(1)设x 第i 班开始上班的人数,i=1,2,3,4,5,6 ???????????=≥≥+≥+≥+≥+≥+≥++++++=且为整数 6,5,4,3,2,1,030 2050607060..min 655443 322161 654321i x x x x x x x x x x x x x t s x x x x x x Z i 解:(2)在题设情况下,可知第五班一定要30个人才能满足轮班需要。则设设i x 第i 班开始上班的人数,i=1,2,3,4。 ??? ????? ?? ??? ??=≥=+++=≥+++=+++=≥+++=+++=≥+++=+++=≥+++++++=4 ,3,2,1,1002 1502 16021702 ,160..30 min i 444342414444433422411434 33323133 443333223113242322212244233222211214131211114413312211114321j i y x y y y y y x y x y x y x y y y y y y x y x y x y x y y y y y y x y x y x y x y y y y y y x y x y x y x y t s x x x x Z ij 变量,—是,,,第四班约束,,第三班约束,,第二班约束,第一班约束 3. 要在长度为l 的一根圆钢上截取不同长度的零件毛坯,毛坯长度有n 种,分别为j a (j=1,2,…n )。问每种毛坯应当截取多少根,才能使圆钢残料最少,试建立本问题的数学模型。 解:设i x 表示各种毛坯的数量,i=1,2,…n 。
《管理运筹学》(第二版)课后习题参考答案 第1章 线性规划(复习思考题) 1.什么是线性规划?线性规划的三要素是什么? 答:线性规划(Lin ear Programming ,LP )是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。 建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。 2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误? 答:(1)唯一最优解:只有一个最优点; (2)多重最优解:无穷多个最优解; (3)无界解:可行域无界,目标值无限增大; (4)没有可行解:线性规划问题的可行域是空集。 当无界解和没有可行解时,可能是建模时有错。 3.什么是线性规划的标准型?松弛变量和剩余变量的管理含义是什么? 答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项0≥i b ,决策变量满足非负性。 如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。 4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。 答:可行解:满足约束条件0≥=X b AX ,的解,称为可行解。 基可行解:满足非负性约束的基解,称为基可行解。 可行基:对应于基可行解的基,称为可行基。 最优解:使目标函数最优的可行解,称为最优解。 最优基:最优解对应的基矩阵,称为最优基。 它们的相互关系如右图所示:
《管理运筹学》考试试卷(A) 一、(20 分)下述线性规划问题 Max z=-5x1+5x2+13x3 ST -x1+x2+3x3 ≤ 20 ——① 12x1+4x2+10x3 ≤ 90 ——② x1,x2,x3 ≥ 0 先用单纯形法求出最优解,然后分析在下列条件下,最优解分别有什么变化? ( 1 )约束条件①的右端常数由20 变为30 ; ( 2 )约束条件②的右端常数由90 变为70 ; ( 3 )目标函数中的x3 的系数由13 变为8 ; ( 4 )增加一个约束条件③2x1+3x2+5x3 ≤ 50 ( 5 )将原有约束条件②变为10x1+5x2+10x3 ≤ 100 二、(10 分)已知线性规划问题 Max z= 2x1+x2+5x3+6x4 对偶变量 2x1 +x3+x4 ≤ 8 y1 2x1+2x2+x3+2x4 ≤ 12 y2 x1,x2,x3,x4 ≥ 0 其对偶问题的最优解为y1*=4 ,y2*=1 ,试用对偶问题的性质,求原问题的最优解。
三、(10 分)某地区有三个化肥厂,除供应外地区需要外,估计每年可供应本地区的数字为:化肥厂 A —— 7 万吨,B —— 8 万吨,C —— 3 万吨。有四个产粮区需要该种化肥,需要量为:甲地区—— 6 万吨,乙地区—— 6 万吨,丙地区—— 3 万吨,丁地区—— 3 万吨。已知从各化肥厂到各产粮区的每吨化肥的运价如下表所示(单位:元/ 吨): 根据上述资料指定一个使总的运费最小的化肥调拨方案。 四、(10 分)需要分配5 人去做5 项工作,每人做各项工作的能力评分见下表。应如何分派,才能使总的得分最大? 五、(10 分)用动态规划方法求解: Max F=4x 1 2 -x 2 2 +2x 3 2 +12 3x 1 +2x 2 +x 3 =9 x1,x2,x3 ≥ 0 六、(10 分)公司决定使用1000 万元开发A 、B 、C 三种产品,。经预测估计开发
《管理运筹学》课程教学改革思考 针对工商管理专业《管理运筹学》课程教学中存在的一些问题,结合《管理运筹学》课程特点,从教学创新与实践改革的必要性出发,提出PBL教学法的改革思路。该教学法在培养学生自主学习能力和解决实际问题能力等方面具有较强的优势,符合新形势下对工商管理类专业人才培养的要求。 标签:PBL;《管理运筹学》;课程教学;教学改革 1引言 古朴的运筹学思想可以追溯到古代先秦时期。我们运筹学的先驱从《史记》“运筹于帷幄之中,决胜于千里之外”一语中摘取“运筹”两字作为这门学科的名称,既显示其军事起源,也表明其朴素的思想早已出现在几千年前的中国。但世上公认的运筹学学科起源于二次世界大战期间,英、美等国的军事部门为战争需要而成立的一些研究小组的活动。其热点是集中多个学科领域的科研人员,对某一特定问题进行全面、系统的分析,提出提高某武器系统效率的操作方法和执行策略。 第二次世界大战结束后,运筹学的研究方法在理论上得到全面发展。作为一种重要的管理决策分析工具,运筹学的应用领域也从军事部门迅速向工商、管理和工业部门转移。运筹学是研究各种广义资源的运用、筹划以及相关决策等问题的近代新兴学科。在我国已有五十多年历史,其目的是根据问题的需求,通过数学的分析和运算,做出综合性的、合理的优化安排,以便更有效地发展有限资源的效益。“运筹学”名称最早于1938年出现在英国,当时称之为“OperationalResearch”,1942年美国开始从事这项研究工作,称之为“OperationsResearch”。运筹学的发展、运筹学在各领域的广泛应用、运筹学的定量分析对于解决实际问题的思路及其特点,适合当今社会发展对高级管理决策人才的迫切需要。本课程是工商管理类专业重要的专业基础课,也是一门实践性和应用型很强的学科。21世纪,科技进步与社会发展提出了培养信息社会高素质人才的要求,高等教育改革不断深化,《管理运筹学》课程教学面临新的挑战, 必须重新对课程原有的教学体系和教学方法进行全面的审视和思考。 2工商管理专业《管理运筹学》课程教学中存在的问题 当前的工商管理专业《管理运筹学》课程教学主要存在以下问题: 一是教学目的不明确,教学方式单一。多数讲授《管理运筹学》课程的教师是学数学出身,缺乏必要的工程技术和管理知识,使得目前《管理运筹学》教学普遍存在着偏重教学理论与解题技巧的传授,将《管理运筹学》当作一门纯数学学科进行教学。这与工商管理专业培养要求相脱节,学生在学习过程中感受不到《管理运筹学》在管理中的应用。在教学方式上,也一直延用传统单一的传授方
运筹学(第3版)习题答案 第1章线性规划 P36 第2章线性规划的对偶理论 P74 第3章整数规划 P88 第4章目标规划 P105 第5章运输与指派问题P142 第6章网络模型 P173 第7章网络计划 P195 第8章动态规划 P218 第9章排队论 P248 第10章存储论P277 第11章决策论P304 第12章 多属性决策品P343 第13章博弈论P371 全书420页 第1章 线性规划 1.1工厂每月生产A 、B 、C 三种产品 ,单件产品的原材料消耗量、设备台时的消耗量、资源限量及单件产品利润如表1-23所示. 310和130.试建立该问题的数学模型,使每月利润最大. 【解】设x 1、x 2、x 3分别为产品A 、B 、C 的产量,则数学模型为 1231231 23123123max 1014121.5 1.2425003 1.6 1.21400 150250260310120130,,0 Z x x x x x x x x x x x x x x x =++++≤??++≤??≤≤?? ≤≤??≤≤?≥?? 1.2建筑公司需要用5m 长的塑钢材料制作A 、B 两种型号的窗架.两种窗架所需材料规格 及数量如表1-24所示:
问怎样下料使得(1)用料最少;(2)余料最少. 【解 设x j (j =1,2,…,10)为第j 种方案使用原材料的根数,则 (1)用料最少数学模型为 10 1 12342567368947910 min 2800212002600223900 0,1,2,,10 j j j Z x x x x x x x x x x x x x x x x x x j ==?+++≥? +++≥?? +++≥??+++≥??≥=?∑L (2)余料最少数学模型为 2345681012342567368947910 min 0.50.50.52800 212002********* 0,1,2,,10 j Z x x x x x x x x x x x x x x x x x x x x x x x x j =++++++?+++≥? +++≥?? +++≥??+++≥??≥=?L 1.3某企业需要制定1~6月份产品A 的生产与销售计划。已知产品A 每月底交货,市场需求没有限制,由于仓库容量有限,仓库最多库存产品A1000件,1月初仓库库存200件。1~6月份产品A 的单件成本与售价如表1-25所示。 (2)当1月初库存量为零并且要求6月底需要库存200件时,模型如何变化。 【解】设x j 、y j (j =1,2,…,6)分别为1~6月份的生产量和销售量,则数学模型为
《管理运筹学》作业题参考答案 一、简答题 1. 试述线性规划数学模型的结构及各要素的特征。 2. 求解线性规划问题时可能出现哪几种结果,哪些结果反映建模时有错误。 3. 举例说明生产和生活中应用线性规划的方面,并对如何应用进行必要描述。 4. 什么是资源的影子价格,同相应的市场价格之间有何区别,以及研究影子价格的意义。 5. 试述目标规划的数学模型同一般线性规划数学模型的相同和异同之点。 (答案参考教材) 二、判断题 1. (√) 2. (√) 3. (×) 4. (√) 5. (√) 三、计算题 1. 用图解法求解下列线性规划问题,并指出各问题是具有唯一最优解、无穷多最优解、无界解或无可行解。 (a) min z =6x 1+4x 2 (b) min z =4x 1+8x 2 ??? ??≥≥+≥+0,5.1431 2.st 2 12121x x x x x x ??? ??≥≥+-≥+0,101022.st 2 12121x x x x x x (c) min z =x 1+x 2 (d) min z =3x 1-2x 2 ?????? ?≥≥-≥+≥+0 ,4212642468.st 2122 121x x x x x x x ??? ??≥≥+≤+0,4221 .st 2 12121x x x x x x (e) min z =3x 1+9x 2 ????? ????≥≤-≤≤+-≤+0 ,0 5264 2263.st 212 122121x x x x x x x x x 2. (a)唯一最优解,z* =3,x 1=1/2,x 2= 0;(b)无可行解;(c)有可行解,但max z 无界;(d )无可行解;(c )无穷多最优解,z*=66;(f )唯一最优解,z*=.3/8,3/20,3 2 3021==x x