
目录
一、 A/D卡设计 (1)
1.1 基于PCI总线的A/D卡 (1)
1.2 基于USB总线的A/D卡 (2)
二、非均匀离散傅立叶变换 (4)
三、不同的插值算法 (6)
1. 拉格朗日多项式插值 (6)
2. 三次样条插值 (7)
3. 牛顿插值 (8)
四、主要算法及程序 (10)
1. 拉格朗日算法 (10)
2. 三次样条插值 (10)
3. Newton算法 (12)
五、算法结果及比较分析 (14)
六、心得体会 (19)
七、参考文献 (20)
一、A/D卡设计
1.1 基于PCI总线的A/D卡
1、PCI总线的含义
PCI是由Intel公司1991年推出的一种局部总线。从结构上看,PCI是在CPU和原来的系统总线之间插入的一级总线,具体由一个桥接电路实现对这一层的管理,并实现上下之间的接口以协调数据的传送。管理器提供了信号缓冲,使之能支持10种外设,并能在高时钟频率下保持高性能,它为显卡、声卡、网卡、MODEM等设备提供了连接接口,它的工作频率为33MHz/66MHz。
PCI是Peripheral Component Interconnect(外设部件互连标准)的缩写,它是目前个人电脑中使用最为广泛的接口,几乎所有的主板产品上都带有这种插槽。PCI插槽也是主板带有最多数量的插槽类型,在目前流行的台式机主板上,ATX结构的主板一般带有5~6个PCI插槽,而小一点的MATX主板也都带有2~3个PCI插槽,可见其应用的广泛性。
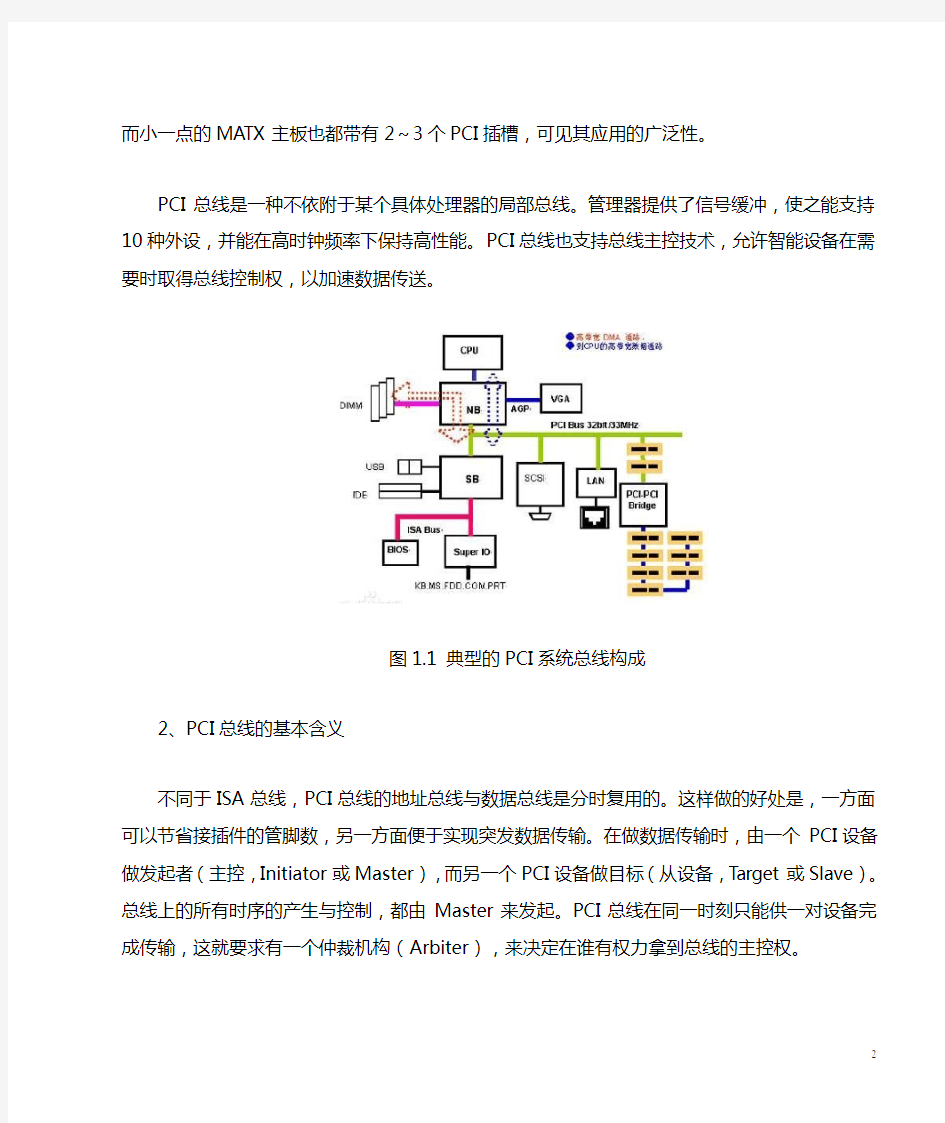
PCI总线是一种不依附于某个具体处理器的局部总线。管理器提供了信号缓冲,使之能支持10种外设,并能在高时钟频率下保持高性能。PCI总线也支持总线主控技术,允许智能设备在需要时取得总线控制权,以加速数据传送。
图1.1 典型的PCI系统总线构成
2、PCI总线的基本含义
不同于ISA总线,PCI总线的地址总线与数据总线是分时复用的。这样做的好处是,
一方面可以节省接插件的管脚数,另一方面便于实现突发数据传输。在做数据传输时,由一个PCI设备做发起者(主控,Initiator或Master),而另一个PCI设备做目标(从设备,Target或Slave)。总线上的所有时序的产生与控制,都由Master来发起。PCI 总线在同一时刻只能供一对设备完成传输,这就要求有一个仲裁机构(Arbiter),来决定在谁有权力拿到总线的主控权。
当PCI总线进行操作时,发起者(Master)先置REQ#,当得到仲裁器(Arbiter)的许可时(GNT#),会将FRAME#置低,并在AD总线上放置Slave地址,同时C/BE#放置命令信号,说明接下来的传输类型。所有PCI总线上设备都需对此地址译码,被选中的设备要置DEVSEL#以声明自己被选中。然后当IRDY#与TRDY#都置低时,可以传输数据。当Master数据传输结束前,将FRAME#置高以标明只剩最后一组数据要传输,并在传完数据后放开IRDY#以释放总线控制权。
1.2 基于USB总线的A/D卡
1.2.1 USB总线介绍
USB总线为通用串行总线,USB接口位于PS/2接口和串并口之间,允许外设在开机状态下热插拔,最多可串接下来127个外设,传输速率可达480Mb/S,P它可以向低压设备提供5伏电源,同时可以减少PC机I/O接口数量。USB是基于通用连接技术,实现外设的简单快速连接,达到方便用户、降低成本、扩展PC连接外设范围的目的。数据采集就是把来自各种传感器的信号数据实时地、准确地测量或汇集起来,用计算机进行实时处理或记录存储,实时完成测试和控制功能。数据采集系统结构通过微机的标准接口连接各种功能模块、仪器仪表和传感器,组成测量系统。
1.2.2 USB接口电路设计
图1.2 USB接口电路结构图
R3是上拉电阻器,它可使USB口的D+端上拉到DS2490S的VB端,表示USB主机系
统是高速设备,同时这个上拉电阻器告诉主机有USB设备插入。该上拉电阻器的设置对适配器的影响很大,它的负载值和1-Wire网络的总长决定1-Wire总线电压上升到5 V 的速度。经过实验测试选择R3的阻值为27 Ω±lO%。R1、R2为USB数据线保护电阻器。L、L2具有禁止高频干扰并且减弱EMI辐射的功能。LF33CV为3.3 V电压稳压器,与周围元件C1、C2组成强上拉部分,给EEPROM或温度传感器等器件提供额外的电源。
1.2.3 USB接口的数据采集系统的设计实现
数据采集系统使用采集卡进行数据采集,然后经过A/D转换器供计算机加工处理。基于USB接口的数据采集与频谱分析系统本系统结构由硬件部分和软件部分组成,硬件部分主要有计算机、I/ O 接口设备. 计算机作为硬件平台的核心可采用台式机,系统采用的I/ O 设备为A/ D 数据采集卡,该采集卡是一种基于USB 总线数据采集产品,可与带USB 接口的各种台式计算机、笔记本电脑、工控机连接构成高性能的数据采集测量系统.整个系统主要由4部分组成:USB接口芯片及外围电路、控制电路、数据缓冲电路和A/D转换电路。USB接口芯片选择了Cypress公司的EZ-USB 2131Q,该芯片内嵌8051控制器,因此整个系统以EZ-USB控制器为核心,由EZ-USB经控制电路实现对A/D转换电路和数据缓冲电路的控制,模拟信号转换后的数据送入数据缓冲器,当数据缓冲器存满之后,通知EZ-USB控制器,由主机取出数据。整个系统框图如图1.3所示。
图1.3 系统框图
1.2.4 A/D转换电路
声卡是计算机对语音信号进行加工的重要部件,它具有对信号滤波、放大、采样保持、A/D和D/A转换等功能。系统中A/D转换芯片采用了MAXIM公司的MAX122,该芯片是12 b的高速的A/D转换器。在完全转换模式下,他的转换时间可以达到2.6μs,采样率为333 kS/s。MAX122有5种工作模式,在数据采集系统中,采用了模式2即连续转换模式。在这种模式下,每次转换需要13~14个时钟脉冲节拍,转换可以不间断地进行,但是需要提供开始转换使能信号,并且要保证使能信号和时钟信号同步,读信号和片选始终处于有效状态。数据输出使能信号一直有效,在转换结束时产生新的数据。
二、非均匀离散傅立叶变换
在过去的几十年里,随着DFT的处理算法的发展,出现了对非均匀离散傅立叶变换的需求(NDFT)。对NDFT来说,数据在时域或者频域进行非均匀采样,,相应的采样点在N个任意但不相同的位置。因此NDFT可以看做是DFT的一般形式,而DFT是NDFT的一种特殊情况。
NDFT问题主要分为五大类:
第1 类:由非等间隔分布的频域采样值估算均匀网格分布的空间域值;
第2 类:由等间隔分布的频率值估算非等间隔指定点的空间域值;
第3 类:由非等间隔分布的空间域值估算均匀网格分布的频域值;
第4 类:由均匀分布的空间域值估算指定频率点的频域值;
第5 类:由非均匀分布的空间域值估算非均匀分布的频域值。
弹光调制干涉信号的相位是非均匀分布的,要实现傅里叶变换,即要处理NDFT的第三类问题。因此,本章将以第3 类NDFT 问题为例分析NDFT 算法。
设有连续的周期信号x(t) ,其傅里叶变换X ( f ) 为:
(2.1)
T 为信号的周期;
将 x(t) 等相位采样,则有数据{xn} , n = 0,1, 2,N -1,其傅里叶变换为 X n ( f ) 。均匀采样信号的离散傅里叶变换,则是将上式积分转换为求和相加的形式。
(2.2)
Ts 为采样间隔,均匀采样时为常数。在计算频谱时是否引入采样间隔常数 Ts
都不影响频谱的检测。因此,均匀信号离散傅里叶变换表达式简化为:
(2.3)
同样,对于连续周期信号 x(t) 进行非等相位采样,其离散傅里叶变换表达式为
(2.4)
在 NDFT 中,每个采样段积分区间的宽度不相等。而采样信号各个频谱的大小和采样间隔成比例关系。所以,在非均匀采样信号的傅里叶变换式中,需引入积分区间宽度
。
利用非均匀采样点拟合整个曲线,再对曲线进行均匀采样,经快速傅里叶变换重建。
三、不同的插值算法
1.拉格朗日多项式插值
已知有n+1 个数据点,满足
(3.1)由这些数据点构造n 次多项式函数,需满足条件:
(3.2)则有
(3.3)l k(x)称为n次插值的基函数。
于是,满足条件(2.3)的插值多项式L
(x),可表示为
n
(3.4)由l
(x)的定义可知,
k
(3.5)公式(2.5)描述的插值多项式 Ln (x) ,称为拉格朗日(Lagrange)插值多项式。
拉格朗日插值多项式结构整齐,容易进行理论分析。然而在计算中,当插值点发生变化时基函数则需要重新计算,计算繁琐。这时可以用重心拉格朗日插值法或牛顿插值法来代替。在插值点比较多的时候,拉格朗日插值多项式的次数可能比较高,将引起龙格现象[,解决的办法是分段用低阶的插值多项式。在本项目研究中,插值的点数比较多,所以采用的是三次或四次分段插值多项式。
重心拉格朗日插值法是拉格朗日插值法的一种改进。设
(3.6)
可以将式(2.6)改写为:
(3.7)
定义重心权:
(3.8)
式(2.8)可简化为
(3.9)
式(2.9)可改写为:
(3.10)
式(2.10)描述了重心拉格朗日插值多项式。
2.三次样条插值
已知有n个节点,且有。
(1) S(x i)=y I (i=0,1,2,…n)
(2)S(x)在每个小区间[x i,x i+1]上是三次多项式;
(3)S(x)在每个小区间[x i,x i+1]上有连续的一阶和二阶导数;
则称 S(x)为三次样条插值函数。由于 S(x)在每个区间都是三次样条插值函数,共有n 个区间,因此应确定4n 个参数。
根据三次样条插值函数 S(x)连续性,以及它的一阶、二阶导数的连续性、节点函数值可确定 4n-2个条件,因此还需确定两个条件。这两个条件一般选择区间的边界条件。边界条件一般有三种:
(1)已知函数在两端点的导数值,S'(x0)=f0,S'(x n)=f n
(2)已知函数在两端点的二阶导数值,S''(x0)=f0'',S''(x n)=f n,在特殊情况下,S ''(x
)=S''(x n)=0
(3) 当函数 S(x) 为周期函数时,有S(x 0 ) = S(x n ) , S ' (x 0 ) = S ' (x n ) , S '' (x 0 ) = S ''
(x n ) 三次样条插值算法的基本思想是在三次样条中,寻找三次多项式用来逼近每对数据点间的曲线。逼近两点间曲线的三次多项式可以有多条,为使得到的三次多项式唯一,对三次多项式做了条件限定。三次样条插值算法具有良好的收敛性、稳定性,以及二阶光滑性。 3. 牛顿插值
假设有n+1个不同的节点及函数在节点上的值(x 0,y 0),……(x n ,y n ),插值多项式有如下形式:
)())(()()()(n 10n 102010n x -x )(x -x x -x x P x x x x x x -??-+??+-++=αααα
(3.11)
其中系数i α(i=0,1,2……n )为特定系数,可由插值样条i i n y x P =)((i=0,1,2……n )确定。
根据均差的定义,把x 看成[a,b]上的一点,可得
f(x)= f (0x )+f[10x x ,](0x -x ) f[x, 0x ]= f[10x x ,]+f[x,10x x ,] (1x -x ) ……
f[x, 0x ,…x 1-n ]= f[x, 0x ,…x n ]+ f[x, 0x ,…x n ](x-x n ) (3.12) 综合以上式子,把后一式代入前一式,可得到:
f(x)= f (0x )+f[10x x ,](0x -x )+ f[210x x x ,,](0x -x )(1x -x )+ …+ f[x, 0x ,…x n ](0x -x )…(x-x n )+ f[x, 0x ,…x n ]n ω= N n (x )+)(x n R 其中 N n (x )= f (0x )+f[10x x ,](0x -x )+ f[210x x x ,,](0x -x )(1x -x )+ …+ f[x, 0x ,…x n ](0x -x )…(x-x n ) (3.13) )
(x n R = f(x)- N n (x )= f[x, 0x ,…x n ]n ω (2.14) n ω=(0x -x )…(x-x n )
Newton 插值的系数i α(i=0,1,2……n )可以用差商表示。一般有
f k =α[k 10x x x ??,] (k=0,1,2,……,n ) (2.15)
把(2.15)代入(1)得到满足插值条件N )()(i i n x f x =(i=0,1,2,……n )的n 次Newton 插值多项式
N n (x )=f (0x )+f[10x x ,](1x -x )+f[210x x x ,,](1x -x )(2x -x )+……
+f[n 10x x x ??,](1x -x )(2x -x )…(1-n x -x ).
其中插值余项为:
)
()!
()
()()()(x 1n f x N -x f x R 1n 1
n n +++==ωξ ξ介于k 10x x x ??,之间。
四、主要算法及程序
1.拉格朗日算法
function f = Language(x,y,x0)
syms t;
if(length(x) == length(y))
n = length(x);
else
disp('x和y的维数不相等!');
return;
end%检错
f = 0.0;
for(i = 1:n)
l = y(i);
for(j = 1:i-1)
l = l*(t-x(j))/(x(i)-x(j));
end;
for(j = i+1:n)
l = l*(t-x(j))/(x(i)-x(j)); %计算拉格朗日基函数end;
f = f + l; %计算拉格朗日插值函数
simplify(f); %化简
if(i==n)
if(nargin == 3)
f = subs(f,'t',x0); %计算插值点的函数值
else
f = collect(f); %将插值多项式展开
f = vpa(f,6); %将插值多项式的系数化成6位精度的小数
end
end
end
2.三次样条插值
function S=sancichazhi(x,y,t)
n=length(x);
z=zeros(n,4);
z(:,1)=y;
%生成前四列的差商表
for i=2:n
for j=2:i
if j==5
break
end
z(i,j)=(z(i,j-1)-z(i-1,j-1))/(x(i)-x(i-j+1));
end
end
%生成系数矩阵
b=linspace(2,2,n);
for k=1:n
if k==1
c(k)=-2; d(k,1)=-12*(x(2)-x(1))*z(4,4);
elseif k==n
a(k)=-2; d(k,1)=12*(x(n)-x(n-1))*z(k,4); c(k)=0;
else
d(k,1)=6*z(k+1,3);c(k)=(x(k+1)-x(k))/(x(k+1)-x(k-1));
a(k)=1-c(k);
end
end
H=[a;b;c;d'];
u(1)=b(1);
r(1)=c(1);
y1(1)=d(1);
for k=2:n
r(k)=c(k);
l(k)=a(k)/u(k-1);
u(k)=b(k)-l(k)*r(k-1);
y1(k)=d(k)-l(k)*y1(k-1);
end
m(n)=y1(n)/u(n);
for k=n-1:-1:1
m(k)=(y1(k)-r(k)*m(k+1))/u(k);
end
a(1)=[];c(n)=[];
a1=diag(a,-1);b1=diag(b);c1=diag(c,1);
M=a1+b1+c1;
%整理三次多项式
for i=2:n
h(i)=x(i)-x(i-1);b1=[x(i),x(i),x(i)];b2=[x(i-1),x(i-1),x(i-1)]; a1=-m(i-1)/(6*h(i))*poly(b1); a2=m(i)/(6*h(i))*poly(b2);
a33=(m(i-1)*(h(i))^2/6-y(i-1))/h(i)*poly(x(i)); a3=[0,0,a33]; a44=-(m(i)*(h(i))^2/6-y(i))/h(i)*poly(x(i-1)); a4=[0,0,a44]; S(i-1,:)=a1+a2+a4+a3;
end
%对于给定的向量,求出三次样条插值函数在某些点的值
l=length(t);
for i=1:l
for j=2:n
if
x(1)+(x(n)-x(1))/(n-1)*(j-2)<=t(i)&&t(i)<=x(1)+(x(n)-x(1))/(n-1)*(j-1) R(i)=polyval(S(j-1,:),t(i));
end
end
end
disp('结果为三次样条插值分段函数的降幂系数')
plot(t,R,'o',x,y,'kd')
title('三次样条插值')
grid on
end
3.Newton算法
function f = Newton(x,y,x0)
syms t;
if(length(x) == length(y))
n = length(x);
c(1:n) = 0.0;
else
disp('x和y的维数不相等!');
return;
end
f = y(1);
y1 = 0;
l = 1;
for(i=1:n-1)
for(j=i+1:n)
y1(j) = (y(j)-y(i))/(x(j)-x(i));
end
c(i) = y1(i+1);
l = l*(t-x(i));
f = f + c(i)*l;
simplify(f);
y = y1;
if(i==n-1)
if(nargin == 3)
f = subs(f,'t',x0);
else
f = collect(f); %将插值多项式展开
f = vpa(f, 6);
end
end
end
调用程序如下
N=1024;
x=[0.5,1.8,2.4,3.6,4.7,5.1,6.5,7.3,8.2,9.8]
y=[0.30886552,0.904582781,0.997978435,0.771243677,0.188851681,-0.061169136, -0.807798281,-0.991820585,-0.90593608,-0.128429604]
y0=zeros(1,101);
x0=[0:0.1:10];
for i=1:101
y0(i)=Language(x,y,x0(i))
end
figure;
plot(x,y);
figure;
plot(x0,y0);
figure;
Y = fft(y0,N); %做FFT变换
Ayy = (abs(Y)); %取模
Ayy=Ayy/(N/2); %换算成实际的幅度
Ayy(1)=Ayy(1)/2;
F=([1:N]-1)*10/N; %换算成实际的频率值
plot(F(1:N/2),Ayy(1:N/2)); %显示换算后的FFT模值结果
title('幅度-频率曲线图');
五、算法结果及比较分析
0246810
-1
-0.5
0.5
1
a
0246810
-1
-0.5
0.5
1
b
0.020.040.060.080.10.12幅度-频率曲线图
c
图5.1 拉格朗日插值结果
上图中,我们对sin (π/5t )进行非均匀采样10个点,如图a 。然后对非均匀信号进行插值,插100个点,如图b 。再对插值后的均匀信号进行fft 变换得到其频谱,如图c 。
-1
-0.5
0.5
1
a
-1
-0.5
0.5
1
B
012
345
0.020.040.060.080.10.12幅度-频率曲线图
图5.2 三次样条插值结果
-1
-0.5
0.5
1
a
0246810
-1
-0.5
0.5
1
b
0.020.040.060.080.10.12幅度-频率曲线图
c
图5.3 牛顿插值结果
再对刚刚信号进行牛顿插值,其结果如上图5.3所示。
拉格朗日插值算法的公式结构整齐紧凑,在理论分析是十分方便,然而在实际操作中,插值点每增加或减少时,所对应的基本多项式就需要全部计算,于是整个计算公式都会改变,十分繁琐。这时可用牛顿法。此外,当插值点比较多时,多项式次数会比较高,数值会不稳定。复杂度是O (n^2)。
牛顿插值公式是n 次插值多项式的又一种构造,它克服拉格朗日差值的缺点,每增加一个插值节点,只要在原牛顿插值公式增添一项可形成高一次的插值公式。但不能全面反映被插值函数的特性不满足实际问题要求的插值函数在各点与被插值函数相同,或者与被插函数的导数值也相等,这时牛顿插值便不符合要求。
三次样条插值鉴于高次插值不收敛又不稳定的特点,低次插值既具有收敛性又具有稳定性,因此低次值更具有实用价值,但是低次插值的光滑性较差。
六、心得体会
通过这三个星期的课程设计,我学到了很多的东西,不仅巩固了我以前所学过的知识, 还让我学到很多在书本上所没有学到过的知识。
同时进一步加深了对插值算法的了解和熟练了对Matlab的使用, 让我对信号处理这门课程有了更加浓厚的兴趣。因为以前都是基于课本上所学的理论知识,然而通过这次课程设计之后才能真正理解其意义。
在这次课程设计的过程中,我做的部分是插值算法编写,在课程设计开始部分,我遇到不少的问题,比如刚开始,无法调用函数,经过后来的改正才可以。还有刚开始由于对非均匀傅立叶变换原理并不是很了解, 不再单单只是懂理论,理论与实际相结合是很重要的, 只有理论知识是远远不够的, 只有把所学的理论知识与实践相结合起来,从理论中得出结论。总的来说,通过这次的课程设计我对语音信号有了全面的认识,对Matlab的知识又有了深刻的理解, 让我感受到只有在充分理解课本知识的前提下,才能更好的应用这个工具。
这次课程设计使我了解了MATLAB的使用方法,学会分析滤波器的优劣和性能,提高了分析和动手实践能力,同时我相信,进一步加强对MATLAB 的学习与研究对我今后的学习将会起到很大的帮助
傅里叶变换在信号处理中的应用 姓名董柱班级电气工程及其自动化学号1109141013 摘要: 傅里叶变换是一种特殊的积分变换。通过傅里叶变换把信号的从时域变换到频域研究,采用频域法较之经典时域的方法有很多突出的优点,虽然傅里叶分析不是信息科学与技术领域中唯一的变换域方法,但是不得不承认,在此领域中,傅里叶变换分析始终有着广泛的应用,通过傅里叶变换实现信号的滤波,调制,抽样是傅里叶变换在信号处理中最主要的作用。通过对信号的调制可以将信号的低频成分调制到高频,实现频谱搬移,减少马间串扰,提高抗噪声新能,有利于信号的远距离传输,另外,对信号采样可以使连续信号离散化,有利于用计算机对信号进行处理,总之,傅里叶变换在信号处理中有着非常重要的作用。傅里叶变换是学习其他频域变换的基础。 关键词: 傅里叶变换,时域,频域,信号处理,信息科学与技术,滤波,调制,抽样。 一傅里叶变换 1.定义 f(t)是t的函数,如果t满足狄里赫莱条件:具有有限个间断点;具有有限个极值点;绝对可积。则有下图①式成立。称为积分运算f(t)的傅立叶变换, ②式的积分运算叫做F(ω)的傅立叶逆变换。F(ω)叫做f(t)的像函数,f(t)叫做 F(ω)的像原函数。F(ω)是f(t)的像。f(t)是F(ω)原像。 ① 傅里叶变换 傅里叶逆变换 2.分类 连续傅立叶变换:一般情况下,若“傅立叶变换”一词的前面未加任何限定语,则指的是“连续傅立叶变换”。“连续傅立叶变换”将平方可积的函数f(t) 表示成复指数函数的积分或级数形式。 f(t) = \mathcal^[F(ω)] = \frac{\sqrt{2π}} \int\limits_{-\infty}^\infty F(ω)e^{iωt}\,dω.
信号与系统的基本思想:把复杂的信号用简单的信号表示,再进行研究。 怎么样来分解信号?任何信号可以用Delta 函数的移位加权和表示。只有系统是线性时不变系统,才可以用单位冲激函数处理,主要讨论各个单位冲激函数移位加权的响应的叠加能得到总的响应。 线性系统(齐次性,叠加定理) 时不变系统 对一个系统输入单位冲激函数,得到的响应为h(t).表征线性时不变系统的非常重要的东西,只要知道了系统对单位冲击函数的响应,就知道了它对任何信号的响应,因为任何信号都可以表示为单位冲激函数的移位加权和。 例如:d(t)__h(t) 那么a*d(t-t0)__a*h(t-t0) -()= ()(t-)d f t f τδττ∝∝? 的响应为-y()=()(-)t f h t d τττ∝ ∝ ? 记为y(t)=f(t)*h(t),称为f(t)和h(t)的卷积 总结为两点:对于现行时不变系统,任何信号可以用单位冲激信号的移位加权和表示,任何信号的响应可以用输入函数和单位冲激函数响应的卷积来表示 连续时间信号和系统的频域分析 时域分析的重点是把信号分解为单位冲激函数的移位加权和,只讨论系统对单位冲激函数的响应。而频域的分析是把信号分解为各种不同频率的正弦函数的加权和,只讨论系统对sinwt 的响应。都是把信号分解为大量单一信号的组合。
周期函数可以展开为傅里叶级数,将矩形脉冲展开成傅里叶级数,得到傅里叶级数的系数 n A sin F = T x x τ 其中0=2 nw x τ。 取样函数sin ()=x S a x 。产生一种震荡,0点的值最大,然后渐渐衰减直至0 第一:对于傅里叶级数的系数,n 是离散的,所以频谱也是离散状的每条谱线都出现在基波频率的整数倍上,其包络是取样函数。 第二:谱线的间距是0w .。零点是0=2nw x τ,02w =T π是谱的基波频率。如果τ不变,T 增大,那么0w 减小,当T 非常大的时候,0w 非常小,谱线近似连续,越来越密,幅度越来越小。 傅里叶变换:非周期函数 正变换:--F jw)= ()iwt f t e dt ∝ ∝?( 反变换:-1()=()2jnwt f t F jw e dw π ∝∝ ? 常用函数的傅里叶变换(典型非周期信号的频谱)
Chirp信号的傅里叶变换的特征比较 Chirp信号即线性调频信号是瞬时频率在某个范围内随时间变化的正弦波,因其良好的频带利用率,具有较强的抗干扰、抗多途效应和抗多普勒衰减以及良好的频带利用率等优点,因此在通信、声呐、雷达等领域具有广泛的应用。本文就瞬时频率范围(信号的调频宽度)和信号的持续时间(信号的周期)对傅里叶变换后的chirp函数的频谱函数的影响做出讨论,运用MATLAB仿真分析比较。 一.信号的调频宽度上下限对频谱函数的影响 1)高频宽度300情况下的频谱函数。信号的采样频率为43000,扫描时间为0.05,初始频率设为19700,结束频率位置为20000。 2)低频宽度300情况下的频谱函数。信号的采样频率为2000,信号的持续时间为0.05,初始频率设为40,结束频率设置为340。 由上面两幅图可以看出,当它们满足,幅度谱的大小基本都在 0.01和0.015之间,这是因为它们的调频上下限之差相同都是300,且时间周 期都为0.05。由公式可知,幅度与信号的调频宽度(表示傅里叶变换后的频带宽度)和时间周期有关。 二.信号的调频宽度对频谱函数的影响 1)高频宽度10000情况下的频谱函数。信号的采样频率为48000,扫描时间为0.05,初始频率设为10000,结束频率位置为20000。
2)低频宽度80情况下的频谱函数。信号的采样频率为1000,信号的持续时间为0.05,初始频率设为40,结束频率设置为120。 上面两图在频带宽度内的幅度谱差异很明显,这是因为只有当时,近似程度才更高。 三.信号的持续时间对频谱函数的影响 1)低频宽度80情况下的频谱函数。信号的采样频率为1000,chirp 脉冲为0.05,信号的持续时间为2,初始频率设为40,结束频率设置为120。 上图的信号周期是2,发射脉冲长度为0.05与之前其它参数相同的图4比较可知,频带宽度基本相同,在频带宽度内的幅度谱没有太大变化,只是频点上的曲线多了些波动。
第一章 信号与系统的基本概念 1.信号、信息与消息的差别? 信号:随时间变化的物理量; 消息:待传送的一种以收发双方事先约定的方式组成的符号,如语言、文字、图像、数据等 信息:所接收到的未知内容的消息,即传输的信号是带有信息的。 2.什么是奇异信号? 函数本身有不连续点或其导数或积分有不连续点的这类函数统称为奇异信号或奇异函数。例如: 单边指数信号 (在t =0点时,不连续), 单边正弦信号 (在t =0时的一阶导函数不连续)。 较为重要的两种奇异信号是单位冲激信号δ(t )和单位阶跃信号u(t )。 3.单位冲激信号的物理意义及其取样性质? 冲激信号:它是一种奇异函数,可以由一些常规函数的广义极限而得到。 它表达的是一类幅度很强,但作用时间很短的物理现象。其重要特性是筛选性,即: ()()()(0)(0)t x t dt t x dt x δδ∞ ∞ -∞ -∞ ==? ? 4.什么是单位阶跃信号? 单位阶跃信号也是一类奇异信号,定义为: 10()00t u t t >?=?
12()()()x t ax t bx t =+,其中a 和b 是任意常数时, 输出信号()y t 是1()y t 和2()y t 的线性叠加,即:12()()()y t ay t by t =+; 且当输入信号()x t 出现延时,即输入信号是0()x t t -时, 输出信号也产生同样的延时,即输出信号是0()y t t -。 其中,如果当12()()()x t x t x t =+时,12()()()y t y t y t =+,则称系统具有叠加性; 如果当1()()x t ax t =时,1()()y t ay t =则称系统具有均匀性。 线性时不变系统是最基本的一类系统,是研究复杂系统,如非线性、时变系统的基础。 6.线性时不变系统的意义与应用? 线性时不变系统是我们本课程分析和研究的主要对象,对线性时不变性进行推广,可以得到线性时不变系统具有微分与积分性质,假设系统的输入与输出信号分别为()x t 和()y t ,则 当输入信号为 ()dx t dt 时,输出信号则为() dy t dt ; 或者当输入信号为()t x d ττ-∞ ?时,输出信号则为()t y d ττ-∞ ?。 另外,线性时不变系统对信号的处理作用可以用冲激响应(或单位脉冲响应)、系统函数或频率响应进行描述。而且多个系统可以以不同的方式进行连接,基本的连接方式为:级联和并联。 假设两个线性时不变系统的冲激响应分别为:1()h t 和2()h t , 当两个系统级联后,整个系统的冲激响应为:12()()*()h t h t h t =; 当两个系统并联后,整个系统的冲激响应为:12()()()h t h t h t =+; 当0t <时,若()0h t =, 则此系统为因果系统; 若|()|h t dt ∞ -∞<∞?, 则此系统为稳定系统。 第二章 连续时间系统的时域分析 1.如何获得系统的数学模型? 数学模型是实际系统分析的一种重要手段,广泛应用于各种类型系统的分析和控制之中。 不同的系统,其数学模型可能具有不同的形式和特点。对于线性时不变系统,其数学模型
时域信号 弧频率表示的 傅里叶变换 注释 1 线性 2 时域平移 3 频域平移, 变换2的频域对应4 如果值较大,则会收缩 到原点附近,而会扩 散并变得扁平. 当 | a | 趋向 无穷时,成为 Delta函数。 5 傅里叶变换的二元性性质。通过 交换时域变量和频域变量 得到. 6 傅里叶变换的微分性质 7 变换6的频域对应 8 表示和的卷积—这
9 矩形脉冲和归一化的sinc 函数 10 变换10的频域对应。矩形函数是理想的低通滤波器,sinc 函数是这类滤波器对反因果冲击的响应。 11 tri 是三角形函数 12 变换12的频域对应 13 高斯函数 exp( ? αt 2) 的傅里叶变换是他本身. 只有当 Re(α) > 0时,这是可积的。 14 15 16 a>0 17 变换本身就是一个公式
18 δ(ω) 代表狄拉克δ函数分布. 这 个变换展示了狄拉克δ函数的重要 性:该函数是常函数的傅立叶变换 19 变换23的频域对应 20 由变换3和24得到. 21 由变换1和25得到,应用了欧拉公 式: cos(at) = (e iat + e?iat) / 2. 22 由变换1和25得到 23 这里, n是一个自然数. δ(n)(ω) 是狄拉克δ函数分布的n阶微分。这 个变换是根据变换7和24得到的。 将此变换与1结合使用,我们可以变 换所有多项式。 24 此处sgn(ω)为符号函数;注意此变 换与变换7和24是一致的. 25 变换29的推广. 26 变换29的频域对应. 27 此处u(t)是单位阶跃函数; 此变换 根据变换1和31得到.
第七章 傅里叶变换 1.求下列函数的傅氏变换: (1)1,10, ()1, 01,0,; t f t t --<? 解: (1)[()]()j t F f t f t e dt ω+∞--∞ =? 1 101 10 1 1 22sin cos | 2(1cos ).j t j t j t j t e dt e dt e dt e dt j i tdt t j ωωωωωωω ωω -----=-+=-+=-= =- -????? (2) ()()j t F f t e dt ωω+∞--∞ =? 0(1)(1)0 11|.11t j t j t j t e e dt e dt e j j ωωωωω ---∞ -∞ --∞====--?? 6.求下列函数的傅氏变换 (1) 1,0,sgn 1,0;t t t -? (2) ()sin(5).3f t t π =+ 解: (1)已知 1 [()](),[1]2(),F u t F j πδωπδωω = +=由sgn 2()1t u t =-有 12[sgn ]2( ())2().F t j j πδωπδωωω =+-= (2) 由于 1()sin(5)sin 5cos5,322f t t t t π=+=+ 故 [()][(5)(5)](5)(5)].2j F f t πδωδωδωδω= +--++- 7.已知00()[()()]F ωπδωωδωω=++-为函数()f t 的傅氏变换,求().f t
傅里叶变换,拉普拉斯变换和Z 变换的意义来源:于理扬的日志 傅里叶变换在物理学、数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学、海洋学、结构动力学等领域都有着广泛的应用(例如在信号处理中, 傅里叶变换的典型用途是将信号分解成幅值分量和频率分量。 傅里叶变换能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数或者它们的积分的线性组合。在不同的研究领域, 傅里叶变换具有多种不同的变体形式, 如连续傅里叶变换和离散傅里叶变换。 傅里叶变换是一种解决问题的方法,一种工具,一种看待问题的角度。理解的关键是:一个连续的信号可以看作是一个个小信号的叠加, 从时域叠加与从频域叠加都可以组成原来的信号,将信号这么分解后有助于处理。 我们原来对一个信号其实是从时间的角度去理解的,不知不觉中,其实是按照时间把信号进行分割, 每一部分只是一个时间点对应一个信号值, 一个信号是一组这样的分量的叠加。傅里叶变换后, 其实还是个叠加问题, 只不过是从频率的角度去叠加, 只不过每个小信号是一个时间域上覆盖整个区间的信号, 但他确有固定的周期,或者说,给了一个周期,我们就能画出一个整个区间上的分信号,那么给定一组周期值(或频率值,我们就可以画出其对应的曲线,就像给出时域上每一点的信号值一样,不过如果信号是周期的话,频域的更简单,只需要几个甚至一个就可以了,时域则需要整个时间轴上每一点都映射出一个函数值。 傅里叶变换就是将一个信号的时域表示形式映射到一个频域表示形式;逆傅里叶变换恰好相反。这都是一个信号的不同表示形式。它的公式会用就可以,当然把证明看懂了更好。 对一个信号做傅里叶变换,可以得到其频域特性,包括幅度和相位两个方面。幅度是表示这个频率分量的大小, 那么相位呢, 它有什么物理意义?频域的相位与时域的相位有关系吗?信号前一段的相位(频域与后一段的相位的变化是否与信号的频率成正比关系。
傅里叶变换 一、傅里叶变换的表述 在数学上,对任意函数f(x),可按某一点进行展开,常见的有泰勒展开和傅里叶展开。泰勒展开为各阶次幂函数的线性组合形式,本质上自变量未改变,仍为x,而傅里叶展开则为三角函数的线性组合形式,同时将自变量由x变成ω,且由于三角函数处理比较简单,具有良好的性质,故被广泛地应用在信号分析与处理中,可将时域分析变换到频域进行分析。 信号分析与处理中常见的有CFS(连续时间傅里叶级数)、CFT (连续时间傅里叶变换)、DTFT(离散时间傅里叶变换)、DFS(离散傅里叶级数)、DFT(离散傅里叶变换)。通过对连续非周期信号x c(t)在时域和频域进行各种处理变换,可推导出以上几种变换,同时可得出这些变换之间的关系。以下将对上述变换进行简述,同时分析它们之间的关系。 1、CFS(连续时间傅里叶级数) 在数学中,周期函数f(x)可展开为 由此类比,已知连续周期信号x(t),周期为T0,则其傅里叶级数为 其中,
为了简写,有 其中, 为了与复数形式联系,先由欧拉公式e j z=cos z+jsin z得 故有
令 则 对于D n,有 n≤0时同理。 故 CFS图示如下:
Figure 1 理论上,CFS对于周期性信号x(t)在任意处展开都可以做到无误差,只要保证n从-∞取到+∞就可以。在实践中,只要n取值范围足够大,就可以保证在某一点附近对x(t)展开都有很高的精度。 2、CFT(连续时间傅里叶变换) 连续非周期信号x(t),可以将其看成一连续周期信号的周期T0→∞。当然,从时域上也可以反过来看成x(t)的周期延拓。将x(t)进行CFS展开,有 若令 则 有
第2章信号分析 本章提要 信号分类 周期信号分析--傅里叶级数非周期信号分析-- 傅里叶变换脉冲函数及其性质 信号:反映研究对象状态和运动特征的物理量信号分析:从信号中提取有用信息的方法和手段 § 2—1 信号的分类 两大类:确定性信号,非确定性信号确定性信号:给定条件下取值是确定的。 进一步分为:周期信号, 非周期信号。
x(t) Acos J% ° m 非确定性信号 (随机信号): 给定条件下 取值是不确定的 按取值情况分类:模拟信号,离散信 号 数字信号:属于离散信号,幅值离散, 并用二进制表示。 信号描述方法 时域描述 如简谐信号 简谐信号及其三个要素 质量—弹簧系 统的力学模型
频域描述 以信号的频率结构来描述信号的方法:将信号看成许多谐波(简谐信号)之和,每一个谐波称作该信号的一 个频率成分,考察信号含有那些频率的谐波,以及各 谐波的幅值和相角。 vpage break〉 § 2-2 周期信号与离散频谱 一、周期信号傅里叶级数的三角函数 形式 周期信号时域表达式 T:周期。注意n的取值:周期信号“无始无终” # 傅里叶级数的三角函数展开式 x(t) a0(a n cosn 0t b n sinn 0t) n 1
(n =1,2, 3 ,…) 傅立叶系数: a 。 1 T T 2 T x(t)dt 2 T 2 2 o tdt a n T T x(t)cos n 2 T 2 2 b n T T x(t)sin n o tdt 2 式中T --周期;0--基频,o =2 /T o 三角函数展开式的另一种形式: 次谐波的幅值 次谐波的频率 信号的均值,直流分量 N 次谐波的相角
目录 用Matlab对信号进行傅里叶变换 (2) Matlab的傅里叶变换实例 (5) Matlab方波傅立叶变换画出频谱图 (7)
用Matlab对信号进行傅里叶变换 1.离散序列的傅里叶变换DTFT(Discrete Time Fourier Transform) 代码: 1 N=8; %原离散信号有8点 2 n=[0:1:N-1] %原信号是1行8列的矩阵 3 xn=0.5.^n; %构建原始信号,为指数信号 4 5 w=[-800:1:800]*4*pi/800; %频域共-800----+800 的长度(本应是无穷,高频分量很少,故省去) 6 X=xn*exp(-j*(n'*w)); %求dtft变换,采用原始定义的方法,对复指数分量求和而得 7 subplot(311) 8 stem(n,xn); 9 title('原始信号(指数信号)'); 10 subplot(312); 11 plot(w/pi,abs(X)); 12 title('DTFT变换') 结果: 分析:可见,离散序列的dtft变换是周期的,这也符合Nyquist采样定理的描述,连续时间信号经周期采样之后,所得的离散信号的频谱是原连续信号频谱的周期延拓。 2.离散傅里叶变换DFT(Discrete Fourier Transform)
与1中DTFT不一样的是,DTFT的求和区间是整个频域,这对 结果图:
分析:DFT只是DTFT的现实版本,因为DTFT要求求和区间无穷,而DFT只在有限点内求和。 3.快速傅里叶变换FFT(Fast Fourier Transform) 虽然DFT相比DTFT缩减了很大的复杂度,但是任然有相当大的计算量,不利于信息的实时有效处理,1965年发现的DFT解决了这一问题。 实现代码: 1 N=64; %原离散信号有8点 2 n=[0:1:N-1] %原信号是1行8列的矩阵 3 xn=0.5.^n; %构建原始信号,为指数信号 4 Xk=fft(xn,N); 5 subplot(221); 6 stem(n,xn); 7 title('原信号'); 8 subplot(212); 9 stem(n,abs(Xk)); 10 title('FFT变换') 效果图: 分析:由图可见,fft变换的频率中心不在0点,这是fft算法造成的,把fft改为fftshift可以将频率中心移到0点。
时域信号 角频率表示的 傅里叶变换 弧频率表示的 傅里叶变换 注释 1 线性 2 时域平移 3 频域平移,变换2 的频域对应 4 如果值较大,则 会收缩到原 点附近,而 会扩 散并变得扁平.当 | a | 趋向无穷 时,成为狄拉克δ 函数。 5 傅里叶变换的二元 性性质。通过交换 时域变量和频域 变量得到. 6 傅里叶变换的微分 性质
7 变换6的频域对应8 表示和 的卷积—这就是卷 积定理 9 变换8的频域对应。[编辑]平方可积函数 时域信号 角频率表示的 傅里叶变换 弧频率表示的 傅里叶变换 注释 10 矩形脉冲和归一 化的sinc函数 11 变换10的频域对 应。矩形函数是理 想的低通滤波器, sinc函数是这类 滤波器对反因果 冲击的响应。
12 tri是三角形函数 13 变换12的频域对应 14 高斯函数exp( ? αt2)的傅里叶变换是他本身.只有当Re(α) > 0时,这是可积的。 15 光学领域应用较多 16 17 18 a>0 19 变换本身就是一个公式
20 J0(t)是0阶第一 类贝塞尔函数。 21 上一个变换的推 广形式; T n(t)是第 一类切比雪夫多 项式。 22 U n (t)是第二类切 比雪夫多项式。[编辑]分布 时域信号 角频率表示的 傅里叶变换 弧频率表示的 傅里叶变换 注释 23 δ(ω)代表狄拉克δ函数 分布.这个变换展示了狄 拉克δ函数的重要性:该 函数是常函数的傅立叶 变换 24 变换23的频域对应
25 由变换3和24得到. 26 由变换1和25得到,应用了欧拉公式: cos(at) = (e iat + e?iat) / 2. 27 由变换1和25得到 28 这里, n是一个自然数.δ(n)(ω)是狄拉克δ函数分布的n阶微分。这个变换是根据变换7和24得到的。将此变换与1结合使用,我们可以变换所有多項式。 29 此处sgn(ω)为符号函数;注意此变换与变换7和24是一致的. 30 变换29的推广. 31 变换29的频域对应. 32 此处u(t)是单位阶跃函数;此变换根据变换1和31得到.
常用傅里叶变换 Document number:NOCG-YUNOO-BUYTT-UU986-1986UT
时域信号 角频率表示的 傅里叶变换 弧频率表示的 傅里叶变换 注释 1 线性 2 时域平移 3 频域平移,变换2 的频域对应 4 如果值较大, 则会收缩 到原点附近,而 会扩 散并变得扁平.当 |?a?|?趋向无穷 时,成为。 5 傅里叶变换的二元 性性质。通过交换 时域变量和频域 变量得到. 6 傅里叶变换的微分 性质 7 变换6的频域对应
8 表示和 的卷积—这就是9 变换8的频域对 应。 []平方可积函数 时域信号 角频率表示的 傅里叶变换 弧频率表示的 傅里叶变换 注释 10 和归一化的 11 变换10的频域对 应。矩形函数是 理想的低通滤波 器,是这类滤波 器对冲击的响 应。 12 tri?是 13 变换12的频域对 应
14 exp( ? αt2)的傅里叶变换是他本身.只有当Re(α) > 0时,这是可积的。 15 领域应用较多 16 17 18 a>0 19 变换本身就是一个公式 20 J0(t)?是。 21 上一个变换的推广形式;?T n(t)?是。 22 ???? U n?(t)是。
[]分布 时域信号 角频率表示的 傅里叶变换 弧频率表示的 傅里叶变换 注释 23 δ(ω)代表分布.这个变换 展示了狄拉克δ函数的 重要性:该函数是常函 数的傅立叶变换 24 变换23的频域对应 25 由变换3和24得到. 26 由变换1和25得到,应 用了:?cos(at) = (e iat?+?e???iat) / 2. 27 由变换1和25得到 28 这里,?n是一个.δ(n)(ω)是 狄拉克δ函数分布的n 阶微分。这个变换是根 据变换7和24得到的。 将此变换与1结合使 用,我们可以变换所 有。
常用函数傅里叶变换 Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】
附录A 拉普拉斯变换及反变换1.表A-1 拉氏变换的基本性质
2.表A-2 常用函数的拉氏变换和z变换表
3. 用查表法进行拉氏反变换 用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。设)(s F 是s 的有理真分式 11 10 111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++==---- (m n >) 式中系数n n a a a a ,,...,,110-,m m b b b b ,,,110- 都是实常数;n m ,是正整数。按代数定理可将)(s F 展开为部分分式。分以下两种情况讨论。 ① 0)(=s A 无重根 这时,F(s)可展开为n 个简单的部分分式之和的形式。 ∑=-=-++-++-+-=n i i i n n i i s s c s s c s s c s s c s s c s F 122 11)( (F-1) 式中,n s s s ,,,21 是特征方程A(s)=0的根。i c 为待定常数,称为F(s)在 i s 处的留数,可按下式计算: )()(lim s F s s c i s s i i -=→ (F-2) 或 i s s i s A s B c ='=)() ( (F-3) 式中,)(s A '为)(s A 对s 的一阶导数。根据拉氏变换的性质,从式(F-1)可求得原函数
关于傅立叶变换,无论是书本还是在网上可以很容易找到关于傅立叶变换的描述,但是大都是些故弄玄虚的文章,太过抽象,尽是一些让人看了就望而生畏的公式的罗列,让人很难能够从感性上得到理解,最近,我偶尔从网上看到一个关于数字信号处理的电子书籍,是一个叫Steven W. Smith, Ph.D.外国人写的,写得非常浅显,里面有七章由浅入深地专门讲述关于离散信号的傅立叶变换,虽然是英文文档,我还是硬着头皮看完了有关傅立叶变换的有关内容,看了有茅塞顿开的感觉,在此把我从中得到的理解拿出来跟大家分享,希望很多被傅立叶变换迷惑的朋友能够得到一点启发,这电子书籍是免费的,有兴趣的朋友也可以从网上下载下来看一下,URL地址是: https://www.doczj.com/doc/ba6185579.html,/pdfbook.htm 要理解傅立叶变换,确实需要一定的耐心,别一下子想着傅立叶变换是怎么变换的,当然,也需要一定的高等数学基础,最基本的是级数变换,其中傅立叶级数变换是傅立叶变换的基础公式。 二、傅立叶变换的提出 让我们先看看为什么会有傅立叶变换?傅立叶是一位法国数学家和物理学家的 名字,英语原名是Jean Baptiste Joseph Fourier(1768-1830), Fourier对热传递很感兴趣,于1807年在法国科学学会上发表了一篇论文,运用正弦曲线来描述温度分布,论文里有个在当时具有争议性的决断:任何连续周期信号可以由一组适当的正弦曲线组合而成。当时审查这个论文的人,其中有两位是历史上著名的数学家拉格朗日(Joseph Louis Lagrange, 1736-1813)和拉普拉斯(Pierre Simon de Laplace, 1749-1827),当拉普拉斯和其它审查者投票通过并要发表这个论文时,拉格朗日坚决反对,在近50年的时间里,拉格朗日坚持认为傅立叶的方法无法表示带有棱角的信号,如在方波中出现非连续变化斜率。法国科学学会屈服于拉格朗日的威望,拒绝了傅立叶的工作,幸运的是,傅立叶还有其它事情可忙,他参加了政治运动,随拿破仑远征埃及,法国大革命后因会被推上断头台而一直在逃避。直到拉格朗日死后15年这个论文才被发表出来。 谁是对的呢?拉格朗日是对的:正弦曲线无法组合成一个带有棱角的信号。但是,我们可以用正弦曲线来非常逼近地表示它,逼近到两种表示方法不存在能量差别,基于此,傅立叶是对的。 为什么我们要用正弦曲线来代替原来的曲线呢?如我们也还可以用方波或三角波来代替呀,分解信号的方法是无穷的,但分解信号的目的是为了更加简单地处理原来的信号。用正余弦来表示原信号会更加简单,因为正余弦拥有原信号所不具有的性质:正弦曲线保真度。一个正弦曲线信号输入后,输出的仍是正弦曲线,只有幅度和相位可能发生变化,但是频率和波的形状仍是一样的。且只有正弦曲线才拥有这样的性质,正因如此我们才不用方波或三角波来表示。
傅里叶变换 那么,到底什么是傅里叶变换算法列?傅里叶变换所涉及到的公式具体有多复 杂列? 傅里叶变换(Fourier transform)是一种线性的积分变换。因其基本思想首先 由法国学者傅里叶系统地提出,所以以其名字来命名以示纪念。 哦,傅里叶变换原来就是一种变换而已,只是这种变换是从时间转换为频率的变化。这下,你就知道了,傅里叶就是一种变换,一种什么变换列?就是一种从时间到频率的变化或其相互转化。 ok,咱们再来总体了解下傅里叶变换,让各位对其有个总体大概的印象,也顺便看看傅里叶变换所涉及到的公式,究竟有多复杂: 以下就是傅里叶变换的4种变体(摘自,维基百科) 连续傅里叶变换 一般情况下,若“傅里叶变换”一词不加任何限定语,则指的是“连续傅里叶变换”。连续傅里叶变换将平方可积的函数f(t)表示成复指数函数的积分或级数 形式。 这是将频率域的函数F(ω)表示为时间域的函数f(t)的积分形式。连续傅里 叶变换的逆变换 (inverse Fourier transform)为: 即将时间域的函数f(t)表示为频率域的函数F(ω)的积分。一般可称函数f(t)为原函数,而称函数F(ω)为傅里叶变换的像函数,原函数和像函数构成一个傅里
叶变换对(transform pair)。除此之外,还有其它型式的变换对,以下两种型式亦常被使用。在通信或是信号处理方面,常以来代换,而形成新的变换对: 或者是因系数重分配而得到新的变换对: 一种对连续傅里叶变换的推广称为分数傅里叶变换(Fractional Fourier Transform)。分数傅里叶变换(fractional Fourier transform,FRFT)指的就是傅里叶变换(Fourier transform,FT)的广义化。 分数傅里叶变换的物理意义即做傅里叶变换 a 次,其中 a 不一定要为整数; 而做了分数傅里叶变换之后,信号或输入函数便会出现在介于时域(time domain)与频域(frequency domain)之间的分数域(fractional domain)。 当f(t)为偶函数(或奇函数)时,其正弦(或余弦)分量将消亡,而可以称这时的变换为余弦变换(cosine transform)或正弦变换(sine transform). 另一个值得注意的性质是,当f(t)为纯实函数时,F(?ω) = F*(ω)成立. 傅 里叶级数 连续形式的傅里叶变换其实是傅里叶级数 (Fourier series)的推广,因为积 分其实是一种极限形式的求和算子而已。对于周期函数,其傅里叶级数是存在的:
弧频率表示的时域信号注释傅里叶变换 线性1 时域平移2 频域平移3 , 变换2的频域对应 会收缩值较大,则如果 4 会扩而到原点附近,a趋向 | | . 散并变得扁平当无穷时,成为函数。 Delta 通过傅里叶变换的二元性性质。
5 交换时域变量和频域变量 . 得到 6 傅里叶变换的微分性质 变换7 6的频域对应 表示和的卷积—这 8就卷积定 9 矩形脉冲和归一化的sinc函数 变换10的频域对应。矩形函数是理
想的低通滤波器,sinc函数是这类10 滤波器对反因果冲击的响应。 tri是三角形函数 11 12 变换12的频域对应 2t) ?α的傅里叶变 exp( 高斯函数 换是他本身. 只有当 Re(α) 13 > 0时,这是可积的。 14 15
a>0 16 17 变换本身就是一个公式 δ(ω) 代表狄拉克δ函数分布. 这个变换展示了狄拉克18 δ函数的重要性:该函数是常函数的傅立叶变换 19 变换23的频域对应 20 由变换3和24得到. 由变换1和25得到,应用了欧拉公 21 iat?iat eeat) / 2. 式: cos() = ( +
22 由变换1和25得到 n)(n(ω) . δ这里, 自然数是一个n阶微分。函数分布的是狄拉克δ 这个变换是根据变换23 7和24得到的。将此变换与1结合使用,我们可以变换所有多项式。 此处sgn(ω)为符号函数;注意此变 24 换与变换7和24是一致的. 25 变换29的推广. 26 变换29的频域对应. ut)是单位阶跃函数此处(; 此变换 27
根据变换1和31得到. uta > 0. ,且()是单位阶跃函数28 狄拉克梳状函数——有助于解释或34 理解从连续到离散时间的转变.
傅里叶变换公式
————————————————————————————————作者: ————————————————————————————————日期:
第2章信号分析 本章提要 ??信号分类 ??周期信号分析--傅里叶级数 ?非周期信号分析--傅里叶变换 ??脉冲函数及其性质 信号:反映研究对象状态和运动特征的物理量信号分析:从信号中提取有用信息的方法 和手段 §2-1信号的分类 ●两大类:确定性信号,非确定性信号 确定性信号:给定条件下取值是确定的。 进一步分为:周期信号, 非周期信号。
质量M 弹簧 刚度K t x (t ) o x 0 质量-弹簧系统的力学模型 x (t ) ? ?? ? ??+=0cos )(?t m k A t x 非确定性信号(随机信号):给定条件下 取值是不确定的 ●?按取值情况分类:模拟信号,离散信号 数字信号:属于离散信号,幅值离散,并用二进制表示。 ● 信号描述方法 时域描述 如简谐信号
)cos(000φω+t x 简谐信号及其三个要素 幅值 频率 相角 频域描述 以信号的频率结构来描述信号的方法:将信号看成许多谐波(简谐信号)之和,每一个谐波称作该信号的一个频率成分,考察信号含有那些频率的谐波,以及各谐波的幅值和相角。
傅里叶变换 对信号和系统的分析研究可以在时间域进行,也可以在频域进行。连续时间信号是时间变量t 的函数,连续时间系统在时间域可以用线性常系数微分方程来描述,也可以用冲激响应来描述。离散时间信号(序列)是序数n 的函数,这里n 可以看成时间参量,离散时间系统在时间域可以用线性常系数差分方程来描述,也可以用单位脉冲响应来描述。 在时间域对信号和系统进行分析研究,比较直观,物理概念清楚,但仅在时间域分析研究并不完善,有些问题研究比较困难。比如,有两个序列,从时间波形上看,一个变化快,一个变化慢,但都混有噪声,希望用滤波器将噪声滤除。从信号波形观察,时域波形变化快,意味着含有更高的频率成分,因此这两个信号的频谱结构不同,那么对滤波器的性能要求也不同。为了设计合适的滤波器,就需要将时域信号转换到频率域,得到其频谱结构,分析其特性,进而得到所要设计的滤波器的技术指标,然后才能进行滤波器的设计。 在连续时间信号与系统中,其频域方法就是拉普拉斯变换与傅里叶变换。在离散时间信号与系统中,频域分析采用z 变换与傅里叶变换作为数学工具。现在针对几种傅里叶变换的基本概念、重要特点、相互关系作详细的介绍。 傅里叶变换的几种可能形式 对傅里叶变换的几种可能形式进行总结,再进一步引出周期序列的离散傅里叶级数及傅里叶变换表示。 一. 非周期连续时间信号的傅里叶变换 在“信号与系统”课程中,这一变换对为 ? ∞ ∞ -Ω-= Ωdt e t x j X t j a a )()( Ω Ω= ? ∞ ∞ -Ωd e j X t x t j a a )(21)(π 这一变换对的时频域示意图(只说明关系,不表示实际的变换对)如图所示。可以看出时域上是非周期连续信号,频域上是连续非周期的频谱。 二. 周期连续时间信号的傅里叶级数及傅里叶变换表示 非周期连续信号及其频谱 t Ω0 Ω-
例9.1 试将图9.3中所示的非正弦周期信号(称为方波信号)展成傅里叶级数。 解 根据图上所示信号的波形,可知其既对称于纵轴,又具有半波对称性质,所以它是兼有奇谐波函数性质的偶函数。依照上述定理,此信号的傅里叶级数中必定只含有余弦的奇次谐波项,因此只需按公式 ()2 04cos T km A f t k tdt T ω= ? 计算A km 。 对图上的波形图可以写出 ()04 42 T A t f t T T A t ?
故有 4044444sin 2sin T T km T A A B t k tdt t A k tdt T T T T ωω?? = -- ??? ?? 参照积分公式 211 sin sin cos x axdx ax x ax a a = -? 可算出 22 22 81,5,9,83,7,11km A k k B A k k ππ?=??=? ?-=? ? 于是所欲求的傅里叶级数 ()2222 8111 sin sin 3sin 5sin 7357 A f t t t t t ωωωωπ?? = -+-+ ??? 。 例9.3 已知一如图9.5所示的信号波形,试求其傅里叶级数。 图9.5 例9.3用图 解 此信号对原点对称,是奇函数,且又是半波横轴对称,所以其傅里叶级数仅是正弦奇次谐波分量组成。由于 ()022 T A t f t T A t T ?
傅里叶变换算法详细介绍
从头到尾彻底理解傅里叶变换算法、上 前言 第一部分、DFT 第一章、傅立叶变换的由来 第二章、实数形式离散傅立叶变换(Real DFT) 从头到尾彻底理解傅里叶变换算法、下 第三章、复数 第四章、复数形式离散傅立叶变换 /**************************************************** ***********************************************/ 这一片的傅里叶变换算法,讲解透彻,希望对大家会有所帮助。感谢原作者们(July、dznlong)的精心编写。 /**************************************************** **********************************************/
前言: “关于傅立叶变换,无论是书本还是在网上可以很容易找到关于傅立叶变换的描述,但是大都是些故弄玄虚的文章,太过抽象,尽是一些让人看了就望而生畏的公式的罗列,让人很难能够从感性上得到理解”---dznlong, 那么,到底什么是傅里叶变换算法列?傅里叶变换所涉及到的公式具体有多复杂列? 傅里叶变换(Fourier transform)是一种线性的积分变换。因其基本思想首先由法国学者傅里叶系统地提出,所以以其名字来命名以示纪念。 哦,傅里叶变换原来就是一种变换而已,只是这种变换是从时间转换为频率的变化。这下,你就知道了,傅里叶就是一种变换,一种什么变换列?就是一种从时间到频率的变化或其相互转化。 ok,咱们再来总体了解下傅里叶变换,让各位对其有个总体大概的印象,也顺便看看傅里叶变换所涉及到的公式,究竟有多复杂: 以下就是傅里叶变换的4种变体(摘自,维基百科)
(正弦和/或余弦函数)或者它们的积分的线性组合。在不同的研究领域,傅立叶变换具有多种不同的变体形式,如连续傅立叶变换和离散傅立叶变换。最初傅立叶分析是作为热过程的解析分析的工具被提出的。 简介 Fourier transform或Transformée de Fourier有多个中文译名,常见的有“傅里叶变换”、“付立叶变换”、“傅立叶转换”、“傅氏转换”、“傅氏变换”、等等。 傅立叶变换是一种分析信号的方法,它可分析信号的成分,也可用这些成分合成信号。许多波形可作为信号的成分,比如正弦波、方波、锯齿波等,傅立叶变换用正弦波作为信号的成分。 傅里叶变换定义 f(t)是t的周期函数,如果t满足狄里赫莱条件:在一个以2T为周期内f(X)连续或只有有限个第一类间断点,附f(x)单调或可划分成有限个单调区间,则F(x)以2T为周期的傅里叶级数收敛,和函数S(x)也是以2T为周期的周期函数,且在这些间断点上,函数是有限值;在一个周期内具有有限个极值点;绝对可积。则有下图①式成立。称为积分运算f(t)的傅立叶变换,
②式的积分运算叫做F(ω)的傅立叶逆变换。F(ω)叫做f(t)的象函数,f(t)叫做 F(ω)的象原函数。F(ω)是f(t)的象。f(t)是F(ω)原象。 ①傅立叶变换 ②傅立叶逆变换 傅里叶变换在物理学、电子类学科、数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学、海洋学、结构动力学等领域都有着广泛的应用(例如在信号处理中,傅里叶变换的典型用途是将信号分解成频率谱——显示与频率对应的幅值大小)。傅里叶变换相关 * 傅里叶变换属于谐波分析。 * 傅里叶变换的逆变换容易求出,而且形式与正变换非常类似; * 正弦基函数是微分运算的本征函数,从而使得线性微分方程的求解可以转化为常系数的代数方程的求解.在线性时不变的物理系统内,频率是个不变的性质,从而系统对于复杂激励的响应可以通过组合其对不同频率正弦信号的响应来获取; *卷积定理指出:傅里叶变换可以化复杂的卷积运算为简单的乘积运算,从而提供了计算卷积的一种简单手段;