简易逻辑考点和题型归纳

简单的逻辑联结词、全称量词与存在量词考点和题型归纳

一、基础知识

1．简单的逻辑联结词

(1)命题中的“且”“或”“非”?叫做逻辑联结词．

①用联结词“且”把命题p和命题q联结起来，得到复合命题“p且q”，记作p∧q；

②用联结词“或”把命题p和命题q联结起来，得到复合命题“p或q”，记作p∨q；

③对命题p的结论进行否定，得到复合命题“非p”，记作非p.?

?“且”的数学含义是几个条件同时满足，“且”在集合中的解释为“交集”；“或”的数学含义是至少满足一个条件，“或”在集合中的解释为“并集”；“非”的含义是否定，“非p”只否定p的结论，“非”在集合中的解释为“补集”.

?“命题的否定”与“否命题”的区别

(1)命题的否定只是否定命题的结论，而否命题既否定其条件，也否定其结论．

(2)命题的否定与原命题的真假总是相对立的，即一真一假，而否命题与原命题的真假无必然联系．

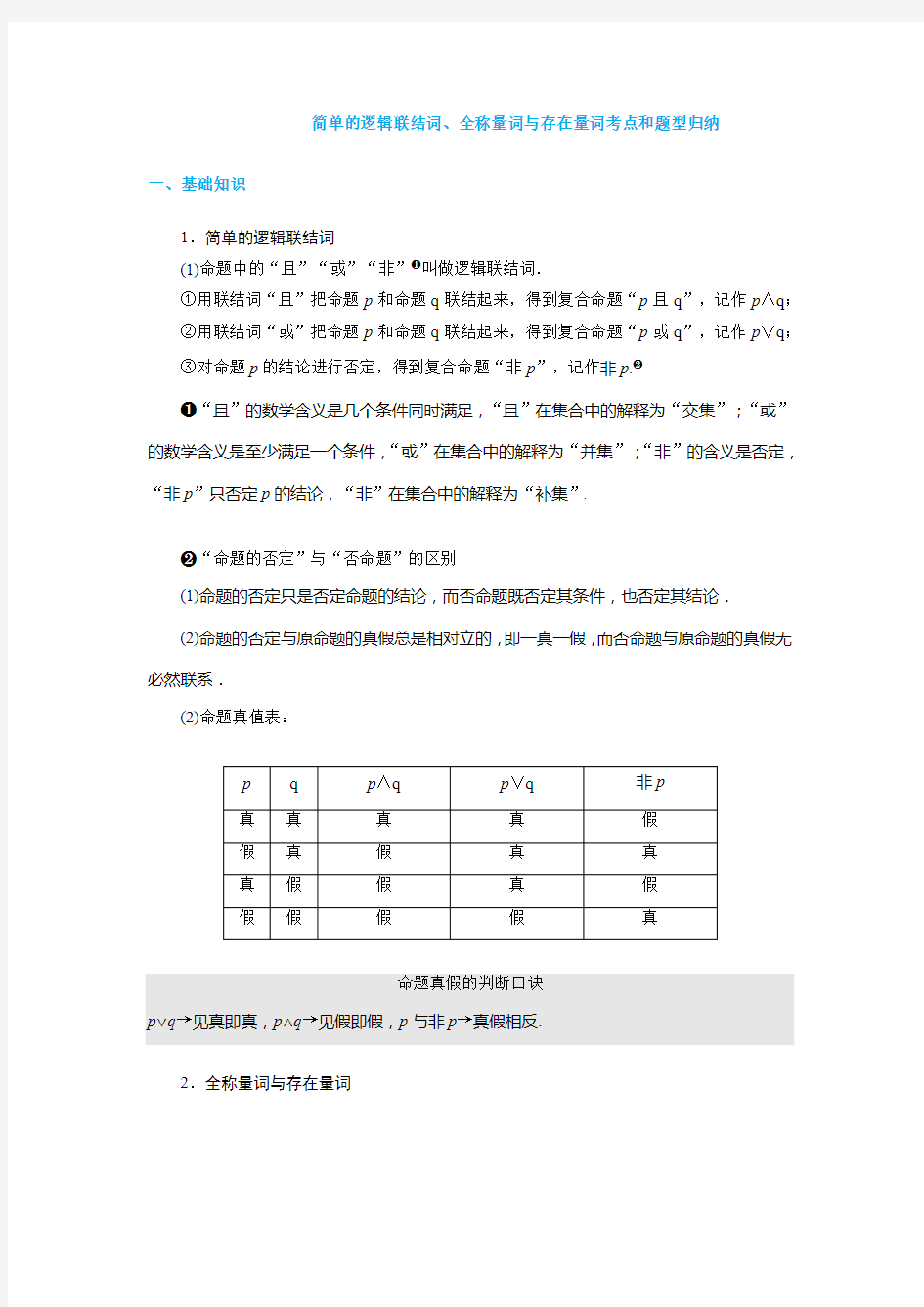
(2)命题真值表：

命题真假的判断口诀

p∨q→见真即真，p∧q→见假即假，p与非p→真假相反.

2．全称量词与存在量词

4．全称命题与特称命题的否定

二、常用结论

含逻辑联结词命题真假的等价关系

(1)p∨q真?p，q至少一个真?(非p)∧(非q)假．

(2)p∨q假?p，q均假?(非p)∧(非q)真．

(3)p∧q真?p，q均真?(非p)∨(非q)假．

(4)p∧q假?p，q至少一个假?(非p)∨(非q)真．

考点一判断含有逻辑联结词命题的真假

[典例](1)(2017·山东高考)已知命题p：?x>0，ln(x＋1)>0；命题q：若a>b，则a2>b2.下列命题为真命题的是()

A．p∧q B．p∧非q

C．非p∧q D．非p∧非q

(2)(2019·安徽安庆模拟)设命题p：?x0∈(0，＋∞)，x0＋1

x0>3；命题q：?x∈(2，＋∞)，

x2>2x，则下列命题为真的是()

A．p∧(非q) B．(非p)∧q

C．p∧q D．(非p)∨q

[解析](1)当x>0时，x＋1>1，因此ln(x＋1)>0，即p为真命题；取a＝1，b＝－2，这时满足a>b，显然a2>b2不成立，因此q为假命题．由复合命题的真假性，知B为真命题．

(2)对于命题p，当x0＝4时，x0＋1

x0＝17

4>3，故命题p为真命题；对于命题q，当x＝4

时，24＝42＝16，即?x0∈(2，＋∞)，使得2x0＝x20成立，故命题q为假命题，所以p∧(非q)为真命题，故选A.

[答案](1)B(2)A

[题组训练]

1．(2019·惠州调研)已知命题p，q，则“非p为假命题”是“p∧q是真命题”的() A．充分不必要条件B．必要不充分条件

C．充要条件D．既不充分也不必要条件

解析：选B充分性：若非p为假命题，则p为真命题，由于不知道q的真假性，所以推不出p∧q是真命题．必要性：p∧q是真命题，则p，q均为真命题，则非p为假命题．所以“非p为假命题”是“p∧q是真命题”的必要不充分条件．

2．已知命题p：“若x2－x>0，则x>1”；命题q：“若x，y∈R，x2＋y2＝0，则xy＝0”．下列命题是真命题的是()

A．p∨(非q)B．p∨q

C．p∧q D．(非p)∧(非q)

解析：选B若x2－x>0，则x>1或x<0，故p是假命题；若x，y∈R，x2＋y2＝0，则x ＝0，y＝0，xy＝0，故q是真命题．则p∨q是真命题．

考点二全称命题与特称命题

[典例](1)命题?x∈R，e x－x－1≥0的否定是()

A．?x∈R，e x－x－1≤0

B．?x∈R，e x－x－1≥0

C．?x0∈R，e x0－x0－1≤0

D．?x0∈R，e x0－x0－1<0

(2)对命题?x0>0，x20>2x0，下列说法正确的是()

A．真命题，其否定是?x0≤0，x20≤2x0

B．假命题，其否定是?x>0，x2≤2x

C．真命题，其否定是?x>0，x2≤2x

D．真命题，其否定是?x≤0，x2≤2x

[解析](1)改全称量词为存在量词，把不等式中的大于或等于改为小于．故选D.

(2)已知命题是真命题，如32＝9>8＝23，其否定是?x>0，x2≤2x.故选C.

[答案](1)D(2)C

[题组训练]

1．命题“?x∈R，?n∈N*，使得n≤x2”的否定形式是()

A．?x∈R，?n∈N*，使得n>x2

B．?x∈R，?n∈N*，使得n>x2

C．?x0∈R，?n∈N*，使得n>x20

D．?x0∈R，?n∈N*，使得n>x20

解析：选D?改写为?，?改写为?，n≤x2的否定是n>x2，则该命题的否定形式为“?x0∈R，?n∈N*，使得n>x20”．

2．已知命题p：?n∈R，使得f(x)＝nxn2＋2n是幂函数，且在(0，＋∞)上单调递增；命题q：“?x0∈R，x20＋2>3x0”的否定是“?x∈R，x2＋2<3x”．则下列命题为真命题的是()

A．p∧q B．(非p)∧q

C．p∧(非q)D．(非p)∧(非q)

解析：选C当n＝1时，f(x)＝x3为幂函数，且在(0，＋∞)上单调递增，故p是真命题，则非p是假命题；“?x0∈R，x20＋2>3x0”的否定是“?x∈R，x2＋2≤3x”，故q是假命题，非q是真命题．所以p∧q，(非p)∧q，(非p)∧(非q)均为假命题，p∧(非q)为真命题，选C.考点三根据命题的真假求参数的取值范围

[典例] 已知p ：存在x 0∈R ，mx 20＋1≤0，q ：任意x ∈R ，x 2

＋mx ＋1>0.若p 或q 为假

命题，求实数m 的取值范围．

[解] 依题意知p ，q 均为假命题，

当p 是假命题时，则mx 2＋1>0恒成立，则有m ≥0； 当q 是真命题时，则Δ＝m 2－4<0，－2

因此由p ，q 均为假命题得{

m ≥0，m ≤－2或m ≥2，即m ≥2. 所以实数m 的取值范围为[2，＋∞)．

[变透练清]

1.(变条件)若本例将条件“p 或q 为假命题”变为“p 且q 为真命题”，其他条件不变，则实数m 的取值范围为________．

解析：依题意，当p 是真命题时，有m <0； 当q 是真命题时，有－2

由?

????

m <0，－2

所以m 的取值范围为(－2,0)． 答案：(－2,0)

2.(变条件)若本例将条件“p 或q 为假命题”变为“p 且q 为假，p 或q 为真”，其他条件不变，则实数m 的取值范围为________．

解析：若p 且q 为假，p 或q 为真，则p ，q 一真一假．

当p 真q 假时?????

m <0，m ≥2或m ≤－2，所以m ≤－2；

当p 假q 真时?

????

m ≥0，

－2

所以m 的取值范围为(－∞，－2]∪[0,2)． 答案：(－∞，－2]∪[0,2)

3.(变条件)若本例将条件q 变为：存在x 0∈R ，x 2

0＋mx 0＋1<0，其他条件不变，则实数m

的取值范围为________．

解析：依题意，当q 是真命题时，Δ＝m 2－4>0，

所以m >2或m <－2.由?

????

m ≥0，

－2≤m ≤2，得0≤m ≤2，

所以m 的取值范围为[0,2]． 答案：[0,2]

[课时跟踪检测]

1．(2019·西安摸底)命题“?x >0，x

x －1>0”的否定是( )

A ．?x 0≥0，x 0

x 0－1≤0

B ．?x 0>0,0≤x 0≤1

C ．?x >0，x

x －1

≤0

D ．?x <0,0≤x ≤1

解析：选B ∵x x －1>0，∴x <0或x >1，∴x

x －1>0的否定是0≤x ≤1，

∴命题的否定是“?x 0>0,0≤x 0≤1”． 2．下列命题中，假命题的是( ) A ．?x ∈R,21－

x >0

B ．?a 0∈R ，y ＝xa 0的图象关于y 轴对称

C ．函数y ＝x a 的图象经过第四象限

D ．直线x ＋y ＋1＝0与圆x 2＋y 2＝1

2

相切

解析：选C 对于A ，由指数函数的性质可知为真命题；对于B ，当a ＝2时，其图象关于y 轴对称；对于C ，当x >0时，y >0恒成立，从而图象不过第四象限，故为假命题；对于D ，因为圆心(0,0)到直线x ＋y ＋1＝0的距离等于

1

2

，等于圆的半径，命题成立． 3．(2019·陕西质检)已知命题p ：对任意的x ∈R ，总有2x >0；q ：“x >1”是“x >2”的充分不必要条件，则下列命题为真命题的是( )

A ．p ∧q

B ．(非p )∧(非q)

C ．(非p )∧q

D ．p ∧(非q)

解析：选D 由指数函数的性质知命题p 为真命题．易知x >1是x >2的必要不充分条件，所以命题q 为假命题．由复合命题真值表可知p ∧(非q)为真命题．

4．(2018·湘东五校联考)下列说法中正确的是( ) A ．“a >1，b >1”是“ab >1”成立的充分条件 B ．命题p ：?x ∈R,2x >0，则非p ：?x 0∈R,2x

0<0 C ．命题“若a >b >0，则1a <1

b ”的逆命题是真命题

D ．“a >b ”是“a 2>b 2”成立的充分不必要条件

解析：选A 对于选项A ，由a >1，b >1，易得ab >1，故A 正确．对于选项B ，全称命题的否定是特称命题，所以命题p ：?x ∈R,2x >0的否定是非p ：?x 0∈R,2x

0≤0，故B 错误．对于选项C ，其逆命题：若1a <1

b ，则a >b >0，可举反例，如a ＝－1，b ＝1，显然是假命

题，故C 错误．对于选项D ，由“a >b ”并不能推出“a 2>b 2”，如a ＝1，b ＝－1，故D 错误．故选A.

5．(2019·唐山五校联考)已知命题p ：“a >b ”是“2a >2b ”的充要条件；命题q ：?x 0∈R ，|x 0

＋1|≤x 0，则( )

A ．(非p )∨q 为真命题

B ．p ∧(非q)为假命题

C ．p ∧q 为真命题

D ．p ∨q 为真命题

解析：选D 由题意可知命题p 为真命题．因为|x ＋1|≤x 的解集为空集，所以命题q 为假命题，所以p ∨q 为真命题．

6．下列说法错误的是( )

A ．命题“若x 2－5x ＋6＝0，则x ＝2”的逆否命题是“若x ≠2，则x 2－5x ＋6≠0”

B ．若命题p ：存在x 0∈R ，x 20＋x 0＋1<0，则非p ：对任意x ∈R ，x 2

＋x ＋1≥0

C ．若x ，y ∈R ，则“x ＝y ”是“xy ≥??

??x ＋y 22

”的充要条件

D ．已知命题p 和q ，若“p 或q ”为假命题，则命题p 与q 中必一真一假

解析：选D 由原命题与逆否命题的关系，知A 正确；由特称命题的否定知B 正确；由xy ≥?

??

??x ＋y 22

?4xy ≥(x ＋y )2?4xy ≥x 2＋y 2＋2xy ?(x －y )2≤0?x ＝y ，知C 正确；对于D ，命题“p 或q ”为假命题，则命题p 与q 均为假命题，所以D 不正确．

7．(2019·长沙模拟)已知命题“?x ∈R ，ax 2＋4x ＋1>0”是假命题，则实数a 的取值范

围是( )

A ．(4，＋∞)

B ．(0,4]

C ．(－∞，4]

D ．[0,4)

解析：选C 当原命题为真命题时，a >0且Δ<0，所以a >4，故当原命题为假命题时，a ≤4.

8．下列命题为假命题的是( ) A ．存在x >y >0，使得ln x ＋ln y <0

B ．“φ＝π

2”是“函数y ＝sin(2x ＋φ)为偶函数”的充分不必要条件

C ．?x 0∈(－∞，0)，使3x 0<4x 0成立

D ．已知两个平面α，β，若两条异面直线m ，n 满足m ?α，n ?β且m ∥β，n ∥α，则α∥β

解析：选C 对于A 选项，令x ＝1，y ＝1

e ，则ln x ＋ln y ＝－1<0成立，故排除A.对于

B 选项，“φ＝π

2”是“函数y ＝sin(2x ＋φ)为偶函数”的充分不必要条件，正确，故排除B.

对于C 选项，根据幂函数y ＝x α，当α<0时，函数单调递减，故不存在x 0∈(－∞，0)，使3x 0<4x 0成立，故C 错误．对于D 选项，已知两个平面α，β，若两条异面直线m ，n 满足m ?α，n ?β且m ∥β，n ∥α，可过n 作一个平面与平面α相交于直线n ′.由线面平行的性质定理可得n ′∥n ，再由线面平行的判定定理可得n ′∥β，接下来由面面平行的判定定理可得α∥β，故排除D ，选C.

9．若命题p 的否定是“?x ∈(0，＋∞)，x ＞x ＋1”，则命题p 可写为________________________．

解析：因为p 是非p 的否定，所以只需将全称量词变为特称量词，再对结论否定即可． 答案：?x 0∈(0，＋∞)，x 0≤x 0＋1

10．已知命题p ：x 2＋4x ＋3≥0，q ：x ∈Z ，且“p ∧q ”与“非q ”同时为假命题，则 x ＝________.

解析：若p 为真，则x ≥－1或x ≤－3， 因为“非q ”为假，则q 为真，即x ∈Z ，

又因为“p ∧q ”为假，所以p 为假，故－3＜x ＜－1， 由题意，得x ＝－2.

答案：－2

11．已知p ：a <0，q ：a 2>a ，则非p 是非q 的________条件(填：充分不必要、必要不充分、充要、既不充分也不必要)．

解析：由题意得非p ：a ≥0，非q ：a 2≤a ，即0≤a ≤1.因为{a |0≤a ≤1}{a |a ≥0}，所以非p 是非q 的必要不充分条件．

答案：必要不充分

12．已知命题p ：a 2≥0(a ∈R)，命题q ：函数f (x )＝x 2－x 在区间[0，＋∞)上单调递增，则下列命题：

①p ∨q ；②p ∧q ；③(非p )∧(非q)；④(非p )∨q. 其中为假命题的序号为________．

解析：显然命题p 为真命题，非p 为假命题． ∵f (x )＝x 2－x ＝????x －122－14

， ∴函数f (x )在区间????1

2，＋∞上单调递增． ∴命题q 为假命题，非q 为真命题．

∴p ∨q 为真命题，p ∧q 为假命题，(非p )∧(非q)为假命题，(非p )∨q 为假命题． 答案：②③④

13．设t ∈R ，已知命题p ：函数f (x )＝x 2－2tx ＋1有零点；命题q ：?x ∈[1，＋∞)， 1x

－x ≤4t 2－1.

(1)当t ＝1时，判断命题q 的真假； (2)若p ∨q 为假命题，求t 的取值范围．

解：(1)当t ＝1时，????1x －x max ＝0，1

x －x ≤3在[1，＋∞)上恒成立，故命题q 为真命题． (2)若p ∨q 为假命题，则p ，q 都是假命题． 当p 为假命题时，Δ＝(－2t )2－4<0，解得－1

1x －x max ≤4t 2－1，即4t 2－1≥0， 解得t ≤－12或t ≥1

2

，

∴当q 为假命题时，－12

2

，

∴t 的取值范围是????－12，12.

常用逻辑用语题型归纳

《常用逻辑用语》 一、判断命题真假 1、下列命题中，真命题是 （ ） A ．221,sin cos 222 x x x R ?∈+= B ．(0,),sin cos x x x π?∈> C ．2,1x R x x ?∈+=- D ．(0,),1x x e x ?∈+∞>+ 2、如果命题“)q p ∨?（”为假命题，则（ ） A. p,q 均为假命题 B. p,q 均为真命题 C. p,q 中至少有一个为真命题 D. p,q 中至多有一个为真命题 3、有四个关于三角函数的命题： 1p ：?x ∈R, 2sin 2x +2cos 2x =12 2p : ?x 、y ∈R, sin(x-y)=sinx-siny 3p : ?x ∈[]0,π,1cos 22 x -=sinx 4p : sinx=cosy ? x+y=2π 其中假命题的是（ ） （A ）1p ，4p （B ）2p ，4p （C ）1p ，3p （D ）2p ，4p 4、给出下列命题： ①在△ABC 中，若∠A ＞∠B ，则sin A ＞sin B ； ②函数y ＝x 3 在R 上既是奇函数又是增函数； ③函数y ＝f(x)的图象与直线x ＝a 至多有一个交点； ④若将函数y ＝sin 2x 的图象向左平移π4个单位，则得到函数y ＝sin ? ????2x ＋π4的图象． 其中正确命题的序号是( ) A ．①② B ．②③ C ．①②③ D ．①②④

5、若命题p ：圆(x －1)2＋(y －2)2 ＝1被直线x ＝1平分；q ：在△ABC 中，若sin 2A ＝sin 2B ，则A ＝B ，则下列结论中正确的是( ) A ．“p∨q”为假 B ．“p∨q”为真 C ．“p∧q”为真 D ．以上都不对 6、已知命题p 1：函数y ＝2x －2－x 在R 上为增函数；p 2：函数y ＝2x ＋2－x 在R 上为减函数， 则在命题q 1：p 1∨p 2，q 2：p 1∧p 2，q 3：(?p 1)∨p 2和q 4：p 1∧(?p 2)中，真命题是( ) 7、下列命题中的假命题．．． 是 ( ) A. ,lg 0x R x ?∈= B. ,tan 1x R x ?∈= C. 3,0x R x ?∈> D. ,20x x R ?∈> 8、下列命题中的假命题是 （ ） A ．?x R ∈,120x -> B. ?*x N ∈,2(1)0x -> C ．? x R ∈,lg 1x < D. ?x R ∈,tan 2x = 9、有以下四个命题： ①ABC ?中，“A B >”是“sin sin A B >”的充要条件； ②若命题:,sin 1,P x R x ?∈≤则:,sin 1p x R x ??∈>； ③不等式210x x >在()0,+∞上恒成立； ④设有四个函数111332,,,,y x y x y x y x -====其中在()0,+∞上是增函数的函数有3个。 其中真命题的序号 二、判断充分、必要条件

近五年高考数学(理科)立体几何题目汇总

高考真题集锦（立体几何部分） 1.(2016.理1）如图是由圆柱和圆锥组合而成的几何体的三视图，则该几何体的表面积是（ ） A 20π B24π C28π D.32π 2. βα，是两个平面，m,n 是两条直线，有下列四个命题： （1）如果m ⊥n,m ⊥α，n ∥β，那么βα⊥； （2）如果m ⊥α，n ∥α，那么m ⊥n. （3）如果αβα?m ，∥那么m ∥β。 （4）如果m ∥n,βα∥，那么m 与α所成的角和n 与β所成的角相等。 其中正确的命题有___________ 3.（2016年理1）如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径．若该几何体的体积是π328，则它的表面积是 A 17π B.18π C.20π D.28π 4.平面α过正方体1111D C B A ABCD -的顶点A ，α//平面11D CB ，?α平面ABCD =m ， ?α平面11A ABB =n,则m,n 所成角的正弦值为（ ） A.23 B.22 C.33 D.3 1 5.（2016年理1）如图，在以A,B,C,D,E,F 为顶点的五面体中，面ABEF 为正方形，AF=2FD ，∠AFD=90°，且二面角D-AF-E 与二面角C-BE-F 都是60° .（12分） （Ⅰ）证明：平面ABEF ⊥平面EFDC ； （Ⅱ）求二面角E-BC-A 的余弦值.

6. (2015年理1）圆柱被一个平面截取一部分后与半球（半径为r ）组成一个几何体，该几何体三视图的正视图和俯视图如图所示，若该几何体的表面积是16+20π，则r=（ ） A.1 B.2 C.7 D.8 7.如图，四边形ABCD 为菱形，∠ABC=120°，E,F 是平面ABCD 同一侧的亮点，BE ⊥平面ABCD,DF ⊥平面ABCD,BE=2DF,AE ⊥EC. (1) 证明：平面AEC ⊥平面AFC; (2) 求直线AE 与直线CF 所成角的余弦值。 8.一个正方体被一个平面截去一部分后，剩余部分的三视图如下图，则截取部分体积和剩余 部分体积的比值为（） 9.如图，长方体1111D C B A ABCD -中，AB = 16，BC = 10，AA1 = 8，点E ，F 分别在1111C D B A ， 上，411==F D E A ，过点E,F 的平面α与此长方体的面相交，交线围成一个正方形。 （1）在图中画出这个正方形（不必说明画法和理由）； （2）求直线AF 与平面α所成的角的正弦值 10.如图，菱形ABCD 的对角线AC 与BD 交于点O ，AB=5，AC=6，点E,F 分别在AD,CD 上，AE=CF=45 ，EF 交BD 于点H.将△DEF 沿EF 折到△DEF 的位置，OD ’=10 （1）证明：D ’H ⊥平面ABCD （2）求二面角B-D ’A-C 的正弦值

绝对值题型归纳总结

. ... .. . 绝对值题型归纳总结 一、知识梳理 模块一绝对值的基本概念 模块二零点分段法（目的：去无围限定的绝对值题型） 模块三几何意义 . . .z

例题分析 题型一 绝对值代数意义及化简 【例1】 ⑴ 下列各组判断中，正确的是 ( ) A ．若a b =，则一定有a b = B ．若a b >，则一定有a b > C. 若a b >，则一定有a b > D ．若a b =，则一定有()2 2a b =- ⑵ 如果2a ＞2b ，则 ( ) A ．a b > B ．a ＞b C ．a b < D a ＜b ⑶ 下列式子中正确的是 ( ) A ．a a >- B ．a a <- C ．a a ≤- D ．a a ≥- ⑷ 对于1m -，下列结论正确的是 ( ) A ．1||m m -≥ B ．1||m m -≤ C ．1||1m m --≥ D ．1||1m m --≤ ⑸若220x x -+-=，求x 的取值围． 【解析】 ⑴ 选择D ．⑵ 选择B ．

. ... .. . . . .z ⑶ 我们可以分类讨论，也可以用特殊值法代入检验，对于绝对值的题目我们一般需要代正数、负数、0，3种数帮助找到准确答案．易得答案为D ． ⑷ 我们可以用特殊值法代入检验，正数、负数、0，3种数帮助找到准确答案C ． ⑸ ()22x x -=--，所以20x -≤，即2x ≤． 【变1】 已知：⑴52a b ==，，且a b <；⑵()2 120a b ++-=，分别求a b ，的值 【解析】 因为55a a ==±，，因为22b b ==±，，又因为a b <，所以22a b =-=±， 即52a b =-=，或52a b =-=-， ⑵由非负性可知12a b =-=， 【例2】 设a b c ，，为整数，且1a b c a -+-=，求c a a b b c -+-+-的值 【解析】 因为a b c ，，为整数，且1a b c a -+-= 故a b -与c a -一个为0，一个为1，从而()()1b c b a a c -=-+-=，原式2= 【例3】 （1）已知1999x =，则2245942237x x x x x -+-++++= ． （2）满足2()()a b b a a b ab -+--=（0ab ≠）有理数a 、b ，一定不满足的关系是（ ） A ． 0ab < B ． 0ab > C ． 0a b +> D ． 0a b +< （3）已知有理数a 、b 的和a b +及差a b -在数轴上如图所示， 化简227a b a b +---． a-b a+b 【解析】 （1）容易判断出，当1999x =时，24590x x -+>，2220x x ++>， 所以 224594223710819982x x x x x x -+-++++=-+=- 这道题目体现了一种重要的“先估算+后化简+再代入求值”的思想． （2）为研究问题首先要先将题干中条件的绝对值符号通过讨论去掉， 若a b ≥时，222()()()()0a b b a a b a b a b ab -+--=---=≠， 若a b <时，2222()()()()2()a b b a a b a b b a a b ab -+--=-+-=-=，

(完整版)空间向量与立体几何题型归纳

空间向量与立体几何 1, 如图，在四棱锥V-ABCD中，底面ABCD是正方形，侧面VAD是正三角形，平面VAD⊥底面ABCD （1）证明AB⊥平面VAD； （2）求面VAD与面VDB所成的二面角的大小 2, 如图所示，在四棱锥P—ABCD中，底面ABCD为矩形，侧棱PA⊥底面ABCD，AB=， BC=1，PA=2，E为PD的中点. （1）求直线AC与PB所成角的余弦值； （2）在侧面PAB内找一点N，使NE⊥平面PAC，并求出N点到AB和AP的距离.(易错点,建系后,关于N点的坐标的设法,也是自己的弱项)

3. 如图，在长方体ABCD ―A 1B 1C 1D 1中，AD=AA 1=1，AB=2，点E 在棱AB 上移动. （1）证明：D 1E ⊥A 1D ； （2）当E 为AB 的中点时，求点A 到面ECD 1的距离； （3）AE 等于何值时，二面角 D 1―EC ―D 的大小为(易错点:在找平面DEC 的法向量的时候,本来法向量就己经存在了,就不必要再去找,但是我认为去找应该没有错吧,但法向量找出来了 ,和那个己经存在的法向量有很大的差别,而且,计算结果很得杂,到底问题出在哪里 ?) 4.如图，直四棱柱ABCD －A 1B 1C 1D 1中，底面ABCD 是等腰梯形，AB ∥CD ，AB ＝2DC ＝2，E 为BD 1的中点，F 为AB 的中点，∠DAB ＝60°． (1)求证：EF ∥平面ADD 1A 1； (2)若2 21BB ，求A 1F 与平面DEF 所成角的正弦值．

N：5题到11题都是运用基底思想解题 5.空间四边形ABCD中，AB=BC=CD，AB⊥BC，BC⊥CD，AB与CD成60度角，求AD与BC所成角的大小。 6.三棱柱ABC-A1B1C1中，底面是边长为2的正三角形，∠A1AB=45°, ∠A1AC=60°,求二面角B-AA1-C的平面角的余弦值。 7.如图，60°的二面角的棱上有A,B两点，直线AC,BD分别在这个二面角的两个半平面内， 且都垂直于AB,已知AB=4,AC=6,BD=8，求CD的长 8.如图，已知空间四边形OABC中，OB=0C, ∠AOB=∠AOC=Θ，求证OA⊥BC。 9．如图，空间四边形OABC各边以及AC，BO的长都是1，点D，E分别是边OA，BC的中点，连接DE。 （1）计算DE的长； （2）求点O到平面ABC的距离。 10．如图，线段AB在平面⊥α，线段AC⊥α，线段BD⊥AB，且AB=7，AC=BD=24，CD=25，求线段BD与平面α所成的角。

常用逻辑用语题型归纳之令狐文艳创作

《常用逻辑用语》 一、 令狐文艳 二、判断命题真假 1、下列命题中，真命题是 （ ） A ．221,sin cos 222 x x x R ?∈+= B ．(0,),sin cos x x x π?∈> C ．2,1x R x x ?∈+=- D ．(0,),1x x e x ?∈+∞>+ 2、如果命题“)q p ∨?（”为假命题，则（ ） A. p,q 均为假命题 B. p,q 均为真 命题 C. p,q 中至少有一个为真命题 D. p,q 中至多有一个 为真命题 3、有四个关于三角函数的命题： 1p ：?x ∈R, 2sin 2x +2cos 2x =122p : ?x 、y ∈R, sin(x- y)=sinx-siny 3p : ?x ∈[]0,π,1cos 22x -=sinx 4p : sinx=cosy ? x+y=2π 其中假命题的是（ ）

（A ）1p ，4p （B ）2p ，4p （C ）1p ，3p （D ）2p ，4p 4、给出下列命题： ①在△ABC 中，若∠A ＞∠B ，则sin A ＞sin B ； ②函数y ＝x 3 在R 上既是奇函数又是增函数； ③函数y ＝f(x)的图象与直线x ＝a 至多有一个交点； ④若将函数y ＝sin 2x 的图象向左平移π4 个单位，则得到函数y ＝sin ? ?????2x ＋π4的图象． 其中正确命题的序号是( ) A ．①② B ．②③ C ．①②③ D ．①②④ 5、若命题p ：圆(x －1)2＋(y －2)2＝1被直线x ＝1平分；q ：在△ABC 中，若sin 2A ＝sin 2B ，则A ＝B ，则下列结论中正确的是( ) A ．“p∨q”为假 B ．“p∨q”为真 C ．“p∧q”为真 D ．以上都不对 6、已知命题p 1：函数y ＝2x －2－x 在R 上为增函数；p 2：函数y ＝2x ＋2－x 在R 上为减函数， 则在命题q 1：p 1∨p 2，q 2：p 1∧p 2，q 3：(?p 1)∨p 2和q 4：p 1∧(?p 2)中，真命题是( ) 7、下列命题中的假命题是 ( ) A. ,lg 0x R x ?∈= B.,tan 1x R x ?∈= C. 3,0x R x ?∈> D. ,20x x R ?∈>

绝对值考点题型总结

绝对值 1、如果| -a | = －a ，下列成立的是（ ) A .a<0 B ．a ≦0 Ｃ.ａ>0 D.a ≧0 2、 的绝对值是8。 3、若11=-b ，则b= ,若==+a a 则,06 ，若a a -=，则a 0 4、若5,3==b a ，则b a +等于( ） A 、2 Ｂ、8 C 、2或8 D 、81--或 ５、已知3a =,且0a a +=，则3 2 1a a a +++=__＿__＿_＿___． 6、绝对值大于 1 小于 4 的整数的和是（ ) A 、０ B 、5 C 、-５ D 、1０ ７、若2 3(2)0m n -++=，则2m n +的值为( ) Ａ．4-? B.1- ?C.０? Ｄ.4 8、在数轴上,距离原点4个单位长度的点所表示的数是 9、如果互为相反数的两个数在数轴上的点相距6个单位长度，这两个数为 10、在数轴上与表示-2的点的距离为３的点所表示的数是 11、已知132x +与1 22 y -互为相反数,求x y +的值。 12、已知()0122 =++-b ab (1) 求a,b 的值，(2)求2008 2008 2?? ? ??-a b 的值 （3）求()()()() ()()2008200812211111--+??+--+--+b a b a b a ab

１3、计算: =-+??+-+-+-99 1100131412131121 14、若ａ＜0,且a ｂ<0,化简|b-a+4｜－|ａ-b-7｜=___＿____＿__. 15、若ab ＜０,－ｂ>0,且b a ，则a+b 0（填“>”“<”） 16、若m>０，ｎ<0，且｜m|>|n|,用“＞”把m 、m -、n 、n -连接起来。 17、已知│x-1│=3,求 -３│1+x │-│x │+5的值. 18、()() 的值。求且若b a c c b a a -?=-=++-3 2 ,21,0212 19、已知｜a |=5,｜b |=2,ab <0. 求:3ａ+2ｂ的值 ２0、已知a 、b 互为相反数，c 、ｄ互为倒数,x 的绝对值比它的相反数大2, 求式子ｘ3+ｃｄｘ+ａ+ｂ+c ｄ的值 21、已知|m|＝５，｜ｎ|＝2,且｜m ＋n|=m ＋n ，求m-n 的值。 22、已知m 、ｎ互为相反数,ｐ、q 互为倒数，a 的绝对值等于2， 求24 1 20052005a pq a n m +-+的值

常用逻辑用语题型归纳

一、判断命题真假 1下列命题中,真命题是 — 2 X 2 X 1 A. X R,sin CoS = 2 2 2 B . -X (0，二）,sin X cosx 2 C. -X R ） X x = —1 X D. —X （0, ：:），e I X 2、 如果命题“ (P q ） ”为假命题,则（ A. p,q 均为假命题 B. p ，q C. p ，q 中至少有一个为真命题 4、给出下列命题: ① 在△ ABC 中，若∠ A>∠ B,贝U Sin A > Sin B ； ② 函数y = X 3 在R 上既是奇函数又是增函数; ③ 函数y = f （x ）的图象与直线X= a 至多有一个交点； ④ 若将函数y = Sin 2x 的图象向左平移 丁个单位，则得到函数 y= Sin 2x+∏的图象。 其中正确命题的序号是（ ） A 。①② B .②③ C 。①②③ D 。①②④ 《常用逻辑用语》 ） 均为真命题 D. p,q 中至多有一个为真命题 .2 X 2 X 1 P I : T X R, Sin —+ COS -- 2 2 2 1 -cos2x P 3： - X 〔0 ,二 1, J ------------ =Sin V 2 其中假命题的是（ ) (A) Pl , P 4 (B ) P 2 , P 4 p 2: ^ X 、y 三 R, sin(x-y)=sinX-Siny p 4 : SinX=COSy =■ x+y=- 2 (C) P ，P 3 (D) p 2，P 4 3、 有四个关于三角函数的命题：

5、若命题 P:圆(X - 1）2+ (y — 2）2 = 1 被直线 X= 1 平分;q ：在厶 ABC 中，若 Sin 2A= Sin 2B ， 则A= B ，则下列结论中正确的是 （ ） A 。 “p ∨ q”为假 B .“p ∨ q”为真 C 。“p ∧ q”为真 D 。以上都不对 6、已知命题p i :函数y = 2x - 2— x 在R 上为增函数；p 2：函数y= 2x + 2— X 在R 上为减函数, 则在命题 q i : p ι∨ p 2， q 2: p ι∧ p 2， q 3： (—p i ） ∨ p 2 和 q 4： p i ∧ ( 一 p 2）中，真命题是 （ ) 7、下列命题中的假命题是（） A. T X R ，Ig X = O B. C. —X R ， X 3 . 0 D. 8、下列命题中的假命题是 （ ） A. -X R ， 2XjL 0 B. —X * N ，（X —1）2 C. —.1 X R , Ig X ：: 1 D 。 -。1 X R , tan X = 2 9、有以下四个命题： ① =ABC 中,“ A B ”是“ Si nA Sin B ”的充要条件; ② 若命题 P: -χ? R ，sin X -1,则一prχ? R ，sin X 1 ； ③ 不等式10x X 2 在上恒成立； 1 1 1 一 - 3 ④ 设有四个函数 y=x ，y = X 2 , y = X 3 ,y = X ，其中在 0,匸：上是增函数的函数有 3 个. 其中真命题的序号 ______ 、判断充分、必要条件 X 三 R,tan X =1 XR,2x 0

立体几何知识点题型整理

立体几何总结（1）空间几何体的知识点： （2）点、直线、面的位置关系： (3)空间直角坐标系: 考点一空间几何体与三视图 1．一个物体的三视图的排列规则是：俯视图放在正视图的下面，长度与正视图的长度一样，侧视图放在正视图的右面，高度与正视图的高度一样，宽度与俯视图的宽度一样．即“长对正、高平齐、宽相等”． 2．画直观图时，与坐标轴平行的线段仍平行，与x轴、z轴平行的线段长度不变，与y轴平行的线段长度减半． 题型一三视图的考察 1、(2009·海南、宁夏) 一个棱锥的三视图如图，则该棱锥的全面积( 单位：cm2) 为（ ) A．48＋12 2 B．48＋24 2 C．36＋12 2 D．36＋24 2 2、如图所示，某几何体的正视图是平行四边形，侧视图和俯视图都是矩形，则该几何体的体积为 ( ) A．6 3 B．9 3 C．12 3 D．18 3 【方法技巧】 1．求三棱锥体积时，可多角度地选择方法．如体积分割、体积差等积转化法是常用的方法．2．与三视图相结合考查面积或体积的计算时，解决时先还原几何体，计算时要结合平面图形，不要弄错相关数量． 3．求不规则几何体的体积常用分割或补形的思想将不规则几何体转化为规则几何体以易于求解． 4．对于组合体的表面积要注意其衔接部分的处理.

题型二 平面图的直观图（斜二测面法） 1、如图所示的直观图，其平面图形的面积为 （ ） A ．3 B.32 2 C ．6 D ．3 2 2、如图所示为一平面图形的直观图，则这个平面图形可能是 （ ） 答案 ：C 题型四 其他类型：展开、投影、截面、旋转体等 1 、面积为3的等边三角形绕其一边中线旋转所得圆锥的侧面积是________． 答案 ：2π 2、 如图，长方体ABCD －A1B1C1D1 中，交于顶点A 的三条棱长分别为AD ＝3 ，AA1 ＝4 ，AB ＝5 ，则从A 点沿表面到 C1 的最短距离为 ( ) A ．5 2 B.74 C ．4 5 D ．310 考点三 球与空间几何体的“切”“接”问题 1．长方体、正方体的外接球其体对角线长为该球的直径． 2．正方体的内切球其棱长为球的直径． 3．正三棱锥的外接球中要注意正三棱锥的顶点、球心及底面正三角形中心共线． 4．正四面体的外接球与内切球的半径之比为3∶1. 若正四面体的棱长为 a a R a a 12 6 ,46 ,36的半径为 正四面的内切球 径正四面体的外接球的半则正四面体的高为= （熟悉常见的补体，特殊的几何体如正三棱柱、正四棱柱、正六棱柱,注意如何确定球心的位置） 1.已知三棱锥ABC S -的三条侧棱两两垂直，且2=SA ，4==SC SB ，则该三棱锥的外接球的半径为（ ）A.3 B.6 C.36 D.9 2、在三棱锥BCD A -中，5,6======BC AD BD AC CD AB ，则该三棱锥的外接球的表面积为（ ）A.π102 B. π54 C. π21 D. π43 变式：在三棱锥BCD A -中，5,4,6======BC AD BD AC CD AB ，则该三棱锥的外接球的表面积为————（π2 77 ） 2、棱长为2的正四面体（四个面均为正三角形）外接球的表面积是（ ） A π3 B π3 C π33 D π2 3 3、在三棱柱C B A ABC '''-中，已知ABC A A 平面⊥'，2='==A A AC AB ，32=BC ，且此三棱柱的各个顶点都在一个球面上，则球的表面积为__________.

绝对值重点题型定稿版

绝对值重点题型精编 W O R D版 IBM system office room 【A0816H-A0912AAAHH-GX8Q8-GNTHHJ8】

绝对值重点题型 例1、已知a0，化简|2a-|a||。 例2、 已知|a|=5，|b|=3，且|a-b|=b-a ，满足条件的a 有 个，则 a+b= 。 例3、已知│a │=2，│b │=3，│c │=6，且│a+b │=a+b ，│a+c │=-（a+c ）， 求a-b-c 的值． 例4、 已知a 、b 、c 在数轴上表示的数如图，化简：|b+c|-|b-a|-|a-c|-|c-b|+|b|+|-2a|。 练习：数a ，b 在数轴上对应的点如图所示，是化简|a+b|+|b-a|+|b|-|a-|a|| 例5、若abc ≠0，则 ||||||c c b b a a ++的所有可能值 例6、已知a 、b 、c 是有理数，且a+b+c=0，abc0，求| |||||c b a b a c a c b +++++的值。 例7、已知3π -=x ，化简：m=|x+1|-|x+2|+|x+3|-|x+4|。 例8、 已知|x+5|+|x-2|=7，求x 的取值范围。 练习: 0 b a c

1、若3|x-2|+|y+3|=0，则x y 的值是多少？ 2、已知a ，b ，c 在数轴上的位置如图所示，化简|a|+|c-b|+|a-c|+|b-a|。 3、有理数a ，b ，c ，d ，满足 1||-=abcd abcd ，求d d c c b b a a ||||||||+++的值。 4、如果0

常用逻辑用语测试题

常用逻辑用语测试题 一 、 选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的） 1．下列语句不是命题的有( ) ①2 30x -=;②与一条直线相交的两直线平行吗③315+=;④536x -> A.①③④ B.①②③ C.①②④ D.②③④ 2．（改编题）命题“a 、b 都是奇数，则a ＋b 是偶数”的逆命题是 （ ） A ．a 、b 都不是奇数，则a ＋b 是偶数 B ．a ＋b 是偶数，则a 、b 都是奇数 C ．a ＋b 不是偶数，则a 、b 都不是奇数 D ．a ＋b 不是偶数，则a 、b 不都是奇数 3．命题“若a ＞b ，则2 2 ac bc >”(这里a 、b 、c 都是实数)与它的逆命题、否命题、逆否命题中，真命题的个数为 （ ） A ．4个 B ．3个 C ．2个 D ．0个 4．命题“若A ∪B ＝A ，则A ∩B=B ”的否命题是（ ） A ．若A ∪ B ≠A ，则A ∩B ≠B B ．若A ∩B ＝B ，则A ∪B=A C ．若A ∩B ≠A ，则A ∪B ≠B D ．若A ∪B ＝B ，则A ∩B ＝A 5．（改编题）下列有关命题的说法中错误的个数是( ) ①若p q ∧为假命题,则p q 、均为假命题 ②“1x =”是“2320x x -+=”的充分不必要条件 ③命题“若2 320x x -+=,则1x =“的逆否命题为:“若1,x ≠则2 320x x -+≠” ④对于命题:,p x R ?∈使得2 10x x ++<,则:,p x R ??∈均有2 10x x ++≥ A 4 B 3 C 2 D 1 6．已知命题:p R x ∈?,022 ≤++a ax x .若命题p 是假命题,则实数a 的取值范围是 ( ) A.(,0][1,)-∞+∞ B.[0,1] C.(,0)(1,)-∞+∞ D.(0,1) 7．（原创题）“ 2a b =-”是“直线20ax y +=垂直于直线1x by +=”的( ) A.充分而不必要条件 B.充分必要条件 C.必要而不充分条件 D.既不充分也不必要条件 8．用反证法证明命题：“a ，b ∈N ，ab 能被5整除，那么a ，b 中至少有一个能被5整除”时，假设的内容是（ ） A ．a 、b 都能被5整除

高考立体几何题型与方法全归纳文科

2019高考立体几何题型与方法全归纳文科 配套练习 1、四棱锥中,⊥底面,,, . (Ⅰ)求证:⊥平面； (Ⅱ)若侧棱上的点满足,求三棱锥的体积。 【答案】 (Ⅰ)证明:因为BC=CD ，即BCD ?为等腰三角形，又ACD ACB ∠=∠,故AC BD ⊥. 因为⊥PA 底面ABCD ，所以BD PA ⊥,从而BD 与平面PAC 内两条相交直线AC PA ,都垂直， 故⊥平面。 (Ⅱ)解：33 2sin 2221sin 21=??=∠??=?πBCD CD BC S BCD . 由⊥PA 底面ABCD 知23233 131=??=??=?-PA S V BCD BDC P . 由,7FC PF =得三棱锥BDC F -的高为PA 8 1, 故：4 132813318131=???=??=?-PA S V BCD BDC F 4 7412=-=-=---BCD F BCD P BDF P V V V 2、如图，四棱锥P ABCD -中，四边形ABCD 为矩形，PAD ?为等腰三角形，90APD ?∠=，平面PAD ⊥ 平面ABCD ，且1,2AB AD ==，,E F 分别为PC 和BD 的中点． （Ⅰ）证明：EF P 平面PAD ； （Ⅱ）证明：平面PDC ⊥平面PAD ；

（Ⅲ）求四棱锥P ABCD -的体积． 【答案】 （Ⅰ）证明：如图，连结AC ． ∵四边形ABCD 为矩形且F 是BD 的中点．∴F 也是AC 的中点． 又E 是PC 的中点，EF AP P ∵EF ?平面PAD ，PA ?平面PAD ，所以EF P 平面PAD ； （Ⅱ）证明：∵平面PAD ⊥ 平面ABCD ，CD AD ⊥，平面PAD I 平面ABCD AD =， 所以平面CD ⊥ 平面PAD ，又PA ?平面PAD ，所以PA CD ⊥ 又PA PD ⊥，,PD CD 是相交直线，所以PA ⊥面PCD 又PA ?平面PAD ，平面PDC ⊥平面PAD ； （Ⅲ）取AD 中点为O ．连结PO ,PAD ?为等腰直角三角形，所以PO AD ⊥， 因为面PAD ⊥面ABCD 且面PAD I 面ABCD AD =， 所以，PO ⊥面ABCD ， 即PO 为四棱锥P ABCD -的高． 由2AD =得1PO =．又1AB =． ∴四棱锥P ABCD -的体积1233 V PO AB AD =??= 考点：空间中线面的位置关系、空间几何体的体积. 3、如图，在四棱锥P ABCD -中，PD ABCD ⊥平面，CD PA ⊥， DB ADC ∠平分，E PC 为的中点，45DAC ∠=o ，AC = O

集合与常用逻辑用语练习测试题.doc

精心整理 第一练集合与常用逻辑用语一.强化题型考点对对练 1.（集合的基本运算）已知集合{|1A x x =≤-或1}x ≥，集合{|01}B x x =<<，则（） A.{}1A B ?= B.A B R ?= C.()(]0,1R C A B ?= D.()R A C B A ?= 【答案】D 2．（集合的基本运算）若集合{}02A x x =<<，且A B B =I ，则集合B 可能是（） A.{}0 2， B.{}0 1， C.{}0 1 2，， D.{}1 【答案】D 【解析】由题意得,因为,所以选B. 3.（集合的基本运算）设集合{}|2M x x =<，{}1,1N =-，则集合M C N 中整数的个数为() A.3 B.2 C.1 D.0 【答案】C 【解析】{}(){}|22,2,1,1M x x N =<=-=-Q ，()()()2,11,11,2,M N ∴=--?-?∴e集合M N e中整数只有0，故个数为1，故选C. 4.（集合间的关系）已知集合 ，若，则（） A.0或1 B.0或2 C.1或2 D.0或1或2 【答案】C 【解析】或.故选C. 5．（充分条件和必要条件）设x R ∈，i 是虚数单位， 则“3x =-”是“复数()()2231z x x x i =+-+-为纯虚数”的 A.充分不必要条 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 【答案】C 【解析】由3x =-，得()()2 22332330x x +-=-+?--=，1314x -=--=-． 而由2230{ 10 x x x +-=-≠，得3x =-．所以“3x =-”是“复数()()2231z x x x i =+-+-为纯数”的充要条件．故选C.

完整版绝对值重点题型.doc

绝对值重点题型 例1、已知a 0，化简|2a-|a||。 例2、 已知|a|=5，|b|=3，且|a-b|=b-a ，满足条件的a 有 个，则a+b= 。 例3、已知│a │=2，│b │=3，│c │=6，且│a+b │=a+b ，│a+c │=-（a+c ）， 求a-b-c 的值． 例4、 已知a 、b 、c 在数轴上表示的数如图，化简：|b+c|-|b-a|-|a-c|-|c-b|+|b|+|-2a|。 练习：数a ，b 在数轴上对应的点如图所示，是化简|a+b|+|b-a|+|b|-|a-|a|| 0 b a c a 0 b

例5、若abc ≠0，则 | |||||c c b b a a ++的所有可能值 例6、已知a 、b 、c 是有理数，且a+b+c=0，abc >0，求 ||||||c b a b a c a c b +++++的值。 例7、已知3π -=x ，化简：m=|x+1|-|x+2|+|x+3|-|x+4|。 例8、 已知|x+5|+|x-2|=7，求x 的取值范围。

练习: 1、若3|x-2|+|y+3|=0，则x y 的值是多少？ 2、已知a ，b |a|+|c-b|+|a-c|+|b-a|。 3、有理数a ，b ，c ，d ，满足 1||-=abcd abcd ，求d d c c b b a a ||||||||+++的值。 4、如果0

常用逻辑用语测试题(含答案)

常用逻辑用语测试题（答案） 1、一个命题与他们的逆命题、否命题、逆否命题这4个命题中（ ） A 、真命题与假命题的个数相同 B 、真命题的个数一定是奇数 C 、真命题的个数一定是偶数 D 、真命题的个数可能是奇数，也可能是偶数 2、下列说法中正确的是（ ） A 、一个命题的逆命题为真，则它的逆否命题一定为真 B 、“a b >”与“ a c b c +>+”不等价 C 、“220a b +=,则,a b 全为0”的逆否命题是“若,a b 全不为0, 则220a b +≠” D 、一个命题的否命题为真，则它的逆命题一定为真 3、给出命题：若函数()y f x =是幂函数，则函数()y f x =的图象不过第四象限．在它的逆命题、否命题、逆否命题三个命题中，真命题的个数是（ ） A 、3 B 、2 C 、1 D 、0 4、命题“设a 、b 、c R ∈，若22ac bc >则a b >”以及它的逆命题、否命题、逆否命题中，真命题的 个数为（ ） A 、0 B 、1 C 、2 D 、3 5、“若x ≠a 且x ≠b，则2()x a b x ab -++≠0”的否命题（ ） A 、若x ＝a 且x ＝b ，则2()x a b x ab -++＝0 B 、若x ＝a 或x ＝b ，则2()x a b x ab -++≠0 C 、若x ＝a 且x ＝b ，则2()x a b x ab -++≠0 D、若x ＝a 或x ＝b ，则2()x a b x ab -++＝0 6、“0x >0>”成立的( ) A 、充分不必要条件. B 、必要不充分条件. C 、充要条件. D 、既不充分也不必要条件. 7、“()24x k k Z π π=+∈”是“tan 1x =”成立的 （ ） A 、充分不必要条件. B 、必要不充分条件. C 、充分条件. D 、既不充分也不必要条件. 8、不等式2 230x x --<成立的一个必要不充分条件是（ ） A 、-1"和"a b e f

实数知识点题型归纳

第六章实数 知识讲解+题型归纳 知识讲解 一、实数的组成 1、实数又可分为正实数，零，负实数 2.数轴：数轴的三要素——原点、正方向和单位长度。数轴上的点与实数一一对应 二、相反数、绝对值、倒数 1. 相反数：只有符号不同的两个数互为相反数。数a的相反数是-a。正数的相反数是负数，负数的相反数是正数，零的相反数是零. 性质：互为相反数的两个数之和为0。 2.绝对值：表示点到原点的距离，数a的绝对值为 3.倒数：乘积为1的两个数互为倒数。非0实数a的倒数为 1 a . 0没有倒数。 4.相反数是它本身的数只有0；绝对值是它本身的数是非负数（0和正数）；倒数是它本身的数是±1. 三、平方根与立方根 1.平方根：如果一个数的平方等于a，这个数叫做a的平方根。数a的平方根记作（a>=0） 特性：一个正数有两个平方根，它们互为相反数，零的平方根还是零。负数没有平方根。 正数a的正的平方根也叫做a的算术平方根，零的算术平方根还是零。 开平方:求一个数的平方根的运算，叫做开平方。 a | |a

2.立方根：如果一个数的立方等于a，则称这个数为a立方根。数a 的立方根用3a表示。 任何数都有立方根，一个正数有一个正的立方根；一个负数有一个负的立方根，零的立方根是零。 开立方：求一个数的立方根（三次方根）的运算，叫做开立方。 四、实数的运算 有理数的加法法则： a）同号两数相加，取相同的符号，并把绝对值相加； b)异号两数相加。绝对值相等时和为0；绝对值不相等时，取绝对值较大的数的符号，并用较大的绝对值减去较小的绝对值. 任何数与零相加等于原数。2.有理数的减法法则：减去一个数等于加上这个数的相反数。 3.乘法法则： a）两数相乘，同号得正，异号得负，并把绝对值相乘；零乘以任何数都得零． b）几个不为0的有理数相乘，积的符号由负因数的个数决定，当负因数的个数为奇数时，积为负，为偶数，积为正 c）几个数相乘，只要有一个因数为0，积就为0 4.有理数除法法则： a）两个有理数相除（除数不为0）同号得正，异号得负，并把绝对值相除。0除以任何非0实数都得0。 b）除以一个数等于乘以这个数的倒数。

高中数学经典错因正解汇总：第一章集合与常用逻辑用语

第一章 集合与常用逻辑用语 §1.1 集合的概念与运算 一、知识导学 1.集合：一般地，一定范围内某些确定的、不同的对象的全体构成一个集合. 2.元素：集合中的每一个对象称为该集合的元素，简称元. 3.子集：如果集合A 的任意一个元素都是集合B 的元素（若A a ?则B a ∈），则称 集合A 为集合B 的子集，记为A ?B 或B ?A ；如果A ?B ，并且A ≠B ，这时集合A 称为集合B 的真子集，记为A B 或B A. 4.集合的相等：如果集合A 、B 同时满足A ?B 、B ?A ，则A=B. 5.补集：设A ?S ，由S 中不属于A 的所有元素组成的集合称为S 的子集A 的补集，记 为 A C s . 6.全集：如果集合S 包含所要研究的各个集合，这时S 可以看做一个全集，全集通常 记作U. 7.交集：一般地，由所有属于集合A 且属于B 的元素构成的集合，称为A 与B 的交集， 记作A ?B. 8.并集：一般地，由所有属于集合A 或者属于B 的元素构成的集合，称为A 与B 的并 集，记作A ?B. 9.空集：不含任何元素的集合称为空集，记作Φ. 10.有限集：含有有限个元素的集合称为有限集. 11.无限集：含有无限个元素的集合称为无限集. 12.集合的常用表示方法：列举法、描述法、图示法（Venn 图）. 13.常用数集的记法：自然数集记作N ，正整数集记作N +或N *，整数集记作Z ，有理数集记作Q ，实数集记作R . 二、疑难知识 1.符号?，，?，，=，表示集合与集合之间的关系，其中“?”包括“”和“=”两种情况，同样“?”包括“”和“=”两种情况.符号∈，?表示元素与集合之间的关系.要注意两类不同符号的区别. 2.在判断给定对象能否构成集合时，特别要注意它的“确定性”，在表示一个集合时，要特别注意它的“互异性”、“无序性”. 3.在集合运算中必须注意组成集合的元素应具备的性质. 4.对由条件给出的集合要明白它所表示的意义，即元素指什么，是什么范围．用集合表示不等式（组）的解集时，要注意分辨是交集还是并集，结合数轴或文氏图的直观性帮助思维判断．空集是任何集合的子集，但因为不好用文氏图形表示，容易被忽视，如在关系式 中，B =Φ易漏掉的情况. 5.若集合中的元素是用坐标形式表示的，要注意满足条件的点构成的图形是什么，用数形结合法解之. 6.若集合中含有参数，须对参数进行分类讨论，讨论时既不重复又不遗漏.

集合与常用逻辑用语,函数知识总结大全

第一章 集合与常用逻辑用语知识结构 【知识概要】 一、集合的概念、关系与运算 1. 集合中元素的特性：确定性、互异性、无序性. 在应用集合的概念求解集合问题时，要特别注意这三个性质在解题中的应用，元素的互异性往往就是检验的重要依椐。 2. 集合的表示方法：列举法、描述法. 有的集合还可用Venn 图表示，用专用符号表示，如,,,,,,N N N Z R Q φ*+等。 3. 元素与集合的关系：我们把研究对象统称为元素，把一些元素组成的总体叫做集合，若元素x 是集合A 的元素，则x A ∈，否则x A ?。 4. 集合与集合之间的关系： ①子集：若x A ∈，则x B ∈，此时称集合A 是集合B 的子集，记作A B ?。 ②真子集：若A B ?，且存在元素x B ∈，且x A ?，则称A 是B 的真子集，记作：A B . ③相等：若A B ?，且A B ?，则称集合A 与B 相等，记作A ＝B .。 5. 集合的基本运算： ①交集：{}A B x x A x B =∈∈I 且 ②并集：{}A B x x A x B =∈∈U 或 ③补集：{|,}U C A x x U x A =∈?且，其中U 为全集，A U ?。 6. 集合运算中常用结论： ①,,A A A A A B B A φφ===I I I I ，A B A A B =??I 。 ②,,A A A A A A B B A φ===U U U U ，A B A B A =??U 。 ③()U A C A U =U ，()U C A A ?=I ， ()()()U U U C A B C A C B =I U ，()()()U U U C A B C A C B =U I 。 ④由n 个元素所组成的集合，其子集个数为2n 个。

关于绝对值的几种题型与解题技巧

关于绝对值的几种题型及解题技巧 所谓绝对值就是只有单纯的数值而没有负号。即0≥a 。但是，绝对值里面的数值可以是正数也可以是负数。怎么理解呢？绝对值符号就相当于一扇门，我们在家里面的时候可以穿衣服也可以不穿衣服，但是，出门的时候一定要穿上衣服。 所以，0≥a ，而a 则有两种可能：o a 和0 a 。如：5=a ，则5=a 和5-=a 。合并写成：5±=a 。 于是我们得到这样一个性质： a 很多同学无法理解，为什么0 a 时，开出来的时候一定要添加一个“负号”呢？a -。因为此时0 a ，也就是说a 是一个负数，负数乘以符号就是正号了。如2)2(=--。因此，当判断绝对值里面的数是一个负数的时候，一定要在这个式子的前面添加一个负号。 例如：0 b a -，则)(b a b a --=-。 绝对值的题解始终围绕绝对值的性质来展开的。我就绝对值的几种题型进行详细讲解，希望能对你们有所帮助。 绝对值的性质： （1） 绝对值的非负性，可以用下式表示：|a|≥0，这是绝对值非常重要的性 质； a （a ＞0） a 0 a 0 0=a a - 0 a

（2） |a|= 0 （a=0） （代数意义） -a (a ＜0) （3） 若|a|=a ，则a ≥0；若|a|=-a ，则a ≤0； （4） 任何一个数的绝对值都不小于这个数，也不小于这个数的相反数， 即|a|≥a ，且|a|≥-a ； （5） 若|a|=|b|，则a=b 或a=-b ；（几何意义） （6） |ab|=|a|·|b|；|b a |=||| |b a （b ≠0）； （7） |a|2=|a 2|=a 2 ； （8） |a+b|≤|a|+|b| |a-b|≥||a|-|b|| |a|+|b|≥|a+b| |a|+|b|≥|a-b| 一：比较大小 典型题型： 【1】已知a 、b 为有理数，且0 a ，0 b ，b a ，则 （ ） A ：a b b a -- ； B ：a b a b -- ； C ：a b b a --； D ：a a b b -- 这类题型的关键是画出数轴，然后将点按照题目的条件进行标记。