
word 可编辑
历年考研数学一真题1987-2017
(答案+解析)
(经典珍藏版)最近三年+回顾过去
最近三年篇(2015-2017)
2015年全国硕士研究生入学统一考试
数学(一)试卷
一、选择题 1—8小题.每小题4分,共32分.
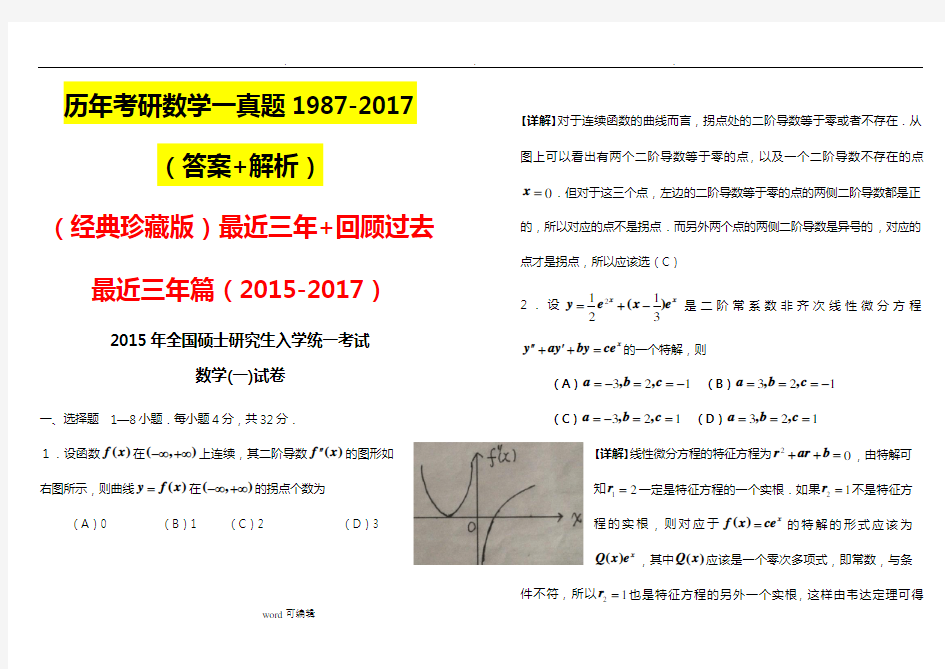
1.设函数()f x 在(,)-∞+∞上连续,其二阶导数()f x ''的图形如右图所示,则曲线()y f x =在(,)-∞+∞的拐点个数为
(A )0 (B )1 (C )2 (D )3
【详解】对于连续函数的曲线而言,拐点处的二阶导数等于零或者不存在.从图上可以看出有两个二阶导数等于零的点,以及一个二阶导数不存在的点
0x =.但对于这三个点,左边的二阶导数等于零的点的两侧二阶导数都是正
的,所以对应的点不是拐点.而另外两个点的两侧二阶导数是异号的,对应的点才是拐点,所以应该选(C ) 2.设211
23
()x x y e x e =
+-是二阶常系数非齐次线性微分方程x y ay by ce '''++=的一个特解,则
(A )321,,a b c =-==- (B )321,,a b c ===- (C )321,,a b c =-== (D )321,,a b c ===
【详解】线性微分方程的特征方程为2
0r ar b ++=,由特解可
知12r =一定是特征方程的一个实根.如果21r =不是特征方程的实根,则对应于()x
f x ce =的特解的形式应该为
()x Q x e ,其中()Q x 应该是一个零次多项式,即常数,与条
件不符,所以21r =也是特征方程的另外一个实根,这样由韦达定理可得
word 可编辑
213212(),a b =-+=-=?=,同时*x y xe =是原来方程的一个解,代入
可得1c =-应该选(A ) 3.若级数
1
n
n a
∞
=∑条件收敛,
则3x x =
=依次为级数1
1()n n n na x ∞
=-∑的
(A)收敛点,收敛点 (B)收敛点,发散点 (C)发散点,收敛点 (D)发散点,发散点 【详解】注意条件级数
1
n
n a
∞
=∑条件收敛等价于幂级数
1
n n
n a
x ∞
=∑在1x =处条件收
敛,也就是这个幂级数的收敛为1,即1
1lim n n n
a a +→∞=,所以11()n n n na x ∞
=-∑的
收敛半径1
11lim
()n
n n na R n a →∞
+==+,绝对收敛域为02(,),
显然3
x x ==依次为收敛点、发散点,应该选(B )
4.设D 是第一象限中由曲线2141,xy xy ==
与直线,y x y ==所围成
的平面区域,函数(,)f x y 在D 上连续,则
(,)D
f x y dxdy =??( )
(A)
13214
22sin sin (cos ,sin )d f r r rdr π
θπθ
θθθ??
(B
)
34
(cos ,sin )d f r r rdr π
πθθθ?
(
C
)
13214
22sin sin (cos ,sin )d f r r dr π
θπθ
θθθ??
(D
)
34
(cos ,sin )d f r r dr π
πθθθ?
【详解】积分区域如图所示,化成极坐标方程:
22121212sin cos sin xy r r r θθθ=?=?=
?=
221
414122sin cos sin xy r r r θθθ
=?=?=
?=
也就是D
:4
3r ππθ?<
所以
(,)D
f x y d x d y =
??34
(cos ,sin )d f r r rdr π
πθθθ?,所以应该选
word 可编辑
(B ).
5.设矩阵2211111214,A a b d a d ???? ? ?
== ? ? ? ?????
,若集合{}12,Ω=,则线性方程组
Ax b =有无穷多解的充分必要条件是
(A ),a d ?Ω?Ω (B ),a d ?Ω∈Ω (C ),a d ∈Ω?Ω (D ),a d ∈Ω∈Ω 【详解】对线性方程组的增广矩阵进行初等行变换:
2222111
1111111111201110111140311001212(,)()()()()B A b a
d a d a d a d a d a a d d ??????
? ? ?==→--→-- ? ? ? ? ? ?------?
?????
方程组无穷解的充分必要条件是3()(,)r A r A b =<,也就是
120120()(),()()a a d d --=--=同时成立,当然应该选(D ).
6.设二次型123(,,)f x x x 在正交变换x Py =下的标准形为222
1232y y y +-,
其中()
123,,P e e e =,若()
132,,Q e e e =-,则123(,,)f x x x 在x Qy =下的标准形为
(A )2221232y y y -+ (B )222
1232y y y +- (C )2221232y y y -- (D ) 222
1232y y y ++
【详解】()()132123100100001001010010,,,,Q e e e e e e P ????
? ?
=-== ? ? ? ?--????,
100001010T T Q P ??
?=- ? ???
211T T T T
f x Ax y PAPy y y ?? ?=== ? ?-??
所以
1
0T T Q AQ P AP ?????
?????
? ? ?????=-=- ? ? ????? ? ? ?????-
--
?
??
??????
?
故选择(A ).
7.若,A B 为任意两个随机事件,则( )
(A )()()()P AB P A P B ≤ (B )()()()P AB P A P B ≥
word 可编辑
(C )2()()()P A P B P AB +≤
(D )2
()()
()P A P B P AB +≥
【详解】()(),()(),P A P AB P B P AB ≥≥所以2
()()
()P A P B P AB +≤故选
择(C ).
8.设随机变量,X Y 不相关,且213,,EX EY DX ===,则
2(())E X X Y +-=( )
(A )3- (B )3 (C ) 5- (D )5 【
详
解
】
222225
(())()()()E X X Y E X E XY EX DX EX EXEY EX +-=+-=++-=
故应该选择(D ).
二、填空题(本题共6小题,每小题4分,满分24分. 把答案填在题中横线上) 9.20ln(cos )
lim
x x x
→= 【详解】2001
22
ln(cos )tan lim
lim x x x x x x →→-==-. 10.
2
21sin cos x x dx x π
π-??
+=
?+??
? . 【详解】只要注意
1sin cos x
x
+为奇函数,在对称区间上积分为零,
所以222
02214sin .cos x x dx xdx x π
π
ππ-??+== ?+?
???
11.若函数(,)z z x y =是由方程2c o s z e x y z
x x +++=确定,则
01(,)|dz = .
【详解】设2(,,)cos z
F x y z e xyz x x =+++-,则
1(,,)sin ,(,,),(,,)z x y z F x y z yz x F x y z xz F x y z e xy '''=+-==+
且
当
01
,x y ==时,
z =,所以
0101010
010
10010010(,)(,)(,,)(,,)|,|,
(,,)
(,,)
y x z z F F z z x y F F ''??=-=-=-=??'' 也就得到01(,)|dz =.dx -
12.设Ω是由平面1x y z ++=和三个坐标面围成的空间区域,则
word 可编辑
23()dxdydz x y z Ω
++=??? .
【详解】注意在积分区域内,三个变量,,x y z 具有轮换对称性,也就是
dxdydz dxdydz dxdydz x y z Ω
Ω
Ω
==?????????
11
2
1
2366314
()dxdydz dxdydz ()z
D x y z z zdz dxdy z z dz Ω
Ω
++===-=??????????
13.n 阶行列式
20021
20
2
002200
12
-=- .
【详解】按照第一行展开,得11
11212122()()n n n n n D D D +---=+--=+,有
1222()n n D D -+=+
由于1226,D D ==,得11
122222()n n n D D -+=+-=-.
14.设二维随机变量(,)X Y 服从正态分布10110(,;,;)N ,
则{}0P XY Y -<= .
【详解】由于相关系数等于零,所以X ,Y 都服从正态分布,
1101~(,),~(,)X N Y N ,且相互独立.
则101~(,)X N -.
{}{}{}{}
010010010(),,P XY Y P Y X P Y X P Y X -<=-<=<->+>-<
三、解答题
15.(本题满分10分)设函数1()ln()sin f x x a x bx x =+++,
3()g x kx =在0x →时为等价无穷小,求常数,,a b k 的取值.
【详解】当0x →时,把函数1()ln()sin f x x a x bx x =+++展开到三阶的马克劳林公式,得
233332331
236123
()(())(())
()()()()
x x f x x a x o x bx x x o x a a
a x
b x x o x =+-+++-+=++-+++ 由于当0x →时,(),()f x g x 是等价无穷小,则有10023
a a
b a k ?
?+=??-+=???=??,
word 可编辑
解得,11123
,,.a b k =-=-
=-
16.(本题满分10分)
设函数)(x f y =在定义域I 上的导数大于零,若对任意的0x I ∈,曲线
)(x f y =在点00(,())x f x 处的切线与直线0x x =及x 轴所围成区域的面积
恒为4,且02()f =,求()f x 的表达式. 【详解】
)(x f y =在点00(,())x f x 处的切线方程为
000()()()y f x x x f x '=-+
令0y =,得000()
()
f x x x f x =-'
曲线)(x f y =在点00(,())x f x 处的切线与直线0x x =及x 轴所围成区域的
面积为
000001
42()()(()()
f x S f x x x f x =
--=' 整理,得218y y '=
,解方程,得118C x y =-,由于02()f =,得1
2
C =
所求曲线方程为8
4.y x
=
- 17.(本题满分10分)
设函数(,)f x y x y xy =++,曲线2
2
3:C x y xy ++=,求(,)f x y 在曲线C 上的最大方向导数. 【详解】显然
11,f f y x x y
??=+=+??. (,)f x y x y xy =++在(,)x y 处的梯度()11,,f f gradf y x x y ??
??==++ ?????
(,)f x y 在(,)x y 处的最大方向导数的方向就是梯度方向,
最大值为梯度的模
gradf =所以此题转化为求函数2
2
11(,)()()
F x y x y =+++在条件
223:C x y xy ++=下的条件极值.用拉格朗日乘子法求解如下:
令2
2
2
2
113(,,)()()()L x y x y x y xy λλ=++++++-
解方程组2
22120
21203()()x y F x x y F y y x x y xy λλλλ?'=+++=??
'=+++=??++=??
,得几个可能的极值点
word 可编辑
()11112112,,(,),(,),(,)----,
进行比较,可得,在点21,x y ==-或12,x y =-=处,方向导数取到最
大,
3.=
18.(本题满分10分)
(1)设函数(),(u x v x 都可导,利用导数定义证明
(()())()()u x v x u x v x u x v x
'''=+; (2)设函数12(),(),,()n u x u x u x 都可导,12()()()
()n f x u x u x u x =,
写出()f x 的求导公式.
【详解】(1)证明:设)()(x v x u y
=
)()()()(x v x u x x v x x u y -++=???
()()()()()()()()u x x v x x u x v x x u x v x x u x v x =+?+?-+?++?-
v x u x x uv ???)()(++=
x
u
x u x x v x u x y ???????)
()(++= 由导数的定义和可导与连续的关系
00'lim
lim[()()]'()()()'()x x y u u
y v x x u x u x v x u x v x x x x
?→?→???==+?+=+???
(2)12()()()
()n f x u x u x u x =
1
1212
12()()()()()()()()()()
(n n n
f x u x u x u x u x u x u x u x u x u x u x ''''=++
+
19.(本题满分10分)
已知曲线L 的方程
为z z x ?=??=??,起点
为00()A ,终点
为
00(,)
B ,
计
算
曲
线
积
分
22()()()L
y z d x z x y d y
+
+-+++?
.
【详解】曲线L
的参数方程为cos ,cos x t y t z t =??
=??=?
起点0()A 对应2
t π
=
,
终点为00(,)B 对应2
t π
=-
.
22222
2
2
2()()()cos )(cos )))(cos )cos L
y z dx z x y dy x y dz
t t d t t d t t d t
π
π-
++-+++=+++-?
?
2
2
02
sin.
tdt
π
==
20.(本题满分11分)
设向量组
123
,,
ααα为向量空间3R的一组基,
11322333
2221
,,()
k k
βααβαβαα
=+==++.
(1)证明:向量组
123
,,
βββ为向量空间3R的一组基;
(2)当k为何值时,存在非零向量ξ,使得ξ在基123
,,
ααα和基
123
,,
βββ
下的坐标相同,并求出所有的非零向量.ξ
【详解】(1)()
123123
201
020
201
(,,),,
k k
βββααα
??
?
= ?
?
+
??
,
因为
201
21
020240
21
201
k k
k k
==≠
+
+
,且
123
,,
ααα显然线性无关,所
以
123
,,
βββ是线性无关的,当然是向量空间3R的一组基.
(2)设非零向量ξ在两组基下的坐标都是123
(,,)
x x x,则由条件
112233112233
x x x x x x
αααβββ
++=++
可整理得:
11322313
20
()()
x k x x k
ααααα
++++=,所以条件转化为线性
方程组
()
13213
20
,,
k k x
ααααα
++=存在非零解.
从而系数行列式应该等于零,也就是
123123
101101
0100100
2020
(,,)(,,
k k k k
αααααα
??
?==
?
?
??
由于
123
,,
ααα显然线性无关,所以
101
0100
20
k k
=,也就是0
k=.
此时方程组化为()
1
121213122
3
,,()
x
x x x x
x
ααααα
??
?
=++=
?
?
??
,
由于
12
,
αα线性无关,所以13
2
x x
x
+=
?
?
=
?
,通解为
1
2
3
x C
x
x C
????
? ?
=
? ?
?
?-
??
??
,其中C为
任意常数.
所以满足条件的0
C
C
ξ
??
?
= ?
?
-
??
其中C为任意不为零的常数.
21.(本题满分11分)
word可编辑
word 可编辑
设矩阵02313312A a -??
?
=-- ?
?
-??
相似于矩阵12000031B b -?? ?= ? ???.
(1)求,a b 的值;
(2)求可逆矩阵P ,使1P AP -为对角矩阵.
【详解】(1)因为两个矩阵相似,所以有trA trB =,A B =.
也就是324
235a b a a b b +=+=?????
-==??
. (2)由2
1
20
05
01500
3
1
()()E B λλλλλλ--=
-=--=--,得A ,B 的特
征值都为12315,λλλ===
解方程组0()E A x -=,得矩阵A 的属于特征值121λλ==的线性无关的特
征向量为12231001.ξξ-???? ? ?
== ? ? ? ?????
;
解方程组50()E A x -=得矩阵A 的属于特征值35λ=的线性无关的特征向量
为3111ξ-??
?= ? ???
令()123231101011,,P ξξξ--?? ?== ? ???,则1100010005.P AP -?? ?
= ? ???
22.(本题满分11分)设随机变量X 的概率密度为220
00ln ,(),x x f x x -?>=?≤?
对X 进行独立重复的观测,直到第2个大于3的观测值出现时停止,记Y 为次
数.
求Y 的分布函数; (1) 求Y 的概率分布; (2) 求数学期望.EY
【详解】(1)X 进行独立重复的观测,得到观测值大于3的概率为
3
1
3228
()ln x P X dx +∞
->==
?
显然Y 的可能取值为234,,
,
且2
2
11117171234888648()(),,,,
k k k P Y k C k k ---????
==??=-= ? ???
??
word 可编辑
(2
)设22
3
2
222
1111()()(),()n n
n n n n x S x n n x
x x x x x ∞
∞
∞-===''''????''=-====< ? ?--????
∑∑∑
2
22171711664
8648()()()k k n E Y kP Y k k k S -∞∞
==??
??
===-=
= ?
?????
∑∑ 23.(本题满分11分) 设总体X 的概率密度为
1
110,(;),x f x θθθ
?≤≤?
=-???其他
其中θ为未知参数,12,,,n X X X 是来自总体的简单样本.
(1)求参数θ的矩估计量; (2)求参数θ的最大似然估计量. 【详解】(1)总体的数学期望为
1
11
112
()()E X x
dx θ
θθ==+-? 令()E X X =,解得参数θ的矩估计量:21?X θ
=-. (2)似然函数为
12121
1
10,,,,()(,,
,;),n n
n x x x L x x x θθθ?≤≤?-=???
其他
显然()L θ是关于θ的单调递增函数,为了使似然函数达到最大,只要使θ尽
可能大就可以,所以
参数θ的最大似然估计量为12
?min(,,,).n x x x θ=