
板材下料优化方法案例
本案例以上海某柴油机厂某车间某年某月所需3种2mm厚度的板材零件下料为例,说明线性规划在下料中的应用及其在提高材料利用率方面所能产生的显著经济效益。同时,该案例所介绍的工作流程还是一种非常简单实用、便于操作、效果良好的板材下料优化方法,可供各企业在生产中参考运用。
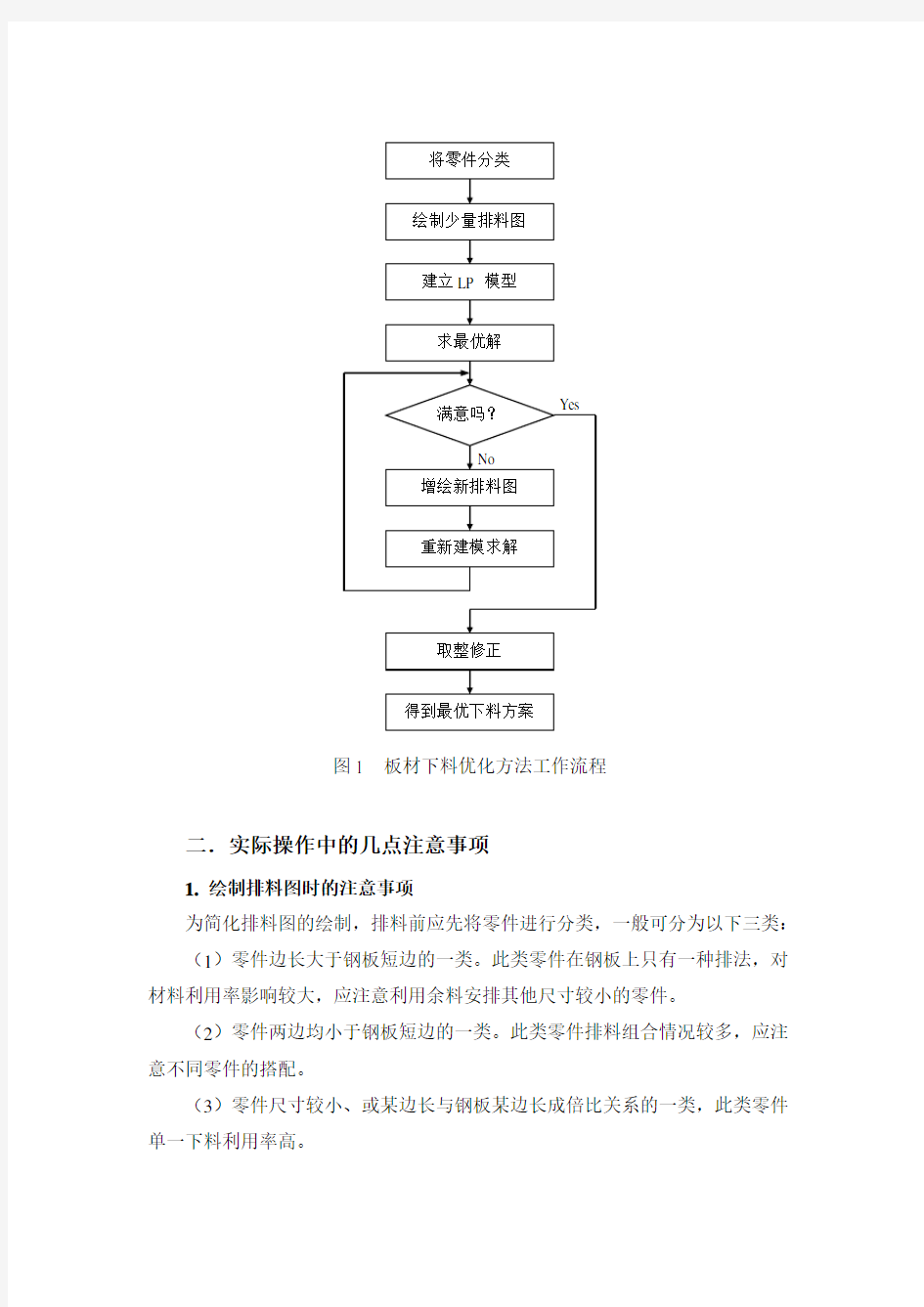
一.板材下料优化方法的特点及其工作流程
用线性规划求解最优下料方案,通常要求首先设计出所有可行合理的下料方式,然后建立LP模型求解最优下料方案。由于板材下料是典型的二维下料,每一种下料方式对应一张排料图,在零件种类较多的情况下,要绘制出所有可行且合理的排料图,不仅工作量非常巨大,而且也是不现实的。为减少绘制排料图的工作量,同时又能达到良好的效果,我们在此给出了一种高效的板材下料优化方法的工作流程。该工作流程有如下特点:
1.对绘制排料图的要求不高。开始时,只需选作少量包含各种零件且材料利用率较高的排料图,这不仅可简化绘图工作量,还可简化模型。
2.对所得最优解进行最优化后分析。若初始最优解效果不理想,则通过有针对性地再增绘少量排料图后重新求解,通常就可达到事半功倍的效果(该步骤属于将在第十一章介绍的敏感性分析中的“增加新的决策变量”,但我们是用计算机求解,故可不涉及敏感性分析的概念)。
3.通常板材下料问题中的变量应当是整数,若采用整数规划求解,则显然会使材料利用率降低。这里我们先采用线性规划求解,对得到的最优解通过舍去小数部分取整,对取整后的零件短缺数,再绘制少量排料图解决。此“取整修正”方法可比使用整数变量求解得到更高的材料利用率。
图1 板材下料优化方法工作流程
二.实际操作中的几点注意事项
1.绘制排料图时的注意事项
为简化排料图的绘制,排料前应先将零件进行分类,一般可分为以下三类:(1)零件边长大于钢板短边的一类。此类零件在钢板上只有一种排法,对材料利用率影响较大,应注意利用余料安排其他尺寸较小的零件。
(2)零件两边均小于钢板短边的一类。此类零件排料组合情况较多,应注意不同零件的搭配。
(3)零件尺寸较小、或某边长与钢板某边长成倍比关系的一类,此类零件单一下料利用率高。
绘制排料图时,应先考虑第一类零件,其次搭配好第二类零件,最后将第三类零件作为余料的填充件,数量较大的第三类零件则还应绘制单一下料图。
2.简化模型的方法
在下料问题的LP模型中,每种零件对应一个约束条件,当一批下料任务中零件种类较多时,不仅会使排料工作复杂化,而且LP模型也会相应复杂,此时可按以下方法进行简化处理。
(1)对尺寸不大且数量较少的零件,在排料时可暂不考虑,它们通常可在取整修正阶段一起解决。
(2)对数量相同,且某边长也相同或相近的两种或多种零件,可组合成一种“新零件”进行排料和建模。
三. 应用案例
上海某柴油机厂某月需要3种2mm厚的板材零件,其工艺尺寸、需要量和单一下料利用率等数据见表1。
表1 零件尺寸、需要量和单一下料利用率
可见,如果采用以往的单一下料方法,则这三种零件总共需要69张钢板,总的材料利用率仅为80.86%。下面,我们采用上述工作流程进行优化。
1. 选作排料图
图2是选作的4张排料图,分别用X1、X2、X3、X4 表示;表9.10给出了各种排料方式下每张钢板可切割的零件数。
表2 各种排料方式下每张钢板可得零件数
2. 建立LP 模型并求最优解
设x 1、x 2、x 3
、x 4 分别为上述各种排料方式的切割钢板数,目标是所耗用的钢板最少。由表2,可得LP 模型为
min x 0 = x 1 + x 2 + x 3 + x 4 21x 1 ≥500 s.t. 28x 2 + 4x 3 ≥600 2x 1 + x 2 +10x 3 +11x 4 ≥250 x 1、x 2 、 x 3 、x 4 ≥ 0 用Excel 软件求解,可得最优解为
x 0* = 60.973,x 1* = 23.810,x 2* =18.806,x 3* =18.357,x 4* = 0
即按排料图x 1切割24张、按x 2和x 3各切割19张,可满足3种零件的需求,
(a) X 1
利用率:86.81% (b) X 2
利用率:94.74%
(c) X 3
利用率:94.26%
(d) X 4
利用率:90.09%
图2 初始排料图
总共需62张钢板,可比单一下料方式少用7张钢板,材料利用率提高到89.99%,但材料利用率仍然偏低,效果还不够理想。
3. 下料方案的最优化后分析
板材下料问题LP模型最优解的效果取决于所绘制的排料图。由于该方法一开始只要求选作若干排料图,因此其初始最优解的效果往往是欠佳的,但这一缺陷可在最优化后分析阶段弥补。
获得初始最优解后,首先应计算其材料利用率,若效果欠佳,则一般有以下两个原因:
(1)最优解中含有某些材料利用率较低的排料图;
(2)各零件在排料图中的数量配比不当(反映在最优解中就是存在较大的剩余变量)。
出现上述情况时,可有针对性地再绘制少量排料图,以它们作为新增变量加入原模型中,重新运算后通常即可得到令人满意的下料方案。
本案例中由于3个剩余变量都为0(都是非基变量,在模型中并未给出,这是由于用软件求解并不要求化为标准型),故不存在数量配比不当的问题。进一步分析可知,x1 = 23.81,数量最大,但排料图x1的材料利用率仅为86.81%,可见这是影响材料利用率的主要原因。分析4张排料图后,可发现仅x1中含有1# 零件,显然应对1# 零件重新设计排料图。再看2# 零件,其需求量最大,且与1# 零件有一边长相近,两者的另一边长之和又恰好与钢板短边成倍比(260+240=500),故可将两者组合后绘制一张新的排料图x5,见图3。该排料图每张可得1# 和2# 零件各14块,3# 零件1块,材料利用率达98.92%。
将x5加入模型,用Excel重新求解,可得新的最优解为
x0* = 57.609,x2* =0.518,x3* =21.377,x5* =35.714,x1*=x4* = 0经进位取整后,只需59张钢板,比初始最优方案又减少了3张,材料利用率则提高到94.56%,已达到令人满意的效果。
4. 对最优方案的取整修正
当最优解中切割方式较多,且钢板总量不是很大时,简单地采用进位取整处理往往会影响材料利用率。下面我们介绍一种简便易行且效果很好的“取整修正法”,步骤如下:
(1)对最优解舍去小数部分取整。本案例经取整后得
x 2 = 0,x 3 = 21,x 5 = 35
(2)计算零件短缺数,见表3。
表3 取整后零件短缺数计算表
(3)对零件短缺数进行套料。通常经取整后的短缺数不会很大,故套料工作量也不会很大。
对于本案例,首先考虑现有排料图。由于x 2每张可得2# 零件28块,3# 零件1块,故应取x 2 =1。这样就只缺1# 零件10块,3# 零件4块,据此再绘制一张排料图x 6 ,见图4,它可裁得1# 零件12块,3# 零件6块,已满足要求。
图3 排料图X 5 图4 排料图X 6
现在已得到最终下料方案:分别按排料图x 2、x 3、x 5
、x 6 各切割1、21、35、1张,总计耗用58张钢板,比进位取整方法又少用1张,材料利用率则进一步提高到96.19%。仅此3个零件,就比单一下料法节约11张钢板,材料利用率提高了15.33%,其经济效益可见一斑。
某金属罐制造厂生产方案的优化案例
一.问题的提出
某金属罐制造厂是制造金属罐的专业厂家,其主要产品有A、B、C、D四种型号的金属罐。近年来,产品销售情况良好,市场对这4种产品的需求量很大,且预测结果表明,需求还有进一步扩大的趋势,许多用户还希望能提供更多的不同功能的新产品。此外,现有产品在质量、性能、成本、工艺等方面也存在进一步改善的余地。对此,该厂已做了一些基本的分析,比如对引进新的制罐技术的可行性分析,对目前产品的成本核算及分析等。但对如何优化当前的生产计划,以获得更大的经济效益;企业目前的各项资源配置是否合理;应如何进一步改进生产条件以满足市场需求;是否下决心引进新技术开发新产品等等一系列问题尚缺乏科学的定量分析依据。为适应日趋激烈的市场竞争环境,不断提高企业的竞争能力和赢利能力,该企业决策者决定聘请某高校的定量分析专家协助,对当前和未来的生产计划进行最优化分析。
二.案例分析
1.产品生产主要过程及其模型的建立
该企业生产的A、B、C、D四种金属罐要经过四道工序:第一道工序是冲压下料,金属板材在冲压车间经冲压机冲压,加工成金属罐所需要的各种板材零件;第二道工序是成形加工,在成形车间里把板材零件冲压成符合要求的形状;第三道工序是焊接装配,在焊接车间将各种成形的零件按技术要求焊接装配成为完整的金属罐;最后一道工序是喷漆,装配好的金属罐送到喷漆车间被喷上防火的瓷漆。
根据工艺要求及成本核算,各单位产品所需的加工时间、利润及目前可供使用的总工时如表11.3所示。
表11.3 单位产品所需加工时间、利润及可利用的工时
该厂仅有一台冲压机,每天工作8小时,共计480 min可供加工使用;另有若干条成形、装配、喷漆生产线分属各车间,除承担本厂生产任务外,还承担着科研实验、新产品开发试制等工作,因此这些生产线每天可利用的总工时分别不超过2400 min、2000 min和3000 min。
由以上分析,可设
x1 为A型金属罐的日产量;
x2为B型金属罐的日产量;
x3 为C型金属罐的日产量;
x4 为D型金属罐的日产量;
并设目标函数为每天的总利润,就可建立日产品计划的线性规划模型如下:max x0 = 9x1+6x2+11x3+8x4
x1+ x2+ x3+ x4≤480
4x1+8x2+ 2x3 + 5x4≤2400
s.t. 4x1+2x2+5x3+ 5x4 ≤2000
6x1+4x2+8x3+ 4x4≤3000
x1, x2 , x3 , x4 ≥0
2.求解最优生产计划
用Excel软件求解该LP问题,图11.2是软件输出的“运算结果报告”。
图11.2 运算结果报告
由图11.2可知,最优解为
X* = ( x1,x2,x3,x4,s1,s2,s3,s4)’
= ( 400,0,70,10,0,610,0,0)’
x0 * = 4450。
其中s1,s2,s3,s4为松弛变量。由软件运行结果可知,为使总利润最大,每天的生产计划应如下安排:A型金属罐400个,C型金属罐70个,D型金属罐10个,不生产B型金属罐,这样日总利润可达4450元。
3.对最优解的初步分析
(1)由最优解中4个松弛变量的值s1 = s3 = s4 =0,s2 =610,说明冲压、装配和喷漆3个工序可利用的加工时间全部用完,但成形工序还剩余610min时间闲置而未被利用。
(2)图11.3是软件输出的“敏感性报告”。
图11.3 敏感性报告
由图11.3可知,冲压时间的影子价格是2.5元,装配时间的影子价格是0.5元,喷漆时间的影子价格是0.75元,其经济意义是上述3道工序资源每增加或减少1min,分别会使利润增加或减少2.5元、0.5元和0.75元。而成形工序的影子价格为0,这是因成形工序有闲置的610min未被利用。由此可知冲压工序是当前生产的关键所在,增加冲压能力将使产品总利润得到较大提高。
4.敏感性分析
为便于分析,下面给出该LP问题的最优单纯型表格,见表11.4。
表11.4 最优单纯型表格
(1)B型金属罐的投产条件分析
在当前的最优生产计划中,不安排B型金属罐的生产,但当前市场对该产品是有需求的,若放弃B型金属罐的市场,将对企业的长期发展产生不利的影响。这就需要分析,在什么条件下,生产B型罐才能与企业利润最大化的目标相一致。
从敏感性分析的角度考虑这一问题,其途径有以下三个:一是通过降本增效,提高B型金属罐的单位利润;二是改进工艺,降低B型金属罐的各工序的加工时间,由此也必将降低B型罐的生产成本从而提高单位利润;三是设法增加某些工序的加工能力,优化配置企业的设备资源,使B型罐得以生产。下面就从这三个方面分别进行分析。
①增加B型金属罐单位利润的分析
由图11.3可知,在不改变当前最优基的条件下,c2允许的增量为0.5;此外由表11.4中x2 的检验数
c= C B B-1 P2 - c2 = 0.5
2
也可知,只要B型金属罐的单位利润c2再增加0.5元以上,则原解就非最优,x2 将被调入基。再由表11.4中不难看出,调入x2后,x1 将被调出基(由最小比值法),结果并不能令人满意。下面假定通过降低物料消耗或提高价格等措施,可将B型金属罐的单位利润由6元增加至7元,用Excel软件重新求解,可得新的最优解为
X* =( x1,x2,x3,x4,s1,s2,s3,s4 )’
= ( 0,133.33,270,76.76,0,410,0,0)’
x0* = 4516.67
即此时新的最优生产计划将调整为:不生产A型金属罐,B、C、D型金属
罐的日产量分别为133.33、270、76.76个。日总利润增加为4516.67元,每天仍有410min 的成形工序时间闲置。由于该方案将放弃A 型金属罐市场,同样可能对企业的长期发展产生不利的影响,故并不能从根本上解决问题。
② 降低B 型金属罐单位资源消耗的分析
设δ1、δ2、δ3、δ4分别为B 型金属罐各道工序单位加工时间的减少量, 则由
'c 2= C B B -1 P 2’ - c 2 = ( 2.5,0,0.5,0.75 ) ?
???
??? ?
?----4321δ4δ2δ8δ1- 6
= 0.5 -2.5δ1 -0.5δ3 - 0.75δ4
可知,只要满足以下三个条件之一,'2c 就将 <0,x 2 就可调入基,该产品就可投入生产。
δ1 > 0.2,或δ3 > 1,或δ4 > 0.67
即冲压时间由1min 降低到1-0.2 = 0.8min 以下;或装配时间由2min 降低到 2-1=1min 以下;或喷漆时间由4min 降低到4 - 0.67 = 3.33 min 以下。
下面我们分别对以上3种情况用Excel 软件进行试算。
a .设.冲压时间由1min 降低到0.7min ,其他工序时间不变,用Excel 软件重新求解,可得新的最优解为
X * = ( x 1,x 2,x 3,x 4,s 1,s 2,s 3,s 4 )’
= ( 203.23,131.18,129.03,55.91,0,0,0,0 )’ x 0 * = 4482.80
既A 、B 、C 、D 四种金属罐都将投入生产,最优日产量分别为203.23、131.18、129.03、55.91个,每天总利润为4482.80元。此时4道工序都恰好用完,资源也得到了充分利用。
b .设.装配时间由2min 降低到0.9min ,其他工序时间不变,用Excel 软件重新求解,可得新的最优解为
X * = ( x 1,x 2,x 3,x 4,s 1,s 2,s 3,s 4 )’
= ( 0,97.56,270,112.44,0,517.32,0,0 )’ x 0 * = 4454.88
即不生产A型罐,B、C、D三种金属罐的日产量分别为97.56、270、112.44个,此时成型工序每天有517.32min空闲时间。
c.设.喷漆时间由4min降低到2.9min,其他工序时间不变,用Excel软件重新求解,可得新的最优解为
X* = ( x1,x2,x3,x4,s1,s2,s3,s4 )’
= ( 0,133.33,306.67,40,0,520,0,0 )’
x0 * = 4453.33
同样不生产A型罐,B、C、D三种金属罐的日产量分别为133.33、306.67、40个,此时成型工序每天有520min空闲时间。
由以上分析可知,只要将B型罐的冲压时间由1min降低到0.7min,4种产品就可同时投入生产,且4种产品的产量相对比较均衡,四道工序时间也都将得到充分利用;而如果采用降低装配或喷漆时间的改进措施,则将导致停产A型罐,成型工序能力也都不能充分利用,放弃A型金属罐市场,同样可能对企业的长期发展产生不利的影响,而且企业资源配置不合理的状况也得不到解决。由此可见,为使B型罐能够生产,设法降低B型罐冲压时间是很好的解决方案。
③增加工序加工能力(优化资源配置)的分析
由图11.3可知,只要将冲压能力增加20min/天以上,或将装配能力增加400min/天以上,或将喷漆能力增加40min/天以上,就将影响当前的最优基。下面我们仍采用试算的方法进行分析。
a.设将冲压能力每天增加60min(可通过加班解决),用Excel软件重新求解,可得新的最优解为
X* = ( x1,x2,x3,x4,s1,s2,s3,s4)’
= ( 887.86,66.67,0,19.05,11.43,0,0,0)’
x0* = 4538.10
即不生产C型罐,A、B、D三种金属罐的日产量分别为887.86、66.67、19.05个,此时冲压工序每天有11.43min空闲时间。由此可知,冲压能力每天只需增加48min,即可使4道工序能力都得到充分利用,但此时将退出C型罐市场,同样将对企业的长期发展产生不利影响。
b.设将装配能力每天增加480min(可通过加班或购置新设备等方法解决),
用Excel软件重新求解,可得新的最优解为
X* = ( x1,x2,x3,x4,s1,s2,s3,s4 )’
= ( 0,0,270,210,0,810,80,0 )’
x0* = 4650
此时不仅B型罐仍不能生产,而且A型罐也将停止生产,成型和装配工序每天将有810min和80min的空闲时间,资源配置更不合理。可见此方案并不能解决问题。
c.设将喷漆能力每天增加60min(可通过加班解决),用Excel软件重新求解,可得新的最优解为
X* = ( x1,x2,x3,x4,s1,s2,s3,s4 )’
= ( 370,10,100,0,0,640,0,0)’
x0 * = 4490
可见增加喷漆能力也不是一个好的解决方案,将放弃D型罐的市场,成型工序每天仍将有640min的空闲时间。
从上述三个不同角度的敏感性分析结果可知,要使B型罐的生产符合利润最大化的目标,而且使所有四种产品都能生产,同时使所有工序能力都得到充分利用的最佳且最容易实现的方案是通过改进工艺,降低B型罐的冲压时间。
(2)关于产品单位利润变动的敏感性分析
由图11.3可知,在不改变原最优解的条件下各产品单位利润的变动范围为
8.83≤c1≤9.5,-∞≤c2≤6.5,10≤c3≤11.33,7≤c4≤9
由此可知,在不影响当前最优基的条件下,各产品单位利润的可变动范围都不大,也即当前最优解对产品单位利润的变化比较敏感,故当企业内外部环境发生变化而引起产品单位利润有较大变化(超出上述范围)时,应重新进行生产计划的优化分析。
(3)关于是否应当引进新产品生产技术的分析
为了满足市场需求,增强企业的发展后劲,该企业计划引进一种新型金属罐(E型罐)的生产技术,生产该产品无需增加新的设备投资。经测算,生产一个该金属罐需要冲压、成型、装配、喷漆的时间分别为1min、2min、6min、12min,产品单位利润为13元。在作出是否引进该金属罐生产技术的决策之前,需要从
企业的整体经济效益出发对引进该产品的效益进行分析。
此问题属于增加一个新的决策变量。可设E 型罐的日产量为x 5 ,由所给条件,c 5 =13,P 5 =(1,2,6,12 )’,则x 5 的检验数为
5c = C B B -1 P 5 - c 5 = ( 2.5,0,0.5,0.75 ) ??????
?
??12621-13 =1.5 >0 故不影响原最优解。5c = 1.5表明,若将E 型罐投入生产,则每生产一个将使企业的总利润减少1.5元。可知从利润最大化的角度考虑不应投产E 型罐。 要使E 型罐的生产符合企业的整体经济效益,与前面(1)中关于B 型罐的生产条件分析完全类似地,可从以下几个方面进行分析。 ① 增加E 型金属罐单位利润的分析
由5c = 1.5可知,如果能通过降低生产成本等措施,将E 型罐的单位利润提高1.5元以上,生产E 型罐就能为企业带来更大的经济效益。下面假定可将B 型金属罐的单位利润由13元增加至15元,用Excel 软件重新求解,可得新的最优解为
X * = ( x 1,x 2,x 3,x 4,x 5,s 1,s 2,s 3,s 4 )’ = ( 428,0,0,24,28,0,512,0,0 )’ x 0 * = 4464
此时将不生产B 型和C 型金属罐,A 、D 、E 型金属罐的日产量分别为428、24、28个,日总利润为4464元,每天仍有512min 的成形工序时间闲置。由于该方案将放弃B 型和C 型金属罐市场,需要慎重考虑。 ② 降低E 型金属罐单位资源消耗的分析
设δ1、δ2、δ3、δ4分别为E 型金属罐各道工序单位加工时间的减少量, 则由
5c = C B B -1 P 5 -c 5 = ( 2.5,0,0.5,0.75 ) ?
???
???
?
?----4321δ12δ6δ2δ1- 13
= 1.5 - 2.5δ1 - 0.5δ3 - 0.75δ4
可知,只要满足
δ1 > 0.6,或δ3 > 3,或δ4 > 2
三个条件之一,E型罐就可投入生产,即:冲压时间由1min降低到0.4min以下;或装配时间由6min降低到3min以下;或喷漆时间由12min降低到10min以下。下面是分别对以上3种情况用Excel软件进行试算的结果。
a.设.冲压时间由1min降低到0.3min,其他工序时间不变,则新的最优解为
X* =(x1,x2,x3,x4,x5,s1,s2,s3,s4 )’
= ( 463.64,0,0,12.12,14.14,0,456.57,0,0 )’
x0 * = 4453.54
同样将不生产B型和C型金属罐,A、D、E型金属罐的日产量分别为463.64、12.12、14.14个,每天总利润为4453.54元,每天仍有456.57min的成形工序时间闲置。
b.设.装配时间由6min降低到2min,其他工序时间不变,则新的最优解为X* =(x1,x2,x3,x4,x5,s1,s2,s3,s4 )’
= ( 0,0,3.33,343.33,133.33,0,410,0,0 )’
x0*= 4516.67
即不生产A型和B型罐,C、D、E三种金属罐的日产量分别为3.33、343.33、133.33个,每天总利润为4516.67元,此时成型工序每天有410min空闲时间。
c.设.喷漆时间由12min降低到9min,其他工序时间不变,则新的最优解为X*= ( x1,x2,x3,x4,x5,s1,s2,s3,s4 )’
= ( 0,205.33,0,58.67,216,0,32,0,0 )’
x0 * = 4509.33
即不生产A型和C型罐,B、D、E三种金属罐的日产量分别为205.33、58.67、216个,每天总利润为4509.33元,此时成型工序每天仅有32min空闲时间。
由以上分析可知,通过降低E型罐某道工序的加工时间,虽然能使E型罐得以投产,但都将导致其他两种产品的停产。如果将停止生产的产品是市场上将逐渐淘汰的产品,则以新产品E型罐取而代之将是可取的,否则就需要慎重考虑。
③增加工序加工能力的分析
图11.4是增加了E型罐的数据后用Excel求解时所输出的“敏感性报告”。
图11.4 敏感性报告
由图11.4可知,只要将冲压能力增加20min/天以上,或将装配能力增加400min/天以上,或将喷漆能力增加40min/天以上,就将影响当前的最优基。
经过多次试算后发现,如果仅单独少量增加以上三道工序的能力,则首先进入基的则是x2即B型罐,这一点其实通过比较B、E两种产品的资源单耗就可知(E型罐所需的装配与喷漆时间都比B型罐要高得多)。由于每个E型罐所需的喷漆时间高达12min,看来要使x5能进入基就需要增加较多的喷漆时间。将喷漆能力每天增加480min后,经试算所得新的最优解为
X*=(x1,x2,x3,x4,x5,s1,s2,s3,s4 )’
= ( 0,155,260,0,65,0,510,0,0)’
x0* = 4635
此时将不生产A型和D型罐,B、C、E三种金属罐的日产量分别为155、260、65个,成型工序每天有510min空闲时间。
从以上分析结果可知,要使E型罐的生产符合利润最大化的目标,就都要放弃另两种金属罐的生产。这就需要对这些产品的市场需求趋势作进一步的分析,选择停止生产即将淘汰的产品的方案。
三.结论及建议
综合以上分析,可以得到如下结论,并提出以下建议:
1.在现有资源及生产工艺条件下,从利润最大化的目标出发,则该企业的最优生产方案为:每天生产A型金属罐400个,C型金属罐70个,D型金属罐10个,不生产B型金属罐,每天总利润可达4450元。此时成形工序每天有610min 的生产能力闲置,企业的资源配置不够合理。
2.考虑到企业现有的产品技术、资源配置、市场需求及竞争的需要,应采取必要措施使B型金属罐得以投产。在各种可供选择的措施中,降低B型罐的冲压时间将是最佳的解决方案。
3.从利润最大化的目标来看,目前引进E型罐生产技术的条件尚不成熟,匆忙上马将导致总利润的下降。如果能够通过改进生产工艺降低资源单耗,或降低产成本提高单位利润,则生产E型罐将是可行的,但要放弃另两种金属罐的生产。这就需要对这些产品的市场需求趋势作进一步分析后再确定最佳解决方案。
4.以上是在利润最大化这个单一目标下所进行的分析。需要指出的是,在市场竞争日趋激烈的环境下,企业不能仅仅考虑眼前的利润目标,更需要从企业的长远发展需要出发对各种优化方案进行具体分析,以上的分析结果能够为该企业的决策者提供许多非常有用的辅助决策信息。
3.6:线性规划 目录: (1)线性规划的基本概念 (2)线性规划在实际问题中的应用 【知识点1:线性规划的基本概念】 (1)如果对于变量x 、y 的约束条件,都是关于x 、y 的一次不等式,则称这些约束条件为__线性约束条件__(),z f x y =是欲求函数的最大值或最小值所涉及的变量x 、y 的解析式,叫做__目标函数_,当(),f x y 是x 、y 的一次解析式时,(),z f x y =叫做_线性目标函数__. (2)求线性目标函数在线性约束条件下的最大值或最小值问题,称为__线性规划问题__ ;满足线性约束条件的解(),x y 叫做__可行解_;由所有可行解组成的集合叫做__可行域_;使目标函数取得最大值或最小值的可行解叫做_最优解__ 例题:若变量x 、y 满足约束条件2 10x y x y +≤?? ≥??≥? ,则z x y =+的最大值和最小值分别为 ( B ) A. 4和3 B. 4和2 C. 3和2 D. 2和0 分析:本题考查了不等式组表示平面区域,目标函数最值求法. 解:画出可行域如图 作020l x y +=: 所以当直线2z x y =+过()20A , 时z 最大,过()1,0B 时z 最小max min 4, 2.z z == 变式1:已知2z x y =+,式子中变量x 、y 满足条件11y x x y y ≤?? +≤??≥-? ,则z 的最大值是__3___ 解:不等式组表示的平面区域如图所示.
作直线0:20l x y +=,平移直线0l ,当直线0l 经过 平面区域的点()21A -,时,z 取最大值2213?-=. 变式2:设2z x y =+,式中变量x 、y 满足条件43 35251x y x y x -≤-?? +≤??≥? ,求z 的最大值和最小值 分析:由于所给约束条件及目标函数均为关于x 、y 的一次式,所以此问题是简单线性 规划问题,使用图解法求解 解:作出不等式组表示的平面区域(即可行域),如图所示. 把2z x y =+变形为2y x z =-+,得到斜率为-2,在y 轴上的截距为z ,随z 变化的一族平行直线. 由图可看出,当直线2z x y =+经过可行域上的点A 时,截距z 最大,经过点B 时,截距z 最小. 解方程组430 35250x y x y -+=??+-=?,得A 点坐标为()5,2, 解方程组1 430x x y =??-+=? ,得B 点坐标为()1,1 所以max min 25212,211 3.z z =?+==?+= 变式3:若变量x 、y 满足约束条件6 321x y x y x +≤?? -≤-??≥? ,则23z x y =+的最小值为( C ) A. 17 B. 14 C. 5 D. 3
第五章线性规划在管理中的应用 某企业停止了生产一些已经不再获利的产品,这样就产生了一部分剩余生产力。管理层考虑将这些剩余生产力用于新产品Ⅰ、Ⅱ、Ⅲ的生产。可用的机器设备是限制新产品产量的主要因素,具体数据如下表: 司的利润最大化。 1、判别问题的线性规划数学模型类型。 2、描述该问题要作出决策的目标、决策的限制条件以及决策的总绩效测度。 3、建立该问题的线性规划数学模型。 4、用线性规划求解模型进行求解。 5、对求得的结果进行灵敏度分析(分别对最优解、最优值、相差值、松驰/剩余量、对偶价格、目标函数变量系数和常数项的变化范围进行详细分析)。 6、若销售部门表示,新产品Ⅰ、Ⅱ生产多少就能销售多少,而产品Ⅲ最少销售18件,请重新完成本题的1-5。 解: 1、本问题是资源分配型的线性规划数学模型。 2、该问题的决策目标是公司总的利润最大化,总利润为: + + 决策的限制条件: 8x1+ 4x2+ 6x3≤500 铣床限制条件 4x1+ 3x2≤350 车床限制条件 3x1+ x3≤150 磨床限制条件 即总绩效测试(目标函数)为: max z= + + 3、本问题的线性规划数学模型 max z= + + S.T.8x1+ 4x2+ 6x3≤500 4x1+ 3x2≤350 3x1+ x3≤150 x1≥0、x2≥0、x3≥0 4、用Excel线性规划求解模板求解结果:最优解(50,25,0),最优值:30元。 5、灵敏度分析
目标函数最优值为: 30 变量最优解相差值 x1 50 0 x2 25 0 x3 0 .083 约束松弛/剩余变量对偶价格 1 0 .05 2 75 0 3 0 .033 目标函数系数范围: 变量下限当前值上限 x1 .4 .5 无上限 x2 .1 .2 .25 x3 无下限.25 .333 常数项数范围: 约束下限当前值上限 1 400 500 600 2 275 350 无上限 3 150 (1)最优生产方案: 新产品Ⅰ生产50件、新产品Ⅱ生产25件、新产品Ⅲ不安排。最大利润值为30元。 (2)x3 的相差值是意味着,目前新产品Ⅲ不安排生产,是因为新产品Ⅲ的利润太低,若要使新产品Ⅲ值得生产,需要将当前新产品Ⅲ利润元/件,提高到元/件。 (3)三个约束的松弛/剩余变量0,75,0,表明铣床和磨床的可用工时已经用完,而车床的可用工时还剩余75个工时; 三个对偶价格,0,表明三种机床每增加一个工时可使公司增加的总利润额。 (4)目标函数系数范围 表明新产品Ⅰ的利润在元/件以上,新产品Ⅱ的利润在到之间,新产品Ⅲ的利润在以下,上述的最佳方案不变。 (5)常数项范围 表明铣床的可用条件在400到600工时之间、车铣床的可用条件在275工时以上、磨铣床的可用条件在到工时之间。各自每增加一个工时对总利润的贡献元,0元,元不变。 6、若产品Ⅲ最少销售18件,修改后的的数学模型是: max z= + + S.T.8x1+ 4x2+ 6x3≤500 4x1+ 3x2≤350 3x1+ x3≤150 x3≥18 x1≥0、x2≥0、x3≥0 这是一个混合型的线性规划问题。 代入求解模板得结果如下: 最优解(44,10,18),最优值:元。 灵敏度报告: 目标函数最优值为: 变量最优解相差值 x1 44 0 x2 10 0 x3 18 0 约束松弛/剩余变量对偶价格
线性规划 线性规划是处理线性目标函数和线性约束的一种较为成熟的方法,目前已经广泛应用于军事、经济、工业、农业、教育、商业和社会科学等许多方面。 8.2.1 基本数学原理 线性规划问题的标准形式是: ????? ??????≥=+++=+++=++++++=0,,,min 21221122222121112 121112211n m n mn m m n n n n n n x x x b x a x a x a b x a x a x a b x a x a x a x c x c x c z 或 ???? ?????=≥===∑∑==n j x m i b x a x c z j n j i j ij n j j j ,,2,1,0,,2,1,min 1 1 写成矩阵形式为: ?? ???≥==O X b AX CX z min 线性规划的标准形式要求使目标函数最小化,约束条件取等式,变量b 非负。不符合这几个条件的线性模型可以转化成标准形式。 MATLAB 采用投影法求解线性规划问题,该方法是单纯形法的变种。 8.2.2 有关函数介绍 在MATLAB 工具箱中,可用linprog 函数求解线性规划问题。 linprog 函数的调用格式如下: ●x=linprog(f,A,b):求解问题minf'*x ,约束条件为A*x<=b 。 ●x=linprog(f,A,b,Aeq,beq):求解上面的问题,但增加等式约束,即Aeq*x=beq 。若没有不等式约束,则令A=[ ],b=[ ]。 ●x=linprog(f,A,b,Aeq,beq,lb,ub):定义设计x 的下界lb 和上界ub ,使得x 始终在该范围内。若没有等式约束,令Aeq=[ ],beq=[ ]。 ●x=linprog(f,A,b,Aeq,beq,lb,ub,x0):设置初值为x0。该选项只适用于中型问题,默认时大型算法将忽略初值。 ●x=linprog(f,A,b,Aeq,beq,lb,ub,x0,options):用options 指定的优化参数进行最小化。 ●[x,fval]=linprog(…):返回解x 处的目标函数值fval 。 ●[x,lambda,exitflag]=linprog(…):返回exitflag 值,描述函数计算的退出条件。 ●[x,lambda,exitflag,output]=linprog(…):返回包含优化信息的输出参数output 。 ●[x,fval,exitflag,output,lambda]=linprog(…):将解x 处的拉格朗日乘子返回到lambda 参数中。
第五章线性规划在管理中的应用 5.1 某企业停止了生产一些已经不再获利的产品,这样就产生了一部分剩余生产力。管理层考虑将这些剩余生产力用于新产品Ⅰ、Ⅱ、Ⅲ的生产。可用的机器设备是限制新产品产量的主要因素,具体数据如下表: 量,使得公司的利润最大化。 1、判别问题的线性规划数学模型类型。 2、描述该问题要作出决策的目标、决策的限制条件以及决策的总绩效测度。 3、建立该问题的线性规划数学模型。 4、用线性规划求解模型进行求解。 5、对求得的结果进行灵敏度分析(分别对最优解、最优值、相差值、松驰/剩余量、对偶价格、目标函数变量系数和常数项的变化范围进行详细分析)。 6、若销售部门表示,新产品Ⅰ、Ⅱ生产多少就能销售多少,而产品Ⅲ最少销售18件,请重新完成本题的1-5。 解: 1、本问题是资源分配型的线性规划数学模型。 2、该问题的决策目标是公司总的利润最大化,总利润为: 0.5x1+ 0.2x2+ 0.25x3 决策的限制条件: 8x1+ 4x2+ 6x3≤500 铣床限制条件 4x1+ 3x2≤350 车床限制条件 3x1+ x3≤150 磨床限制条件 即总绩效测试(目标函数)为: max z= 0.5x1+ 0.2x2+ 0.25x3 3、本问题的线性规划数学模型 max z= 0.5x1+ 0.2x2+ 0.25x3 S.T.8x1+ 4x2+ 6x3≤500 4x1+ 3x2≤350 3x1+ x3≤150 x1≥0、x2≥0、x3≥0 4、用Excel线性规划求解模板求解结果:最优解(50,25,0),最优值:30元。 5、灵敏度分析
目标函数最优值为 : 30 变量最优解相差值 x1 50 0 x2 25 0 x3 0 .083 约束松弛/剩余变量对偶价格 1 0 .05 2 75 0 3 0 .033 目标函数系数范围 : 变量下限当前值上限 x1 .4 .5 无上限 x2 .1 .2 .25 x3 无下限 .25 .333 常数项数范围 : 约束下限当前值上限 1 400 500 600 2 275 350 无上限 3 37.5 150 187.5 (1)最优生产方案: 新产品Ⅰ生产50件、新产品Ⅱ生产25件、新产品Ⅲ不安排。最大利润值为30元。 (2)x3 的相差值是0.083意味着,目前新产品Ⅲ不安排生产,是因为新产品Ⅲ的利润太低,若要使新产品Ⅲ值得生产,需要将当前新产品Ⅲ利润0.25元/件,提高到0.333元/件。 (3)三个约束的松弛/剩余变量0,75,0,表明铣床和磨床的可用工时已经用完,而车床的可用工时还剩余75个工时; 三个对偶价格0.05,0,0.033表明三种机床每增加一个工时可使公司增加的总利润额。 (4)目标函数系数范围 表明新产品Ⅰ的利润在0.4元/件以上,新产品Ⅱ的利润在0.1到0.25之间,新产品Ⅲ的利润在0.333以下,上述的最佳方案不变。 (5)常数项范围 表明铣床的可用条件在400到600工时之间、车铣床的可用条件在275工时以上、磨铣床的可用条件在37.5到187.5工时之间。各自每增加一个工时对总利润的贡献0.05元,0元,0.033元不变。 6、若产品Ⅲ最少销售18件,修改后的的数学模型是: max z= 0.5x1+ 0.2x2+ 0.25x3 S.T.8x1+ 4x2+ 6x3≤500 4x1+ 3x2≤350 3x1+ x3≤150 x3≥18 x1≥0、x2≥0、x3≥0 这是一个混合型的线性规划问题。 代入求解模板得结果如下: 最优解(44,10,18),最优值:28.5元。 灵敏度报告: 目标函数最优值为 : 28.5 变量最优解相差值 x1 44 0 x2 10 0
线性规划应用案例
市场营销应用 案例一:媒体选择 在媒体选择中应用线性规划的目的在于帮助市场营销经理将固定的广告预算分配到各种广告媒体上,可能的媒体包括报纸、杂志、电台、电视和直接邮件。在这些媒体中应用线性规划,目的是要使宣传范围、频率和质量最大化。对于应用中的约束条件通常源于对公司政策、合同要求及媒体的可用性。在下面的应用中,我们将介绍如何应用线性规划这一工具来建立模型进而解决媒体选择问题。 REL发展公司正在私人湖边开发一个环湖社区。湖边地带和住宅的主要市场是距离开发区100英里以内的所有中上收入的家庭。REL公司已经聘请BP&J 来设计宣传活动。 考虑到可能的广告媒体和要覆盖的市场,BP&J建议将第一个月的广告局限于5种媒体。在第一个月末,BP&J将依据本月的结果再次评估它的广告策略。BP&J已经收集到了关于受众数量、广告单价、各种媒体一定周期内可用的最大次数以及评定5种媒体各自宣传质量的数据。质量评定是通过宣传质量单位来衡量的。宣传质量单位是一种用于衡量在各个媒体中一次广告的相对价值的标准,它建立于BP&J在广告业中的经验,将众多因素考虑在内,如受众层次(年龄、收入和受众受教育的程度)、呈现的形象和广告的质量。表4-1列出了收集到的这些信息。 表4-1 REL发展公司可选的广告媒体
REL发展公司提供给BP&J第一个月广告活动的预算是30000美元。而且,REL公司对BP&J如何分配这些资金设置了如下限制:至少要使用10次电视广告,达到的受众至少要有50000人,并且电视广告的费用不得超过18000美元。应当推荐何种广告媒体选择计划呢? 案例二:市场调查 公司开展市场营销调查以了解消费者个性特点、态度以及偏好。专门提供此种信息的市场营销调查公司,经常为客户机构开展实际调查。市场营销调查公司提供的典型服务包括涉及计划、开展市场调查、分析收集数据、提供总结报告和对客户提出意见。在调查设计阶段,应当对调查对象的数量和类型设定目标或限额。市场营销调查公司的目标是以最小的成本满足客户要求。 市场调查公司(MSI)专门评定消费者对新的产品、服务和广告活动的反映。一个客户公司要求MSI帮助确定消费者对一种近期推出的家具产品的反应。在与客户会面的过程中,MSI统一开展个人入户调查,以从有儿童的家庭和无儿童的家庭获得回答。而且MSI还同意同时开展日间和晚间调查。尤其是,客户的合同要求依据以下限制条款进行1000个访问: ●至少访问400个有儿童的家庭; ●至少访问400个无儿童的家庭; ●晚间访问的家庭数量必须不少于日间访问的家庭数量; ●至少40%有儿童的家庭必须在晚间访问; ●至少60%无儿童的家庭必须在晚间访问。 因为访问有儿童的家庭需要额外的访问时间,而且晚间访问者要比日间访问者获得更多收入,所以成本因访问的类型不同而不同。基于以往的调查研究,预计的访问费用如下表所示: 以最小总访问成本满足合同要求的家庭——时间访问计划是什么样的
线性规划的实际应用举例 即两为了便于同学们掌握线性规划的一般理论和方法,本文拟就简单的线性规划( 的实际应用举例加以说明。个变量的线性规划) 1 物资调运中的线性规划问题 万个40万个和30万个,由于抗洪抢险的需要,现需调运1 A,B两仓库各有编织袋50例/元万个、180/万个到乙地。已知从A仓库调运到甲、乙两地的运费分别为120元到甲地,20元/万个。问如何调运,能150/万个、万个;从B仓库调运到甲、乙两地的运费分别为100元? ?总运费的最小值是多少使总运费最小仓库调Bz元。那么需从x万个到甲地,y万个到乙地,总运费记为解:设从A仓库调运40-x万个到甲 地,调运运万个到乙地。20-y 从而有 。z=120x+180y+100(40-x)+150·(20-y)=20x+30y+7000 1)(图,即可行域。作出以上不等式组所表示的平面区域 z'=z-7000=20x+30y. 令 :20x+30y=0,作直线l 且与原点距离最小,0),,l的位置时,直线经过可行域上的点M(30l把直线向右上方平移至l y=0时,即x=30,亦取得最小值,取得最小值,从而z=z'+7000=20x+30y+7000z'=20x+30y 元)。30+30×z=20× 0+7000=7600(min 万个到乙地,可使总万个到甲地,20B30万个到甲地,从仓库调运10A答:从仓库调运元。运费最小,且总运费的最小值为7600 2 产品安排中的线性规划问题 吨,麦麸0.4吨需耗玉米某饲料厂生产甲、乙两种品牌的饲料,已知生产甲种饲料2例1O.4
吨,其余添加剂0.2. 吨甲种1吨,其余添加剂0.2吨。每吨;生产乙种饲料1吨需耗玉米0.5吨,麦麸0.3元。可供饲料厂生产的玉米供应500元,每1吨乙种饲料的利润是饲料的利润是400吨。问甲、乙300吨,麦麸供应量不超过500吨,添加剂供应量不超过量不超过600 ? ?最大利润是多少两种饲料应各生产多少吨(取整数),能使利润总额达到最大 1。分析:将已知数据列成下表 2表1例表 元,那么吨、y吨,利润总额为z解:设生产甲、乙两种饲料分别为x z=400x+500y。 即可行域。(图2)作出以上不等式组所表示的平面区域 平行,所以线段l4x+5y=6000与。并把400x+500y=0l向右上方平移,由于l:作直线l:1。,N(0,1200)M(250MN上所有坐标都是整数的点(整点)都是最优解。易求得,1000) ,y=1000时,1000)取整点M(250,,即x=250 。元1000=600000()=60(万元)=400×z250+500×max 吨,能使利润总额达到最大。最大利润为1000可安排生产甲种饲料250吨,乙种饲料答:万元。60 使我们认识到最优解的个数还例2课本题中出现的线性规划问题大都有唯一的最优解。注:有其他可能,这里不再深入探究。
线性规划模型在生活中的实际应用 一、线性规划的基本概念 线性规划是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支,它是辅助人们进行科学管理的一种数学方法.在经济管理、交通运输、工农业生产等经济活动中,提高经济效果是人们不可缺少的要求,而提高经济效果一般通过两种途径:一是技术方面的改进,例如改善生产工艺,使用新设备和新型原材料.二是生产组织与计划的改进,即合理安排人力物力资源.线性规划所研究的是:在一定条件下,合理安排人力物力等资源,使经济效果达到最好.一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题.满足线性约束条件的解叫做可行解,由所有可行解组成的集合叫做可行域.决策变量、约束条件、目标函数是线性规划的三要素. 二、线性规划模型在实际问题中的应用 (1)线性规划在企业管理中的应用范围 线性规划在企业管理中的应用广泛,主要有以下八种形式: 1.产品生产计划:合理利用人力、物力、财力等,是获利最大. 2.劳动力安排:用最少的劳动力来满足工作的需要. 3.运输问题:如何制定运输方案,使总运费最少. 4.合理利用线材问题:如何下料,使用料最少. 5.配料问题:在原料供应的限制下如何获得最大利润. 6.投资问题:从投资项目中选取方案,是投资回报最大. 7.库存问题:在市场需求和生产实际之间,如何控制库存量从而获得更高利益. 8.最有经济计划问题:在投资和生产计划中如何是风险最小 . (2)如何实现线性规划在企业管理中的应用 在线性规划应用前要建立经济与金融体系的评价标准及企业的计量体系,摸清企业的资
源.首先通过建网、建库、查询、数据采集、文件转换等,把整个系统的各有关部分的特征进行量化,建立数学模型,即把组成系统的有关因素与系统目标的关系,用数学关系和逻辑关系描述出来,然后白较好的数学模型编制成计算机语言,输入数据,进行计算,不同参数获取的不同结果与实际进行分析对比,进行定量,定性分析,最终作出决策.
简单的线性规划问题 [学习目标] 1.了解线性规划的意义以及约束条件、目标函数、可行解、可行域、最优解等基本概念.2.了解线性规划问题的图解法,并能应用它解决一些简单的实际问题. 知识点一 线性规划中的基本概念 知识点二 1.目标函数的最值 线性目标函数z =ax +by (b ≠0)对应的斜截式直线方程是y =-a b x +z b ,在y 轴上的截距是z b ,当z 变化时,方程表 示一组互相平行的直线. 当b >0,截距最大时,z 取得最大值,截距最小时,z 取得最小值; 当b <0,截距最大时,z 取得最小值,截距最小时,z 取得最大值. 2.解决简单线性规划问题的一般步骤 在确定线性约束条件和线性目标函数的前提下,解决简单线性规划问题的步骤可以概括为:“画、移、求、答”四步,即, (1)画:根据线性约束条件,在平面直角坐标系中,把可行域表示的平面图形准确地画出来,可行域可以是封闭的多边形,也可以是一侧开放的无限大的平面区域. (2)移:运用数形结合的思想,把目标函数表示的直线平行移动,最先通过或最后通过的顶点(或边界)便是最优解. (3)求:解方程组求最优解,进而求出目标函数的最大值或最小值. (4)答:写出答案. 知识点三 简单线性规划问题的实际应用 1.线性规划的实际问题的类型 (1)给定一定数量的人力、物力资源,问怎样运用这些资源,使完成的任务量最大,收到的效益最大; (2)给定一项任务,问怎样统筹安排,使完成这项任务耗费的人力、物力资源量最小. 常见问题有: ①物资调动问题 例如,已知两煤矿每年的产量,煤需经两个车站运往外地,两个车站的运输能力是有限的,且已知两煤矿运往两个车站的运输价格,煤矿应怎样编制调动方案,才能使总运费最小?
线性规划的应用 线性规划是运筹学中一个重要分支,它是研究线性约束条件下线性目标函数的极值问题的数学理论和方法。广泛应用于军事作战、经济分析、经营管理和工程技术等方面。如:经济管理、交通运输、工农业生为合理地利用有限的人力、物力、财力等资源作出的最优决策,提供科学的依据。 线性规划作为运筹学的一个研究较早、发展较快、应用广泛、方法较成熟的重要分支,它在日常生活中的典型应用主要有:1合理利用线材问题:如何下料使用材最少 2配料问题:在原料供应量的限制下如何获取最大利润 3投资问题:从投资项目中选取方案,使投资回报最大 4产品生产计划:合理利用人力、物力、财力等,使获利最大 5劳动力安排:用最少的劳动力来满足工作的需要 6运输问题:如何制定调动方案,使总运费最小 其实,也就是说,线性规划在运筹学中的研究对象主要是在有一定的人力、财力、资源条件下,如何合理安排使用,效益最高和在某项任务确定后,如何安排人、财、物,使之最省。 例如: 某公司现有三条生产线来生产两种新产品,其主要数据如表1.1所示。请问如何生产可以让公司每周利润最大?
表1 产品组合问题的数据表 此问题是在生产线可利用时间受到限制的情形下寻求每周利润最大化的产品组合问题。 在建立产品组合模型的过程中,以下问题需要得到回答: (1)要做出什么决策? (2)做出的决策会有哪些条件限制? (3)这些决策的全部评价标准是什么? (1)变量的确定 要做出的决策是两种新产品的生产水平,记x1为每周生产产品甲的产量,x2为每周生产产品乙的产量。一般情况下,在实际问题中常常称为变量(决策变量)。 (2)约束条件 求目标函数极值时的某些限制称为约束条件。如两种产品在相应生产线上每周生产时间不能超过每条生产线的可得时间,对于生产线一,有x1≤4,类似地,其它生产线也有不等式约束。 (3)目标函数 对这些决策的评价标准是这两种产品的总利润,即目标函数是要求每周的生产利润(可记为z,以百元为计量单位)为最大 这样,可以把产品组合问题抽象地归结为一个数学模型: max z = 3x1+5x2 s.t. x1 ≤4 2x2 ≤12 3x1+ 2x2 ≤18 x1≥0,x2 ≥0
密封线 线性规划的实际应用 摘要线性规划模型是科学与工程领域广泛应用的数学模型。本文应用线性规划模型,以 某水库输水管的选择为研究对象,以实现输水管的选择既能保证供水,又能使造价最低为 目标,根据水库的特点和实际运行情况,分析了其输水管选择过程中线性规划模型的建立 方法,并分别通过单纯形法和MATLAB软件进行求解。 关键词线性规划模型单纯形法 MATLAB 一、专著背景简介 《最优化方法》介绍最优化模型的理论与计算方法,其中理论包括对偶理论、非线性规划的最优性理论、非线性半定规划的最优性理论、非线性二阶锥优化的最优性理论;计算方法包括无约束优化的线搜索方法、线性规划的单纯形方法和内点方法、非线性规划的序列二次规划方法、非线性规划的增广Lagrange方法、非线性半定规划的增广Lagrange方法、非线性二阶锥优化的增广Lagrange方法以及整数规划的Lagrange松弛方法。《最优化方法》注重知识的准确性、系统性和算法论述的完整性,是学习最优化方法的一本入门书。 最优化方法(也称做运筹学方法)是近几十年形成的,它主要运用数学方法研究各种系统的优化途径及方案,为决策者提供科学决策的依据。最优化方法的主要研究对象是各种有组织系统的管理问题及其生产经营活动。最优化方法的目的在于针对所研究的系统,求得一个合理运用人力、物力和财力的最佳方案,发挥和提高系统的效能及效益,最终达到系统的最优目标。实践表明,随着科学技术的日益进步和生产经营的日益发展,最优化方法已成为现代管理科学的重要理论基础和不可缺少的方法,被人们广泛地应用到公共管理、经济管理、工程建设、国防等各个领域,发挥着越来越重要的作用。本章将介绍最优化方法的研究对象、特点,以及最优化方法模型的建立和模型的分析、求解、应用。主要是线性规划问题的模型、求解(线性规划问题的单纯形解法)及其应用-运输问题;以及动态规划的模型、求解、应用-资源分配问题。 二、专著的主要结构内容 《最优化方法》是一本着重实际应用又有一定理论深度的最优化方法教材,内容包括线
8.2 线性规划 线性规划是处理线性目标函数和线性约束的一种较为成熟的方法,目前已经广泛应用于军事、经济、工业、农业、教育、商业和社会科学等许多方面。 8.2.1 基本数学原理 线性规划问题的标准形式是: ????? ??????≥=+++=+++=++++++=0,,,min 21221122222121112 121112211n m n mn m m n n n n n n x x x b x a x a x a b x a x a x a b x a x a x a x c x c x c z ΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛ 或 ???? ?????=≥===∑∑==n j x m i b x a x c z j n j i j ij n j j j ,,2,1,0,,2,1,min 1 1ΛΛ 写成矩阵形式为: ?? ???≥==O X b AX CX z min 线性规划的标准形式要求使目标函数最小化,约束条件取等式,变量b 非负。不符合这几个条件的线性模型可以转化成标准形式。 MATLAB 采用投影法求解线性规划问题,该方法是单纯形法的变种。 8.2.2 有关函数介绍 在MATLAB 工具箱中,可用linprog 函数求解线性规划问题。 linprog 函数的调用格式如下: ●x=linprog(f,A,b):求解问题minf'*x ,约束条件为A*x<=b 。 ●x=linprog(f,A,b,Aeq,beq):求解上面的问题,但增加等式约束,即Aeq*x=beq 。若没有不等式约束,则令A=[ ],b=[ ]。 ●x=linprog(f,A,b,Aeq,beq,lb,ub):定义设计x 的下界lb 和上界ub ,使得x 始终在该范围内。若没有等式约束,令Aeq=[ ],beq=[ ]。 ●x=linprog(f,A,b,Aeq,beq,lb,ub,x0):设置初值为x0。该选项只适用于中型问题,默认时大型算法将忽略初值。 ●x=linprog(f,A,b,Aeq,beq,lb,ub,x0,options):用options 指定的优化参数进行最小化。 ●[x,fval]=linprog(…):返回解x 处的目标函数值fval 。 ●[x,lambda,exitflag]=linpro g(…):返回exitflag 值,描述函数计算的退出条件。 ●[x,lambda,exitflag,output]=linprog(…):返回包含优化信息的输出参数output 。 ●[x,fval,exitflag,output,lambda]=linprog(…):将解x 处的拉格朗日乘子返回到
市场营销应用 案例一:媒体选择 在媒体选择中应用线性规划的目的在于帮助市场营销经理将固定的广告预算分配到各种广告媒体上,可能的媒体包括报纸、杂志、电台、电视和直接邮件。在这些媒体中应用线性规划,目的是要使宣传范围、频率和质量最大化。对于应用中的约束条件通常源于对公司政策、合同要求及媒体的可用性。在下面的应用中,我们将介绍如何应用线性规划这一工具来建立模型进而解决媒体选择问题。 REL发展公司正在私人湖边开发一个环湖社区。湖边地带和住宅的主要市场是距离开发区100英里以内的所有中上收入的家庭。REL公司已经聘请BP&J 来设计宣传活动。 考虑到可能的广告媒体和要覆盖的市场,BP&J建议将第一个月的广告局限于5种媒体。在第一个月末,BP&J将依据本月的结果再次评估它的广告策略。BP&J已经收集到了关于受众数量、广告单价、各种媒体一定周期内可用的最大次数以及评定5种媒体各自宣传质量的数据。质量评定是通过宣传质量单位来衡量的。宣传质量单位是一种用于衡量在各个媒体中一次广告的相对价值的标准,它建立于BP&J在广告业中的经验,将众多因素考虑在内,如受众层次(年龄、收入和受众受教育的程度)、呈现的形象和广告的质量。表4-1列出了收集到的这些信息。 表4-1 REL发展公司可选的广告媒体
REL发展公司提供给BP&J第一个月广告活动的预算是30000美元。而且,REL公司对BP&J如何分配这些资金设置了如下限制:至少要使用10次电视广告,达到的受众至少要有50000人,并且电视广告的费用不得超过18000美元。应当推荐何种广告媒体选择计划呢? 案例二:市场调查 公司开展市场营销调查以了解消费者个性特点、态度以及偏好。专门提供此种信息的市场营销调查公司,经常为客户机构开展实际调查。市场营销调查公司提供的典型服务包括涉及计划、开展市场调查、分析收集数据、提供总结报告和对客户提出意见。在调查设计阶段,应当对调查对象的数量和类型设定目标或限额。市场营销调查公司的目标是以最小的成本满足客户要求。 市场调查公司(MSI)专门评定消费者对新的产品、服务和广告活动的反映。一个客户公司要求MSI帮助确定消费者对一种近期推出的家具产品的反应。在与客户会面的过程中,MSI统一开展个人入户调查,以从有儿童的家庭和无儿童的家庭获得回答。而且MSI还同意同时开展日间和晚间调查。尤其是,客户的合同要求依据以下限制条款进行1000个访问: ●至少访问400个有儿童的家庭; ●至少访问400个无儿童的家庭; ●晚间访问的家庭数量必须不少于日间访问的家庭数量; ●至少40%有儿童的家庭必须在晚间访问; ●至少60%无儿童的家庭必须在晚间访问。 因为访问有儿童的家庭需要额外的访问时间,而且晚间访问者要比日间访问者获得更多收入,所以成本因访问的类型不同而不同。基于以往的调查研究,预计的访问费用如下表所示: 以最小总访问成本满足合同要求的家庭——时间访问计划是什么样的呢?
线性规划的实际应用 The Standardization Office was revised on the afternoon of December 13, 2020
线性规划的实际应用 摘要线性规划模型是科学与工程领域广泛应用的数学模型。本文应用线性规划模 型,以某水库输水管的选择为研究对象,以实现输水管的选择既能保证供水,又能使 造价最低为目标,根据水库的特点和实际运行情况,分析了其输水管选择过程中线性 规划模型的建立方法,并分别通过单纯形法和M A T L A B软件进行求解。 关键词线性规划模型单纯形法M A T L A B 一、专著背景简介 《最优化方法》介绍最优化模型的理论与计算方法,其中理论包括对偶理论、非线性规划的最优性理论、非线性半定规划的最优性理论、非线性二阶锥优化的最优性理论;计算方法包括无约束优化的线搜索方法、线性规划的单纯形方法和内点方法、非线性规划的序列二次规划方法、非线性规划的增广L ag ra ng e 方法、非线性半定规划的增广La gr an ge方法、非线性二阶锥优化的增广 La gr an ge方法以及整数规划的L ag ra n ge松弛方法。《最优化方法》注重知识的准确性、系统性和论述的完整性,是学习最优化方法的一本入门书。 最优化方法(也称做方法)是近几十年形成的,它主要运用研究各种系统的优化途径及方案,为决策者提供科学决策的依据。最优化方法的主要研究对象是各种有的管理问题及其生产经营活动。最优化方法的目的在于针对所研究的系统,求得一个合理运用人力、物力和财力的最佳方案,发挥和提高系统的效能及效益,最终达到系统的最优目标。实践表明,随着科学技术的日益进步和生产经营的日益发展,最优化方法已成为的重要理论基础和的方法,被人们广泛地应用到、、工程建设、国防等各个领域,发挥着越来越重要的作用。本章将介绍最优化方法的研究对象、特点,以及最优化方法模型的建立和模型的分析、求解、应用。主要是线性规划问题的模型、求解(线性规划问题的单纯形解法)及其应用-运输问题;以及动态规划的模型、求解、应用-资源分配问题。 二、专著的主要结构内容 《最优化方法》是一本着重实际应用又有一定理论深度的最优化方法教材,内容包括线性规划、运输问题、整数规划、目标规划、非线性规划(无约束最优化与约束最优化)、动态规划等最基本、应用最广又最有代表性的最优化方
LP (Linear Programming)
Alex 有一个家庭农场。除了农场上的农作物以外,他还饲养了一些猪拿到市场上出售,猪可获得的饲料及其所含成分如下表:Alex如何喂养猪更好? 成分/每公斤 玉米槽料苜蓿每日最小需求量碳水化合物 蛋白质 维他命 成本(美分)903010842080207240606060200180150 问题1:科学养猪线性规划建模(猪饲料的配方)饲养成本最小
--- 每天玉米、槽料、苜蓿各喂多少公斤? --- 必须满足要求12--- 追求成本最低 Min. 84x 1+ 72x 2+ 60x 3 3x 1x 2x 3 知识点 建模三要素 决策变量约 束目标 90x 1+ 20x 2+ 40x 3 ≥ 20030x 1+ 80x 2+ 60x 3 ≥ 18010x 1+ 20x 2+ 60x 3 ≥ 150 x i ≥0 , i =1,2,3 成分/每公 斤 玉米槽料苜蓿每日最小需求量碳水化合物 蛋白质 维他命 成本(美分)903010842080207240606060200180150
s.t. 90x 1+ 20x 2+ 40x 3 ≥ 200 30x 1 + 80x 2+ 60x 3 ≥ 180 10x 1+ 20x 2+ 60x 3 ≥ 150 x i ≥0 , i =1,2,3 Min . 84x 1+ 72x 2+ 60x 3 目标函数约束函数符号中必含等号符号的右侧为常数线性--变量均为1次方 Max. 或 Min.线性--所有变量均为1次方常规约束:变量非负!知识点 模型表示
?线性规划模型能求解出来吗? 能!--- 万能的单纯形法 结合软件 QSB应用
诚信声明 我声明,所呈交的毕业论文是本人在老师指导下进行的研究工作及取得的研究成果。据我查证,除了文中特别加以标注和致谢的地方外,论文中不包含其他人已经发表或撰写过的研究成果,我承诺,论文中的所有内容均真实、可信。 毕业论文作者签名:签名日期:年月日
摘要:在企业生产过程中,生产资源的分配直接影响到企业的经济效益。因此,企业在制定生产计划时,人力物力和时间等资源的优化配制是首要面对的关键问题,而建立线性规划模型则是目前解决该问题的有效方法之一。本文旨在针对上述有限资源条件的约束下,通过建立相应的线性规划模型来制定生产计划以实现企业资源最优化、利益最大化,同时利用LINGO 11.0软件求解线性规划模型并分析在某些资源变动时对该模型所产生的影响并寻求最优生产方案。 关键词:企业生产计划;线性规划;数学模型;LINGO 11.0
Abstract:In the enterprise production process, the allocation of production resources directly affects the economic efficiency of enterprises. Therefore, enterprises in the development of production plan, formulated to optimize the resources of manpower and time is the key problem of face. And to establish the linear programming model is one of the effective ways to solve the problem. This paper aimed at the limited resource constraints, by establishing linear programming model corresponding to make production plan in order to realize the maximization of enterprise resource optimization, interest, and using LINGO11.0 software to solve the linear programming model and analysis the influence on the model in some resource changes and seek the optimal production plan. Key words:Production plan;Linear programming;Mathematical model; LINGO 11.0 目录
第五章运筹学线性规划在管理中的应用案例 -标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII
第五章线性规划在管理中的应用 5.1 某企业停止了生产一些已经不再获利的产品,这样就产生了一部分剩余生产力。管理层考虑将这些剩余生产力用于新产品Ⅰ、Ⅱ、Ⅲ的生产。可用的 三种新产品的单位利润分别为0.5元、0.2元、0.25元。目标是要确定每种新产品的产量,使得公司的利润最大化。 1、判别问题的线性规划数学模型类型。 2、描述该问题要作出决策的目标、决策的限制条件以及决策的总绩效测度。 3、建立该问题的线性规划数学模型。 4、用线性规划求解模型进行求解。 5、对求得的结果进行灵敏度分析(分别对最优解、最优值、相差值、松驰/剩余量、对偶价格、目标函数变量系数和常数项的变化范围进行详细分析)。 6、若销售部门表示,新产品Ⅰ、Ⅱ生产多少就能销售多少,而产品Ⅲ最少销售18件,请重新完成本题的1-5。 解: 1、本问题是资源分配型的线性规划数学模型。 2、该问题的决策目标是公司总的利润最大化,总利润为:
0.5x1+ 0.2x2+ 0.25x3 决策的限制条件: 8x1+ 4x2+ 6x3≤500 铣床限制条件 4x1+ 3x2≤350 车床限制条件 3x1 + x3≤150 磨床限制条件 即总绩效测试(目标函数)为: max z= 0.5x1+ 0.2x2+ 0.25x3 3、本问题的线性规划数学模型 max z= 0.5x1+ 0.2x2+ 0.25x3 S.T. 8x1+ 4x2+ 6x3≤500 4x1+ 3x2≤350 3x1 + x3≤150 x1≥0、x2≥0、x3≥0 4、用Excel线性规划求解模板求解结果:最优解(50,25,0),最优值:30元。 5、灵敏度分析 目标函数最优值为 : 30 变量最优解相差值 x1 50 0 x2 25 0 x3 0 .083 约束松弛/剩余变量对偶价格 1 0 .05 2 75 0 3 0 .033 目标函数系数范围 : 变量下限当前值上限 x1 .4 .5 无上限 x2 .1 .2 .25 x3 无下限 .25 .333 常数项数范围 : 约束下限当前值上限 1 400 500 600 2 275 350 无上限 3 37.5 150 187.5
1. 人力资源分配问题 设司机和乘务人员分别在各时间段开始时上班,并连续工作8小时,问该公交线路应怎样安排司机和乘务人员,既能满足工作需要,又使配备司机和乘务人员的人数最少? 解:设x i 表示第i班次时开始上班的司机和乘务人员数, 这样我们建立如下的数学模型。 目标函数:Min x1 + x2 + x3 + x4 + x5 + x6 约束条件:s.t. x1 + x6 ≥60 x1 + x2 ≥70 x2 + x3 ≥60 x3 + x4 ≥50 x4 + x5 ≥20 x5 + x6 ≥30 x1,x2,x3,x4,x5,x6 ≥0 运用lingo求解: Min=x1 + x2 + x3 + x4 + x5 + x6; x1 + x6 >=60; x1 + x2>= 70; x2 + x3>= 60; x3 + x4>=50; x4 + x5>= 20; x5 + x6>=30; Objective value: 150.0000 ariable Value Reduced Cost X1 60.00000 0.000000 X2 10.00000 0.000000 X3 50.00000 0.000000 X4 0.000000 0.000000 X5 30.00000 0.000000 X6 0.000000 0.000000 也可以是 Global optimal solution found. Objective value: 150.0000 Total solver iterations: 6 Variable Value Reduced Cost X1 40.00000 0.000000