
实验1 典型时间序列模型分析
1、实验目的
熟悉三种典型的时间序列模型:AR 模型,MA 模型与ARMA 模型,学会运用Matlab 工具对对上述三种模型进行统计特性分析,通过对2 阶模型的仿真分析,探讨几种模型的适用范围,并且通过实验分析理论分析与实验结果之间的差异。
2、实验原理
AR 模型分析:
设有 AR(2)模型,
X(n)=-0.3X(n-1)-0.5X(n-2)+W(n)
其中:W(n)是零均值正态白噪声,方差为4。
(1)用MA TLAB 模拟产生X(n)的500 观测点的样本函数,并绘出波形 (2)用产生的500 个观测点估计X(n)的均值和方差 (3)画出理论的功率谱
(4)估计X(n)的相关函数和功率谱
【分析】给定二阶的AR 过程,可以用递推公式得出最终的输出序列。或者按照一个白噪声 通过线性系统的方式得到,这个系统的传递函数为:
1
2
1
()10.30.5H z z z --=
++
这是一个全极点的滤波器,具有无限长的冲激响应。 对于功率谱,可以这样得到,
()()
2
2
12
12exp 11x w
z jw P w a z a z σ--==++
可以看出,
()
x P w 完全由两个极点位置决定。
对于 AR 模型的自相关函数,有下面的公式:
这称为 Yule-Walker 方程,当相关长度大于p 时,由递推式求出:
这样,就可以求出理论的 AR 模型的自相关序列。
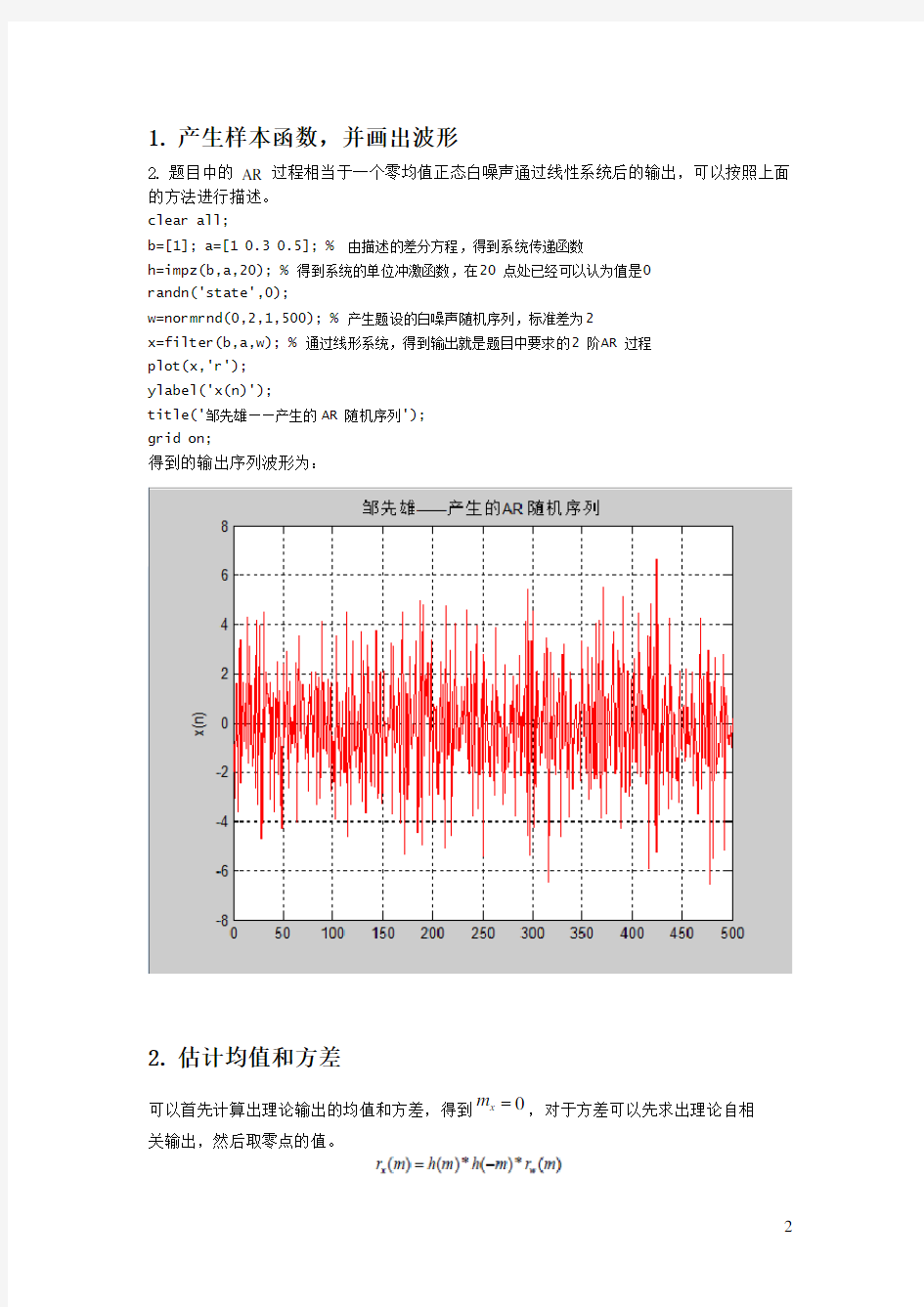
1.产生样本函数,并画出波形
2.题目中的AR 过程相当于一个零均值正态白噪声通过线性系统后的输出,可以按照上面的方法进行描述。
clear all;
b=[1]; a=[1 0.3 0.5]; % 由描述的差分方程,得到系统传递函数
h=impz(b,a,20); % 得到系统的单位冲激函数,在20 点处已经可以认为值是0
randn('state',0);
w=normrnd(0,2,1,500); % 产生题设的白噪声随机序列,标准差为2
x=filter(b,a,w); % 通过线形系统,得到输出就是题目中要求的2 阶AR 过程
plot(x,'r');
ylabel('x(n)');
title('邹先雄——产生的AR 随机序列');
grid on;
得到的输出序列波形为:
2.估计均值和方差
可以首先计算出理论输出的均值和方差,得到
x
m
,对于方差可以先求出理论自相
关输出,然后取零点的值。
并且,,带入有
在最大值处输出的功率,也就是方差,为
对实际数据进行估计,均值为mean(x)=-0.0703,而方差为var(x)=5.2795,两者合理论值吻合得比较好。
程序及运行结果图如下,其中y_mean表示均值,y_var表示方差。
3.画出理论的功率谱密度曲线
理论的功率谱为,
用下面的语句产生:
delta=2*pi/1000;
w_min=-pi;
w_max=pi;
Fs=1000;
w=w_min:delta:w_max; % 得到数字域上的频率取样点,范围是[-pi,pi]
Gx=4*(abs(1./(1+0.3*exp(-i*w)+0.5*exp(-2*i*w))).^2); % 计算出理论值
Gx=Gx/max(Gx); % 归一化处理
f=w*Fs/(2*pi); % 转化到模拟域上的频率
plot(f,Gx);
title('邹先雄——理论功率谱密度曲线');
grid on;
得到的图形为:
可以看出,这个系统是带通系统。
4.估计自相关函数和功率谱密度
用实际数据估计自相关函数和功率谱的方法前面已经讨论过,在这里仅给出最后的仿真图形。
Mlag=20; % 定义最大自相关长度
Rx=xcorr(x,Mlag,'coeff');
m=-Mlag:Mlag;
stem(m,Rx,'r.');
title('邹先雄——自相关函数');
最终的值为
可以看出,它和上面的理论输出值吻合程度很好。实际的功率谱密度可以用类似于上面的方法进行估计,
window=hamming(20); % 采用hanmming 窗,长度为20
noverlap=10; % 重叠的点数
Nfft=512; % 做FFT 的点数
Fs=1000; % 采样频率,为1000Hz
b=[1]; a=[1 0.3 0.5]; % 由描述的差分方程,得到系统传递函数
h=impz(b,a,20); % 得到系统的单位冲激函数,在20 点处已经可以认为值是0
randn('state',0);
w=normrnd(0,2,1,500); % 产生题设的白噪声随机序列,标准差为2
x=filter(b,a,w); % 通过线形系统,得到输出就是题目中要求的2 阶AR 过程
[Px,f]=pwelch(x,window,noverlap,Nfft,Fs, 'onesided'); % 估计功率谱密度
f=[-fliplr(f) f(1:end)]; % 构造一个对称的频率,范围是[-Fs/2, Fs/2]
Py=[-fliplr(Px) Px(1:end)]; % 对称的功率谱
plot(f,10*log10(Py),'b');
title('邹先雄——实际的功率谱密度曲线');
估计出来的功率谱密度为,
将两幅图画在一起,可以看到拟合的情况比较好(两者相位刚好相反,但是基本波形相似):代码如下:
clear all;
delta=2*pi/1000;
w_min=-pi;
w_max=pi;
Fs=1000;
w=w_min:delta:w_max; % 得到数字域上的频率取样点,范围是[-pi,pi]
Gx=4*(abs(1./(1+0.3*exp(-i*w)+0.5*exp(-2*i*w))).^2); % 计算出理论值
Gx=Gx/max(Gx); % 归一化处理
f=w*Fs/(2*pi); % 转化到模拟域上的频率结束
plot(f,Gx,'r');
hold on;
title('邹先雄——理论和实际的功率谱密度曲线拟合');
window=hamming(20); % 采用hanmming 窗,长度为20
noverlap=10; % 重叠的点数
Nfft=512; % 做FFT 的点数
Fs=1000; % 采样频率,为1000Hz
b=[1]; a=[1 0.3 0.5]; % 由描述的差分方程,得到系统传递函数
h=impz(b,a,20); % 得到系统的单位冲激函数,在20 点处已经可以认为值是0
randn('state',0);
w=normrnd(0,2,1,500); % 产生题设的白噪声随机序列,标准差为2
x=filter(b,a,w); % 通过线形系统,得到输出就是题目中要求的2 阶AR 过程
[Px,f]=pwelch(x,window,noverlap,Nfft,Fs, 'onesided'); % 估计功率谱密度
f=[-fliplr(f) f(1:end)]; % 构造一个对称的频率,范围是[-Fs/2, Fs/2]
Py=[-fliplr(Px) Px(1:end)]; % 对称的功率谱
Py=-10*log10(Py);
Py=Py/max(Py);
Py=-Py;Py=3*Py;Py=Py+2.6;%用来归一处理,使两者吻合
plot(f,Py,'b');
legend('实际值','理论值');
grid on;
ARMA 模型分析
设有ARMA(2,2)模型,
X(n)+0.3X(n-1)-0.2X(n-2)=W(n)+0.5W(n-1)-0.2W(n-2)
W(n)是零均值正态白噪声,方差为4。
(1)用MA TLAB 模拟产生X(n)的500 观测点的样本函数,并绘出波形
(2)用产生的500 个观测点估计X(n)的均值和方差
(3)画出理论的功率谱
(4)估计X(n)的相关函数和功率谱
【分析】给定(2,2) 的ARMA 过程,也可以用递推公式得出最终的输出序列。或者按照一个白噪声通过线性系统的方式得到,这个系统的传递函数为:
对于功率谱,可以这样得到,
对于ARMA 过程,当模型的所有极点均落在单位圆内时,才是一个渐进平稳的随机过程。这个过程的自相关函数不能简单地写成Yule-Walker 方程形式,它于模型的参数具有高度的非线性关系。
1. 产生样本函数,并画出波形
题目中的ARMA 过程相当于一个零均值正态白噪声通过线性系统后的输出,可以按照
上面的方法进行描述。
clear all;
b=[1 0.5 -0.2]; a=[1 0.3 -0.2]; % 由描述的差分方程,得到系统传递函数
h=impz(b,a,10); % 得到系统的单位冲激函数,在10点处已经可以认为值是0
randn('state',0);
w=normrnd(0,2,1,500); % 产生题设的白噪声随机序列,标准差为2
x=filter(b,a,w); % 通过线形系统,得到输出就是题目中要求的(2,2)阶ARMA过程
plot(x,'r');
title('邹先雄——输出的AR 随机序列');
得到的输出序列波形为:
2. 估计均值和方差
可以首先计算出理论输出的均值和方差,得到
x
m
,对于方差可以先求出理论自相
关输出,然后取零点的值。
并且,,带入有
在最大值处就是输出的功率,也就是方差,为
对实际数据进行估计,均值为mean(x)= -0.0547,而方差为var(x)=3.8,两者和理论值吻合的比较好。
附代码及运行结果截图如下:
3. 画出理论的功率谱密度曲线
理论的功率谱为,
用下面的语句产生:
delta=2*pi/1000;w_min=-pi;w_max=pi;Fs=1000;
w=w_min:delta:w_max; % 得到数字域上的频率取样点,范围是[-pi,pi]
NS=1+0.5*exp(-i*w)-0.2*exp(-2*i*w); % 分子
DS=1+0.3*exp(-i*w)-0.2*exp(-2*i*w); % 分母
Gx=4*(abs(NS./DS).^2); % 计算出理论值
Gx=Gx/max(Gx);f=w*Fs/(2*pi); % 转化到模拟域上的频率
plot(f,Gx,'b');
title('邹先雄——理论的功率谱密度曲线');
grid on;
4. 估计相关函数和功率谱密度曲线
用实际数据估计自相关函数和功率谱的方法前面已经讨论过,在这里仅给出仿真图形。% 计算理论和实际的自相关函数序列
Mlag=20; % 定义最大自相关长度
Rx=xcorr(x,Mlag,'coeff');
m=-Mlag:Mlag;
stem(m,Rx,'r.');
title('邹先雄——估计自相关函数');
最终的值为
实际的功率谱密度可以用类似于上面的方法进行估计,
window=hamming(20); % 采用hanmming窗,长度为20
noverlap=10; % 重叠的点数
Nfft=512; % 做FFT的点数
Fs=1000; % 采样频率,为1000Hz
b=[1 0.5 -0.2]; a=[1 0.3 -0.2]; % 由描述的差分方程,得到系统传递函数
h=impz(b,a,10); % 得到系统的单位冲激函数,在10点处已经可以认为值是0 randn('state',0);
w=normrnd(0,2,1,500); % 产生题设的白噪声随机序列,标准差为2
x=filter(b,a,w); % 通过线形系统,得到输出就是题目中要求的(2,2)阶ARMA过程[Px,f]=pwelch(x,window,noverlap,Nfft,Fs, 'onesided'); % 估计功率谱密度
f=[-fliplr(f) f(1:end)]; % 构造一个对称的频率,范围是[-Fs/2, Fs/2]
Py=[fliplr(Px) Px(1:end)]; % 对称的功率谱
plot(f,10*log10(Py),'b');
title('邹先雄——实际的功率谱密度曲线');
估计出来的功率谱密度为
把两幅图画在一起,可以得到下面的图形,可以看出两者的吻合度比较高。delta=2*pi/1000;w_min=-pi;w_max=pi;Fs=1000;
w=w_min:delta:w_max; % 得到数字域上的频率取样点,范围是[-pi,pi]
NS=1+0.5*exp(-i*w)-0.2*exp(-2*i*w); % 分子
DS=1+0.3*exp(-i*w)-0.2*exp(-2*i*w); % 分母
Gx=4*(abs(NS./DS).^2); % 计算出理论值
Gx=Gx/max(Gx);f=w*Fs/(2*pi); % 转化到模拟域上的频率
plot(f,Gx,'r');
title('邹先雄——理论和实际的功率谱密度曲线的拟合');
hold on;
window=hamming(20); % 采用hanmming窗,长度为20
noverlap=10; % 重叠的点数
Nfft=512; % 做FFT的点数
Fs=1000; % 采样频率,为1000Hz
b=[1 0.5 -0.2]; a=[1 0.3 -0.2]; % 由描述的差分方程,得到系统传递函数
h=impz(b,a,10); % 得到系统的单位冲激函数,在10点处已经可以认为值是0 randn('state',0);
w=normrnd(0,2,1,500); % 产生题设的白噪声随机序列,标准差为2
x=filter(b,a,w); % 通过线形系统,得到输出就是题目中要求的(2,2)阶ARMA过程[Px,f]=pwelch(x,window,noverlap,Nfft,Fs, 'onesided'); % 估计功率谱密度
f=[-fliplr(f) f(1:end)]; % 构造一个对称的频率,范围是[-Fs/2, Fs/2]
Py=[fliplr(Px) Px(1:end)]; % 对称的功率谱
Py=10*log10(Py);
Py=Py/max(Py);
Py=-Py;Py=3*Py;Py=Py+4;%用来归一处理,使两者吻合
plot(f,Py,'b');
legend('实际值','理论值');
grid on;
3、实验内容
1、熟悉实验原理,将实验原理上的程序应用matlab 工具实现;
2、设有MA(2)模型,
W(n)是零均值正态白噪声,方差为4。
(1)用MA TLAB 模拟产生X(n)的500 观测点的样本函数,并绘出波形(2)用产生的500 个观测点估计X(n)的均值和方差
(3)画出理论的功率谱
(4)估计X(n)的相关函数和功率谱
完成4个问题的源代码如下
clear all;
%产生样本函数,并画出波形
b=[1 -0.3 0.2]; a=[1]; % 由描述的差分方程,得到系统传递函数
h=impz(b,a,10); % 得到系统的单位冲激函数,在10点处已经可以认为值是0 randn('state',0);
w=normrnd(0,2,1,500); % 产生题设的白噪声随机序列,标准差为2
x=filter(b,a,w); % 通过线形系统,得到输出就是题目中要求的(2,2)阶ARMA过程figure(1);
plot(x,'r');
title('邹先雄——样本函数');
Py_mean=mean(x)
Py_var=var(x)
%画出理论的功率谱密度曲线
delta=2*pi/1000;w_min=-pi;w_max=pi;Fs=1000;
w=w_min:delta:w_max; % 得到数字域上的频率取样点,范围是[-pi,pi]
NS=1-0.3*exp(-i*w)+0.2*exp(-2*i*w); % 分子
DS=1; % 分母
Gx=4*(abs(NS./DS).^2); % 计算出理论值
Gx=Gx/max(Gx);f=w*Fs/(2*pi); % 转化到模拟域上的频率
figure(2);
plot(f,Gx,'b');
title('邹先雄——理论的功率谱密度曲线');
%估计相关函数
Mlag=20; % 定义最大自相关长度
Rx=xcorr(x,Mlag,'coeff');
m=-Mlag:Mlag;
figure(3);
stem(m,Rx,'r.');
title('邹先雄——估计相关函数');
%画出估计的功率谱密度曲线
window=hamming(20); % 采用hanmming窗,长度为20
noverlap=10; % 重叠的点数
Nfft=512; % 做FFT的点数
Fs=1000; % 采样频率,为1000Hz
[Px,f]=pwelch(x,window,noverlap,Nfft,Fs, 'onesided'); % 估计功率谱密度
f=[-fliplr(f) f(1:end)]; % 构造一个对称的频率,范围是[-Fs/2, Fs/2]
Py=[fliplr(Px) Px(1:end)]; % 对称的功率谱
figure(4);
plot(f,10*log10(Py),'b');
title('邹先雄——估计的功率谱密度曲线');
%对实际和估计两功率谱密度曲线进行拟合
delta=2*pi/1000;w_min=-pi;w_max=pi;Fs=1000;
w=w_min:delta:w_max; % 得到数字域上的频率取样点,范围是[-pi,pi]
NS=1-0.3*exp(-i*w)+0.2*exp(-2*i*w); % 分子
DS=1; % 分母
Gx=4*(abs(NS./DS).^2); % 计算出理论值
Gx=Gx/max(Gx);f=w*Fs/(2*pi); % 转化到模拟域上的频率
figure(5);
plot(f,Gx,'r');
title('邹先雄——实际和估计两功率谱密度曲线的拟合');
hold on;
window=hamming(20); % 采用hanmming窗,长度为20
noverlap=10; % 重叠的点数
Nfft=512; % 做FFT的点数
Fs=1000; % 采样频率,为1000Hz
b=[1 -0.3 0.2]; a=[1]; % 由描述的差分方程,得到系统传递函数
h=impz(b,a,10); % 得到系统的单位冲激函数,在10点处已经可以认为值是0 randn('state',0);
w=normrnd(0,2,1,500); % 产生题设的白噪声随机序列,标准差为2
x=filter(b,a,w); % 通过线形系统,得到输出就是题目中要求的(2,2)阶ARMA过程[Px,f]=pwelch(x,window,noverlap,Nfft,Fs, 'onesided'); % 估计功率谱密度
f=[-fliplr(f) f(1:end)]; % 构造一个对称的频率,范围是[-Fs/2, Fs/2]
Py=[fliplr(Px) Px(1:end)]; % 对称的功率谱
Py=10*log10(Py);
Py=Py/max(Py);
Py=-Py;Py=3*Py;Py=Py+4;%用来归一处理,使两者吻合
plot(f,Py,'b');
legend('实际值','理论值');
grid on;
样本函数波形为:
理论功率谱密度曲线为:
估计相关函数波形为:
估计功率谱密度曲线为:
实际和估计两功率谱密度曲线的拟合截图如下:
附程序运行后得到的均值与方差的截图,其中y_mean为均值,大小为-0.1127;y_var为方差,大小为3.9324:
4.实验总结:
通过实验,让我更加的了解了随机序列的均值、方差、功率谱密度以及自相关函数。通过软件的编程运行结果,加深了对书上理论知识的理解与掌握。
首先第一个实验中两个随机序列的练习让我更容易着手于本次的实验。通过实验,我对matlab有了更深的认识,在使用matlab的过程中,经常产生问题、发现问题并解决问题,这让我对matlab使用的更加熟练。这次统计信号实验并不是我第一次接触matlab,以前对matlab的应用让我有了一些基础,这次的实验更是让我学到了不少东西,从选题到做题,让我学到了以前没有接触过的matlab知识。比如要在一幅图中显示多条曲线时,可以使用hold on语句来实现,或者在画图函数中的参数进行设定(如:plot(f,(Py),'r',f,Gy,'b');),这在以前没有学过。
第二章习题答案 2.1 (1)非平稳 (2)0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376 (3)典型的具有单调趋势的时间序列样本自相关图 2.2 (1)非平稳,时序图如下 (2)-(3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相关图
2.3 (1)自相关系数为:0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 -0.139 -0.034 0.206 -0.010 0.080 0.118 (2)平稳序列 (3)白噪声序列 2.4 ,序列 LB=4.83,LB统计量对应的分位点为0.9634,P值为0.0363。显著性水平=0.05 不能视为纯随机序列。 2.5 (1)时序图与样本自相关图如下
(2) 非平稳 (3)非纯随机 2.6 (1)平稳,非纯随机序列(拟合模型参考:ARMA(1,2)) (2)差分序列平稳,非纯随机 第三章习题答案 3.1 解:1()0.7()()t t t E x E x E ε-=?+ 0)()7.01(=-t x E 0)(=t x E t t x ε=-)B 7.01( t t t B B B x εε)7.07.01()7.01(221Λ+++=-=- 229608.149 .011 )(εεσσ=-= t x Var 49.00212==ρφρ 022=φ 3.2 解:对于AR (2)模型: ?? ?=+=+==+=+=-3.05 .02110211212112011φρφρφρφρρφφρφρφρ 解得:???==15/115 /72 1φφ 3.3 解:根据该AR(2)模型的形式,易得:0)(=t x E 原模型可变为:t t t t x x x ε+-=--2115.08.0 2212122 ) 1)(1)(1(1)(σφφφφφφ-+--+-= t x Var 2) 15.08.01)(15.08.01)(15.01() 15.01(σ+++--+= =1.98232σ ?????=+==+==-=2209.04066.06957.0)1/(1221302112211ρφρφρρφρφρφφρ ?? ? ??=-====015.06957.033222111φφφρφ
应用时间序列分析实验报告
单位根检验输出结果如下:序列x的单位根检验结果:
1967 58.8 53.4 1968 57.6 50.9 1969 59.8 47.2 1970 56.8 56.1 1971 68.5 52.4 1972 82.9 64.0 1973 116.9 103.6 1974 139.4 152.8 1975 143.0 147.4 1976 134.8 129.3 1977 139.7 132.8 1978 167.6 187.4 1979 211.7 242.9 1980 271.2 298.8 1981 367.6 367.7 1982 413.8 357.5 1983 438.3 421.8 1984 580.5 620.5 1985 808.9 1257.8 1986 1082.1 1498.3 1987 1470.0 1614.2 1988 1766.7 2055.1 1989 1956.0 2199.9 1990 2985.8 2574.3 1991 3827.1 3398.7 1992 4676.3 4443.3 1993 5284.8 5986.2 1994 10421.8 9960.1 1995 12451.8 11048.1 1996 12576.4 11557.4 1997 15160.7 11806.5 1998 15223.6 11626.1 1999 16159.8 13736.5 2000 20634.4 18638.8 2001 22024.4 20159.2 2002 26947.9 24430.3 2003 36287.9 34195.6 2004 49103.3 46435.8 2005 62648.1 54273.7 2006 77594.6 63376.9 2007 93455.6 73284.6 2008 100394.9 79526.5 run; proc gplot; plot x*t=1 y*t=2/overlay; symbol1c=black i=join v=none; symbol2c=red i=join v=none w=2l=2; run; proc arima data=example6_4; identify var=x stationarity=(adf=1); identify var=y stationarity=(adf=1); run; proc arima; identify var=y crrosscorr=x; estimate methed=ml input=x plot; forecast lead=0id=t out=out; proc aima data=out; identify varresidual stationarity=(adf=2); run;
青海民族大学 毕业论文 论文题目:时间序列分析方法及应用—以青海省GDP 增长为例研究 学生姓名:学号: 指导教师:职称: 院系:数学与统计学院 专业班级:统计学 二○一五年月日
时间序列分析方法及应用——以青海省GDP增长为例研究 摘要: 人们的一切活动,其根本目的无不在于认识和改造世界,让自己的生活过得更理想。时间序列是指同一空间、不同时间点上某一现象的相同统计指标的不同数值,按时间先后顺序形成的一组动态序列。时间序列分析则是指通过时间序列的历史数据,揭示现象随时间变化的规律,并基于这种规律,对未来此现象做较为有效的延伸及预测。时间序列分析不仅可以从数量上揭示某一现象的发展变化规律或从动态的角度刻画某一现象与其他现象之间的内在数量关系及其变化规律性,达到认识客观世界的目的。而且运用时间序列模型还可以预测和控制现象的未来行为,由于时间序列数据之间的相关关系(即历史数据对未来的发展有一定的影响),修正或重新设计系统以达到利用和改造客观的目的。从统计学的内容来看,统计所研究和处理的是一批有“实际背景”的数据,尽管数据的背景和类型各不相同,但从数据的形成来看,无非是横截面数据和纵截面数据两类。本论文主要研究纵截面数据,它反映的是现象以及现象之间的关系发展变化规律性。在取得一组观测数据之后,首先要判断它的平稳性,通过平稳性检验,可以把时间序列分为平稳序列和非平稳序列两大类。主要采用的统计方法是时间序列分析,主要运用的数学软件为Eviews软件。大学四年在青海省上学,基于此,对青海省的GDP十分关注。本论文关于对1978年到2014年以来的中国的青海省GDP(总共37个数据)进行时间序列分析,并且对未来的三年中国的青海省GDP进行较为有效的预测。希望对青海省的发展有所贡献。 关键词: 青海省GDP 时间序列白噪声预测
时间序列预测模型时间序列是指把某一变量在不同时间上的数值按时间先后顺序排列起来所形成的序列,它的时间单位可以是分、时、日、周、旬、月、季、年等。时间序列模型就是利用时间序列建立的数学模型,它主要被用来对未来进行短期预测,属于趋势预测法。一、简单一次移动平均预测法例1.某企业1月~11月的销售收入时间序列如下表所示.取n 4,试用简单一次移动平均法预测第12月的销售收入,并计算预测的标准误差. 二、加权一次移动平均预测法简单一次移动平均预测法,是把参与平均的数据在预测中所起的作用同等对待,但参与平均的各期数据所起的作用往往是不同的。为此,需要采用加权移动平均法进行预测,加权一次移动平均预测法是其中比较简单的一种。三、指数平滑预测法 1、一次指数平滑预测法一元线性回归模型 * 项数n的数值,要根据时间序列的特点而定,不宜过大或过小.n过大会降低移动平均数的敏感性,影响预测的准确性;n过小,移动平均数易受随机变动的影响,难以反映实际趋势.一般取n的大小能包含季节变动和周期变动的时期为好,这样可消除它们的影响.对于没有季节变动和周期变动的时间序列,项数n的取值可取较大的数;如果历史数据的类型呈上升或下降型的发展趋势,则项数n的数值应取较小的数,这样能取得较好的预测效果. 1102.7 1015.1 963.9 892.7 816.4 772.0 705.1 649.8 606.9 574.6 533.8 销售收入 11 10 9 8 7 6 5 4 3 2 1 月份 t 158542.7 993.6 12 12950.4 19016.4 17662.4 24617.6 27989.3
基于ARMA模型的社会融资规模增长分析 ————ARMA模型实验
第一部分实验分析目的及方法 一般说来,若时间序列满足平稳随机过程的性质,则可用经典的ARMA模型进行建模和预则。但是, 由于金融时间序列随机波动较大,很少满足ARMA模型的适用条件,无法直接采用该模型进行处理。通过对数化及差分处理后,将原本非平稳的序列处理为近似平稳的序列,可以采用ARMA模型进行建模和分析。 第二部分实验数据 2.1数据来源 数据来源于中经网统计数据库。具体数据见附录表5.1 。 2.2所选数据变量 社会融资规模指一定时期(每月、每季或每年)实体经济从金融体系获得的全部资金总额,为一增量概念,即期末余额减去期初余额的差额,或当期发行或发生额扣除当期兑付或偿还额的差额。社会融资规模作为重要的宏观监测指标,由实体经济需求所决定,反映金融体系对实体经济的资金量支持。 本实验拟选取2005年11月到2014年9月我国以月为单位的社会融资规模的数据来构建ARMA模型,并利用该模型进行分析预测。 第三部分 ARMA模型构建 3.1判断序列的平稳性 首先绘制出M的折线图,结果如下图:
图3.1 社会融资规模M曲线图 从图中可以看出,社会融资规模M序列具有一定的趋势性,由此可以初步判断该序列是非平稳的。此外,m在每年同时期出现相同的变动趋势,表明m还存在季节特征。下面对m的平稳性和季节性·进行进一步检验。 为了减少m的变动趋势以及异方差性,先对m进行对数化处理,记为lm,其时序图如下: 图3.2 lm曲线图
对数化后的趋势性减弱,但仍存在一定的趋势性,下面观察lm的自相关图 表3.1 lm的自相关图 上表可以看出,该lm序列的PACF只在滞后一期、二期和三期是显著的,ACF随着滞后结束的增加慢慢衰减至0,由此可以看出该序列表现出一定的平稳性。进一步进行单位根检验,由于存在较弱的趋势性且均值不为零,选择存在趋势项的形式,并根据AIC自动选择之后结束,单位根检验结果如下: 表3.2 单位根输出结果 Null Hypothesis: LM has a unit root Exogenous: Constant, Linear Trend Lag Length: 0 (Automatic - based on SIC, maxlag=12) t-Statistic Prob.*
实验1典型时间序列模型分析 1、实验目的 熟悉三种典型的时间序列模型: AR 模型,MA 模型与ARMA 模型,学会运用Matlab 工具对 对上述三种模型进行统计特性分析,通过对2阶模型的仿真分析,探讨几种模型的适用范围, 并且通过实验分析理论分析与实验结果之间的差异。 2、实验原理 AR 模型分析: 设有AR(2)模型, X( n)=-0.3X( n-1)-0.5X( n-2)+W( n) 其中:W(n)是零均值正态白噪声,方差为 4。 (1 )用MATLAB 模拟产生X(n)的500观测点的样本函数,并绘出波形 (2) 用产生的500个观测点估计X(n)的均值和方差 (3) 画出理论的功率谱 (4) 估计X(n)的相关函数和功率谱 【分析】给定二阶的 AR 过程,可以用递推公式得出最终的输出序列。或者按照一个白噪声 通过线性系统的方式得到,这个系统的传递函数为: 这是一个全极点的滤波器,具有无限长的冲激响应。 对于功率谱,可以这样得到, 可以看出, FX w 完全由两个极点位置决定。 对于AR 模型的自相关函数,有下面的公式: \(0) 打⑴ 匚⑴… ^(0) ■ 1' G 2 W 0 JAP) 人9-1)… 凉0) _ 这称为Yule-Walker 方程,当相关长度大于 p 时,由递推式求出: r (r) + -1) + -■ + (7r - JJ )= 0 这样,就可以求出理论的 AR 模型的自相关序列。 H(z) 二 1 1 0.3z , P x w +W 1 1 a 才 a 2z^
1. 产生样本函数,并画出波形 2. 题目中的AR过程相当于一个零均值正态白噪声通过线性系统后的输出,可以按照上面的方法进行描述。 clear all; b=[1]; a=[1 0.3 0.5]; % 由描述的差分方程,得到系统传递函数 h=impz(b,a,20); % 得到系统的单位冲激函数,在20点处已经可以认为值是0 randn('state',0); w=normrnd(0,2,1,500); % 产生题设的白噪声随机序列,标准差为 2 x=filter(b,a,w); % 通过线形系统,得到输出就是题目中要求的2阶AR过程 plot(x,'r'); ylabel('x(n)'); title(' 邹先雄——产生的AR随机序列'); grid on; 得到的输出序列波形为: 邹先雄——产生的AR随机序列 2. 估计均值和方差 可以首先计算出理论输出的均值和方差,得到m x =0 ,对于方差可以先求出理论自相 关输出,然后取零点的值。
Lecture 6 6. Time series analysis: Multivariate models 6.1Learning outcomes ?Vector autoregression (VAR) ?Cointegration ?Vector error correction model (VECM) ?Application: pairs trading 6.2Vector autoregression (VAR)向量自回归 The classical linear regression model assumes strict exogeneity; hence, there is no serial correlation between error terms and any realisation of any independent variable (lead or lag). As we discovered, serial correlation (or autocorrelation) is very common in financial time series and panel data. Furthermore, we assumed a pre-defined relation of causality: explanatory variable affect the dependent variable? 传统的线性回归模型假设严格的外主性,误差项与可实现的独立变量之间没有序列相关性。金融时间序列及面板数据往往都有很强的自相关性,假定解释变量影响因变量。 We now relax bo什]assumptions using a VAR model. VAR models can be regarded as a generalisation of AR(p) processes by adding additional time series. Hence, we enter the field of multivariate time series analysis. VAR模型可以'"l作是在一般的自回归过程中加入时间序列。 Lefs look at a standard AR(p) process for hvo variables (y( and xj? (1)%= Ql + 琅]仇『一 +仏 (2)x t = a2 + - + £2t The next step is to allow that lagged values of xt can affect y( and vice versa. This means that we obtain a system of equations for two dependent variables(y(and xj?Both dependent variables are influenced by past realisations of y(and x t. By doing that, we violate strict exogeneity (see Lecture 2); however, we can use a more relaxed concept, namely weak exogeneity?As we use lagged values of bodi dependent variables, we can argue that these lagged values are known to us, as we observed them in the previous period? We call these variables predetermined? Predetermined (lagged) variables fulfil weak exogeneity in the sense that they have to be uncorrelated with the contemporaneoiis error term in t? We can still use OLS to estimate the following system of equations, which is called a VAR in reduced form. (3)+y 仇1化_丫+sr=i ^12 +£it (4)X t = a2+2X1021”—, + _i + f2t
【时间简“识”】 说明:本文摘自于经管之家(原人大经济论坛) 作者:胖胖小龟宝。原版请到经管之家(原人大经济论坛) 查看。 1.带你看看时间序列的简史 现在前面的话—— 时间序列作为一门统计学,经济学相结合的学科,在我们论坛,特别是五区计量经济学中是热门讨论话题。本月楼主推出新的系列专题——时间简“识”,旨在对时间序列方面进行知识扫盲(扫盲,仅仅扫盲而已……),同时也想借此吸引一些专业人士能够协助讨论和帮助大家解疑答惑。 在统计学的必修课里,时间序列估计是遭吐槽的重点科目了,其理论性强,虽然应用领域十分广泛,但往往在实际操作中会遇到很多“令人发指”的问题。所以本帖就从基础开始,为大家絮叨絮叨那些关于“时间”的故事! Long long ago,有多long估计大概7000年前吧,古埃及人把尼罗河涨落的情况逐天记录下来,这一记录也就被我们称作所谓的时间序列。记录这个河流涨落有什么意义当时的人们并不是随手一记,而是对这个时间序列进行了长期的观察。结果,他们发现尼罗河的涨落非常有规律。掌握了尼罗河泛滥的规律,这帮助了古埃及对农耕和居所有了规划,使农业迅速发展,从而创建了埃及灿烂的史前文明。
好~~从上面那个故事我们看到了 1、时间序列的定义——按照时间的顺序把随机事件变化发展的过程记录下来就构成了一个时间序列。 2、时间序列分析的定义——对时间序列进行观察、研究,找寻它变化发展的规律,预测它将来的走势就是时间序列分析。 既然有了序列,那怎么拿来分析呢 时间序列分析方法分为描述性时序分析和统计时序分析。 1、描述性时序分析——通过直观的数据比较或绘图观测,寻找序列中蕴含的发展规律,这种分析方法就称为描述性时序分析 描述性时序分析方法具有操作简单、直观有效的特点,它通常是人们进行统计时序分析的第一步。 2、统计时序分析 (1)频域分析方法 原理:假设任何一种无趋势的时间序列都可以分解成若干不同频率的周期波动 发展过程: 1)早期的频域分析方法借助富里埃分析从频率的角度揭示时间序列的规律 2)后来借助了傅里叶变换,用正弦、余弦项之和来逼近某个函数 3)20世纪60年代,引入最大熵谱估计理论,进入现代谱分析阶段 特点:非常有用的动态数据分析方法,但是由于分析方法复杂,结果抽象,有一定的使用局限性 (2)时域分析方法
时间序列分析法原理及步骤 ----目标变量随决策变量随时间序列变化系统 一、认识时间序列变动特征 认识时间序列所具有的变动特征, 以便在系统预测时选择采用不同的方法 1》随机性:均匀分布、无规则分布,可能符合某统计分布(用因变量的散点图和直方图及其包含的正态分布检验随机性, 大多服从正态分布 2》平稳性:样本序列的自相关函数在某一固定水平线附近摆动, 即方差和数学期望稳定为常数 识别序列特征可利用函数 ACF :其中是的 k 阶自 协方差,且 平稳过程的自相关系数和偏自相关系数都会以某种方式衰减趋于 0, 前者测度当前序列与先前序列之间简单和常规的相关程度, 后者是在控制其它先前序列的影响后,测度当前序列与某一先前序列之间的相关程度。实际上, 预测模型大都难以满足这些条件, 现实的经济、金融、商业等序列都是非稳定的,但通过数据处理可以变换为平稳的。 二、选择模型形式和参数检验 1》自回归 AR(p模型
模型意义仅通过时间序列变量的自身历史观测值来反映有关因素对预测目标的影响和作用,不受模型变量互相独立的假设条件约束,所构成的模型可以消除普通回归预测方法中由于自变量选择、多重共线性的比你更造成的困难用 PACF 函数判别 (从 p 阶开始的所有偏自相关系数均为 0 2》移动平均 MA(q模型 识别条件
平稳时间序列的偏相关系数和自相关系数均不截尾,但较快收敛到 0, 则该时间序列可能是 ARMA(p,q模型。实际问题中,多数要用此模型。因此建模解模的主要工作时求解 p,q 和φ、θ的值,检验和的值。 模型阶数 实际应用中 p,q 一般不超过 2. 3》自回归综合移动平均 ARIMA(p,d,q模型 模型含义 模型形式类似 ARMA(p,q模型, 但数据必须经过特殊处理。特别当线性时间序列非平稳时,不能直接利用 ARMA(p,q模型,但可以利用有限阶差分使非平稳时间序列平稳化,实际应用中 d (差分次数一般不超过 2. 模型识别 平稳时间序列的偏相关系数和自相关系数均不截尾,且缓慢衰减收敛,则该时间序列可能是 ARIMA(p,d,q模型。若时间序列存在周期性波动, 则可按时间周期进
季节性时间序列分析方 法 LG GROUP system office room 【LGA16H-LGYY-LGUA8Q8-LGA162】
第七章季节性时间序列分析方法 由于季节性时间序列在经济生活中大量存在,故将季节时间序列从非平稳序列中抽出来,单独作为一章加以研究,具有较强的现实意义。本章共分四节:简单随机时间序列模型、乘积季节模型、季节型时间序列模型的建立、季节调整方法X-11程序。 本章的学习重点是季节模型的一般形式和建模。 §1 简单随机时序模型 在许多实际问题中,经济时间序列的变化包含很多明显的周期性规律。比如:建筑施工在冬季的月份当中将减少,旅游人数将在夏季达到高峰,等等,这种规律是由于季节性(seasonality)变化或周期性变化所引起的。对于这各时间数列我们可以说,变量同它上一年同一月(季度,周等)的值的关系可能比它同前一月的值的相关更密切。 一、季节性时间序列 1.含义:在一个序列中,若经过S个时间间隔后呈现出相似性,我们说该序列具有以S为周期的周期性特性。具有周期特性的序列就称为季节性时间序列,这里S为周期长度。 注:①在经济领域中,季节性的数据几乎无处不在,在许多场合,我们往往可以从直观的背景及物理变化规律得知季节性的周期,如季度数据(周期为4)、月度数据(周期为12)、周数据(周期为7);②有的时间序列也可能包含长度不同的若干种周期,如客运量数据(S=12,S=7) 2.处理办法: (1)建立组合模型; (1)将原序列分解成S个子序列(Buys-Ballot 1847)
对于这样每一个子序列都可以给它拟合ARIMA 模型,同时认为各个序列之间是相互独立的。但是这种做法不可取,原因有二:(1)S 个子序列事实上并不相互独立,硬性划分这样的子序列不能反映序列{}t x 的总体特征;(2)子序列的划分要求原序列的样本足够大。 启发意义:如果把每一时刻的观察值与上年同期相应的观察值相减,是否能将原序列的周期性变化消除( 或实现平稳化),在经济上,就是考查与前期相比的净增值,用数学语言来描述就是定义季节差分算子。 定义:季节差分可以表示为S t t t S t S t X X X B X W --=-=?=)1(。 二、 随机季节模型 1.含义:随机季节模型,是对季节性随机序列中不同周期的同一周期点之间的相关关系的一种拟合。 AR (1):t t S t S t t e W B e W W =-?+=-)1(11??,可以还原为:t t S S e X B =?-)1(1?。 MA (1):t S t S t t t e B W e e W )1(11θθ-=?-=-,可以还原为:t S t S e B X )1(1θ-=?。 2.形式:广而言之,季节型模型的ARMA 表达形式为 t S t S e B V W B U )()(= (1) 这里,?? ? ??----=----=?=qS q S S S pS P S S S t d S t B V B V B V B V B U B U B U B U X W 2212211)(1)()(平稳。 注:(1)残差t e 的内容;(2)残差t e 的性质。 §2 乘积季节模型 一、 乘积季节模型的一般形式 由于t e 不独立,不妨设),,(~m d n ARIMA e t ,则有
Eviews时间序列分析实例 时间序列是市场预测中经常涉及的一类数据形式,本书第七章对它进行了比较详细的介绍。通过第七章的学习,读者了解了什么是时间序列,并接触到有关时间序列分析方法的原理和一些分析实例。本节的主要内容是说明如何使用Eviews软件进行分析。 一、指数平滑法实例 所谓指数平滑实际就是对历史数据的加权平均。它可以用于任何一种没有明显函数规律,但确实存在某种前后关联的时间序列的短期预测。由于其他很多分析方法都不具有这种特点,指数平滑法在时间序列预测中仍然占据着相当重要的位置。 (-)一次指数平滑 一次指数平滑又称单指数平滑。它最突出的优点是方法非常简单,甚至只要样本末期的平滑值,就可以得到预测结果。 一次指数平滑的特点是:能够跟踪数据变化。这一特点所有指数都具有。预测过程中添加最新的样本数据后,新数据应取代老数据的地位,老数据会逐渐居于次要的地位,直至被淘汰。这样,预测值总是反映最新的数据结构。 一次指数平滑有局限性。第一,预测值不能反映趋势变动、季节波动等有规律的变动;第二,这种方法多适用于短期预测,而不适合作中长期的预测;第三,由于预测值是历史数据的均值,因此与实际序列的变化相比有滞后现象。 指数平滑预测是否理想,很大程度上取决于平滑系数。Eviews提供两种确定指数平滑系数的方法:自动给定和人工确定。选择自动给定,系统将按照预测误差平方和最小原则自动确定系数。如果系数接近1,说明该序列近似纯随机序列,这时最新的观测值就是最理想的预测值。 出于预测的考虑,有时系统给定的系数不是很理想,用户需要自己指定平滑系数值。平滑系数取什么值比较合适呢?一般来说,如果序列变化比较平缓,平滑系数值应该比较小,比如小于0.l;如果序列变化比较剧烈,平滑系数值可以取得大一些,如0.3~0.5。若平滑系数值大于0.5才能跟上序列的变化,表明序列有很强的趋势,不能采用一次指数平滑进行预测。 [例1]某企业食盐销售量预测。现在拥有最近连续30个月份的历史资料(见表l),试预测下一月份销售量。 表1 某企业食盐销售量单位:吨 解:使用Eviews对数据进行分析,第一步是建立工作文件和录入数据。有关操作在本
现代时间序列分析模型§1 时间序列平稳性和单位根检验§2 协整与误差修正模型经典时间序列分析模型: MA、AR、ARMA 平稳时间序列模型分析时间序列自身的变化规律现代时间序列分析模型:分析时间序列之间的关系单位根检验、协整检验现代宏观计量经济学§1 时间序列平稳性和单位根检验一、时间序列的平稳性二、单整序列三、单位根检验一、时间序列的平稳性 Stationary Time Series ⒈问题的提出经典计量经济模型常用到的数据有:时间序列数据(time-series data ;截面数据cross-sectional data 平行/面板数据(panel data/time-series cross-section data 时间序列数据是最常见,也是最常用到的数据。经典回归分析暗含着一个重要假设:数据是平稳的。数据非平稳,大样本下的统计推断基础――“一致性”要求――被破怀。数据非平稳,往往导致出现“虚假回归”(Spurious Regression)问题。表现为两个本来没有任何因果关系的变量,却有很高的相关性。例如:如果有两列时间序列数据表现出一致的变化趋势(非平稳的),即使它们没有任何有意义的关系,但进行回归也可表现出较高的可决系数。 2、平稳性的定义假定某个时间序列是由某一随机过程(stochastic process)生成的,即假定时间序列 Xt (t 1, 2, …)的每一个数值都是从一个概率分布中随机得到,如果满足下列条件:均值E Xt ?是与时间t 无关的常数;方差Var Xt ?2是与时间t 无关的常数;协方差Cov Xt,Xt+k ?k 是只与时期间隔k有关,与时间t 无关的常数;则称该随机时间序列是平稳的(stationary ,
基于Excel的时间序列预测与分析 1 时序分析方法简介 1.1时间序列相关概念 1.1.1 时间序列的内涵以及组成因素 所谓时间序列就是将某一指标在不同时间上的不同数值,按照时间的先后顺序排列而成的数列。如经济领域中每年的产值、国民收入、商品在市场上的销量、股票数据的变化情况等,社会领域中某一地区的人口数、医院患者人数、铁路客流量等,自然领域的太阳黑子数、月降水量、河流流量等等,都形成了一个时间序列。人们希望通过对这些时间序列的分析,从中发现和揭示现象的发展变化规律,或从动态的角度描述某一现象和其他现象之间的内在数量关系及其变化规律,从而尽可能多的从中提取出所需要的准确信息,并将这些知识和信息用于预测,以掌握和控制未来行为。 时间序列的变化受许多因素的影响 ,有些起着长期的、决定性的作用 ,使其呈现出某种趋势和一定的规律性;有些则起着短期的、非决定性的作用,使其呈现出某种不规则性。在分析时间序列的变动规律时,事实上不可能对每个影响因素都一一划分开来,分别去作精确分析。但我们能将众多影响因素,按照对现象变化影响的类型,划分成若干时间序列的构成因素,然后对这几类构成要素分别进行分析,以揭示时间序列的变动规律性。影响时间序列的构成因素可归纳为以下四种: (1)趋势性(Trend),指现象随时间推移朝着一定方向呈现出持续渐进地上升、下降或平稳的变化或移动。这一变化通常是许多长期因素的结果。 (2)周期性(Cyclic),指时间序列表现为循环于趋势线上方和下方的点序列并持续一年以上的有规则变动。这种因素是因经济多年的周期性变动产生的。比如,高速通货膨胀时期后面紧接的温和通货膨胀时期将会使许多时间序列表现为交替地出现于一条总体递增 地趋势线上下方。 (3)季节性变化(Seasonal variation),指现象受季节性影响 ,按一固定周期呈现出的周期波动变化。尽管我们通常将一个时间序列中的季节变化认为是以1年为期的,但是季节因素还可以被用于表示时间长度小于1年的有规则重复形态。比如,每日交通量数据表现出为期1天的“季节性”变化,即高峰期到达高峰水平,而一天的其他时期车流量较小,从午夜到次日清晨最小。
第六节时间序列模型的建立与预测 ARIMA过程y t用 Φ (L) (Δd y t)= α+Θ(L) u t 表示,其中Φ (L)和Θ (L)分别是p, q阶的以L为变数的多项式,它们的根都在单位圆之外。α为Δd y t过程的漂移项,Δd y t表示对y t 进行d次差分之后可以表达为一个平稳的可逆的ARMA 过程。这是随机过程的一般表达式。它既包括了AR,MA 和ARMA过程,也包括了单整的AR,MA和ARMA过程。 可取 图建立时间序列模型程序图 建立时间序列模型通常包括三个步骤。(1)模型的识别,(2)模型参数的估计,(3)诊断与检验。
模型的识别就是通过对相关图的分析,初步确定适合于给定样本的ARIMA模型形式,即确定d, p, q的取值。 模型参数估计就是待初步确定模型形式后对模型参数进行估计。样本容量应该50以上。 诊断与检验就是以样本为基础检验拟合的模型,以求发现某些不妥之处。如果模型的某些参数估计值不能通过显著性检验,或者残差序列不能近似为一个白噪声过程,应返回第一步再次对模型进行识别。如果上述两个问题都不存在,就可接受所建立的模型。建摸过程用上图表示。下面对建摸过程做详细论述。 1、模型的识别 模型的识别主要依赖于对相关图与偏相关图的分析。在对经济时间序列进行分析之前,首先应对样本数据取对数,目的是消除数据中可能存在的异方差,然后分析其相关图。 识别的第1步是判断随机过程是否平稳。由前面知识可知,如果一个随机过程是平稳的,其特征方程的根都应在单位圆之外;如果 (L) = 0的根接近单位圆,自相关函数将衰减的很慢。所以在分析相关图时,如果发现其衰减很慢,即可认为该时间序列是非平稳的。这时应对该时间序列进行差分,同时分析差分序列的相关图以判断差分序列的平稳性,直至得到一个平稳的序列。对于经济时间序列,差分次数d通常只取0,1或2。 实际中也要防止过度差分。一般来说平稳序列差分得到的仍然是平稳序列,但当差分次数过多时存在两个缺点,(1)序列的样本容量减小;(2)方差变大;所以建模过程中要防止差分过度。对于一个序列,差分后若数据的极差变大,说明差分过度。 第2步是在平稳时间序列基础上识别ARMA模型阶数p, q。表1给出了不同ARMA模型的自相关函数和偏自相关函数。当然一个过程的自相关函数和偏自相关函数通常是未知的。用样本得到的只是估计的自相关函数和偏自相关函数,即相关图和偏相关图。建立ARMA模型,时间序列的相关图与偏相关图可为识别模型参数p, q提供信息。相关图和偏相关图(估计的自相关系数和偏自相关系数)通常比真实的自相关系数和偏自相关系数的方差要大,并表现为更高的自相关。实际中相关图,偏相关图的特征不会像自相关函数与偏自相关函数那样“规范”,所以应该善于从相关图,偏相关图中识别出模型的真实参数p, q。另外,估计的模型形式不是唯一的,所以在模型识别阶段应多选择几种模型形式,以供进一步选择。
第 39卷 第 2期 2007年 4月 西 安 建 筑 科 技 大 学 ( 学 报 ( 自然科学版) ) V ol.39 No.2 Apr . 2007 J 1Xi ’an Univ . of Arch . & Tech . Natural Scie nce Editio n 多因素时间序列的灰色预测模型 苏变萍 ,曹艳平 ,王 婷 (西安建筑科技大学理学院 ,陕西 西安 710055) 摘 要:对于传统的单因素时间序列预测法在实际应用中的不足之处 ,提出采用灰色 DGM (1 ,1) 模型和多元 线性回归原理相结合的方法 ,综合各种因素建立多因素时间序列的灰色预测模型。它首先利用 DGM (1 ,1) 模 型对影响事物发展趋势的各项因素进行预测 ;然后利用多元线性回归法将各种因素综合起来 ,以预测事物的 发展趋势。最后将该模型应用于预测分析陕西省的就业状况 ,取得了较好的预测效果 ,同时也验证了此模型 的可行性。 关键词: 时间序列 ;单因素 ;多因素 ;预测模型 中图分类号:TB114 文献标识码:A 文章编号 :100627930 2007 022******* ( ) 多年以来 ,对时间序列的预测研究 ,大多是停留在对单因素时间序列上 ,对其预测通常采用的是趋 势外推法 ,而且该方法适合于原始时间序列规律性较好的情况 ,若时间序列中包含了随机因素的影 响 ,再采用这种方法得出的预测结果可能会失真. 同时 ,客观世界又是复杂多变的 ,事物的发展通常不 是由某个单个因素决定 ,往往是许多错综复杂的因素综合作用的结果 ,为了对某项事物的发展做出更加 符合实际的预测 ,这就需要来探讨多因素时间序列的预测问题 ,正是基于这些 ,本文在应用灰色 D GM (1 ,1)模型对单因素时间序列预测的基础上 ,结合多元回归原理 ,提出建立多因素时间序列的灰色预测 模型 ,这样就充分发挥了二者的优点 ,既克服了时间序列的随机因素影响 ,又综合考虑了影响事物发展 的多种因素 ,从而达到提高预测精度和增加预测结果可靠性的效果. 1 模型的建立 设 Y = (y (1) , y (2) , …, y( n)) 表示事物发展的特征因素时间序列, X i = (x i (1) , x i (2) , …, x i ( n)) (i = 1 ,2 , …, p) 表示影响事物发展的单因素时间序列. 1.1 单因素时间序列的 DGM(1 ,1) 模型 对于单因素原始时间序列{ X i } (i = 1 ,2 , …, p) ,根据灰色系统理论建模方法 ,得 D GM (1 ,1) 模 型 : x i (1) a (1 - a) + a b ,t > 1 1.2 多因素时间序列的预测模型 为了能将影响事物发展的众多因素结合起来进行综合预测和相关因素的预测分析 ,在经过多次研 究与比较后,采用多元回归的原理建立多因素时间序列的灰色预测模型: y t = a 0 + a 1 x 1 t + a 2 x 2 t + …+ a p x p t 2 式中 y t 为该事物在 t 时刻的预测值;x i t i = 1 ,2 , …, p 为第 i 个单因素 ,通过应用上述的灰色 3收稿日期 :2005201209 修改稿日期:2006204212 基金项目 :陕西省教育厅专项基金项目 01J K133( ) 作者简介 :苏变萍 19632( ) ,女 ,山西忻州人 ,副教授 ,博士研究生 ,研究方向为计量经济学. [122] (0) (0) (0) ( ) ( ) [4] (0) x (1) = x (1) ^ x (t) = (1) ( ) ^ ^ ^ ^ ^ ^
传统的经济计量方法是以经济理论为基础来描述变量关系的模型。但是,经济理论通常并不足以对变量之间的动态联系提供一个严密的说明,而且内生变量既可以出现在方程的左端又可以出现在方程的右端使得估计和推断变得更加复杂。为了解决这些问题而出现了一种用非结构性方法来建立各个变量之间关系的模型。本章所要介绍的向量自回归模型(vector autoregression ,VAR)和向量误差修正模型(vector error correction model ,VEC)就是非结构化的多方程模型。 向量自回归(VAR)是基于数据的统计性质建立模型,VAR 模型把系统中每一个内生变量作为系统中所有内生变量的滞后值的函数来构造模型,从而将单变量自回归模型推广到由多元时间序列变量组成的“向量”自回归模型。VAR 模型是处理多个相关经济指标的分析与预测最容易操作的模型之一,并且在一定的条件下,多元MA 和ARMA 模型也可转化成VAR 模型,因此近年来VAR 模型受到越来越多的经济工作者的重视。 VAR(p ) 模型的数学表达式是 t=1,2,…..,T 其中:yt 是 k 维内生变量列向量,xt 是d 维外生变量列向量,p 是滞后阶数,T 是样本个数。k ?k 维矩阵Φ1,…, Φp 和k ?d 维矩阵H 是待估计的系数矩阵。εt 是 k 维扰动列向量,它们相互之间可以同期相关,但不与自己的滞后值相关且不与等式右边的变量相关,假设 ∑ 是εt 的协方差矩阵,是一个(k ?k )的正定矩阵。 11t t p t p t t --=+???+++y Φy Φy Hx ε
注意,由于任何序列相关都可以通过增加更多的yt 的滞后而被消除,所以扰动项序列不相关的假设并不要求非常严格。 以1952一1991年对数的中国进、出口贸易总额序列为例介绍VAR 模型分析,其中包括;① VAR 模型估计;②VAR 模型滞后期的选择;③ VAR 模型平隐性检验;④VAR 模型预侧;⑤协整性检验 VAR 模型佑计 数据 εε εε
第二篇 预测方法与模型 预测是研究客观事物未来发展方向与趋势的一门科学。统计预测是以统计调查资料为依据,以经济、社会、科学技术理论为基础,以数学模型为主要手段,对客观事物未来发展所作的定量推断和估计。根据社会、经济、科技的预测结论,人们可以调整发展战略,制定管理措施,平衡市场供求,进行各种各样的决策。预测也是制定政策,编制规划、计划,具体组织生产经营活动的科学基础。20世纪三四十年代以来,随着人类社会生产力水平的不断提高和科学技术的迅猛发展,特别是近年来以计算机为主的信息技术的飞速发展,更进一步推动了预测技术在国民经济、社会发展和科学技术各个领域的应用。 预测包含定性预测法、因果关系预测法和时间序列预测法三类。本篇对定性预测法不加以介绍,对后两类方法选择以下几种介绍方法的原理、模型的建立和实际应用,分别为:时间序列分析、微分方程模型、灰色预测模型、人工神经网络。 第五章 时间序列分析 在预测实践中,预测者们发现和总结了许多行之有效的预测理论和方法,但以概率统计理论为基础的预测方法目前仍然是最基本和最常用的方法。本章介绍其中的时间序列分析预测法。此方法是根据预测对象过去的统计数据找到其随时间变化的规律,建立时间序列模型,以推断未来数值的预测方法。时间序列分析在微观经济计量模型、宏观经济计量模型以及经济控制论中有广泛的应用。 第一节 时间序列简介 所谓时间序列是指将同一现象在不同时间的观测值,按时间先后顺序排列所形成的数列。时间序列一般用 ,,,,21n y y y 来表示,可以简记为}{t y 。它的时间单位可以是分钟、时、日、周、旬、月、季、年等。
一、时间序列预测法 时间序列预测法就是通过编制和分析时间序列,根据时间序列所反应出来的发展过程、方向和趋势,进行类推或延伸,借以预测下一段时间或以后若干年可能达到的水平。其容包括:收集与整理某种社会现象的历史资料;将这些资料进行检查鉴别,排成数列;分析时间序列,从中寻找该社会现象随时间变化而变化的规律,得出一定的模型,以此模型去预测该社会现象将来的情况。 二、时间序列数据的特点 通常,时间序列经过合理的函数变换后都可以看作是由三个部分叠加而成,这三个部分是趋势项部分、周期项部分和随机项部分。 1. 趋势性 许多序列的一个最主要的特征就是存在趋势。这种趋势可能是向下的也可能是向上的,也许比较陡,也许比较平缓,或者是指数增长,或者近似线性。总之,时间序列的趋势性是依据时间序列进行预测的本质所在。 2. 季节性/周期性 当数据按照月或季观测时,通常的情况是这样的:时间序列会呈现出明显的季节性。对季节性也不存在一个非常精确的定义。通常,当某个季节的观测值具有与其它季节的观测值明显不同的特征时,就称之为季节性。 3. 异常观测值 异常观测值指那些严重偏离趋势围的特殊点。异常观测值的出现往往是由于某些不可抗 1958 年自然灾害和1966年左右“文化大革命”对我国经拒的外部条件的影响。如1960 济的影响,造成经济指标陡然下降现象;1992年,我国银行紧缩政策造成的房地产业泡沫破灭,而使得房地产业的经济数据发生突然变化的例子等等。 4. 条件异方差性 所谓条件异方差性,表现出来就是异常数据观测值成群地出现,故也称为“波动积聚性”。由于方差是风险的测度,因此波动存在的积聚性的预测对于评估投资决策是很有用的,对于期权和其它金融衍生产品的买卖决策也是有益的。 5. 非线性 对非线性的最好定义就是“线性以外的一切”。非线性常常表现为“机制转换”(regime witches)或者“状态依赖”(State pendence)。其中状态依赖意味着时间序列的特征依赖于其现时的状态;不同的时刻,其特征不一样。当时间序列的特征在所有的离散状态都不一样时,就成为机制转换特性。 三、时间序列的分类 1. 按研究的对象的多少可分为单变量时间序列和多变量时间序列。 如果所研究的对象是一个变量,如某个国家的国生产总值,即为单变量时间序列。果所研究的对象是多个变量,如按年、月顺序排列的气温、气压、雨量数据,为多变量时间序列。多变量时间序列不仅描述了各个变量的变化规律,而且还表示了各变量间相互依存关系的动态规律性。 2. 按时间的连续性可将时间序列分为离散时间序列和连续时间序列。 如果某一序列中的每一个序列值所对应的时间参数为间断点,则该序列就是一个离散时间序列。如果某一序列中的每个序列值所对应的时间参数为连续函数,则该序列就是一个连续时间序列。 3. 按序列的统计特性可分为平稳时间序列和非平稳时间序列两类。