实验一 典型连续时间信号和离散时间信号
一、实验目的
掌握利用Matlab 画图函数和符号函数显示典型连续时间信号波形、典型时间离散信号、连续时间信号在时域中的自变量变换。
二、实验内容
1、典型连续信号的波形表示(单边指数信号、复指数信号、抽样信号、单位阶
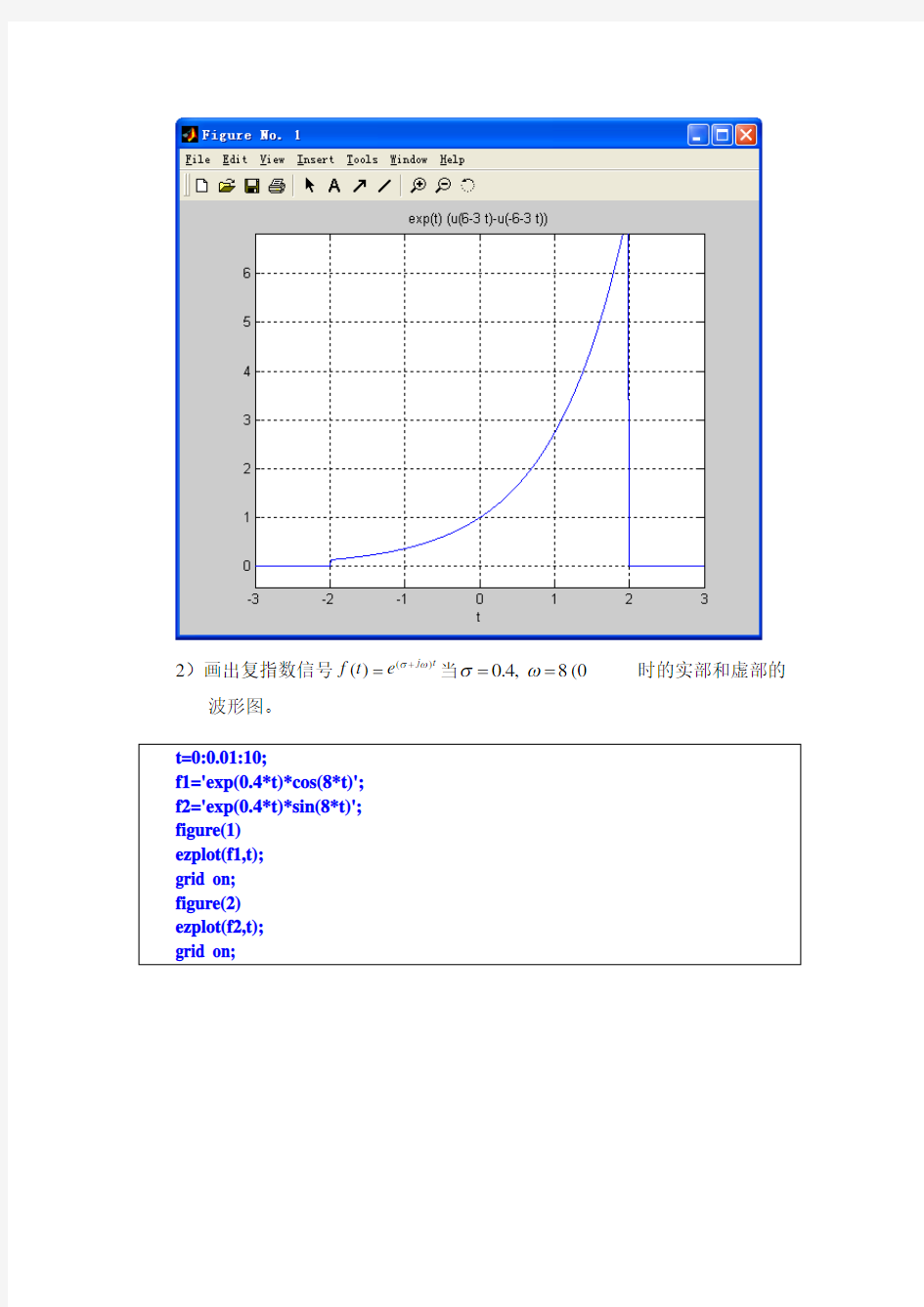
跃信号、单位冲击信号) 1)画出教材P28习题1-1(3) ()[(63)(63)]t f t e u t u t =----的波形图。
2)画出复指数信号()()j t f t e σω+=当0.4, 8σω==(0 波形图。 t=0:0.01:10; f1='exp(0.4*t)*cos(8*t)'; f2='exp(0.4*t)*sin(8*t)'; figure(1) ezplot(f1,t); grid on; figure(2) ezplot(f2,t); grid on; t=-10:0.01:10; f='sin(t)/t'; ezplot(f,t); grid on; t=0:0.01:10; f='(sign(t-3)+1)/2'; ezplot(f,t); grid on; 5)单位冲击信号可看作是宽度为?,幅度为1/?的矩形脉冲,即t=t 1处的冲击信号为 11111 ()()0 t t t x t t t other δ??<<+? ?=-=???? 画出0.2?=, t 1=1的单位冲击信号。 t=0:0.01:2; f='5*(u(t-1)-u(t-1.2))'; ezplot(f,t); grid on; axis([0 2 -1 6]); 2、典型离散信号的表示(单位样值序列、单位阶跃序列、实指数序列、正弦序 列、复指数序列) 编写函数产生下列序列: 1)单位脉冲序列,起点n0,终点n f,在n s处有一单位脉冲。 2)单位阶跃序列,起点n0,终点n f,在n s前序列值为0,在n s后序列值为1。 对于1)、2)小题,最后以参数n0= -10,n f=10,n s= -3为例,画出各自 波形。 、 n0=-10;nf=10;ns=-3;n=n0:nf; x1=[zeros(1,ns-n0),1,zeros(1,nf-ns)]; figure(1); stem(n,x1); title('单位脉冲序列'); x2=[zeros(1,ns-n0),1,ones(1,nf-ns)]; figure(2); stem(n,x2); title('单位阶跃序列'); 3)画出教材P21图1-26,即[][]n x n a u n =当a =1.2, 0.6, -1.5, -0.8的单边指数序 列(-2≤n ≤5)。 n=-2:5; subplot(2,2,1) x1=1.2.^n.*u(n);stem(n,x1); title('1.2^n*u(n)'); subplot(2,2,2) x2=0.6.^n.*u(n);stem(n,x2); title('0.6^n*u(n)'); subplot(2,2,3) x3=(-1.5).^n.*u(n);stem(n,x3); title('(-1.5)^n*u(n)'); subplot(2,2,4) x4=(-0.8).^n.*u(n);stem(n,x4); title('(-0.8)^n*u(n)'); 4)画出教材P21图1-27,即00[]sin(), 7 x n n π =ΩΩ= 的正弦序列(-7≤n ≤14)。 n=-7:14; x=sin(pi/7*n); stem(n,x); title('x[n]=sin(\Omega_0n) 正弦序列'); 5)画出复指数序列/6[]j n x n e π=和3[]j n x n e =的实部和虚部(-50≤n ≤50)。 n=-50:50; figure(1) x1=cos(pi/6*n);stem(n,x1); title('cos(n\pi/6) 实部'); figure(2) x2=sin(pi/6*n);stem(n,x2); title('sin(n\pi/6) 虚部'); figure(3) x3=cos(3*n);stem(n,x3); title('cos(3*n) 实部'); figure(4) x4=sin(3*n);stem(n,x4); title('sin(3*n) 虚部'); 3、信号的自变量变换 1)编写程序(函数),画出教材P10图1-13(a)即f(t)的波形(-6 2)利用1)中建立的函数,通过自变量替换方式依次画出图1-13(b)、(c)、 (d)即f(t+5)、f(-t+5)、f(-2t+5)的波形(-6 syms t; f='u(t)-u(t-2)'+(1+t)*'u(t+1)-u(t)'; subplot(2,2,1);ezplot(f,[-2,3]); axis([-2 3 -0.2 1.2]);title('f(t)');grid on; f1=subs(f,t,t+5); subplot(2,2,2);ezplot(f1,[-7,-2]); axis([-7 -2 -0.2 1.2]);title('f(t+5)');grid on; f2=subs(f,t,-t+5); subplot(2,2,3);ezplot(f2,[2,7]); axis([2 7 -0.2 1.2]);title('f(-t+5)');grid on; f3=subs(f,t,-2*t+5); subplot(2,2,4);ezplot(f3,[-1,4]); axis([-1 4 -0.2 1.2]);title('f(-2t+5)');grid on; 实验二连续和离散时间LTI系统的响应及卷积一、实验目的 掌握利用Matlab工具箱求解连续时间系统的冲激响应、阶跃响应,离散时间系统的单位样值响应,理解卷积概念。 二、实验内容 1、连续时间系统的冲击响应、阶跃响应 a. 利用impulse函数画出教材P44例2-15: LTI系统 () 3()2() dy t y t x t dt +=的冲击 响应的波形。 a=[0 1 3]; b=[0 2]; impulse(b,a); b. 利用step函数画出教材P45例2-17: LTI系统 1 ''()3'()2()'()2()2 y t y t y t x t x t ++=+的阶跃响应的波形。 a=[1 3 2]; b=[0.5 2]; step(b,a); 2、离散时间系统的单位样值响应 利用impz 函数画出教材P48例2-21: []3[1]3[2][3][]y n y n y n y n x n --+---=的单位样值响应的图形。 a=[1 -3 3 -1]; b=[0 1]; impz(b,a); 3、连续时间信号卷积 画出函数f1(t)=(1+t)[u(t)-u(t-1)]和f2(t)=u(t-1)-u(t-2)的图形,并利用附在后面的sconv.m函数画出卷积积分f1(t)* f2(t)图形。 function sconv(f1,f2,k1,k2) f3=conv(f1,f2); ks=k1(1)+k2(1); ke=k1(end)+k2(end); k=length(k1)+length(k2)-1; k3=linspace(ks,ke,k); subplot(2,2,1) plot(k1,f1) title('f1(t)') xlabel('t') ylabel('f1(t)') subplot(2,2,2) plot(k2,f2) title('f2(t)') xlabel('t') ylabel('f2(t)') subplot(2,2,3) plot(k3,f3); h=get(gca,'position'); h(3)=2.5*h(3); set(gca,'position',h) title('f(t)=f1(t)*f2(t)') xlabel('t') ylabel('f(t)') t=-1:0.01:3; f1=(1+t).*(0.5*sign(t)-0.5*sign(t-1)); f2=(0.5*sign(t-1)-0.5*sign(t-2)); sconv(f1,f2,t,t); 4、画出教材P60例2-28中h[n]、x[n]的图形(图2-14(a)(b)),并利用conv函数求出 卷积x[n]*h[n]并画出图形(图2-14(f))。 function dconv(x1,x2,k1,k2) x3=conv(x1,x2); 实验三连续时间周期信号的傅里叶级数 一、实验目的 掌握连续时间周期信号的傅里叶级数的展开和合成,理解吉布斯现象,掌握周期矩形脉冲信号的频谱及脉冲宽度、周期对周期信号频谱的影响。 二、实验内容 1、周期信号的傅里叶级数的展开和合成 画出如下图对称方波(取E=1、T=1),并采用有限项傅里叶级数对原函数进行逼近,画出对称方波的1、3、5、7、9、11次谐波的傅里叶级数合成波形,观察吉布斯现象。 function F_series(m) sum=0; t=-3:0.01:3; E=1;T=1; ta=T/2;w=2*pi/T; for n=1:2*m-1 fn=(2*E*ta/T)*sin(w*ta*n/2)/(w*ta*n/2); f=(E*ta/T)+cos(n*w*t)*fn-E/2; sum=sum+f; end figure(m) plot(t,sum);grid on; title([num2str(2*m-1) '次谐波的傅里叶级数合成波形']); for i=1:6 F_series(i); end 产生离散衰减正弦序列()π0.8sin 4n x n n ?? = ??? , 010n ≤≤,并画出其波形图。 n=0:10; x=sin(pi/4*n).*0.8.^n; stem(n,x);xlabel( 'n' );ylabel( 'x(n)' ); 用MATLAB 生成信号()0sinc at t -, a 和0t 都是实数,410t -<<,画波形图。观察并分析a 和0t 的变化对波形的影响。 t=linspace(-4,7); a=1; t0=2; y=sinc(a*t-t0); plot(t,y); t=linspace(-4,7); a=2; t0=2; y=sinc(a*t-t0); plot(t,y); t=linspace(-4,7); a=1; t0=2; y=sinc(a*t-t0); plot(t,y); 三组对比可得a 越大最大值越小,t0越大图像对称轴越往右移 某频率为f 的正弦波可表示为()()cos 2πa x t ft =,对其进行等间隔抽样,得到的离散样值序列可表示为()()a t nT x n x t ==,其中T 称为抽样间隔,代表相邻样值间的时间间隔,1 s f T = 表示抽样频率,即单位时间内抽取样值的个数。抽样频率取40 Hz s f =,信号频率f 分别取5Hz, 10Hz, 20Hz 和30Hz 。请在同一张图中同时画出连续信号()a x t t 和序列()x n nT 的波形图,并观察和对比分析样值序列的变化。可能用到的函数为plot, stem, hold on 。 fs = 40; t = 0 : 1/fs : 1 ; % ?μ?ê·?±e?a5Hz,10Hz,20Hz,30Hz f1=5; xa = cos(2*pi*f1*t) ; subplot(1, 2, 1) ; 《信号与系统MATLAB实践》第一次上机作业 实验一、熟悉MATLAB基本操作 三、基本序列运算 1.数组的加减乘除和乘方运算 A=[1 2 3]; B=[4 5 6]; C=A+B; D=A-B; E=A.*B; F=A./B; G=A.^B; subplot(2,4,1);stem(A) subplot(2,4,2);stem(B) subplot(2,4,3);stem(C) subplot(2,4,4);stem(D) subplot(2,4,5);stem(E) subplot(2,4,6);stem(F) subplot(2,4,7);stem(G) 2.绘制函数波形 (1)t=0:0.001:10 x=3-exp(-t); plot(t,x) ylabel('f(t)'); xlabel('t'); title('(1)'); (2)t=0:0.001:10 x=5*exp(-t)+3*exp(-2*t); plot(t,x) ylabel('f(t)'); xlabel('t'); title('(2)'); (3)t=0:0.001:3 x=exp(-t).*sin(2*pi*t); plot(t,x) ylabel('f(t)'); xlabel('t'); title('(3)'); (4)t=0:0.001:3 x=sin(3*t)./(3*t); plot(t,x) ylabel('f(t)'); xlabel('t'); title('(4)'); (5)k=1:1:6 x=(-2).^(-k); stem(k) xlabel('k'); ylabel('f(k)'); title('(5)'); 《信号与系统》MATLAB实验报告 院系:专业: 年级:班号: 姓名:学号: 实验时间: 实验地点: 实验一 连续时间信号的表示及可视化 实验题目: )()(t t f δ=;)()(t t f ε=;at e t f =)((分别取00<>a a 及); )()(t R t f =;)()(t Sa t f ω=;)2()(ft Sin t f π=(分别画出不同周期个数 的波形)。 解题分析: 以上各类连续函数,先运用t = t1: p:t2的命令定义时间范围向量,然后调用对应的函数,建立f 与t 的关系,最后调用plot ()函数绘制图像,并用axis ()函数限制其坐标范围。 实验程序: (1) )()(t t f δ= t=-1:0.01:3 %设定时间变量t 的范围及步长 f=dirac(t) %调用冲激函数dirac () plot(t,f) %用plot 函数绘制连续函数 axis([-1,3,-0.5,1.5]) %用axis 函数规定横纵坐标的范围 (2) )()(t t f ε= t=-1:0.01:3 %设定时间变量t 的范围及步长 f=heaviside(t) %调用阶跃函数heaviside () plot(t,f) %用plot 函数绘制连续函数 title('f(t)=heaviside(t)') %用title 函数设置图形的名称 axis([-1,3,-0.5,1.5]) %用axis 函数规定横纵坐标的范围 (3) at e t f =)( a=1时: t=-5:0.01:5 %设定时间变量t 的范围及步长 f=exp(t) %调用指数函数exp () M2-3 (1) function yt=x(t) yt=(t).*(t>=0&t<=2)+2*(t>=2&t<=3)-1*(t>=3&t<=5); (2)function yt=x (t) yt=(t).*(t>=0&t<=2)+2*(t>=2&t<=3)-1*(t>=3&t<=5); t=0:0.001:6; subplot(3,1,1) plot(t,x2_3(t)) title('x(t)') axis([0,6,-2,3]) subplot(3,1,2) plot(t,x2_3(0.5*t)) title('x(0.5t)') axis([0,11,-2,3]) subplot(3,1,3) plot(t,x2_3(2-0.5*t)) title('x(2-0.5t)') axis([-6,5,-2,3]) 图像为: M2-5 (3) function y=un(k) y=(k>=0) untiled3.m k=[-2:10] xk=10*(0.5).^k.*un(k); stem(k,xk) title('x[k]') axis([-3,12,0,11]) M2-5 (6) k=[-10:10] xk=5*(0.8).^k.*cos((0.9)*pi*k) stem(k,xk) title('x[k]') grid on M2-7 A=1; t=-5:0.001:5; w0=6*pi; xt=A*cos(w0*t); plot(t,xt) hold on A=1; k=-5:5; w0=6*pi; xk=A*cos(w0*0.1*k); stem(k,xk) axis([-5.5,5.5,-1.2,1.2]) title('x1=cos(6*pi*t)&x1[k]') 习题三 绘制典型信号及其频谱图 1.更改参数,调试程序,绘制单边指数信号的波形图和频谱图。观察参数a对信号波形 及其频谱的影响。 程序代码: close all; E=1;a=1; t=0:0.01:4; w=-30:0.01:30; f=E*exp(-a*t); F=1./(a+j*w); plot(t,f);xlabel('t');ylabel('f(t)'); figure; plot(w,abs(F));xlabel('\omega');ylabel('|F(\omega)|'; E=1,a=1,波形图频谱图更改参数E=2,a=1; 更改参数a,对信号波形及其频谱的影响。(保持E=2)上图为a=1图像 a=2时 a=4时 随着a的增大,f(t)曲线变得越来越陡,更快的逼近0,而对于频谱图,随着a增大,图像渐渐向两边张开,峰值减小,陡度减小,图像整体变得更加平缓。 2.矩形脉冲信号 程序代码: close all; E=1;tao=1; t=-4:0.1:4; w=-30:0.1:30; f=E*(t>-tao/2&tao/2)+0*(t<=-tao/2&t>=tao/2); F=(2*E./w).*sin(w*tao/2); plot(t,f);xlabel('t');ylabel('f(t)'); figure; plot(w,abs(F));xlabel('\omega');ylabel('|F(\omega)|') ; figure; plot(w,20*log10(abs(F))); xlabel('\omega');ylabel('|F(\omega)| in dB'); figure; plot(w,angle(F));xlabel('\omega');ylabel('\phi(\omega )'); 实验一 名称:连续时间信号分析 姓名:王嘉琦 学号:201300800636 班级:通信二班 一、实验目的 (一)掌握使用Matlab 表示连续时间信号 1、学会运用Matlab 表示常用连续时间信号的方法 2、观察并熟悉常用信号的波形和特性 (二)掌握使用Matlab 进行连续时间信号的相关运算 1、学会运用Matlab 进行连续时间信号的时移、反褶和尺度变换 2、学会运用Matlab 进行连续时间信号微分、积分运算 3、学会运用Matlab 进行连续时间信号相加、相乘运算 4、学会运用Matlab 进行连续时间信号卷积运算 二、实验条件 Matlab 三、实验内容 1、利用Matlab 命令画出下列连续信号的波形图。 (1))4/3t (2cos π+ 代码: k=2;w=3;phi=pi/4; t=0:0.01:3; ft=k*cos(w*t+phi); plot(t,ft),grid on; axis([0,3,-2.2,2.2]) title('余弦信号') (2) )t (u )e 2(t -- 代码: k=-1;a=-1; t=0:0.01:3; ft=2-k*exp(a*t); plot(t,ft),grid on axis([0,3,2,3]) title('指数信号') (3))]2()(u )][t (cos 1[--+t u t π 代码: k=1;w=pi;phi=0; t=0:0.01:2; ft=1+k*cos(w*t+phi); plot(t,ft),grid on; axis([0,3,0,2]) title('余弦信号') 2016-2017学年第一学期 信号与系统实验报告 班级: 姓名: 学号: 成绩: 指导教师: 实验一常见信号的MATLAB 表示及运算 一.实验目的 1.熟悉常见信号的意义、特性及波形 2.学会使用MATLAB 表示信号的方法并绘制信号波形 3. 掌握使用MATLAB 进行信号基本运算的指令 4. 熟悉用MATLAB 实现卷积积分的方法 二.实验原理 信号一般是随时间而变化的某些物理量。按照自变量的取值是否连续,信号分为连续时间信号和离散时间信号,一般用()f t 和()f k 来表示。若对信号进行时域分析,就需要绘制其波形,如果信号比较复杂,则手工绘制波形就变得很困难,且难以精确。MATLAB 强大的图形处理功能及符号运算功能,为实现信号的可视化及其时域分析提供了强有力的工具。 根据MATLAB 的数值计算功能和符号运算功能,在MATLAB 中,信号有两种表示方法,一种是用向量来表示,另一种则是用符号运算的方法。在采用适当的MATLAB 语句表示出信号后,就可以利用MATLAB 中的绘图命令绘制出直观的信号波形了。下面分别介绍连续时间信号和离散时间信号的MATLAB 表示及其波形绘制方法。 1.连续时间信号 所谓连续时间信号,是指其自变量的取值是连续的,并且除了若干不连续的点外,对于一切自变量的取值,信号都有确定的值与之对应。从严格意义上讲,MATLAB 并不能处理连续信号。在MATLAB 中,是用连续信号在等时间间隔点上的样值来近似表示的,当取样时间间隔足够小时,这些离散的样值就能较好地近似出连续信号。在MATLAB 中连续信号可用向量或符号运算功能来表示。 ⑴ 向量表示法 对于连续时间信号()f t ,可以用两个行向量f 和t 来表示,其中向量t 是用形如12::t t p t 的命令定义的时间范围向量,其中,1t 为信号起始时间,2t 为终止时间,p 为时间间隔。向量f 为连续信号()f t 在向量t 所定义的时间点上的样值。 说明:plot 是常用的绘制连续信号波形的函数。 严格说来,MATLAB 不能表示连续信号,所以,在用plot()命令绘制波形时,要对自变量t 进行取值,MATLAB 会分别计算对应点上的函数值,然后将各个数据点通过折线连接起来绘制图形,从而形成连续的曲线。因此,绘制的只是近似波形,而且,其精度取决于t 的取样间隔。t 的取样间隔越小,即点与点之间的距离越小,则近似程度越好,曲线越光滑。例如:图1-1是在取样间隔为p=0.5时绘制的波形,而图1-2是在取样间隔p=0.1时绘制的波形,两相对照,可以看出图1-2要比图1-1光滑得多。 连续时间系统 (1) 离散时间系统 (2) 拉普拉斯变换 (4) Z变换 (5) 傅里叶 (7) 连续时间系统 %%%%%%%%%%向量法%%%%%%%%%%%%%%%% t1=-2:0.01:5; f1=4*sin(2*pi*t1-pi/4); figure(1) subplot(2,2,1),plot(t1,f1),grid on %%%%%%%%%符号运算法%%%%%%%%%%%% syms t f1=sym('4*sin(2*pi*t-pi/4)'); figure(2) subplot(2,2,1),ezplot(f1,[-2 5])跟plot相比,ezplot不用指定t,自动生成。axis([-5,5,-0.1,1])控制坐标轴的范围xx,yy; 求一个函数的各种响应 Y’’(t)+4y’(t)+2y(t)=f”(t)+3f(t) %P187 第一题 %(2) clear all; a1=[1 4 2]; b1=[1 0 3]; [A1,B1,C1,D1]=tf2ss(b1,a1); t1=0:0.01:10; x1=exp(-t1).*Heaviside(t1); rc1=[2 1];(起始条件) figure(1) subplot(3,1,1),initial(A1,B1,C1,D1,rc1,t1);title('零输入响应') subplot(3,1,2),lsim(A1,B1,C1,D1,x1,t1);title('零状态响应') subplot(3,1,3),lsim(A1,B1,C1,D1,x1,t1,rc1);title('全响应') Y=lsim(A1,B1,C1,D1,x1,t1,rc1);title('全响应')则是输出数值解 subplot(2,1,1),impulse(b1,a1,t1:t:t2可加),grid on,title('冲激响应') subplot(2,1,2),step(b1,a1,t1:t:t2可加),grid on,title('阶跃响应') 卷积 %第九题 P189 clear all; %(1) t1=-1:0.01:3; 实验一 基本信号的产生与运算 一、 实验目的 学习使用MATLAB 产生基本信号、绘制信号波形、实现信号的基本运算。 二、 实验原理 MATLAB 提供了许多函数用于产生常用的基本信号:如阶跃信号、脉冲信号、指数信号、正弦信号和周期方波等等。这些信号是信号处理的基础。 1、 利用MATLAB 产生下列连续信号并作图。 (1)51),1(2)(<<---=t t u t x (2)300),3 2 sin()(3.0<<=-t t e t x t (3)1.01.0,3000cos 100cos )(<<-+=t t t t x (4)2000),8.0cos()1.0cos()(<<=t t t t x ππ 答:(1)、 >> t=-1:0.02:5; >> x=(t>1); >> plot(t,-2*x); >> axis([-1,5,-3,1]); >> title('杨婕婕 朱艺星'); >> xlabel('x(t)=-2u(t-1)'); (2)、 >> t=0:0.02:30; >> x=exp(-0.3*t).*sin(2/3*t); >> plot(t,x); >> title('杨婕婕朱艺星'); >> xlabel('x(t)=exp(-0.3*t).*sin(2/3*t)'); 因为原函数在t=15后x(t)取值接近于零,所以将横坐标改成0到15,看得更清晰 axis([0,15,-0.2,0.6]); (3)>> t=-0.1:0.01:0.1;x=cos(100*t)+cos(3000*t);plot(t,x); >> title('杨婕婕朱艺星'); >>xlabel('x=cos(100*t)+cos(3000*t)'); 因为t的间隔取太大,以至于函数不够准确,缩小t的间隔:t=-0.1:0.002:0.2;x=cos(100*t)+cos(3000*t); plot(t,x);title('杨婕婕') 实验一常用连续时间信号的实现 一、实验目的 (1)了解连续时间信号的特点; (2)掌握连续时间信号表示的向量法和符号法; (3)熟悉MA TLABPlot函数等的应用。 二、涉及的MATLAB函数 1.plot函数 功能:在X轴和Y轴方向都按线性比例绘制成二维图形。 2.ezplot函数 功能:绘制符号函数在一定范围内的二维图形,简易绘制函数曲线。 3.Sym函数 功能:定义信号为符号变量。 4.subplot函数 功能:产生多个绘图区间。 三、实验内容与方法 1.正弦交流信号f(t)=sin(ωt+φ) (1)符号推理法生成正弦交流信号。 MATLAB程序:. t=-0:0.001:1; f=sym('sin(2*pi*t)'); ezplot(f,[0,1]); xlabel('时间(t)'); ylabei('幅值(f)'); title(‘正弦交流信号'); 用符号法生成的正弦交流信号如图所示: (2)数值法生成正弦交流信号。 MATLAB程序:. t=-0:0.001:1; y=sin(2*pi*t); plot(t,y,'k'); xlabel('时间(t)'); ylabei('幅值(f)'); title('正弦交流信号'); 用数值法生成的正弦交流信号如图所示: 2.单边衰减指数信号. MATLAB程序: t1=-1;t2=10;dt=0.1; t=t1:dt:t2; A1=1; %斜率 a1=0.5; %斜率 n=A1*exp(-a1*t); plot(t,n); axis([t1,t2,0,1]); xlabel('时间(t)'); ylabel('幅值(f)'); title('单边衰减指数信号'); 用数值法生成的单边衰减指数信号如图所示: 本科毕业(论文) 题 目 (中、英文 ) in The Signal System 分类 号 学号 密级 公开 学校代码 1107044431 TN911.6 基于MATLAB 的信号系统仿真及应用 The Application of MATLAB in The Signal System 工科 作者姓名 指导教师 学科门类 专业名称 电气工程及其自动化 提交论文日期 成绩评定 二零一五年五月 摘要 当前的科学信息技术正在日新月异的高速发展,而通过应用数字信号处理的方法,已成为一个非常重要的技术手段被广泛应用在通信、音频和图像、遥感,视频等领域。为了更好地了解信号与系统的基本理论和掌握其方法,从而更好地理解和掌握数字信号处理的理论知识,因此在实验过程中我们就需要通过MATLAB 计算机辅助设计平台。 本论文主要探究MATALB在信号与系统中的连续信号和离散信号中的应用,主要从连续和离散两方面入手,进一步掌握信号系统中的相关知识。同时引进计算机软件—MATLAB,对信号系统二阶系统的时域和频域分析,通过它在计算机上对程序进行仿真,阐述信号与系统理论应用与实际相联系。以此激发学习兴趣,变被动接受为主动探知,从而提升学习效果,培养主动思维,学以致用的思维习惯,也可以让人们进一步了解MATLAB软件 关键词:采样定理;MATLAB;信号与系统;抽样定理 Abstract Current, the rapid development of science and information technology are changing and through the application of digital signal processing method, has become a very important technology is widely used in communication, audio and video, remote sensing, video, etc. In order to better understand the basic theory of signal and system, and grasp the method, to better understand and master the theoretical knowledge of digital signal processing, so we need in the process of experiment by MATLAB computer aided design platform. This thesis mainly explores MATALB in signal and system, the application of discrete and continuous signals, mainly from the two aspects of the continuous and discrete, further to master relevant knowledge of signal system. Introduction of computer software - MATAB at the same time, the signal system of second order system time domain and frequency domain analysis, through its d on program on computer simulation, signal and system theory associated with the actual application. To stimulate interest in learning, change passive accept to active detection, so as to improve learning effect, active thinking, to practice habits of thinking, also can let people learn more about MATLAB software. Key words:Sampling theorem; MATLAB; Signals and systems; The sampling theorem (1) t=-2:0.001:4; T=2; xt=rectpuls(t-1,T); plot(t,xt) axis([-2,4,-0.5,1.5]) 图象为: (2) t=sym('t'); y=Heaviside(t); ezplot(y,[-1,1]); grid on axis([-1 1 -0.1 1.1]) 图象为: A=10;a=-1;B=5;b=-2; t=0:0.001:10; xt=A*exp(a*t)-B*exp(b*t); plot(t,xt) 图象为: (4) t=sym('t'); y=t*Heaviside(t); ezplot(y,[-1,3]); grid on axis([-1 3 -0.1 3.1]) 图象为: A=2;w0=10*pi;phi=pi/6; t=0:0.001:0.5; xt=abs(A*sin(w0*t+phi)); plot(t,xt) 图象为: (6) A=1;w0=1;B=1;w1=2*pi; t=0:0.001:20; xt=A*cos(w0*t)+B*sin(w1*t); plot(t,xt) 图象为: A=4;a=-0.5;w0=2*pi; t=0:0.001:10; xt=A*exp(a*t).*cos(w0*t); plot(t,xt) 图象为: (8) w0=30; t=-15:0.001:15; xt=cos(w0*t).*sinc(t/pi); plot(t,xt) axis([-15,15,-1.1,1.1]) 图象为: (1)function yt=x2_3(t) yt=(t).*(t>=0&t<=2)+2*(t>=2&t<=3)-1*(t>=3&t<=5); (2)function yt=x2_3(t) yt=(t).*(t>=0&t<=2)+2*(t>=2&t<=3)-1*(t>=3&t<=5); t=0:0.001:6; subplot(3,1,1) plot(t,x2_3(t)) title('x(t)') axis([0,6,-2,3]) subplot(3,1,2) plot(t,x2_3(0.5*t)) title('x(0.5t)') axis([0,11,-2,3]) subplot(3,1,3) plot(t,x2_3(2-0.5*t)) title('x(2-0.5t)') axis([-6,5,-2,3]) 图像为: 实验一、MATLAB 编程基础及典型实例 一、实验目的 (1)熟悉MATLAB 软件平台的使用; (2)熟悉MATLAB 编程方法及常用语句; (3)掌握MATLAB 的可视化绘图技术; (4)结合《信号与系统》的特点,编程实现常用信号及其运算。 示例一:在两个信号进行加、减、相乘运算时,参于运算的两个向量要有相同的维数,并且它们的时间变量范围要相同,即要对齐。编制一个函数型m 文件,实现这个功能。function [f1_new,f2_new,n]=duiqi(f1,n1,f2,n2) a=min(min(n1),min(n2)); b=max(max(n1),max(n2)); n=a:b; f1_new=zeros(1,length(n)); f2_new=zeros(1,length(n)); tem1=find((n>=min(n1))&(n<=max(n1))==1); f1_new(tem1)=f1; tem2=find((n>=min(n2))&(n<=max(n2))==1); f2_new(tem2)=f2; 四、实验内容与步骤 (2)绘制信号x(t)=)3 2sin(2t e t ?的曲线,t 的范围在0~30s ,取样时间间隔为0.1s 。t=0:0.1:30; y=exp(-sqrt(2)*t).*sin(2*t/3); plot(t,y); (3)在n=[-10:10]范围产生离散序列:?? ?≤≤?=Other n n n x ,033,2)(,并绘图。n=-10:1:10; z1=((n+3)>=0); z2=((n-3)>=0); x=2*n.*(z1-z2); stem(n,x);(4)编程实现如下图所示的波形。 t=-2:0.001:3; f1=((t>=-1)&(t<=1)); f2=((t>=-1)&(t<=2)); f=f1+f2; plot(t,f); axis([-2,3,0,3]); 《信号与系统及MATLAB实现》实验指导书 前言 长期以来,《信号与系统》课程一直采用单一理论教学方式,同学们依靠做习题来巩固和理解教学内容,虽然手工演算训练了计算能力和思维方法,但是由于本课程数学公式推导较多,概念抽象,常需画各种波形,作题时难免花费很多时间,现在,我们给同学们介绍一种国际上公认的优秀科技应用软件MATLAB,借助它我们可以在电脑上轻松地完成许多习题的演算和波形的绘制。 MATLAB的功能非常强大,我们此处仅用到它的一部分,在后续课程中我们还会用到它,在未来地科学研究和工程设计中有可能继续用它,所以有兴趣的同学,可以对MATLAB 再多了解一些。 MATLAB究竟有那些特点呢? 1.高效的数值计算和符号计算功能,使我们从繁杂的数学运算分析中解脱出来; 2.完备的图形处理功能,实现计算结果和编程的可视化; 3.友好的用户界面及接近数学表达式的自然化语言,易于学习和掌握; 4.功能丰富的应用工具箱,为我们提供了大量方便实用的处理工具; MATLAB的这些特点,深受大家欢迎,由于个人电脑地普及,目前许多学校已将它做为本科生必须掌握的一种软件。正是基于这些背景,我们编写了这本《信号与系统及MATLAB实现》指导书,内容包括信号的MATLAB表示、基本运算、系统的时域分析、频域分析、S域分析、状态变量分析等。通过这些练习,同学们在学习《信号与系统》的同时,掌握MATLAB的基本应用,学会应用MATLAB的数值计算和符号计算功能,摆脱烦琐的数学运算,从而更注重于信号与系统的基本分析方法和应用的理解与思考,将课程的重点、 难点及部分习题用MATLAB进行形象、直观的可视化计算机模拟与仿真实现,加深对信号与系统的基本原理、方法及应用的理解,为学习后续课程打好基础。另外同学们在进行实验时,最好事先预习一些MATLAB的有关知识,以便更好地完成实验,同时实验中也可利用MATLAB的help命令了解具体语句以及指令的使用方法。 实验一基本信号在MATLAB中的表示和运算 一、实验目的 1.学会用MATLAB表示常用连续信号的方法; 2.学会用MATLAB进行信号基本运算的方法; 二、实验原理 1.连续信号的MATLAB表示 MATLAB提供了大量的生成基本信号的函数,例如指数信号、正余弦信号。 表示连续时间信号有两种方法,一是数值法,二是符号法。数值法是定义某一时间范围和取样时间间隔,然后调用该函数计算这些点的函数值,得到两组数值矢量,可用绘图语句画出其波形;符号法是利用MATLAB的符号运算功能,需定义符号变量和符号函数,运算结果是符号表达的解析式,也可用绘图语句画出其波形图。 例1-1指数信号指数信号在MATLAB中用exp函数表示。 如at )(,调用格式为ft=A*exp(a*t) 程序是 f t Ae 实验一 基本信号的产生与运算 一、 实验目的 学习使用MATLAB 产生基本信号、绘制信号波形、实现信号的基本运算。 二、 实验原理 MATLAB 提供了许多函数用于产生常用的基本信号:如阶跃信号、脉冲信号、指数信号、正弦信号和周期方波等等。这些信号是信号处理的基础。 1、 利用MATLAB 产生下列连续信号并作图。 (1)51),1(2)(<<---=t t u t x (2)300),3 2sin()(3.0<<=-t t e t x t (3)1.01.0,3000cos 100cos )(<<-+=t t t t x (4)2000),8.0cos()1.0cos()(<<=t t t t x ππ 答:(1)、 >> t=-1:0.02:5; >> x=(t>1); >> plot(t,-2*x); >> axis([-1,5,-3,1]); >> title('杨婕婕 朱艺星'); >> xlabel('x(t)=-2u(t-1)'); (2)、 >> t=0:0.02:30; >> x=exp(-0.3*t).*sin(2/3*t); >> plot(t,x); >> title('杨婕婕朱艺星'); >> xlabel('x(t)=exp(-0.3*t).*sin(2/3*t)'); 因为原函数在t=15后x(t)取值接近于零,所以将横坐标改成0到15,看得更清晰 axis([0,15,-0.2,0.6]); (3)>> t=-0.1:0.01:0.1;x=cos(100*t)+cos(3000*t);plot(t,x); >> title('杨婕婕朱艺星'); >>xlabel('x=cos(100*t)+cos(3000*t)'); 因为t的间隔取太大,以至于函数不够准确,缩小t的间隔: t=-0.1:0.002:0.2;x=cos(100*t)+cos(3000*t); plot(t,x);title('杨婕婕') >> t=-0.1:0.0001:0.1; x=cos(100*t)+cos(3000*t); >> plot(t,x);title('杨婕婕朱艺星'); 实验报告 实验课程:信号与系统—Matlab综合实验学生姓名: 学号: 专业班级: 2012年5月20日 基本编程与simulink仿真实验 1—1编写函数(function)∑=m n k n 1并调用地址求和∑∑∑===++100 11-8015012 n n n n n n 。实验程序: Function sum=qiuhe(m,k)Sum=0For i=1:m Sum=sum+i^k End 实验结果; qiuhe(50,2)+qiuhe(80,1)+qiuhe(100,-1) ans=4.6170e+004。 1-2试利用两种方式求解微分方程响应 (1)用simulink对下列微分方程进行系统仿真并得到输出波形。(2)编程求解(转移函数tf)利用plot函数画图,比较simulink图和plot图。)()(4)(6)(5)(d 22t e t e d d t r t r d d t r d t t t +=++在e(t)分别取u(t)、S(t)和sin(20пt)时的情况! 试验过程 (1) (2) a=[1,5,6]; b=[4,1]; sys=tf(b,a); t=[0:0.1:10]; step(sys) 连续时间系统的时域分析3-1、已知某系统的微分方程:)()()()()(d 2t e t e d t r t r d t r t t t +=++分别用两种方法计算其冲激响应和阶跃响应,对比理论结果进行验证。 实验程序: a=[1,1,1];b=[1,1];sys=tf(b,a);t=[0:0.01:10];figure;subplot(2,2,1);step(sys);subplot(2,2,2);x_step=zeros(size(t));x_step(t>0)=1;x_step(t==0)=1/2;lsim(sys,x_step,t);subplot(2,2,3);impulse(sys,t);title('Impulse Response');xlabel('Time(sec)');ylabel('Amplitude');subplot(2,2,4);x_delta=zeros(size(t));x_delta(t==0)=100;[y1,t]=lsim(sys,x_delta,t);y2=y1;plot(t,y2);title('Impulse Response'); 《信号与系统》MATLAB 实验报告 院系: 专业: 年级: 班号: 姓名: 学号: 实验时间: 实验地点: 实验一 连续时间信号的表示及可视化 实验题目: )()(t t f δ=;)()(t t f ε=;at e t f =)((分别取00<>a a 及); )()(t R t f =;)()(t Sa t f ω=;)2()(ft Sin t f π=(分别画出不同周期个数的波形)。 解题分析: 以上各类连续函数,先运用t = t1: p:t2的命令定义时间范围向量,然后调用对应的函数,建立f 与t 的关系,最后调用plot ()函数绘制图像,并用axis ()函数限制其坐标范围。 实验程序: (1))()(t t f δ= t=-1:0.01:3 %设定时间变量t 的范围及步长 f=dirac(t) %调用冲激函数dirac () plot(t,f) %用plot 函数绘制连续函数 axis([-1,3,-0.5,1.5]) %用axis 函数规定横纵坐标的范围 (2))()(t t f ε= t=-1:0.01:3 %设定时间变量t 的范围及步长 f=heaviside(t) %调用阶跃函数heaviside () plot(t,f) %用plot 函数绘制连续函数 title('f(t)=heaviside(t)') %用title 函数设置图形的名称 axis([-1,3,-0.5,1.5]) %用axis 函数规定横纵坐标的范围 (3)at e t f =)( a=1时: t=-5:0.01:5 %设定时间变量t 的范围及步长 f=exp(t) %调用指数函数exp () plot(t,f) %用plot 函数绘制连续函数 title('f=exp(t)') %用title 函数设置图形的名称 axis([-5,5,-1,100]) %用axis 函数规定横纵坐标的范围 a=2时: t=-5:0.01:5 f=exp(2*t) %调用指数函数exp () plot(t,f) title('f=exp(2*t)') axis([-5,5,-1,100]) a=-2时: t=-5:0.01:5 f=exp(-2*t) plot(t,f) title('f=exp(-2*t)') axis([-5,5,-1,100]) (4))()(t R t f = t=-5:0.01:5 f=rectpuls(t,2) %用rectpuls(t,a)表示门函数,默认以零点为中心,宽度为a plot(t,f) title('f=R(t)') axis([-5 5 -0.5 1.5]) (5))()(t Sa t f ω= ω=1时: 考核人数______ 考核班次_______________ 任课教员_________ 出题教员签名________ 任课教研室主任签名_______日期_______ 队别__________ 教学班次___________ 学号___________ 姓名____________ …………………………密………………………………封………………………………线……………………………………… 通信系统仿真题目 1.学习电路时已知LC 谐振电路具有选择频率的作用,当输入正弦信号频率与LC 电路的谐 振频率一致时,将产生较强的输出响应,而当输入信号频率适当偏离时,输出响应相对值很弱,几乎为零(相当于窄带通滤波器)。利用这一原理可以从非正弦周期信号中选择所需的正弦频率成分。题图所示RLC 并联电路和电流1()i t 都是理想模型。已知电路的谐振频率为 0100f kHz = =,100R k =Ω谐振电路品质因素Q 足够高(可滤除邻近频率成分) 1()i t 为周期矩形波,幅度为1 mA 当1()i t 的参数(,)T τ为下列情况时,粗略地画出输出电压 2()t υ的波形,并注明幅度值。 (1)510s T s τμμ== (2)1020s T s τμμ== (3)1530s T s τμμ== 2.设()x n 为一限长序列,当0n <和n N ≥时,()0x n =,且N 等于偶数。已知[()]DFT x n = ()X k ,试用()X k 表示以下各序列的DFT 。 (1)1()(1)x n x N n =-- (2)2()(1)()n x n x n =- (3) 3() (01)()()(21)0()x n n N x n x n N N n N n ≤≤-?? =-≤≤-??? 为其他值 (4) 4()()(01) ()2 2 () N N x n x n n x n n ?≠+≤≤ -? =???为其他值 (5) 5()(01)()0 (21)0() x n n N x n N n N n ≤≤-?? =≤≤-??? 为其他值 (6) 6() ()20()n x n x n n ??? ? ?=????? 为偶数为奇数 (DFT 有限长度取2N ,k 取偶数。) (7) 7()(2)x n x n =(DFT 有限长度取 2 N )。 3.已知三角脉冲1() f t 的傅里叶变换为21()24E F Sa τωτω??= ??? 试利用有关定理求210()cos()2f t f t t τω?? =- ??? 的傅里叶变换2()F ω。1()f t 、2()f t 的波形如下图所示。 4.求下图所示半波余弦信号的傅里叶级数。若E=10V ,f=10kHz ,大致画出幅度谱。 5.求下图所示()F ω的傅里叶逆变换()f t 。 基于Matlab 的信号与系统实验指导 实验一 连续时间信号在Matlab 中的表示 一、实验目的 1、学会运用Matlab 表示常用连续时间信号的方法 2、观察并熟悉这些信号的波形和特性 二、实验原理及实例分析 1、信号的定义与分类 2、如何表示连续信号? 连续信号的表示方法有两种;符号推理法和数值法。 从严格意义上讲,Matlab 数值计算的方法不能处理连续时间信号。然而,可利用连续信号在等时间间隔点的取样值来近似表示连续信号,即当取样时间间隔足够小时,这些离散样值能被Matlab 处理,并且能较好地近似表示连续信号。 3、Matlab 提供了大量生成基本信号的函数。如: (1)指数信号:K*exp(a*t) (2)正弦信号:K*sin(w*t+phi)和K*cos(w*t+phi) (3)复指数信号:K*exp((a+i*b)*t) (4)抽样信号:sin(t*pi) 注意:在Matlab 中用与Sa(t)类似的sinc(t)函数表示,定义为:)t /()t (sin )t (sinc ππ= (5)矩形脉冲信号:rectpuls(t,width) (6)周期矩形脉冲信号:square(t,DUTY),其中DUTY 参数表示信号的占空比 DUTY%,即在一个周期脉冲宽度(正值部分)与脉冲周期的比值。占空比默认为0.5。 (7)三角波脉冲信号:tripuls(t, width, skew),其中skew 取值范围在-1~+1之间。 (8)周期三角波信号:sawtooth(t, width) (9)单位阶跃信号:y=(t>=0) 三、实验内容 1、验证实验内容 直流及上述9个信号 2、程序设计实验内容 (1)利用Matlab 命令画出下列连续信号的波形图。 (a ))4/3t (2cos π+ (b ) )t (u )e 2(t -- (c ))]2()(u )][t (cos 1[--+t u t π (2)利用Matlab 命令画出复信号) 4/t (j 2e )t (f π+=的实部、虚部、模和辐角。 四、实验报告要求 1、格式:实验名称、实验目的、实验原理、实验环境、实验内容、实验思考等 2、实验内容:程序设计实验部分源代码及运行结果图示。信号与系统matlab实验及答案
信号与系统——MATLAB基本实验
信号与系统MATLAB实验报告
信号与系统 matlab答案
(完整word版)信号与系统matlab实验
MATLAB实验报告
信号与系统MATLAB实验
matlab信号与系统代码整理
matlab信号与系统实验报告
信号与系统作业
基于MATLAB的信号与系统仿真及应用
信号与系统课后matlab作业.
信号与系统MATLAB实验总汇
信号与系统MATLAB实验
matlab信号与系统实验报告
信号与系统MATLAB实验报告
信号与系统 MATLAB实验报告
信号与系统MATLAB仿真题目
根据Matlab的信号与系统实验指导材料