
2 3 x 1
3 3 2 3 x 3 3 3 3 2019 中考数学压轴题
52.(2017 内蒙古赤峰市,第 21 题,10 分)如图,一次函数
于点 A 、B ,以线段 AB 为边在第一象限作等边△ABC.
y = k
y = -
3
x +1 3
的图象与 x 轴、y 轴分别交 (1) 若点 C 在反比例函数 x 的图象上,求该反比例函数的解析式;
(2) 点 P ( 2 ,m )在第一象限,过点 P 作 x 轴的垂线,垂足为 D ,当△PAD 与△OAB 相似时,P 点 是否在(1)中反比例函数图象上?如果在,求出 P 点坐标;如果不在,请加以说明.
【答案】(1)
y =
;(2)P ( 2 ,1)在反比例函数图象上. 【分析】(1)由直线解析式可求得 A 、B 坐标,在 Rt△AOB 中,利用三角函数定义可求得∠BAO=30°,
且可求得 AB 的长,从而可求得 CA⊥OA,则可求得 C 点坐标,利用待定系数法可求得反比例函数解析式; (2)分△PAD∽△ABO 和△PAD∽△BAO 两种情况,分别利用相似三角形的性质可求得 m 的值,可求得 P 点坐标,代入反比例函数解析式进行验证即可.
【解析】(1)在 y = - 3
x +1 3
中,令 y=0 可解得 x= ,令 x=0 可得 y=1,∴A( ,0),B (0,1),∴
OB = = tan∠BAO=
OA 3
3 ,∴∠BAO=30°,∵△ABC 是等边三角形,∴∠BAC=60°,∴∠CAO=90°, y = k
在Rt △BOA 中,由勾股定理可得 AB=2,∴AC=2,∴C( ,2),∵点 C 在反比例函数 x 的图象上,∴k=2
× =
2 y =
,∴反比例函数解析式为 ;
PD =
AD
(2)∵P( 2
m =
,m )在第一象限,∴AD=OD﹣OA= 2 ﹣ = ,PD=m ,当△ADP∽△AOB 时,则有
OB OA ,即 1 ,解得 m=1,此时 P 点坐标为( 2 ,1);
3 3 3 3 3 3 3 3 3
3
PD =
AD m = 当△PDA∽△AOB 时,则有 OA OB ,即
y = 3 1 ,解得 m=3,此时 P 点坐标为( 2 ,3);
把 P (
2 ,3)代入 x 可得 3≠ ,∴P( 2 ,3)不在反比例函数图象上,把 P ( 2 ,1)
代入反比例函数解析式得 1= ,∴P( 2 ,1)在反比例函数图象上;
综上可知 P 点坐标为( 2 ,1).
点睛:本题为反比例函数的综合应用,涉及待定系数法、等边三角形的性质、三角函数、勾股定理、
相似三角形的性质及分类讨论思想等知识.在(1)中求得 C 点坐标是解题的关键,在(2)中利用相似三角形的性质得到 m 的方程是解题的关键,注意分两种情况.本题考查知识点较多,综合性较强, 难度适中.
考点:反比例函数综合题;分类讨论;综合题.
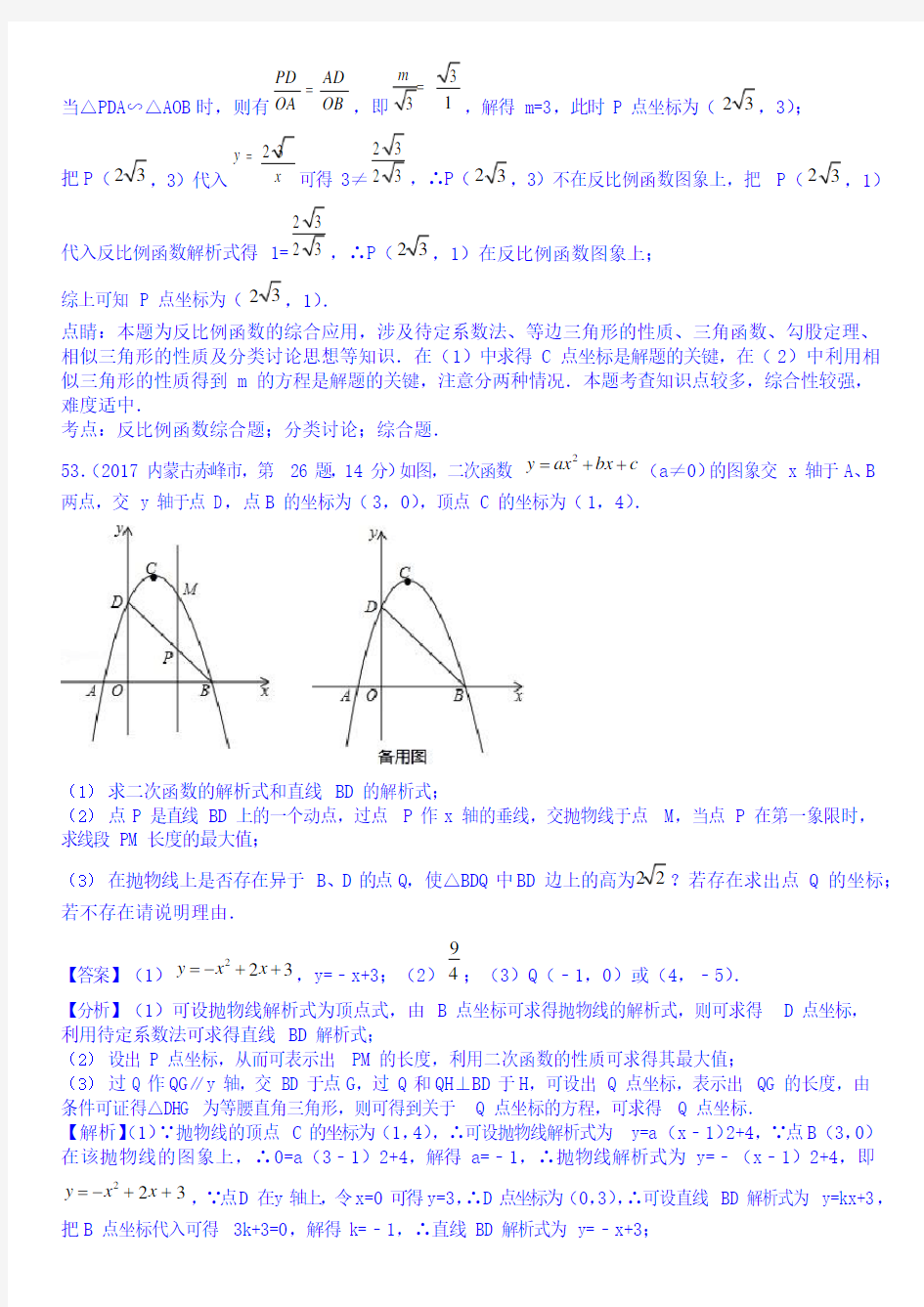
53.(2017 内蒙古赤峰市,第 26 题,14 分)如图,二次函数 y = ax 2
+ bx + c (a≠0)的图象交 x 轴于 A 、B
两点,交 y 轴于点 D ,点 B 的坐标为(3,0),顶点 C 的坐标为(1,4).
(1) 求二次函数的解析式和直线 BD 的解析式;
(2) 点 P 是直线 BD 上的一个动点,过点 P 作 x 轴的垂线,交抛物线于点 M ,当点 P 在第一象限时,
求线段 PM 长度的最大值;
(3) 在抛物线上是否存在异于 B 、D 的点 Q ,使△BDQ 中 BD 边上的高为2 若不存在请说明理由.
?若存在求出点 Q 的坐标;
9
【答案】(1) y = -x 2
+ 2x + 3 ,y=﹣x+3;(2) 4 ;(3)Q (﹣1,0)或(4,﹣5).
【分析】(1)可设抛物线解析式为顶点式,由 B 点坐标可求得抛物线的解析式,则可求得 D 点坐标,
利用待定系数法可求得直线 BD 解析式; (2) 设出 P 点坐标,从而可表示出 PM 的长度,利用二次函数的性质可求得其最大值; (3) 过 Q 作 QG∥y 轴,交 BD 于点 G ,过 Q 和 QH⊥BD 于 H ,可设出 Q 点坐标,表示出 QG 的长度,由条件可证得△DHG 为等腰直角三角形,则可得到关于 Q 点坐标的方程,可求得 Q 点坐标. 【解析】(1)∵抛物线的顶点 C 的坐标为(1,4),∴可设抛物线解析式为 y=a (x ﹣1)2+4,∵点 B (3,0)在该抛物线的图象上,∴0=a (3﹣1)2+4,解得 a=﹣1,∴抛物线解析式为 y=﹣(x ﹣1)2+4,即 y = -x 2 + 2x + 3 ,∵点 D 在y 轴上,令 x=0 可得 y=3,∴D 点坐标为(0,3),∴可设直线 BD 解析式为 y=kx+3,把 B 点坐标代入可得 3k+3=0,解得 k=﹣1,∴直线 BD 解析式为 y=﹣x+3;
3 3 2 3
2 3 2 3 3 3 2 3
2 3 3 3 2
(2)设P 点横坐标为m(m>0),则P(m,﹣m+3),M(m,﹣m2+2m+3),∴PM=﹣m2+2m+3﹣(﹣m+3)
=﹣m2+3m=
-(m -3
)2+
9 3 9
2 4 ,∴当 m= 2 时,PM 有最大值4 ;
点睛:本题为二次函数的综合应用,涉及待定系数法、二次函数的性质、等腰直角三角形的性质及方程思想等知识.在(1)中主要是待定系数法的考查,注意抛物线顶点式的应用,在(2)中用 P 点坐标表示出 PM 的长是解题的关键,在(3)中构造等腰直角三角形求得 QG 的长是解题的关键.本题考查知识点较多,综合性较强,难度适中.
考点:二次函数综合题;二次函数的最值;最值问题;分类讨论;压轴题.
54.
(2017 内蒙古通辽市,第26 题,12 分)在平面直角坐标系xOy 中,抛物线y=ax2+bx+2过点A(﹣2,0),B(2,2),与 y 轴交于点 C.
(1)求抛物线y =ax
2 +bx + 2 的函数表达式;
(2)若点 D 在抛物线y =ax
2 +bx + 2 的对称轴上,求△ACD的周长的最小值;
(3)在抛物线y =ax
2 +bx + 2 的对称轴上是否存在点 P,使△ACP是直角三角形?若存在直接写出点 P 的坐标,若不存在,请说明理由.
5 5 2 5 5 4a + 2b + 2 = 2
【答案】(1)
y =
- 1 x 2 + 1 x + 2 4 2
;(2) 2 + 2 ;(3)存在,P (1,1)或(1,﹣3). 【分析】(1)利用待定系数法求抛物线的函数表达式;
(2) 由轴对称的最短路径得:因为 B 与 C 关于对称轴对称,所以连接 AB 交对称轴于点 D ,此时△ACD 的周长最小,利用勾股定理求其三边相加即可; (3) 存在,当 A 和 C 分别为直角顶点时,画出直角三角形,设 P (1,y ),根据三角形相似列比例式可得 P 的坐标.
【解析】(1)把点 A (﹣2,0),B (2,2)代入抛物线
?
a = - 1
y = ax 2 + bx + 2 ?4a - 2b + 2 = 0
? 中,得: ? ,解得: ? ?
?b = ? 4
1
2 ,∴抛物线函数表达式为: y = - 1 x 2 + 1 4 2
x + 2
;
(2)∵ y = - 1 x 2 + 1 x + 2 4 2 - 1 (x -1)2 + 9
= 4 4 ,∴对称轴是:直线 x=1,如图 1,过 B 作 BE⊥x 轴于 E ,∵C(0, 2),B (2,2),对称轴是:x=1,∴C 与 B 关于 x=1 对称,∴CD=BD,连接 AB 交对称轴于点 D ,此时△ACD
的周长最小,∵BE=2,AE=2+2=4,OC=2,OA=2,∴AB= =
2 ,AC= = 2 ,∴△ACD
的周长=AC+CD+AD=AC+BD+AD=AC+AB=
2 + 2 .
答:△ACD 的周长的最小值是2 (3)存在,分两种情况:
+ 2 ;
①当∠ACP=90°时,△ACP 是直角三角形,如图 2,过 P 作 PD⊥y 轴于D ,设 P (1,y ),则△CGP∽△AOC,∴ PG = CG 1 = CG
OC AO ,∴ 2 2 ,∴CG=1,∴OG=2﹣1=1,∴P(1,1);
AE =
PE
②当∠CAP=90°时,△ACP 是直角三角形,如图 3,设 P (1,y ),则△PEA∽△AOC,∴
OC AO ,∴
3 =
PE
2 2 ,∴PE=3,∴P(1,﹣3);
2 22 + 42 22 + 22
2 2 ?
3 3 3 3 综上所述,△ACP 是直角三角形时,点 P 的坐标为(1,1)或(1,﹣3).
点睛:本题是二次函数的综合题,难度适中,考查了利用待定系数法求二次函数的解析式、轴对称的最短路径问题、直角三角形问题,第 3 问采用了分类讨论的思想,与三角形相似结合,列比例式可解决问题.
考点:二次函数综合题;最值问题;分类讨论;存在型;压轴题. 55.(2017 吉林省,第 23 题,8 分)如图①,BD 是矩形 ABCD 的对角线,∠ABD=30°,AD=1.将△BCD 沿射线 BD 方向平移到△B'C'D'的位置,使 B'为 BD 中点,连接 AB',C'D ,AD',BC',如图②. (1) 求证:四边形 AB'C'D 是菱形; (2) 四边形 ABC'D′的周长为 ; (3) 将四边形 ABC'D'沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.
【答案】(1)证明见解析;(2) 4 ;(3)6+ 或 2 +3.
【分析】(1)有一组邻边相等的平行四边形是菱形,据此进行证明即可;
(2) 先判定四边形 ABC'D'是菱形,再根据边长AB=
AD= ,
即可得到四边形 ABC'D′的周长为4 ; (3)
根据两种不同的拼法,分别求得可能拼成的矩形周长.
【解析】(1)∵BD 是矩形 ABCD 的对角线,∠ABD=30°,∴∠ADB=60°,由平移可得,B'C'=BC=AD ,∠ D'B'C'=∠DBC=∠ADB=60°,∴AD∥B'C'
1
∴四边形 AB'C'D 是平行四边形,∵B'为 BD 中点,∴Rt△ABD 中,AB'= 2 BD=DB',又∵∠ADB=60°,∴△ ADB'是等边三角形,∴AD=AB',∴四边形 AB'C'D 是菱形; (2) 由平移可得,AB=C'D',∠ABD'=∠C'D'B=30°,∴AB∥C'D',∴四边形 ABC'D'是平行四边形,
由(1)可得,AC'⊥B'D,∴四边形 ABC'D'是菱形,∵AB=
AD= ,∴四边形 ABC'D′的周长为4 ,
故答案为:
4 ; (3) 将四边形 ABC'D'沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形如下:
3 3 3 3 3 3
3 3 x
? ?
∴矩形周长为 6+ 或 2 +3.
点睛:本题主要考查了菱形的判定与性质,矩形的性质以及勾股定理的运用,解题时注意:有一组邻边相等的平行四边形是菱形;对角线互相垂直的平行四边形是菱形.
考点:菱形的判定与性质;矩形的性质;图形的剪拼;平移的性质;操作型;分类讨论. 56.(2017 吉林省,第 25 题,10 分)如图,在 Rt △ABC 中,∠ACB=90°,∠A=45°,
AB=4cm .点 P 从点 A 出发,以 2cm/s 的速度沿边 AB 向终点 B 运动.过点 P 作 PQ⊥AB 交折线 ACB 于点 Q ,D 为 PQ 中点,以 DQ 为边向右侧作正方形 DEFQ .设正方形 DEFQ 与△ABC 重叠部分图形的面积是 y (cm2),点 P 的运动时间为 x (s ).
(1) 当点 Q 在边 AC 上时,正方形 DEFQ 的边长为 cm (用含 x 的代数式表示); (2) 当点 P 不与点 B 重合时,求点 F 落在边 BC 上时 x 的值; (3) 当 0<x <2 时,求 y 关于 x 的函数解析式; (4) 直接写出边 BC 的中点落在正方形 DEFQ 内部时 x 的取值范围.
? 2
(0 < x
≤ 4)
5 ? y = ?- ? 23 x 2 + 20x - 8 ( 4 2 5 < x ≤ 1)
4 【答案】(1)x ;(2)x=
5 ;(3) ? 1 x 2
- 2x + 2 (1 < x < 2)
? 2 3 ;(4)1<x <
2 . 【分析】(1)国际已知条件得到∠AQP=45°,求得 PQ=AP=2x ,由于 D 为 PQ 中点,于是得到 DQ=x ;
(2) 如图①,延长 FE 交 AB 于 G ,由题意得 AP=2x ,由于 D 为 PQ 中点,得到 DQ=x ,求得 GP=2x ,列方程于是得到结论;
4 4
(3) 如图②,当 0<x≤ 5 时,根据正方形的面积公式得到 y=x2;如图③,当 5 <x≤1 时,过 C 作 CH⊥AB 于 H ,交 FQ 于 K ,则 CH=2,根据正方形和三角形面积公式得到 y 的解析式;如图④,当 1<x <2 时,
PQ=4﹣2x ,根据三角形的面积公式得到结论;
(4) 当 Q 与 C 重合时,E 为 BC 的中点,得到 x=1,当 Q 为 BC 的中点时,BQ= 得到结论.
,得到 x 的值,于是
【解析】(1)∵∠ACB=90°,∠A=45°,PQ⊥AB,∴∠AQP=45°,∴PQ=AP=2x,∵D 为 PQ 中点,∴ DQ=x ,故答案为:x ; (2) 如图①,延长 FE 交 AB 于 G ,由题意得 AP=2x ,∵D 为 PQ 中点,∴DQ=x,∴GP=2x,∴2x+x+2x=4,∴x=
2 ?
2 x
? ? 4 5 ;
4
(3)
如图②,当 0<x≤ 5 时,y=S 正方形 DEFQ=DQ2=x2,∴ y = x 2
;
4 1
如图③,当 5 <x≤1 时,过 C 作 CH⊥AB 于 H ,交 FQ 于 K ,则 CH=
2 AB=2,∵PQ=AP=2x,CK=2﹣2x ,∴
1 1
MQ=2CK=4﹣4x ,FM=x ﹣(4﹣4x )=5x ﹣4,∴y=S 正方形 DEFQ ﹣S△MNF=DQ2﹣ 2 FM2,∴y=x2﹣ 2 (5x ﹣4) y = - 23
x 2 + 20x - 8
2,∴ 2 ;
1 1
y = 1
x 2 - 2x + 2
如图④,当 1<x <2 时,PQ=4﹣2x ,∴DQ=2﹣x ,∴y=S△DEQ= 2 DQ2,∴y= 2 (2﹣x )2,∴ 2 ;
? 2
(0 < x ≤ 4)
5 ? y = ?- ? 23 x 2 + 20x - 8 ( 4 2 5 < x ≤ 1)
综上所述: ? 1 x 2 - 2x + 2 (1 < x < 2) ? 2
(4)
当Q 与C 重合时,E 为BC 的中点,即2x=2,∴x=1,当Q 为BC 的中点时,BQ= ,PB=1,∴AP=3,∴2x=3,
3 3
∴x=
2 ,∴边 BC 的中点落在正方形 DEFQ 内部时 x 的取值范围为:1<x < 2 .
点睛:本题考查了等腰直角三角形的性质,正方形的性质,图形面积的计算,正确的作出图形是解题的关键.
考点:四边形综合题;动点型;分类讨论;分段函数;压轴题. 57.(2017 吉林省,第 26 题,10 分)《函数的图象与性质》拓展学习片段展示:
?
【问题】如图①,在平面直角坐标系中,抛物线
则 a= .
y = a (x - 2)2
- 4
3 经过原点 O ,与 x 轴的另一个交点为 A , 【操作】将图①中抛物线在 x 轴下方的部分沿 x 轴折叠到 x 轴上方,将这部分图象与原抛物线剩余部分的图象组成的新图象记为 G ,如图②.直接写出图象 G 对应的函数解析式.
【探究】在图②中,过点 B (0,1)作直线 l 平行于 x 轴,与图象 G 的交点从左至右依次为点 C ,D ,E ,F , 如图③.求图象 G 在直线 l 上方的部分对应的函数 y 随 x 增大而增大时 x 的取值范围.
【应用】P 是图③中图象 G 上一点,其横坐标为 m ,连接 PD ,PE .直接写出△PDE 的面积不小于 1 时 m 的取值范围.
?1
(x - 2)2 - 4 (x ≤ 0或x ≥ 4) y = ?3 3 1 【答案】【问题】: 3 ;【操作】: ? ?- 1 (x - 2)2 + 4 ? 3 3
(0 < x < 4)
;【探究】:当 1<x <2 或 x >2+
时,函数 y 随 x 增大而增大;【应用】:m=0 或 m=4 或 m≤2﹣ 10 或 m≥2+ 10 .
【分析】【问题】:把(0,0)代入可求得 a 的值;
【操作】:先写出沿 x 轴折叠后所得抛物线的解析式,根据图象可得对应取值的解析式;
【探究】:令 y=0,分别代入两个抛物线的解析式,分别求出四个点 CDEF 的坐标,根据图象呈上升趋势的部分,即 y 随 x 增大而增大,写出 x 的取值;
【应用】:先求 DE 的长,根据三角形面积求高的取值 h≥1; 分三部分进行讨论:
1 (m - 2)
2 - 4 ①当 P 在 C 的左侧或 F 的右侧部分时,设 P[m ,
3 3 ],根据 h≥1,列不等式解出即可; ②如图③,作对称轴由最大面积小于 1 可知:点 P 不可能在 DE 的上方;
③P 与 O 或 A 重合时,符合条件,m=0 或 m=4. 【解析】【问题】
y = a (x - 2)2 - 4 0 = a (0 - 2)2 - 4 1 1
∵抛物线
3 经过原点 O ,∴ y = 1 (x - 2)2 - 4
3 ,a= 3 ,故答案为: 3 ; 【操作】:如图①,抛物线: 3
3 ,对称轴是:直线 x=2,由对称性得:A (4,0),沿 x 轴折叠后所得抛物线为:
y = - 1 (x - 2)2 + 4
3 3 ,如图②,图象 G 对应的函数解析式为: 7
7 ?1
(x - 2)2 - 4 (x ≤ 0或x ≥ 4) y = ?3 3 ? ?- 1 (x - 2)2 + 4 ? 3 3
(0 < x < 4) ;
【探究】:如图③,由题意得:
1 (x - 2)
2 - 4 当 y=1 时,
3 3 =0,解得:x1=2+ - 1 (x - 2)2 + 4
= 0
,x2=2﹣ ,∴C(2﹣
,1),F (2+
,1),当 y=1
时, 3
3 ,解得:x1=3,x2=1,∴D (1,1),E (3,1),由图象得:图象 G 在直线 l 上 方的部分,当 1<x <2 或 x >2+ 时,函数 y 随 x 增大而增大;
1
【应用】:∵D(1,1),E (3,1),∴DE=3﹣1=2,∵S△PDE=
2 DE?h≥1,∴h≥1; 1 (m - 2)2 -
4
1 (m - 2)
2 - 4
①
当
P
在C 的
左侧或F
的右侧部分
4 4 1 ②如图③,作对称轴交抛物线 G 于 H ,交直线 CD 于 M ,交 x 轴于 N ,∵H(2, 3 ),∴HM=
3 ﹣1= 3 <1,∴ 当点 P 不可能在 DE 的上方; ③∵MN=1,且 O (0,0),a (4,0),∴P 与 O 或 A 重合时,符合条件,∴m=0 或 m=4; 综上所述,△PDE 的面积不小于 1 时,m 的取值范围是:m=0 或 m=
4 或 m≤2﹣ 10 或 m≥2+ 10 . 点睛:本题是二次函数的综合题,考查了利用待定系数法求二次函数的解析式、对称性、二次函数的性质、图形和坐标特点、折叠的性质;运用了数形结合的思想和分类讨论的思想,应用部分有难度, 根据面积的条件,先求出底边的长和确定高的取值是关键. 考点:二次函数综合题;翻折变换(折叠问题);分类讨论;阅读型;压轴题. 58.(2017 吉林省长春市,第 23 题,10 分)如图①,在 Rt△ABC 中,∠C=90°,AB=10,BC=6,点 P 从点 A 出发,沿折线 AB ﹣BC 向终点 C 运动,在 AB 上以每秒
5 个单位长度的速度运动,在 BC 上以每 4
秒 3 个单位长度的速度运动,点 Q 从点 C 出发,沿 CA 方向以每秒 3 个单位长度的速度运动,P ,Q 两 点同时出发,当点 P 停止时,点 Q 也随之停止.设点 P 运动的时间为 t 秒. (1) 求线段 AQ 的长;(用含 t 的代数式表示) (2)
连结 PQ ,当 PQ 与△ABC 的一边平行时,求 t 的值; (3) 如图②,过点 P 作 PE⊥AC 于点 E ,以 PE ,EQ 为邻边作矩形 PEQF ,点 D 为 AC 的中点,连结 7 7 7 7 ?
102 - 62
? DF .设矩形 PEQF 与△ABC 重叠部分图形的面积为 S .
①当点 Q 在线段 CD 上运动时,求 S 与 t 之间的函数关系式;
②直接写出 DF 将矩形 PEQF 分成两部分的面积比为 1:2 时 t 的值.
?
-16t 2 + 24t (0 ≤ t ≤ 3) ?
?
S = ?- ? 16 t 2
+ 40t - 48 ( 3 3 2 2 < t ≤ 2)
4 3 ?- 20 t 2
+ 30t - 24 (2 < t ≤ 3)
【答案】(1)AQ=8﹣ 3 t (0≤t≤4);(2)t= 2 s 或 3s ;(3)① ?? 3
;②t=
3 6
5 s 或 5 s .
【分析】(1)利用勾股定理先求出 AC ,根据 AQ=AC ﹣CQ 即可解决问题; (2) 分两种情形列出方程求解即可;
3 3
(3) ①分三种情形 a 、如图 1 中,当 0≤t≤ 2 时,重叠部分是四边形 PEQF .b 、如图 2 中,当 2 <t≤2 时,重叠部分是四边形 PNQE .C 、如图 3 中,当 2<t≤3 时,重叠部分是五边形 MNPBQ .分别求解即可;
②分两种情形 a 、如图 4 中,当 DE :DQ=1:2 时,DF 将矩形 PEQF 分成两部分的面积比为 1:2.b 、如图 5 中,当 NE :PN=1:2 时,DF 将矩形 PEQF 分成两部分的面积比为 1:2.分别列出方程即可解决问题; 【解析】(1)在 Rt△ABC 中,∵∠C=90°,AB=10,BC=6
4
= =8,∵CQ= 3 t ,∴
4
AQ=8﹣ 3 t (0≤t≤4).
AP =
AQ
5t =
8 - 4 t 3 3 (2) ①当 PQ∥BC 时, AB AC ,∴
10 8 4 t
,∴t= 2 s . CQ =
CP 3 = 6 - 3(t - 2) ②当 PQ∥AB 时, CA CB ,∴ 8 6 ,∴t=3.
3
综上所述,t=
2 s 或 3s 时,当 PQ 与△ABC 的一边平行. 3
(3) ①如图 1 中,a 、当 0≤t≤
2 时,重叠部分是四边形 PEQF . AB 2 - BC 2
4
S=PE?EQ=3t?(8﹣4t﹣3 t)= -16t 2 + 24t .
3
b、如图 2 中,当2 <t≤2 时,重叠部分是四边形 PNQE.
1 4 5 4 3 5 4
S=S 四边形 PEQF﹣S△PFN=(16t2﹣24t)﹣2 ?5 [5t﹣4 (8﹣3 t)]?5 [5t﹣4 (8﹣3 t0]=
-16
t 2+ 40t - 48 3 .
C.如图 3 中,当 2<t≤3 时,重叠部分是五边形 MNPBQ.
4 1 4 3 4
S =S 四边形 PBQF -S△FNM= 3 t?[6﹣3(t﹣2)]﹣2 ?[3 t﹣4(t﹣2)]?4 [ 3 t﹣4(t﹣2)]=
-20
t 2+ 30t - 24 3 .
? ?
-16t 2 + 24t (0 ≤ t ≤ 3) ?
?
S =
?- ? 16 t 2 + 40t - 48 ( 3 3 2 2 < t ≤ 2) ?- 20 t 2
+ 30t - 24 (2 < t ≤ 3)
综上所述: ?
? 3
;
②a、如图 4 中,当 DE :DQ=1:2 时,DF 将矩形 PEQF 分成两部分的面积比为 1:2.
4 3 则有(4﹣4t ):(4﹣
3 t )=1:2,解得 t= 5 s ; b 、如图 5 中,当 NE :PN=1:2 时,DF 将矩形 PEQF 分成两部分的面积比为 1:2.
4 6
∴DE:DQ=NE :FQ=1:3,∴(4t ﹣4):(4﹣
3 t )=1:3,解得 t= 5 s .
3 6
综上所述,当 t=
5 s 或 5 s 时,DF 将矩形 PEQF 分成两部分的面积比为 1:2. 点睛:本题考查四边形综合题、矩形的性质、勾股定理、相似三角形的性质和判定、平行线分线段成
比例定理等知识,解题的关键是学会用分类讨论的思想思考问题,学会构建方程解决问题,属于中考压轴题.
考点:相似三角形的判定与性质;四边形综合题;分段函数;分类讨论;动点型;压轴题. 59.(2017 吉林省长春市,第 24 题,12 分)定义:对于给定的两个函数,任取自变量 x 的一个值,当 x <0 时,它们对应的函数值互为相反数;当 x≥0 时,它们对应的函数值相等,我们称这样的两个
??-x +1( x < 0) y = ?
函数互为相关函数.例如:一次函数 y=x ﹣1,它的相关函数为 ??
x -1( x ≥ 0) .
(1) 已知点 A (﹣5,8)在一次函数 y=ax ﹣3 的相关函数的图象上,求 a 的值;
?ax - 3(x ≥ 0) ? ?
(2) 已知二次函数
y = -x 2 + 4x - 1
2 .
3
①当点 B (m ,
2 )在这个函数的相关函数的图象上时,求 m 的值; y = -x 2 + 4x - 1
②当﹣3≤x≤3 时,求函数
2 的相关函数的最大值和最小值;
1 9
(3) 在平面直角坐标系中,点 M ,N 的坐标分别为(﹣ 2 ,1),( 2 ,1}),连结 MN .直接写出线段 MN
与二次函数
y = -x 2
+ 4x + n 的相关函数的图象有两个公共点时 n 的取值范围.
43 1
【答案】(1)1;(2)①m=2﹣ 或 m=2+ 或 m=2﹣ ;②最大值为 2 ,最小值为﹣
2 ;(3)﹣3<n≤
5
﹣1 或 1<n≤
4 .
【分析】(1)函数 y=ax ﹣3 的相关函数为求解即可;
y = ?-ax + 3(x < 0)
? ,将然后将点 A (﹣5,8)代入 y=﹣ax+3
?x 2
- 4x + 1 (x < 0) y = ? 2 1
1 (2) 二次函数 y = -x
2 + 4x -
2 的相关函数为 ?-x 2 + 4x - ? (x ≥ 0)
2 ,①分为 m <0 和 m≥0 两种情况
将点 B 的坐标代入对应的关系式求解即可;②当﹣3≤x<0 时,
y = -x 2 + 4x - 1
y = -x 2 + 4x - 1
2 ,然后可 此时的最大 值和最小值,当 0≤x≤
3 时,函数3 时的最大值和最小值;
2 ,求得此时的最大值和最小值,从而可得到当﹣3≤x≤ (3) 首先确定出二次函数
y = -x 2
+ 4x + n 的相关函数与线段 MN 恰好有 1 个交点、2 个交点、3 个交点时 n 的值,然后结合函数图象可确定出 n 的取值范围.
y = ?-ax + 3(x < 0)
ax - 3(x ≥ 0)
【解析】(1)函数 y=ax ﹣3 的相关函数为 ? ,将点 A (﹣5,8)代入 y=﹣ax+3 得:5a+3=8,解得:a=1.
5 2 2
②当﹣3≤x<0 时,y =x2- 4x
+ 1
2 ,抛物线的对称轴为
x=2,此时 y 随x 的增大而减小,∴此时 y 的
43
最大值为2 .
y =-x2+ 4x -
1 1
当0≤x≤3时,函数 2 ,抛物线的对称轴为 x=2,当 x=0 有最小值,最小值为﹣2 ,当x=2
7
时,有最大值,最大值 y= 2 .
综上所述,当﹣3≤x≤3时,函数y =-x2+ 4x -
1
2 的相关函数的最大值为
43 1
2 ,最小值为﹣2 ;
(3)如图 1 所示:线段 MN 与二次函数y =-x2 + 4x +n 的相关函数的图象恰有 1 个公共点.
所以当 x=2 时,y=1,即﹣4+8+n=1,解得 n=﹣3.
如图 2 所示:线段 MN 与二次函数y =-x2 + 4x +n 的相关函数的图象恰有 3 个公共点
∵抛物线y =-x2 + 4x +n 与y 轴交点纵坐标为 1,∴﹣n=1,解得:n=﹣1,∴当﹣3<n≤﹣1 时,线段MN 与二次函数y =-x2 + 4x +n 的相关函数的图象恰有 2 个公共点.
如图 3 所示:线段 MN 与二次函数y =-x2 + 4x +n 的相关函数的图象恰有 3 个公共点.
∵抛物线y=-x2+4x+n经过点(0,1),∴n=1.
如图 4 所示:线段 MN 与二次函数y =-x2 + 4x +n 的相关函数的图象恰有 2 个公共点.
1 1 5 5
∵抛物线y=x2-4x-n经过点 M(﹣2,1),∴ 4+2﹣n=1,解得:n= 4,∴1<n≤4时,线段 MN 与二次函数y =-x2 + 4x +n 的相关函数的图象恰有 2 个公共点.
5
综上所述,n 的取值范围是﹣3<n≤﹣1 或1<n≤4 .
点睛:本题主要考查的是二次函数的综合应用,解答本题主要应用了二次函数的图象和性质、函数图象上点的坐标与函数解析式的关系,求得二次函数y =-x2 + 4x +n 的相关函数与线段 MN 恰好有 1 个交点、2 个交点、3 个交点时 n 的值是解题的关键.
? 考点:二次函数综合题;新定义;二次函数的最值;最值问题;分类讨论;压轴题.
60.(2017 四川省内江市,第 28 题,12 分)如图,在平面直角坐标系中,抛物线
y = ax 2
+ bx + c (a≠0)与 y 轴交与点 C (0,3),与 x 轴交于 A 、B 两点,点 B 坐标为(4,0),抛物线的对称轴方程为 x=1.
(1) 求抛物线的解析式; (2) 点 M 从 A 点出发,在线段 AB 上以每秒 3 个单位长度的速度向 B 点运动,同时点 N 从 B 点出发, 在线段 BC 上以每秒 1 个单位长度的速度向 C 点运动,其中一个点到达终点时,另一个点也停止运动, 设△MBN 的面积为 S ,点 M 运动时间为 t ,试求 S 与 t 的函数关系,并求 S 的最大值; (3) 在点 M 运动过程中,是否存在某一时刻 t ,使△MBN 为直角三角形?若存在,求出 t 值;若不存在,请说明理由.
【答案】(1)
y = - 3 x 2 + 3 x + 3 8 4
;(2)S= - 9 t 2 + 9 t
10 5 9 ,运动 1 秒使△PBQ 的面积最大,最大面积是10 ;
24 30
(3)t=
17 或 t= 19 . 【分析】(1)把点 A 、B 、C 的坐标分别代入抛物线解析式,列出关于系数 a 、b 、c 的解析式,通过解
方程组求得它们的值; (2) 设运动时间为 t 秒.利用三角形的面积公式列出 S△MBN 与 t 的函数关系式.利用二次函数的图象性质进行解答; (3) 根据余弦函数,可得关于 t 的方程,解方程,可得答案. 【解析】(1)∵点 B 坐标为(4,0),抛物线的对称轴方程为 x=1,∴A(﹣2,0),把点 A (﹣2,0)、B (4,0)、
?
a = - 3 ?
? ?
点 C (0,3),分别代入 y = ax 2
+ bx + c ?4a - 2b + 3 = 0 (a≠0),得: ?16a + 4b + 3 = 0 ?b = ? ?c = 3 ,解得: ?? ,所以该抛物
线的解析式为:
y = - 3 x 2 + 3
x + 3
8 4 ; (2) 设运动时间为 t 秒,则 AM=3t ,BN=t ,∴MB=6﹣3t .由题意得,点 C 的坐标为(0,3).在 Rt△BOC
HN = BN
中,BC= =5.如图
1,过点 N 作 NH⊥AB 于点 H ,∴NH∥CO,∴△BHN∽△BOC,∴ OC BC ,即
HN =
t 3 1 1 3 - 9 t 2 + 9 t - 9 (t -1)2 + 9 3 5 ,∴ HN= 5 t ,∴ S△ MBN= 2 MB?HN= 2 ( 6﹣3t )? 5 t ,即 S= 10 5 = 10 10 ,当△ PBQ
9
存在时,0<t <2,∴当 t=1 时,S△PBQ 最大= 10 .
32 + 42
4 3
8
9答:运动 1 秒使△PBQ 的面积最大,最大面积是10 ;
OB
=
4
(3)如图2,在Rt△OBC中,cos∠B=BC 5 .
设运动时间为 t 秒,则 AM=3t,BN=t,∴MB=6﹣3t.
BN
=4 t
=
4 24
①当∠MNB=90°时,cos∠B=MB 5 ,即6 - 3t 5 ,化简,得 17t=24,解得 t= 17 ;
6 - 3t
=4 30
②当∠BMN=90°时,cos∠B= t 5 ,化简,得19t=30,解得t= 19 .
24 30
综上所述:t= 17 或t= 19 时,△MBN为直角三角形.
点睛:本题是二次函数的综合题型,其中涉及到的知识点有待定系数法求二次函数解析式和三角形的面积求法.在求有关动点问题时要注意该点的运动范围,即自变量的取值范围.
考点:二次函数综合题;最值问题;二次函数的最值;动点型;存在型;分类讨论;压轴题.61.(2017 四川省南充市,第 25 题,10 分)如图 1,已知二次函数y=ax2+bx+c(a、b、c 为常数,a≠0)
-8
的图象过点 O(0,0)和点 A(4,0),函数图象最低点 M 的纵坐标为 3 ,直线 l 的解析式为 y=x.
(1)求二次函数的解析式;
(2)直线 l 沿x 轴向右平移,得直线l′,l′与线段 OA 相交于点 B,与x 轴下方的抛物线相交于点C,过点 C 作CE⊥x轴于点 E,把△BCE沿直线l′折叠,当点 E 恰好落在抛物线上点E′时(图2),求直线l′的解析式;
(3)在(2)的条件下,l′与y 轴交于点 N,把△BON绕点O 逆时针旋转135°得到△B′ON′,P 为l′
上的动点,当△PB′N′为等腰三角形时,求符合条件的点 P 的坐标.
y =2
x2-
8
x 3 2 + 3 -3 3 3 2 - 3 - 3 3
【答案】(1) 3 3 ;(2)y=x﹣3;(3)P 坐标为(0,﹣3)或( 2 , 2 )
3 2 + 3 + 3 3 或(2
3 2 - 3 + 3 3
, 2 ).
-
8
y =a(x - 2)2-
8
【分析】(1)由题意抛物线的顶点坐标为(2, 3 ),设抛物线的解析式为 3 ,把(0,0)
2
代入得到 a= 3 ,即可解决问题;
2
m2-8
m -
2
m2+
11
m
(2)如图1 中,设E(m,0),则C(m,3 3
m + (-2
m2+
11
m)
3 3
),B( 3 3,0),由E、B 关于对称轴对称,
可得2=2,由此即可解决问题;
(3)分两种情形求解即可①当 P1 与N 重合时,△P1B′N′是等腰三角形,此时 P1(0,﹣3).②当N′=N′B′时,设 P(m,m﹣3),列出方程解方程即可;
-8
【解析】(1)由题意抛物线的顶点坐标为(2, 3 ),设抛物线的解析式为y =a(x - 2)2-
8
3 ,把(0,0)
2
代入得到 a= 3 ,∴抛物线的解析式为y =
2
(x - 2)2-
8
3 3 ,即
2
m2-
8
m
y =
2
x2-
8
x
3 3 .
-
2
m2+
11
m
(2)如图1 中,设E(m,0),则C(m,3 3),B( 3 3,0),
∵E′在抛物线上,∴E、B 关于对称轴对称,∴m + (-
2
m2+
11
m)
3 3
2 =2,解得m=1 或6(舍弃),∴B(3,0),C
(1,﹣2),∴直线l′的解析式为 y=x﹣3.
(3)如图 2 中,①当 P1 与N 重合时,△P1B′N′是等腰三角形,此时 P1(0,﹣3).
(m -3 2
)2+ (m - 3 -
3 2
)2= (3 2)2 3 2 + 3 - 3 3
②当N′=N′B′时,设P(m,m﹣3),则有 2 2 ,解得m= 2
3 2 + 3 + 3 3
或2,∴P2(
3 2 + 3 - 3 3
2
3 2 - 3 - 3 3
, 2 ),P3(
3 2 + 3 + 3 3
2
3 2 - 3 + 3 3
, 2 ).
综上所述,满足条件的点 P 坐标为(0,﹣3)或(
3 2 - 3 + 3 3
3 2 + 3 - 3 3
2
3 2 - 3 - 3 3
, 2 )或(
3 2 + 3 + 3 3
2 ,
2 ).
点睛:本题考查二次函数综合题、待定系数法、等腰三角形的判定和性质、两点间距离公式等知识,
解题的关键是学会用分类讨论的思想思考问题,学会根据方程,属于中考压轴题.
考点:二次函数综合题;几何变换综合题;分类讨论;压轴题.
62.
(2017 四川省宜宾市,第24 题,12 分)如图,抛物线y=-x2+bx+c与x 轴分别交于A(﹣1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)在第二象限内取一点 C,作 CD 垂直X 轴于点 D,链接 AC,且 AD=5,CD=8,将Rt△ACD沿x 轴向
右平移 m 个单位,当点 C 落在抛物线上时,求 m 的值;
(3)在(2)的条件下,当点 C 第一次落在抛物线上记为点 E,点 P 是抛物线对称轴上一点.试探究:
在抛物线上是否存在点 Q,使以点 B、E、P、Q 为顶点的四边形是平行四边形?若存在,请出点 Q 的坐标;若不存在,请说明理由.
-25 + 5b + c = 0 c = 5 【答案】(1)
y = -x 2 + 4x + 5 ;(2)m 的值为 7 或 9;(3)Q 点的坐标为(﹣2,﹣7)或(6,﹣7) 或(4,5).
【分析】(1)由 A 、B 的坐标,利用待定系数法可求得抛物线的解析式; (2) 由题意可求得 C 点坐标,设平移后的点 C 的对应点为 C′,则 C′点的纵坐标为 8,代入抛物线解析式可求得 C′点的坐标,则可求得平移的单位,可求得 m 的值; (3) 由(2)可求得 E 点坐标,连接 BE 交对称轴于点 M ,过 E 作 EF⊥x 轴于点 F ,当 BE 为平行四边形的边时,过 Q 作对称轴的垂线,垂足为 N ,则可证得△PQN≌△EFB,可求得 QN ,即可求得 Q 到对称轴的距离,则可求得 Q 点的横坐标,代入抛物线解析式可求得 Q 点坐标;当 BE 为对角线时,由 B 、E 的坐标可求得线段 BE 的中点坐标,设 Q (x ,y ),由 P 点的横坐标则可求得 Q 点的横坐标,代入抛物线解析式可求得 Q 点的坐标. 【解析】
(1) ∵抛物线
?b = 4
y = -x 2 + bx + c ?-1- b + c = 0
? 与
x 轴分别交于 A (﹣1,0),B (5,0)两点,∴ ? ,解得: ?
?
,∴抛物线解析式为 y = -x 2 + 4x + 5 ; (2) ∵AD=5,且 OA=1,∴OD=6,且 CD=8,∴C (﹣6,8),设平移后的点 C 的对应点为 C′,则 C′
点的纵坐标为 8,代入抛物线解析式可得 8=
-x 2 + 4x + 5 ,解得 x=1 或 x=3,∴C′点的坐标为(1,8) 或(3,8),∵C(﹣6,8),∴当点 C 落在抛物线上时,向右平移了 7 或 9 个单位,∴m 的值为 7 或 9;
(3)∵ y = -x 2 + 4x + 5 = -(x - 2)2
+ 9 坐标为(1,8),分两种情况讨论:
,∴抛物线对称轴为 x=2,∴可设 P (2,t ),由(2)可知 E 点
①当 BE 为平行四边形的边时,连接 BE 交对称轴于点 M ,过 E 作 EF⊥x 轴于点 F ,当 BE 为平行四边形的边时,过 Q 作对称轴的垂线,垂足为 N ,如图,则∠BEF=∠BMP=∠QPN,在△PQN 和△EFB 中,∵∠QPN=∠ BEF ,∠PNQ=∠EFB,PQ=BE ,∴△PQN≌△EFB(AAS ),∴NQ=BF=OB﹣OF=5﹣1=4,设 Q (x ,y ),则 QN=|x ﹣2|, ∴|x﹣2|=4,解得x=﹣2 或x=6,当x=﹣2 或x=6 时,代入抛物线解析式可求得y=﹣7,∴Q 点坐标为(﹣2, ﹣7)或(6,﹣7);
②当 BE 为对角线时,∵B(5,0),E (1,8),∴线段 BE 的中点坐标为(3,4),则线段 PQ 的中点坐标为(3,4),设 Q (x ,y ),且 P (2,t ),∴x+2=3×2,解得 x=4,把 x=4 代入抛物线解析式可求得 y=5,∴Q (4,5);
综上可知 Q 点的坐标为(﹣2,﹣7)或(6,﹣7)或(4,5).
点睛:本题为二次函数的综合应用,涉及待定系数法、平移的性质、全等三角形的判定和性质、平行四边形的性质、方程思想及分类讨论思想等知识.在(1)注意待定系数法的应用,在(2)中求得平