
目录
题目一 (2)
(一)状态反馈加积分器校正的输出反馈系统设计 (2)
(1)建立被控对象的状态空间模型,并判断系统性质 (2)
(2)状态反馈增益矩阵和积分增益常数的设计 (4)
(3)全维观测器设计 (6)
(4)如何在闭环调速系统中增加限流环节 (8)
(二)二次型最优全状态反馈控制和按负载扰动前馈补偿的复合控制系统设计 (8)
(1)线性二次型最优全状态反馈设计 (8)
(2)降维观测器设计 (13)
题目二 (15)
(1)判断系统是否存在最优控制律 (15)
(2)非零给定点的最优控制设计和仿真分析 (16)
(3)权矩阵的各权值对动态性能影响分析 (17)
题目一
(一)状态反馈加积分器校正的输出反馈系统设计 (1)建立被控对象的状态空间模型,并判断系统性质
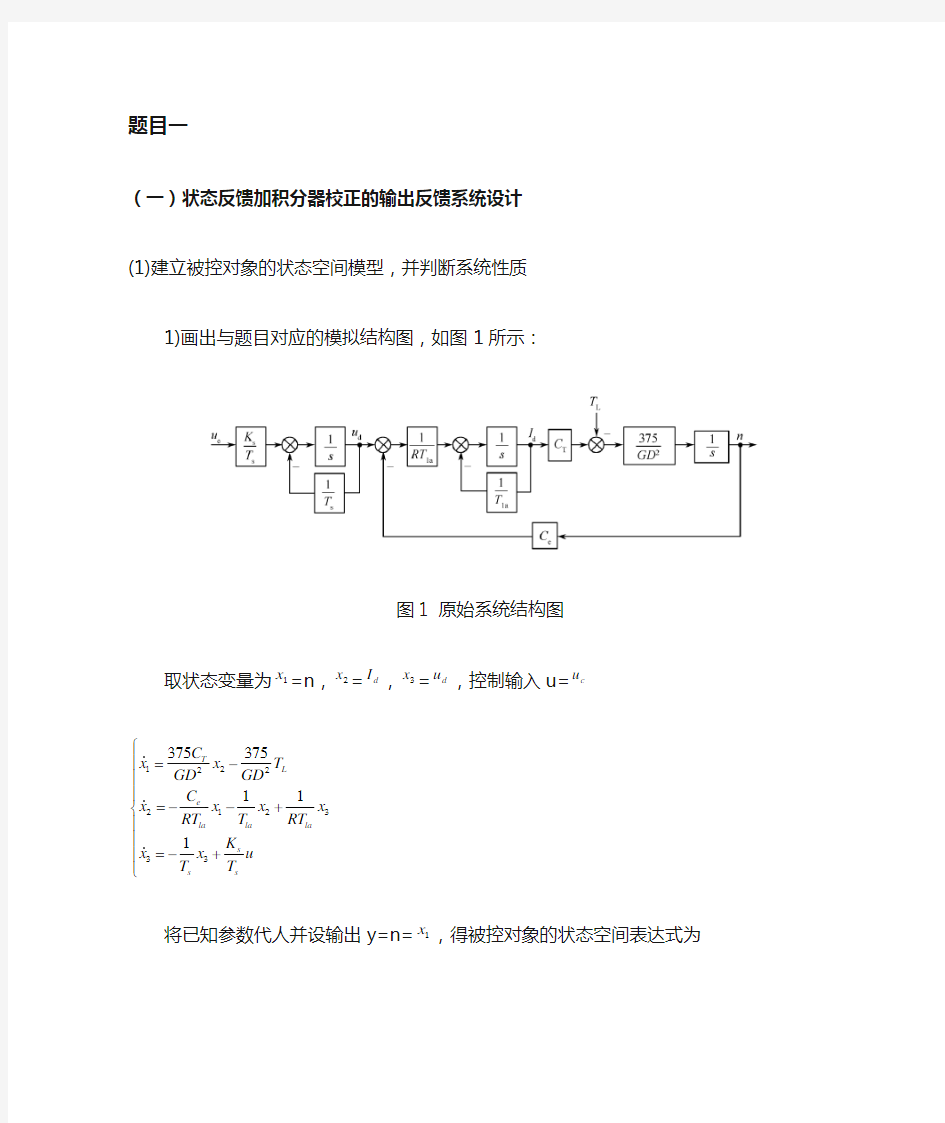
1)画出与题目对应的模拟结构图,如图1所示:
图1原始系统结构图
取状态变量为1x =n ,2x =d I ,3x =d u ,控制输入u=c u
1222212333375375111
T L
e la la la s s s C x x T GD GD C x x x x RT T RT K x
x u T T ?=-???=--+???=-+??
将已知参数代人并设输出y=n=1x ,得被控对象的状态空间表达式为
L x Ax Bu ET y Cx
=++=
其中,2
37500039.768011=-3.696-17.85727.05600-588.2351
00
T e
la la
la s C GD C A RT T RT T ????
?
???????=-
-??????
??????-???
?
,
000=023529.41s s B K T ??????????=????????????????
,2375-30.4880=000GD E ??-????????=????????
?
?????,[]100C = 2)检查被控系统的结构性质
判断系统能控性、能观性、稳定性 程序如下:
A=[0 39.768 0;-3.696 -17.857 27.056;0 0 -588.235]; B=[0;0;23529.41];C=[1 0 0]; Qc=ctrb(A,B); Qo=obsv(A,C); L=length(A); if rank(Qc)==L
disp('系统是状态完全能控'); else
disp('系统是状态不完全能控'); end
if rank(Qo)==L
disp('系统是状态完全能观'); else
disp('系统是状态不完全能观'); end
disp(eig(A))%利用A 的特征值判断系统稳定性 运行结果:
系统是状态完全能控 系统是状态完全能观 1.0e+02 *
-0.0893 + 0.0820i -0.0893 - 0.0820i -5.8823 + 0.0000i
由于矩阵A 全部特征值均具有负实部,因此系统渐近稳定。 原系统
设负载转矩为0,输入为阶跃信号,系统simulink 仿真如下:
图2原始开环系统结构框图
图3原始开环系统仿真
分析:由系统仿真图可以看出,调节时间大于0.5s ,不满足性能指标。
(2)状态反馈增益矩阵和积分增益常数的设计
由于原系统能控,可以使用状态反馈。为满足设计指标,采用状态反馈加积分器校正的输出反馈系统。因增广系统能控,故可采用线性状态反馈控制律12u K x K w =-+。 将闭环系统极点配置到复平面左半开平面的任意期望位置且可消除阶跃扰动及阶跃参考输入作用下的稳态误差。
式中:[
]111
12
13=K K K K ,[]12
3=T
x x x x ,w v y =-,v 为系统参考输入。
由经典控制理论,闭环极点为1,2n j λζωω=-±的欠阻尼二阶线性定常系统的
超调量及调节时间为%=100%e
σ?, 3.5
s n
t ζω=
。
系统需满足%%σ≤8,0.5s s t ≤,计算可得0.6266ζ≥,n ω≥11.1714,取=0.7ζ,
=n ω12,设计指标的期望闭环主导极点对为*
1,28.48.57j λ=-±。选择2个期望的闭环非主
导极点离虚轴为主导极点5倍以上,取*
3,450λ=-,据期望闭环极点,采用MATLAB 极点配置函数可求出增广系统状态反馈增益阵,程序如下:
A=[0 39.768 0;-3.696 -17.857 27.056;0 0 -588.235]; B=[0;0;23529.41];C=[1 0 0];
Az=[A [0;0;0];-C 0];Bz=[B;0];Cz=[C 0]; P=[-8.4+j*8.57;-8.4-j*8.57;-50;-50]; Km=acker(Az,Bz,P);
K=[Km(1,1),Km(1,2),Km(1,3),-Km(1,4)] 运行程序可得:
[]
[]
11
1213
2=0.001650.003780.02080.0142K K K K K =-
系统simulink 仿真如下:
图4状态反馈加积分器校正系统结构框图
图5状态反馈加积分器校正系统仿真
由图可知,超调量%(
1.0420-1)/1 4.2%8%σ==<,调节时间0.5s s t <,满足要求。
图6 加负载扰动后系统状态反馈加积分器校正系统仿真
0时刻扰动,最终系统稳定在1,因此系统稳态误差为0。
(3)全维观测器设计
由于系统能观,可以使用状态观测器。
2
37500039.768011=-3.696-17.85727.05600-588.2351
00
????
?
???????=-
-??????
??????-???
?
T e la la
la s C GD C A RT T RT T , 000=023529.41s s B K T ??????????=???????
?
????????
,[]100C =,
[][]1111213=0.001650.003780.0208=-K K K K
2
111121337500039.768011-=-3.696-17.85727.056-38.8235-88.9412-98.82331?
?
??
?
???????=-
-??????????
??-
---??
?
?
T e
la la
la
s s s s s s s C GD C A BK RT T RT K K K K K K T T T T 新系统的特征根为:-61,27.807212.1936j -±,基于通常选择观测器的响应速度
比所考虑的状态反馈闭环系统快2-5倍这一经验规则,取观测器期望极点为:-150,-60,-70。
应用MATLAB 极点配置函数求解新系统全维观测器,程序如下: A=[0 39.768 0;-3.696 -17.857 27.056;-38.8235 -88.9412 -98.8233]; B=[0;0;23529.41];C=[1 0 0]; P=[-150;-60;-70];
Gt=acker(A',C',P);%求对偶系统的状态反馈增益阵G G=Gt';%求系统的观测器偏差反馈增益矩阵G 运行程序可得:
163.3197G=8.1911129.8454??
??????-??
。
带观测器的状态反馈加积分调节系统仿真结构图如下:
图7带观测器的状态反馈加积分器校正系统结构框图
图8系统加全维观测器波形图
图9全维观测器波形图
由仿真图可知,系统的稳态误差为0,动态误差满足超调量%% ≤8,调节时间0.5s s t ≤的要求。
状态估计误差收敛速度与状态观测器极点的配置有关。一般而言状态观测器极点在复平面的左半开平面距离虚轴距离越远,则估计误差收敛速度越快。但是,观测器响应速度过快会产生大量噪声,影响系统的正常工作故不宜取值过大。综合工程实际出发,一般取为比状态反馈闭环系统快2—5倍。
(4)如何在闭环调速系统中增加限流环节
从加快启动电动机的角度来看,闭环调速系统应允许有较大的启动电流,而造成堵转的故障消失后,系统电流应能自动恢复正常。所以常规的熔断器或过流继电器在这里均不能作为限流保护措施。因为它们是通过切断电路来保护设备的,虽然能起到保护作用,但故障消失后,系统无法自动恢复正常。为了充分利用设备的过流能力,又保证设备的安全运行,电流截止负反馈则可以限制电流的大小。
电流截止负反馈的作用是:当电枢电流大于某一截止值时,电流负反馈起作用,限制电流不能过大。当电枢电流小于截止值时,电流反馈被截止,对系统的稳态运行不产生影响。电动机启动时,因为电流截止负反馈作用,从而限制启动电流。正常工作时,电流截止负反馈作用很小。电动机发生堵转时,由于电流截止负反馈的作用,使Ud 大大下降,因而使Ia 不致过大。允许的堵转电流一般为电动机额定电流的2~2.5倍。系统工作在额定值时,由于电流截止负反馈起作用,从而保证系统设备的安全。 电流截止负反馈如图所示:
图10 电流截止负反馈结构图
(二)二次型最优全状态反馈控制和按负载扰动前馈补偿的复合控制系统设计 (1)线性二次型最优全状态反馈设计
1)判断系统是否存在最优控制律
要使系统阶跃响应具有良好的动、静态特性,可按非零给定点的最优控制律设计,即()()g u t Kx t u *=-+,由于输入维数和输出维数相等,所以1()()(0)c w u t Kx t W y *-=-+。
由于系统完全能控,因此,最优控制()u t *存在。 最优控制性能指标为:0
1
()()()()2
T T
t
J x t Qx t u t Ru t dt ∞
??=
+???,其中Q 为状态加
权系数矩阵,R 为控制加权系数矩阵。
2)非零给定点的最优控制设计和仿真分析
由图可知,系统输出响应发散,可引入最优控制1()()(0)c w u t Kx t W y *-=-+。
选取设
????????
=????????
???
?112233001000000=01000100q Q q q ,R=1。
程序如下:
A=[0 39.768 0;-3.696 -17.857 27.056;0 0 -588.235]; B=[0;0;23529.41]; C=[1 0 0]; D=0; R=1;
Q=[100 0 0;0 1 0;0 0 1]; K=lqr(A,B,Q,R); ac=A-B*K;
W=inv((-C/(A-B*K))*B); bc=B*W; cc=C; dc=D;
step(ac,bc,cc,dc); grid
运行结果如下:[]K=9.8635 4.87020.9809,110.0009c W -=。
图11非零给定点最优控制系统单位阶跃响应
3)权矩阵的各权值对动态性能影响分析
a)固定控制加权系数矩阵R=1,且另22q 、33q 都为1,11q 取不同值时,研究非零给定点的最优控制仿真曲线。程序如下:
a_color=['r','g','b','y','c', 'm','k'];
A=[0 39.768 0;-3.696 -17.857 27.056;0 0 -588.235]; B=[0;0;23529.41];
C=[1 0 0];
D=0; R=1;
syms Q q11;
N=[1 100,200,500,1000,10000]; syms i K; for i=1:6
q11=N(i);
Q=[q11 0 0;0 1 0;0 0 1] K=lqr(A,B,Q,R); ac=A-B*K;
W=inv(-C/(A-B*K)*B); bc=B*W; cc=C; dc=D;
sys(i)=ss(ac,bc,cc,dc); end figure(1)
step(sys(1),a_color(1),sys(2),a_color(2),sys(3),a_color(3),sys(4),a_color(4),sys(5),a_color(5) ,sys(6),a_color(6));
grid
结果曲线如下:
图1211q 取不同值时二次型最优全状态反馈曲线
红色:111q =,绿色:11100q =,蓝色:11200q =,黄色:11500q =,蓝绿色:111000q =,紫红1110000q =。
由图可知,随着11q 的增大,调节时间减少;如果11q 过大,超调量会增大。
b)固定控制加权系数矩阵R=1,11q 、22q 、33q 分别取相同值时,研究非零给定点的最优控制仿真曲线。程序如下:
a_color=['r','g','b'];
A=[0 39.768 0;-3.696 -17.857 27.056;0 0 -588.235]; B=[0;0;23529.41]; C=[1 0 0]; D=0; R=1;
syms Q q11 q22 q33; for i=1:3 q11=1; q22=1; q33=1;
Q=[q11 0 0;0 q22 0;0 0 q33]; Q(i,i)=100;
K=lqr(A,B,Q,R); ac=A-B*K;
W=inv(-C/(A-B*K)*B); bc=B*W; cc=C; dc=D;
sys(i)=ss(ac,bc,cc,dc); end
figure(1)
step(sys(1),a_color(1),sys(2),a_color(2),sys(3),a_color(3)); grid
结果曲线如下:
图1311q 、22q 、33q 分别取相同值时二次型最优全状态反馈曲线
红色:
11100
q=,绿色:
22100
q=,蓝色:
33100
q=。
由图可知,
11100
q=时,调节时间最小,系统动态性能比另外两个好。
c)当状态加权系数矩阵Q不变,控制加权系数矩阵R取不同值时。研究非零给定点的最优控制仿真曲线。程序如下:
a_color=['r','g','b','y','c'];
A=[0 39.768 0;-3.696 -17.857 27.056;0 0 -588.235];
B=[0;0;23529.41];
C=[1 0 0];
Q=[100 0 0;0 1 0;0 0 1];
D=0;
syms R;
N=[1,100,1000,1500,10000];
for i=1:5
R=N(i);
K=lqr(A,B,Q,R);
ac=A-B*K;
W=inv(-C/(A-B*K)*B);
bc=B*W;
cc=C;
dc=D;
sys(i)=ss(ac,bc,cc,dc);
end
figure(1)
step(sys(1),a_color(1),sys(2),a_color(2),sys(3),a_color(3),sys(4),a_color(4),sys(5),a_color(5) );
grid
结果曲线如下:
图14 R取不同值时二次型最优全状态反馈曲线
由图可知,R 越大时,调节时间也越大。
(2)降维观测器设计
由于L T 平稳变化,n 、d I 、d u 均可准确测量,对负载转矩进行估计的降维观测器的设计需要对原系统结构进行变化参考文献[3],系统增广矩阵的状态方程可写成:
220
00
00375375000110010000
00030.488039.7680=0 3.69617.85727.056000588.235T
L L e d d la la la s d d s s C T T GD GD n
n C u I I RT T RT K u u T T ????????????-??
????????
????????=
+--????????
???????????
???????????-???
?????-????--?
-?? 000
23529.41L d d T n u
I u ????
????????+?????????
??
??, 010*********L d d T n y I u ??
????
????=????
????
????
。 参考文献[1],将直接可测的与不能直接可测的状态变量分开:
1111121
2221222X B A A X u X B A A X ??????
??=+?????????
??
??????????? , []12201X y X X ??
==????
。
式中,11=0A ,[]12=000A ,21-30.488=00A ??????
????
,
22039.7680-3.696-17.85727.05600-588.235A ????=??????
,
1=0B ,20=023529.41B ??????????,1L X T =,2d d n X I u ??
??=??
????
。
需要设计一维观测器重构。设降维观测器的反馈阵[
]12
3G g g g =。
则降维观测器特征多项式为:
11211()det[()]30.488f I A GA g λλλ=--=-。
选择降维观测器期望极点为闭环极点的2-5倍,取=-150λ*
,则可得1=-4.920g 。引入降维观测器状态方程:
[]11211211211222
[-][-][(-)+-]=-150738195.660=-150738+195.66d
W A GA W B GB u A GA G A GA y W y W n I =++++
1+=-4.92X W Gy W n =
引入非零给定点最优控制,如:[]K=9.8635 4.87020.9809,110.0009c W -=。选取比例调节的前馈补偿:
3210.980940 4.8702401
0.42540 1.304410.0009
s s p c s T R K K K K K W K C +++?+?=
=?=?。
降维观测器仿真如下:
图15降维观测器仿真结构图
图16降维观测器无扰动时仿真波形
图17降维观测器1s 扰动时仿真波形
题目二
(1)判断系统是否存在最优控制律
要使系统阶跃响应具有良好的动、静态特性,可按非零给定点的最优控制律设计,即()()g u t Kx t u *=-+,由于输入维数和输出维数相等,所以1()()(0)c w u t Kx t W y *-=-+。
由于系统为能控标准型,所以系统完全能控,因此,最优控制()u t *存在。 最优控制性能指标为:0
1
()()()()2
T T
t
J x t Qx t u t Ru t dt ∞
??=
+???,其中Q 为状态加
权系数矩阵,R 为控制加权系数矩阵。
(2)非零给定点的最优控制设计和仿真分析
[]??
?
???
?=??????????+??????????--=x x x 0011008180100010y u 原系统动态仿真模型如下:
图18原系统结构框图
图19原系统单位阶跃响应
由图可知,系统输出响应发散,可引入最优控制1()()(0)c w u t Kx t W y *-=-+。选取设
????????
=????????
???
?112233001000000=01000100q Q q q ,R=1。
程序如下:
A=[0 1 0;0 0 1;0 -18 -8]; B=[0;0;1]; C=[1 0 0]; R=1;
Q=[100 0 0;0 1 0;0 0 1]; K=lqr(A,B,Q,R);
W=inv((-C/(A-B*K))*B);
运行结果如下:[]K=10
4.28320.5771,110c W -=。
非零给定点最有控制系统动态仿真模型如下:
图20非零给定点最有控制系统结构框图
图21非零给定点最优控制系统单位阶跃响应
(3)权矩阵的各权值对动态性能影响分析
1)固定控制加权系数矩阵R=1,且另22q 、33q 都为1,11q 取不同值时,研究非零给定点的最优控制仿真曲线。程序如下:
a_color=['r','g','b','y','c','k']; A=[0 1 0;0 0 1;0 -18 -8]; B=[0;0;1]; C=[1 0 0]; D=0; R=1;
syms Q q11;
N=[100,200,500,1000,10000];
syms i K; for i=1:5
q11=N(i);
Q=[q11 0 0;0 1 0;0 0 1] K=lqr(A,B,Q,R); ac=A-B*K;
k1=inv(-C/(A-B*K)*B); bc=B*k1; cc=C; dc=D;
sys(i)=ss(ac,bc,cc,dc); end figure(1)
step(sys(1),a_color(1),sys(2),a_color(2),sys(3),a_color(3),sys(4),a_color(4),sys(5),a_color(5));
grid
结果曲线如下:
图2211q 取不同值时二次型最优全状态反馈曲线
红色:11100q =,绿色:11200q =,蓝色:11500q =,黄色:111000q =,蓝绿色:
1110000q =。
由图可知,随着11q 的增大,调节时间减少;如果11q 过大,超调量会增大。
2) 固定控制加权系数矩阵R=1,11q 、22q 、33q 分别取相同值时,研究非零给定点的最优控制仿真曲线。程序如下:
a_color=['r','g','b'];
A=[0 1 0;0 0 1;0 -18 -8]; B=[0;0;1]; C=[1 0 0]; D=0; R=1;
syms Q q11 q22 q33; for i=1:3 q11=1; q22=1; q33=1;
Q=[q11 0 0;0 q22 0;0 0 q33]; Q(i,i)=100;
K=lqr(A,B,Q,R); ac=A-B*K;
W=inv(-C/(A-B*K)*B); bc=B*W; cc=C; dc=D;
sys(i)=ss(ac,bc,cc,dc); end
figure(1)
step(sys(1),a_color(1),sys(2),a_color(2),sys(3),a_color(3)); grid
结果曲线如下:
图2311q 、22q 、33q 分别取相同值时二次型最优全状态反馈曲线
红色:11100q =,绿色:22100q =,蓝色:33100q =。
由图可知,
11100
q 时,系统动态性能比另外两个好。
3)当状态加权系数矩阵Q不变,控制加权系数矩阵R取不同值时。研究非零给定点的最优控制仿真曲线。程序如下:
a_color=['r','g','b','y','c'];
A=[0 1 0;0 0 1;0 -18 -8];
B=[0;0;1];
C=[1 0 0];
Q=[100 0 0;0 1 0;0 0 1];
D=0;
syms R;
N=[1,100,1000,1500,10000];
for i=1:5
R=N(i);
K=lqr(A,B,Q,R);
ac=A-B*K;
W=inv(-C/(A-B*K)*B);
bc=B*W;
cc=C;
dc=D;
sys(i)=ss(ac,bc,cc,dc);
end
figure(1)
step(sys(1),a_color(1),sys(2),a_color(2),sys(3),a_color(3),sys(4),a_color(4),sys(5),a_color(5) );
grid
结果曲线如下:
图24 R取不同值时二次型最优全状态反馈曲线
由图可知,R越大时,调节时间也越大。
审定成绩: 重庆邮电大学 硕士研究生课程设计报告 (《线性系统理论》) 设计题目:汽车机器人建模 学院名称:自动化学院 学生姓名: 专业:控制科学与工程 仪器科学与技术 班级:自动化1班、2班 指导教师:蔡林沁 填表时间:2017年12月
重庆邮电大学
摘要 汽车被广泛的应用于城市交通中,它的方便、快速、高效给人们带来了很大便利,这大大改变了人们的生活. 研制出一种结构简单、控制有效、行驶安全的城市用无人智能驾驶车辆,将驾驶员解放出来,是大大降低交通事故的有效方法之一,应用现代控制理论设计出很多控制算法,对汽车进行控制是非常必要的,本文以汽车机器人为研究对象,对其进行建模和仿真,研究了其模型的能控能观性、稳定性,并通过极点配置和状态观测器对其进行控制,达到了一定的性能要求。这些研究为以后研究汽车的自动驾驶和路径导航,打下了一定的基础。 关键字:建模、能控性、能观性、稳定性、极点配置、状态观测器
目录 第一章绪论 (1) 第一节概述 (1) 第二节任务分工 (2) 第二章系统建模 (2) 2 系统建模 (2) 2.1运动学模型 (2) 2.2自然坐标系下模型 (4) 2.3具体数学模型 (6) 第三章系统分析 (7) 3.1 能控性 (7) 3.1.1 能控性判据 (7) 3.1.2 能控性的判定 (8) 3.2 能观性 (10) 3.2.1 能观性判据 (10) 3.2.2 能观测性的判定 (12) 3.3 稳定性 (13) 3.3.1 稳定性判据 (13) 3.3.2 稳定性的判定 (14) 第四章极点配置 (15) 4.1 极点配置概念 (15) 4.2 极点配置算法 (15) 4.3 极点的配置 (16) 4.4 极点配置后的阶跃响应 (17) 第五章状态观测器 (18) 5.1概念 (19) 5.2带有观测器的状态反馈 (20) 5.3代码实现 (21) 5.4 极点配置和状态观测器比较 (23)
摘要 神经网络自适应控制是基于自适应的基本原理,利用神经网络的特点设计而成的。它发挥了自适应与神经网络的各自长处,为非线性控制的研究提供了一种新方法。 本文基于Lyapunov稳定性理论,采用神经网络直接自适应控制的思想设计控制器,研究了一类带干扰的不确定非线性系统的控制问题。控制器主要是针对不确定非线性系统中存在的两类未知项——未知函数和未知外界干扰而设计,其中未知函数利用径向基函数神经网络来近似,外界干扰利用非线性阻尼项来抑制,这样可以充分利用神经网络的逼近特性,克服复杂系统难以建模等困难,并且系统稳定性和收敛性在给出的假设的条件下均能得到保证。最后设计程序进行仿真验证,在程序设计中,以高斯函数作为基函数,仿真结果表明在权值和控制的有界性方面取得了一定的效果。 本文第一章到第三章详细介绍了人工神经网络及神经网络控制的发展和研究现状;第四章主要介绍了径向基函数神经网络,并对其逼近能力进行仿真; 在结束语中展望了神经网络控制的发展前景,提出以后的研究方向。 关键词:RBF神经网络,自适应控制,不确定非线性系统 Abstract Neural network adaptive control is proposed combining adaptive control's advantages with neural network's characters and provides a new method for nonlinear control. Based on Lyapunov stability theorem and neural network direct adaptive control idea the control problem of a class of uncertain nonlinear system with disturbance is researched. The controller is designed arming at two kinds of uncertainties existing in nonlinear system--the unknown functions and the uncertain disturbance. In controller. the radial basis function neural network is used as approximation model for the unknown functions. and nonlinear damping term is used to counteract the disturbances. so neural network's better approximation capabilities can be utilized richly and the modeling difficulties can be avoided. Meanwhile. the controlled system's stability and convergence can be guaranteed under some assumptions. At last the program is designed to verify the effectiveness of the controller. In presented programs. Guassian function is used as basis function. Simulation results show that
电子通讯与控制职务说明书格式 第九研究室部门职务说明书电子控制与通讯岗位职务说明书岗位编号:205-905 编写日期:2003-11-27 岗位名称:电子通讯与控制在岗人数:6~7 所在部门:第九研究室编写人:直接上级:第九研究室主任.项目负责人直接下级:直接下级人数:审定人:本职概述:从事光电子和红外热成像技术及产品有关的电子通讯与控制组件的设计与研究工作。 跟踪.分析.报告国内外有关电子通讯与控制组件设计技术和热成像处理电子学的最新进展,了解和掌握电子电路加工与制造工艺技术.电子设计.产品和市场的动态。 职责一:参与产品开发或技术研究总体方案论证平均占工作时间百分比:15% 工作任务结合国内外电子控制技术和市场发展动态,及时报告.申请拟开展立项论证研究的课题结合总体方案论证的需求开展相关电子控制与通讯系统设计方案可行性论证,开展国内外相关技术调研建议.实施与信号处理论证研究直接相关的内部技术分析研讨会或关键技术的演示验证试验编制并提交产品开发或技术研究项目的电子控制与通讯系统论证报告工作权限工作责任工作频次工作关系内部关系外部关系建议权执行权有限责任每2~3年一次每次5~7周项目负责人.总体设计.光机结构设计.电子信号处理.可靠性预计
第七.第等专业研究室和试制研究中心职责二:设计输入控制平均占工作时间百分比:20% 工作任务根据总体下达的光机设计技术要求,制定电子通讯与控制系统的总体设计方案(基本组成.结构.布局和性能)确定电子通讯与控制组部件的技术性能要求,明确所选用元器件的电气特性.使用环境和工艺制造条件。 按照上级设计师系统下达的电子通讯与控制性能指标要求,制定电子通讯与控制系统的设计规范,明确规定电子通讯与控制系统的输入信号.控制输入与输出.功率输入.输出信号.噪声控制要求.通讯接口标准.通道带宽.通道增益和传递函数.环境适应性等性能设计方面的技术要求。 工作权限工作责任工作频次工作关系内部关系外部关系执行权全部每2~3年一次每次2~3个月项目负责人.总体设计.光机结构设计.电子信号处理.可靠性预计 第研究室和试制研究中心职责三:设计输出控制平均占工作时间百分比:40 % 工作任务按计划开展项目与产品的技术研究和电子电路设计工作根据产品研制或技术设计工作需要,组织开展关键技术试验.实验和联合技术攻关,制定联合攻关的技术方案报告或关键技术和产品的试验.实验大纲。 在保证产品研制工作质量的条件下,严格控制各项研制成本在产品研制的各阶段要注意收集和积累能够反映产品研制工作进展和技术状态控制的各种相关资料(包括文字材料.图片.音频和
北京化工大学 攻读博士学位研究生入学考试 《线性系统理论》考试大纲 一、适用的招生专业 控制理论与控制工程; 二、考试的基本要求 要求考试比较系统地理解线性系统状态空间设计方法的基本概念和基本理论,掌握线 性系统的状态空间分析和设计方法,要求考试具有抽象思维能力、逻辑推理能力、运算能力 和综合运用所学的知识分析问题和解决问题的能力。 三、考试的主要内容与要求 (▲表示应掌握;■表示应理解;?表示应了解) 1.▲线性系统的状态空间描述 传递函数表达与状态空间描述之间的相互转换;代数等价;组合系统的状态空间描述。2.线性系统的运动分析 ▲状态转移矩阵的定义、性质;▲定常和时变系统的状态转移矩阵求解;▲定常和时变系统的状态运动分析;■连续系统的离散化;■离散系统的运动分析。 3.线性系统能控性和能观性分析 ▲能控性及能观性定义;▲时变和定常系统的能控性及能观测性判别;■对偶原理;▲能控、能观规范型;?结构分解。 4.线性系统稳定性分析 ▲Lyapunov意义下的运动稳定性定义;■Lyapunov稳定性理论;■线性系统的Lyapunov稳定性分析;?离散系统的状态运动稳定性及判据。 5.线性系统的综合设计理论 ▲状态反馈和输出反馈的比较;极点配置问题的定义,▲极点配置条件;单变量系统的极点配置算法;■状态反馈的镇定问题;?输入——输出静态、动态解耦的定义、条件和算法;?跟踪控制;?线性二次型最优问题;▲观测器的提法、分类、与存在条件;▲全维状态观测器的设计;?降维状态观测器的设计;■观测器状态反馈控制系统及分离原理。 四、考试参考书 郑大钟,线性系统理论。北京:化学工业出版社。
目录 题目一 (2) (一)状态反馈加积分器校正的输出反馈系统设计 (2) (1)建立被控对象的状态空间模型,并判断系统性质 (2) (2)状态反馈增益矩阵和积分增益常数的设计 (4) (3)全维观测器设计 (6) (4)如何在闭环调速系统中增加限流环节 (8) (二)二次型最优全状态反馈控制和按负载扰动前馈补偿的复合控制系统设计 (8) (1)线性二次型最优全状态反馈设计 (8) (2)降维观测器设计 (13) 题目二 (15) (1)判断系统是否存在最优控制律 (15) (2)非零给定点的最优控制设计和仿真分析 (16) (3)权矩阵的各权值对动态性能影响分析 (17)
题目一 (一)状态反馈加积分器校正的输出反馈系统设计 (1)建立被控对象的状态空间模型,并判断系统性质 1)画出与题目对应的模拟结构图,如图1所示: 图1原始系统结构图 取状态变量为1x =n ,2x =d I ,3x =d u ,控制输入u=c u 1222212333375375111 T L e la la la s s s C x x T GD GD C x x x x RT T RT K x x u T T ?=-???=--+???=-+?? 将已知参数代人并设输出y=n=1x ,得被控对象的状态空间表达式为 L x Ax Bu ET y Cx =++= 其中,2 37500039.768011=-3.696-17.85727.05600-588.2351 00 T e la la la s C GD C A RT T RT T ???? ? ???????=- -?????? ??????-??? ? ,
1绪论 1.1计算机控制系统 计算机控制系统是在自动化控制技术和计算机技术的飞速发展的基础上产生的,20世纪50年代中期,经典控制理论已经发展成熟,并在不少工程技术领域得到了成功的应用。随着复杂系统的设计和复杂控制规律的实现上很难满足更高的要求。现代控制理论的发展为自动控制系统的分析、设计与综合增添了理论基础,而计算机技术的发展为新型控制方法的实现提供了非常有效的手段,两者的结合极大的推动了自动控制技术的发展。进而计算机控制系统广泛的应用于工厂生产,逐渐融入于生产中,各类大型工厂均离不开计算机控制系统。 1.1.1系统的分类 按系统性能分:线性系统和非线性系统;连续系统和离散系统;定常系统和时变系统;确定系统和不确定系统。 1、线性连续系统:用线性微分方程式来描述,如果微分方程的系数为常数,则为定常系统;如果系数随时间而变化,则为时变系统。今后我们所讨论的系统主要以线性定常连续系统为主。 2、线性定常离散系统:离散系统指系统的某处或多处的信号为脉冲序列或数码形式。这类系统用差分方程来描述。 3、非线性系统:系统中有一个元部件的输入输出特性为非线性的系统。 1.1.2系统的数学模型 在线性系统理论中,一般常用的数学模型形式有:传递函数模型(系统的外部模型)、状态方程模型(系统的内部模型)、零极点增益模型和部分分式模型等。这些模型之间都有着内在的联系,可以相互进行转换。 1.2计算机模拟控制系统 模拟控制系统由给定输入、模糊控制器、控制对象、检测变送装置、反馈信号与给定输入的相加环节等组成。模拟控制系统的各处均为连续信号,在模拟系统中,给定值与反馈值经过比较器比较产生偏差,控制器对偏差进行调节计算,产生控制信号驱动执行机构,从而被控参数的值达到预期值。其典型结构如下图所示:
一. 极点配置原理 假设原系统的状态空间模型为: ???=+=Cx y Bu Ax x 若系统是完全可控的,则可引入状态反馈调节器,且: 这时,闭环系统的状态空间模型为: ()x A BK x Bv y Cx =-+?? =? 二. 状态观测器设计原理 假设原系统的状态空间模型为: ???=+=Cx y Bu Ax x 若系统是完全可观的,则可引入全维状态观测器,且: ??(y y)??x Ax Bu G y Cx ?=++-??=?? 设?x x x =-,闭环系统的状态空间模型为: ()x A GC x =- 解得: (A GC)t (0),t 0x e x -=≥ 由上式可以看出,在t 0≥所有时间内,如果(0)x =0,即状态估计值x 与x 相等。如果(0)0x ≠,两者初值不相等,但是()A GC -的所有特征值具有负实部,这样 x 就能渐进衰减至零,观测器的状态向量?x 就能够渐进地逼近实际状态向量x 。状态逼近的速度取决于G 的选择和A GC -的特征配置。 三. 状态观测的实现 为什么要输出y 和输入u 对系统状态x 进行重构。 u Kx v =-+
证明 输出方程对t 逐次求导,并将状态方程x Ax Bu =+代入整理,得 2(n 1)(n 2)(n 3)21n n y Cx y CBu CAx y CBu CABu CA x y CBu CABu CA Bu CA x -----=??-=??--=????----=? 将等号左边分别用z 的各分量12,, ,n z z z 表示,有 121(n 1)(n 2)(n 3) 2 n n n y C z y CBu CA z z y CBu CABu x Qx z CA y CBu CABu CA Bu -----?? ???????? -?? ????? ? ? ?????==--==?? ????????????????????----?? ? 如果系统完全能观,则 rankQ n = 即 1?(Q Q)T T x Q z -= (类似于最小二乘参数估计) 综上所述,构造一个新系统z ,它是以原系统的输出y 和输入u ,其输出经过变 换1(Q Q)T T Q -后得到状态向量?x 。也就是说系统完全能观,状态就能被系统的输入输出以及各阶倒数估计出来。 四. 实例 给定受控系统为 再指定期望的闭环极点为12,341,1,2i λλλ*** =-=-±=-,观测器的特征值为 12,33,32i λλ=-=-±,试设计一个观测器和一个状态反馈控制系统,并画出系统 的组成结构图。 []0100000101000100 05 021000x x u y x ???? ????-????=+????????-???? =
研 究 生 课 程 论 文 (2014-2015学年第一学期) 线性系统的基本特性 研究生:
线性系统理论的研究对象为线性系统。线性系统是最为简单和最为基本的一类动态系统。线性系统理论是系统控制理论中研究最为充分、发展最为成熟和应用最为广泛的一个分支。线性系统理论中的很多概念和方法,对于研究系统控制理论的其他分支,如非线性系统理论、最优控制理论、自适应控制理论、鲁棒控制理论、随机控制理论等,同样也是不可缺少的基础。 线性系统的一个基本特征是其模型方程具有线性属性即满足叠加原理。叠加原理是指,若表系统的数学描述为L ,则对任意两个输入变量u 1和u 2以及任意两个非零有限常数c 1和c 2必成立关系式: 11221122()()()L c u c u c L u c L u +=+ 对于线性系统,通常还可进一步细分为线性时不变系统(linear time-invariant systems)和线性时变系统(linear time-varying systems)两类。 线性时不变系统也称为线性定常系统或线性常系数系统。其特点是,描述系统动态过程的线性微分方程或差分方程中,每个系数都是不随时间变化的函数。从实际的观点而言,线性时不变系统也是实际系统的一种理想化模型,实质上是对实际系统经过近似化和工程化处理后所导出的一类理想化系统。但是,由于线性时不变系统在研究上的简便性和基础性,并且为数很多的实际系统都可以在一定范围内足够精确地用线性时不变系统来代表,因此自然地成为线性系统理论中的主要研究对象。 线性时变系统也称为线性变系数系统。其特点是,表征系统动态过程的线性微分方程或差分方程中,至少包含一个卷数为随时间变化的函数。在视实世界中,由于系统外部和内部的原因,参数的变化是不可避免的,因此严格地说几乎所有系统都属于时变系统的范畴。但是,从研究的角度,只要参数随时间
分数: ___________ 任课教师签字:___________ 华北电力大学研究生结课作业 学年学期:第一学年第一学期 课程名称:线性系统理论 学生姓名: 学号:
提交时间:目录
弹簧-质量-阻尼系统的建模与控制系统设计 1 研究背景及意义 弹簧、阻尼器、质量块是组成机械系统的理想元件。由它们组成的弹簧-质量-阻尼系统是最常见的机械振动系统,在生活中具有相当广泛的用途,缓冲器就是其中的一种。缓冲装置是吸收和耗散过程产生能量的主要部件,其吸收耗散能量的能力大小直接关系到系统的安全与稳定。缓冲器在生活中处处可见,例如我们的汽车减震装置和用来消耗碰撞能量的缓冲器,其缓冲系统的性能直接影响着汽车的稳定与驾驶员安全;另外,天宫一号在太空实现交会对接时缓冲系统的稳定与否直接影响着交会对接的成功。因此,对弹簧-质量-阻尼系统的研究有着非常深的现实意义。 2 弹簧-质量-阻尼模型 数学模型是定量地描述系统的动态特性,揭示系统的结构、参数与动态特性之间关系的数学表达式。其中,微分方程是基本的数学模型,不论是机械的、液压的、电气的或热力学的系统等都可以用微分方程来描述。微分方程的解就是系统在输入作用下的输出响应。所以,建立数学模型是研究系统、预测其动态响应的前提。通常情况下,列写机械振动系统的微分方程都是应用力学中的牛顿定律、质量守恒定律等。 弹簧-质量-阻尼系统是最常见的机械振动系统。机械系统如图所示,
图2-1弹簧-质量-阻尼系统机械结构简图 其中、表示小车的质量,表示缓冲器的粘滞摩擦系数,表示弹簧的弹性系数,表示小车所受的外力,是系统的输入即,表示小车的位移,是系统的输出,即,i=1,2。设缓冲器的摩擦力与活塞的速度成正比,其中,, ,,,。系统的建立 由图,根据牛顿第二定律,分别分析两个小车的受力情况,建立系统的动力学模型如下: 对有: 对有:
东南大学自动化学院 实 验 报 告 课程名称: 自动控制基础 实验名称: 状态观测器的设计 院 (系): 自动化学院 专 业: 自动化 姓 名: 吴静 学 号: 08008419 实 验 室: 机械动力楼417室 实验组别: 同组人员: 实验时间:2011年05月13日 评定成绩: 审阅教师: 一、实验目的 1. 理解观测器在自动控制设计中的作用 2. 理解观测器的极点设置 3. 会设计实用的状态观测器 二、实验原理 如果控制系统采用极点配置的方法来设计,就必须要得到系统的各个状态,然后才能用状态反馈进行极点配置。然而,大多数被控系统的实际状态是不能直接得到的,尽管系统是可以控制的。怎么办?如果能搭试一种装置将原系统的各个状态较准确地取出来,就可以实现系统极点任意配置。于是提出了利用被控系统的输入量和输出量重构原系统的状态,并用反馈来消除原系统和重构系统状态的误差,这样原系统的状态就能被等价取出,从而进行状态反馈,达到极点配置改善系统的目的,这个重构的系统就叫状态观测器。 另外,状态观测器可以用来监测被控系统的各个参量。 观测器的设计线路不是唯一的,本实验采用较实用的设计。 给一个被控二阶系统,其开环传递函数是G (s )=12 (1)(1)K T s T s ++ ,12 K K K =观测器如图示。
设被控系统状态方程 构造开环观测器,X ∧ Y ∧ 为状态向量和输出向量估值 由于初态不同,估值X ∧ 状态不能替代被控系统状态X ,为了使两者初态跟随,采用输出误差反馈调节,加入反馈量H(Y-Y)∧ ,即构造闭环观测器,闭环观测器对重构造的参数误差也有收敛作用。 也可写成 X =(A-HC)X +Bu+HY Y CX ? ∧ ∧ ∧∧ = 只要(A-HC )的特征根具有负实部,状态向量误差就按指数规律衰减,且极点可任意配置,一般地,(A-HC )的收敛速度要比被控系统的响应速度要快。工程上,取小于被控系统最小时间的3至5倍,若响应太快,H 就要很大,容易产生噪声干扰。 实验采用X =A X +Bu+H(Y-Y)? ∧ ∧∧ 结构,即输出误差反馈,而不是输出反馈形式。 取:1212min 35 20,5,2,0.5,0.2K K T T t λ-= =====,求解12g g ?????? 三、实验设备: THBDC-1实验平台 THBDC-1虚拟示波器 Matlab/Simulink 软件 四、实验步骤 按要求设计状态观测器 (一) 在Matlab 环境下实现对象的实时控制 1. 将ZhuangTai_model.mdl 复制到E:\MATLAB6p5\work 子目录下,运行matlab ,打开ZhuangTai_model.mdl 注:‘实际对象’模块对应外部的实际被控对象,在simulink 下它代表计算机与外部接口: ● DA1对应实验面板上的DA1,代表对象输出,输出通过数据卡传送给计算机; ● AD1对应实验面板上的AD1,代表控制信号,计算机通过数据卡将控制信号送给实际对象;
RC 有源带通滤波器设计与仿真 摘要:简要介绍Pspice10.5的特点以及其实现有源滤波器仿真的基本方法,实现了带通滤波器设计,用仿真软件Pspice 对设计结果进行了仿真。 关键词:有源模拟滤波器;Pspice;仿真;设计 引言 随着数字化进程的不断推进,数字滤波器越来越广泛的应用在各个领域之中。但是模拟滤波器凭借自身的优势仍然有很高的研究价值。所有数字系统的前端,一般需要一个对微弱信号预处理的部分;在抽样量化之前,还需要一个对信号最高频率进行限制的处理。这些都只能使用模拟滤波器。RC 有源滤波器是模拟滤波器中最实用、应用范围最广泛的滤波器。其标准化电路的种类很少,仅使用及R 、C 元件,因此非常便于集成,这给推广应用带来革命性影响。因为不使用电感、特别是大型电感,也因为运放在性能的飞速提高的同时价格却一降再降,所以在成本方面有源滤波器已经变得比无源滤波器还有优势。本文基于这一点简单介绍了RC 有源滤波器的结构,以基于实现带通波器设计为例,完成了其设计过程,并利用电子仿真软件Pspice 进行了仿真。 1、OrCAD/Pspice10.5简介 对于仿真技术而言,目前最流行的是以美国伯克利分校开发的Spice 为核心的仿真软件,而以Spice 为核心开发的最好的仿真软件是OrCAD/Pspice10.5。它之所以流行就是因为他能很好地运行在PC 平台上且能很好地进行模拟数字混合信号的仿真,而且能解决很多设计上的实际问题。OrCAD10.5在以前版本的基础上扩展了许多功能,包括供设计输入的OrCADCaptureR ,供类比与混合讯号模拟用的PspiceRA/DBasics ,供电路板设计的 OrCADLayoutR 以及供高密度电路板自动绕线的SPECCTRAR 4U 。新加入的SPECCTRA ,用以支援设计日益复杂的各种高速、高密度印刷电路板设计。 OrCAD/PSpice 10.5软件的功能特点有: (1)对模拟电路不仅可进行直流、交流、瞬态等基本电路特性分析,而且可进行参数扫描分析和统计分析。 (2)以OrCAD/Capture 作为前端,除了以利用Capture 的电路图输入这一基本功能外,还可以实现OrCAD 中设计项目统一管理。 (3)将电路模拟结果和波形显示分析两个模块集成在一起。Probe 只是其中的一个窗口,在屏幕上可同时显示波形和输出文本等内容,Probe 还具有电路性能分析功能。 (4)使用PSpice 优化器能调整电路,在一定的约束条件下,对电路的某些参数进行调整,直到电路的性能达到要求为止。 2、RC 有源滤波器的设计 根据线性系统理论,n 阶滤波器的传递函数的一般形式为 11 10 111)()()(a s a s a s b s b s b s b s U s U s A n n n m m m m i o ++++++++==---- (1) (1)式中,m ≤n ;一个复杂的传递函数可以分解成几个简单的传递函数的乘积。上式中, 若n 为偶数,可分解为n/2个二阶滤波器的级联;而若n 为奇数,则可分解成一个一阶滤波器和(n-1)/2个二阶滤波器的级联。一阶、二阶滤波器是构成高阶滤波器的基本单元,二阶 滤波器单元传递函数可以写为:0 120 122)(a s a s b s b s b s A ++++=,其中分子系数0b 、1b 、2b 决定了 传递函数的零点位置,即决定滤波器类型(低通、高通、带通、带阻),分母系数1a 、0a 决
毕 业 设 计 (论 文) 设计(论文)题目:_ 三阶随动系统串联校正的频率 __ 特性法设计及仿真研究_______ 单 位(系别):______自动化系______ 学 生 姓 名:___ 陈海龙_________ 专 业:__电气工程及其自动化__ 班 级:___ 05111106________ 学 号:___ 0511110629______ 指 导 教 师:_______汪纪锋_________ 答辩组负责人:______________________ 填表时间: 20 15 年 6 月 重庆邮电大学移通学院教务处制 编 号:____________ 审定成绩:____________
重庆邮电大学移通学院毕业设计(论文)任务书 设计(论文)题目三阶随动系统串联校正的频率特性法设计及仿真研究 学生姓名陈海龙系别自动化系专业电气工程及其自动化班级 05111106 指导教师汪纪峰职称教授联系电话 42871150 教师单位自动化系下任务日期__2014 __年_12_月_ 20_ 日 毕业设计(论文)开始后一周内完成。
重庆邮电大学移通学院 毕业设计任务书(简明)技术资料 一、设计题目: 题目16 三阶随动系统串联校正的频率特性法设计及仿真研究 二、系统说明: 设三阶系统开环结构如下 (s)(s)(s)(0.11)(0.21) y k Gp r s s s =++ 三、系统参量: 校正前:系统输入信号:r (t );系统输出信号:y (t ); 校正后:系统输入信号:u (t );系统输出信号:y (t ); 四、设计指标: 1. 设定:在输入为r (t )=u (t )=a+bt ,(其中:a=4,b=1 sec. ) 2. 在保证静态速度误差系数Kv =30 1sec.的前提下,其动态期望指标: 040?γ≥ ; 2.3c rad s ω≥ 。 五、设计要求: 基于频率特性法,试设计一个串联校正闭环系统(如图示),以满足系统设计指 标。 重庆邮电大学移通学院 自动化系 指导教师: 汪纪峰 2014.12
Linear Systems Theory: A Structural Decomposition Approach 线性系统理论: 结构分解法 Ben M. Chen (陈本美) 新加坡国立大学 Zongli Lin(林宗利) 美国弗吉尼亚大学 Yacov Shamash (雅科夫 司马诩) 美国纽约州立大学石溪分校
此书献给我们的家人 前两位作者谨以这中译版献给他们的母校 厦门大学
目录 绪论 1 导论和预览 1.1 背景 1.2 各章预览 1.3 符号和术语 2 数学基础 2.1 导论 2.2 矢量空间和子空间 2.3 矩阵代数和特性 2.3.1 行列式、逆和求导 2.3.2 秩、特征值和约当型 2.3.3 特殊矩阵 2.3.4 奇异值分解 2.4 范数 2.4.1 矢量范数 2.4.2矩阵范数 2.4.3 连续时间信号范数 2.4.4 离散时间信号范数 2.4.5 连续时间系统范数 2.4.6 离散时间系统范数 3 线性系统理论复习 3.1 导论 3.2 动态响应 3.3 系统稳定性 3.4 可控性和可观性 3.5 系统可逆性 3.6 常态秩、有限零点和无限零点3.7 几何子空间 3.8 状态反馈和输出馈入的特性3.9 练习
4 无驱动和/或无检测系统的分解 4.1 导论 4.2 自治系统 4.3 无驱动系统 4.4 无检测系统 4.5 练习 5. 正则系统的分解 5.1 导论 5.2 SISO系统 5.3 严格正则系统 5.4 非严格正则系统 5.5 结构化分解特性的证明 5.6 系统矩阵的Kronecker型和Smith型5.7 离散时间系统 5.8 练习 6 奇异系统的分解 6.1 导论 6.2 SISO奇异系统 6.3 MIMO描述系统 6.4 定理6.3.1的证明和性质 6.5 离散时间奇异系统 6.6 练习 7 双线性变换的结构化映射 7.1 导论 7.2 连续到离散时间系统的映射 7.3 离散时间到连续时间系统的映射7.4 定理7.2.1的证明 7.5 练习 8 系统因子分解 8.1 导论 8.2 严格正则系统 8.3 非严格正则系统 8.4 离散时间系统 8.5 练习 9 通过选择传感器/执行器实现的结构配置9.1 导论 9.2 同时有限和无限零点结构配置 9.2.1 SISO系统 9.2.2 MIMO系统
信息光学习题答案 第一章 线性系统分析 1.1 简要说明以下系统是否有线性和平移不变性. (1)()();x f dx d x g = (2)()();?=dx x f x g (3)()();x f x g = (4)()()()[];2 ? ∞ ∞ --= αααd x h f x g (5) ()()απξααd j f ?∞ ∞ --2exp 解:(1)线性、平移不变; (2)线性、平移不变; (3)非线性、平移不变; (4)线性、平移不变; (5)线性、非平移不变。 1.2 证明)()ex p()(2x comb x j x comb x comb +=?? ? ??π 证明:左边=∑∑∑∞ -∞ =∞-∞=∞-∞=-=??? ???-=??? ??-=??? ??n n n n x n x n x x comb )2(2)2(2122δδδ ∑∑∑∑∑∑∞ -∞ =∞ -∞ =∞ -∞=∞ -∞=∞ -∞ =∞ -∞ =--+-= -+-=-+-= +=n n n n n n n n x n x n x jn n x n x x j n x x j x comb x comb ) () 1()() ()exp()() ()exp()()exp()()(δδδπδδπδπ右边 当n 为奇数时,右边=0,当n 为偶数时,右边=∑∞ -∞ =-n n x )2(2δ 所以当n 为偶数时,左右两边相等。 1.3 证明)()(sin x comb x =ππδ 证明:根据复合函数形式的δ函数公式 0)(,) () ()]([1 ≠''-= ∑ =i n i i i x h x h x x x h δδ 式中i x 是h(x)=0的根,)(i x h '表示)(x h 在i x x =处的导数。于是 )() ()(sin x comb n x x n =-=∑∞ -∞ =π δπ ππδ
课程名称: MATLAB及在电子信息课程中的应用实验名称:图像的傅里叶变换及其应用 设计四图像的傅里叶变换及其应用
一、设计目的 通过该设计,掌握傅里叶变换的定义及含义。 二、设计内容及主要的MATLAB 函数 1、图像的离散傅里叶变换 假设),(n m f 是一个离散空间中的二维函数,则该函数的二维傅里叶变换定义为 n j m j e e n m f f 21),()2,1(ωωωω--∞∞-∞∞-∑∑= 其中21ωω和是频域变量,单位是弧度/采样单元。函数),(21ωωf 为函数),(n m f 的频谱。 二维傅里叶反变换的定义为21212121),(),(ωωωωωωπ πωππωd d e e f n m f n j m j ??-=-== 因此,函数),(n m f 可以用无数个不同频率的复指数信号的和表示,在频率),(21ωω处复指数信号的幅度和相位为),(21ωωf MATLAB 提供的快速傅里叶变换函数 1)fft2:用于计算二维快速傅里叶变换,其语法格式为 b=fft2(I),返回图像I 的二维傅里叶变换矩阵,输入图像I 和输出图像B 大小相同; b=fft2(I,m,n),通过对图像I 剪切或补零,按用户指定的点数计算二维傅里叶变换,返回矩阵B 的大小为m ?n 。 很多MATLAB 图像显示函数无法显示复数图像,为了观察图像傅里叶变换后的结果,应对变换后的结果求模,方法是对变换结果使用abs 函数。 2)fftn :用于计算n 维快速傅里叶变换,其语法格式为 b=fftn(I),计算图像的n 维傅里叶变换,输出图像B 和输入图像I 大小相同; b=fftn(I, size),通过对图像I 剪切或补零,按size 指定的点数计算n 维傅里叶变换,返回矩阵B 的大小为size 。 3) fftshift :用于将变换后的图像频谱中心从矩阵的原点移到矩阵的中心,其语法格式为 b=fftshift(I),将变换后的图像频谱中心从矩阵的原点移到矩阵的中心。
说明: 姚老师是从07还是08年教这门课的,之前的考题有多少参考价值不敢保证,也只能供大家参考了,重点的复习还是以课件为主,把平时讲的课件内容复习好了,考试不会有问题(来自上届的经验)。 祝大家考试顺利! (这个文档内部交流用,并感谢董俊青和兰天同学,若有不足请大家见谅。) 2008级综合大题 []4001021100101 1 2x x u y x ???? ????=-+????????-????= 1 能否通过状态反馈设计将系统特征值配置到平面任意位置? 2 控规范分解求上述方程的不可简约形式? 3 求方程的传递函数; 4 验证系统是否渐近稳定、BIBO 稳定、李氏稳定; 5 可能通过状态反馈将不可简约方程特征值配置到-2,-3?若能,确定K ,若不能,请说明理由; 6 能否为系统不可简约方程设计全阶状态观测器,使其特征值为-4,-5; 7画出不可简约方程带有状态观测器的状态反馈系统结构图。 参考解答: 1. 判断能控性:能控矩阵2 14161 24,() 2.0 0M B AB A B rank M ?? ?? ??==-=???????? 系统不完全可控,不能任意配置极点。
2 按可控规范型分解 取M 的前两列,并加1与其线性无关列构成1 1 401200 1P -?? ??=-?????? ,求得120331 1066 00 1P ?? ????? ?=-????????? ? 进行变换[] 1 1 20831112,0,2 2 26000 1 A PAP B PB c cP --? ? ?? ???? ????=-====???? ??????????? ? 所以系统不可简约实现为[]08112022x x u y x ?????=+???????????=? 3. 1 2(1)(1)2(1)()()(4)(2)(1) (4)(2) s s s G s c sI A B s s s s s --+-=-= = -++-+ 4. det()(4)(2)(1)sI A s s s -=-++, 系统有一极点4,位于复平面的右部,故不是渐近稳定。 1 2(1)()()(4)(2) s G s c sI A B s s --=-= -+,极点为4,-2,存在位于右半平面的极点,故系统不 是BIBO 稳定。 系统发散,不是李氏稳定。 5. 可以。令11 228,12T k k k k A Bk k +???? =+=??? ??? ?? 则特征方程[]2 112()det ()(2)28f s sI A Bk s k s k k =-+=-++-- 期望特征方程* 2 ()(2)(3)56f s s s s s =++=++
实 验 报 告 课程 线性系统理论基础 实验日期 2016年 6月 6 日 专业班级 学号 同组人 实 验 名 称 全 维 状 态 观 测 器 的 设 计 评分 批阅教师签字 一、实验目的 1. 学习用状态观测器获取系统状态估计值的方法,了解全维状态观测器的极点对状态的估计误差的影响; 2. 掌握全维状态观测器的设计方法; 3. 掌握带有状态观测器的状态反馈系统设计方法。 二、实验容 开环系统? ??=+=cx y bu Ax x ,其中 []0100001,0,10061161A b c ????????===????????--???? a) 用状态反馈配置系统的闭环极点:5,322-±-j ; b) 设计全维状态观测器,观测器的极点为:10,325-±-j ; c) 研究观测器极点位置对估计状态逼近被估计值的影响; d) 求系统的传递函数(带观测器及不带观测器时);
绘制系统的输出阶跃响应曲线。 三、实验环境 MATLAB6.5 四、实验原理(或程序框图)及步骤 利用状态反馈可以使闭环系统的极点配置在所希望的位置上,其条件是必须对全部状态变量都能进行测量,但在实际系统中,并不是所有状态变量都能测量的,这就给状态反馈的实现造成了困难。因此要设法利用已知的信息(输出量y和输入量x),通过一个模型重新构造系统状态以对状态变量进行估计。该模型就称为状态观测器。若状态观测器的阶次与系统的阶次是相同的,这样的状态观测器就称为全维状态观测器或全阶观测器。 设系统完全可观,则可构造如图4-1所示的状态观测器 图4-1 全维状态观测器 为求出状态观测器的反馈ke增益,与极点配置类似,也可有两种方法: 方法一:构造变换矩阵Q,使系统变成标准能观型,然后根据特征方程求出k e ; 方法二:是可采用Ackermann公式:
学士论文 基于FPGA的FIR数字滤波器设计 摘要 随着公元的第二十一个世纪的到来,今天我们进入了一个科技日新月异的时代。在现代电子数字系统中,滤波器都以一个不可缺少的身份出现。其中,FIR数字滤波器又以其良好的线性特性被广泛和有针对性的大量使用。众所周知,灵活性和实时性是工程实践中对数字信号处理的基本要求。在以往使用的各种滤波器技术中,不难发现有许许多多的问题。但是,随着现代计算机技术在滤波问题上的飞跃,派生出一个全新的分支——数字滤波器。利用可编程逻辑器件和EDA技术,使用FPGA来实现FIR滤波器,可以同时兼顾实时性和灵活性。基于FPGA的FIR数字滤波器的研究势在必行。 本论文讨论基于FPGA的FIR数字滤波器设计,针对该毕业设计要做的基本工作有如下几点:(一)掌握有限冲击响应FIR(Finite Impulse Response,FIR)的基本结构,研究现有的实现方法。对各种方案和步骤进行比较和论证分析,然后针对目前FIR数字滤波器需要的特点,速度快和硬件规模小,作为指导思想进行设计计算。 (二)基于硬件FPGA的特点,利用Matlab软件以及窗函数法设计滤波器。对整个FPGA元件,计划采用模块化、层次化设计思想,从而对各个部分功能进行更为详细的理解和分工设计。最终FIR数字滤波器的设计语言选择VHDL硬件编程语言。 (三)设计中的软件仿真使用Altera公司的综合性PLD开发软件Quartus II,并且利用Matlab工具进行对比仿真,在仿真的过程中,对比证明,本论文设计的滤波器的技术指标已经全部达标。 关键词:数字滤波器Matlab 可编程逻辑元件模块化算法 Based On FPGA Design Of FIR Digital Filters Major:Electronic And Information Engineering Department(Information Engineering)
2008级综合大题 []400102110010112x x u y x ????????=-+????????-????=& 1 能否通过状态反馈设计将系统特征值配置到平面任意位置? 2 控规范分解求上述方程的不可简约形式? 3 求方程的传递函数; 4 验证系统是否渐近稳定、BIBO 稳定、李氏稳定;(各种稳定之间的关系和判定方法!) 5 可能通过状态反馈将不可简约方程特征值配置到-2,-3?若能,确定K ,若不能,请说明理由; 6 能否为系统不可简约方程设计全阶状态观测器,使其特征值为-4,-5; 7画出不可简约方程带有状态观测器的状态反馈系统结构图。 参考解答: 1. 判断能控性:能控矩阵21416124,() 2.000M B AB A B rank M ?? ????==-=???? ???? 系统不完全 可控,不能任意配置极点。 2 按可控规范型分解 取M 的前两列,并加1与其线性无关列构成1140120001P -????=-??????,求得1203311066 001P ?? ?? ?? ??=-?????? ???? 进行变换[]11 20831112,0,22260001A PAP B PB c cP --? ??????? ????=-====???? ???????? ????
所以系统不可简约实现为[]08112022x x u y x ?????=+?????????? ?=? & 3. 12(1)(1)2(1) ()()(4)(2)(1)(4)(2) s s s G s c sI A B s s s s s --+-=-= =-++-+ 4. det()(4)(2)(1)sI A s s s -=-++,系统有一极点4,位于复平面的右部,故不是渐近稳定。 12(1) ()()(4)(2) s G s c sI A B s s --=-= -+,极点为4,-2,存在位于右半平面的极点,故系统不 是BIBO 稳定。 系统发散,不是李氏稳定。 5. 可以。令11228,12T k k k k A Bk k +???? =+=???????? 则特征方程[]2 112()det ()(2)28f s sI A Bk s k s k k =-+=-++-- 期望特征方程*2 ()(2)(3)56f s s s s s =++=++ 比较上两式求得:728T k -?? =??-?? 6. 可以。设12l L l ??=????,则11222821222l l A LC l l --?? -=? ?--?? 特征方程2 2121()(222)1628f s s l l s l l =+-++-- 期望特征方程*2 ()(4)(5)920f s s s s s =++=++ 比较得:103136L ???? =????????