
第六节最速下降法与共轭梯度法
6.1 最速下降法
当方程组
Ax = b (1)
中的A为对称正定矩阵时,方程组Ax=b的解正好是二次函数
(2)
的唯一极小值点。求解方程组(1)的问题等价与求
(3)
问题。求解问题(3)的最简单的方法是所谓最速下降法,即从某个初始点x(0)出发,沿φ(x)在点x(0)处的负梯度方向
(4)
(称为搜索方向)求得φ(x)的极小值点x(1) , 即
(5)
然后从x(1)出发,重复上面的过程得到x(2)。如此下去,得到序列{x(k) }
(6)
可以证明,从任一初始点x(0)出发,用最速下降法所得到的序列{x(k)}均收敛于问题(3)的解,也就是方程组(1)的解。其收敛速度取决于
其中λ1 ,λn分别为A的最小,最大特征值。最速下降法迭代格式:给定初值x(0) ,x(k)按如下方法决定
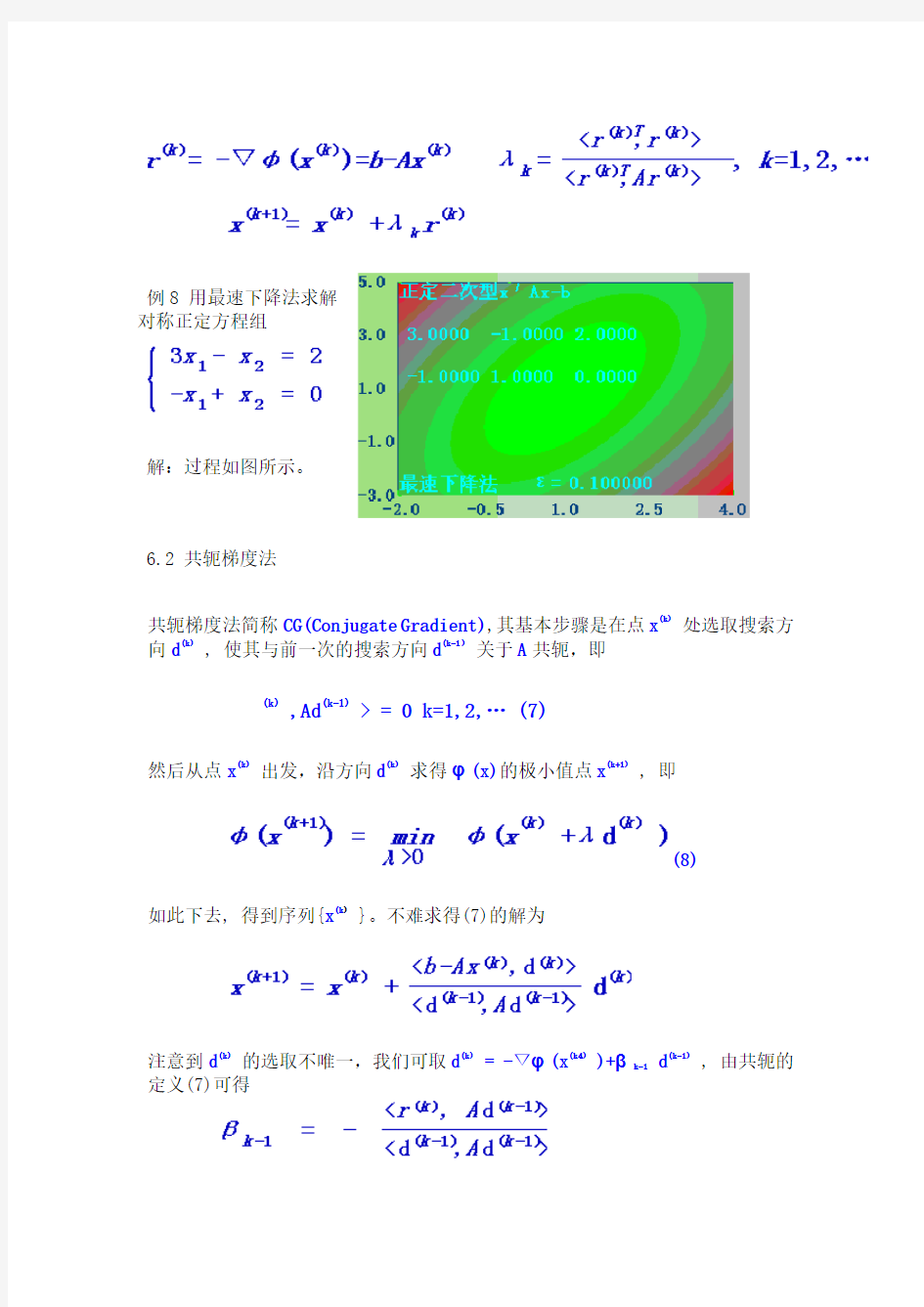
对称正定方程组
解:过程如图所示。
6.2 共轭梯度法
共轭梯度法简称CG(Conjugate Gradient),其基本步骤是在点x(k)处选取搜索方向d(k) , 使其与前一次的搜索方向d(k-1)关于A共轭,即
然后从点x(k)出发,沿方向d(k)求得φ(x)的极小值点x(k+1) , 即
(8)
如此下去, 得到序列{x(k)}。不难求得(7)的解为
注意到d(k)的选取不唯一,我们可取d(k) = -▽φ(x(k4) )+βk-1 d(k-1) , 由共轭的定义(7)可得
共轭梯度法的计算过程如下:
第一步:去初始向量x(0) , 计算
第k+1步(k=1,2,…):计算
例8 用共轭梯度法求解对称正定方程组
解
迭代过程如图所示
故x2 = (1,1)T就是φ(x)的最小点,也就是索求方程的解。
16梯度法和共轭梯度法基本原理和特点
16梯度法和共轭梯度法基本原理和特点? 梯度法又称最速下降法,基本原理是在迭代点附近采用使目标函数值下降最快的负梯度方向作为搜索方向, 求目标函数的极小值,特 点;迭代计算简单,只需求一阶偏导数,所占的存储单 元少,对初始点的要求不 高,在接近极小点位置时收敛速度很慢,共轭的特点为 在梯度法靠近极值点收敛速度放慢时,它可以构造共轭方向使其收敛速度加快, 迭代计算比较简单,效果 好,在每一步迭代过程中都要构造共轭的、方向,比较繁琐。17迭代终止准则有哪三种? 1)当设计变量在相邻两点之间的移动距离充分小时,可用相邻两点的矢量差的模作为终止的判据, 2)当相邻两点目标函数值之差达到充分小时,可 用两次迭代的目标函数之 差作为终止判据。 3)当迭代点逼近极值点时,目标函数在该点的梯度已达到充分小时,可用梯度的模作为 终止判据。
18 .无约束设计法,1)powell法,它是在下降迭代过 运算中只需计算和比较目标函数值的大小,不需计算偏导数的方法,是较好的一种直接搜索 算法。 2)梯度法,又称最速下降法,它是采用使目标 函数值下降最快的负梯度方向作为搜索方向来求目标函数的极小值。 3)共轭梯度法,又称FR法,是利用目标函数的 梯度确定共轭方向,使得计算简便而效 果好,只需利用相邻两点的梯度就可以构造一个共轭方向,这种方式产生共轭方 向并进行迭代的算法称为 共轭梯度法。 4)变尺度法,又称DFP法,为了得到既有快速收敛的性质,又能避免计算二阶导数矩阵及逆矩阵,减少计算工作量。迭代公式X=X+aS, 19有约束设计法? 1)复合形法,在可行域中选取k个设计点作为 初始复合形的顶点,然后比较复合形个各项目标函数值的大小,其中目标函数值最大的点为坏点,以坏
16梯度法和共轭梯度法基本原理和特点? 梯度法又称最速下降法,基本原理是在迭代点附近采用使目标函数值下降最快的负梯度方向作为搜索方向, 求目标函数的极小值,特 点;迭代计算简单,只需求一阶偏导数,所占的存储单 元少,对初始点的要求不 高,在接近极小点位置时收敛速度很慢,共轭的特点为 在梯度法靠近极值点收敛速度放慢时,它可以构造共轭方向使其收敛速度加快, 迭代计算比较简单,效果 好,在每一步迭代过程中都要构造共轭的、方向,比较繁琐。 17迭代终止准则有哪三种? 1)当设计变量在相邻两点之间的移动距离充分小时,可用相邻两点的矢量差的模作为终止的判据, 2)当相邻两点目标函数值之差达到充分小时,可 用两次迭代的目标函数之 差作为终止判据。 3)当迭代点逼近极值点时,目标函数在该点的梯度已达到充分小时,可用梯度的模作为
终止判据。 18 .无约束设计法,1)powell法,它是在下降迭代过运算中只需计算和比较目标函数值的大小,不需计算偏导数的方法,是较好的一种直接搜索 算法。 2)梯度法,又称最速下降法,它是采用使目标 函数值下降最快的负梯度方向作为搜索方向来求目标函数的极小值。 3)共轭梯度法,又称FR法,是利用目标函数的梯度确定共轭方向,使得计算简便而效 果好,只需利用相邻两点的梯度就可以构造一个共轭方向,这种方式产生共轭方 向并进行迭代的算法称为 共轭梯度法。 4)变尺度法,又称DFP法,为了得到既有快速收敛的性质,又能避免计算二阶导数矩阵及逆矩阵,减少计算工作量。迭代公式X=X+aS, 19有约束设计法? 1)复合形法,在可行域中选取k个设计点作为
初始复合形的顶点,然后比较复合形个各项 目标函数值的大小,其中目标函数值最大的点为坏点,以坏点之外其余各点的中心为映 射中心,寻坏点的映射点,以映射点替换坏点,并与原复合 型除坏点之外其余各点构成就k 顶点的新的复合型,这样反复迭代直到达到精度找到最优点, 2)简约梯度法,用来解决线性约束非线性规划问题。3)罚函数法,是把一个有约束的问 题转化为一系列无约束的问 题求解,逐渐逼近最优值。 . 可靠性工程包括的三个方面? 1可靠性设计,包括设计方面的分析,对比评价,必要时也包 括可靠性实验,生产制造中的质量控制设计 及使用维修规程的设计。 2可靠性分析,主要是失效分析,也包括故障分析 3可靠性数学, 这是数理统计方法在开展 可靠性工作中发展起来的 数学分支。 常用的可靠
#include printf("\n"); printf("input the Maxtr X\n"); /*给X0输入一个初始向量*/ for(i=0;i 最优化课程设计--共轭梯度法算法分析与实现(设计程序) 题目共轭梯度法算法分析与实现 班级 / 学号 14140101/2011041401011 学生姓名黄中武指导教师王吉波王微微 课程设计任务书 课程名称最优化方法课程设计院(系) 理学院专业信息与计算科学 课程设计题目共轭梯度法算法分析与实现课程设计时间: 2014 年 6月 16日至 2014 年 6月 27日 课程设计的要求及内容: [要求] 1. 学习态度要认真,要积极参与课程设计,锻炼独立思考能力; 2. 严格遵守上机时间安排; 3. 按照MATLAB编程训练的任务要求来编写程序; 4. 根据任务书来完成课程设计论文; 5. 报告书写格式要求按照沈阳航空航天大学“课程设计报告撰写规范”; 6. 报告上交时间:课程设计结束时上交报告; 7. 严禁抄袭行为,一旦发现,课程设计成绩为不及格。 一、运用共轭梯度法求解无约束最优化问题 要求:1)了解求解无约束最优化问题的共轭梯度法; 2)绘出程序流程图; 3)编写求解无约束最优化问题的共轭梯度法MATLAB程序; 4)利用编写文件求解某无约束最优化问题; 5)给出程序注释。 指导教师年月日 负责教师年月日 学生签字年月日 沈阳航空航天大学 课程设计成绩评定单 课程名称最优化理论与算法课程设计院(系) 理学院专业信息与计算科学课程设计题目共轭梯度法算法分析与实现学号 2011041401011 姓名黄中武指导教师评语: 课程设计成绩 指导教师签字 年月日 最优化方法课程设计沈阳航空航天大学课程设计用纸目录 目录 一、正 文 (1) 二、总结 ............................................................... 8 参考文 献 ............................................................... 9 附录 .. (10) 第 I 页 最优化方法课程设计沈阳航空航天大学课程设计用纸正文 一、正文 一无约束最优化问题的共轭梯度法 最优化方法第四次作业 题目:利用FR-共轭梯度法求解无约束优化问题222 12122min ()44412x R f x x x x x x ∈=+--。初始点(0)(0.5,1).T x =- () ()T k k T k k k k k k k g g g g k d g k g d 111110.0,;0,-----=???≥+-=-=ββ 一、程序 function [x,val,k]=frcg(fun,gfun,x0) %功能:用FR 共轭梯度法求解无约束问题min f (x ) %输入:x0是初始点,fun,gfun 分别是求目标函数和梯度 %输出:x,val 分别是近似最优点和最优值,k 是迭代次数 maxk=5000; rho=0.6; sigma=0.4; k=0; epsilon=1e-4; n=length(x0); while (k while (m<20) %用Armijo 搜索求步长 if (feval(fun,x0+rho^m*d) 一种修正的DY 共轭梯度法的全局收敛性 敖卫斌 (重庆师范大学 数学学院,重庆 401331) 摘要:本文提出了一种新的非线性修正的DY 共轭梯度算法(MDYCG ),该算法得到的搜索方向为下降方向,它既不受线搜索规则的影响,也不受目标函数的凸性影响。在精确线搜索下,MDYCG 算法化归为标准的DY 共轭梯度算法。证明了该方法在Armijo 型线搜索下的全局收敛性,给出了初步的数值结果。 关键词:无约束优化;共轭梯度法;Armijo 型线搜索;全局收敛性 中图分类号:0182.1 1. 引言 考虑无约束优化问题: min (),,n f x x R ∈ (1) 其中:n f R R →为连续可微函数,其梯度向量记为() g x ,简记为g 。 共轭梯度法是求解大规模无约束优化问题的有效算法之一,它像最速下降法一样在每步迭代中不需要存储和计算矩阵,其迭代格式为: 1k k k k x x d α+=+ (2) 1,1;,1, k k k k k g k d g d k β--=?=?-+>? (3) 其中,()k k g f x =?,k d 为搜索方向,k α是通过一维线搜索获得的步长,k β为标量。不同的k β对应着不同的共轭梯度算法。1964, Fletcher 和 Reeves 首先提出非线性共轭梯度法参数k β,它定义为 22 1 k FR k k g g β-= ([2]). 还有其他著名的k β,比如 1 2 1 T PRP k k k k g y g β --= ( [3-4]), 111T HS k k k T k k g y d y β ---=([5]), 111 T LS k k k T k k g y d g β---=-([6]), 2 11 k DY k k k g d y βT --= ([7]), 2 11 k CD k k k g d g βT --=- ([8]); 收稿日期:2013-05-07; 作者简介: 敖卫斌(1987-),男,重庆九龙坡人,硕士研究生,主要从事最优化理论与研究. 第六节最速下降法与共轭梯度法 6.1 最速下降法 当方程组 Ax = b (1) 中的A为对称正定矩阵时,方程组Ax=b的解正好是二次函数 (2) 的唯一极小值点。求解方程组(1)的问题等价与求 (3) 问题。求解问题(3)的最简单的方法是所谓最速下降法,即从某个初始点x(0)出发,沿φ(x)在点x(0)处的负梯度方向 (4) (称为搜索方向)求得φ(x)的极小值点x(1) , 即 (5) 然后从x(1)出发,重复上面的过程得到x(2)。如此下去,得到序列{x(k) } (6) 可以证明,从任一初始点x(0)出发,用最速下降法所得到的序列{x(k)}均收敛于问题(3)的解,也就是方程组(1)的解。其收敛速度取决于 其中λ1 ,λn分别为A的最小,最大特征值。最速下降法迭代格式:给定初值x(0) ,x(k)按如下方法决定 对称正定方程组 解:过程如图所示。 6.2 共轭梯度法 共轭梯度法简称CG(Conjugate Gradient),其基本步骤是在点x(k)处选取搜索方向d(k) , 使其与前一次的搜索方向d(k-1)关于A共轭,即 共轭梯度法的计算过程如下: 第一步:去初始向量x(0) , 计算 第k+1步(k=1,2,…):计算 例8 用共轭梯度法求解对称正定方程组 解 迭代过程如图所示 最优化方法课程设计报告 题目:共轭梯度软件设计 院(系): 专业: 学生姓名: 指导教师: 题目类型:实验研究工程设计软件开发 2010 年1月15 日 摘要 共轭梯度法最早是由Hestenes 和Stiefle (1952)提出来的,用于解正定系数矩阵的线性方程组,在这个基础上,Fletcher 和Reeves (1964)首先提出了解非线性最优化问题的共轭梯度法。 共轭梯度法是解决无约束非线性最优化问题的重要的方法之一(Conjugate gradient method to solve unconstrained nonlinear optimization problem, one of the important ways.),因为共轭梯度法是介于最速下降法与牛顿法之间的一个方法,它仅需利用一阶导数信息,但克服了最速下降法收敛慢的缺点,又避免了牛顿法需要存储和计算Hesse 矩阵并求逆的缺点,共轭梯度法不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法一。 共轭梯度对于无约束优化问题Mlnf(x),x ∈R n 给出一初始值x1,算法选代产生x2,x3,x4,x 5,….希望某一k X 是目标函数解或点收敛于解,在我们这次的运筹学课程设计当中我们正是用这种方法要求解最小问题的最优解的。 关键字:共轭梯度法;无约束优化 Abstract Conjugate gradient method was first used by Hestenes and Stiefle (1952) put forward for the solution of positive definite coefficient matrix of linear equations, on this basis, Fletcher and Reeves (1964) first put forward about the problem of nonlinear optimization conjugate gradient method. The conjugate gradient method to solve unconstrained nonlinear optimization problems, one of the important ways, as the conjugate gradient method is between steepest descent method and Newton's method between a method, it requires the use of a first-order derivative information, But the steepest descent method to overcome the shortcomings of slow convergence, but also avoid the need to store and calculate Newton's method and the inverse Hesse matrix of the shortcomings of the conjugate gradient method is not only a large-scale linear equations to solve one of the ways the most useful, but also large-scale solution nonlinear optimization algorithm is the most effective one. Conjugate gradient for the unconstrained optimization problem Mlnf (x), x ∈ given an initial value of x1, the election algorithm is generated on behalf of the x2, x3, x4, x 5, .... Hope that is the objective function of a solution or point of convergence in the solution, in our curriculum design, operations research this is exactly what we were using this method requires the smallest solution of the problem the optimal solution. Keywords: conjugate gradient method;unconstrained nonlinear optimization 目录 一、共轭梯度法的概念....................................................... 错误!未定义书签。 一、共轭梯度法 共轭梯度法(Conjugate Gradient)是共轭方向法的一种,因为在该方向法中每一个共轭向量都是依靠赖于迭代点处的负梯度而构造出来的,所以称为共轭梯度法。由于此法最先由Fletcher和Reeves (1964)提出了解非线性最优化问题的,因而又称为FR 共轭梯度法。由于共轭梯度法不需要矩阵存储,且有较快的收敛速度和二次终止性等优点,现在共轭梯度法已经广泛地应用于实际问题中。共轭梯度法是一个典型的共轭方向法,它的每一个搜索方向是互相共轭的,而这些搜索方向d仅仅是负梯度方向与上一次迭代的搜索方向的组合,因此,存储量少,计算方便,效果好。 二、共轭梯度法的原理 设有目标函数 f(X)=1/2X T HX+b T X+c 式1 式中,H作为f(X)的二阶导数矩阵,b为常数矢量,b=[b1,b2,b3,...b n]T 在第k次迭代计算中,从点X(k)出发,沿负梯度方向作一维搜索,得 S(K)=-?f(X(k))式2 X(k+1)=X(k)+ɑ(k)S(k) 式3 在式中,ɑ(k)为最优步长。 设与S(k)共轭的下一个方向S(k+1)由点S(k)和点X(k+1)负梯度的线性组 合构,即 S (k+1)=-?f (X (k+1))+β(k)S (k) 式4 根据共轭的条件有 [S (k)]T ?2f (X (k))S (k+1)=0 式5 把式2和式4带入式5,得 -[?f(X (k))]T ?2f (X (k))[-?f (X (k+1))+β(k)S (k) ]=0 式6 对于式1,则在点X (k)和点X (k+1)的梯度可写为 ?f(X (k))=HX (k)+b 式7 ?f (X (k+1))=HX (k+1)+b 式8 把上面两式相减并将式3代入得 ɑ(k)H S (k)=?f (X (k+1))-?f(X (k)) 式9 将式4和式9两边分别相乘,并代入式5得 -[?f (X (k+1))+β(k)?f(X (k))]T [?f (X (k+1))-?f(X (k)]=0 式10 将式10展开,并注意到相邻两点梯度间的正交关系,整理后得 β (k ) =2 2 ||))((||||))1((||k X f k X f ?+? 式11 把式11代入式4和式3,得 S (k+1)=-?f (X (k))+β (k ) S (k ) X (k+1)=X (k )+ɑ(k )S (k ) 由上可见,只要利用相邻两点的梯度就可以构造一个共轭方向。以这种方式产生共轭方向并进行迭代运算的方法,即共轭梯度法。 最速下降法 1.最速下降方向 函数f(x)在点x处沿方向d的变化率可用方向导数来表示。对于可微函数,方向导数等于梯度与方向的内积,即: Df(x;d) = ▽f(x)T d, 因此,求函数f(x)在点x处的下降最快的方向,可归结为求解下列非线性规划: min ▽f(x)T d s.t. ||d|| ≤ 1 当 d = -▽f(x) / ||▽f(x)|| 时等号成立。因此,在点x处沿上式所定义的方向变化率最小,即负梯度方向为最速下降方向。 2.最速下降算法 最速下降法的迭代公式是 x(k+1) = x(k) + λk d(k) , 其中d(k)是从x(k)出发的搜索方向,这里取在x(k)处的最速下降方向,即 d = -▽f(x(k)). λk是从x(k)出发沿方向d(k)进行一维搜索的步长,即λk满足 f(x(k) + λk d(k)) = min f(x(k)+λd(k)) (λ≥0). 计算步骤如下: (1)给定初点x(1) ∈ R n,允许误差ε> 0,置k = 1。 (2)计算搜索方向d = -▽f(x(k))。 (3)若||d(k)|| ≤ε,则停止计算;否则,从x(k)出发,沿d(k)进行一维搜索,求λk,使 f(x(k) + λk d(k)) = min f(x(k)+λd(k)) (λ≥0). (4)令x(k+1) = x(k) + λk d(k),置k = k + 1,转步骤(2)。 共轭梯度法 1.共轭方向 无约束问题最优化方法的核心问题是选择搜索方向。 以正定二次函数为例,来观察两个方向关于矩阵A共轭的几何意义。 设有二次函数: f(x) = 1/2 (x - x*)T A(x - x*) , 其中A是n×n对称正定矩阵,x*是一个定点,函数f(x)的等值面 1/2 (x - x*)T A(x - x*) = c 是以x*为中心的椭球面,由于 ▽f(x*) = A(x - x*) = 0, A正定,因此x*是f(x)的极小点。 设x(1)是在某个等值面上的一点,该等值面在点x(1)处的法向量 ▽f(x(1)) = A(x(1) - x*)。 最速下降法and 共轭梯度法 分类:matlab 2011-04-17 17:02 961人阅读评论(2) 收藏举报算法出版优化 注明:程序中调用的函数jintuifa.m golddiv.m我在之前的笔记中已贴出 最速下降法 %最速下降法求解f = 1/2*x1*x1+9/2*x2*x2的最小值,起始点为x0=[9 1] %算法根据最优化方法(天津大学出版社)97页算法3.2.1编写 %v1.0 author: liuxi BIT %format long syms x1 x2 alpha; f = 1/2*x1*x1+9/2*x2*x2;%要最小化的函数 df=jacobian(f,[x1 x2]);%函数f的偏导 epsilon=1e-6;%0.000001k=0; x0=[9 1];%起始点 xk=x0; gk=subs(df,[x1 x2],xk);%起始点的梯度 gk=double(gk); while(norm(gk)>epsilon)%迭代终止条件||gk||<=epsilon pk=-gk;%负梯度方向 f_alpha=subs(f,[x1 x2],xk+alpha*pk);%关于alpha的函数 [left right] = jintuifa(f_alpha,alpha);%进退法求下单峰区间 [best_alpha best_f_alpha]=golddiv(f_alpha,alpha,left,right);%黄金分割法求最优步长xk=xk+best_alpha*pk; k=k+1; gk=subs(df,[x1 x2],xk); gk=double(gk); end best_x=xk;%最优点 best_fx=subs(f,[x1 x2],best_x);%最优值 共轭梯度法 最优化课程设计--共轭梯度法算法分析与实现 (设计程序) 题目共轭梯度法算法分析与实现 班级 / 学号 14140101/11 学生姓名黄中武指导教师王吉波王微微 课程设计任务书 课程名称最优化方法课程设计院(系) 理学院专业信息与计算科学 课程设计题目共轭梯度法算法分析与实现课程设计时间: 2014 年 6月 16日至2014 年 6月 27日 课程设计的要求及容: [要求] 1. 学习态度要认真,要积极参与课程设计,锻炼独立思考能力; 2. 严格遵守上机时间安排; 3. 按照MATLAB编程训练的任务要求来编写程序; 4. 根据任务书来完成课程设计论文; 5. 报告书写格式要求按照航空航天大学“课程设计报告撰写规”; 6. 报告上交时间:课程设计结束时上交报告; 7. 严禁抄袭行为,一旦发现,课程设计成绩为不及格。 一、运用共轭梯度法求解无约束最优化问题 要求:1)了解求解无约束最优化问题的共轭梯度法; 2)绘出程序流程图; 3)编写求解无约束最优化问题的共轭梯度法MATLAB程序; 4)利用编写文件求解某无约束最优化问题; 5)给出程序注释。 指导教师年月日 负责教师年月日 学生签字年月日 航空航天大学 课程设计成绩评定单 课程名称最优化理论与算法课程设计院(系) 理学院专业信息与计算科学课程设计题目共轭梯度法算法分析与实现学号 11 黄中武指导教师评语: 课程设计成绩 指导教师签字 年月日 最优化方法课程设计航空航天大学课程设计用纸目录 目录 一、正文 ............................................................... 1 二、总 结 ............................................................... 8 参考文 献 ............................................................... 9 附 录 (10) 第 I 页 最优化方法课程设计航空航天大学课程设计用纸正文 一、正文 一无约束最优化问题的共轭梯度法 共轭梯度法最初是由Hesteness和Stiefel于1952年为求解线形方程组而提出的。后来,人们把这种方法用于求解无约束最优化问题,使之成为一种重要的最优化方法。 下面,重点介绍Fletcher-Reeves共轭梯度法,简称FR法。 共轭梯度法 1.算法思想: 共轭梯度法是利用目标函数梯度逐步产生共轭方向作为线搜索方向的方法,每次搜索方向都是在目标函数梯度的共轭方向,搜索步长通过一维极值算法确定。 2.算法步骤: 用共轭梯度法求无约束多维极值问题min (),n f x x R ∈的算法步骤如下: (1) 给定初始点(0)x ,及精度0ε>; (2) 若 (0)()f x ε ?≤,停止,极小值点为(0)x ,否则转步骤(3); (3) 取(0)(0)()p f x =-?,且置0k =; (4) 用一维搜索法求k t ,使得()()()()()0 ()min k k k k k t f x t p f x tp ≥+=+,令,(1)()()k k k k x x t p +=+,转步骤5; (5) 若 (1)()k f x ε +?≤,停止,极小值点为(1)k x +,否则转步骤(6); (6) 若1k n +=,令(0)()n x x =,转步骤(3),否则转步骤(7); (7) 令(1)(1)()()k k k k p f x p λ++=-?+,2(1)2 () () () k k k f x f x λ+?=?,置1k k =+,转 步骤(4)。 3.算法源程序: #include #define N 10 #define eps pow(10,-6) double f(double x[],double p[],double t) { double s; s=pow(x[0]+t*p[0],2)+25*pow(x[1]+t*p[1],2); return s; } /*以下是进退法搜索区间源程序*/ void sb(double *a,double *b,double x[],double p[]) { double t0,t1,t,h,alpha,f0,f1; int k=0; t0=2.5; /*初始值*/ h=1; /*初始步长*/ alpha=2; /*加步系数*/ f0=f(x,p,t0); t1=t0+h; f1=f(x,p,t1); while(1) { 牛顿法 迭代公式:(1)2()1()[()]()k k k k x x f x f x +-=-?? Matlab 代码: function [x1,k] =newton(x1,eps) hs=inline('(x-1)^4+y^2'); 写入函数 ezcontour(hs,[-10 10 -10 10]); 建立坐标系 hold on; 显示图像 syms x y 定义变量 f=(x-1)^4+y^2; 定义函数 grad1=jacobian(f,[x,y]); 求f 的一阶梯度 grad2=jacobian(grad1,[x,y]); 求f 的二阶梯度 k=0; 迭代初始值 while 1 循环 grad1z=subs(subs(grad1,x,x1(1)),y,x1(2)); 给f 一阶梯度赋初值 grad2z=subs(subs(grad2,x,x1(1)),y,x1(2)); 给f 二阶梯度赋初值 x2=x1-inv(grad2z)*(grad1z)'; 核心迭代公式 if norm(x1-x2) end end end 优点:在极小点附近收敛快 缺点:但是要计算目标函数的hesse 矩阵 最速下降法 1. :选取初始点xo ,给定误差 2. 计算一阶梯度。若一阶梯度小于误差,停止迭代,输出 3. 取()()()k k p f x =? 4. 10 t ()(), 1.min k k k k k k k k k k t f x t p f x tp x x t p k k +≥+=+=+=+进行一维搜索,求,使得令转第二步 例题: 求min (x-2)^4+(x-2*y)^2.初始值(0,3)误差为0.1 (1)编写一个目标函数,存为f.m function z = f( x,y ) z=(x-2.0)^4+(x-2.0*y)^2; end (2)分别关于x 和y 求出一阶梯度,分别存为fx.m 和fy.m function z = fx( x,y ) z=2.0*x-4.0*y+4.0*(x-2.0)^3; end 和 function z = fy( x,y ) 共轭梯度法及其基本性质 预备知识 定义1 设是对称正定矩阵。称是A-共轭的,是指 性质1 设有是彼此共轭的维向量,即 则一定是线性无关的。 [证明]若有一组数满足 则对一切一定有 注意到,由此得出:即所有的=0.因此, 是线性无关的. 性质2设向量是线性无关的向量组,则可通过它们的线性组合得出一组向量,而是两两共轭的. [证明]我们用构造法来证实上面的结论. S0:取; S1:令,取. …… Sm:令 取 容易验证:符合性质2的要求. 性质3设是两两A-共轭的,是任意指定的向量,那么从出发,逐次沿方向搜索求的极小值,所得序列,满足: . [证明]由下山算法可知,从出发,沿方向搜索,获得 从而 性质4设是两两A共轭的,则从任意指定的出发,依次沿搜索,所得序列满足: (1) (2),其中是方程组(5.1.1)的解. [证明](1)是性质3的直接推论,显然成立. (2)由于是两两A共轭的,故是线性无关的.所以对于向量可用线性表出,即存在一组数使 由于及,得出 , 于是,再由得出 于是,与得出一样地,我们可以陆续得出: 对比和的表达式可知, 证明完毕 性质4是性质3的直接推论.但它给出了一种求(5.1.1)的算法,这种算法称之为共轭方向法.结合性质2,我们可以得到如下的性质5. 性质5设是上的一组线性无关的向量,则从任意指定的出发,按以下迭代产生的序列: S1:取,,; S2:计算,取; 计算,得出; 如此进行下去,直到第n步: Sn:计算取 计算,得出. 显然: 根据性质4可知,不论采用什么方法,只要能够构造个两两A共轭的向量作为搜索方向,从任一初始向量出发,依次沿两两A共轭的方向进行搜索,经 步迭代后,便可得到正定方程组的解. 最优化课程设计 题目:共轭梯度法 姓名:田鑫 指导老师:智红英 学号: 201118030216 班级:信息与计算科学111802班 共轭梯度法(Conjugate Gradient) 是介于最速下降法与牛顿法之间的一个方法,它仅需利用一阶导数信息,但克服了最速下降法收敛慢的缺点,又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点,共轭梯度法不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法之一。在各种优化算法中,共轭梯度法是非常重要的一种。其优点是所需存储量小,具有步收敛性,稳定性高,而且不需要任何外来参数。 设我们要求解下列线性系统 其中n-×-n矩阵A是对称的(也即,A T = A),正定的(也即,x T Ax > 0对于所有非0向量x属于R n),并且是实系数的。 将系统的唯一解记作x*。 最后算法 经过一些简化,可以得到下列求解Ax = b的算法,其中A是实对称正定矩阵。x := 0 k := 0 r := b repeat until r k is "sufficiently small": k := k + 1 if k = 1 p := r0 1 else end if x := x k-1 + αk p k k r := r k-1 - αk A p k k end repeat 结果为x k 共轭梯度法程序源代码 #include 应用共轭梯度法求解方程组121242 x x x x +=??-=?的根。初始值(0)(0,0)T x = 分析:将方程组Ax b =转化为优化问题中的极值问题然后应用共轭梯度法进行求解。 令()R x Ax b =-,只需求得x ,使得()R x 取得最小值。则有: min ()R x ?2min ()R x min T R R ? ()() ()() ()()()()2T T T T T T T T T T T T T T T T T T T T T T T T T T R R Ax b Ax b X A b Ax b X A AX X A b b Ax b b X A AX X A b b Ax b b X A A X b AX b Ax b b X A A X b AX b b =--=--=--+=--+=--+=-+这是一个数 与1()2 T T f x x Gx b x c =++比较 则有:2,()22T T T G A A g x A A A b ==- 回到题目问题中,则对应有124124012,,04444x G g b x --??????=== ? ? ?--?????? 也就是应用共轭梯度法求点使221212()2212420f x x x x x =+--+取得最小值。 程序清单: #include 题目:共轭梯度法及其数值实现 院系:数理科学与工程学院应用数学系 专业:数学与应用数学 姓名学号:************ ************ ************ ************ 指导教师:张世涛 日期:2015 年7 月 5 日 最优化是一门应用性很强的学科,近年来,随着计算机的发展以及实际问题的需要,大规模优化问题越来越受到重视。共轭梯度法是最优化中最常见的方法之一,他具有算法简单、存储需求少、有较快的收敛速度和二次终止性且易于实现等优点,十分适合于大规模优化问题。 非线性共轭梯度法已有五十多年的历史,最早由计算数学家Hestenes和几何学家Stiefel 为求解线性方程组Ax=b,n R x∈而独立提出的。较著名的有FR方法、PRP方法、HS方法和LS方法等。非线性最优化的共轭梯度算法的收敛性分析,也就是讨论各种共轭梯度算法在不同搜索下的收敛性质。本文主要研究求解无约束优化问题的非线性共轭梯度法,并用Matlab软件对其数值实现。 关键词:无约束规划;非线性共轭梯度法;迭代;最优解;数值实现 Abstract Optimization is strong discipline applied. In recent years, with the development of computer and practical issues,large-scale optimization problems are given more and more attention. Conjugate gradient method is one of the most commonly used methods in optimization. It is simply, storage needs less, easy to practice with faster convergence speed and quadratic termination. It is suitable for large-scale optimization problem. The conjugate gradient method have been more than 50 years of history. The pioneers were mathematician Hestenes and geometrician Stiefel. They independently proposed this method for solving system of linear equations Ax=b,n R x∈. Well-known conjugate gradient method is FR method, PRP method, HS method, LS method and so on. The convergence analysis of the conjugate gradient algorithm for nonlinear optimization is also the convergence of various conjugate gradient algorithms under different search conditions. Global convergence and numerical result of nonlinear conjugate gradient method of unconstrained optimization is investigated in this paper. Besides, we use Matlab to get its numerical solution. Keywords:Unconstrained programming; Nonlinear conjugate gradient method; Iteration; Optimal solution; Numerical implementation最优化课程设计--共轭梯度法算法分析与实现
作业4-FR共轭梯度法
(修改稿)一种新的修正DY共轭梯度法的全局收敛性
第六节 最速下降法与共轭梯度法
共轭梯度法课程设计
共轭梯度法程序
共轭梯度法
共轭梯度法
最优化课程设计--共轭梯度法算法分析与实现
共轭梯度法
最优化牛顿法最速下降法共轭梯度法matlab代码
共轭梯度法和基本性质
共轭梯度法c++程序
共轭梯度法求极小值
共轭梯度法