
静安区2019学年第二学期教学质量检测高三数学试卷
参考答案与评分标准
一. 1.31
; 2.2-; 3.20; 4.()2,2-;
5.2021
; 6.4; 7.π; 8.0;
9.5.26; 10.1; 11.4
1
.
二、12.B .13.A .;14.C .
三、15.(本题满分14分,第1小题7分,第2小题满分7分)
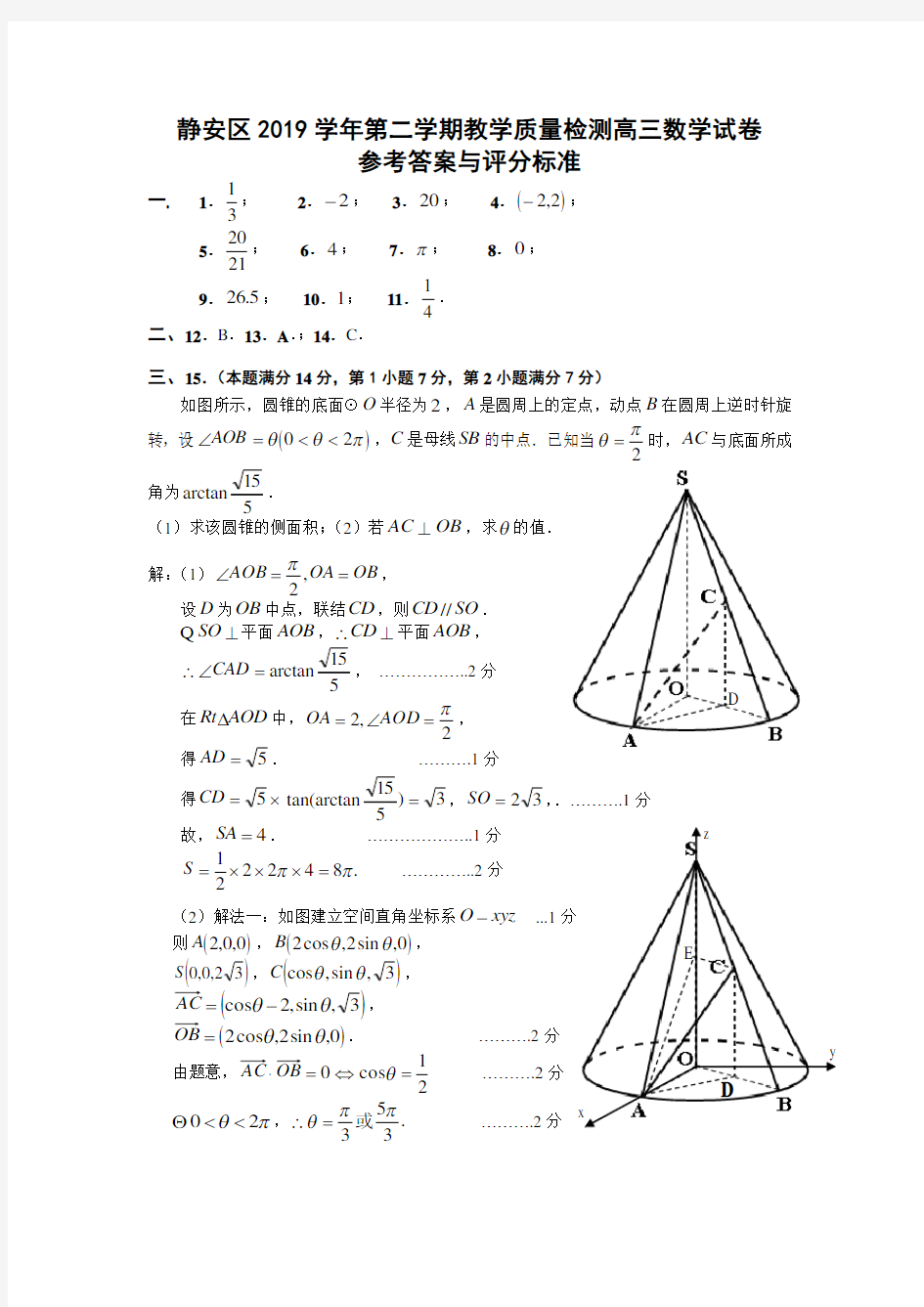
如图所示,圆锥的底面⊙O 半径为2,A 是圆周上的定点,动点B 在圆周上逆时针旋转,设()πθθ20<<=∠AOB ,C 是母线SB 的中点.已知当2
π
θ=时,AC 与底面所成
角为5
15
arctan
. (1)求该圆锥的侧面积;(2)若⊥AC OB ,求θ的值. 解:(1)OB OA AOB ==
∠,2
π
,
设D 为OB 中点,联结CD ,则SO CD //.
SO ⊥Q 平面AOB ,CD ∴⊥平面AOB ,
5
15
arctan
=∠∴CAD , ……………..2分 在Rt AOD ?中,2
,2π
=∠=AOD OA ,
得5=AD . ……….1分 得?=
5CD 3)5
15
tan(arctan
=,32=SO ,.……….1分 故,4=SA . ………………..1分
.84222
1
ππ=???=
S …………..2分 (2)解法一:如图建立空间直角坐标系xyz O - ...1分则()0,0,2A ,()0,sin 2,cos 2θθB ,
(
)32,0,0S ,(
)
3,sin ,cos θθC ,
(
)
3,sin ,2cos θθ-=AC ,
()0,sin 2,cos 2θθ=OB . ……….2分
由题意,2
1
cos 0=?=?θOB AC ……….2分
πθ20<<Θ,.3
53ππθ或=∴ ……….2分
D
D
x
y
z
E
解法二:设D 为OB 中点,联结CD ,则SO CD //.
OB CD ⊥∴. ……….2分 又⊥AC ΘOB ,可得⊥OB 平面ADC OB AD ⊥?,
AB OA =∴. ……….2分 AOB ?∴是等边三角形. ………1分
故,3π
θ=
或
3
5π
. ……….2分
解法三:设E 为SO 中点,联结CE ,AE ,
CE AC ⊥∴. ………1分 设D 为OB 中点,联结CD ,AD ,
AD CD ⊥∴. ………1分
在ADO ?中,由余弦定理,有θcos 452
-=AD , ………1分
所以,在ADC Rt ?中,θcos 482
-=AC .
在AOE ?中,有72
=AE ,
所以,在ACE Rt ?中,2
22CE AC AE +=,
即得2
1
cos =θ. ………2分
πθ20<<Θ,.3
53π
πθ或=∴ ………2分
16.(本题满分14分;第1小题6分,第2小题8分)
若函数()()sin (0,0,0)f x A x A ω?ω?π=+>>≤<满足下列条件:①()f x 的图像向左平移π个单位时第一次和原图像重合;对任意的R x ∈都有()26f x f π??
≤= ???
成立. (1)求()f x 的解析式;
(2)若锐角ABC ?的内角B 满足()1f B =,且B ∠的对边1b =,求ABC ?的周长l 的取
值范围. 16.解:(1)由题意,可得最小正周期T π=,
由2T π
πω
=
=,解得2ω=. ………………..2分
()26f x f π??
≤= ???
Q ,2A ∴=, ………………..2分
2262
k ππ?π+=+g ,26k π
?π∴=+,
(Z k ∈) 又0?π≤ ?∴= . ………………..2分 故()2sin 26f x x π? ?=+ ?? ?. (2)2sin 216B π? ?+= ?? ?Q ,3B π∴=, ………………..1分 又02B A ππ<-- A ππ ∴<<.………………..1分 sin sin sin 3b a c B A A ππ== ??-- ???Q ,22sin A a c π??- ? ∴== 22sin 12sin 16A l A ππ??- ? ??∴=+=++ ? ? ?.………………..4分 2,633A πππ??+∈ ??? Q . 所以,周长( 1l ?∈? . ………………..2分 17.(本题满分19分,第1小题5分,第2小题7分,第3小题7分) 已知抛物线Γ:2 4y x =的焦点为F ,若ABC ?的三个顶点都在抛物线Γ上,且 0FA FB FC ++=u u u r u u u r u u u r r ,则称该三角形为“核心三角形”. (1)是否存在“核心三角形”,其中两个顶点的坐标分别为(0,0)和(1,2)?请说明理由; (2)设“核心三角形”ABC 的一边AB 所在直线的斜率为4,求直线AB 的方程; (3)已知ABC ?是“核心三角形”,证明:点A 的横坐标小于2. 解:(1)第三个顶点的坐标为3(1,0)(0,0)(1,2)(2,2)--=-. 但点(2,2)-不在抛物线Γ上 所以这样的“核心三角形”不存在.(反证法叙述同样给分) ………………..5分 (2)设直线AB 的方程为t x y +=4,与2 4y x =联立,得02 =+-t y y . …..2分 设()()()112233,,,,,A x y B x y C x y .2 41)2(41,1212121t t y y x x y y -=-+= +=+ 由()()123123,3,0x x x y y y ++++=得411 23+=t x ,31y =-.……………..3分 代入方程2 4y x =,解得5m =-,所以直线AB 的方程为450x y --=.…..2分 (3)设直线BC 的方程为x ny m =+,与2 4y x =联立,得2 440y ny m --=...1分 因为直线BC 与抛物线Γ相交,故判别式() 2160n m ?=+>. ……………..1分 234y y n +=, 所以,2 2342x x n m +=+. 点A 的坐标为( ) 2 423,4n m n --+-, 又因为点A 在抛物线Γ上,故2 2 1616812n n m =--+,得2 342 m n =-+ . 2m n >-Q ,212 n ∴< . 故,点A 的横坐标2 2 2 2 4234842n m n n n --+=-+=<. ………………..5分 注:(3)也可以用反证法证明,同样给分. 18.(本题满分19分,第1小题6分,第2小题6分,第3小题7分) 设数列{}n a 的每一项均为正数,对于给定的正整数k ,k n n n a a b +?=)N (* ∈n ,若{} n b 是等比数列,则称{}n a 为)(k B 数列. (1)求证:若{}n a 是等比数列,则{}n a 是)(k B 数列; (2)请你写出一个不是等比数列的)1(B 数列的通项公式; (3)设{}n a 为)1(B 数列,且满足312 2a a a ?=,请用数学归纳法证明:{}n a 是等比数列. 解:(1)设{}n a 是公比为q 的等比数列, 对于给定的正整数k ,k n n n a a b +?=)N (* ∈n , k n n n a a b ++++?=∴111. 02111>=??=+++++q a a a a b b k n n k n n n n . 又,0111>?=+k a a b . 所以{}n b 是等比数列. 故{}n a 为)(k B 数列. ………………..6分 (2)?????=-==--k n q a k n q a a k k n 2,,12,1 21 1(q a a 2 122≠).(答案不唯一)………………..6分 简洁的例子如:?? ?=-==k n k n a n 2,2, 12,1)N (*∈k . (3)因为{}n a 为)1(B 数列,所以,{}n b 是等比数列,其中1+?=n n n a a b )N (* ∈n , n n n n n n n n a a a a a a b b 21211+++++=??=∴)N (*∈n , ? ?????∴+n n a a 2)N (*∈n 是常数列,设常数为2q ,即22q a a n n =+)N (*∈n . 以下用数学归纳法证明(一)221++?=n n n a a a )N (* ∈n . (i )由已知312 2a a a ?=,可得当1=n 时命题成立. ………………..1分 (ii )假设1-=k n )2,N (≥∈* k n 时命题成立,即,112+-?=k k k a a a .…..1分 当k n =时,? ???? ?+n n a a 2Θ)N (* ∈n 是常数列. ………………..2分 1 1 2-++=∴ k k k k a a a a )2,N (≥∈*k k , 211122+-++=?=?∴k k k k k k a a a a a a . ………………..2分 等式也成立. 根据(i )和(ii )可以断定,221++?=n n n a a a 对任何* ∈N n 都成立,即{}n a 是等比数 列. ………………..1分 令n n n a a c 1+= ,以下用数学归纳法证明(二)q c n =)N (* ∈n . (i )3122a a a ?=Θ,1223a a a a =∴,2 2 1213q a a a a =??? ? ??=∴,q a a =∴12,即,q c =1. 故,当1=n 时命题成立. ………………..1分 假设k n =)1,N (≥∈* k k 时命题成立,即q c k =(q a a k k =+1).………………..1分 (ii )当1+=k n 时,q a a q a a a a a a c k k k k k k k =?=?==+++++2 1212121. …………..4分 等式也成立. 根据(i )和(ii )可以断定,q c n =对任何* ∈N n 都成立,即{}n a 是等比数列. …………..1分 注:其它表述方法同样给分.