
1.
2.
(2011-重庆)曲线尸?X 3+3X 2在点(I,
2)
A. y=3x - 1
B. y=-3x+5
(201b 山东)曲线 y=x 3+l 1 在点 P (1, 12)
处的切线方程为(
)
C. y=3x+5
D. y=2x
处的切线与y 轴交点的纵坐标是(
15 3. A. [- 1,-岑]
B ?[?1, 0]
C. [0, II
D.[兰,1]
乙
那么导函数y=f (x )的图象可能是(
函数q : g (x ) =x 2 - 4x+3m 不存在零点则
p 是
D.既不充分也不必要条件
导数与反函数练习题
选择题
(2011 ?杭州)如图是导函数尸f (x )的图象,则下列命题错误的是(
)
A .导函数y=f (x )在x=xi 处有极小值
B .导函数y=F (x )在x=x?处有极大值 C.函数y=f (x )在x=X3 处有极小值 D.函
数y=f (x )在x=X4处有极小值
4. (2011 ?福建)若a>0, b>0,且函数f (x ) =4x 3 - ax 2 - 2bx+2在x=l 处有极值,则ab 的最大值等于(
)
A. 2
B. 3
C. 6
D. 9
5. (2010*江西)若 f (x ) =ax 4+bx 2+c 满足 f (I ) =2,则 f ( - 1)=(
)
A. -4
B. - 2
C. 2
D. 4
6. (2009?江西)若存在过点(1, 0)的直线与曲线尸x3和y=ax 2+^X- 9都相切,则a 等于(
)
方
91 7 9R
7
A. - 1 或一竺
B. - 1
C. 一」或一竺
D. 一 ■或 7
64
4 4 64 4
°
TT
7. (2008?辽宁)设P 为曲线C : y=x~+2x+3上的点,且曲线C 在点P 处切线倾斜角的取值范围是[0,—],则点P 横
4
坐标的取值范围是( )
A.充分不必要条件
B.必要不充分条件
C.
充分必要条件8.(2008?福建)如果函数y=f (x )的图象如图,
q 的( )
(0)
13. A. 4x-y ?3=0 B. x+4y - 5=0
C. 4x ?y+3=0
D. x+4y+3=0
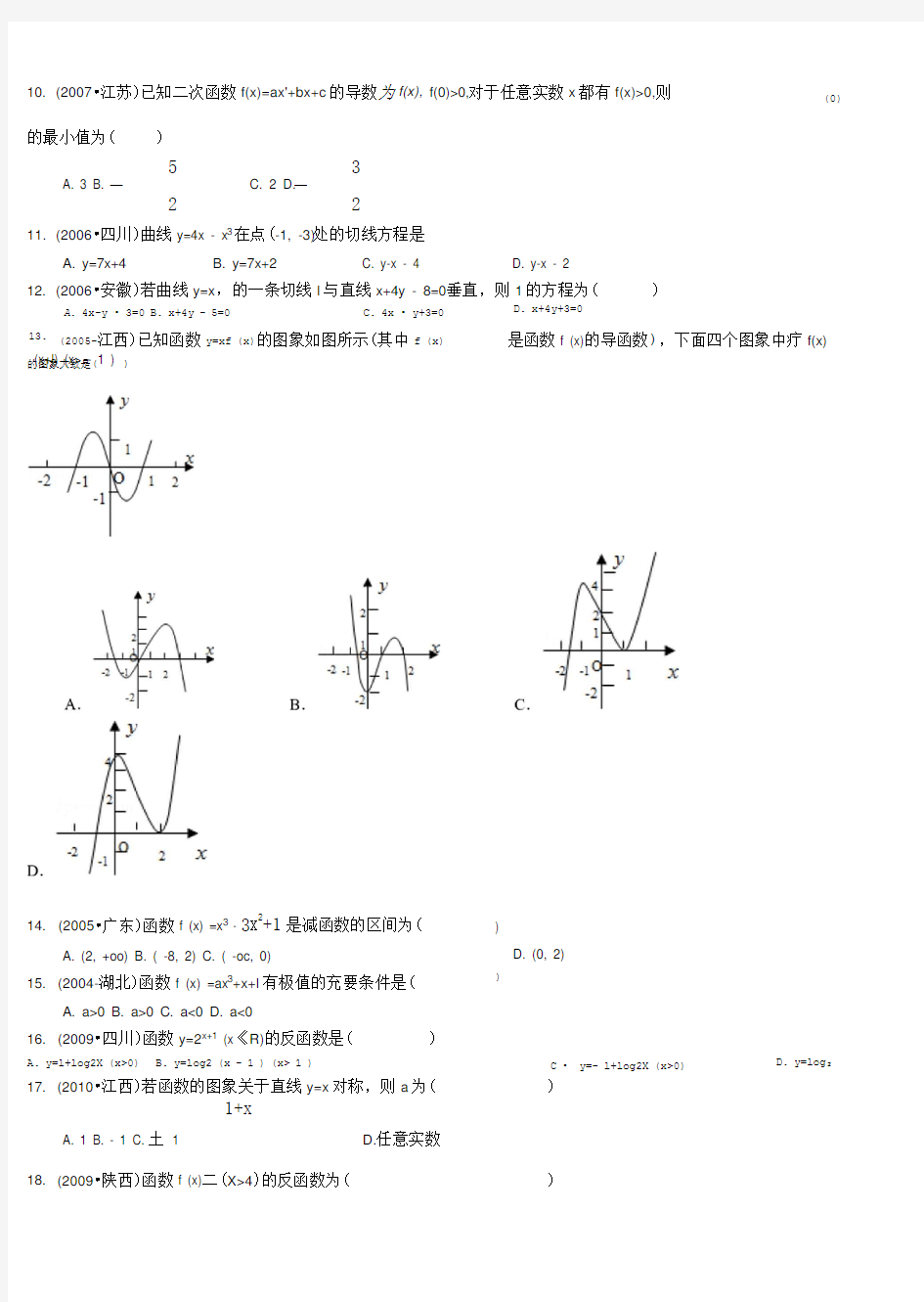
(2005-江西)已知函数y=xf (x)的图象如图所示(其中f (x)
是函数f (x)的导函数),下面四个图象中疔f(x)
14. (2005?广东)函数f (x) =x 3
- 3X
2
+1是减函数的区间为(
A. (2, +oo)
B. ( -8, 2)
C. ( -oc, 0)
15. (2004-湖北)函数f (x) =ax 3+x+l 有极值的充要条件是(
A. a>0
B. a>0
C. a<0
D. a<0
16. (2009?四川)函数y=2x+1 (x 《R)的反函数是(
)
A. y=l+log2X (x>0)
B. y=log2 (x - 1 ) (x> 1 )
)
D. (0, 2)
)
C ? y=- l+log2X (x>0)
D. y=log 2
10. (2007?江苏)已知二次函数f(x)=ax'+bx+c 的导数为f(x), f(0)>0,对于任意实数x 都有f(x)>0,则
的最小值为(
)
5
3 A. 3 B. ―
C. 2
D.―
2
2
11. (2006?四川)曲线y=4x - x 3在点(-1, -3)处的切线方程是
A. y=7x+4
B. y=7x+2
C. y-x - 4
D. y-x - 2
12. (2006?安徽)若曲线y=x ,的一条切线I 与直线x+4y - 8=0垂直,则1的方程为(
)
(x+l) (x> - 1 ) 17.
(2010?江西)若函数的图象关于直线
y=x 对称,则
a 为( )
1+x
A. 1
B. - 1
C. 土 1
D.任意实数
18. (2009?陕西)函数f (x)二(X>4)的反函数为(
)
的图象大致是( )
A. fT (x)蓦x?+2 (x 》0) c. f-1 (x) *+4 (Qo)
B . fT (x) *+2 (x 》2)
D. f-1 (x) *+4(x 》2)
x — 2 19?(2009?湖北)函数y= --- (xER, 2x ~ 1 且好岑)的反函数是( A. y=^-~Y ( xE R, 且 2x ~
1 2
B. C. 广 x+2 ( xE R, 且x 尹4)
2 1 _ 20. (2009-湖北)设a 为非零实数,函数y= ax 1+ax
且 X#1 ) 1 _ ax 1
A. y=— ----------- (xWR,.且 x 尹 ) 1+ax
a
1 - X
D. V= ? ----------- r — (x£R, B. 21. (2009?广A. log2X 22. (2009?广A. log2X
23. 24. 25. 26. D.
y=——( xE R,且x 尹2) x _
2
— 1 y=_ ( x€ R,且好 - 2) (xeR,且乂具)的反函数是(
a
1+ax y=
l
- ax
(xER,且 x£) a c
y= y
a (1-x)
(xER,
且 x^--) a 若函数y=f (x)是函数y=a x (a>0,且狎1) B. log —x C. —D. x 2
2 2X
的反函数,其图象经过点(崩,a ),则f (x )=(
若函数y=f (x )是函数y=a x a (a>0, Jla/1)的反函数,旦f △) =1,则函数y=( C. log ]X
2
函数 y=10x2-1 (0
(2008?重庆)
的反函数是(
B . y^Vl+lgx
(x>—)
10
C- y= - Jl+lgx (— 10 D . y^l+lgx (— ------------ 10 _ 函数 1) 2 (l A. y= (x- (0 (2008,天津) A. f 1 (x) C. f'1 (x) (2008?湖南) (0 ) B. y= (x- 1) 2 (0 C. 7 y=x -1(1 D. y=x 2 (OVxVl ) 1- Vx 在其定义域上是增函数旦最大值为1 在其定义域上是减函数且最大值为1 设函数f 的反函数为f-1 (x), B . r 1(X )在其定义域上是减函数旦最小值为o D. fT (x )在其定义域上是增函数且最小值为0 函数y=log 2 (x2 -2x+1) (x>l) 的反函数为尸f-】(x ),则fT (2)等于( A. 3 B. 2 C. 0 D ??2 27. (2007?天津)函数 y=log 2 (x+1) +1 (x>0)的反函数为( A. y=2x , - 1 (x>l) B. y=2x , +l (x>l) ) C. y=2x+l - 1 (x>0) D.y=2x+1+l(x>0) 28. (2007-辽宁)若函数y=f (x)的反函数图象过点(1, 5),则函数y=f (x)的图象必过点( ) A. (1, 1) B. (1, 5) C. (5, 1) D. (5, 5) 29. (2004?黑龙江)函数疔口^ (x/-5)的反函数是( ) x+5 A. y旦-5 (x,0) B. y=x+5 (x^R) C. y=i-5 (x/0) D. y=x - 5 (xGR) X X 30. (2004-陕西)记函数y=l+3”的反函数为尸g (x),则g (10)等于( ) A. 2 B. - 2 C. 3 D. - 1 二、反函数的导数法则 定理1:设)(x f y =为)(y x ?=的反函数,若)(y ?在0y 的某邻域内连续,严格单调,且0)(0≠'y ?,则)(x f 在0x (即)(0y f 点有导数),且) (1 )(00y x f ?'= '。 证明:0 0000)()(1 lim )()(lim )()(lim 000 y y y y y y y y x x x f x f y y y y x x --=--=--→→→???? )(1 )()(lim 100 00y y y y y y y ???'=--= → 所以 ) (1 )(00y x f ?'='。 注1:00 y y x x →? →,因为)(y ?在0y 点附近连续,严格单调; 2:若视0x 为任意,并用x 代替,使得)(1)(y x f ?'= '或)(1 dy dx dx dy =,其中dy dx dx dy , 均为整体记号,各代表不同的意义; 3:)(x f '和)(y ?'的“′”均表示求导,但意义不同; 4:定理1即说:反函数的导数等于直接函数导数的倒数; 5:注意区别反函数的导数与商的导数公式。 【例1】 求x y arcsin =的导数, 解:由于]1,1[,arcsin -∈=x x y ,是]2 ,2[,sin π π- ∈=y y x 的反函数,由定理1 得: 2211 sin 11cos 1)(sin 1)(arcsin x y y y x -= -=='='。 注1:同理可证:2 22 11 )tan (,11)(arctan ,11)(arccos x x arcc x x x x +-='+= '-- ='; 高阶导数 1. 填空题. (1)x y 10=,则()()=0n y . (2)y x =sin2,则()()y x n = .. 2. 选择题. (1)设f x ()在()-∞+∞,内为奇函数且在()0,+∞内有'>f x ()0,''>f x ()0,则f x ()在()-∞,0内是( ) A. ' 隐函数及由参数方程所确定的函数的导数 1. 设y e y x x sin 22=-,求.dx dy 2. 设063sin 33=+-+y x y x ,求.0 =x dx dy 3.求曲线??? ????+=+=222 1313t t y t t x 在2=t 处的切线方程和法线方程. 4.利用对数求导法求导数. (1).1sin x e x x y -= (2)().sin ln x x y = 反三角函数求导公式的证明 §2.3 反函数的导数,复合函数的求导法则 一、反函数的导数 设)(y x ?=是直接函数,)(x f y =是它的反函数,假定)(y x ?=在I y 内单调、可 导,而且0)(≠'y ?,则反函数)(x f y =在间},)(|{y x I y y x x I ∈==?内也是单调、可 导的,而且 )(1 )(y x f ?'=' (1) 证明: ?∈x I x ,给x 以增量x ?),0(x I x x x ∈?+≠? 由 )(x f y = 在 I x 上的单调性可知 0)()(≠-?+=?x f x x f y 于是 y x x y ??=??1因直接函数)(y x ?=在I y 上单调、可导,故它是连续的,且反函数)(x f y =在I x 上也是连续的,当0→?x 时,必有0→?y )(11lim lim 00y y x x y y x ?'=??=??→?→?即:)(1)(y x f ?'=' 【例1】试证明下列基本导数公式 ().(arcsin )().()().(log )ln 11 1211312 2 x x arctgx x a x a x '=-'=+'= 证1、设y x sin =为直接函数,x y arcsin =是它的反函数 函数 y x sin =在 )2,2(ππ-=y I 上单调、可导,且 '=≠x y cos 0 因此,在 )1,1(-=x I 上, 有 y x cos 1)arcsin (= ' 注意到,当)2,2(π π-∈y 时,0cos >y ,221sin 1cos x y y -=-= 因此, 211)arcsin (x x -= ' 证2 设x tgy =,)2,2(ππ-=y I 则y arctgx =,I x =-∞+∞(,) tgy x = 在 I y 上单调、可导且 0cos 12>='y x 故 2221111cos )(1)(x y tg y tgy arctgx +=+=='= ' 证3 a x a a a a y y x ln 1ln 1)(1)log (=='= ' 类似地,我们可以证明下列导数公式: 反函数定义 一般地,设函数y=f(x)(x∈A)的值域是C,根据这个函数中x,y 的关系,用y 把x表示出,得到x= g(y). 若对于y在C中的任何一个值,通过x= g(y),x在A 中都有唯一的值和它对应,那么,x= g(y)就表示y是自变量,x是因变量y的函数,这样的函数x= g(y)(y∈C)叫做函数y=f(x)(x∈A)的反函数,记作y=f^-1(x). 反函数y=f^-1(x)的定义域、值域分别是函数y=f(x)的值域、定义域. 反函数性质 (1)互为反函数的两个函数的图象关于直线y=x对称; 函数及其反函数的图形关于直线y=x对称 (2)函数存在反函数的充要条件是,函数的定义域与值域是一一映射; (3)一个函数与它的反函数在相应区间上单调性一致; (4)大部分偶函数不存在反函数(唯一有反函数的偶函数是f(x)=a^x,x∈{0},但是y=k(常数)无法通过水平线测试,所以没有反函数。)。奇函数不一定存在反函数。被与y轴垂直的直线截时能过2个及以上点即没有反函数。若一个奇函数存在反函数,则它的反函数也是奇函数。 (5)一切隐函数具有反函数; (6)一段连续的函数的单调性在对应区间内具有一致性; (7)严格增(减)的函数一定有严格增(减)的反函数【反函数存在定理】。 (8)反函数是相互的且具有唯一性 (9)定义域、值域相反对应法则互逆(三反) (10)原函数一旦确定,反函数即确定(三定)(在有反函数的情况下,即满足(2)) 例:y=2x-1的反函数是y=0.5x+0.5 y=2^x的反函数是y=log2 x 例题:求函数3x-2的反函数 解:y=3x-2的定义域为R,值域为R. 由y=3x-2解得 x=1/3(y+2) 将x,y互换,则所求y=3x-2的反函数是 y=1/3(x+2)(x属于R) (11)反函数的导数关系:如果X=F(Y)在区间I上单调,可导,且F‘(Y)不等于0,那么他的反函数Y=F’(X)在区间S={X|X=F(Y),Y属于I }内也可导,且[F‘(X)]'=1\[F’(Y)]'。 反函数说明 ⑴在函数x=f’(y)中,y是自变量,x是函数,但习惯上,我们一般用x表示自变量,用y 表示函数,为此我们常常对调函数x=f‘(y)中的字母x,y,把它改写成y=f’(x),今后凡无特别说明,函数y=f(x)的反函数都采用这种经过改写的形式。 §2.2 求导法则与导数的基本公式 教学目标与要求 1. 掌握并能运用函数的和、差、积、商的求导法则 2. 理解反函数的导数并能应用; 3. 理解复合函数的导数并会求复合函数的导数; 4. 熟记求导法则以及基本初等函数的导数公式。 教学重点与难度 1. 会用函数的和、差、积、商的求导法则求导; 2. 会求反函数的导数; 3. 会求复合函数的导数 前面,我们根据导数的定义,求出了一些简单函数的导数。但是,如果对每一个函数都用定义去求它的导数,有时候将是一件非常复杂或困难的事情。因此,本节介绍求导数的几个基本法则和基本初等函数的导数公式。鉴于初等函数的定义,有了这些法则和公式,就能比较方便地求出常见的函数——初等函数的导数。 一、函数的和、差、积、商求导法则 1.函数的和、差求导法则 定理1 函数()u x 与()v x 在点x 处可导,则函数()()y u x v x =±在点x 处也可导,且 [()()]()()y u x v x u x v x ''''=±=± 同理可证:' ' ' [()()]()()u x v x u x v x -=- 即证。 注意:这个法则可以推广到有限个函数的代数和,即 12''' ' 12[()()()]()()()n n u x u x u x u x u x u x ±± ±=±±±, 即有限个函数代数和的导数等于导数的代数和。 例1 求函数4 cos ln 2 y x x x π =+++ 的导数 解 4 c o s l n 2y x x x π'??'=+++ ?? ? ()()()4 cos ln 2x x x π'??'''=+++ ??? 3 1 4s i n x x x =-+ 2.函数积的求导公式 定理2 函数()u x 与()v x 在点x 处可导,则函数()()y u x v x =在点x 也可导,且 ''''[()()]()()()()y u x v x u x v x u x v x ==+。 注意:1)特别地,当u c =(c 为常数)时, '''[()]()y cv x cv x ==, 即常数因子可以从导数的符号中提出来。而且将其与和、差的求导法则结合,可得: ''''[()()]()()y au x bv x au x bv x =±=±。 2)函数积的求导法则,也可以推广到有限个函数乘积的情形,即 ''' '12 1212 12 ()n n n n u u u u u u u u u u u u =+++。 例2 求下列函数的导数。 1)32 3254sin y x x x x =+-+; 解 ()()()()3 2 3254sin y x x x x '''''=+-+ 反函数的导数 首先证明反函数的求导公式: 定理:设)(x f y =为)(y x ?=的反函数,若)y (?在点y 0的某邻域内连续,严格单 调且()0' 0≠y ?,则()x f 在点()()00y x x ?=可导,且()() 00'1 'y x f ?= 证:设()()00y y y x ??-?+=?,()()00x f x x f y -?+=?因为?在0y 的某邻域内连续且 严格单调,故1-=?f 在0x 的某邻域内连续且严格单调,从而当且仅当0=?y 时0=?x , 并 且 当 且仅当 →?y 时 0→?x ,由()0'0≠y ?,可得 ()()00000'1 lim 1lim lim 'y y x x y x y x f y y x ?= ??=??=??=→?→?→?。 例6 证明: (i )(a a a x x ln )'(=其中) 1.0(≠>a a 特别地()x x e e =' . (ii) )arcsin ' (x = x 2 -11; ()x arccos '=— x 2 -11 (iii) () x arctan ' = x 2 11 +;() x arc cot ' =— x 2 11 + 证 (i )由于R x y a x ∈= .为对数函数 ,y x a log = .),0(+∞∈y 的反函数,故由公 式(6)得到 ()a x '=) (log ' 1 y a = e y a log = a a x ln . (ii )由于)1,1(,arcsin -∈=x x y 是) 2.2(,sin π π-∈=y y x 的反函数,故由公式(6)得到 ()x arcsin ' = () y sin ' 1 = y cos 1 = y sin 2 -11= )1,1(.-112 -∈x x 同理可 证:()x arccos ' =—)1,1(.-11 2 -∈x x 反函数求导法则 刘云 (天水师范学院数学与统计学院数学与应用数学11级六班 甘肃天水 741000) 摘 要:主要叙述了反函数求导定理,基本初等函数的导数和微分公式,求导定理的推广以及在实际例题中的应用。 关键词:反函数;基本初等函数;求导 引 言 除了少数几个最简单的函数之外,可以直接用定义较方便地求出导数的函数实在是微乎其微,因而就有必要对一般的函数导出一系列的求导运算法则,故本节主要讨论反函数的求导法则以及应用。 1. 反函数求导定理 若函数)(x f y =在()b a ,上连续、严格单调、可导并且0)(≠'x f ,记α))(),(min(-+=b f a f ,))(),(max(-+=b f a f β,则它的反函数)(y f x '=在()b a ,上可导,且有 [])(1)(1x f y f '='-. 证明: 因为函数)(x f y =在()b a ,上连续且严格单调,由反函数连续定理,它的反函数)(1y f x -=在),(βα上存在、连续、且严格单调,这时0)()(≠-?+=?x f x x f y 等价于0)()(11≠-?+=?--y f y y f x ,并且当0→?y 时有0→?x 。 因此 []y y f y y f y f y ?-?+='--→?-)()(lim )(1101 )()(lim 0x f x x f x x -?+?=→? )(1)()(lim 10x f x x f x x f x '=?-?+=→?. 2.基本初等函数的导数和微分公式: 0)(='C 0*0)(==dx C d 1)(-='a a ax x dx ax x d a a 1)(-= x x cos )(sin =' xdx x d cos )(sin = x x sin )(cos -=' xdx x d sin )(cos -= x x 2sec )(tan =' xdx x d 2sec )(tan = x x 2csc )(cot -=' xdx x d 2csc )(cot -= x x x sec tan )(sec =' xdx x x d sec tan )(sec = x x x csc cot )(csc -=' xdx x x d csc cot )(csc -= 3.求导定理的推广 (1)多个函数线性组合的导函数 ∑∑=='='?? ????n i i i n i i i x f c x f c 11)()(, 其中),,3,2,1(n i c i =为常数。 (2)多个函数乘积的导函数 ∑∏∏=≠==?? ????????'='??????n j n j i i i j n i i x f x f x f 111)()()(. §2.3 反函数的导数,复合函数的求导法则 一、反函数的导数 设)(y x ?=是直接函数,)(x f y =是它的反函数,假定)(y x ?=在I y 内单调、可导,而且0)(≠'y ?,则反函数)(x f y =在间 },)(|{y x I y y x x I ∈==?内也是单调、可导的,而且 )(1 )(y x f ?'=' (1) 证明: ?∈x I x ,给x 以增量x ?),0(x I x x x ∈?+≠? 由 )(x f y = 在 I x 上的单调性可知 0)()(≠-?+=?x f x x f y 于是 y x x y ??=??1 因直接函数)(y x ?=在I y 上单调、可导,故它是连续的,且反函数)(x f y =在I x 上也是连续的,当0→?x 时,必有0→?y )(11lim lim 00y y x x y y x ?'=??=??→?→?即:)(1)(y x f ?'=' 【例1】试证明下列基本导数公式 ().(arcsin )().()().(lo g )ln 11121131 2 2x x a rctg x x a x a x '= -'= +'= 证1、设y x sin =为直接函数,x y arcsin =是它的反函数 函数 y x sin =在 )2,2(ππ-=y I 上单调、可导,且 '=≠x y cos 0 因此,在 )1,1(-=x I 上, 有 y x cos 1)arcsin (= ' 注意到,当)2,2(π π-∈y 时,0cos >y ,2 21sin 1cos x y y -=-= 因此, 211 )arcsin (x x -=' 证2 设 x tgy =,)2,2(ππ-=y I 则y arctgx =,I x =-∞+∞(,) tgy x = 在 I y 上单调、可导且 0cos 12>='y x 故 22211 11 cos )(1)(x y tg y tgy arctgx +=+=='=' 证3 a x a a a a y y x ln 1ln 1)(1 )log (=='=' 四、基本求导法则与导数公式 1. 基本初等函数的导数公式和求导法则 基本初等函数的求导公式和上述求导法则,在初等函数的基本运算中起着重要的作用,我们必须熟练的掌握它,为了便于查阅,我们把这些导数公式和求导法则归纳如下: 基本初等函数求导公式 (1) 0)(='C (2) 1 )(-='μμμx x (3) x x cos )(sin =' (4) x x sin )(cos -=' (5) x x 2sec )(tan =' (6) x x 2csc )(cot -=' (7) x x x tan sec )(sec =' (8) x x x cot csc )(csc -=' (9) a a a x x ln )(=' (10) (e )e x x '= (11) a x x a ln 1 )(log = ' (12) x x 1)(ln = ', (13) 211)(arcsin x x -= ' (14) 211)(arccos x x -- =' (15) 21(arctan )1x x '= + (16) 21(arccot )1x x '=- + 函数的和、差、积、商的求导法则 设 )(x u u =,)(x v v =都可导,则 (1) v u v u '±'='±)( (2) u C Cu '=')((C 是常数) (3) v u v u uv '+'=')( (4) 2v v u v u v u '-'=' ??? ?? 反函数求导法则 若函数 )(y x ?=在某区间y I 内可导、单调且0)(≠'y ?,则它的反函数)(x f y =在对应 区间x I 内也可导,且 昨天的文章中提到过反函数的求导法则。反函数的求导法则是:反函数的导数是原函数导数的倒数。这话听起来很简单,不过很多人因此犯了迷糊: y=x3的导数是y'=3x2,其反函数是y=x1/3,其导数为y'=1/3x-2/3.这两个压根就不是互为倒数嘛! 出现这样的疑问,其实是对反函数的概念未能充分理解,反函数是说,将f(x)的自变量当成因变量,因变量当成自变量,得到的新函数x=f(y)就是原函数的反函数。所以y=x3的反函数严格来说应该是x=1/3y-2/3,只不过为了符合习惯,经常将x写成y,y写成x而已,这一点,因为在中学的时候没怎么强调,所以到了大学就有些不适应。因此: y=x1/3的导函数应该这样求y‘=1/(y3)'=1/(3y2) (因为y的反函数是x=y3), =1/(3x2/3)=1/3x-2/3.(将y=x1/3带入即可) 实际上反函数求导法则是根据下面的原则 所以反函数求导法则的意思是说,反函数的导数,等于x对y求导的倒数。我们再以反三角函数来作为例子,希望学到这点的朋友能够真正理解他。 例题:求y=arcsinx的导函数。首先,函数y=arcsinx的反函数为x=siny,所以:y‘=1/sin’y=1/cosy 因为x=siny,所以cosy=√1-x2;(那个啥,这个符号输入有点蛋疼,不过各位应该能看懂) 所以y‘=1/√1-x2。 同理大家可以求其他几个反三角函数的导数。所以以后在求涉及到反函数的导数时,先将反函数求出来,只是这里的反函数是以x为因变量,y为自变量,这个要和我们平时的区分开。最后将y想法设法换成x即可。 相信大家对这一点应该有所明白的吧!大家可以试着求y=arctanx的导函数,然后与结果进行对照。 第十二讲 高阶导数习题 一、选择题 1. 设x e x f 2)(=,则(0)f '''=【 】 A. 8 B. 2 C. 0 D. 1 2. 设x x x f cos )(=,则()f x ''=【 】 A. x x sin cos + B. x x x sin cos - C. x x x sin 2cos -- D. x x x sin 2cos + 3. 设y=sinx ,则y (10)|x=0=【 】 A. 1 B. -1 C. 0 D. 2n 4. 已知ln ,=y x x 则()6y =【 】 A. 5 1x - B. 51x C. 54!x D. 54!x - 二、填空题 1. 设函数)(x f 有任意阶导数且)()('2 x f x f =,则()f x '''= 。 2. 已知函数2x y e =,则y '''=_____________. 3. 设函数)(x f 在2=x 的某邻域内可导,且)()(x f e x f =',1)2(=f ,则=''')2(f _____________. 4. 设函数)(y f x =的反函数)(1x f y -=及)]([1x f f -'、)]([1x f f -''均存在,且 0)]([1≠'-x f f ,则=-212dx )x (f d _____________. 5. 设x x x f +-=11)(,则=)x (f )n (_____________. 6. 设x x y 44cos sin -=,则=) n (y ____________. 7. 184、设x x x y cos sin sin 3+=,则=) n (y ____________. §3.2 求导法则(一) 教学内容 1.函数的和、差、积、商的求导法则; 2.反函数的求导法则; 3.复合函数的求导法则. 教学重点与难点 导数的运算法则及导数基本公式. 简要复习上节内容 1.导数的定义; 2.导数的定义的几种形式; 3.可导的充要条件; 4.函数可导与连续的关系; 5.导数的几何意义、物理意义. 一、导数的四则运算法则 设),(x u u =)(x v v =都在x 处可导,则有 ①v u v u '±'='±)(; ②v u v u uv '+'=')(; u c cu '=')(; ③2 )(v v u u v v u '-'='. 我们现在只证明②. 证 设=)(x f )()(x v x u 则 h x f h x f x f h )()(lim )(0-+='→=h x v x u h x v h x u h ) ()()()(lim 0-++→ =h x v x u x v h x u x v h x u h x v h x u h )()()()()()()()(lim 0-+++-++→ =h x v h x v h x u h )()()(lim 0-++→+=-+→h x u h x u x v h ) ()() (lim 0=v u v u '+' 例1 2sin cos 4)(3π -+=x x x f ,求)(x f ',)2(π f '. 解 )(x f '=x x sin 432-, )2(πf '=443 2-π. 例2 求21 log 3tan sin a y x x x x =++的导数. 解 x x x a x x x x y a 2 22sin cos sec 3ln log 2-+++='. 第十二讲高阶导数习 题 精品文档 收集于网络,如有侵权请联系管理员删除 第十二讲 高阶导数习题 一、选择题 1. 设x e x f 2)(=,则(0)f '''=【 】 A. 8 B. 2 C. 0 D. 1 2. 设x x x f cos )(=,则()f x ''=【 】 A. x x sin cos + B. x x x sin cos - C. x x x sin 2cos -- D. x x x sin 2cos + 3. 设y=sinx ,则y (10)|x=0=【 】 A. 1 B. -1 C. 0 D. 2n 4. 已知ln ,=y x x 则()6y =【 】 A. 5 1x - B. 51x C. 54!x D. 54!x - 二、填空题 1. 设函数)(x f 有任意阶导数且)()('2x f x f =,则()f x '''= 。 2. 已知函数2x y e =,则y '''=_____________. 3. 设函数)(x f 在2=x 的某邻域内可导,且)()(x f e x f =',1)2(=f ,则 =''')2(f _____________. 4. 设函数)(y f x =的反函数)(1x f y -=及)]([1x f f -'、)]([1x f f -''均存在,且 0)]([1≠'-x f f ,则=-2 12dx ) x (f d _____________. 5. 设x x x f +-=11)(,则=)x (f )n (_____________. 6. 设x x y 44cos sin -=,则=) n (y ____________. 7. 184、设x x x y cos sin sin 3+=,则=) n (y ____________. 8. 设)()()(x a x x f n ?-=,其中)(x ?在点a 的一个邻域内有)1(-n 阶连续导数,则 浅析莱布尼兹公式在求高阶导数中的应用 导数的计算在我们整个考研数学是一个比较简单的考点了,只需灵活运用函数求导法则、导数四则运算、复合函数求导、反函数求导以及隐函数求导都可以解决。然而在考研过程中还涉及一些题型,即求某函数的高阶导数,通常为n 阶等。对于高阶导数的计算,核心思路在于找规律以及运用莱布尼兹公式进行求解,而莱布尼兹公式为导数计算考点中的一个核心考点,但很多同学往往把握不到位。因此,本文介绍一下莱布尼兹公式在求高阶导数中的应用。 一、莱布尼兹公式 莱布尼兹公式主要用来计算两个函数乘积的高阶导数。 设u(x),v(x)均有n 阶导数,则有 ∑=-=n k k n k k n n x v x u C x v x 0)()()() ()()]()(u [这个公式为莱布尼兹公式抽象形式,从这个公式中可以看到,我们在应用莱布尼茨公式时会求函数n 阶导数,因此对于常用的函数高阶导数公式需非常熟悉,具体总结如下: ()()()()()()1()11.,2.,(ln )(0,1) 3.y sinx,sin()2 4.cos ,cos()2 5.,(1).......1)1 6.,(1)! 7.ln ,(1)(1)!x n x x n x n n n a n a n n n n n n n y e y e y a y a a a a n y x n y x y x y x y a a a n x y y n x x y x y n x ππ-----====>≠==+ ==+==--+==-==--(有了这些公式,我们应用莱布尼茨公式就比较方便了。 二、公式应用 例1.设2 ),1(,ln )()(2≥=n f x x x f n 其中求代入由莱布尼兹公式得: ()2()02()12'(1)12''(2)2()(1)-2(2)-1(3)-()(1)()(ln )ln ()ln ()ln 04()-1n-1)!2-1n-2)!n-1)-1n-3)!(1)2-1n n n n n n n n n n n n n n n n n f x x x C x x C x x C x x x f x x n x x n x f ---+-+--==++=+?+=因为的三阶导数已经为了,所以莱布尼茨公式的第项开始我们就不用写了 所以,()(()((()(()n-3)! (分析与提炼 由例1可知,莱布尼兹公式运用过程中通常题型为幂函数与上述常用可求高阶导数函数结合求高阶导数,其原因在于幂函数在求有限次导数之后会变为0,使得高阶导数便于计算。除了记忆莱布尼茨公式,常用函数高阶导数公式外,求两个函数乘积的高阶导数时,我们还要注意最后一步组合数的计算和整个式子的化简,不要再这里出错。 中公祝全体考生考试成功! 反函数的导数、反三角函数的导数教案1 教学目的 1(通过复习提问使学生巩固反函数的概念; 2(使学生掌握反函数求导法则及其推导方法; 3(使学生会用反函数求导公式推导并熟练掌握四个反三角函数的求导公式( 教学重点和难点 反函数的求导法则和四个反三角函数的求导公式是本节课的重点(本节课的难点是反函数的求导( 教学过程 一、复习提问 1(什么叫函数 y,f(x)的反函数, (请一名学生回答(因为反函数是高中一年级所学内容,学生已经生疏,可能答得不好,可由其他学生补充或纠正,最后教师应准确地给学生讲述反函数概念(另外,上一节课应布置学生预先复习反函数概念() -1 如果给定函数y,f(x)的对应关系f是一一对应,那么f的逆对应f所确定的函数x, -1 f(y)就叫做函数y,f(x)的反函数( -1 强调指出:这里所说的函数关系f应是一一对应,否则就没有逆对应f,也就不可 -1能有反函数x,f(y)( 2(下列函数有反函数吗,若有请写出它的反函数表示式: n (1)y,2x,3;(2)y,x(n为正整数)( (请一名学生板演() n为偶数时,函数关系不是一一对应,故没有反函数( 二、引入新课 为求反函数的导数,自然会想到互为反函数的两个函数的导数之间有无关系,如果有,其规律是什么,为此,我们先就提问第2题的两个实例进行探讨( (1)求y,2x,3的导数( x y',2( n (2)求函数y,x(n为奇数)的导数 xn-1 y',nx( 观察:由(1)可见 那么(2)是否也有同样的规律呢,不妨试一试: 讲解新课 如果Δy?0,上等式显然成立( 事实上,当Δx?0时,一定有Δy?0(为什么,请学生思考并回答)(否则不等 至此,我们可以肯定上面所提出的反函数的求导法则如下: 或记作 2(几何解释(图2,7): 由导数的几何意义可知 x y',tanα,x',tanβ( y 反函数的导数的几何直观解释 高一数学组彭晶晶 反函数的导数的概念比较难理解,如果用几何直观方法将有利于我们理解它的意义,下面我们从几何直观法来探讨它. 设函数() y f x =的反函数存在,我们把() f x反函数1() x f y - =记为() x g y =,同时还要满足以下条件: (i)'()0 f x≠, (ii)1() x f y - =的导数存在. 于是,在同一坐标系中,函数() y f x =与它的反函数1() x f y - =的图像重合,如图9所示. 图9 我们已经知道结论: 1 dx dx dy dy =. 它的严格推导过程较复杂,且我们不容易理解, 如果用几何直观方法作辅助,将有利于我们理解它,下面我们就利用几何直观法来分析说明. 我们已经了解了函数() y f x =在点x处的导数为'() f x,它的几何意义是:曲线() y f x =在点(,) x y处的切线斜率,若α表示这条切线l与x轴正向的夹角,如图10所示,则 '()tan f x α=, 所以 '()tan dy f x dx α==. 图10 同理,我们可以知道,函数1()x f y -=在相应的点y 处的导数为'()g y ,'()g y 是曲线()x g y = 在点(,)x y 处的切线斜率.若θ表示切线l 与y 轴正向的夹角,则'()tan g y θ=,则有 '()tan dx g y dy θ==. 由图10可以得到 2ππθπα-+-= , 即32παθ+=,所以3tan tan 2πθα??=- ??? ,则 1tan tan θα =. 由以上分析,我们这样描述反函数的导数的几何意义: 函数1()x f y -=在相应的点y 处的导数为'()g y ,'()g y 是曲线()x g y =在点(,)x y 处的切线斜率.若α表示这条切线l 与x 轴正向的夹角,θ表示切线l 与y 轴正向的夹角,则 1tan tan θα =. 由于函数()y f x =可以是满足条件(i),(ii)的任意函数,所以以上结论具 高阶导数 1. 填空题. (1)x y 10=,则()()=0n y . (2)y x =sin 2,则()()y x n = .. 2. 选择题. (1)设 f x ()在()-∞+∞,内为奇函数且在()0,+∞内有'>f x ()0,''>f x ()0,则f x ()在()-∞,0内是( ) A. ' 隐函数及由参数方程所确定的函数的导数 1. 设y e y x x sin 22=-,求.dx dy 2. 设063sin 33=+-+y x y x ,求 .0=x dx dy 3.求曲线??? ????+=+=222 1313t t y t t x 在2=t 处的切线方程和法线方程. 4.利用对数求导法求导数. (1).1sin x e x x y -= (2)().sin ln x x y = 两个重要极限 第一个重要极限:1sin lim 0=→x x x 推论:0tan lim 1x x x →=,0arcsin lim 1x x x →=,0arctan lim 1x x x →= 第二个重要极限:1 lim(1)x x e x →∞ += 其他形式:()10 1lim(1),lim 1x x n n e x e n →∞→+=+= 推论:00log (1)1lim ln ln(1) lim 1x a x x a x x x →→++?== 0011lim ln lim 1x x x x a a e x x →→--?== 等价无穷小 当1x →时,ln 1x x - (这个等价无穷小很有用。) 证明:ln ln[1(1)]1x x x =+-- (10x -→ ) 导 数 高阶导数 函数f (x )在点x 0注 如果函数f (x )在点x 0处的二阶可导,则函数f (x )在点x 0的某个邻域内必须有连续的导数 ()f x '。 两个函数乘积的高阶导数(莱布尼茨公式): () () ()() k k n n k k n n v u C uv -=∑=0 或 () ()() (1)...(1)() !n n n k k k n n n k uv u v k -=--+=∑ 求导法则和方法 导数的四则运算法则 和差的导数:()u v u v '''±=± 乘积的导数:()uv u v uv '''=+ 特例:()Cu Cu ''= 商的导数:2u u v uv v v '''-??= ??? 特例:2 1v v v ' '??=- ??? 复合函数的求导法则(链式法则) 设()y f u =和()u x ?=可导,则 dy dy du dx du dx =? 或 ()()dy f u x dx ?''=? 或 {[()]}[()]()f x f x x ???'''=? 复合函数的二阶导数 设()y f u =和()u x ?=二阶可导,则复合函数(())y f x ?=也二阶可导,且 2222222 ()d y d y du dy d u dx du dx dx dx =?+? 或 2 (())()(())()y f x x f x x ????''''''''=+ 反函数的求导法则 设()y f x =是单调的可导函数,则其反函数1 ()x f y -=也可导,且 1dx dy dy dx = 或 1 1()()() f y f x -'='(其中()y f x =) 参数方程求导公式 参数方程()()x x t y y t =???=?? 确定的函数()y y x =的导数:()()y t dy dx x t '=' 二阶导数: 2 23( )()()()()()() t dy d y y t x t y t x t dx dx x t x t ' ''''''-=='' 三阶导数:2323()() t d y d y dx dx x t ' =' 几种常见函数的导数 教学目的 1.通过复习提问使学生巩固反函数的概念; 2.使学生掌握反函数求导法则及其推导方法; 3.使学生会用反函数求导公式推导并熟练掌握四个反三角函数的求导公式. 教学重点和难点 反函数的求导法则和四个反三角函数的求导公式是本节课的重点.本节课的难点是反函数的求导. 教学过程 一、复习提问 1.什么叫函数 y=f(x)的反函数? (请一名学生回答.因为反函数是高中一年级所学内容,学生已经生疏,可能答得不好,可由其他学生补充或纠正,最后教师应准确地给学生讲述反函数概念.另外,上一节课应布置学生预先复习反函数概念.) 如果给定函数y=f(x)的对应关系f是一一对应,那么f的逆对应f-1所确定的函数x= f-1(y)就叫做函数y=f(x)的反函数. 强调指出:这里所说的函数关系f应是一一对应,否则就没有逆对应f-1,也就不可能有反函数x=f-1(y). 2.下列函数有反函数吗?若有请写出它的反函数表示式: (1)y=2x-3;(2)y=x n(n为正整数). (请一名学生板演.) n为偶数时,函数关系不是一一对应,故没有反函数. 二、引入新课 为求反函数的导数,自然会想到互为反函数的两个函数的导数之间有无关系,如果有,其规律是什么?为此,我们先就提问第2题的两个实例进行探讨. (1)求y=2x-3的导数. y x'=2. (2)求函数y=x n(n为奇数)的导数 y x'=nx n-1. 观察:由(1)可见 那么(2)是否也有同样的规律呢?不妨试一试: 讲解新课 如果Δy≠0,上等式显然成立. 事实上,当Δx≠0时,一定有Δy≠0(为什么?请学生思考并回答).否则不等 至此,我们可以肯定上面所提出的反函数的求导法则如下: 或记作 反三角函数求导公式的证明 § 反函数的导数,复合函数的求导法则 一、反函数的导数 设)(y x ?=是直接函数,)(x f y =是它的反函数,假定)(y x ?=在I y 内单调、可 导,而且0)(≠'y ?,则反函数)(x f y =在间},)(|{y x I y y x x I ∈==?内也是单调、可 导的,而且 )(1 )(y x f ?'=' (1) 证明: ?∈x I x ,给x 以增量x ?),0(x I x x x ∈?+≠? 由 )(x f y = 在 I x 上的单调性可知 0)()(≠-?+=?x f x x f y 于是 y x x y ??=??1因直接函数)(y x ?=在I y 上单调、可导,故它是连续的,且反函数)(x f y =在I x 上也是连续的,当0→?x 时,必有0→?y )(11lim lim 00y y x x y y x ?'=??=??→?→?即:)(1)(y x f ?'=' 【例1】试证明下列基本导数公式 ().(arcsin )().()().(log )ln 11 1211312 2 x x arctgx x a x a x '=-'=+'= 证1、设y x sin =为直接函数,x y arcsin =是它的反函数 函数 y x sin =在 )2,2(ππ-=y I 上单调、可导,且 '=≠x y cos 0 因此,在 )1,1(-=x I 上, 有 y x cos 1)arcsin (= ' 注意到,当)2,2(ππ-∈y 时,0cos >y ,221sin 1cos x y y -=-= 因此, 211 )arcsin (x x -=' 证2 设x tgy = ,)2,2(ππ-=y I 则y arctgx =,I x =-∞+∞(,) tgy x = 在 I y 上单调、可导且 0cos 12>='y x 故 2221111cos )(1)(x y tg y tgy arctgx +=+=='= '反函数和复合函数的求导法则
高阶、隐函数的导数和微分练习题
反角函数求导公式的证明
反函数定义
求导法则与求导公式
反函数的导数
反函数求导法则
反三角函数求导公式证明
求导基本法则和公式
反函数的求导法则辨析
第十二讲高阶导数习题
求导法则(一)
第十二讲高阶导数习题资料讲解
浅析莱布尼兹公式在求高阶导数中的应用
反函数的导数、反三角函数的导数教案1
反函数的导数的几何直观解释.
(完整)高阶、隐函数的导数和微分练习题
高等数学公式 极限与导数
人教版高中数学(理科)选修几种常见函数的导数
反三角函数求导公式的证明