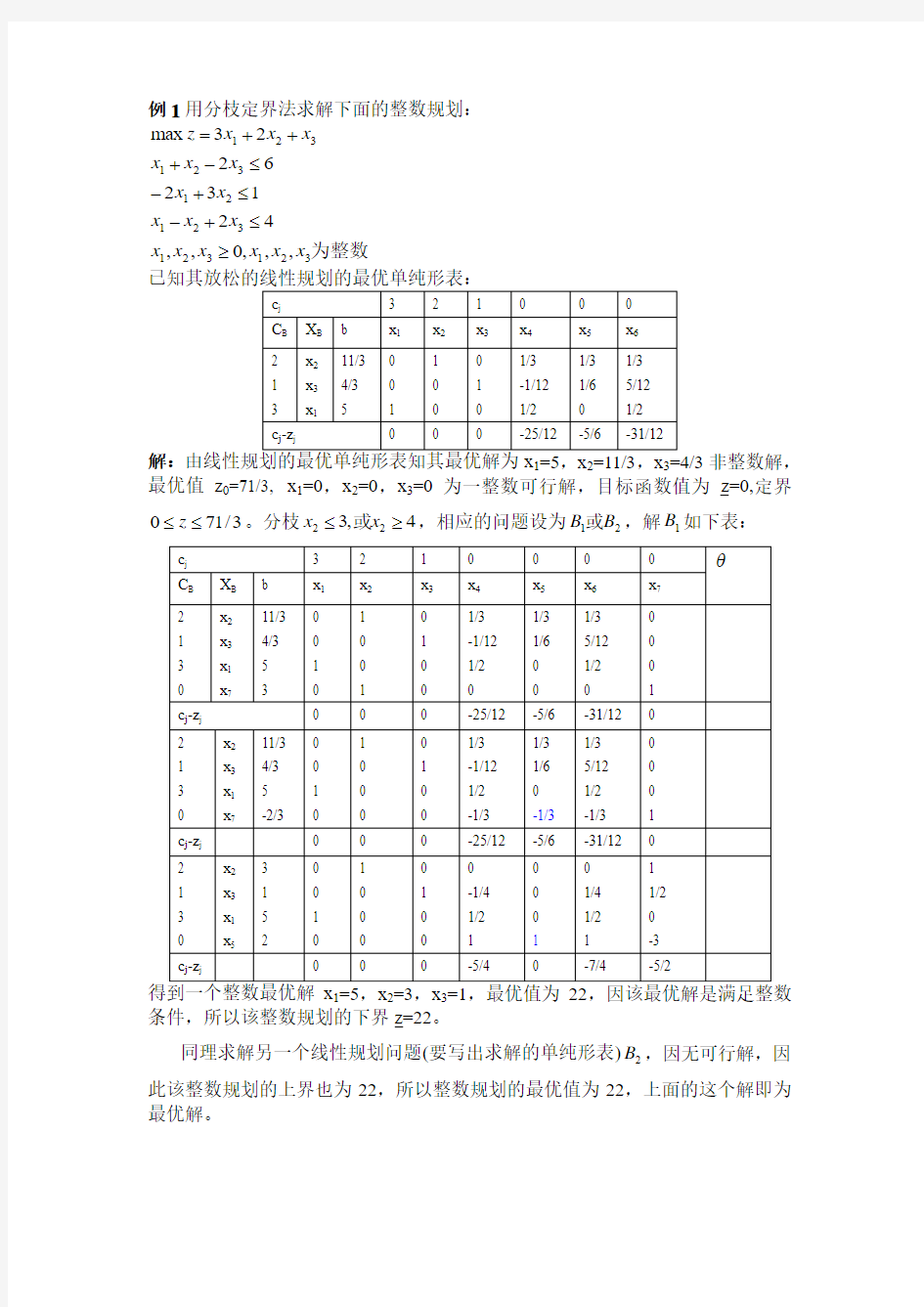
例1用分枝定界法求解下面的整数规划: 为整数
321321*********
21,,,0,,4
21326223max x x x x x x x x x x x x x x x x x z ≥≤+-≤+-≤-+++=
解:123非整数解,最优值z 0=71/3, x 1=0,x 2=0,x 3=0为一整数可行解,目标函数值为z=0,定界
3/710≤≤z 。分枝4,322≥≤x x 或,相应的问题设为21B B 或,解1B 如下表:
123条件,所以该整数规划的下界z=22。
同理求解另一个线性规划问题(要写出求解的单纯形表)2B ,因无可行解,因此该整数规划的上界也为22,所以整数规划的最优值为22,上面的这个解即为最优解。
function [x,y]=lpint(f,G,h,lb,ub,x,n,id) % 整数线性规划分枝定界法,可求解线性全整数或线性混合整数规划% 此程序基于Matlab优化工具箱的lp函数写成 % 此程序为GreenSim团队原创作品,转载请注明 % 欢迎访问GreenSim团队的主页https://www.doczj.com/doc/5714409607.html,/greensim % y = min f'x subject to: Gx <= h x为整 % x % 用法 % [x,y]=lpint(f,G,h) % [x,y]=lpint(f,G,h,lb,ub) % [x,y]=lpint(f,G,h,lb,ub,x) % [x,y]=lpint(f,G,h,lb,ub,x,n) % [x,y]=lpint(f,G,h,lb,ub,x,n,id) % 参数说明 % x: 最优解列向量 % y: 目标函数最小值 % f: 目标函数系数列向量 % G: 约束条件系数矩阵 % h: 约束条件右端列向量 % lb: 解的的下界列向量(Default: -inf) % ub: 解的的上界列向量(Default: inf) % x: 迭代初值列向量 % n: 等式约束数(Default: 0) % id: 整数变量指标列向量。1-整数,0-实数(Default: 1) % 举例 % min Z=x1+4x2 % s.t. 2x1+x2<=8 % x1+2x2>=6 % x1, x2>=0且为整数 %先将x1+2x2>=6化为 - x1 - 2x2<= -6 %》[x,y]=lpint([1;4],[2 1;-1 -2],[8;-6],[0;0]) % Y. MA & L.J. HU 1999 global upper opt c N x0 A b ID; if nargin<8, id=ones(size(f));end if nargin<7|isempty(n), n=0;end if nargin<6, x=[];end if nargin<5|isempty(ub), ub=inf*ones(size(f));end if nargin<4|isempty(lb), lb=zeros(size(f));end
第五章整数规划练习 题答案
精品资料 仅供学习与交流,如有侵权请联系网站删除 谢谢2 第五章 整数规划练习题答案 一. 判断下列说法是否正确 1. 用分枝定界法求解一个极大化的整数规划问题时,任何一个可行整数解的目标函数值是 该问题目标函数值的下界。( ) 2. 用割平面法求解整数规划时,构造的割平面有可能切去一些不属于最优解的整数解。( ) 3. 用割平面法求解纯整数规划时,要求包括松弛变量在内的全部变量必须取整数值。( ) 4. 指派问题数学模型的形式与运输问题十分相似,故也可以用表上作业法求解。( ) 二. 设有五项工作要分派给五个工人,每人的作业产值如下表所示,为了使总产值最大,问 应如何分配这五项工作,并求得最大产值。 答案: 设原矩阵为A ,因求极大问题,令B=[M-a ij ],其中M=Max {a ij }=10,则: 16425105 3140 42132 510425 1042 4003B 13752102641015406241515130450203057470574704646111 -???? ?? ? ? ? ? ? ? ? ? ? =→→- ? ? ?- ? ? ? ? ? ??????? --- m 4n 5 l m 44213421324324315415452352346464646=<===???? ? ??? ? ? ? ?→→????→?? ? ? ?? ? ? ? ???????0 3102340031 15406020303535?? ? ? ? ? ? ??? 31234311546233535??? ?? ? ?→ ?? ? ??? m=5=n ,得最优解。解矩阵*00 01000100X 00 0010100010000?? ? ? ?= ? ? ??? 。
割平面法 求解整数规划问题: Max Z=3x 1+2x 2 2x 1+3x 2?14 4x 1+2x 2?18 x 1,x 2?0,且为整数 解:首先,将原问题的数学模型标准化,这里标准化有两层含义:(1)将不等式转化为等式约束,(2)将整数规划中所有非整数系数全部转化为整数,以便于构造切割平面。从而有: Max Z=3x 1+2x 2 2x 1+3x 2+x 3=14 2x 1+x 2+x 4=9 x 1,x 2?0,且为整数 利用单纯形法求解,得到最优单纯形表,见表1: 表1
最优解为:x 1=13/4, x 2=5/2, Z=59/4 根据上表,写出非整数规划的约束方程,如: x 2+1/2x 3-1/2x 4=5/2 (1) 将该方程中所有变量的系数及右端常数项均改写成“整数与非负真分数之和”的形式,即: (1+0)x 2+(0+1/2)x 3+(-1+1/2)x 4=2+1/2 把整数及带有整数系数的变量移到方程左边,分数及带有分数系数的变量称到方程右边,得: x 2 - x 4-2 =1/2-(1/2x 3+1/2x 4) (2) 由于原数学模型已经“标准化”,因此,在整数最优解中,x 2和x 4也必须取整数值,所以(2)式左端必为整数或零,因而其右端也必须是整数。又因为x 3,x 4?0,所以必有:
由于(2)式右端必为整数,于是有: 1/2-(1/2x 3+1/2x 4)?0 (3) 或 x 3+x 4?1 (4) 这就是考虑整数约束的一个割平面约束方程,它是用非基变量表示的,如果用基变量来表示割平面约束方程,则有: 2x 1+2x 2?11 (5) 从图1中可以看出,(5)式所表示的割平面约束仅割去线性规划可行域中不包含整数可行解的部分区域,使点E(3.5,2)成为可行域的一个极点。 图1 在(3)式中加入松弛变量x 5,得: -1/2x 3-1/2x 4+x 5=-1/2 (6) 将(6)式增添到问题的约束条件中,得到新的整数规划问题: Max Z=3x 1+2x 2 2x 1+3x 2+x 3=14 2x 1+x 2+x 4=9
整数规划分支定界算法matlab通用源程序 %整数规划分支定界算法matlab通用源程序 %各参数的意义同matlab优化工具箱的线性规划函数linprog %调用前,输入参数要化成matlab的标准形式 [x,val]=kfz-f-3(n,f,a,b,aeq,beq,lb,ub) x=zeros(n,1); x1=zeros(n,1); m1=2; m2=1; [x1,val1]=linprog(f,a,b,aeq,beq,lb,ub); if (x1==0) x=x1; val=val1; elseif (round(x1)==x1) x=x1; val=val1; else e1={0,a,b,aeq,beq,lb,ub,x1,val1}; e(1,1)={e1}; zl=0; zu=-val1; while (zu~=zl) for c=1:1:m2 if (m1~=2) if (cell2mat(e{m1-1,c}(1))==1) e1={1,[],[],[],[],[],[],[],0}; e(m1,c*2-1)={e1}; e(m1,c*2)={e1}; continue; end; end; x1=cell2mat(e{m1-1,c}(8)); x2=zeros(n,1); s=0; s1=1; s2=1; lb1=cell2mat(e{m1-1,c}(6)); ub1=cell2mat(e{m1-1,c}(7)); lb2=cell2mat(e{m1-1,c}(6)); ub2=cell2mat(e{m1-1,c}(7)); for d=1:1:n if (abs((round(x1(d))-x1(d)))>0.0001)&(s==0) s=1;
题目:割平面法及其数值实现 院系:数理科学与工程学院应用数学系 专业:数学与应用数学 姓名学号:*** 1****** *** 1****** *** 1****** *** 1****** 指导教师:张世涛 日期:2015 年 6 月11 日
整数规划与线性规划有着密不可分的关系,它的一些基本算法的设计都是从相应的线性规划的最优解出发的。整数规划问题与我们的实际生活有着密切的联系,如合成下料问题、建厂问题、背包问题、投资决策问题、旅行商问题、生产顺序表问题等都是求解整数模型中的著名问题。所以要想掌握生活中这些解决问题的方法,研究整数规划是必然的路径。用于解决整数规划的方法主要有割平面法,分支定界法,小规模0-1规划问题的解法,指派问题和匈牙利法。本文重要对整数规划中经常用的割平面法加以介绍及使用Matlab 软件对其数值实现。 割平面法从线性规划问题着手,在利用单纯型法的时候,当约束矩阵中出现分数,给出一种"化分为整"的方法。然后在割平面方法来解决整数线性规划的理论基础上,把"化分为整"的方法进行到底,直到求解出最有整数解。 关键词:最优化;整数规划;割平面法;数值实现;最优解;Matlab软件。 Abstract The integer programming are closely related to the linear programming. Some of the basic algorithms of the former are designed from the optimal solution of the corresponding linear programming. What’s more, our daily life has a close relationship with it as well, such as synthesis problem, plant problem, knapsack problem, investment decision problem, traveling salesman problem and production sequence table problems. They are famous questions in solving integer model. So, to study the integer programming is the inevitable way to master the methods of solving these problems in life. The methods used in solving the integer programming include cutting plane method, branch and bound method, and solving the problem of small-scale 0-1 programming, assignment problem and Hungarian method. In this paper, we introduce the cutting plane method and use Matlab to get its numerical implementation in the integer programming. Cutting plane method, giving us a "integrated" method when we meet the constraint matrix scores in the use of simplex method, starts from the linear programming problem. Then, based on the theory of cutting plane method to solve the integer linear programming, we use “integrated” method until the most integer solution is solved. Keywords:Optimization; Integer programming; Cutting plane method; Numerical implementation; Optimal solution; Matlab software.
割平面法 求解整数规划问题: Max Z=3x1+2x2 2x1+3x2?14 4x1+2x2?18 x1,x2?0,且为整数 解:首先,将原问题的数学模型标准化,这里标准化有两层含义:(1)将不等式转化为等式约束,(2)将整数规划中所有非整数系数全部转化为整数,以便于构造切割平面。从而有:Max Z=3x1+2x2 2x1+3x2+x3=14 2x1+x2+x4=9 x1,x2?0,且为整数 利用单纯形法求解,得到最优单纯形表,见表1: 表1
最优解为:x1=13/4, x2=5/2, Z=59/4 根据上表,写出非整数规划的约束方程,如:x2+1/2x3-1/2x4=5/2 (1) 将该方程中所有变量的系数及右端常数项均改写成“整数与非负真分数之和”的形式,即:(1+0)x2+(0+1/2)x3+(-1+1/2)x4=2+1/2 把整数及带有整数系数的变量移到方程左边,分数及带有分数系数的变量称到方程右边,得:x2 - x4-2 =1/2-(1/2x3+1/2x4) (2) 由于原数学模型已经“标准化”,因此,在整数最优解中,x2和x4也必须取整数值,所以(2)式左端必为整数或零,因而其右端也必须是整数。又因为x3,x4?0,所以必有: 1/2-(1/2x3+1/2x4)<1 由于(2)式右端必为整数,于是有: 1/2-(1/2x3+1/2x4)?0 (3) 或 x3+x4?1 (4) 这就是考虑整数约束的一个割平面约束方程,它是用非基变量表示的,如果用基变量来表示割平面约束方程,则有: 2x1+2x2?11 (5)
从图1中可以看出,(5)式所表示的割平面约束仅割去线性规划可行域中不包含整数可行解的部 分区域,使点E,2)成为可行域的一个极点。 图1 在(3)式中加入松弛变量x5,得: -1/2x3-1/2x4+x5=-1/2 (6) 将(6)式增添到问题的约束条件中,得到新的整数规划问题: Max Z=3x1+2x2 2x1+3x2+x3=14 2x1+x2+x4=9 -1/2x3-1/2x4+x5=-1/2 x i?0,且为整数,i=1,2,…,5 该问题的求解可以在表1中加入(6)式,然后运用对偶单纯形法求出最优解。具体计算过程见表2: 表2
1、概念: 分支定界算法(Branch and bound,简称为BB、B&B, or BnB)始终围绕着一颗搜索树进行的,我们将原问题看作搜索树的根节点,从这里出发,分支的含义就是将大的问题分割成小的问题。大问题可以看成是搜索树的父节点,那么从大问题分割出来的小问题就是父节点的子节点了。分支的过程就是不断给树增加子节点的过程。而定界就是在分支的过程中检查子问题的上下界,如果子问题不能产生一比当前最优解还要优的解,那么砍掉这一支。直到所有子问题都不能产生一个更优的解时,算法结束。 2、例子: 用BB算法求解下面的整数规划模型 因为求解的是最大化问题,我们不妨设当前的最优解BestV为-INF,表示负无穷。 1.
首先从主问题分出两支子问题: 通过线性松弛求得两个子问题的upper bound为Z_LP1 = 12.75,Z_LP2 = 12.2。由于Z_LP1 和Z_LP2都大于BestV=-INF,说明这两支有搞头,继续往下。 2. 3.
从节点1和节点2两个子问题再次分支,得到如下结果: 子问题3已经不可行,无需再理。子问题4通过线性松弛得到最优解为10,刚好也符合原问题0的所有约束,在该支找到一个可行解,更新BestV = 10。 子问题5通过线性松弛得到upper bound为11.87>当前的BestV = 10,因此子问题5还有戏,待下一次分支。而子问题6得到upper bound为9<当前的BestV = 10,那么从该支下去找到的解也不会变得更好,所以剪掉! 4.
对节点5进行分支,得到: 子问题7不可行,无需再理。子问题8得到一个满足原问题0所有约束的解,但是目标值为4<当前的BestV=10,所以不更新BestV,同时该支下去也不能得到更好的解了。 6.
第五章 整数规划练习题答案 一. 判断下列说法是否正确 1. 用分枝定界法求解一个极大化的整数规划问题时,任何一个可行整数解的目标函数值是 该问题目标函数值的下界。() 2. 用割平面法求解整数规划时,构造的割平面有可能切去一些不属于最优解的整数解。() 3. 用割平面法求解纯整数规划时,要求包括松弛变量在内的全部变量必须取整数值。() 4. 指派问题数学模型的形式与运输问题十分相似,故也可以用表上作业法求解。() 二. 设有五项工作要分派给五个工人,每人的作业产值如下表所示,为了使总产值最大,问 应如何分配这五项工作,并求得最大产值。 工作 工人 A & B C D E 甲 9 4 6 8 5 \ 乙 8 5 9 10 6 丙 9 7 3 ' 5 8 丁 4 8 6 9 5 戊 10 ; 5 3 6 3 答案: 设原矩阵为A ,因求极大问题,令B=[M-a ij ],其中M=Max {a ij }=10,则: 16425105 3140 42 13251042510424003B 1 3752102 64 10 154062415151 3045 020305 7470574704646111-?????? ? ? ? ? ? ? ? ? ? =→→- ? ? ?- ? ? ? ? ? ??????? --- m 4n 5l m 4 4 21342132432431541545235234 6 4 64 6 4 6=<===? ??? ? ??? ? ? ? ?→→????→?? ? ??? ? ? ? ???? ? ? ? 031023 4003115406020303535?? ? ? ? ? ? ?? ? 31234311546233 5 3 5? ?? ?? ? ?→ ?? ? ?? ? m=5=n ,得最优解。解矩阵*0001000100X 0000101 00010000?? ? ? ?= ? ? ??? 。
整数规划分支定界法MATLAB程序 1.这种方法绝对能都解出答案,而且答案正确 function [x,val]=fzdj(n,f,a,b,aeq,beq,lb,ub) x=zeros(n,1); x1=zeros(n,1); m1=2; m2=1; [x1,val1]=linprog(f,a,b,aeq,beq,lb,ub); if (x1==0) x=x1; val=val1; elseif (round(x1)==x1) x=x1; val=val1; else e1={0,a,b,aeq,beq,lb,ub,x1,val1}; e(1,1)={e1}; zl=0; zu=-val1; while (zu~=zl) for c=1:1:m2 if (m1~=2) if (cell2mat(e{m1-1,c}(1))==1) e1={1,[],[],[],[],[],[],[],0}; e(m1,c*2-1)={e1}; e(m1,c*2)={e1}; continue; end; end; x1=cell2mat(e{m1-1,c}(8)); x2=zeros(n,1); s=0; s1=1; s2=1; lb1=cell2mat(e{m1-1,c}(6)); ub1=cell2mat(e{m1-1,c}(7)); lb2=cell2mat(e{m1-1,c}(6)); ub2=cell2mat(e{m1-1,c}(7)); for d=1:1:n if (abs((round(x1(d))-x1(d)))>0.0001)&(s==0) s=1; lb1(d)=fix(x1(d))+1;
〈运筹学〉补充例题 例题 1.1 某工厂可以生产产品A和产品B两种产品。生产单位产品A和B所需要的机时、人工工时的数量以及可利用资源总量由下表给出。这两种产品在市场上是畅销产品。该工厂经理要制订季度的生产计划,其目标是使工厂的销售额最大。 产品A 产品B 资源总量 机器(时) 6 8 120 人工(时) 10 5 100 产品售价(元) 800 300 MAX 800X1 +300X2 ST 6X1 +8X2 <= 120 10X1 +5X2 <= 100 X1, X2 >=0 例题 1.2该工厂根据产品A和产品B的销售和竞争对手的策略,调整了两种产品的售价。产品A和B的价格调整为600元和400元。假设其它条件不变,请你帮助该工厂经理制订季度的生产计划,其目标仍然是使工厂的销售额最大。 X 600X1 +400X2 ST 6X1 +8X2 <= 120 10X1 +5X2 <= 100 X1, X2 >=0 例题 1.3由于某些原因,该工厂面临产品原料供应的问题。因此,工厂要全面考虑各种产品所需要的机时、人工工时、原材料的资源数量及可用资源的总量、产品的售价等因素。有关信息在下表中给出。 产品A 产品B 资源总量 机器(时) 6 8 120 人工(时) 10 5 100 原材料(公斤) 11 8 130 产品售价(元) 600 400 MAX 600X1 +400X2 ST 6X1 +8X2 <= 120 10X1 +5X2 <= 100 11X1 +8X2 <= 130 X1, X2 >=0 例题 1.4随着企业改革的不断深化,该企业的经理的管理思想产生了变化,由原来的追求销售额变为注重销售利润,因此,要考虑资源的成本。工厂的各种产品所需要的机时、人
Linprogdis子程序: function [x,fval,exitflag,output,lambda]=... linprogdis(ifint,f,A,b,Aeq,beq,lb,ub,x0,options) %Title: % 分支定届法求解混合整数线性规划模型 % %初步完成:2002年12月 %最新修订: 2004-03-06 %最新注释:2004-11-20 %数据处理 [t1,t2] = size(b); if t2~=1, b=b';%将b转置为列向量 end %调用线性规划求解 [x,fval,exitflag,output,lambda] = linprog(f,A,b,Aeq,beq,lb,ub,x0,options); if exitflag<=0,%如果线性规划失败,则本求解也失败 return end %得到有整数约束的决策变量的序号 v1=find(ifint==1);%整数变量的index tmp=x(v1);%【整数约束之决策变量】的当前值 if isempty(tmp), %无整数约束,则是一般的线性规划,直接返回即可 return end v2=find(checkint(tmp)==0);%寻找不是整数的index if isempty(v2), %如果整数约束决策变量确实均为整数,则调用结束 return end %第k个决策变量还不是整数解 %注意先处理第1个不满足整数约束的决策变量 k=v1(v2(1)); %分支1:左分支 tmp1=zeros(1,length(f));%线性约束之系数向量 tmp1(k)=1; low=floor(x(k)); %thisA 分支后实际调用线性规划的不等式约束的系数矩阵A %thisb 分支后实际调用线性规划的不等式约束向量b if ifrowinmat([tmp1,low],[A,b])==1 %如果分支的约束已经存在旧的A,b中,则不改变约束 thisA= A; thisb= b;
练习4.9 连续投资问题 某公司现有资金10万元,拟在今后五年考虑用于下列项目的投资: 项目A:从第一年到第四年每年年初需要投资,并于次年收回本利115%,但要求第一年投资最低金额为4万元,第二.三.四年不限. 项目B:第三年初需要投资,到第五年末能收回本利128%,但规定最低投资金额为3万元,最高金额为5万元. 项目C:第二年初需要投资,到第五年末能收回本利140%,但规定其投资金额或为2万元,或为4万元,或为6万元,或为8万元. 项目D:五年每年年初都可购买公债,于当年末归还,并获利6%,此项目投资金额不限. 试问该公司应图和确定这些项目的每年投资金额,使到第五年末拥有最大的资金收益. (1) x 为项目各年月初投入向量。 (2) ij x 为 i 种项目j 年的月初的投入。 (3) 向量c 中的元素 ij c 为i 年末j 种项目收回本例的百分比。 (4) 矩阵A 中元素 ij a 为约束条件中每个变量ij x 的系数。 (5) Z 为第5年末能拥有的资金本利最大总额。 因此目标函数为 4325max 1.15 1.28 1.40 1.06A B C D Z x x x x =+++ 束条件应是每年年初的投资额应等于该投资者年初所拥有的资金. 第1年年初该投资者拥有10万元资金,故有 11100000A D x x +=. 第2年年初该投资者手中拥有资金只有()116%D x +,故有 22211.06A C D D x x x x ++=. 第3年年初该投资者拥有资金为从D 项目收回的本金: 21.06D x ,及从项目A 中第1年投资收回的本金: 11.15A x ,故有 333121.15 1.06A B D A D x x x x x ++=+ 同理第4年、第5年有约束为 44231.15 1.06A D A D x x x x +=+, 5341.15 1.06D A D x x x =+
整数规划分支定界法MATLAB 程序 1.这种方法绝对能都解出答案,而且答案正确function [x,val]=fzdj(n,f,a,b,aeq,beq,lb,ub) x=zeros(n,1); x1=zeros(n,1); m1=2; m2=1; [x1,val1]=linprog(f,a,b,aeq,beq,lb,ub); if (x1==0) x=x1; val=val1; elseif (round(x1)==x1) x=x1; val=val1; else e1={0,a,b,aeq,beq,lb,ub,x1,val1}; e(1,1)={e1}; zl=0; zu=-val1; while (zu~=zl) for c=1:1:m2 if (m1~=2) if (cell2mat(e{m1-1,c}(1))==1) e1={1,[],[],[],[],[],[],[],0}; e(m1,c*2-1)={e1}; e(m1,c*2)={e1}; continue; end; end; x1=cell2mat(e{m1-1,c}(8)); x2=zeros(n,1); s=0; s1=1; s2=1; lb1=cell2mat(e{m1-1,c}(6)); ub1=cell2mat(e{m1-1,c}(7)); lb2=cell2mat(e{m1-1,c}(6)); ub2=cell2mat(e{m1-1,c}(7)); for d=1:1:n if (abs((round(x1(d))-x1(d)))>0.0001)&(s==0) s=1; lb1(d)=fix(x1(d))+1; if (a*lb1<=b) s1=0; end; ub2(d)=fix(x1(d)); if (a*lb2<=b) s2=0; end; end; end; e1={s1,a,b,aeq,beq,lb1,ub1,[],0}; e2={s2,a,b,aeq,beq,lb2,ub2,[],0}; e(m1,c*2-1)={e1}; e(m1,c*2)={e2}; end; m1=m1+1;
第章整数规划割平面法 This manuscript was revised on November 28, 2020
割平面法 求解整数规划问题: Max Z=3x1+2x2 2x1+3x214 4x1+2x218 x1,x20,且为整数 解:首先,将原问题的数学模型标准化,这里标准化有两层含义:(1)将不等式转化为等式约束,(2)将整数规划中所有非整数系数全部转化为整数,以便于构造切割平面。从而有:Max Z=3x1+2x2 2x1+3x2+x3=14 2x1+x2+x4=9 x1,x20,且为整数 利用单纯形法求解,得到最优单纯形表,见表1: 表1
最优解为:x1=13/4, x2=5/2, Z=59/4 根据上表,写出非整数规划的约束方程,如:x2+1/2x3-1/2x4=5/2 (1) 将该方程中所有变量的系数及右端常数项均改写成“整数与非负真分数之和”的形式,即:(1+0)x2+(0+1/2)x3+(-1+1/2)x4=2+1/2 把整数及带有整数系数的变量移到方程左边,分数及带有分数系数的变量称到方程右边,得: x2 - x4-2 =1/2-(1/2x3+1/2x4) (2)由于原数学模型已经“标准化”,因此,在整数最优解中,x2和x4也必须取整数值,所以(2)式左端必为整数或零,因而其右端也必须是整数。又因为x3,x40,所以必有: 1/2-(1/2x3+1/2x4)<1 由于(2)式右端必为整数,于是有: 1/2-(1/2x3+1/2x4)0 (3) 或 x3+x41 (4)
这就是考虑整数约束的一个割平面约束方程,它是用非基变量表示的,如果用基变量来表示割平面约束方程,则有: 2x1+2x211 (5) 从图1中可以看出,(5)式所表示的割平面约束仅割去线性规划可行域中不包含整数可行解的部分区域,使点E,2)成为可行域的一个极点。 图1 在(3)式中加入松弛变量x5,得: -1/2x3-1/2x4+x5=-1/2 (6) 将(6)式增添到问题的约束条件中,得到新的整数规划问题: Max Z=3x1+2x2 2x1+3x2+x3=14 2x1+x2+x4=9 -1/2x3-1/2x4+x5=-1/2 x i 0,且为整数,i=1,2,…,5 该问题的求解可以在表1中加入(6)式,然后运用对偶单纯形法求出最优解。具体计算过程见表2: 表2
第五章 整数规划练习题答案 一. 判断下列说法是否正确 1. 用分枝定界法求解一个极大化的整数规划问题时,任何一个可行整数解的目标函数值是 该问题目标函数值的下界。() 2. 用割平面法求解整数规划时,构造的割平面有可能切去一些不属于最优解的整数解。() 3. 用割平面法求解纯整数规划时,要求包括松弛变量在内的全部变量必须取整数值。() 4. 指派问题数学模型的形式与运输问题十分相似,故也可以用表上作业法求解。() 二. 设有五项工作要分派给五个工人,每人的作业产值如下表所示,为了使总产值最大,问 应如何分配这五项工作,并求得最大产值。 工作 工人 A B C D E 甲 9 4 6 8 5 乙 8 5 9 10 6 丙 9 7 3 5 8 丁 4 8 6 9 5 戊 10 5 3 6 3 答案: 设原矩阵为A ,因求极大问题,令B=[M-a ij ],其中M=Max {a ij }=10,则: 16425105 3140 42 13251042510424003B 1 3752102 6410 1540 62 415151 3045 020305 7470574704646111-?????? ? ? ? ? ? ? ? ? ? =→→- ? ? ?- ? ? ? ? ? ??????? --- m 4n 5l m 4 4 21342132432431541545235234 6 4 64 6 4 6=<===? ??? ? ??? ? ? ? ?→→????→?? ? ??? ? ? ? ???? ? ? ? 031023 4003115406020303535?? ? ? ? ? ? ???
分支定界法和割平面法 在上学期课程中学习的线性规划问题中,有些最优解可能是分数或消失,但现实中某些具体的问题,常要求最优解必须是整数,这样就有了对于整数规划的研究。 整数规划有以下几种分类:(1)如果整数规划中所有的变量都限制为(非负)整数,就称为纯整数规划或全整数规划;(2)如果仅一部分变量限制为整数,则称为混合整数规划;(3)整数规划还有一种特殊情形是0-1规划,他的变量取值仅限于0或1。本文就适用于纯整数线性规划和混合整数线性规划求解的分支定界法和割平面法,做相应的介绍。 一、分支定界法 在求解整数规划是,如果可行域是有界的,首先容易想到的方法就是穷举变量的所有可行的整数组合,然后比较它们的目标函数值以定出最优解。对于小型问题,变量数量很少,可行的整数组合数也是很小时,这个方法是可行的,也是有效的。而对于大型的问题,可行的整数组合数很大时,这种方法就不可取了。所以我们的方法一般是仅检查可行的整数组合的一部分,就能定出最有的整数解。分支定界法就是其中一个。 分枝定界法可用于解纯整数或混合的整数规划问题。在二十世纪六十年代初由Land Doig 和Dakin 等人提出。由于这方法灵活且便于用计算机求解,所以现在它已是解整数规划的重要方法。目前已成功地应用于求解生产进度问题、旅行推销员问题、工厂选址问题、背包问题及分配问题等。 设有最大化的整数规划问题A ,与它相应的线性规划为问题B ,从解问题B 开始,若其最优解不符合A 的整数条件,那么B 的最优目标函数必是A 的最优目标函数z *的上界,记作z ;而A 的任意可行解的目标函数值将是z *的一个下界z 。分枝定界法就是将B 的可行域分成子区域再求其最大值的方法。逐步减小z 和增大z ,最终求到z *。现用下例来说明: 例1 求解下述整数规划 219040Max x x z += ??? ??≥≥+≤+且为整数0,7020756792 12121x x x x x x 解 (1)先不考虑整数限制,即解相应的线性规划B ,得最优解为: 124.81, 1.82,356 x x z === 可见它不符合整数条件。这时z 是问题A 的最优目标函数值z *的上界,记作z 。而X 1=0,X 2=0显然是问题A 的一个整数可行解,这时0=z ,是z * 的一个下界,记作z ,即0≤z *≤356 。 (2)因为X 1X 2当前均为非整数,故不满足整数要求,任选一个进行分枝。设选X 1进行分枝,于是对原问题增加两个约束条件: [][]114.814, 4.8115 x x ≤=≥+= 于是可将原问题分解为两个子问题B 1和B 2(即两支),给每支增加一个约束条件并不影响问题A 的可行域,不考虑整数条件解问题B 1和 B 2 ,称此为第一次迭代。得到最优解
整数线性规划之分支定界法 摘要 最优化理论和方法是在上世纪 40 年代末发展成为一门独立的学科。1947年,Dantaig 首先提出求解一般线性规划问题的方法,即单纯形算法,随后随着工业革命、计算机技术的巨大发展,以及信息革命的不断深化,到现在的几十年时间里,它有了很快的发展。目前,求解各种最优化问题的理论研究发展迅速,例如线性规划、非线性规划以及随机规划、非光滑规划、多目标规划、几何规划、整数规划等,各种新的方法也不断涌现,并且在军事、经济、科学技术等方 面应用广泛,成为一门十分活跃的学科。 整数规划(integer programming)是一类要求要求部分或全部决策变量取整数值的数学规划,实际问题中有很多决策变量是必须取整数的。本文主要介绍求解整数线性规划问题的分支定界法及其算法的matlb实现。 关键词:整数线性规划;分支定界法;matlb程序;
1.引言 1.1优化问题发展现状 最优化理论与算法是一个重要的数学分支,它所讨论的问题是怎样在众多的方案中找到一个最优的方案.例如,在工程设计中,选择怎样的设计参数,才能使设计方案既满足要求又能降低成本;在资源分配中,资源有限时怎样分配,才能使分配方案既可以满足各方面的要求,又可以获得最多的收益;在生产计划安排中,怎样设计生产方案才能提高产值和利润;在军事指挥中,确定怎样的最佳作战方案,才能使自己的损失最小,伤敌最多,取得战争的胜利;在我们的生活中,诸如此类问题,到处可见.最优化作为数学的一个分支,为这些问题的解决提供了一些理论基础和求解方法. 最优化是个古老的课题.长期以来,人们一直对最优化问题进行着探讨和研究.在二十世纪四十年代末,Dantzig 提出了单纯形法,有效地解决了线性规划问题,从而最优化成为了一门独立的学科。目前,有关线性规划方面的理论和算法发展得相当完善,但是关于非线性规划问题的理论和算法还有待进一步的研究,实际应用中还有待进一步的完善。传统的非线性全局最优化方法只能求出问题的局部最优解,但由于许多问题的局部最优解不一定是全局最优解,使得传统的非线性最优化方法不能直接成功地应用于求解非线性全局最优化问题。另外,没有一个固定的评判标准来判断得到的局部最优解是否为全局最优解。随着科学技术的发展和计算机计算能力的提高,最优化理论在最近这几年来得到了迅速的发展,涌现出了许多新的算法, 如打洞函数法,填充函数法,lagrangian 乘子函数方法,信赖域方法,虑子方法等。 本文主要介绍求解整数线性规划问题的分支定界法及其算法的matlb实现。 1.2整数线性规划及其数学模型 整数规划主要有以下三大类: (1)全整数规划(all integer programming):所有的决策变量都取整数值,也称为纯整数规划(pure integer programming); (2)混合整数规划(mixed integer programming):仅要求一部分决策变量取整数值; (3)0-1规划(zero-one integer programming):该类问题的决策变量只能取0或1. 本文主要讨论的整数线性规划问题模型为:
一、编程 利用Matlab的线性规划指令: [x,fval]=linprog(f,A,b,Aeq,beq,lb,ub) 编写计算整数规划函数,输入与输出与上述指令相同 分枝定界法(递归实现) function [x,fval,status] = intprog(f,A,B,I,Aeq,Beq,lb,ub,e) %整数规划求解函数 intprog() % 其中 f为目标函数向量 % A和B为不等式约束 Aeq与Beq为等式约束 % I为整数约束 % lb与ub分别为变量下界与上界 % x为最优解,fval为最优值 %例子: % maximize 20 x1 + 10 x2 % S.T. % 5 x1 + 4 x2 <=24 % 2 x1 + 5 x2 <=13 % x1, x2 >=0 % x1, x2是整数 % f=[-20, -10]; % A=[ 5 4; 2 5]; % B=[24; 13]; % lb=[0 0]; % ub=[inf inf]; % I=[1,2]; % e=0.000001; % [x v s]= IP(f,A,B,I,[],[],lb,ub,,e) % x = 4 1 v = -90.0000 s = 1 % 控制输入参数 if nargin < 9, e = 0.00001; if nargin < 8, ub = []; if nargin < 7, lb = []; if nargin < 6, Beq = []; if nargin < 5, Aeq = []; if nargin < 4, I = [1:length(f)]; end, end, end, end, end, end %求解整数规划对应的线性规划,判断是否有解 options = optimset('display','off'); [x0,fval0,exitflag] = linprog(f,A,B,Aeq,Beq,lb,ub,[],options); if exitflag < 0
第五章 整数规划习题 5.1 考虑下列数学模型 )()(m in 2211x f x f z += 且满足约束条件 (1)或101≥x ,或102≥x ; (2)下列各不等式至少有一个成立: ??? ??≥+≥+≥+15 215152212121x x x x x x (3)021=-x x 或5或10 (4)01≥x ,02≥x 其中 )(11x f =?? ?=>+0,0 0,520111x x x 如如 =)(2 2x f ?? ?=>+0,00,612222x x x 如如 将此问题归结为混合整数规划的模型。 解:2211612510m in x y x y z +++= ? ? ?????????????? ????=≥≥=+++++-+-=-≤++-≥+-≥+-≥+?--≥?-≥?≤?≤),,=(或,)()()(;)(11.110;00)4(1 11105503215215152)1(1010102111 1098711109872165462152142132312211i y x x y y y y y y y y y y x x y y y M y x x M y x x M y x x M y x M y x M y x M y x i 5.2 试将下述非线性的0-1规划问题转换成线性的0-1规划问题 3 3 3221max x x x x z -+= ?? ?==≤++-) ,(或3,2,110332321j x x x x j
解:令=y ???==否则,当,01132x x 故有y x x =32,又21x ,3 1x 分别与1x ,3x 等价,因此题中模型可转换为 31m ax x y x z -+= ? ???? ?? ??-+≤+≤≤≤++-变量均为10,,,1 3 323213 23 2321y x x x y x x x y x y x x x 5.3 某科学实验卫星拟从下列仪器装置中选若干件装上。有关数据资料见表5-1 要求:(1)装入卫星的仪器装置总体积不超过V ,总质量不超过W ;(2)A 1与A 3中最多安装一件;(3)A 2与A 4中至少安装一件;(4)A 5同A 6或者都安上,或者都不安。总的目的是装上取的仪器装置使该科学卫星发挥最大的实验价值。试建立这个问题的数学模型。 解: j j j x c z ∑==6 1 max ??? ?? ?????????????==≥+≤+≤≤∑∑==否则 仪器安装,0,111 654231 6 1 6 1j j j j j j j j A x x x x x x x W x w V x v 5.4 某钻井队要从以下10个可供选择的井位中确定5个钻井探油,使总的钻探费用最小。若10个井位的代号为s 1 ,s 2,…s 10,相应的钻探费用为c 1 ,c 2,…,c 10,并且井位选择上要满足下列限制条件: