
?????????
??????
?????=01
00000001001010000
010*********
Edge 第8章 图
8-1 画出1个顶点、2个顶点、3个顶点、4个顶点和5个顶点的无向完全图。试证明在n 个顶点的无向完全图中,边的条数为n(n -1)/2。 【解答】 【证明】
在有n 个顶点的无向完全图中,每一个顶点都有一条边与其它某一顶点相连,所以每一个顶点有n -1
条边与其他n -1个顶点相连,总计n 个顶点有n(n -1)条边。但在无向图中,顶点i 到顶点j 与顶点j 到顶点i 是同一条边,所以总共有n(n -1)/2条边。
8-2 右边的有向图是强连通的吗?请列出所有的简单路径。 【解答】
判断一个有向图是否强连通,要看从任一顶点出发是否能够回到该顶
点。右面的有向图做不到这一点,它不是强连通的有向图。各个顶点自成强连通分量。
所谓简单路径是指该路径上没有重复的顶点。
从顶点A 出发,到其他的各个顶点的简单路径有A →B ,A →D →B ,A →B →C ,A →D →B →C ,A →D ,A →B →E ,A →D →E ,A →D →B →E ,A →B →C →F →E ,A →D →B →C →F →E ,A →B →C →F ,A →D →B →C →F 。
从顶点B 出发,到其他各个顶点的简单路径有B →C ,B →C →F ,B →E ,B →C →F →E 。 从顶点C 出发,到其他各个顶点的简单路径有C →F ,C →F →E 。
从顶点D 出发,到其他各个顶点的简单路径有D →B ,D →B →C ,D →B →C →F ,D →E ,D →B →E ,D →B →C →F →E 。
从顶点E 出发,到其他各个顶点的简单路径无。 从顶点F 出发,到其他各个顶点的简单路径有F →E 。
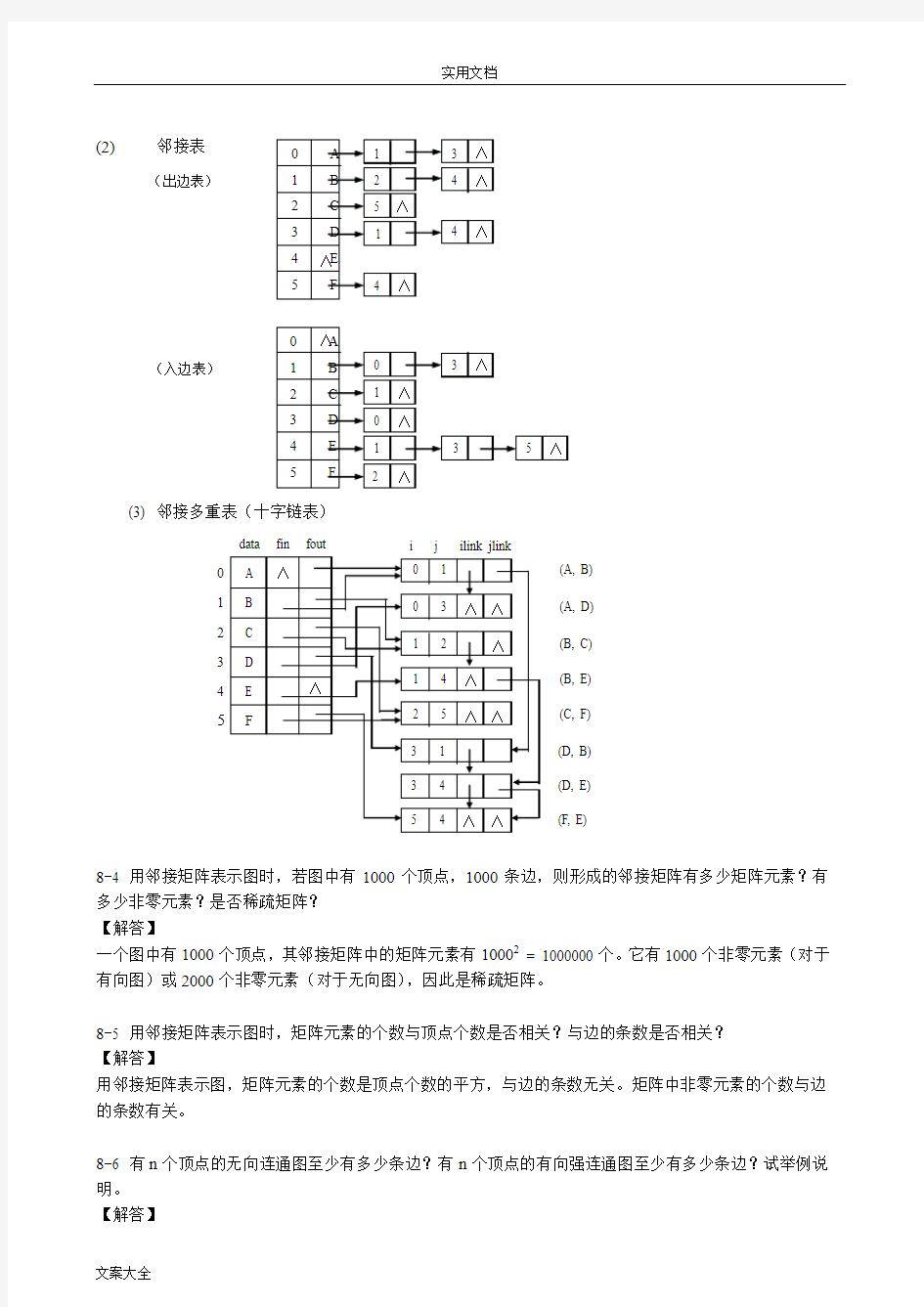
8-3 给出右图的邻接矩阵、邻接表和邻接多重表表示。 【解答】 (1) 邻接矩阵
1个顶点的 无向完全图
2个顶点的 无向完全图
3个顶点的 无向完全图 4个顶点的 无向完全图
5个顶点的 无向完全图
(2) 邻接表
(3) 邻接多重表(十字链表)
8-4 用邻接矩阵表示图时,若图中有1000个顶点,1000条边,则形成的邻接矩阵有多少矩阵元素?有多少非零元素?是否稀疏矩阵? 【解答】
一个图中有1000个顶点,其邻接矩阵中的矩阵元素有10002 = 1000000个。它有1000个非零元素(对于有向图)或2000个非零元素(对于无向图),因此是稀疏矩阵。
8-5 用邻接矩阵表示图时,矩阵元素的个数与顶点个数是否相关?与边的条数是否相关? 【解答】
用邻接矩阵表示图,矩阵元素的个数是顶点个数的平方,与边的条数无关。矩阵中非零元素的个数与边的条数有关。
8-6 有n 个顶点的无向连通图至少有多少条边?有n 个顶点的有向强连通图至少有多少条边?试举例说明。 【解答】
(出边表)
(入边表)
12345data fin fout (A, B) (A, D) (B, C)
(B, E) (C, F) (D, B) (D, E) (F, E)
①②
①
②③
④⑤或
①
②③
④⑤
①
②③
④⑤
③
④⑤
n个顶点的无向连通图至少有n-1条边,n个顶点的有向强连通图至少有n条边。例如:
特例情况是当n = 1时,此时至少有0条边。
8-7对于有n个顶点的无向图,采用邻接矩阵表示,如何判断以下问题:图中有多少条边?任意两个顶点i和j之间是否有边相连?任意一个顶点的度是多少?
【解答】
用邻接矩阵表示无向图时,因为是对称矩阵,对矩阵的上三角部分或下三角部分检测一遍,统计其中的非零元素个数,就是图中的边数。如果邻接矩阵中A[i][j] 不为零,说明顶点i与顶点j之间有边相连。此外统计矩阵第i行或第i列的非零元素个数,就可得到顶点i的度数。
8-8对于如右图所示的有向图,试写出:
(1) 从顶点①出发进行深度优先搜索所得到的深度优先生成树;
(2) 从顶点②出发进行广度优先搜索所得到的广度优先生成树;
【解答】
(1) 以顶点①为根的深度优先生成树(不唯一):②③④⑤⑥
(2) 以顶点②为根的广度优先生成树:
8-9 试扩充深度优先搜索算法,在遍历图的过程中建立生成森林的左子女-右兄弟链表。算法的首部为void Graph::DFS ( const int v, int visited [ ], TreeNode
【解答】
为建立生成森林,需要先给出建立生成树的算法,然后再在遍历图的过程中,通过一次次地调用这个算法,以建立生成森林。
te mplate
//从图的顶点v出发, 深度优先遍历图, 建立以t (已在上层算法中建立)为根的生成树。
Visited[v] = 1; int first = 1; TreeNode
int w = GetFirstNeighbor ( v );//取第一个邻接顶点
while ( w != -1 ) {//若邻接顶点存在
if ( vosited[w] == 0 ) { //且该邻接结点未访问过
p = new TreeNode
if ( first == 1 ) //若根*t还未链入任一子女
{ t->setFirstChild ( p );first = 0; }//新结点*p成为根*t的第一个子女
else q->setNextSibling ( p );//否则新结点*p成为*q的下一个兄弟
q = p;//指针q总指示兄弟链最后一个结点
DFS_Tree ( w, visited, q );//从*q向下建立子树
}
w = GetNextNeighbor ( v, w );//取顶点v排在邻接顶点w的下一个邻接顶点}
}
下一个算法用于建立以左子女-右兄弟链表为存储表示的生成森林。
template
//从图的顶点v出发, 深度优先遍历图, 建立以左子女-右兄弟链表表示的生成森林T。
T.root = NULL; int n =NumberOfVertices ( ); //顶点个数
TreeNode
int * visited = new int [ n ];//建立访问标记数组
for ( int v = 0; v < n; v++ ) visited[v] = 0;
for ( v = 0; v < n; v++ ) //逐个顶点检测
if ( visited[v] == 0 ) {//若尚未访问过
p = new TreeNode
if ( T.root == NULL ) T.root = p;//原来是空的生成森林, 新结点成为根
else q-> setNextSibling ( p );//否则新结点*p成为*q的下一个兄弟
q = p;
DFS_Tree ( v, visited, p );//建立以*p为根的生成树
}
}
8-10 用邻接表表示图时,顶点个数设为n,边的条数设为e,在邻接表上执行有关图的遍历操作时,时间代价是O(n*e)?还是O(n+e)?或者是O(max(n,e))?
【解答】
在邻接表上执行图的遍历操作时,需要对邻接表中所有的边链表中的结点访问一次,还需要对所有的顶点访问一次,所以时间代价是O(n+e)。
8-11 右图是一个连通图,请画出
(1) 以顶点①为根的深度优先生成树;
(2) 如果有关节点,请找出所有的关节点。
(3)如果想把该连通图变成重连通图,至少在图中加几条边?如何加?
【解答】
(1) 以顶点①为根的深度优先生成树:⑩①②
③④
⑥
⑦
⑧
⑨
(2) 关节点为 ①,②,③,⑦,⑧
(3) 至少加四条边 (1, 10), (3, 4), (4, 5), (5, 6)。从③的子孙结点⑩到③的祖先结点①引一条边,从②
的子孙结点④到根①的另一分支③引一条边,并将⑦的子孙结点⑤、⑥与结点④连结起来,可使其变为重连通图。
8-12试证明在一个有n 个顶点的完全图中,生成树的数目至少有2n-1-1。 【证明】略
8-13 编写一个完整的程序,首先定义堆和并查集的结构类型和相关操作,再定义Kruskal 求连通网络的最小生成树算法的实现。并以右图为例,写出求解过程中堆、并查集和最小生成树的变化。 【解答】 求解过程的第一步是对所有的边,按其权值大小建堆:
①
② ③
④ ⑤
⑥
11
7
6
8
5
10
9
7
⑩
① ②
③
④
⑥ ⑦ ⑧
⑨
⑩
① ②
③
④
⑤
⑥ ⑦
⑧
⑨
加(1, 2), (1, 3),
(2,3)
加(2, 4)
加(3, 4)
加(3, 5) 加(3, 6)
加(5, 6)
求解过程中并查集与堆的变化:
最后得到的生成树如下
完整的程序如下:
#include
template
MinHeap ( int Maxsize = MaxHeapSize ); MinHeap ( Type Array[ ], int n ); void Insert ( const Type &ele ); void RemoveMin ( Type &Min );
void Output ();
private: void FilterDown ( int start , int end ); void FilterUp ( int end ); Type *pHeap ; int HMaxSize ; int CurrentSize ;
};
class UFSets { public:
3 1 -6 3 3 5 1 3 11 3 5 7
2 4 9
2 3 10
3 6 8 ①
② ③
④ ⑤
⑥
6
7
5
7
9
③ ④
选(3,4,5)
③ ④ ⑤ ⑥
选(5,6,6)
③ ④ ⑤ ⑥
选(1,2,7)
① ② ③ ④ ⑤
⑥
选(3,5,7) ① ② 1 3 11
2 4 9 2
3 10
3 6 8
③ ④ ⑤
⑥ 选(3,6,8), 在同一连通分量上, 不加 ① ② 1 3 11
2 3 10 2 4 9
③ ④ ⑤
⑥ 选(2,4,9), 结束
① ②
1 3 11
2 3 10
0 1 2 3 4 5 6
并查集的存储表示
enum { MaxUnionSize = 50 };
UFSets ( int MaxSize = MaxUnionSize );
~UFSets () { delete [ ] m_pParent; }
void Union ( int Root1, int Root2 );
int Find ( int x );
private:
int m_iSize;
int *m_pParent;
};
class Graph {
public:
enum { MaxVerticesNum = 50 };
Graph( int Vertices = 0) { CurrentVertices = Vertices; InitGraph(); }
void InitGraph ();
void Kruskal ();
int GetVerticesNum () { return CurrentVertices; }
private:
int Edge[MaxVerticesNum][MaxVerticesNum];
int CurrentVertices;
};
class GraphEdge {
public:
int head, tail;
int cost;
int operator <= ( GraphEdge &ed );
};
GraphEdge :: operator <= ( GraphEdge &ed ) {
return this->cost <= ed.cost;
}
UFSets :: UFSets ( int MaxSize ) {
m_iSize = MaxSize;
m_pParent = new int[m_iSize];
for ( int i = 0; i < m_iSize; i++ ) m_pParent[i] = -1;
}
void UFSets :: Union ( int Root1, int Root2 ) {
m_pParent[Root2] = Root1;
}
int UFSets :: Find ( int x ) {
while ( m_pParent[x] >= 0 ) x = m_pParent[x];
return x;
}
template
HMaxSize = Maxsize;
pHeap = new Type[HMaxSize];
CurrentSize = -1;
}
template
pHeap = new Type[HMaxSize];
for ( int i = 0; i < n; i++ ) pHeap[i] = Array[i];
CurrentSize = n-1;
int iPos = ( CurrentSize - 1 ) / 2;
while ( iPos >= 0 ) {
FilterDown ( iPos, CurrentSize );
iPos--;
}
}
template
Type Temp = pHeap[i];
while ( j <= end ) {
if ( j < end && pHeap[j+1] <= pHeap[j] ) j++;
if ( Temp <= pHeap[j] ) break;
pHeap[i] = pHeap[j];
i = j; j = 2 * j + 1;
}
pHeap[i] = Temp;
}
template
int i = end, j = ( end - 1 ) / 2;
Type Temp = pHeap[i];
while ( i > 0 ) {
if ( pHeap[j] <= Temp ) break;
pHeap[i] = pHeap[j];
i = j; j = ( j - 1 ) / 2;
}
pHeap[i] = Temp;
}
template
CurrentSize++;
if ( CurrentSize == HMaxSize ) return;
pHeap[CurrentSize] = ele;
FilterUp ( CurrentSize );
}
template
if ( CurrentSize < 0 )return;
Min = pHeap[0];
pHeap[0] = pHeap[CurrentSize--];
FilterDown ( 0, CurrentSize );
}
template
for ( int i = 0; i <= CurrentSize; i++ ) cout << pHeap[i] << " ";
cout << endl;
}
void Graph :: InitGraph( ) {
Edge[0][0] = -1;Edge[0][1] = 28;Edge[0][2] = -1;Edge[0][3] = -1;Edge[0][4] = -1;Edge[0][5] = 10;
Edge[0][6] = -1;
Edge[1][1] = -1;Edge[1][2] = 16;Edge[1][3] = -1;Edge[1][4] = -1;Edge[1][5] = -1;Edge[1][6] = 14;
Edge[2][2] = -1; Edge[2][3] = 12;Edge[2][4] = -1; Edge[2][5] = -1;Edge[2][6] = -1;
Edge[3][3] = -1;Edge[3][4] = 22;Edge[3][5] = -1;Edge[3][6] = 18;
Edge[4][4] = -1;Edge[4][5] = 25; Edge[4][6] = 24;
Edge[5][5] = -1;Edge[5][6] = -1;
Edge[6][6] = -1;
for ( int i = 1; i < 6; i++ )
for ( int j = 0; j < i; j ++ ) Edge[i][j] = Edge[j][i];
}
void Graph :: Kruskal( ) {
GraphEdge e;
int VerticesNum = GetVerticesNum ( );
int i, j, count;
MinHeap
UFSets set ( VerticesNum );
for ( i = 0; i < VerticesNum; i++ )
for ( j = i + 1; j < VerticesNum; j++ )
if ( Edge[i][j] > 0 ) { e.head = i ; e.tail = j ; e.cost = Edge[i][j]; heap.Insert ( e );
}
count = 1;
while ( count < VerticesNum ) { heap.RemoveMin ( e ); i = set.Find ( e.head ); j = set.Find ( e.tail ); if ( i != j ) { set.Union ( i, j ); count++;
cout << "( " << e.head << ", " << e.tail << ", " <<
e.cost << " )" << endl;
}
}
}
8-14 利用Dijkstra 算法的思想,设计一个求最小生成树的算法。 【解答】
计算连通网络的最小生成树的Dijkstra 算法可描述如下:将连通网络中所有的边以方便的次序逐步加入到初始为空的生成树的边集合T 中。每次选择并加入一条边时,需要判断它是否会与先前加入T 的边构成回路。如果构成了回路,则从这个回路中将权值最大的边退选。 下面以邻接矩阵作为连通网络的存储表示,并以并查集作为判断是否出现回路的工具,分析算法的
执行过程。
①
②
⑤ ④
③
⑥ 18 14
16 26
21
19
11 9
5
6
?????
?
??
?
?
?
?--
-
---------∞∞-
-∞-∞∞=02601118060199502114160Edge ① ② ③ ④ ⑤ ⑥
①
②③④⑤⑥
① ②
⑤
④
③
⑥
14 16
21
① ② ⑤ ⑥
并查集, 表明4个结点在同一连通分量上
①
②
⑤
④
③
⑥
14
16
21
①
② ⑤ ⑥
19
9
5
? ③ ④ ① ②
⑤
④
③
⑥ 14 16
①
② ⑤
⑥ 5
③
19 9
6
?
①
②
⑤
④
③
⑥
14
16
①
② ⑤
⑥
5
③ ④ 6
19
11
?
最终得到的最小生成树为
实现算法的过程为
const int MaxNum = 10000; void Graph :: Dijkstra ( ) { GraphEdge e ;
int VerticesNum = GetVerticesNum ( ); int i , j , p, q, k ;
int disJoint[VerticesNum];
//并查集
for ( i = 0; i < VerticesNum ; i++ ) disJoint[i] = -1;
//并查集初始化
for ( i = 0; i < VerticesNum -1; i++ )
//检查所有的边
for ( j = i + 1; j < VerticesNum ; j++ ) if ( Edge[i][j] < MaxNum ) {
//边存在
p = i ; q = j ;
//判结点i 与j 是否在同一连通分量上
while ( disJoint[p] >= 0 ) p = disJoint[p]; while ( disJoint[q] >= 0 ) p = disJoint[q]; if ( p != q ) disJoint[j] = i ; // i 与j 不在同一连通分量上, 连通之 } else {
// i 与j 在同一连通分量上
p = i ;
//寻找离结点i 与j 最近的祖先结点
while ( disJoint[p] >= 0 ) {
//每变动一个p, 就对q 到根的路径检测一遍
q = j ;
while ( disJoint[q] >= 0 && disJoint[q] == disJoint[p] )
q = disJoint[q];
if ( disJoint[q] == disJoint[p] ) break;
else p = disJoint[p];
}
k = disJoint[p];
//结点k 是i 和j 的最近的共同祖先 p = i ; q = disJoint[p]; max = -MaxNum ; //从i 到k 找权值最大的边(s1, s2)
while ( q <= k ) { if ( Edge[q][p] > max ) { max = Edge[q][p]; s1 = p ; s2 = q ; }
p =q ; q = disJoint[p];
}
p = j ; q = disJoint[p]; max = -MaxNum ; //从j 到k 找权值最大的边(t1, t2)
while ( q <= k ) { if ( Edge[q][p] > max ) { max = Edge[q][p]; t1 = p ; t2 = q ; }
p =q ; q = disJoint[p];
}
max = Edge[i][j]; k1 = i ; k2 = j ;
if ( max < Edge[s1][s2] ) { max = Edge[s1][s2]; k1 = s1; k2 = s2; }
①
②
⑤
④
③
⑥
14
16
5
6
11
if ( max < Edge[t1][t2] ) { max = Edge[t1][t2]; k1 = t1; k2 = t2; }
if ( max != Edge[i][j] ) { //当Edge[i][j] == max时边不改
if ( disJoint[k1] == k2 ) disJoint[k1] = -1;
else disJoint[k2] = -1; //删除权值最大的边
disJoint[j] = i; //加入新的边
Edge[j][i] = - Edge[j][i];
}
}
}
8-15以右图为例,按Dijkstra算法计算得到的从顶点①(A)到其它各个顶点的最短路径和最短路径长度。【解答】
C
8-16 在以下假设下,重写Dijkstra算法:
(1) 用邻接表表示带权有向图G,其中每个边结点有3个域:邻接顶点vertex,边上的权值length 和边链表的链接指针link。
(2) 用集合T = V(G) - S代替S (已找到最短路径的顶点集合),利用链表来表示集合T。
试比较新算法与原来的算法,计算时间是快了还是慢了,给出定量的比较。
【解答】
(1)用邻接表表示的带权有向图的类定义:
const int DefaultSize = 10; //缺省顶点个数
class Graph; //图的前视类定义
struct Edge { //边的定义
friend class Graph;
int vertex; //边的另一顶点位置
float length; //边上的权值
Edge *link; //下一条边链指针
Edge ( ) { }//构造函数
Edge ( int num, float wh ) : vertex (num), length (wh), link (NULL) { }//构造函数
int operator < ( const Edge & E ) const { return length != E.length;}//判边上权值小否
}
struct Vertex { //顶点的定义
friend class Graph;
char data; //顶点的名字
Edge *adj; //边链表的头指针
}
①
②
③
④
⑤
class Graph {
//图的类定义
private:
Vertex *NodeTable ; //顶点表 (各边链表的头结点) int NumVertices ; //当前顶点个数 int NumEdges ;
//当前边数
int GetVertexPos ( const Type vertex ); //给出顶点vertex 在图中的位置
public:
Graph ( int sz ); //构造函数 ~Graph ( );
//析构函数
int NumberOfVertices ( ) { return NumVertices ; } //返回图的顶点数 int NumberOfEdges ( ) { return NumEdges ; }
//返回图的边数
char GetValue ( int i )
//取位置为i 的顶点中的值
{ return i >= 0 && i < NumVertices ? NodeTable[i].data : ‘ ’; } float GetWeight ( int v1, int v2 ); //返回边(v1, v2)上的权值 int GetFirstNeighbor ( int v );
//取顶点v 的第一个邻接顶点
int GetNextNeighbor ( int v, int w ); //取顶点v 的邻接顶点w 的下一个邻接顶点
}
(2) 用集合T = V(G) - S 代替S (已找到最短路径的顶点集合),利用链表来表示集合T 。
8-17 试证明:对于一个无向图G = (V , E),若G 中各顶点的度均大于或等于2,则G 中必有回路。 【解答】
反证法:对于一个无向图G=(V ,E ),若G 中各顶点的度均大于或等于2,则G 中没有回路。此时从某一个顶点出发,应能按拓扑有序的顺序遍历图中所有顶点。但当遍历到该顶点的另一邻接顶点时,又可能回到该顶点,没有回路的假设不成立。
8-18 设有一个有向图存储在邻接表中。试设计一个算法,按深度优先搜索策略对其进行拓扑排序。并以右图为例检验你的算法的正确性。 【解答】 (1) 利用题8-16定义的邻接表结构。
增加两个辅助数组和一个工作变量:
? 记录各顶点入度 int indegree[NumVertices]。 ? 记录各顶点访问顺序 int visited[NumVertices],初始时让visited[i] = 0, i = 1, 2, , NumVertices 。 ? 访问计数int count ,初始时为0。
(2) 拓扑排序算法
void Graph :: dfs ( int visited[ ], int indegree[ ], int v, int & count ) {
count++; visited[v] = count ;
cout << NodeTable[v].data << endl;
Edge *p = NodeTable[v].adj ;
while ( p != NULL ) { int w = p ->vertex ; indegree[w]--;
if ( visited[w] == 0 && indegree[w] == 0 ) dfs ( visited, indegree, w, count );
p = p->link;
}
}
主程序
int i, j; Edge *p; float w;
cin >> NumVertices;
int * visited = new int[NumVertices+1];
int * indegree = new int[NumVertices+1];
for ( i = 1; i <= NumVertices; i++ ) {
NodeTable[i].adj = NULL; cin >> NodeTable[i].data; cout << endl;
visited[i] = 0; indegree[i] = 0;
}
int count = 0;
cin >> i >> j >> w; cout << endl;
while ( i != 0 && j != 0 ) {
p = new Edge ( j, w );
if ( p == NULL ) { cout << “存储分配失败!” << endl; exit(1); }
indegree[j]++;
p->link = NodeTable[i].adj;NodeTable[i].adj = p;
NumEdges++;
cin >> i >> j >> w; cout << endl;
}
for (i = 1; i <= NumVertices; i++ )
if ( visited[i] == 0 && indegree[i] == 0 )dfs ( visited, indegree, i, count );
if (count < NumVertices ) cout<< “排序失败!” << endl;
else cout<< “排序成功!” < delete [ ] visited; delete [ ] indegree; 8-19试对右图所示的AOE网络,解答下列问 题。 (1) 这个工程最早可能在什么时间结束。 (2) 求每个事件的最早开始时间Ve[i]和最迟开 始时间Vl[I]。 (3) 求每个活动的最早开始时间e( )和最迟开始时间l( )。 (4) 确定哪些活动是关键活动。画出由所有关键活动构成的图,指出哪些活动加速可使整个工程提前完成。 【解答】 按拓扑有序的顺序计算各个顶点的最早可能开始时间Ve和最迟允许开始时间Vl。然后再计算各个活动的最早可能开始时间e和最迟允许开始时间l,根据l - e = 0? 来确定关键活动,从而确定关键路径。 此工程最早完成时间为43。关键路径为<1, 3><3, 2><2, 5><5, 6> 8-20 若AOE网络的每一项活动都是关键活动。令G是将该网络的边去掉方向和权后得到的无向图。 (1) 如果图中有一条边处于从开始顶点到完成顶点的每一条路径上,则仅加速该边表示的活动就能减少整个工程的工期。这样的边称为桥(bridge)。证明若从连通图中删去桥,将把图分割成两个连通分量。 (2) 编写一个时间复杂度为O(n+e)的使用邻接表表示的算法,判断连通图G中是否有桥,若有。输出这样的桥。 数据结构实验指导书 实验一线性表的顺序存储结构 一、实验学时 4学时 二、背景知识:顺序表的插入、删除及应用。 三、目的要求: 1.掌握顺序存储结构的特点。 2.掌握顺序存储结构的常见算法。 四、实验内容 1.从键盘随机输入一组整型元素序列,建立顺序表。(注意:不可将元素个数和元素值写死在程序中) 2.实现该顺序表的遍历(也即依次打印出每个数据元素的值)。 3.在该顺序表中顺序查找某一元素,如果查找成功返回1,否则返回0。 4.实现把该表中某个数据元素删除。 5.实现在该表中插入某个数据元素。 6.实现两个线性表的归并(仿照课本上P26 算法2.7)。 7. 编写一个主函数,调试上述6个算法。 五、实现提示 1.存储定义 #include typedef int ElemType;//元素类型 typedef struct list{ ElemType *elem;//静态线性表 int length; //表的实际长度 int listsize; //表的存储容量 }SqList;//顺序表的类型名 2.建立顺序表时可利用随机函数自动产生数据。 3.为每个算法功能建立相应的函数分别调试,最后在主函数中调用它们。 六、注意问题 插入、删除元素时对于元素合法位置的判断。 七、测试过程 1.先从键盘输入元素个数,假设为6。 2.从键盘依次输入6个元素的值(注意:最好给出输入每个元素的提示,否则除了你自己知道之外,别人只见光标在闪却不知道要干什么),假设是:10,3,8,39,48,2。 3.遍历该顺序表。 4.输入待查元素的值例如39(而不是待查元素的位置)进行查找,因为它在表中所以返回1。假如要查找15,因为它不存在,所以返回0。 5.输入待删元素的位置将其从表中删掉。此处需要注意判断删位置是否合法,若表中有n个元素,则合法的删除位 2014 上数据结构期末复习大纲 一. 期中前以期中考试试卷复习,算法要真正理解 二、二叉树、图、排序算法将是考试重点(占60%左右) 三、要掌握的算法 1. 二叉树的链表表示 2.建立二叉树的链表存储结构 3. 先序、中序、后序遍历二叉树(递归算法) 4. 遍历算法的应用(如求二叉树的结点数) 5.建立huffman树和huffman编码 6. 图的邻接矩阵表示和邻接链表表示 7.图的深度优先遍历和广度优先遍历算法 8. 有向图求最短路径(迪杰斯特拉算法) 9. 直接插入排序算法 10. shell 排序(排序过程) 12. 堆排序(排序过程) 练习题 1. 有8个结点的无向图最多有 B 条边。 A .14 B. 28 C. 56 D. 112 2. 有8个结点的无向连通图最少有 C 条边。 A .5 B. 6 C. 7 D. 8 3. 有8个结点的有向完全图最多有 C 条边。 A .14 B. 28 C. 56 D. 112 4. 用邻接表表示图进行广度优先遍历时,通常是采用 B 来实现算法的。 A .栈 B. 队列 C. 树 D. 图 5. 用邻接表表示图进行深度优先遍历时,通常是采用 A 来实现算法的。 A .栈 B. 队列 C. 树 D. 图 6. 已知图的邻接矩阵,根据算法思想,则从顶点0出发按深度优先遍历的结点序列是*( C ) A .0 2 4 3 1 5 6 B. 0 1 3 6 5 4 2 C. 0 4 2 3 1 6 5 ??? ? ?? ? ? ? ? ? ???????????0100011101100001011010110011001000110010011011110 实验报告 实验六图的应用及其实现 一、实验目的 1.进一步功固图常用的存储结构。 2.熟练掌握在图的邻接表实现图的基本操作。 3.理解掌握AOV网、AOE网在邻接表上的实现以及解决简单的应用问题。 二、实验内容 一>.基础题目:(本类题目属于验证性的,要求学生独立完成) [题目一]:从键盘上输入AOV网的顶点和有向边的信息,建立其邻接表存储结构,然后对该图拓扑排序,并输出拓扑序列. 试设计程序实现上述AOV网 的类型定义和基本操作,完成上述功能。 [题目二]:从键盘上输入AOE网的顶点和有向边的信息,建立其邻接表存储结构,输出其关键路径和关键路径长度。试设计程序实现上述AOE网类型定义和基本操作,完成上述功能。 测试数据:教材图7.29 【题目五】连通OR 不连通 描述:给定一个无向图,一共n个点,请编写一个程序实现两种操作: D x y 从原图中删除连接x,y节点的边。 Q x y 询问x,y节点是否连通 输入 第一行两个数n,m(5<=n<=40000,1<=m<=100000) 接下来m行,每行一对整数 x y (x,y<=n),表示x,y之间有边相连。保证没有重复的边。 接下来一行一个整数 q(q<=100000) 以下q行每行一种操作,保证不会有非法删除。 输出 按询问次序输出所有Q操作的回答,连通的回答C,不连通的回答D 样例输入 3 3 1 2 1 3 2 3 5 Q 1 2 D 1 2 Q 1 2 D 3 2 Q 1 2 样例输出 C C D 【题目六】 Sort Problem An ascending sorted sequence of distinct values is one in which some form of a less-than operator is used to order the elements from smallest to largest. For example, the sorted sequence A, B, C, D implies that A < B, B < C and C < D. in this problem, we will give you a set of relations of the form A < B and ask you to determine whether a sorted order has been specified or not. 【Input】 Input consists of multiple problem instances. Each instance starts with a line containing two positive integers n and m. the first value indicated the number of objects to sort, where 2 <= n<= 26. The objects to be sorted will be the first n characters of the uppercase alphabet. The second value m indicates the number of relations of the form A < B which will be given in this problem instance. 1 <= m <= 100. Next will be m lines, each containing one such relation consisting of three characters: an uppercase letter, the character "<" and a second uppercase letter. No letter will be outside the range of the first n letters of the alphabet. Values of n = m = 0 indicate end of input. 【Output】 For each problem instance, output consists of one line. This line should be one of the following three: Sorted sequence determined: y y y… y. Sorted sequence cannot be determined. Inconsistency found. 第七章图:习题 习题 一、选择题 1.设完全无向图的顶点个数为n,则该图有( )条边。 A. n-l B. n(n-l)/2 C.n(n+l)/2 D. n(n-l) 2.在一个无向图中,所有顶点的度数之和等于所有边数的( )倍。 A.3 B.2 C.1 D.1/2 3.有向图的一个顶点的度为该顶点的( )。 A.入度 B. 出度 C.入度与出度之和 D.(入度+出度)/2 4.在无向图G (V,E)中,如果图中任意两个顶点vi、vj (vi、vj∈V,vi≠vj)都的,则称该图是( )。 A.强连通图 B.连通图 C.非连通图 D.非强连通图 5.若采用邻接矩阵存储具有n个顶点的一个无向图,则该邻接矩阵是一个( )。 A.上三角矩阵 B.稀疏矩阵 C.对角矩阵 D.对称矩阵 6.若采用邻接矩阵存储具有n个顶点的一个有向图,顶点vi的出度等于邻接矩阵 A.第i列元素之和 B.第i行元素之和减去第i列元素之和 C.第i行元素之和 D.第i行元素之和加上第i列元素之和 7.对于具有e条边的无向图,它的邻接表中有( )个边结点。 A.e-l B.e C.2(e-l) D. 2e 8.对于含有n个顶点和e条边的无向连通图,利用普里姆Prim算法产生最小生成时间复杂性为( ),利用克鲁斯卡尔Kruskal算法产生最小生成树(假设边已经按权的次序排序),其时间复杂性为( )。 A. O(n2) B. O(n*e) C. O(n*logn) D.O(e) 9.对于一个具有n个顶点和e条边的有向图,拓扑排序总的时间花费为O( ) A.n B.n+l C.n-l D.n+e 10.在一个带权连通图G中,权值最小的边一定包含在G的( )生成树中。 A.最小 B.任何 C.广度优先 D.深度优先 二、填空题 1.在一个具有n个顶点的无向完全图中,包含有____条边;在一个具有n个有向完全图中,包含有____条边。 2.对于无向图,顶点vi的度等于其邻接矩阵____ 的元素之和。 3.对于一个具有n个顶点和e条边的无向图,在其邻接表中,含有____个边对于一个具有n个顶点和e条边的有向图,在其邻接表中,含有_______个弧结点。 4.十字链表是有向图的另一种链式存储结构,实际上是将_______和_______结合起来的一种链表。 5.在构造最小生成树时,克鲁斯卡尔算法是一种按_______的次序选择合适的边来构造最小生成树的方法;普里姆算法是按逐个将_______的方式来构造最小生成树的另一种方法。 6.对用邻接表表示的图进行深度优先遍历时,其时间复杂度为一;对用邻接表表示的图进行广度优先遍历时,其时间复杂度为_______。 7.对于一个具有n个顶点和e条边的连通图,其生成树中的顶点数为_______ ,边数为_______。 8.在执行拓扑排序的过程中,当某个顶点的入度为零时,就将此顶点输出,同时将该顶点的所有后继顶点的入度减1。为了避免重复检测顶点的入度是否为零,需要设立一个____来存放入度为零的顶点。 知识点: 01.绪论 02.顺序表 03.链表 04.栈 05.链队列 06.循环队列 07.串 08.数组的顺序表示 09.稀疏矩阵 10.广义表 11.二叉树的基本概念 12.二叉树遍历、二叉树性质 13.树、树与二叉树的转换 14.赫夫曼树 15.图的定义、图的存储 16.图的遍历 17.图的生成树 18.静态查找(顺序表的查找、有序表的查找) 19.动态查找(二叉排序树、平衡树、B树) 20.哈希查找 21.插入排序(直接插入、折半插入、2路插入、希尔排序)22.选择排序(简单选择、树形选择、堆排序) 23.快速排序、归并排序 101A1(1).数据的逻辑结构是(A)。 A.数据的组织形式 B.数据的存储形式 C.数据的表示形式 D.数据的实现形式 101A1(2).组成数据的基本单位是(C)。 A.数据项 B.数据类型 C.数据元素 D.数据变量 101B1(3).与顺序存储结构相比,链式存储结构的存储密度(B)。 A.大 B.小 C.相同 D.以上都不对 101B2(4).对于存储同样一组数据元素而言,(D)。 A.顺序存储结构比链接结构多占空间 B.在顺序结构中查找元素的速度比在链接结构中查找要快 C.与链接结构相比,顺序结构便于安排数据元素 D.顺序结构占用整块空间而链接结构不要求整块空间101B2(5).下面程序的时间复杂度为(B)。 x=0; for(i=1;i /* *题目:编写按键盘输入的数据建立图的邻接矩阵存储 * 编写图的深度优先遍历程序 * 编写图的广度优先遍历程序 * 设计一个选择式菜单形式如下: * 图子系统 * *********************************** * * 1------更新邻接矩阵* * * 2------深度优先遍历* * * 3------广度优先遍历* * * 0------ 返回* * *********************************** * 请选择菜单号(0--3): */ #include #include 第8章 图 8-1 画出1个顶点、2个顶点、3个顶点、4个顶点和5个顶点的无向完全图。试证明在n 个顶点的无向完全图中,边的条数为n(n-1)/2。 【解答】 【证明】 在有n 个顶点的无向完全图中,每一个顶点都有一条边与其它某一顶点相连,所以每一个顶点有 n-1条边与其他n-1个顶点相连,总计n 个顶点有n(n-1)条边。但在无向图中,顶点i 到顶点j 与顶点j 到顶点i 是同一条边,所以总共有n(n-1)/2条边。 8-2 右边的有向图是强连通的吗?请列出所有的简单路径。 【解答】 点,它不是强连通的有向图。各个顶点自成强连通分量。 所谓简单路径是指该路径上没有重复的顶点。 从顶点A 出发,到其他的各个顶点的简单路径有A →B ,A →D →B ,A →B →C ,A →D →B →C ,A →D ,A →B →E ,A →D →E ,A →D →B →E ,A →B →C →F →E ,A →D →B →C →F →E ,A →B →C →F ,A 1个顶点的 无向完全图 2个顶点的 无向完全图 3个顶点的 无向完全图 4个顶点的 无向完全图 5个顶点的 无向完全图 A D ????????? ?????? ?????=01 00000001001010000 010*********Edge →D →B →C →F 。 从顶点B 出发,到其他各个顶点的简单路径有B →C ,B →C →F ,B →E ,B →C →F →E 。 从顶点C 出发,到其他各个顶点的简单路径有C →F ,C →F →E 。 从顶点D 出发,到其他各个顶点的简单路径有D →B ,D →B →C ,D →B →C →F ,D →E ,D →B →E ,D →B →C →F →E 。 从顶点E 出发,到其他各个顶点的简单路径无。 从顶点F 出发,到其他各个顶点的简单路径有F →E 。 8-3 给出右图的邻接矩阵、邻接表和邻接多重表表示。 【解答】 (1) 邻接矩阵 A D 实验六图的应用及其实现 一、实验目的 1.进一步功固图常用的存储结构。 2.熟练掌握在图的邻接表实现图的基本操作。 3.理解掌握AOE网在邻接表上的实现及解决简单的应用问题。 二、实验内容 [题目]:从键盘上输入AOE网的顶点和有向边的信息,建立其邻接表存储结构,输出其关键路径和关键路径长度。试设计程序实现上述AOE网类型定义和基本操作,完成上述功能。 三、实验步骤 (一)、数据结构与核心算法的设计描述 本实验题目是基于图的基本操作以及邻接表的存储结构之上,着重拓扑排序算法的应用,做好本实验的关键在于理解拓扑排序算法的实质及其代码的实现。 (二)、函数调用及主函数设计 以下是头文件中数据结构的设计和相关函数的声明: typedef struct ArcNode // 弧结点 { int adjvex; struct ArcNode *nextarc; InfoType info; }ArcNode; typedef struct VNode //表头结点 { VertexType vexdata; ArcNode *firstarc; }VNode,AdjList[MAX_VERTEX_NUM]; typedef struct //图的定义 { AdjList vertices; int vexnum,arcnum; int kind; }MGraph; typedef struct SqStack //栈的定义 { SElemType *base; SElemType *top; int stacksize; }SqStack; int CreateGraph(MGraph &G);//AOE网的创建 int CriticalPath(MGraph &G);//输出关键路径 (三)、程序调试及运行结果分析 (四)、实验总结 在做本实验的过程中,拓扑排具体代码的实现起着很重要的作用,反复的调试和测试占据着实验大量的时间,每次对错误的修改都加深了对实验和具体算法的理解,自己的查错能力以及其他各方面的能力也都得到了很好的提高。最终实验结果也符合实验的预期效果。 四、主要算法流程图及程序清单 1、主要算法流程图: 2、程序清单: 创建AOE网模块: int CreateGraph(MGraph &G) //创建有向网 { int i,j,k,Vi,Vj; ArcNode *p; cout<<"\n请输入顶点的数目、边的数目"< 邻接矩阵的实现 1. 实验目的 (1)掌握图的逻辑结构 (2)掌握图的邻接矩阵的存储结构 (3)验证图的邻接矩阵存储及其遍历操作的实现2. 实验内容 (1)建立无向图的邻接矩阵存储 (2)进行深度优先遍历 (3)进行广度优先遍历3.设计与编码MGraph.h #ifndef MGraph_H #define MGraph_H const int MaxSize = 10; template int vertexNum, arcNum; }; #endif MGraph.cpp #include 数据结构实验 实验四、图遍历的演示。 【实验学时】5学时 【实验目的】 (1)掌握图的基本存储方法。 (2)熟练掌握图的两种搜索路径的遍历方法。 【问题描述】 很多涉及图上操作的算法都是以图的遍历操作为基础的。试写一个程序,演示连通的无向图上,遍历全部结点的操作。 【基本要求】 以邻接多重表为存储结构,实现连通无向图的深度优先和广度优先遍历。以用户指定的结点为起点,分别输出每种遍历下的结点访问序列和相应生成树的边集。 【测试数据】 教科书图7.33。暂时忽略里程,起点为北京。 【实现提示】 设图的结点不超过30个,每个结点用一个编号表示(如果一个图有n个结点,则它们的编号分别为1,2,…,n)。通过输入图的全部边输入一个图,每个边为一个数对,可以对边的输入顺序作出某种限制。注意,生成树的边是有向边,端点顺序不能颠倒。 【选作内容】 (1)借助于栈类型(自己定义和实现),用非递归算法实现深度优先遍历。(2)以邻接表为存储结构,建立深度优先生成树和广度优先生成树,再按凹入表或树形打印生成树。 (3)正如习题7。8提示中分析的那样,图的路径遍历要比结点遍历具有更为广泛的应用。再写一个路径遍历算法,求出从北京到广州中途不过郑州的所有简单路径及其里程。 【源程序】 #include 数据流图(DFD)画法要求 一、数据流图(DFD) 1.数据流图的基本符号 数据流图由基本符号组成,见图5-4-1所示。 图5-4-1 数据流图的基本符号 例:图5-4-2是一个简单的数据流图,它表示数据X从源S流出,经P加工转换成Y,接着经P加工转换为Z,在加工过程中从F中读取数据。 图5-4-2数据流图举例 下面来详细讨论各基本符号的使用方法。 2.数据流 数据流由一组确定的数据组成。例如“发票”为一个数据流,它由品名、规格、单位、单价、数量等数据组成。数据流用带有名字的具有箭头的线段表示,名字称为数据流名,表示流经的数据,箭头表示流 向。数据流可以从加工流向加工,也可以从加工流进、流出文件,还可以从源点流向加工或从加工流向终点。 对数据流的表示有以下约定: 对流进或流出文件的数据流不需标注名字,因为文件本身就足以说明数据流。而别的数据流则必须标出名字,名字应能反映数据流的含义。 数据流不允许同名。 两个数据流在结构上相同是允许的,但必须体现人们对数据流的不同理解。例如图5-4-3(a)中的合理领料单与领料单两个数据流,它们的结构相同,但前者增加了合理性这一信息。 两个加工之间可以有几股不同的数据流,这是由于它们的用途不同,或它们之间没有联系,或它们的流动时间不同,如图5-4-3(b)所示。 (a)(b)(c) 图5-4-3 简单数据流图举例 数据流图描述的是数据流而不是控制流。如图5-4-3 (c)中,“月末”只是为了激发加工“计算工资”,是一个控制流而不是数据流,所以应从图中删去。 3.加工处理 加工处理是对数据进行的操作,它把流入的数据流转换为流出的数据流。每个加工处理都应取一个名字表示它的含义,并规定一个编号用来标识该加工在层次分解中的位置。名字中必须包含一个动词,例如“计算”、“打印”等。 对数据加工转换的方式有两种: 改变数据的结构,例如将数组中各数据重新排序; 绪论 一、填空题 1.数据的逻辑结构被分为集合、(线性结构)、(树形结构)和(图状结构)四种。 2. 物理结构是数据结构在计算机中的表示,又称为(存储结构)。 3. 数据元素的逻辑结构包括(线性)、(树)和图状结构3 种类型,树形结构和图状结构合称为(非线性结构)。 4. (数据元素)是数据的基本单位,(数据项)是数据不可分割的最小单位。 5. 线性结构中元素之间存在(一个对一个)关系,树形结构中元素之间存在(一个对多个)关系,图状结构中元素之间存在(多个对多个)关系。 ? 6.数据结构是一门研究非数值计算的程序设计问题中:计算机的(数据元素)以及它们之间的(关 系)和(运筹)等的学科。 7. 算法的五个重要特性为有穷性、确定性、(输入)、(输出)和(可行性)。 二、选择题 1. 数据的不可分割的基本单位是(D)。 A.元素 B.结点C数据类型D.数据项 *2. 线性表的逻辑顺序与存储顺序总是一致的,这种说法(B)。 A.正确 B.不正确C不确定 D.无法选择 3. 线性结构是指数据元素之间存在一种(D)。 A.一对多关系 B.多对多关系C多对一关系D.—对一关系 4. 在数据结构中,从逻辑上可以把数据结构分成(A)。 A.动态结构和静态结构 B.紧凑结构和非紧凑结构 C线性结构和非线性结构D.内部结构和外部结构 5. 线性表若采用链式存储结构时,要求内存中可用存储单元的地址(D)。 A.必须是连续的 B.部分地址必须是连续的 C. 一定是不连续的 D.连续不连续都可以 三、简答题 1. 算法的特性是什么。 答:有穷性确定性可行性有0 或多个输入有 1 或多个输出 线性结构 一、填空题 1?在一个长度为n的线性表中删除第i个元素(1< i产时,需向前移动(n-i)个元素。 2. 从循环队列中删除一个元素时,其操作是(先移动队首指针,后取出元素)。 3?在线性表的单链接存储中,若一个元素所在结点的地址为p,则其后继结点的地址为(p-> next)。 4. 在一个单链表中指针p所指向结点的后面插入一个指针q所指向的结点时,首先把(p->next)的值赋给q->next,然后(q->date)的值赋给p->next。 5. 从一个栈删除元素时,首先取出(栈顶元素),然后再使(栈顶指针)减1。 6. 子串的定位操作通常称做串的(模式匹配)。 7. 设目标T= ‘ abccdcdccba,模式P= ‘ cdc则第(六)次匹配成功。。 8. 顺序栈S 中,出栈操作时要执行的语句序列中有S->top(--);进栈操作时要执行的语句序列中有S->top(++)。 从数据流程图导出初始结构图方法 下面分别讨论经过”变换分析”和”事务分析”技术, 导出”变换型”和”事务型”初始结构图的技术。 1.变换分析 根据系统说明书, 能够决定数据流程图中, 哪些是系统的主处理。主处理一般是几股数据流汇合处的处理, 也就是系统的变换中心, 即逻辑输入和逻辑输出之间的处理。 确定逻辑输入——离物理输入端最远的, 但仍可被看作系统输入的那个数据流即为逻辑输入。确定方法是从物理输入端开始, 一步步向系统的中间移动, 直至达到这样一个数据流: 它已不能再被看作为系统的输入, 则其前一个数据流就是系统的逻辑输入。确定逻辑输出——离物理输出端最远的, 但仍可被看作系统输出的那个数据流即为逻辑输出。方法是从物理输出端开始, 一步步向系统的中间反方向移动, 直至达到这样一个数据流: 它已不能再被看作为系统的输出, 则其后一个数据流就是系统的逻辑输出。对系统的每一股输入和输出, 都用上面的方法找出相应的逻辑输入、输出。逻辑输入和逻辑输出之间的加工, 就是系统的主加工。如图4-24所示。 图4-24(a)初始DFD图 图4-24(b)找系统的主加工 2) 设计模块的顶层和第一层 ”顶层模块”也叫主控模块, 其功能是完成整个程序要做的工作。在与主加工对应的位置上画出主模块。系统结构的”顶层”设计后, 下层的结构就按输入、变换、输出等分支来分解。 设计模块结构的第一层: 为逻辑输入设计一个输入模块, 它的功能是向主模块提供数据; 为逻辑输出设计一个输出模块, 它的功能是输出主模块提供的数据; 为主加工设计一个变换模块, 它的功能是将逻辑输入变换成逻辑输出。 第一层模块同顶层主模块之间传送的数据应与数据流程图相对应。这里主模块控制并协调第一层的输入、变换、输出模块的工作。( 3) 设计中、下层模块 由自顶向下、逐步细化的过程, 为每一个上层模块设计下属模块。输入模块的功能是向它的调用模块提供数据, 由两部分组成: 一部分是接受输入数据; 另一部分是将这些数据变换成其调用模块所 第7章图 一、单选题 01、在一个图中,所有顶点的度数之和等于图的边数的倍。A.1/2 B.1 C.2 D.4 02、在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和的倍。 A.1/2 B.1 C.2 D.4 03、有8个结点的无向图最多有条边。 A.14 B.28 C.56 D.112 04、有8个结点的无向连通图最少有条边。 A.5 B.6 C.7 D.8 05、有8个结点的有向完全图有条边。 A.14 B.28 C.56 D.112 06、用邻接表表示图进行广度优先遍历时,通常是采用来实现算法的。 A.栈 B.队列 C.树 D.图 07、用邻接表表示图进行深度优先遍历时,通常是采用来实现算法的。 A.栈 B.队列 C.树 D.图 08、一个含n个顶点和e条弧的有向图以邻接矩阵表示法为存储结构,则计算该有向图中某个顶点出度的时间复杂度为。 A.O(n) B.O(e) C.O(n+e) D.O(n2) 09、已知图的邻接矩阵,根据算法思想,则从顶点0出发按深度优先遍历的结点序列是。 A.0 2 4 3 1 5 6 B.0 1 3 6 5 4 2 C.0 1 3 4 2 5 6 D.0 3 6 1 5 4 2 10、已知图的邻接矩阵同上题,根据算法,则从顶点0出发,按广度优先遍历的结点序列是。 A.0 2 4 3 6 5 1 B.0 1 2 3 4 5 6 C.0 4 2 3 1 5 6 D.0 1 3 4 2 5 6 11、已知图的邻接表如下所示,根据算法,则从顶点0出发按深度优先遍历的结点序列是。 A.0 1 3 2 B.0 2 3 1 C.0 3 2 1 D.0 1 2 3 12、已知图的邻接表如下所示,根据算法,则从顶点0出发按广度优先遍历的结点序列是。 A.0 3 2 1 B.0 1 2 3 C.0 1 3 2 D.0 3 1 2 13、图的深度优先遍历类似于二叉树的。 A.先序遍历 B.中序遍历 C.后序遍历 D.层次遍历14、图的广度优先遍历类似于二叉树的。 A.先序遍历 B.中序遍历 C.后序遍历 D.层次遍历15、任何一个无向连通图的最小生成树。 A.只有一棵 B.一棵或多棵 C.一定有多棵 D.可能不存在 ( )16、对于一个具有n个结点和e条边的无向图,若采用邻接表表示,则顶点表的大小为,所有边链表中边结点的总数为。 A.n、2e B.n、e C.n、n+e D.2n、2e 17、判断有向图是否存在回路,可以利用算法。 A.关键路径 B.最短路径的Dijkstra C.拓扑排序D.广度优先遍历 18、若用邻接矩阵表示一个有向图,则其中每一列包含的“1”的个数为。 A.图中每个顶点的入度 B.图中每个顶点的出度 C.图中弧的条数 D.图中连通分量的数目 19、求最短路径的Dijkstra算法的时间复杂度是___。A.O(n) B.O(n+e) C.O(n2) D.O(n*e) 20、设图G采用邻接表存储,则拓扑排序算法的时间复杂度为。 A.O(n) B.O(n+e) C.O(n2) D.O(n*e) 21、带权有向图G用邻接矩阵A存储,则顶点i的入度等于A中。 A.第i行非∞的元素之和 B.第i列非∞的元素之和 C.第i行非∞且非0的元素个数 D.第i列非∞且非0的元素个数 22、一个有n个顶点的无向图最多有条边。 A.n B.n(n-1) C.n(n-1)/2 D.2n 23、对于一个具有n个顶点的无向图,若采用邻接矩阵表示,则该矩阵的大小是。 A.n B.(n-1)2 C.n-1 D.n2 24、对某个无向图的邻接矩阵来说,。 A.第i行上的非零元素个数和第i列的非零元素个数一定相等 B.矩阵中的非零元素个数等于图中的边数 C.第i行上,第i列上非零元素总数等于顶点v i的度数D.矩阵中非全零行的行数等于图中的顶点数 25、已知图的表示如下,若从顶点a出发按深度搜索法进行遍历,则可能得到的一种顶点序列为。 图 1. 填空题 ⑴ 设无向图G中顶点数为n,则图G至少有()条边,至多有()条边;若G为有向图,则至少有()条边,至多有()条边。 【解答】0,n(n-1)/2,0,n(n-1) 【分析】图的顶点集合是有穷非空的,而边集可以是空集;边数达到最多的图称为完全图,在完全图中,任意两个顶点之间都存在边。 ⑵ 任何连通图的连通分量只有一个,即是()。 【解答】其自身 ⑶ 图的存储结构主要有两种,分别是()和()。 【解答】邻接矩阵,邻接表 【分析】这是最常用的两种存储结构,此外,还有十字链表、邻接多重表、边集数组等。 ⑷ 已知无向图G的顶点数为n,边数为e,其邻接表表示的空间复杂度为()。 【解答】O(n+e) 【分析】在无向图的邻接表中,顶点表有n个结点,边表有2e个结点,共有n+2e个结点,其空间复杂度为O(n+2e)=O(n+e)。 ⑸ 已知一个有向图的邻接矩阵表示,计算第j个顶点的入度的方法是()。 【解答】求第j列的所有元素之和 ⑹ 有向图G用邻接矩阵A[n][n]存储,其第i行的所有元素之和等于顶点i的()。 【解答】出度 ⑺ 图的深度优先遍历类似于树的()遍历,它所用到的数据结构是();图的广度优先遍历类似于树的()遍历,它所用到的数据结构是()。 【解答】前序,栈,层序,队列 ⑻ 对于含有n个顶点e条边的连通图,利用Prim算法求最小生成树的时间复杂度为(),利用Kruskal 算法求最小生成树的时间复杂度为()。 【解答】O(n2),O(elog2e) 【分析】Prim算法采用邻接矩阵做存储结构,适合于求稠密图的最小生成树;Kruskal算法采用边集数组做存储结构,适合于求稀疏图的最小生成树。 ⑼ 如果一个有向图不存在(),则该图的全部顶点可以排列成一个拓扑序列。 【解答】回路 ⑽ 在一个有向图中,若存在弧、、,则在其拓扑序列中,顶点vi, vj, vk的相对次序为()。 【解答】vi, vj, vk 【分析】对由顶点vi, vj, vk组成的图进行拓扑排序。 2. 选择题 ⑴ 在一个无向图中,所有顶点的度数之和等于所有边数的()倍。 A 1/2 B 1 C 2 D 4 【解答】C 【分析】设无向图中含有n个顶点e条边,则。 ⑵ n个顶点的强连通图至少有()条边,其形状是()。 A n B n+1 C n-1 D n×(n-1) E 无回路 F 有回路 G 环状 H 树状 【解答】A,G ⑶ 含n 个顶点的连通图中的任意一条简单路径,其长度不可能超过()。 A 1 B n/2 C n-1 D n 【解答】C 【分析】若超过n-1,则路径中必存在重复的顶点。 数据结构教案第七章图 第7章图 【学习目标】 1.领会图的类型定义。 2.熟悉图的各种存储结构及其构造算法,了解各种存储结构的特点及其选用原则。 3.熟练掌握图的两种遍历算法。 4.理解各种图的应用问题的算法。 【重点和难点】 图的应用极为广泛,而且图的各种应用问题的算法都比较经典,因此本章重点在于理解各种图的算法及其应用场合。 【知识点】 图的类型定义、图的存储表示、图的深度优先搜索遍历和图的广度优先搜索遍历、无向网的最小生成树、最短路径、拓扑排序、关键路径 【学习指南】 离散数学中的图论是专门研究图性质的一个数学分支,但图论注重研究图的纯数学性质,而数据结构中对图的讨论则侧重于在计算机中如何表示图以及如何实现图的操作和应用等。图是较线性表和树更为复杂的数据结构,因此和线性表、树不同,虽然在遍历图的同时可以对顶点或弧进行各种操作,但更多图的应用问题如求最小生成树和最短路径等在图论的研究中都早已有了特定算法,在本章中主要是介绍它们在计算机中的具体实现。这些算法乍一看都比较难,应多对照具体图例的存储结构进行学习。而图遍历的两种搜索路径和树遍历的两种搜索路径极为相似,应将两者的算法对照学习以便提高学习的效益。 【课前思考】 1. 你有没有发现现在的十字路口的交通灯已从过去的一对改为三对,即每个方向的直行、左拐和右拐能否通行都有相应的交通灯指明。你能否对某个丁字路口的6条通路画出和第一章绪论中介绍的"五叉路口交通管理示意图"相类似的图? 2. 如果每次让三条路同时通行,那么从图看出哪些路可以同时通行? 同时可通行的路为:(AB,BC,CA),(AB,BC,BA),(AB,AC,CA),(CB,CA,BC) 云南大学软件学院数据结构实验报告 (本实验项目方案受“教育部人才培养模式创新实验区(X3108005)”项目资助)实验难度: A □ B □ C □ 学期:2010秋季学期 任课教师: 张德海 实验题目: 图及其应用 姓名: 申平 学号: 20091120185 电子邮件: 完成提交时间: 2010 年 12 月 27 日 云南大学软件学院2010学年秋季学期 《数据结构实验》成绩考核表 学号:姓名:本人承担角色: 综合得分:(满分100分) 指导教师:年月日(注:此表在难度为C时使用,每个成员一份。) (下面的内容由学生填写,格式统一为,字体: 楷体, 行距: 固定行距18,字号: 小四,个人报告按下面每一项的百分比打分。难度A满分70分,难度B满分90分) 一、【实验构思(Conceive)】(10%) 1.本演示程序中,元素限定为char型。 2.演示程序以用户和计算机的对话方式执行,即在计算机终端显示“提示信息“后,由用户在 键盘上输入符合演示程序中规则的图的边数,结点数;相应的先序和按层遍历会显示其后。 3.程序执行命令包括:1)根据用户给出的图字符串进行对临接表的先序构建2)输出构建的临 接表 4.测试数据 用户输入:abc//d//e// 结果:DLR:abcde LDR:cbdae LRD:cdbea Ceng:abecd 用户输入:ab/cd///e// 结果:DLR:abcde LDR:bdcae LRD:dcbea Ceng:abecd 二、【实验设计(Design)】(20%) (本部分应包括:抽象数据类型的功能规格说明、主程序模块、各子程序模块的伪码说明,主程序模块与各子程序模块间的调用关系) 为实现上述程序功能,需要三个抽象数据类型:队列和图 1.图的抽象数据类型定义为: ?ADT Graph{ ?数据对象V:顶点集 ?数据关系R:R={VR} ?VR={数据结构实验
上数据结构期末图习题答案
数据结构_实验六_报告
数据结构图习题
数据结构习题库
数据结构:图子系统
数据结构第六章实验
数据结构-图习题
数据结构实验六 图的应用及其实现
数据结构实验报告图实验
数据结构实验四五六
数据流图画法
数据结构考试题库
从数据流程图导出初始结构图方法模板
最新数据结构习题与答案--图
数据结构 第六章 图 练习题及答案详细解析(精华版)
(完整版)数据结构详细教案——图
数据结构实验报告六 图