
第4章 控制系统的状态空间设计
要点:
1状态反馈
2单输入系统的极点配置
3观测器及其设计 4用状态观测器的反馈系统概念 难点: 观测器及其设计
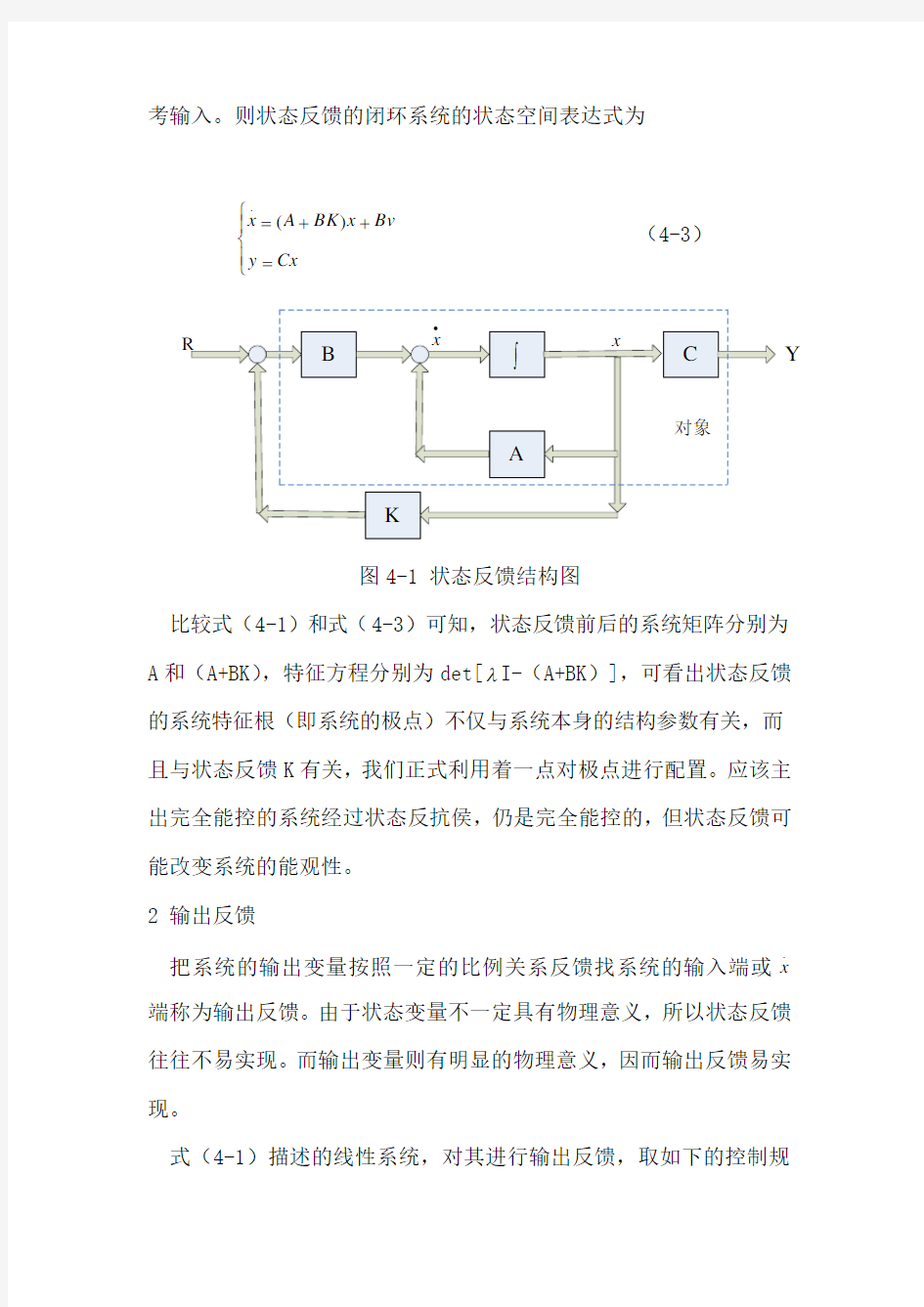
闭环系统极点的分布情况决定于系统的稳定性和动态品质,因此,可以根据对系统动态品质的要求,规定闭环系统的极点应有的分布情况,把极点的布置作为系统的动态品质指标。这种把极点不止在希望的位置的过程成为极点配置。在空间状态法中,一般采用反馈系统状态变量或输出变量的方法,实现系统的极点配置。 一 状态反馈与输出反馈 1 状态反馈
把系统状态变量按照一定的比例关系,反馈到系统的输出端称为状态反馈。
设线性系统为
????
?=+=?
Cx
y Bu
Ax x (4-1) 而反馈规律为
u=Kx+v (4-2)
其中A ,B ,C ,K 分别为n ×n 、n ×m 、p ×n 及m ×n 矩阵,v 为参
考输入。则状态反馈的闭环系统的状态空间表达式为
????
?=++=Cx
y Bv
x BK A x )(.
(4-3)
Y
图4-1 状态反馈结构图
比较式(4-1)和式(4-3)可知,状态反馈前后的系统矩阵分别为A 和(A+BK ),特征方程分别为det[λI-(A+BK )],可看出状态反馈的系统特征根(即系统的极点)不仅与系统本身的结构参数有关,而且与状态反馈K 有关,我们正式利用着一点对极点进行配置。应该主出完全能控的系统经过状态反抗侯,仍是完全能控的,但状态反馈可能改变系统的能观性。 2 输出反馈
把系统的输出变量按照一定的比例关系反馈找系统的输入端或.
x 端称为输出反馈。由于状态变量不一定具有物理意义,所以状态反馈往往不易实现。而输出变量则有明显的物理意义,因而输出反馈易实现。
式(4-1)描述的线性系统,对其进行输出反馈,取如下的控制规
律。
~
Ky V u += (4-4) 式中~
K 为1×P 矩阵,称为输出反馈增益矩阵。将式(4-4)可将输出反馈侯的系统方程为
????
?=++=Cx
y Bv
x C K B A x )(~
.
(4-5)
Y
图4-2 输出反馈结构图
比较(4-1)和(4-5)式可以看到反馈前后的系统特征方程分别为det[]A I -λ和det[)],(~
C K B A I +-λ从而可见输出反馈后的系统极点与输出反抗矩阵~
K 有关。当我们把图4-2输出反馈结构图中的B 矩阵移到第一个相加点之前时,就时输出变量反馈到.
x 端的情况如图4-3所示。
Y
R
图4-3 输出反馈.
x 结构图
此时,系统的状态方程为
????
?=+-=Cx
y Bu
x GC A x )(.
(4-6) 式中G 为n ×p 矩阵,也称为输出反馈增益矩阵。 输出反馈不改变系统的能观性。
状态反馈和输出反馈(主要指输出反馈至.
x 的情况)都能够对系统进行极点配置,且一般经验认为,用简单的比例反馈(即K ,~
K 或G 为常数矩阵)就能使问题得到解决。 二 极点配置
1 应用状态反馈实现预期的极点配置
定理4-1 系统∑=),,(C B A 采用状态反馈使闭环系统极点可任意配置的充要条件使系统完全能控。
证:由于系统∑=),,(C B A 完全能控,故可用变换∧
=x TX 化为能控标准形。
即 ???????????
??
?--=∧-∧
∧-∧
111
00a a a I A n n n Λ
M , ?????
?
??????=∧
100M ΘB
取 []1,,1∧
-∧∧K K K n n Λ 则
??????
???
?????---=+∧
∧-∧
-∧
∧∧-∧∧∧11111
0a k a k a k I K B A n n n
n n Λ
M
其特征方程为
f(λ)=dat ??
????+-∧∧∧)(K B A I λ=n
λ+(-∧
K
1
+∧
a 1)λ
n-1
+…
+(-∧K n-1+∧a n-1)λ+(-∧k n +∧
a n )=0 (4-7) 设希望闭环系统特征根为对称复数复合:
Λ =
{}λλλn
Λ,,2
1
则对应的特征方成为
(λ-λ1)(λ-λ2)…(λ-λn )=λn +α1λn-1+…+α-1λ+αn =0 (4-8) 式中的α1,α2…αn 全为实数
根据特性值不变原理,式(4-7)和式(4-8)应具有相同的特征根,则两个方程系数应分别相等,即
α 1=(-∧
k 1+∧
a 1),…,α
n-1
=-∧k n-1+∧a n-1,αn =-∧k n +∧
a n
所以只要取?????????+-=+-=+-=∧--∧
-∧
a k a k a k n n n n n n 1
11111αααM
(i=1,2,…n )
原系统∑=(A,B,C )的状态反馈阵K 可通过线性逆变换求得
?
∧
x =T ?x =(u B x K B A ∧
∧∧∧∧++)
以上可有
u B x T K B A x T T ∧
-?
∧∧∧-?
++=1
1
)(
Bu x T K B A x ++=∧
∧?)( (4-9)
上式与式(4-3)比较可得
K=T K ∧
(4-10)
只要按上(4-10)式选取K 阵即可保证状态反馈系统具有给定的(预期)的极点配置。证毕。
对于由能控标准型状态方程描述的系统可不经变化直接选取K 值,即相当于T=I
例1 已知系统的传递函数为
)()(S U S Y =s
s s 231
23++ 试确定状态反馈矩阵K ,以使闭环系统的极点配置在s 1=-2,s 2,3=-1±j
解:因所给系统的传递函数无对消银子,故系统能控,是能控标准形的状态方程为
?
x =x ??????????--32010001
0+u ??
??
??????100 设K=[]123K K K
则A+BK=?????
?????+-+-12
3
32100
10
K K K 是特征多项式为
f(λ)=[]()I A BK λ-+32213)2()3(K K K --+-+λλλ 因要求状态反馈后,系统的特征多项式为
f *(λ)=)1)(1)(2(j j -+-++λλλ=46423+++λλλ 故令上两式相等,便可求得
??
?
??=-=-=-4
6243321k k k 解得:k 3=-4, k 2=-4, k 1=1 所以 K=[]123k k k =[]144-- 2 不完全能控系统的极点配置
设不完全能控的多输入系统为
Bu Ax x +=& (4-11)
经过坐标变换,即经过能控结构分解,式(4-11)可写成
u B x x A A A x
x NC C NC C ??
?
???+????????????=????
??001221211&& (4-12) 式中,(A 11,B 1)为能控子系统,式(4-11)和式(4-12)的极点集为
)()(0
2211221211
A A A A A σσσ?=??
?
?
?? (4-13) 极点)(11A σ为能控极点,)(22A σ为不能控极点。考虑式(4-12)系统的任意状态反馈 []v x x K K u NC C NC C +??
?
?
??= (4-14) 在此反馈作用下,闭环系统为
v B x x A K B A K B A x
x NC C NC C NC C ??
?
???+????????????++=??????001221212111&& (4-15) 闭环系统极点为
)()(22111A K B A C σσ?+ (4-16) 由于),(111B A 是能控的,所以适当选择K C ,可使闭环系统)(111C K B A +σ部分的极点能任意配置。而不能控部分22A 的特征值在任意状态下反馈都不会改变。如果22A 的特征值均具有负实部,则可以选择C K 使能控部分的闭还极点)(111C K B A +σ均具有负的实部,因此存在状态反馈,使闭环系统稳定。若)(22A σ不具有负实部,显然不存在状态反馈使闭环系统稳定。
定理4-2 系统式(4-11)用状态反馈使闭环系统稳定的充分必要条件为系统的不能控极点)(22A σ都具有负实部。 三 状态观测器设计 1 观测器的设计思路
状态观测器实质上是一个状态估计器(或动态补偿器),它是利用被控对象的输入变量u 和输出y 对系统的状态x 进行估计,从而解决某些状态变量不能直接测量的难题。
考虑线性定常系统
?
??=+=Cx y Bu Ax x
& (4-17)
式(4-17)系统构造的状态观测器,其输入是输出y 和输入u 的综合,其输出z ,使0)(lim =-∞
→x z t ,则z 可以作为x 的估计值,从而实现状态
重构。
为了得到估计值z ,用模拟部件去再实现系统式(4-17),即构造系统式(4-17)的模拟系统
Bu Az z +=& (4-18)
由于式(4-18)是构造的,故都是可测量的的信息,若以z 去作为x 的估值,则其估计误差为x z e z -=,用式(4-18)减去式(4-17),则误差满足方程
z z Ae e =& (4-19)
由于它是一个开环系统,当估计值产生误差时,没有反馈不能消除误
差。所以,一个改进的措施是利用输出估计的误差y Cz y y
y -=-=??作为反馈。
此时,构造的动态系统,即龙伯格状态观测器的状态方程为
)(y Cz K Bu Az z
z --+=& 即 Bu y K z C K A z
z z ++-=)(& (4-20) 式中,z K 为反馈增益阵。用式(4-20)减去式(4-17)得估计误差z e 方程为
z z z e C K A e )(-=& (4-21)
如果选择合适的z K ,使式(4-21)稳定,即)(C K A z -σ都具有负实部,则对应的任意初值)0(z e ,)0(x 以及任意输入u 均有0)(lim lim =-=∞
→∞
→x z e t z t 。
因而z 可以用为x 的估值,故式(4-21)为系统式(4-17)的一个观测器。
2全维状态观测器的设计
定理4-3 系统式(4-17)存在观测器,且观测器的极点可以任意配置的充分必要条件是该系统完全能观。
推理: 若系统式(4-17)是不完全能观的,则其存在观测器的充分必要条件是其不能观的部分的极点具有负实部,并称这类系统是能检
测的。
现在来讨论式(4-17)给出的n 阶完全能观性系统,显然其对偶系统
?????=+=x
B y u
C x A x T
T T & (4-22) 是完全能控的,若对这个对偶系统给以状态反馈v x K u T +=,则其闭环极点,即(T T T K C A +)的特征值是可以任意配置的,而且(T T T K C A +)与(KC A +)具有相同的特征值。因此,对式(4-17)的被控对象设计观测器就可以归之于对其对偶系统(4-22)求状态反馈,使对偶系统的闭环极点等于观测器所要求的极点,且观测器中的反馈增益矩阵K K z -=。这表明,观测器设计是极点配置的问题。 例2 二阶系统
[][]
T
x x y u x x x x 21
212112110001-=??????+????????????=???
???&& 设计全阶观测器,要求观测器的极点为{-1,-1}。
解: 容易验证系统是完全能观的,其对偶系统的系统阵和输入阵分别为
??
????-=?
?????=12,0001T T
C A 按从前给出的极点配置方法,有
???
???=???
?
????-=??
????-=-121,11210,02121a Q Q c c
1
2)1()()det(0121
21
222
++=+=-=-?????????
??
?=??????=s s s s f s
s A sI aA a T d T T
则反馈增益 [][]T z K K T K K K =--='=--=',12,
31
所以,观测器的反馈增益为[]T Z K 12=
[]??
?
???--=-??????-??????=-122312120001C K A Z 观测器方程为
u y z z z z ???
???+??????+???????????
?---=??????111212232121&&