初中数学——求几何面积的方法
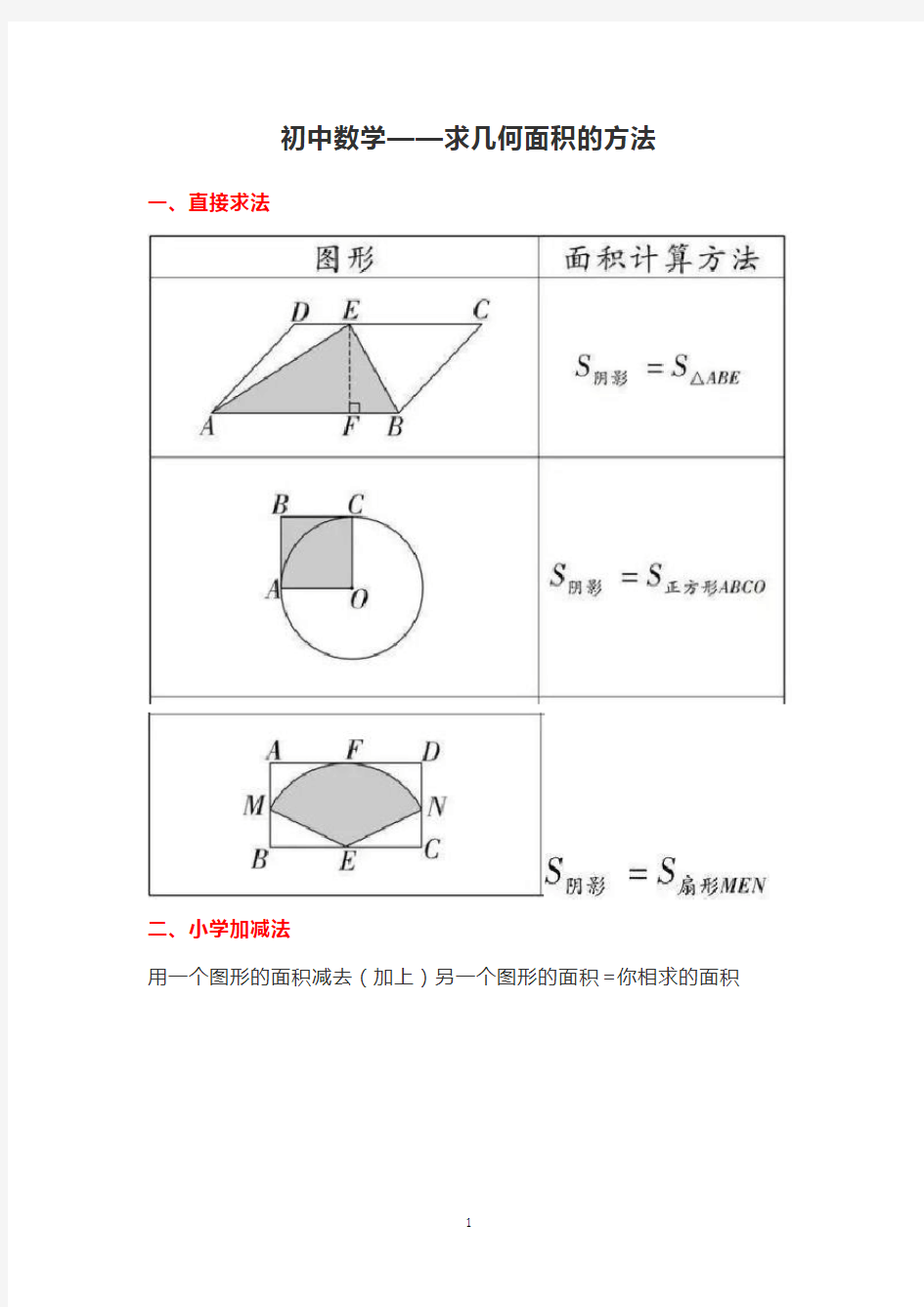
一、直接求法
二、小学加减法
用一个图形的面积减去(加上)另一个图形的面积=你相求的面积
三、神笔马良
发现运用加减法已经无法得出答案的时候
记得机会是给有准备的人的,试着画条辅助线,然后试着运用上面第二种方法。
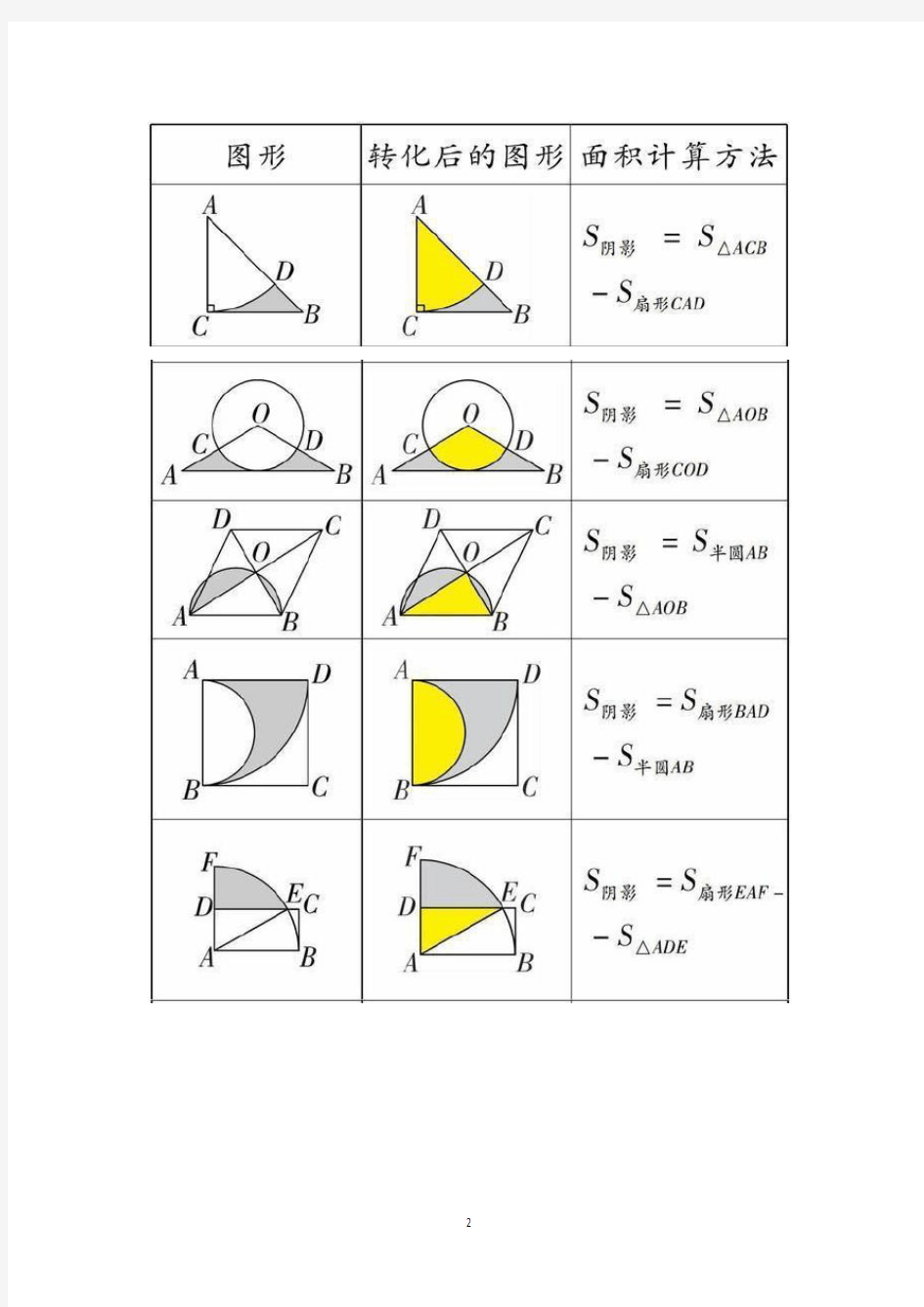
四、乾坤大挪移
BOC
AOC S S S ?+=扇形阴影
小结:(一)解决面积问题常用的理论依据
1、三角形的中线把三角形分成两个面积相等的部分。
2、同底同高或等底等高的两个三角形面积相等。
3、平行四边形的对角线把其分成两个面积相等的部分。
4、同底(等底)的两个三角形面积的比等于高的比。同高(或等高)的两个三角形
面积的比等于底的比。
5、基本几何图形面积公式:三角形、平行四边形、、菱形、矩形、梯形、圆、扇形。
6、相似三角形面积之比等于相似比的平方
7、反比例函数中k的几何含义
8、在直角坐标系中函数图像构成的图形面积常常利用图形顶点的坐标构造高去求面积
(二)证明面积问题常用的证题思路和方法
1、分解法:通常把一个复杂的图形,分解成几个三角形。
2、补全法:通过平移、旋转、翻折变换把分散的图形拼成一个规则的几何基本图形
3、作平行线法:通过平行线找出同高(或等高)的三角形
与圆有关的阴影部分的面积 [自学笔记] 1. 圆心角为n °,半径为R 的扇形的面积为 2. 半径为r 的圆的面积为 3. 弓形的面积为 4. 边长为a 的等边三角形的面积为 [自学检测] 1.图中阴影部分的面积为 2. 如图,扇形AOB 的圆心角为直角,若OA =2,以AB 为直径作半圆,则阴影部分的面积为 3. 如图,在正方形ABCD 中,以A 为顶点作等边△AEF ,交BC 边于E ,交DC 边于F ;又以A 为圆心,AE 的长为半径作弧EF 。若△AEF 4.如图,三个小正方形的边长都是1,则图中阴影部分面积和是 5. 在两个同心圆中,三条直径把大圆分成相等的六部分,若大圆半径为 2,则阴影部分的面积为
6. 如图,AB 是⊙O 的直径,弦CD ⊥AB ,∠CDB=30°,CD= 32 ,则阴影部分图形的面积为( ) A .4π B 2π C.π D 3 2π 7. 如图,圆O 的半径为1cm,正六边形ABCDEF 内接于圆O,则图中阴影部分面积为 cm2 8. 在?ABC 中,∠BAC=90°,AB=AC=2,以AB 为直径的圆交BC 于D ,则图中阴影部分的面积为 9. 矩形ABCD 中,BC=2,DC=4,以AB 为直径的半圆O 与DC 相切于点E,则阴影部分的面积是 [基础夯实] 1.正方形ABCD 边长为2,以C 点为圆心,AC 长为半径作弧,则图中阴影部分的面积为 . 2..如图,⊙A 、⊙B 、⊙C 相外离,它们的半径都是1,顺次连接三个圆心得到△ABC ,则图中三个扇形(阴影部分)的面积之和是 . 3.某种商品的商标图案如图(阴影部分) 已知菱形ABCD 的边长为4,∠A=60°,弧BD 是以A 为圆心AB 长为半径的弧,弧DC 是以B 为圆心BC 为半径的弧,则该商标图案的面积为 [解惑提升] D C
初中数学之求阴影面积方法总结 一、公式法 这属于最简单的方法,阴影面积是一个常规的几何图形,例如三角形、正方形等等。简单举出2个例子: 二、和差法 攻略一直接和差法 这类题目也比较简单,属于一目了然的题目。只需学生用两个或多个常见的几何图形面积进行加减。
攻略二构造和差法 从这里开始,学生就要构建自己的数学图形转化思维了,学会通过添加辅助线进行求解。 三、割补法 割补法,是学生拥有比较强的转化能力后才能轻松运用的,否则学生看到这样的题目还是会无从下手。尤其适用于直接求面积较复杂或无法计算时,通过对图形的平移、旋转、割补等,为利用公式法或和差法求解创造条件。 攻略一全等法
攻略二对称法
攻略三平移法
攻略四旋转法 小结:(一)解决面积问题常用的理论依据 1、三角形的中线把三角形分成两个面积相等的部分。 2、同底同高或等底等高的两个三角形面积相等。 3、平行四边形的对角线把其分成两个面积相等的部分。 4、同底(等底)的两个三角形面积的比等于高的比。同高(或等高)的两个三角形面积的比等于底的比。 5、基本几何图形面积公式:三角形、平行四边形、、菱形、矩形、梯形、圆、扇形。 6、相似三角形面积之比等于相似比的平方 7、反比例函数中k的几何含义 8、在直角坐标系中函数图像构成的图形面积常常利用图形顶点的坐标构造高去求面积 (二)证明面积问题常用的证题思路和方法 1、分解法:通常把一个复杂的图形,分解成几个三角形。 2、补全法:通过平移、旋转、翻折变换把分散的图形拼成一个规则的几何基本图形 3、作平行线法:通过平行线找出同高(或等高)的三角形。
初中数学几何最值问题 典型例题 TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-
初中数学《最值问题》典型例题 一、解决几何最值问题的通常思路 两点之间线段最短; 直线外一点与直线上所有点的连线段中,垂线段最短; 三角形两边之和大于第三边或三角形两边之差小于第三边(重合时取到最值) 是解决几何最值问题的理论依据,根据不同特征转化是解决最值问题的关键.通过转化减少变量,向三个定理靠拢进而解决问题;直接调用基本模型也是解决几何最值问题的高效手段. 1.如图:点P 是∠AOB 内一定点,点M 、N 分别在边OA 、OB 上运动,若∠AOB =45°,OP =PMN 的周长的最小值为 . 【分析】作P 关于OA ,OB 的对称点C ,D .连接OC ,OD .则当M ,N 是CD 与OA ,OB 的交点时,△PMN 的周长最短,最短的值是CD 的长.根据对称的性质可以证得:△COD 是等腰直角三角形,据此即可求解. 【解答】解:作P 关于OA ,OB 的对称点C ,D .连接OC ,OD .则当M ,N 是CD 与OA ,OB 的交点时,△PMN 的周长最短,最短的值是CD 的长. ∵PC 关于OA 对称, ∴∠COP =2∠AOP ,OC =OP 同理,∠DOP =2∠BOP ,OP =OD ∴∠COD =∠COP +∠DOP =2(∠AOP +∠BOP )=2∠AOB =90°,OC =OD . ∴△COD 是等腰直角三角形. 则CD OC . 【题后思考】本题考查了对称的性质,正确作出图形,理解△PMN 周长最小的条件是解题的关键. 2.如图,当四边形PABN 的周长最小时,a = .
初中数学几何最值问题综合测试卷 一、单选题(共6道,每道16分) 1.如图,已知∠MON=40°,P为∠MON内一定点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,求∠APB的度数为( ) A.100° B.110° C.140° D.80° 答案:A 解题思路:作定点P关于直线OM,ON的对称点,然后利用两点之间线段最短解题. 试题难度:三颗星知识点:最值问题 2.如图,当四边形PABN的周长最小时,a的值为( ) A. B.1 C.2 D. 答案:A 解题思路:先平移AP或BN使P,N重合,然后作其中一个定点关于定直线l的对称点,然后利用两点之间线段最短解题. 试题难度:三颗星知识点:最值问题 3.如图,已知两点A,B在直线l的异侧,A到直线l的距离AC=6,B到直线l的距离BD=2,CD=3,点
P在直线l上运动,则的最大值为( ) A. B.3 C.1 D.5 答案:D 解题思路:作其中一个定点关于定直线l的对称点,然后利用三角形三边关系解题. 试题难度:三颗星知识点:最值问题 4.如图,直角梯形纸片ABCD中,AD⊥AB,AB=4,AD=2,CD=3,点E,F分别在线段AB,AD上,将△AEF 沿EF翻折,点A的落点记为P.当点P落在直角梯形ABCD内部时,PD的最小值为( ) A.2 B.1 C. D.3 答案:C 解题思路:找运动过程中的不变特征进行转化,转化成求DP+PE+EB的最大值,减少变量,然后利用两点之间线段最短来解题. 试题难度:三颗星知识点:最值问题 5.如图,∠MON=90°,等腰Rt△ABC的顶点A,B分别在OM,ON上,当点B在ON上运动时,点A
初中数学之求阴影面积 方法总结 Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】
初中数学之求阴影面积方法总结一、公式法 这属于最简单的方法,阴影面积是一个常规的几何图形,例如三角形、正方形等等。简单举出2个例子: 二、和差法 攻略一直接和差法 这类题目也比较简单,属于一目了然的题目。只需学生用两个或多个常见的几何图形面积进行加减。 攻略二构造和差法 从这里开始,学生就要构建自己的数学图形转化思维了,学会通过添加辅助线进行求解。 三、割补法 割补法,是学生拥有比较强的转化能力后才能轻松运用的,否则学生看到这样的题目还是会无从下手。尤其适用于直接求面积较复杂或无法计算时,通过对图形的平移、旋转、割补等,为利用公式法或和差法求解创造条件。 攻略一全等法 攻略二对称法 攻略三平移法 攻略四旋转法 小结:(一)解决面积问题常用的理论依据 1、三角形的中线把三角形分成两个面积相等的部分。 2、同底同高或等底等高的两个三角形面积相等。 3、平行四边形的对角线把其分成两个面积相等的部分。 4、同底(等底)的两个三角形面积的比等于高的比。同高(或等高)的两个三角形面积的比等于底的比。 5、基本几何图形面积公式:三角形、平行四边形、、菱形、矩形、梯形、圆、扇形。 6、相似三角形面积之比等于相似比的平方 7、反比例函数中k的几何含义 8、在直角坐标系中函数图像构成的图形面积常常利用图形顶点的坐标构造高去求面积 (二)证明面积问题常用的证题思路和方法 1、分解法:通常把一个复杂的图形,分解成几个三角形。
2、补全法:通过平移、旋转、翻折变换把分散的图形拼成一个规则的几何基本图形 3、作平行线法:通过平行线找出同高(或等高)的三角形。
阴影部分的面积专题 解题方法: 1、熟悉三角形、四边形、圆、扇形面积的公式 2、利用各种图形面积之间的相加或相减的办法 一、选择 1、如图,圆的半径是6,空白部分的圆心角分别是60°与 30°,则阴影部分的面积是 ( ) A 、9π B 、27π C 、6π D 、3π 2. 如图1,扇形OAB 的圆心角为90,且半径为1,分别以OA ,OB 为 直径在扇形内作半圆,P 和Q 分别表示两个阴影部分的面积, 那么P 和Q 的大小关系是( ) A.P Q = B.P Q > C.P Q < D.无法确定 3. 如图2,矩形ABCD 中,1AB =,3BC =,以BC 的中点 为圆心的MPN 与AD 相切,则图中的阴影部分的面积为( ) A.23π B.34π C.3 π D.π3 4. 如图,△ABC 中,105A ∠=,45B ∠=,22AB =,AD BC ⊥,为垂足,以为圆心,以AD 为半径画弧EF ,则图中阴影部分的面积为( ) A.7236- π B.7 236- π+2 C.5 236 -π D.5 236 -π+2 5.如图两个同心圆的圆心为0,大圆的弦AB 切小圆于点P ,两圆的半径分别为6,3则图中阴影部分的面积为( ) A 、93-π B 、63-π C 、93-3π D 、63-2π Q O A P C C N D P A M C D B E A F
O E F B C D A A A ' P O Q B O ' B ' A D E 二、填空 1.如图,在Rt △ABC 中,∠C=90°,CA=CB=2。分别以A 、B 、C 为圆心, 以 2 1 AC 为半径画弧,三条弧与边AB 所围成的阴影部分的面积是______. 3. 如图,AB 是半圆O 的直径,以O 为圆心,OE 为半径的半圆交AB 于,两点,弦AC 是小半圆的切线,为切点,若4OA =,2OE =,则图中阴影部分的面积为 . 3 4 5 4. 如图,两个半径为1,圆心角是90的扇形OAB 和扇形O A B '''叠放在一起,点O '在AB 上,四边形OPO Q '是正方形,则阴影部分的面积等于 . 5.在△ABC 中,AB=AC=2cm , ∠B=300,以A 为圆心,AB 为半径BEC , 以BC 为直径作半圆BFC .则商标图案面积等于 7.如图,圆心角都是90°的扇形OAB 与扇形OCD 叠放在一起,OA=3,OC=1,分别连结AC 、BD ,则图中阴影部分的面积为 A B C D 7 8 9 8.如图,A 是半径为2的⊙O 外一点,OA=4,AB 是⊙O 的切线,点B 是切点,弦BC ∥OA ,连结AC ,则图中阴影部分的面积为_________. 9.如图,两个半圆中,长为6的弦CD 与直径AB 平行且与小半圆相切,那么图中阴影部分的面积等于_____. 10、如图,以正方形ABCD 的边AD 、BC 、CD 为直径画半圆,阴影部分的面积记为m ,空白部分的面积记为 n ,则m 与n 的关系为_____________. 11、如图,正方形ABCD 边长为4,以BC 为直径的半圆O 交对角线BD 于E .则直线CD 与⊙O 的位置关系是 ,阴影部分面积为 .
“最值问题”集锦 ●平面几何中的最值问题 (01) ●几何的定值与最值 (07) ●最短路线问题 (14) ●对称问题 (18) ●巧作“对称点”妙解最值题 (22) ●数学最值题的常用解法 (26) ●求最值问题 (29) ●有理数的一题多解 (34) ●4道经典题 (37) ●平面几何中的最值问题 在平面几何中,我们常常遇到各种求最大值和最小值的问题,有时它和不等式联系在一起,统称最值问题.如果把最值问题和生活中的经济问题联系起来,可以达到最经济、最节约和最高效率.下面介绍几个简例. 在平面几何问题中,当某几何元素在给定条件变动时,求某几何量(如线段的长度、图形的面积、角的度数)的最大值或最小值问题,称为最值问题。 最值问题的解决方法通常有两种: (1)应用几何性质: ①三角形的三边关系:两边之和大于第三边,两边之差小于第三边; ②两点间线段最短; ③连结直线外一点和直线上各点的所有线段中,垂线段最短; ④定圆中的所有弦中,直径最长。 ⑵运用代数证法: ①运用配方法求二次三项式的最值; ②运用一元二次方程根的判别式。 例1、A、B两点在直线l的同侧,在直线L上取一点P,使PA+PB最小。 分析:在直线L上任取一点P’,连结A P’,BP’,
在△ABP’中AP’+BP’>AB,如果AP’+BP’=AB,则P’必在线段AB上,而线段AB 与直线L无交点,所以这种思路错误。 取点A关于直线L的对称点A’,则AP’= AP, 在△A’BP中A’P’+B’P’>A’B,当P’移到A’B与直线L的交点处P点时 A’P’+B’P’=A’B,所以这时PA+PB最小。 1 已知AB是半圆的直径,如果这个半圆是一块铁皮,ABDC是内接半圆的梯形,试问怎样剪这个梯形,才能使梯形ABDC的周长最大(图3-91)? 分析本例是求半圆AB的内接梯形的最大周长,可设半圆半径为R.由于AB∥CD,必有AC=BD.若设CD=2y,AC=x,那么只须求梯形ABDC的半周长u=x+y+R的最大值即可.解作DE⊥AB于E,则x2=BD2=AB·BE=2R·(R-y)=2R2-2Ry, 所以 所以求u的最大值,只须求-x2+2Rx+2R2最大值即可. -x2+2Rx+2R2=3R2-(x-R)2≤3R2, 上式只有当x=R时取等号,这时有 所以2y=R=x. 所以把半圆三等分,便可得到梯形两个顶点C,D, 这时,梯形的底角恰为60°和120°. 2 .如图3-92是半圆与矩形结合而成的窗户,如果窗户的周长为8米(m),怎样才能得出 最大面积,使得窗户透光最好? 分析与解设x表示半圆半径,y表示矩形边长AD,则必有2x+2y+πx=8,
初中数学《最值问题》典型例题 一、解决几何最值问题的通常思路 两点之间线段最短; 直线外一点与直线上所有点的连线段中,垂线段最短; 三角形两边之和大于第三边或三角形两边之差小于第三边(重合时取到最值) 是解决几何最值问题的理论依据,根据不同特征转化是解决最值问题的关键.通过转化减少变量,向三个定理靠拢进而解决问题;直接调用基本模型也是解决几何最值问题的高效手段. 轴 对 称 最 值 图形 l P B A N M l B A A P B l 原理两点之间线段最短两点之间线段最短三角形三边关系 特征 A,B为定点,l为定直 线,P为直线l上的一 个动点,求AP+BP的 最小值 A,B为定点,l为定直线, MN为直线l上的一条动线 段,求AM+BN的最小值 A,B为定点,l为定直线, P为直线l上的一个动 点,求|AP-BP|的最大值转化 作其中一个定点关于定 直线l的对称点 先平移AM或BN使M,N 重合,然后作其中一个定 点关于定直线l的对称点 作其中一个定点关于定 直线l的对称点 折 叠 最 值 图形 B' N M C A B 原理两点之间线段最短 特征 在△ABC中,M,N两点分别是边AB,BC上的动点,将△BMN沿MN翻折, B点的对应点为B',连接AB',求AB'的最小值. 转化转化成求AB'+B'N+NC的最小值 1.如图:点P是∠AOB内一定点,点M、N分别在边OA、OB上运动,若∠AOB=45°,OP=32,则△PMN 的周长的最小值为. 【分析】作P关于OA,OB的对称点C,D.连接OC,OD.则当M,N是CD与OA,OB的交点时,△PMN 的周长最短,最短的值是CD的长.根据对称的性质可以证得:△COD是等腰直角三角形,据此即可求解.【解答】解:作P关于OA,OB的对称点C,D.连接OC,OD.则当M,N是CD与OA,OB的交点时,△PMN的周长最短,最短的值是CD的长. ∵PC关于OA对称, ∴∠COP=2∠AOP,OC=OP 同理,∠DOP=2∠BOP,OP=OD
知识板块 考点一:几何图形中的最小值问题 方法: 1.找对称点求线段的最小值; 步骤:①找已知点的对称点,动点在哪条线上动,就是对称轴; ②连接对称点与另一个已知点; ③与对称轴的交点即是要找的点;通常用勾股定理求线段长; 2.利用三角形三边关系:两边之差小于第三边; 3.转化成其他线段,间接求线段的最小值;例如:用点到直线的距离最短,通过作垂线求最值; 4.用二次函数中开口向上的函数有最小值; 考点二:几何图形中的最大值问题 方法: 1.当两点位于直线的同侧时,与动点所在的直线的交点,这三点在同一直线时,线段差有最大值; 2.当两点位于直线的异侧时,先找对称点,同样三点位于同一直线时,线段差有最大值; 3.利用三角形三边关系:两边之和大于第三边; 4.用二次函数中开口向下的函数有最大值; 例题板块 考点一:几何图形中的最小值问题 例1.如图1,在正方形ABCD 中,E 是AB 上一点,BE=2,AE=3BE ,P 是AC 上一动点,则PB+PE 的最小值是 _________ . 图1 图2 图3 例2.如图2,在锐角△ABC 中,AB=4,∠BAC=45°,∠BAC 的平分线交BC 于点D ,M 、N 分别是AD 和AB 上的动点,则BM+MN 的最小值是 . 例3.如图3,点P 是Rt △ABC 斜边AB 上的一点,PE ⊥AC 于E ,PF ⊥BC 于F ,BC=6,AC=8,则线段EF 长的最小值为 ; 第一节 几何最值问题专项
例4.如图,在Rt △ABC 中,AB=BC=6,点E ,F 分别在边AB ,BC 上,AE=3,CF=1,P 是斜边AC 上的一个动点,则△PEF 周长的最小值为 . 图4 图5 例5.如图,在平面直角坐标系中,Rt △OAB 的顶点A 的坐标为(9,0),点C 的坐标为(2,0),tan ∠BOA= A .67 B .231 C. 6 D .193+ 例6.如图6,等腰Rt △ABC 中,∠ACB=90°,AC=BC=4,⊙C 的半径为1,点P 在斜边AB 上,PQ 切⊙O 于点Q ,则切线长PQ 长度的最小值为( ) 图6 图7 图8 例7.如图7,矩形ABCD 中,AB=4,BC=8,E 为CD 的中点,点P 、Q 为BC 上两个动点,且PQ=3,当CQ= _________ 时,四边形APQE 的周长最小. 考点二:几何图形中的最大值问题 例1.已知点A (1,2)、B (4,-4),P 为x 轴上一动点. (1)若|PA |+|PB |有最小值时,求点P 的坐标; (2)若|PB |-|PA |有最大值时,求点P 的坐标. 例2.如图8所示,已知A 11 (,y )2,B 2(2,y )为反比例函数1y x =图像上的两点,动点P (x,0)在x 正半轴上运动,当线段AP 与线段BP 之差达到最大时,点P 的坐标是 .
几何的定值与最值 几何中的定值问题,是指变动的图形中某些几何元素的几何量保持不变,或 几何元素间的某些几何性质或位置关系不变的一类问题,解几何定值问题的基本 方法是:分清问题的定量及变量,运用特殊位置、极端位置,直接计算等方法, 先探求出定值,再给出证明. 几何中的最值问题是指在一定的条件下,求平面几何图形中某个确定的量 (如线段长度、角度大小、图形面积)等的最大值或最小值,求几何最值问题的基 本方法有: 1.特殊位置与极端位置法; 2.几何定理(公理)法; 3.数形结合法等. 注:几何中的定值与最值近年广泛出现于中考竞赛中,由冷点变为热点.这 是由于这类问题具有很强的探索性(目标不明确),解题时需要运用动态思维、数 形结合、特殊与一般相结合、 逻辑推理与合情想象相结合等思想方法. 【例题就解】 【例1】 如图,已知AB=10,P 是线段AB 上任意一点,在AB 的同侧分别以 AP 和PB 为边作等边△APC 和等边△BPD ,则CD 长度的最小值为 . 思路点拨 如图,作CC ′⊥AB 于C ,DD ′⊥AB 于D ′, DQ ⊥CC ′,CD 2=DQ 2+CQ 2,DQ=2 1AB 一常数,当CQ 越小,CD 越小, 本例也可设AP=x ,则PB=x 10,从代数角度探求CD 的最小值. 注:从特殊位置与极端位置的研究中易得到启示,常能找到解题突破口,特 殊位置与极端位置是指: (1)中点处、垂直位置关系等; (2)端点处、临界位置等. 【例2】 如图,圆的半径等于正三角形ABC 的高,此圆在沿底边AB 滚动,切点为T ,圆交AC 、BC 于M 、N ,则对于所有可能的圆的位置而言, MTN 为的度 数( ) ⌒
初中数学复习(圆) 1、已知:如图,AB为半圆⊙O的直径,C、D为半圆⊙O的三等分点,若AB=12,求阴影部分的面积。 2、如图,已知:∠AOB=90°,AC∥OB,AO=3,分别以O点,A点为圆心,AO、AB为半径画弧,交OB、AC于B、C,求阴影部分的周长和面积。 3、如图,已知半径分别为1和3的⊙O1和⊙O2外切于P,AB切二圆于A、B两点,求图中阴影部分的面积。 4、如图,已知:⊙O1与⊙O2相交于B、D,AB为⊙O1直径,BC=AD,若AB=12,DE=30,求圆中阴影部分的面积。 6、一个扇形的半径等于一个圆的半径的2倍,如果这个扇形的面积与圆的面积相等,则这个扇形的圆心角等于( ) A.180° B.90° C.45° D.22.5° π,则大圆的面积为,小圆的面积为7、两圆的半径之比为3∶5,面积相差32 ;正三角形的内切圆与外接圆的面积之比为。 8、圆心角为40°,半径为6的扇形的面积为; 半径为3,弧长为4的扇形的面积为; 弧长为2π,面积为4π的扇形的半径为,圆心角为; 圆心角为60°,弧长为6π的扇形的半径为,面积为。
9、如图,四个等圆两两外切,半径均为2cm ,且∠O 2O 1O 4=90°,求图中的阴影部分的面 积为S 。 10、已知扇形的圆心角为60°,面积为6π,求这个扇形的周长。 11、如图,在菱形ABCD 中,AC 与BD 相交于点O ,AC=4,34BD = ,以B 为圆心,BO 为 半径画弧交AB 于E ,交BC 于F ,以D 为圆心,DO 为半径画弧交AD 于G ,交DC 于H ,求阴影部分的面积S 。 12、如图,PA 、PB 是⊙O 的切线,A 、B 是切点,∠P=60°,AB=12,求阴影部分的面积。 13如图,已知△ABC 中,∠C=90°,AC=8,BC=6,M 为AB 的中点,分别以A 、B 为圆心,AM 为 半径画弧交AC 于D ,交BC 于E ,求阴影部分的面积。
六年级阴影部分的面积 1.求阴影部分的面积。(单位:厘米) 解:割补后如右图,易知,阴影部分面积为一个梯形。梯形上底DE=7-4=3厘米, 1S =S =DE AB)AD 2?+?阴梯形(=1 37)42 ?+?(=20(平方厘米) 2、求阴影部分的面积。 解:S =S 阴梯形,梯形的上底是圆的直径,下底、高是 圆的半径,S =S 阴梯形=1 24)22 ?+?(=6(2cm ) 3、如图,平行四边形的高是6厘米,面积是54平方厘米,求阴影三角形的面积。 解:S =AD AO ?ABCD =54平方厘米,且AO=6厘米,所以AD=9厘米。由图形可知AED ?是等腰直角三角形,所以AE=AD ,OE=OF=AE-AO=9-6=3cm ,BO=BC-OC=9-3=6cm 。 1S =BO OF 2??阴=1 S =632??阴=92cm 。
4、如图是一个平行四边形,面积是50平方厘米,求阴影积分的面积。 解:方法一:过C 点作CF AD ⊥交AD 于点F ,可知AECF 是长方形,面积=5×6=302cm ,ABE CFD S =S ??=(50-30)÷2=102cm 。 方法二:BC=S ABCD ÷AE=50÷5=10cm ,BE=BC-EC=10-6=4cm ,ABE S ?=BE ×AE ÷2 =4×5÷2=102cm 5、下图是一个半圆形,已知AB=10厘米,阴影部分的面积为24.25平方厘米,求图形中三角形的高。 解:S =S -S ?阴半圆=2 1AB 22π???? ? ??-24.25 =2 1103.1422?? ?? ???-24.25=152cm , 三角形的高=2S ?÷AB=2×15÷10=3cm 。 6、如图,一个长方形长是10cm ,宽是4cm ,以A 点和C 点为圆心各画一个扇形,求画中阴影部分的面积是多少平方厘米? 解:BECD 1S =S -S 4阴大圆=ABCD 11S -S S 44?? - ??? 大圆小圆 =ABCD 11S +S -S 44大圆小圆=()221 3.1410-4-1044??? =25.942cm 。
一.压轴题专项训练 25.阅读材料: (1)对于任意两个数a b 、的大小比较,有下面的方法: 当0a b ->时,一定有a b >; 当0a b -=时,一定有a b =; 当0a b -<时,一定有a b <. 反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”. (2)对于比较两个正数a b 、的大小时,我们还可以用它们的平方进行比较: ∵22()()a b a b a b -=+-,0a b +> ∴(22a b -)与(a b -)的符号相同 当22a b ->0时,a b ->0,得a b >; 当22a b -=0时,a b -=0,得a b = 当22a b -<0时,a b -<0,得a b < 解决问题: (1)课堂上,老师让同学们制作几种几何体,张丽同学用了3张A4纸,7张B5纸;李明 同学用了2张A4纸,8张B5纸.设每张A4纸的面积为x ,每张B5纸的面积为y ,且x >y ,张丽同学的用纸总面积为W 1,李明同学的用纸总面积为W 2.回答下列问题: ① W 1= (用x 、y 的式子表示),W 2= (用x 、y 的式子表示) ② 请你分析谁用的纸面积最大. (2)如图1所示,要在燃气管道l 上修建一个泵站,分别向A .B 两镇供气,已知A 、B 到 l 的距离分别是3km 、4km (即AC =3km ,BE =4km ),AB =x km ,现设计两种方案: 方案一:如图2所示,AP ⊥l 于点P ,泵站修建在点P 处,该方案中管道长度1a AB AP =+. 方案二:如图3所示,点A ′与点A 关于l 对称,A ′B 与l 相交于点P ,泵站修建在点P 处,该方案中管道长度. ① 在方案一中,a 1= km (用含x 的式子表示); ② 在方案二中,a 2= km 用含x 的式子表示); ③ 请你分析要使铺设的输气管道较短,应选择方案一还是方案二.
最新人教版六年级数学几何典型题解:阴影部分的面积 1.求阴影部分的面积。(单位:厘米) 解:割补后如右图,易知,阴影部分面积为一个梯形。梯形上底DE=7-4=3厘米, 1S =S =DE AB)AD 2?+?阴梯形(=1 37)42 ?+?(=20(平方厘米) 2、求阴影部分的面积。 解:S =S 阴梯形,梯形的上底是圆的直径,下底、高是 圆的半径,S =S 阴梯形=1 24)22 ?+?(=6(2cm ) 3、如图,平行四边形的高是6厘米,面积是54平方厘米,求阴影三角形的面积。 解:S =AD AO ?ABCD =54平方厘米,且AO=6厘米,所以AD=9厘米。由图形可知AED ?是等腰直角三角形,所以AE=AD ,OE=OF=AE-AO=9-6=3cm ,BO=BC-OC=9-3=6cm 。 1S =BO OF 2??阴=1 S =632??阴=92cm 。
4、如图是一个平行四边形,面积是50平方厘米,求阴影积分的面积。 解:方法一:过C 点作CF AD ⊥交AD 于点F ,可知AECF 是长方形,面积=5×6=302cm ,ABE CFD S =S ??=(50-30)÷2=102cm 。 方法二:BC=S ABCD ÷AE=50÷5=10cm ,BE=BC-EC=10-6=4cm ,ABE S ?=BE ×AE ÷2 =4×5÷2=102cm 5、下图是一个半圆形,已知AB=10厘米,阴影部分的面积为24.25平方厘米,求图形中三角形的高。 解:S =S -S ?阴半圆=2 1AB 22π???? ? ??-24.25 =2 1103.1422?? ?? ???-24.25=152cm , 三角形的高=2S ?÷AB=2×15÷10=3cm 。 6、如图,一个长方形长是10cm ,宽是4cm ,以A 点和C 点为圆心各画一个扇形,求画中阴影部分的面积是多少平方厘米? 解:BECD 1S =S -S 4阴大圆=ABCD 11S -S S 44?? - ??? 大圆小圆 =ABCD 11S +S -S 44大圆小圆=()221 3.1410-4-1044??? =25.942cm 。
初中数学最值问题专题分类讲解全书 ●平面几何中的最值问题 ●几何的定值与最值 ●最短路线问题 ●对称问题 ●巧作―对称点‖妙解最值题 ●数学最值题的常用解法 ●求最值问题 ●有理数的一题多解
●平面几何中的最值问题 在平面几何中,我们常常遇到各种求最大值和最小值的问题,有时它和不等式联系在一起,统称最值问题.如果把最值问题和生活中的经济问题联系起来,可以达到最经济、最节约和最高效率.下面介绍几个简例. 在平面几何问题中,当某几何元素在给定条件变动时,求某几何量(如线段的长度、图形的面积、角的度数)的最大值或最小值问题,称为最值问题。 最值问题的解决方法通常有两种: (1)应用几何性质: ①三角形的三边关系:两边之和大于第三边,两边之差小于第三边; ②两点间线段最短; ③连结直线外一点和直线上各点的所有线段中,垂线段最短; ④定圆中的所有弦中,直径最长。 ⑵运用代数证法: ①运用配方法求二次三项式的最值; ②运用一元二次方程根的判别式。 例1、A、B两点在直线l的同侧,在直线L上取一点P,使PA+PB最小。 分析:在直线L上任取一点P’,连结A P’,BP’, 在△ABP’中AP’+BP’>AB,如果AP’+BP’=AB,则P’必在线段AB上,而线段AB与直线L无交点,所以这种思路错误。 取点A关于直线L的对称点A’,则AP’=AP,
在△A’BP中A’P’+B’P’>A’B,当P’移到A’B与直线L的交点处P点时A’P’+B’P’=A’B,所以这时PA+PB最小。 1 已知AB是半圆的直径,如果这个半圆是一块铁皮,ABDC是内接半圆的梯形,试问怎样剪这个梯形,才能使梯形ABDC的周长最大(图3-91)? 分析本例是求半圆AB的内接梯形的最大周长,可设半圆半径为R.由于AB∥CD,必有AC=BD.若设CD=2y,AC=x,那么只须求梯形ABDC的半周长u=x+y+R的最大值即可. 解作DE⊥AB于E,则x2=BD2=AB·BE=2R·(R-y)=2R2-2Ry, 所以 所以求u的最大值,只须求-x2+2Rx+2R2最大值即可. -x2+2Rx+2R2=3R2-(x-R)2≤3R2, 上式只有当x=R时取等号,这时有 所以2y=R=x. 所以把半圆三等分,便可得到梯形两个顶点C,D, 这时,梯形的底角恰为60°和120°. 2 .如图3-92是半圆与矩形结合而成的窗户,如果窗户的周长为8米(m),怎样才能得出 最大面积,使得窗户透光最好?
中考压轴题突破:几何最值问题大全(将军饮马、造桥选址、胡 不归、阿波罗尼斯圆等) 一、基本图形 所有问题的老祖宗只有两个:①[定点到定点]:两点之间,线段最短;②[定点到定线]:点线之间,垂线段最短。 由此派生:③[定点到定点]:三角形两边之和大于第三边;④[定线到定线]:平行线之间,垂线段最短;⑤[定点到定圆]:点圆之间,点心线截距最短(长);⑥[定线到定圆]:线圆之间,心垂线截距最短;⑦[定圆到定圆]:圆圆之间,连心线截距最短(长)。 余不赘述,下面仅举一例证明:[定点到定圆]:点圆之间,点心线截距最短(长)。 已知⊙O半径为r,AO=d,P是⊙O上一点,求AP的最大值和最小值。
证明:由“两点之间,线段最短”得AP≤AO+PO,AO≤AP+PO,得d-r≤AP≤d+r,AP最小时点P在B处,最大时点P在C处。即过圆心和定点的直线截得的线段AB、AC分别最小、最大值。(可用“三角形两边之和大于第三边”,其实质也是由“两点之间,线段最短”推得)。 上面几种是解决相关问题的基本图形,所有的几何最值问题都是转化成上述基本图形解决的。 二、考试中出现的问题都是在基本图形的基础上进行变式,如圆与线这些图形不是直接给出,而是以符合一定条件的动点的形式确定的;再如过定点的直线与动点所在路径不相交而需要进行变换的。类型分三种情况:(1)直接包含基本图形;(2)动点路径待确定;(3)动线(定点)位置需变换。 (一)直接包含基本图形 例1.在⊙O中,圆的半径为6,∠B=30°,AC是⊙O的切线,则CD的最小值是。
简析:由∠B=30°知弧AD一定,所以D是定点,C是直线AC上的动点,即为求定点D到定线AC的最短路径,求得当CD⊥AC时最短为3。 (二)动点路径待确定 例2.,如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是。 简析:A是定点,B'是动点,但题中未明确告知B'点的运动路径,所以需先确定B'点运动路径是什么图形,一般有直线与圆两类。此题中B'的路径是以C为圆心,BC为半径的圆弧,从而转化为定点到定圆的最短路径为AC-B'C=1。 例3.在△ABC中,AB=AC=5,cos∠ABC=3/5,将△ABC绕点C顺时针旋转,得到△A'B'C,点E是BC上的中点,点F为线段AB上
一、基本图形 余不赘述,下面仅举一例证明: [定点到定圆]:点圆之间,点心线截距最短(长)。 已知⊙O半径为r,AO=d,P是⊙O上一点,求AP的最大值和最小值。
证明:由“两点之间,线段最短”得AP≤AO+PO, AO≤AP+PO,得d-r≤AP≤d+r,AP最小时点P在B处,最大时点P在C处。即过圆心和定点的直线截得的线段AB、AC分别最小、最大值。(可用“三角形两边之和大于第三边”,其实质也是由“两点之间,线段最短”推得)。 上面几种是解决相关问题的基本图形,所有的几何最值问题都是转化成上述基本图形解决的。 二、考试中出现的问题都是在基本图形的基础上进行变式,如圆与线这些图形不是直接给出,而是以符合一定条件的动点的形式确定的;再如过定点的直线与动点所在路径不相交而需要进行变换的。 类型分三种情况:(1)直接包含基本图形;(2)动点路径待确定;(3)动线(定点)位置需变换。 (一)直接包含基本图形。 例1.在⊙O中,圆的半径为6,∠B=30°,AC是⊙O的切线,则CD的最小值是。
简析:由∠B=30°知弧AD一定,所以D是定点,C是直线AC上的动点,即为求定点D到定线AC的最短路径,求得当CD⊥AC时最短为3。 (二)动点路径待确定。 例2.,如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB 边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是。 简析:A是定点,B'是动点,但题中未明确告知B'点的运动路径,所以需先确定B'点运动路径是什么图形,一般有直线与圆两类。此题中B'的路径是以C为圆心,BC为半径的圆弧,从而转化为定点到定圆的最短路径为AC-B'C=1。
中考数学求阴影部分面积的几种常见方法 Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】
阴影部分面积的几种常见方法 在初中数学中,求阴影部分的面积问题是一个重要内容,在近年来的各地中考试题中屡见不鲜.这类试题大多数都是求不规则图形的面积,具有一定的难度,因此,正确把握求阴影部分面积问题的解题方法,显得尤为重要.本文举例介绍解决这类问题的常见方法. 一、直接求解法 例1如图1,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD边落在 AB边上,AD变到AD 1位置,折痕为AE.再将△AED 1 以D 1 E为折痕,向右折叠, AE变到A 1E位置,且A 1 E交BC于点F.求图中阴影部分的面积. 分析因为阴影部分是一个规则的几何图形Rt△CEF,故根据已知条件可以直接计算阴影部分面积. 解如图1,根据对称性可得 AD=AD 1=A 1 D 1 =6. 由已知条件易知: EC=D 1 B=4,BC=6; Rt△FBA 1 ∽Rt△FCE.设FC为x,则FB=6-x.二、间接求解法 例2如图2,⊙O 1与⊙O 2 外切于点C,且两圆分别和直线l相切于A、B两 点,若⊙O 1半径为3cm;⊙O 2 半径为1cm,求阴影部分面积. 分析这是求一个不规则图形的面积,没有现成的面积公式,因此应采用间接的方法,设法转化为规则图形的面积的和或差去计算. 三、整体合并法 例3如图3,⊙A、⊙B、⊙C两两不相交,且半径都是0.5cm,求三个阴影部分面积之和. 分析所求的阴影部分面积是三个扇形面积之和,因为三个扇形圆心角度数不知道,所以无法单独求解,但仔细观察发现,三个扇形的圆心角分别是△ABC的三个内角,其和为180°,而扇形半径都相等,所以三个扇形能合并成一个半圆.于是问题获解. 解如图3,因为三个圆的半径相等,三个扇形圆心角之和是180°,所以其面积就是半圆面积. 四、等积变换法 例4如图4,A是半径为R的⊙O外一点,弦BC为3R,OA∥BC,求阴影部分 面积. 分析本题的阴影部分是不规则的图形,求其面积较困难, 但灵活运用等积变换,就可以把它的面积转化为扇形OBC的面 积,从而获解. 解连接OC,OB, 五、分割法
初中数学几何旋转最值最短路径问题专题训练专练3 最短路径模型——旋转最值类 基本模型图: 【典例1】如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC边上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连 结B′D,则B′D的 最小值是(). A. B.6 C. D.4 【思路探究】根据E为AB中点,BE=B′E可知,点A、B、B′在以点E为圆心,AE长为半径的圆上,D、E为定点,B′是动点,当E、B′、D三点共线时,B′D的长最小,此时B′D=DE-EB′,问题得解. 【解析】∵AE=BE,BE=B′E,由圆的定义可知,A、B、B′在以点E为圆心,AB长为直径的圆上,如图所示. B′D的长最小值= DE-EB′.故选A. 22 -=-
【启示】此题属于动点(B′)到一定点(E )的距离为定值(“定点定长”),联想到以E 为圆心,EB′为半径的定圆,当点D 到圆上的最小距离为点D 到圆心的距离-圆的半径.当然此题也可借助三角形三边关系解决,如,当且仅当点E 、B′、D 三点共线B D DE B E ''≤-时,等号成立. 【典例2】如图,E 、F 是正方形ABCD 的边AD 上两个动点,满足AE =DF ,连接CF 交BD 于点G ,连结BE 交AG 于点H ,若正方形的边长是2,则线段DH 长度的最小值是 . 【思路探究】根据正方形的轴对称性易得∠AHB =90°,故点H 在以AB 为直径的圆上.取AB 中点O ,当D 、H 、O 三点共线时,DH 的值最小,此时DH =OD -OH ,问题得解. 【解析】由△ABE ≌△DCF ,得∠ABE =∠DCF ,根据正方形的轴对称性,可得∠DCF =∠DAG ,∠ABE =∠DAG ,所以∠AHB =90°,故点H 在以AB 为直径的圆弧上.取AB 中 点O ,OD 交⊙O 于点H ,此时DH 最小,∵OH =, OD =,∴DH 的最小值为112 AB =OD -OH . 1【启示】此题属于动点是斜边为定值的直角三角形的直角顶点,联想到直径所对圆周角为直角(定弦定角),故点H 在以AB 为直径的圆上,点D 在圆外,DH 的最小值为DO -OH .当然此题也可利用的基本模型解决. DH OD OH ≤-【针对训练 】 1. 如图,在△ABC 中,∠ACB =90°,AC =2,BC =1,点A ,C 分别在x 轴,y 轴上,当点A 在轴正半轴上运动时,点C 随之在轴上运动,在运动过程中,点B 到原点O 的最大x y 距离为( ). A B C . D .31
初中数学之阴影部分面积 一、直接法 1、如图1,在Rt △ABC 中,∠ABC=90°,AB=8cm,BC=6cm,分别以A 、C 为圆心, 以 2 AC 为半径作圆,将Rt △ABC 截去两个扇形,则剩余(阴影)部分的面积为( )cm 2 A 、24-π425 B 、π425 C 、24-π4 5 D 、24-π625 2、如图2,将△ABC 绕点B 逆时针旋转到△A 1BC 1使A 、B 、C 1在同一直线上, 若∠BCA=90°,∠BAC=30°,AB=4cm,则图2中的阴影部分面积为 cm 2 3、如图3,正方形的边长为a ,以各顶点为圆心,2 1 a 为半径画弧。再以正方形的中心 为圆心, 2 1 a 为半径画圆,则阴影部分的面积等于 二、割补法 4、如图4,△ABC 是直角边长为a 的等腰直角三角形,直角边AB 是半圆O 1的直径, 半圆O 2过C 点且与半圆O 1相切,则图中阴影部分的面积是( ) A 、 2 36 7a π- B 、2365a π- C 、2367a D 、2365a 5、如图5,AB=EF=4cm,BC=AE=3cm,则阴影部分面积为 6、如图6,中的圆均为等圆,且相邻两圆外切,圆心连线构成正三角形, 记各阴影部分面积从左至右依次为S 1,S 2,S 3,…S n ,则S 12:S 4的值等于 三、平移法 7、如图7,平行于y 轴的直线l 被 抛物线y=21x 2+1,y=2 1x 2 -1所截, 当直线l 向右平移3个单位时, 直线l 被两条抛物线所截得的 线段扫过的图形面积为 8、在长为a m,宽为b m 的一块草坪上修一条宽1 m 的笔直小路, 则余下草坪的面积可表示为 m 2 ; 现为了增加美感,把这条小路改为宽恒为1 m 的弯曲小路(如图8) 则余下草坪的面积为 m 2 四、对称法 9、如图9,⊙O 的半径为2,C 1是函数y= 21x 2的图象,C 2是函数y= -2 1x 2 的图象, 则阴影部分的面积是 10、如图10,⊙A 和⊙B 都与x 轴和y 轴相切, 圆心A 和圆心B 都在反比例函数y=x 1 图象上, 则图中阴影部分的面积等于 五、旋转法 11、如图11,半圆O 的直径AB=20,将半圆O 绕着点B 顺时针 旋转54°得到半圆O 1,弧A 1B 交AB 于点P (1)求AP 的长;(2)求图中阴影部分的面积(结果精确到0.1) 图 2 1O 图4 图 5 图6 第1个 第3个 图11 图3