
2017届湖南长沙长郡中学高三入学考试数学(文)试题
一、选择题
1.设全集{|1}U x x =>,集合{|2}A x x =>,则U C A =( ) A .{|12}x x <≤ B .{|12}x x << C .{|2}x x > D .{|2}x x ≤ 【答案】A
【解析】试题分析:{|12}U C A x x =<≤,故选A. 【考点】集合的运算.
2.设i 是虚数单位,则复数25
()2i i
-+=+( ) A .22i - B .1i - C .3i - D .115i -
【答案】B
【解析】试题分析:2
55(2)()11212(2)(2)
i i i i i i i --+=-+=-+-=-++-,故选B. 【考点】复数的运算. 3.已知(cos
,sin )66a π
π=,55(cos ,sin )66
b ππ
=,则||a b -=( ) A .1 B
.2
.2
【答案】C
【解析】
试题分析:因为55(cos
cos
,sin sin )6
666
a b π
πππ
-=--=,所以||3a b -=,故选C.
【考点】向量的坐标运算.
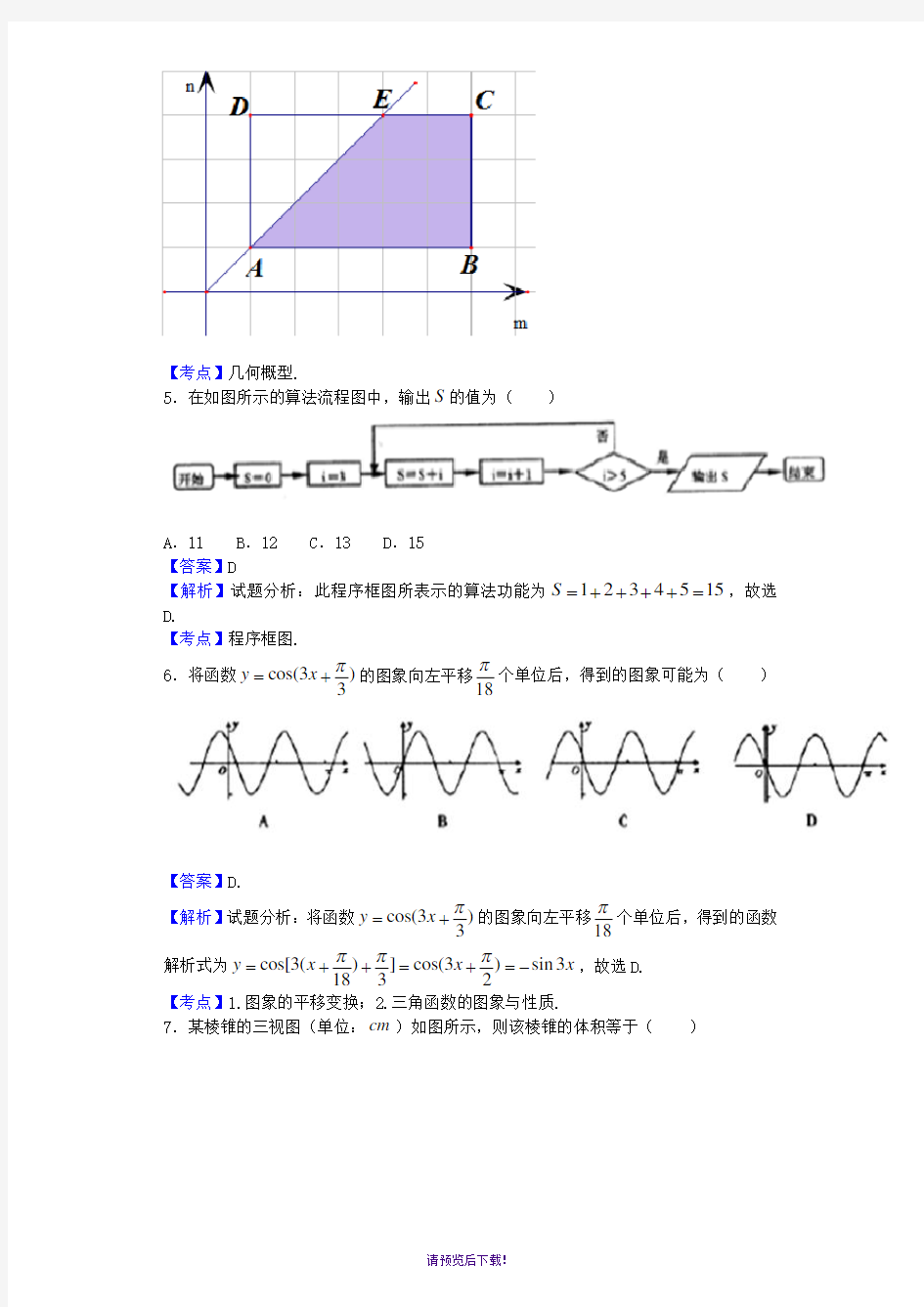
4.分别在区间[1,6]和[1,4]内任取一个实数,依次记为m 和n ,则m n >的概率为( ) A .
710 B .310 C .35 D .2
5
【答案】A
【解析】试题分析:分别在区间[1,6]和[1,4]内任取一个实数,依次记为m 和n ,则点
(,)P m n 构成的平面区域为一矩形ABCD ,在矩形内且m n >的区域为梯形ABCE ,
如下图所示,所以所求概率21
7
21510
ABCE ABCD
S P S =
==梯形矩形,故选A.
【考点】几何概型.
5.在如图所示的算法流程图中,输出S 的值为( )
A .11
B .12
C .13
D .15 【答案】D
【解析】试题分析:此程序框图所表示的算法功能为1234515S =++++=,故选D.
【考点】程序框图. 6.将函数cos(3)3
y x π
=+
的图象向左平移
18
π
个单位后,得到的图象可能为( )
【答案】D.
【解析】试题分析:将函数cos(3)3
y x π
=+的图象向左平移
18
π
个单位后,得到的函数解析式为cos[3()]cos(3)sin 31832
y x x x πππ
=+
+=+=-,故选D. 【考点】1.图象的平移变换;2.三角函数的图象与性质.
7.某棱锥的三视图(单位:cm )如图所示,则该棱锥的体积等于( )
A .310cm
B .320cm
C .330cm
D .340cm
【答案】B
【解析】试题分析:由三视图可知,该几何体为如下图所示的四棱锥P ABCD -,所以其体积1
543203
V =
???=,故选B. B
【考点】1.三视图;2.多面体的体积. 8.已知点(1,2)-和3
(3
在直线:10l ax y -+=(0)a ≠的同侧,则直线l 倾斜角的取值范围是( ) A .(
,)43ππ
B .3(0,)(,)34πππ
C .35(,)46ππ
D .23(,)34
ππ
【答案】D
【解析】试题分析:因为点(1,2)-和3
3
在直线:10l ax y -+=(0)a ≠的同侧, 所以3
(21)(
01)03
a a --+-+>,即(1)(3)0a a ++<,所以31a <<-,又直线l 的斜率k a =,即31k <<-,所以倾斜角的范围为23(,)34
ππ
,故选D. 【考点】1.直线的倾斜角与斜率;2.线性规划.
9.若不等式组
10
10
1
2
x y
x y
y
?
?+-≤
?
-+≥
?
?
?+≥
?
表示的区域Ω,不等式22
11
()
24
x y
-+≤表示的区域为Γ,
向Ω区域均匀随机撒360颗芝麻,则落在区域Γ中芝麻约为()
A.114 B.10 C.150 D.50
【答案】A
【解析】试题分析:在坐标系内作出可行域如下图所示,其中芝麻落在区域Γ内的概率为
2
31111
32
42222
1336
3
22
P
π
π
??
??+??
?+
??
==
??
,所以落在区域Γ中芝麻约为
32
360114
36
π+
?≈,故选A.
【考点】1.线性规划;2.几何概型.
【名师点睛】本题考查几何概型与线性规划,属中档题.概率问题是高考的必考见容,概率问题通常分为古典概型与几何概型两种,几何概型求概率是通过线段的长度比或区域的面积比、几何体的体积比求解的,本题是用的区域的面积比,但求面积是通过线性规划相关知识来完成的,把线性规划与几何概型有机的结合在一起是本题的亮点.
10.已知双曲线
22
122
:1(0,0)
x y
C a b
a b
-=>>的右焦点F也是抛物线
2
2
:2(0)
C y px p
=>的焦点,
1
C与
2
C的一个交点为P,若PF x
⊥轴,则双曲线
1
C 的离心率为()
A21 B2 C21 D31
【答案】A
【解析】试题分析:由题意可知
2
2
,2
2
p b
c p
a
==,所以
2
2
4
b
c
a
=,即222
c a ac
-=
,所以2210e e --=
,解之得1e =,故选A.
【考点】1.双曲线的标准方程与几何性质;2.抛物线的标准方程与几何性质. 11.已知函数
22
()
()()
n n f n n n ??=?-??为奇数为偶数且()(1)n a f n f n =++,则12350a a a a ++++=( )
A .50
B .60
C .70
D .80
【答案】A
【解析】试题分析:由题意可知2
2
1123a =-=-,2
2
2235a =-+=,
223347a =-=-,224459a =-+=,4950,99,101a a =-=,所以
1235012344950()()
()25250a a a a a a a a a a +++
+=+++++=?=,故选A.
【考点】1.数列的表示;2.数列求和.
【名师点睛】本题考查数列的表示以及数列求和,属中档题;数列求和问题是高考常考内容之一,数列求和的主要方法有:1.公式法;2.分组求和法;3.倒序相加法;4.错位相减法;5.裂项相消法.其中错位相减法与裂项相消法是考试的重点内容,本题主要采用的是分组求和法. 12.若函数()()b
f x x b R x
=+
∈的导函数在区间(1,2)上有零点,则()f x 在下列区间上单调递增的是( )
A .(,1]-∞-
B .(1,0)-
C .(0,1)
D .(2,)+∞ 【答案】D
【解析】试题分析:函数()()b
f x x b R x
=+
∈的导函数在区间(1,2)上有零点,由22()10b x b
f x x x
-'=-==得2x b =
,所以1b <<且函数()f x 的单调递增区间
为(,)-∞+∞,所以函数()f x 在区间(2,)+∞上单调递增,故选D. 【考点】1.导数与函数的单调性;2.函数与方程
【名师点睛】本题考查导数与函数的单调性、函数与方程,属中档题;导数与函数的单调性是高考的必考内容,也是难点,导数与单调性关系:()0()f x f x '>?单调递增,
()0()f x f x '
二、填空题
13.已知()ln 1,(0,)f x ax x x =+∈+∞()a R ∈,'()f x 为()f x 的导函数,'
(1)2f =,
则a = . 【答案】2
【解析】试题分析:因为1
()ln (ln 1)f x a x ax a x x
'=+?
=+,所以(1)(ln11)2f a a '=+==.
【考点】导数的运算.
14.若,x y 满足约束条件20210220x y x y x y +-≤??
-+≤??-+≥?
,则3z x y =+的最大值为 .
【答案】4
【解析】试题分析:在坐标系内作出可行域如下图所示的三角形区域,由图可知,目标函数3z x y =+取得最大值时的最优解为(1,1)B ,此时max 3114z =?+=.
【考点】线性规划.
15.抛物线22(0)x py p =>的焦点为F ,其准线与双曲线22
1x y -=相交于,A B 两
点,若ABF ?为等边三角形,则p = . 【答案】3【解析】试题分析:抛物线2
2(0)x py p =>的焦点为(
,0)2p F ,准线方程为2
p x =-,与双曲线2
2
1x y -=的交点为2244((,)22p p p p
A B ----,
又若ABF ?为等边三角形,
所以2
24043222
AF p p k p p --=
==--,解之得:23p = 【考点】1.抛物线的标准方程与几何性质;2.双曲线的标准方程与几何性质.
【名师点睛】本题考查抛物线的标准方程与几何性质与双曲线的标准方程与几何性质,属中档题;高考对圆锥曲线的考查主要是考查定义、标准方程、几何性质,小题和大题中均有.本题主要考查双曲线与抛物线的对称性的应用.
16.若定义在区间D 上的函数()y f x =满足:对,x D M R ?∈?∈,使得|()|f x M ≤恒成立,则称函数()y f x =在区间D 上有界,则下列函数中有界的是 .
①sin y x =;②1y x x
=+
;③tan y x =;④x x
x
x
e e y e e ---=+;⑤
321(44)y x ax bx x =+++-≤≤,其中,a b R ∈.
【答案】①④⑤
【解析】试题分析:因为sin 1x ≤,所以sin y x =为有界函数;1
2x x
+
≥,无上界,所以②不是有界函数;tan y x =的值域为(,)-∞+∞,是无界函数;
22212111x x x x x x x e e e y e e e e ----===-+++,因为22021x e <<+,所以221111
x e -<-<+,即
1y <,所以x x
x x e e y e e
---=+是有界函数;对于⑤,函数321y x ax bx =+++ 为实数上
连续函数,所以在区间[4,4]-上一定有最大值和最小值,所以是有界函数,故应填①④⑤.
【考点】1.新定义问题;2.值域及求法.
【名师点睛】本题主要考查新定义问题、值域及求法.函数值域的求解是难点,主要方法有:配方法、单调性法、数形结合法、换元法、基本不等式法、导数法、利用已知函数的有界性法等方法. 三、解答题
17.已知函数2()2sin cos cos sin sin (0)2
f x x x x ?
??π=+-<<在x π=处取最小
值.
(1)求?的值;
(2)在ABC ?中,,,a b c 分别为内角,,A B C 的对边,已知1,()a b f A ===
,求角C . 【答案】(1)
2π;(2)712π或12
π 【解析】试题分析:(1)利用三角恒等变换公式化简函数解析式得()sin()f x x ?=+,
由在x π=处取最小值及0?π<<查求得2
π
?=
;(2)由()f A =
可得6
A π
=,再由正弦定理求出sin B ,从而求出角B 的值,即可求角C . 试题解析:(1)1cos ()2sin cos sin sin 2
f x x x x ?
?+=?
+-
sin sin cos cos sin sin x x x x ??=++- sin cos cos sin sin()x x x ???=+=+
因为函数()f x 在x π=处取最小值,所以sin()1π?+=-, 由诱导公式知sin 1?=,因为0?π<<,所以2
π
?=.
所以()sin()cos 2
f x x x π
=+
=.
(2)因为3()f A =,所以3cos A =,因为角A 为ABC ?的内角,所以6A π=. 又因为1,2a b ==
,所以由正弦定理,得
sin sin a b
A B
=
, 也就是sin 12
sin 222
b A B a =
=?=, 因为b a >,所以4B π
=
或34
B π
=
.
当4B π=时,76412C ππππ=--=;
当34B π=时,36412
C ππππ=--=.
【考点】1.三角恒等变换;2.正弦定理;3.三角函数的图象与性质.
【名师点睛】本题考查三角恒等变换、正弦定理、三角函数的图象与性质,属中档题.在解有关三角形的题目时,要有意识地考虑用哪个定理更适合,或是两个定理都要用,要抓住能够利用某个定理的信息.一般地,如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果式子中含有角的正弦或边的一次式,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理都有可能用到.
18.如图,在四棱锥P ABCD -中,AB ⊥平面BCP ,//CD AB ,2AB BC CP BP ====,1CD =.
(1)求点B 到平面DCP 的距离; (2)点M 为线段AB 上一点(含端点),设直线MP 与平面DCP 所成角为α,求sin α的取值范围.
【答案】(13;(2)63
]
【解析】试题分析:(1) 要求点B 到平面DCP 的距离,只要能过点B 作出平面DCP 的垂线即可,由题意可知CD ⊥平面CPB ,所以CD ⊥平面CPB 内的任意一条直线,因此只要在平面CPB 内过点B 作BF PC ⊥即可得到BF ⊥平面DCP ,求出BF 的长即可;(2)由(1)可知点M 到平面DCP 的距离即点B 到平面DCP 的距离,所以
sin BF MP α=
,即只要求出BF
MP
的取值范围即可. 试题解析:(1)过点B 作BF PC ⊥,由平面DCP ⊥平面BCP 可知,BF 即点B 到面DCP 的距离,在正PBC ?中,3BF =
,即点B 到平面DCP 的距离为3.
(2)∵//CD AB ,所以点M 到平面DCP 的距离即点B 到平面DCP 的距离, 而[2,22]MP ∈,
所以63
sin [,]42
BF MP α=
∈. 【考点】1.线面垂直的判定与性质;2.直线与平面所成的角.
【名师点睛】本题考查线面垂直的判定与性质、直线与平面所成的角,属中档题;文科立体几何解答题主要考查线面位置关系的证明及几何体体积的计算,空间中线面位置关系的证明主要包括线线、线面、面面三者的平行与垂直关系,其中推理论证的关键是结合空间想象能力进行推理,要防止步骤不完整或考虑不全致推理片面,该类题目难度不大,以中档题为主.
19.某校对高一年级学生寒假参加社区服务的次数进行了统计,随机抽取了M 名学生作为样本,得到这M 名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如下:
(1)求表中,n p 的值和频率分布直方图中a 的值,并根据频率分布直方图估计该校高一学生寒假参加社区服务次数的中位数;
(2)如果用分层抽样的方法从样本服务次数在[10,15)和[25,30)的人中共抽取6人,再从这6人中选2人,求2人服务次数都在[10,15)的概率. 【答案】(1)0.625,0.075n p ==,0.125a =,中位数为17;(2)
2
3
【解析】试题分析:(1)由第一组内频数为20,频率为0.25可求出总人数为
20800.25M =
=,由此可求出第二组的频率为50
0.62580
n ==,并可求频率直方图中
0.1255
n
a =
=,由频率之和为1可求出p ,频率分布直方图求出面积的一半处求出中位数即可;(2)分分层抽样的原则先求出共抽取6人时在[10,15)和[25,30)的人数,再列出所有基本事件,可求2人服务次数都在[10,15)的概率. 试题解析:(1)因200.25M ÷=,所以80M =,所以50
0.62580
n =
=, 3
10.250.6250.050.07540
p =---==, 1
0.12558
n a =
==. 中位数位于区间[15,20),设中位数为(15)x +,
则0.1250.25x =,所以2x =,所以学生参加社区服务区次数的中位数为17次. (2)由题意知样本服务次数在[10,15)有20人,样本服务次数在[25,30)有4人, 如果用分层抽样的方法从样本服务次数在[10,15)和[25,30)的人中共抽取6人,则抽取的服务次数在[10,15)和[25,30)的人数分别为:206524?
=和46124
?=. 记服务次数在[10,15)为12345,,,,a a a a a ,在[25,30)的为b . 从已抽取的6人任选两人的所有可能为:
121314151232425234(,),(,),(,),(,),(,),(,),(,),(,),(,),(,),a a a a a a a a a b a a a a a a a b a a 3534545(,),(,),(,),(,),(,),a a a b a a a b a b 共15种,
设“2人服务次数都在[10,15)”为事件A ,则事件A 包括
1213141523242534(,),(,),(,),(,),(,),(,),(,),(,),a a a a a a a a a a a a a a a a 3545(,),(,)a a a a
共10种, 所有102
()153
P A =
=. 【考点】1.频率分布表;2.频率分布直方图;3.古典概型.
20.已知椭圆:C 22
221(0)x y a b a b
+=>>上的左、右顶点分别为,A B ,1F 为左焦点,
且1||2AF =,又椭圆C 过点(0,. (1)求椭圆C 的方程;
(2)点P 和Q 分别在椭圆C 和圆22
16x y +=上(点,A B 除外),设直线,PB QB 的斜
率分别为12,k k ,若123
4
k k =
,证明:,,A P Q 三点共线.
【答案】(1)22
11612
x y +=;(2)见解析 【解析】试题分析:(1)1||2AF a c ==-,由椭圆C
过点(0,
可得b =,由椭圆中,,a b c 关系求出,,a b c 的值即可;(2)由(1)知,(4,0),(4,0)A B -,设
1122(,),(,)P x y Q x y ,
由此可得211112
1114416
PA y y y k k x x x ?=?=+--,又因为22113124y x =-,1234k k =,由此可得21PA k k ?=-,同理可得21QA k k ?=-,所以PA QA k k =,即可证,,A P Q 三点共线.
试题解析:(1
)由已知可得2,a c b -==,又222
12b a c =-=,解得4a =,
故所求椭圆C 的方程为
22
11612
x y +=. (2)由(1)知,(4,0),(4,0)A B -,设1122(,),(,)P x y Q x y ,
所以2
11112
1114416
PA y y y k k x x x ?=?=+--,因为11(,)P x y 在椭圆C 上, 所以
221
1
11612x y +=,即22113124
y x =-,所以21
12131234164PA x k k x -
?==--. 又因为123
4
k k =
,所以21PA k k ?=-.(a ) 由已知点22(,)Q x y 在圆22
16x y +=上,AB 为圆的直径,
所以QA QB ⊥,所以21QA k k ?=-(b )
由(a )(b )可得PA QA k k =,因为直线,PA QA 有共同点A , 所以,,A P Q 三点共线.
【考点】1.椭圆的标准方程与几何性质;2.直线与椭圆的位置关系. 21.已知函数()ln f x x x =.
(1)求函数()y f x =的单调区间和最小值; (2)若函数()()f x a F x x -=
在[1,]e 上的最小值为3
2
,求a 的值; (3)若k Z ∈,且()(1)0f x x k x +-->对任意1x >恒成立,求k 的最大值.
【答案】(1)()f x 的单调递增区间为1
[,)e +∞,单调减区间为1(0,]e ,min 1()f x e
=-.
(2)a =(3)3
【解析】试题分析:(1)求导'()ln 1(0)f x x x =+>,解不等式'()0f x ≥与'
()0
f x ≤可得函数()f x 的单调区间;(2)求函数()ln a F x x x =-
的导数'2
()x a
F x x +=,分0a ≥与0a <讨论函数()ln a F x x x =-在区间[1,]e 的单调性与最小值,由min 3
()2
f x =求之
即可;(3)由题意分离参数得ln 1
x x x
k x +<-对任意1x >恒成立,构造函数
ln ()1
x x x h x x +=
-,求导'2ln 2()(1)x x h x x --=-,'
2
ln 2()(1)x x h x x --=-的符号由分子()ln 2(1)x x x x ?=-->确定,且函数()x ?在(1,)+∞上单调递增,所以方程()0
x ?=在(1,)+∞上存在唯一的实根0x ,且0(3,4)x ∈,由此可知函数()h x 在0(1,)x 上递减,在
0(,)x +∞上单调递增,所以min 0()k g x x <=,可证结论成立.
试题解析:(1)因为'()ln 1(0)f x x x =+>,令'()0f x ≥,即1
ln 1ln x e -≥-=,所
以1
x e
≥
, 同理,令'
()0f x ≤,可得1(0,]x e
∈,所以()f x 的单调递增区间为1[,)e
+∞,单调减
区间为1(0,]e
.
所以min 1111()()ln f x f e
e e e ==
=-. (2)()ln a F x x x =-,'2
()x a
F x x +=,
Ⅰ.当0a ≥时,'
()0F x >,()F x 在[1,]e 上单调递增,min 3()(1)2
F x F a ==-=
,所以3
[0,)2
a =-
?+∞,舍去. Ⅱ.当0a <时,()F x 在(0,)a -上单调递减,在(,)a -+∞上单调递增, ①若(1,0)a ∈-,()F x 在[1,]e 上单调递增,min 3
()(1)2
F x F a ==-=
,所以3
[0,)2
a =-?+∞,舍去,
②若[,1]a e ∈--,()F x 在[1,]a -上单调递减,在[,]a e -上单调递增,
所以min 3
()(1)ln()2
F x F a a ==-+=
,解得[,1]a e =--.
③若(,)a e ∈-∞-,()F x 在[1,]e 上单调递减,min 3
()()12
a F x
F e e ==-
=,所以(,)2
e
a e =-?-∞-,舍去,综上所述,a e =-.
(3)由题意得:(1)ln k x x x x -<+对任意1x >恒成立,即ln 1
x x x
k x +<-对任意1x >恒成立. 令ln ()1
x x x h x x +=
-,则'
2
ln 2()(1)x x h x x --=-,令()ln 2(1)x x x x ?=-->,则'1
1
()10x x x x
?-=-=
>, 所以函数()x ?在(1,)+∞上单调递增,
因为方程()0x ?=在(1,)+∞上存在唯一的实根0x ,且0(3,4)x ∈,当01x x <<时,
()0x ?<,即'()0h x <,
当0x x >时,()0x ?>,即'
()0h x >.
所以函数()h x 在0(1,)x 上递减,在0(,)x +∞上单调递增. 所以0000min 0000(1ln )(12)
()()(3,4)11
x x x x h x h x x x x ++-==
==∈--
所以min 0()k g x x <=,又因为0(3,4)x ∈,故整数k 的最大值为3.
【考点】1.导数与函数的单调性、最值;2.函数与不等式.
【名师点睛】本题主要考查导数与函数的单调性、最值;函数与不等式,属难题.本题覆盖面广,对考生计算能力要求较高,是一道难题.解答本题,准确求导数是基础,恰当分类讨论是关键,易错点是分类讨论不全面、不彻底、不恰当.本题能较好的考查考生的逻辑思维能力、基本计算能力、分类讨论思想等.
22.如图,圆周角BAC ∠的平分线与圆交于点D ,过点D 的切线与弦AC 的延长线交于点E ,AD 交BC 于点F .
(1)求证://BC DE ;
(2)若,,,D E C F 四点共圆,且AC BC =,求BAC ∠. 【答案】(1)见解析;(2)
27
π
【解析】试题分析:(1)要证//BC DE ,只要证EDC DCB ∠=∠即可,由弦切角和圆周角关系可得EDC DAC ∠=∠,由角平分线性质得EDC DAC ∠=∠,又同弧上的圆周角相等,所以DAB DCB ∠=∠,即可证得EDC DCB ∠=∠;(2)由,,,D E C F 四点共圆及(1)得CFA ACF ∠=∠,设DAC DAB x ∠=∠=,在等腰三角形ACF 中,列出方程7CFA ACF CAF x π=∠+∠+∠=,解之即可. 试题解析: (1)∵BAC ∠的平分线与圆交于点D ∴EDC DAC ∠=∠,DAC DAB ∠=∠,
∵BD BD =,∴DAB DCB ∠=∠,∴EDC DCB ∠=∠, ∴//BC DE .
(2)因为,,,D E C F 四点共圆,所以CFA CED ∠=∠, 由(1)知,ACF CED ∠=∠, 所以CFA ACF ∠=∠. 设DAC DAB x ∠=∠=,
因为AC BC =,所以2CBA BAC x ∠=∠=, 所以3CFA FBA FAB x ∠=∠+∠=,
在等腰三角形ACF 中,7CFA ACF CAF x π=∠+∠+∠=, 则7
x
π
=
,所以227
BAC x π∠==
.
【考点】1.圆的性质;2.等腰三角形性质;3.圆内接四边形性质.
23.已知直线112:3x t l y ?=+??
??=??(t 为参数),曲线1cos :sin x C y θθ=??=?(θ为参数).
(1)设l 与1C 相交于,A B 两点,求||AB ;
(2)若把曲线1C 上各点的横坐标压缩为原来的
1
2
3倍,得
到曲线2C ,设点P 是曲线2C 上的一个动点,求它到直线l 的距离的最小值.
【答案】(1)1;(26
21)