
1.4 定积分与微积分基本定理
1.4.1曲边梯形面积与定积分
【提出问题】
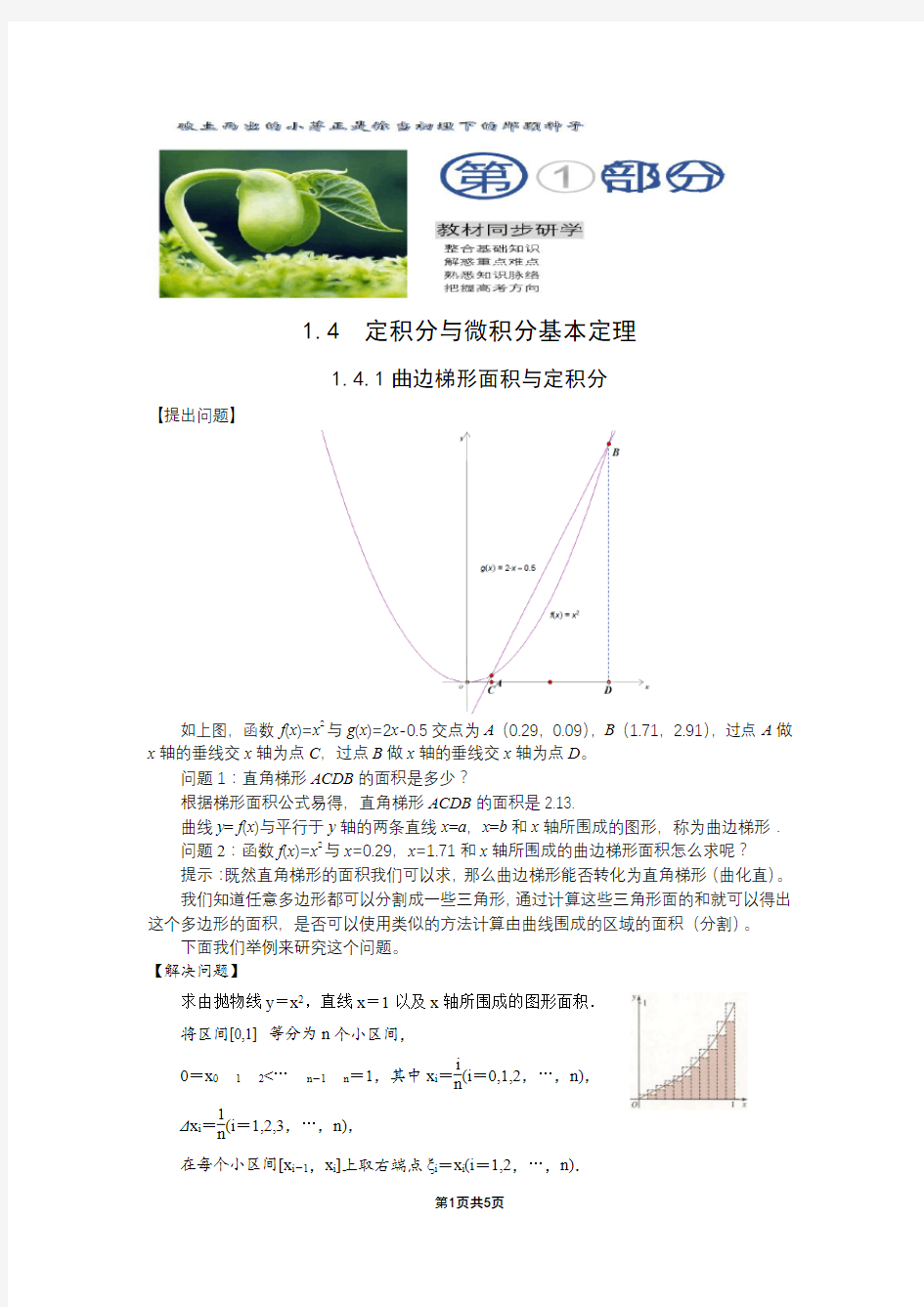
如上图,函数f(x)=x2与g(x)=2x-0.5交点为A(0.29,0.09),B(1.71,2.91),过点A做x轴的垂线交x轴为点C,过点B做x轴的垂线交x轴为点D。
问题1:直角梯形ACDB的面积是多少?
根据梯形面积公式易得,直角梯形ACDB的面积是2.13.
曲线y=f(x)与平行于y轴的两条直线x=a,x=b和x轴所围成的图形,称为曲边梯形.问题2:函数f(x)=x2与x=0.29,x=1.71和x轴所围成的曲边梯形面积怎么求呢?
提示:既然直角梯形的面积我们可以求,那么曲边梯形能否转化为直角梯形(曲化直)。
我们知道任意多边形都可以分割成一些三角形,通过计算这些三角形面的和就可以得出这个多边形的面积,是否可以使用类似的方法计算由曲线围成的区域的面积(分割)。
下面我们举例来研究这个问题。
【解决问题】
求由抛物线y=x2,直线x=1以及x轴所围成的图形面积.
将区间[0,1] 等分为n个小区间,
0=x0 n(i=0,1,2,…,n), Δx i=1 n(i=1,2,3,…,n), 在每个小区间[x i-1,x i]上取右端点ξi=x i(i=1,2,…,n). 于是曲线之下小矩形的面积为ξi 21 n (i =0,1,2,…,n-1) 所以曲线之下小矩形的面积和为 S n =(0n ) 2?1n +(1n ) 2?1n +(2n ) 2?1n +…+(n?1n ) 2?1 n = 02+12+22+?+(n?1)2 n 3 =1 6(1?1 n )(2?1 n ) 由此得到 S =lim n →∞ S n =lim n →∞ 16 (1?1n )(2?1n )=1 3 . 从图形上看,当n 越来越大时,划分越来越细,阴影部分的面积与曲边梯形面积相差越来越小,当n 趋于正无穷时,阴影部分趋近于曲边三角形,因此可以将1 3视为此曲边三角形的面积。 【获得新知】 类似的问题还很多,它们都可以归结为求这种和式的极限。牛顿等数学家经过艰苦研究,得到了解决这类问题的一般方法:求函数的定积分。 定积分的定义 设函数y =f(x)定义在区间[a ,b]上(如图).用分点a =x 0 Δx i =x i +1-x i ,i =0,1,2,…,n -1. 记λ为这些小区间长度的最大者.当λ趋近于0时,所有的小区间长度都趋近于0.在每个小区间内任取一点ξi ,作和式S n = 当λ→0时,如果和式的极限存在,我们把和式S n 的极限叫做函数f(x)在区间[a ,b]上的定积分,记作 ()b a f x dx ? ,即()b a f x dx ?= 其中f(x)叫做被积函数,a 叫做积分 下限,b 叫积分上限,f(x)d x 叫做被积式.此时称函数f(x)在区间[a ,b]上可积. 【概念领悟】 1.定积分的几何意义 (1)当f(x)在区间[a ,b]上大于0时,()b a f x dx ?表示由直线x =a ,x =b(a ≠b),y =0及 曲线y =f(x)所围成的曲边梯形的面积. (2)当f(x)在区间[a ,b]上小于0时, ()b a f x dx ? 表示由直线x =a ,x =b(a ≠b),y =0及 曲线y =f(x)所围成的曲边梯形的面积的相反数. (3)当f(x)在区间[a ,b]上有正有负时, ()b a f x dx ? 表示介于x 轴、曲线y =f(x)以及直线 x =a ,x =b 之间各部分的面积之和,在x 轴上方的面积取正号,在x 轴下方的面积取负号. 2.定积分的性质 (1) ()()b b a a kf x dx k f x dx =? ?(k 为常数); (2) ()()()()b b a a a b f x g x dx f x dx g x dx ±=±? ??; (3) ()()() ()b c b a a c f x dx f x dx f x dx a c b =+< ??. 【经典例题】 例1 利用定积分的定义计算由抛物线y =x 2,直线x =2以及x 轴所围成的图形面积. 解:将区间[0,2]n 等分, 0=x 0 n (i =0,1,2,…,n), Δx i =2 n (i =1,2,3,…,n), 在每个小区间[x i -1,x i ]上取右端点ξi =x i-1(i =1,2,…,n). 于是曲线之下小矩形的面积为ξi 22 n (i =1,2,…,n) 所以曲线之下小矩形的面积和为 S n =4[(0 n ) 2?2 n +(1 n ) 2?2 n +(2 n ) 2?2 n +…+( n?1n ) 2?2n ] =8? 02+12+22+?+(n?1)2 n 3 =43 (1?1 n )(2?1 n ) 由此得到 S =lim n →∞ S n =lim n →∞ 43(1?1n )(2?1n )=8 3. 【规律技巧】求曲边梯形面积的四个步骤: 第一步:分割,在区间[a ,b]上插入n -1个分点,将这个区间n 等分,即将它分成n 个小区间[x i -1,x i ](i =1,2,…,n ).区间[x i -1,x i ]的长度Δx i =x i -x i -1; 第二步:近似代替,“以直代曲”,用矩形的面积近似代替小曲边梯形的面积,求出每个小曲边梯形面积的近似值; 第三步:求和,即求这些小矩形面积的和; 第四步:取极限. 例2 利用定积分的几何意义求∫√4?x 2dx 2 0的值。 解:因为被积函数为y =√4?x 2, 其表示的曲线为以原点为圆心,2为半径的四分之一圆, 由定积分的几何意义可知,所求的定积分即为四分之一圆的面积, 所以∫√4?x 22 0dx =14 ·π·22=π. 【规律技巧】利用定积分的几何意义求定积分 ()b a f x dx ? ,关键是确定由曲线y =f (x )和直 线x =a ,x =b 及x 轴所围成的图形的形状,若图形是三角形、梯形、矩形、圆(或一部分),则可用相应面积公式计算. 例3 利用定积分表示由抛物线y 2=x (y >0)与直线5x +y -6=0及y =0所围成图形的面积. 解:由题意,作图形,并解方程组{y 2=x (y >0), 5x +y ?6=0 得x =1,y =1. 所以y 2=x 与直线5x +y -6=0的交点为(1,1). 所以所求面积为 S =∫√xdx 1 0+∫(6?5x )dx 6 51 . 【规律技巧】 ①当函数f (x )在区间[a ,b ]上恒为正时,定积分()b a f x dx ? 的几何意义是以曲线f (x )为曲边的曲边梯形的面积.一般情况下,如图,定积分 ()b a f x dx ? 的几何意义是介于x 轴、函数 f (x )的图像以及直线x =a 、x =b 之间各部分面积的代数和,在x 轴上方的面积取正号,在x 轴下方的面积取负号. ②利用定积分表示曲线围成的面积时,关键是弄清定积分的几何意义,特别注意符号问题.定积分的值可正可负可为零,而面积是正值. 【总结提炼】这节内容我们通过“曲化直”与“分割”的思想方法研究了曲边梯形的面 积,定义了定积分运算。这些数学核心思想方法要注意理解。