
第二章 空间向量与立体几何(A)
(时间:120分钟 满分:150分)
一、选择题(本大题共10小题,每小题5分,共50分) 1.以下命题中,不正确的个数为( )
①|a |-|b |=|a +b |是a ,b 共线的充要条件;②若a∥b ,则存在唯一的实数λ,使a =λb ;③若a·b =0,b·c =0,则a =c ;④若a ,b ,c 为空间的一个基底,则a +b ,b +c ,c +a 构成空间的另一个基底; ⑤|(a·b )·c |=|a |·|b |·|c |.
A .2
B .3
C .4
D .5
2.直三棱柱ABC —A 1B 1C 1中,若CA →=a ,CB →=b ,CC 1→=c ,则A 1B →
等于( ) A .a +b -c B .a -b +c C .-a +b +c D .-a +b -c 3.已知a =(2,4,5),b =(3,x ,y ),若a∥b ,则( ) A .x =6,y =15 B .x =3,y =
152
C .x =3,y =15
D .x =6,y =15
2
4.已知空间三点A (0,2,3),B (-2,1,6),C (1,-1,5).若|a |=3,且a 分别与AB →,AC
→
垂直,则向量a 为( ) A .(1,1,1)
B .(-1,-1,-1)
C .(1,1,1)或(-1,-1,-1)
D .(1,-1,1)或(-1,1,-1)
5.已知A (-1,0,1),B (0,0,1),C (2,2,2),D (0,0,3),则sin 〈AB →,CD →
〉等于( ) A .-23 B.23 C.53 D .-53
6.在正三棱柱ABC —A 1B 1C 1中,若AB =
2BB 1,则AB 1与C 1B 所成角的大小为( )
A .60°
B .90°
C .105°
D .75°
7.若两个不同平面α,β的法向量分别为u =(1,2,-1),v =(-3,-6,3),则( ) A .α∥β B .α⊥β
C .α,β相交但不垂直
D .以上均不正确
8.若两点A (x,5-x,2x -1),B (1,x +2,2-x ),当|AB →
|取最小值时,x 的值等于( ) A .19 B .-87 C.87 D.19
14
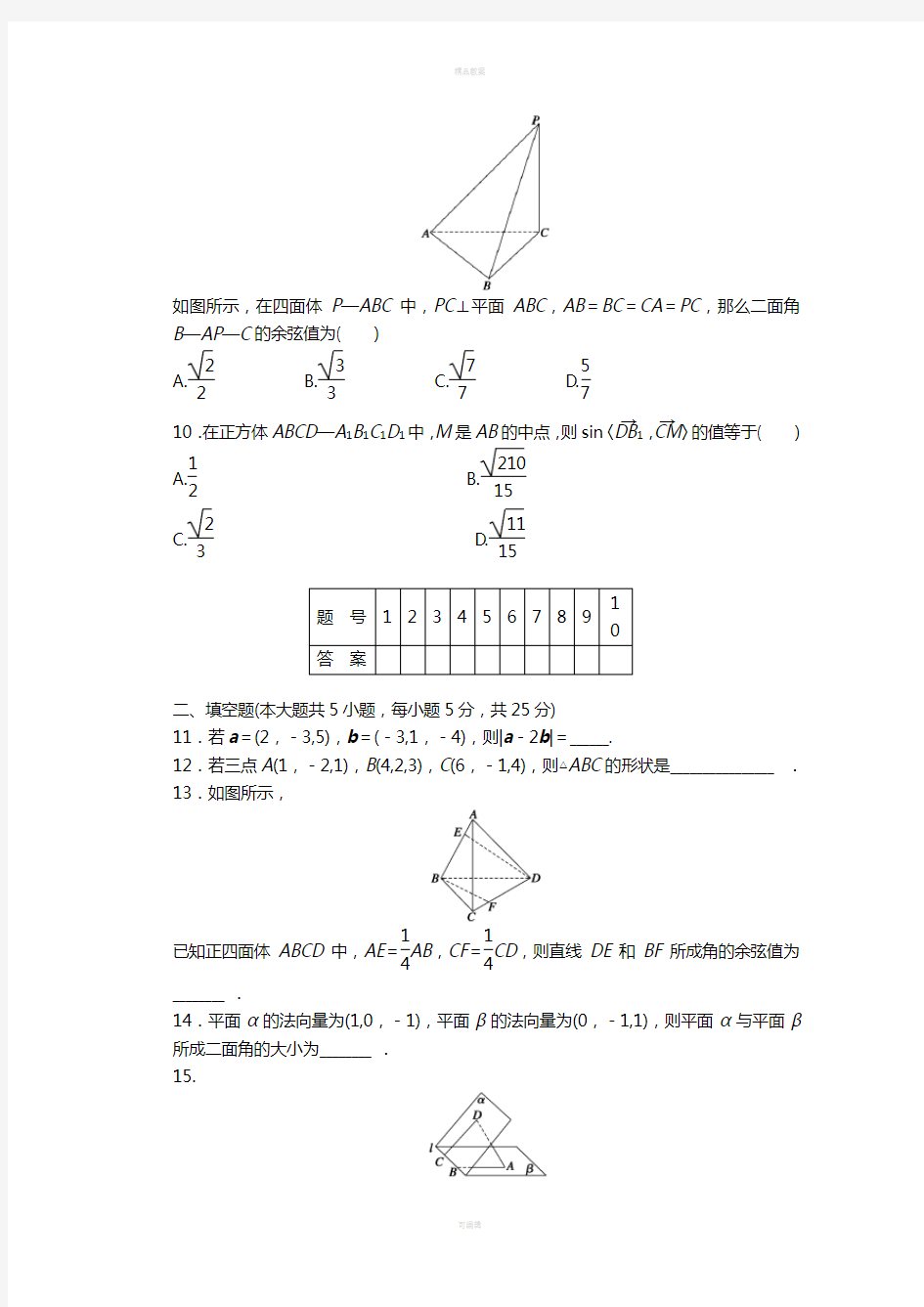
9.
如图所示,在四面体P —ABC 中,PC ⊥平面ABC ,AB =BC =CA =PC ,那么二面角
B —AP —
C 的余弦值为( )
A.22
B.33
C.77
D.57
10.在正方体ABCD —A 1B 1C 1D 1中,M 是AB 的中点,则sin 〈DB 1→,CM →〉的值等于( ) A.12 B.21015 C.23 D.1115
题 号 1 2 3 4 5 6 7 8 9 10 答 案
二、填空题(本大题共5小题,每小题5分,共25分) 11.若a =(2,-3,5),b =(-3,1,-4),则|a -2b |=______.
12.若三点A (1,-2,1),B (4,2,3),C (6,-1,4),则△ABC 的形状是________________. 13.如图所示,
已知正四面体ABCD 中,AE =14AB ,CF =1
4CD ,则直线DE 和BF 所成角的余弦值为
________.
14.平面α的法向量为(1,0,-1),平面β的法向量为(0,-1,1),则平面α与平面β所成二面角的大小为________. 15.
如图所示,已知二面角α—l —β的平面角为θ ? ??
??
θ∈? ????0,π2,AB ⊥BC ,BC ⊥CD ,AB
在平面β内,BC 在l 上,CD 在平面α内,若AB =BC =CD =1,则AD 的长为______. 三、解答题(本大题共6小题,共75分)
16.(12分)在直三棱柱ABC —A 1B 1C 1中,AB 1⊥BC 1,CA 1⊥BC 1.求证:AB 1=CA 1.
17.(12分)已知四边形ABCD 的顶点分别是A (3,-1,2),B (1,2,-1),C (-1,1, -3),D (3,-5,3).
求证:四边形ABCD 是一个梯形.
18.(12分)
如图所示,在棱长为2的正方体ABCD—A1B1C1D1中,E、F分别为A1D1和CC1的中点.
(1)求证:EF∥平面ACD1;
(2)求异面直线EF与AB所成角的余弦值.
19.(12分)
如图所示,已知平行六面体ABCD—A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD =∠BCD.
求证:C1C⊥BD.
20.(13分)
如图,在空间四边形OABC中,OA=8,AB=6,AC=4,BC=5,∠OAC=45°,∠OAB =60°,求OA与BC所成角的余弦值.
21.(14分)
如图,在长方体ABCD —A 1B 1C 1D 1中,E 、F 分别是棱BC ,CC 1上的点,CF =AB =2CE ,
AB ∶AD ∶AA 1=1∶2∶4.
(1)求异面直线EF 与A 1D 所成角的余弦值; (2)证明AF ⊥平面A 1ED ;
(3)求二面角A 1—ED —F 的正弦值.
第二章 空间向量与立体几何(A)
1.C [只有命题④正确.] 2.D
[如图,A 1B →=AB →-AA 1→=CB →-CA →-AA 1→=CB →-CA →
-CC 1→
=b -a -c .]
3.D
[∵a∥b ,∴存在实数λ,使????
? 3=2λx =4λ
y =5λ
,∴?????
x =6y =15
2
.]
4.C [设a =(x ,y ,z ),∵AB →
=(-2,-1,3),
AC →=(1,-3,2),又|a |=3,a ⊥AB →
,a ⊥AC →
,
∴????
? x 2+y 2+z 2=3,
-2x -y +3z =0,x -3y +2z =0.
∴?????
x =1,
y =1,z =1
或????
?
x =-1,
y =-1,z =-1.
∴a =(1,1,1)或a =(-1,-1,-1).] 5.C [∵AB →=(1,0,0),CD →
=(-2,-2,1), ∴cos 〈AB →
,CD →
〉=AB →·CD
→
|AB →|·|CD →|
=-2
3,
∴sin 〈AB →
,CD →
〉=5
3
.]
6.B [
建立如图所示的空间直角坐标系,设BB 1=1,则A (0,0,1),B 1? ??
???62,22,0,
C 1(0,2,0), B ? ??
???62,22,1.
∴AB 1→=? ??
???62,22,-1,
C 1B →=? ??
???62,-22,1,∴AB 1→·C 1B →=64-24-1=0,即AB 1与C 1B 所成角的大小为90°.]
7.A [∵v =-3u ,∴v ∥u .故α∥β.] 8.C [AB →
=(1-x,2x -3,-3x +3), 则|AB →|=1-x
2+
2x -32+-3x +3
2
=
14x 2-32x +19=
14? ????x -872+57
. 故当x =87时,|AB →
|取最小值.]
9.C [如图所示,
作BD ⊥AP 于D ,作CE ⊥AP 于E ,设AB =1,则易得CE =22,EP =2
2,PA =PB =
2,
可以求得BD =144,ED =2
4
.
∵BC →=BD →+DE →+EC →,
∴BC →2=BD →2+DE →2+EC →2+2BD →·DE →+2DE →·EC →+2EC →·BD →. ∴EC →·BD →=-14,∴cos 〈BD →,EC →
〉=-77,
即二面角B —AP —C 的余弦值为7
7.]
10.B
[以D 为原点,DA 、DC 、DD 1分别为x 轴、y 轴、z 轴建立空间直角坐标系,设正方
体棱长为1,易知DB 1→
=(1,1,1),CM →
=? ??
??1,-1
2,0,
故cos 〈DB 1→
,CM →
〉=15
15
,
从而sin 〈DB 1→,CM →
〉=21015
.]
11.
258
解析 ∵a -2b =(8,-5,13), ∴|a -2b |=
82+-5
2+132=
258.
12.不等边的锐角三角形
解析 AB →=(3,4,2),AC →=(5,1,3),BC →=(2,-3,1),AB →·AC →>0,得∠A 为锐角;CA →·CB →
>0,得∠C 为锐角;BA →·BC →>0,得∠B 为锐角,所以△ABC 是锐角三角形且|AB →|=29,
|AC →|=35,|BC →|=
14.
13.4
13
解析 因四面体ABCD 是正四面体,顶点A 在底面BCD 内的射影为△BCD 的垂心,所以有BC ⊥DA ,AB ⊥CD .设正四面体的棱长为4,
则BF →·DE →=(BC →+CF →)·(DA →+AE →)=0+BC →·AE →+CF →·DA →
+0=4×1×cos 120°+1×4×cos 120°=-4,
BF =DE =42+12-2×4×1×cos 60°=13,
所以异面直线DE 与BF 的夹角θ的余弦值为:
cos θ=|BF →·DE →|
|BF →||DE →|=4
13.
14.π3或2π3
解析 设n 1=(1,0,-1),n 2=(0,-1,1),
则cos 〈n 1,n 2〉=1×0+0×-1+-1×12·2
=-1
2,
∴〈n 1,n 2〉=2π
3.因平面α与平面β所成的角与〈n 1,n 2〉相等或互补,所以α与β所
成的角为π3或2π
3.
15.
3-2cos θ
解析 因为AD →=AB →+BC →+CD →
,
所以AD →2=AB →2+BC →2+CD →2+2AB →·CD →+2AB →·BC →+2BC →·CD →
=1+1+1+2cos(π-θ)=3-2cos θ. 所以|AD →|=3-2cos θ, 即AD 的长为
3-2cos θ.
16.证明 以A 为原点,AC 为x 轴,AA 1为z 轴建立空间直角坐标系. 设B (a ,b,0),C (c,0,0),A 1(0,0,d ),
则B 1(a ,b ,d ),C 1(c,0,d ),AB 1→
=(a ,b ,d ),
BC 1→=(c -a ,-b ,d ),CA 1→
=(-c,0,d ),
由已知AB 1→·BC 1→
=ca -a 2-b 2+d 2=0,
CA 1→·BC 1→
=-c (c -a )+d 2=0,可得c 2=a 2+b 2.
再由两点间距离公式可得: |AB 1|2=a 2+b 2+d 2, |CA 1|2=c 2+d 2=a 2+b 2+d 2, ∴AB 1=CA 1.
17.证明 因为AB →=(1,2,-1)-(3,-1,2)=(-2,3,-3),CD →
=(3,-5,3)-(-1,1,-3)=(4,-6,6),因为-24=3-6=-3
6,
所以AB →和CD →
共线,即AB ∥CD .
又因为AD →
=(3,-5,3)-(3,-1,2)=(0,-4,1),
BC →
=(-1,1,-3)-(1,2,-1)=(-2,-1,-2),
因为0-2≠-4-1≠1-2,所以AD →与BC →不平行,
所以四边形ABCD 为梯形. 18.(1)证明
如图所示,分别以DA 、DC 、DD 1所在的直线为x 轴、y 轴、z 轴建立空间直角坐标系,由已知得D (0,0,0),
A (2,0,0),
B (2,2,0),
C (0,2,0),B 1(2,2,2),
D 1(0,0,2),
E (1,0,2),
F (0,2,1).
易知平面ACD 1的一个法向量是DB 1→
=(2,2,2).
又∵EF →=(-1,2,-1),由EF →·DB 1→=-2+4-2=0,∴EF →⊥DB 1→. 又∵EF 平面ACD 1,∴EF ∥平面ACD 1. (2)解 ∵AB →
=(0,2,0),
cos 〈EF →,AB →
〉=EF →·AB
→
|EF →||AB →|=426=63.
19.证明 设CD →=a ,CB →=b ,CC 1→
=c , 依题意,|a |=|b |,
又设CD →,CB →,CC 1→
中两两所成夹角为θ, 于是BD →=CD →-CB →
=a -b ,
CC 1→·BD →
=c ·(a -b )=c·a -c·b
=|c||a |cos θ-|c||b |cos θ=0, 所以C 1C ⊥BD .
20.解 因为BC →=AC →-AB →
, 所以OA →·BC →=OA →·AC →-OA →·AB →
=|OA →||AC →|cos 〈OA →,AC →〉-|OA →||AB →|cos 〈OA →,AB →〉 =8×4×cos 135°-8×6×cos 120°=-16
2+24.
所以cos 〈OA →
,BC →
〉=OA →·BC
→
|OA →||BC →|
=24-1628×5=
3-2
25.
即OA 与BC 所成角的余弦值为
3-2
25
.
21.(1)解 如图所示,建立空间直角坐标系,点A 为坐标原点.设AB =1,依题意得
D (0,2,0),F (1,2,1),A 1(0,0,4),
E ? ??
??
1,32,0.
易得EF →
=? ??
??0,12,1,A 1D →
=(0,2,-4),
于是cos 〈EF →,A 1D →
〉 =EF →·A 1D
→
|EF →||A 1D →|
=-3
5. 所以异面直线EF 与A 1D 所成角的余弦值为3
5.
(2)证明 易知AF →
=(1,2,1), EA 1→
=? ????-1,-32,4,ED →=? ??
??-1,1
2,0,
于是AF →·EA 1→=0,AF →·ED →
=0. 因此,AF ⊥EA 1,AF ⊥ED .
又EA 1∩ED =E ,所以AF ⊥平面A 1ED . (3)设平面EFD 的法向量u =(x ,y ,z ),
则??
?
u ·EF
→
=0,u ·ED
→
=0,即?????
1
2y +z =0,
-x +12y =0.
不妨令x =1,可得u =(1,2,-1), 由(2)可知,AF →
为平面A 1ED 的一个法向量, 于是cos 〈u ,AF →
〉=u ·AF
→
|u ||AF →|
=2
3,
从而sin〈u,AF→〉=
5 3 .
所以二面角A1—ED—F的正弦值为
5 3 .