
第十三章轴对称
【典型例题讲解】
拓展天地(1)
以给定的图形“○○,△△,=”(两个圆,两个三角形,两条平行线)为构件,构思独特而有意义的轴对称图形,如下左图所示,是符合要求的图形,请你在图中方框里构思出一幅其他的图形,并写出一两句贴切、诙谐的解说词.
两盏电灯
【解析】两条平行线可看成2,两个圆看成两个0,由200联想到2008,两个三角形正好可组成一个8,再结合2008北京奥运会得出答案.
【解】如图所示:
解说词:北京好运
拓展天地(2)
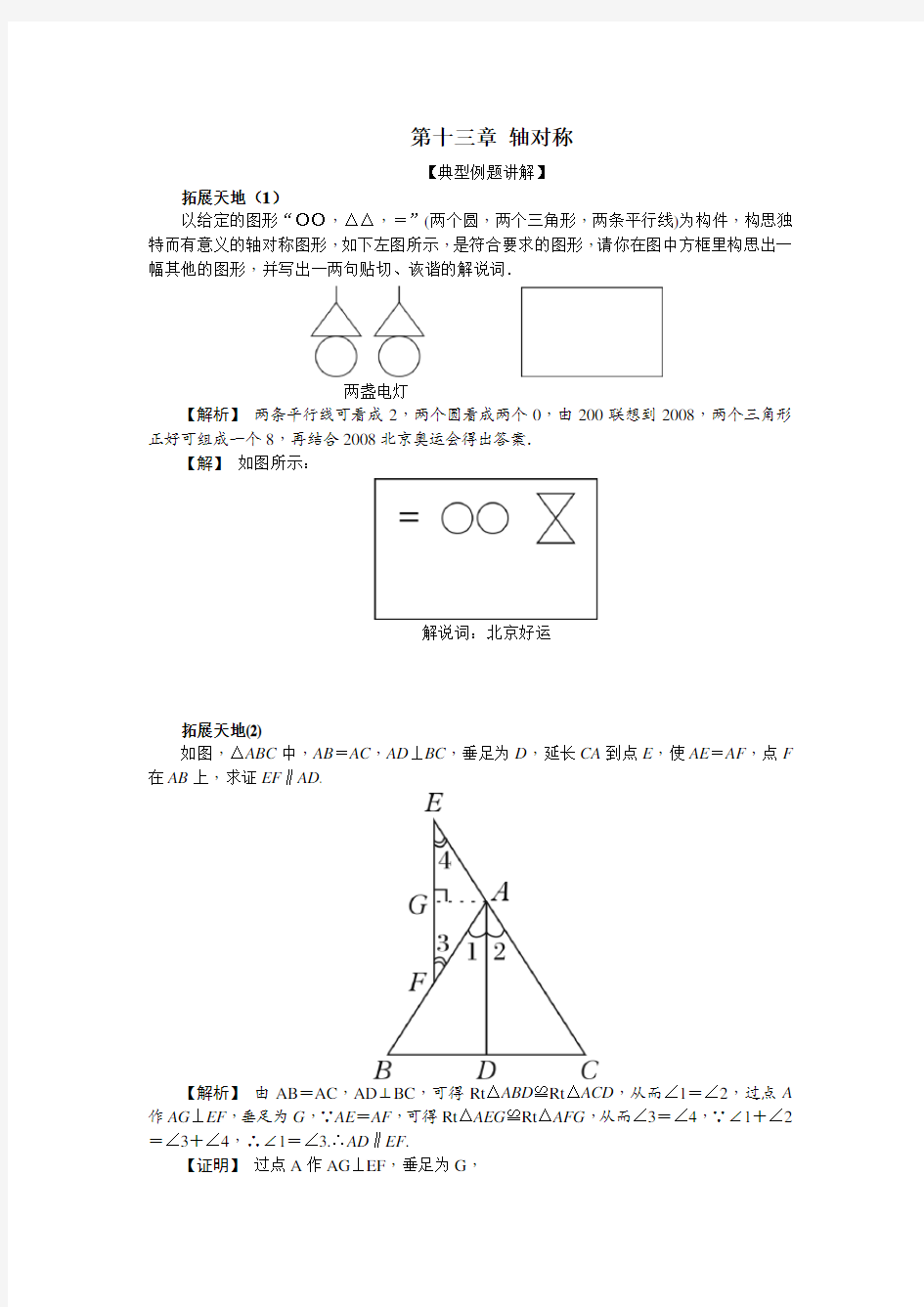
如图,△ABC中,AB=AC,AD⊥BC,垂足为D,延长CA到点E,使AE=AF,点F 在AB上,求证EF∥AD.
【解析】由AB=AC,AD⊥BC,可得Rt△ABD≌Rt△ACD,从而∠1=∠2,过点A 作AG⊥EF,垂足为G,∵AE=AF,可得Rt△AEG≌Rt△AFG,从而∠3=∠4,∵∠1+∠2=∠3+∠4,∴∠1=∠3.∴AD∥EF.
【证明】过点A作AG⊥EF,垂足为G,
在Rt△AEG和Rt△AFG中,AE=AF,AG=AG,
∴Rt△AEG≌Rt△AFG,∴∠3=∠4,
同理,∠1=∠2,
∵∠BAC=∠3+∠4,即∠1+∠2=∠3+∠4,
∴2∠1=2∠3,∴∠1=∠3.∴AD∥EF.
拓展天地(3)
如图,左边的树经过几次轴对称变换,可以变成右边的树?你能设计一种变换方案吗?
【解析】本题会有许多种不同的解法,一般需作四次轴对称变换,最少的是两次轴对称变换.
【解】如图所示,经过两次轴对称变换就可以将左边的树变成右边的树.
拓展天地(4)
如图所示,(1)A,B是直线m异侧的两点,在直线m上求一点P,使P A+PB的长度最短.
(2)C,D是直线n同侧的两点,在直线n上求一点Q,使QC+QD的长度最短.
【解析】(1)连接AB交直线m于点P,则点P为所求点.
(2)C,D是直线n同侧的两点,可考虑将它们转化为(1)的情形,不妨设想将点C转化为关于直线n的对称点C′,即不论直线n上任何一点Q,都应满足QC=QC′,这样,C,D 与直线n上任意一点的距离之和就转化为C′,D与直线n上任意一点的距离之和.由QC=QC′知,点Q在线段CC′的垂直平分线上,由Q的任意性知,直线n是线段CC′的垂直平分线.
(1)(2)
【解】(图略)(1)连接AB,交直线m于点P,则点P即为所求的点.
(2)作点C关于直线n的对称点C′,连接C′D交直线n于点Q,则点Q即为所求的点.
拓展天地(5)
在平面直角坐标系内画出下列各点:(3,-2),(-5,3),(-2,2),(-1,-3).将各点绕坐标原点旋转180°,求旋转后各点的坐标,并指出旋转前后点的坐标的变化规律.
【解析】 利用平面直角坐标系中的网格及全等三角形的判定,容易发现已知点绕原点旋转180°后的坐标.
【解】 点(3,-2)绕原点旋转180°后所得点的坐标为(-3,2),点(-5,3)绕原点旋转180°后所得点的坐标为(5,-3),点(-2,2)绕原点旋转180°后所得点的坐标为(2,-2),点(-1,-3)绕原点旋转180°后所得点的坐标为(1,3).变化规律是:旋转后所得点的横、纵坐标都是旋转前点的横、纵坐标的相反数.
拓展天地(6)
如图,已知∠AOB =α,在射线OA ,OB 上分别取点A 1,B 1,使得OA 1=OB 1,连接A 1B 1;在B 1A 1,B 1B 上分别取点A 2,B 2,使B 1B 2= B 1 A 2,连接A 2B 2…按此规律下去,记∠A 2B 1B 2=θ1,∠A 3B 2B 3=θ2,…,∠A n +1B n B n +1=θn ,则
(1)θ1=________________;
(2)θn =________________.
【解析】 这是一个已知等腰三角形的顶角求其底角度数的问题.由∠AOB =α可求得∠θ1=180°+α2,由∠θ1=180°+α2可求得∠θ2=3×180°+α4,由∠θ2=3×180°+α4
可求得∠θ3=7×180°+α8
,…以此类推. 【答案】 (1)∠θ1=180°+α2 (2)∠θn =(2n -1)180°+α2n
拓展天地(7)
已知如图,锐角△ABC 的两条高BE ,CD 相交于点O ,且OB =OC ,求证△ABC 是等腰三角形.
【解析】 由OB =OC ,可得∠OBC =∠OCB ,即∠BCD =∠CBE ,再由BE ,CD 是高,可发现题中隐含全等三角形: △BDC ≌△CEB ,从而得∠DBC =∠ECB ,∴AB =AC ,即△ABC 是等腰三角形.
【证明】 ∵OB =OC ,∴∠OBC =∠OCB.
∵BE ,CD 是两条高,∴∠BDC =∠CEB =90°.
又∵BC =CB ,∴△BDC ≌△CEB ,
∴∠DBC =∠ECB ,∴AB =AC ,∴△ABC 是等腰三角形.
拓展天地(8)
如图,C 是AB 上一点,△ACD ,△BCE 都是等边三角形,AE ,CD 相交于点M ,BD ,CE 相交于点N ,求证 △CMN 是等边三角形.
【解析】 由已知条件易知,∠MCN =60°,因此,只需证明△MCN 中有两边相等,就可以证明△MCN 是等边三角形.
【证明】 ∵△ACD ,△BCE 都是等边三角形,
∴AC =CD ,BC =CE ,∠1=∠2=60°,
∴∠3=180°-∠1-∠2=60°,∴∠ACE =∠DCB =120°.
在△ACE 和△DCB 中,AC =DC ,CE =CB ,∠ACE =∠DCB ,
∴△ACE ≌△DCB ,∴∠4=∠5.
在△BCN 和△ECM 中,∠2=∠3,BC =CE ,∠5=∠4,
∴△BCN ≌△ECM ,∴CM =CN ,
又∵∠3=60°,∴△CMN 是等边三角形.
拓展天地(9)
如图,△ABC 中,∠ACB =90°,BC =12
AB ,求证∠A =30°.
【解析】 本题是“含30°角的直角三角形性质”中将问题的结论与其中一个条件交换
而得的,对于BC =12AB ,其处理方法仍是“截半”或“倍长”.
【解】 如图,作AB 的垂直平分线DE ,交AB 于点D ,交AC 于点E ,连接EB.
∵DE 垂直平分AB ,∴BD =12
AB ,∠EDB =90°,AE =EB ,∴∠A =∠1. ∵BC =12AB ,BD =12
AB ,∴BD =BC , 又∵∠ACB =∠EDB =90°,
又∵BD =BC ,BE =BE ,
∴Rt △BDE ≌Rt △BCE ,∴∠BED =∠BEC ,∴∠1=∠2.
∵∠A =∠1,∴∠A =∠2=∠1,
∵∠ACB =90°,∴∠A +∠2+∠1=90°,
∴3∠A =90°,∴∠A =30°.