
模式1:平行四边形 分类标准:讨论对角线
例如:请在抛物线上找一点p 使得P C B A 、、、四点构成平行四边形,则可分成以下几种情况
(1)当边AB 是对角线时,那么有BC AP // (2)当边AC 是对角线时,那么有CP AB // (3)当边BC 是对角线时,那么有BP AC //
例题1:(山东省阳谷县育才中学模拟10)本题满分14分)在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点. (1)求抛物线的解析式;
(2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S.求S 关于m 的函数关系式,并求出S 的最大值;
(3)若点P 是抛物线上的动点,点Q 是直线y=-x 上的动点,判断有几个位置能使以点P 、Q 、B 、0为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标.
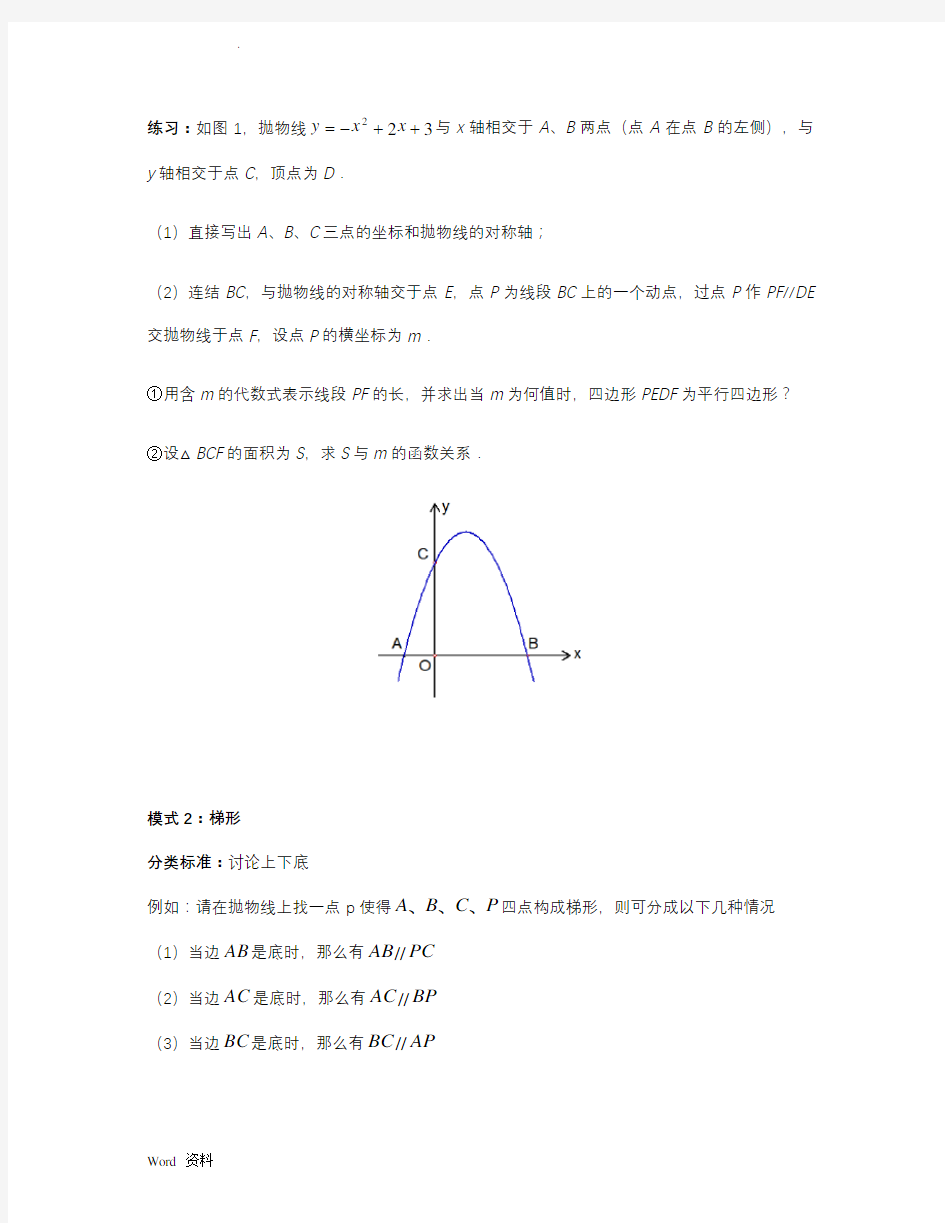
练习:如图1,抛物线322
++-=x x y 与x 轴相交于A 、B 两点(点A 在点B 的左侧),与
y 轴相交于点C ,顶点为D .
(1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴;
(2)连结BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF //DE 交抛物线于点F ,设点P 的横坐标为m .
①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形?
②设△BCF 的面积为S ,求S 与m 的函数关系.
模式2:梯形
分类标准:讨论上下底
例如:请在抛物线上找一点p 使得P C B A 、、、四点构成梯形,则可分成以下几种情况 (1)当边AB 是底时,那么有PC AB // (2)当边AC 是底时,那么有BP AC // (3)当边BC 是底时,那么有AP BC //
例题2:已知,矩形OABC 在平面直角坐标系中位置如图1所示,点A 的坐标为(4,0),点C 的坐标为)20(-,,直线x y 3
2
-
=与边BC 相交于点D . (1)求点D 的坐标;
(2)抛物线c bx ax y ++=2
经过点A 、D 、O ,求此抛物线的表达式;
(3)在这个抛物线上是否存在点M ,使O 、D 、A 、M 为顶点的四边形是梯形?若存在,请求出所有符合条件的点M 的坐标;若不存在,请说明理由.
练习:已知二次函数的图象经过A (2,0)、C (0,12) 两点,且对称轴为直线x =4,设顶点为点P ,与x 轴的另一交点为点B .
(1)求二次函数的解析式及顶点P 的坐标;
(2)如图1,在直线 y =2x 上是否存在点D ,使四边形OPBD 为等腰梯形?若存在,求出点
D 的坐标;若不存在,请说明理由;
(3)如图2,点M 是线段OP 上的一个动点(O 、P 两点除外),以每秒2个单位长度的速度由点P 向点O 运动,过点M 作直线MN //x 轴,交PB 于点N . 将△PMN 沿直线MN 对
折,得到△P 1MN . 在动点M 的运动过程中,设△P 1MN 与梯形OMNB 的重叠部分的面积为
S ,运动时间为t 秒,求S 关于t 的函数关系式.
模式3:直角三角形
分类标准:讨论直角的位置或者斜边的位置
例如:请在抛物线上找一点p 使得P B A 、、三点构成直角三角形,则可分成以下几种情况 (1)当A ∠为直角时,AB AC ⊥ (2)当B ∠为直角时,BA BC ⊥ (3)当C ∠为直角时,CB CA ⊥
例题3:如图1,已知抛物线y =x 2
+bx +c 与x 轴交于A 、B 两点(点A 在点B 左侧),与y 轴交于点C (0,-3),对称轴是直线x =1,直线BC 与抛物线的对称轴交于点D .
(1)求抛物线的函数表达式;
(2)求直线BC 的函数表达式;
(3)点E 为y 轴上一动点,CE 的垂直平分线交CE 于点F ,交抛物线于P 、Q 两点,且点P 在第三象限.
①当线段3
4
PQ AB =
时,求tan ∠CED 的值;
②当以C 、D 、E 为顶点的三角形是直角三角形时,请直接写出点P 的坐标.
练习:如图1,直线43
4
+-=x y 和x 轴、y 轴的交点分别为B 、C ,点A 的坐标是(-2,0).
(1)试说明△ABC 是等腰三角形;
(2)动点M 从A 出发沿x 轴向点B 运动,同时动点N 从点B 出发沿线段BC 向点C 运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M 运动t 秒时,△MON 的面积为S . ① 求S 与t 的函数关系式;
② 设点M 在线段OB 上运动时,是否存在S =4的情形?若存在,求出对应的t 值;若不存在请说明理由;
③在运动过程中,当△MON 为直角三角形时,求t 的值.
模式4:等腰三角形
分类标准:讨论顶角的位置或者底边的位置
例如:请在抛物线上找一点p 使得P B A 、、三点构成等腰三角形,则可分成以下几种情况 (1)当A ∠为顶角时,AB AC = (2)当B ∠为顶角时,BA BC = (3)当C ∠为顶角时,CB CA =
例题4:已知:如图1,在平面直角坐标系xOy 中,矩形OABC 的边OA 在y 轴的正半轴上,
OC 在x 轴的正半轴上,OA =2,OC =3,过原点O 作∠AOC 的平分线交AB 于点D ,连接DC ,过点D 作DE ⊥DC ,交OA 于点E .
(1)求过点E 、D 、C 的抛物线的解析式;
(2)将∠EDC 绕点D 按顺时针方向旋转后,角的一边与y 轴的正半轴交于点F ,另一边与线段OC 交于点G .如果DF 与(1)中的抛物线交于另一点M ,点M 的横坐标为5
6
,那么EF =2GO 是否成立?若成立,请给予证明;若不成立,请说明理由;
A
B C
O
P Q
D
y
x
(3)对于(2)中的点G ,在位于第一象限内的该抛物线上是否存在点Q ,使得直线GQ 与
AB 的交点P 与点C 、G 构成的△PCG 是等腰三角形?若存在,请求出点Q 的坐标;若不存在
成立,请说明理由.
练习:(2012江汉市中考模拟)已知抛物线y =ax 2
+bx +c (a >0)经过点B (12,0)和C (0,-6),对称轴为x =2. (1)求该抛物线的解析式.
(2)点D 在线段AB 上且AD =AC ,若动点P 从A 出发沿线段AB 以每秒1个单位长度的速度匀速运动,同时另一个动点Q 以某一速度从C 出发沿线段CB 匀速运动,问是否存在某一时刻,使线段PQ 被直线CD 垂直平分?若存在,请求出此时的时间t (秒)和点Q 的运动速度;若存在,请说明理由.
(3)在(2)的结论下,直线x =1上是否存在点M ,使△MPQ 为等腰三角形?若存在,请求出所有点M 的坐标;若不存在,请说明理由.
模式5:相似三角形
突破口:寻找比例关系以及特殊角
例题5:(据荆州资料第58页第2题改编)在梯形ABCD 中,AD ∥BC ,BA ⊥AC ,∠B = 450
,AD = 2,BC = 6,以BC 所在直线为x 轴,建立如图所示的平面直角坐标系,点A 在y 轴
上。
(1) 求过A 、D 、C 三点的抛物线的解析式。
(2) 求△ADC 的外接圆的圆心M 的坐标,并求⊙M 的半径。
(3) E 为抛物线对称轴上一点,F 为y 轴上一点,求当ED +EC +FD +FC 最小时,EF 的长。
(4) 设Q 为射线CB 上任意一点,点P 为对称轴左侧抛物线上任意一点,问是否存在这样的点P 、Q ,使得以P 、Q 、C 为顶点的△与△ADC 相似?若存在,直接写出点P 、Q 的坐标,若不存在,则说明理由。
模拟题汇编之动点折叠问题
1.(2012深圳模拟)(本题12分)已知二次函数c bx x y ++=2
与x 轴交于A (-1,0)、B (1,0)两点.
(1)求这个二次函数的关系式;
(2)若有一半径为r 的⊙P ,且圆心P 在抛物线上运动,当⊙P 与两坐标轴都相切时,求半径
r 的值.
(3)半径为1的⊙P 在抛物线上,当点P 的纵坐标在什么范围内取值时,⊙P 与y 轴相离、相交?
2.如图,在平面直角坐标系中,二次函数c bx x y ++=2
的图象与x 轴交于A 、B 两点, A 点在原点的左侧,B 点的坐标为(3,0),与y 轴交于C (0,-3)点,点P 是直线BC 下方的抛物线上一动点.(1)分别求出图中直线和抛物线的函数表达式;
(2)连结PO 、PC ,并把△POC 沿C O 翻折,得到四边形POP ′C , 那么是否存在点P ,使四边形POP ′C 为菱形?若存在,请求出此时点P 的坐标;若不存在,请说明理由.
解:将B 、C 两点的坐标代y=kx+b, 0=3k-3, k=1,∴y=x-3…………1分
将B 、C 两点的坐标代入得:??
?-==+303c c b ,解得:???-=-=3
2
c b
所以二次函数的表达式为:322
--=x x y .…………………3分
(2)存在点P ,使四边形POP /
C 为菱形.设P 点坐标为(x ,322
--x x ),
PP /交CO 于E.若四边形POP /
C 是菱形,则有PC =PO .…………………5分
连结PP /
则PE ⊥CO 于E ,∴OE=EC =23
∴y =23-.∴322
--x x =2
3- .………………………………6分
解得1x =
2102+
,2x =2
10
2-(不合题意,舍去) ∴P 点的坐标为(
210
2+,2
3-).…………………………9分
3.(2012江西模拟)已知抛物线2
34y x x =-++交y 轴于点A ,交x 轴于点B ,C (点B 在点C 的右侧).过点A 作垂直于y 轴的直线l. 在位于直线l 下方的抛物线上任取一点P ,过点P 作直线PQ 平行于y 轴交直线l 于点Q .连接AP . (1)写出A ,B ,C 三点的坐标; (2)若点P 位于抛物线的对称轴的右侧:
①如果以A ,P ,Q 三点构成的三角形与△AOC 相似,求出点P 的坐标;
②若将△APQ 沿AP 对折,点Q 的对应点为点M .是否存在点P ,使得点M 落在x 轴上.若存在,求出点P 的坐标;若不存在,请说明理由.
4.(2012安庆模拟)在直角梯形ABCD 中,∠B =90°,AD =1,AB =3,BC =4,M 、N 分别
C
D
N
是底边BC 和腰CD 上的两个动点,当点M 在BC 上运动时,始终保持AM ⊥MN 、NP ⊥BC . (1)证明:△CNP 为等腰直角三角形;
(2)设NP =x ,当△ABM ≌△MPN 时,求x 的值;
(3)设四边形ABPN 的面积为y ,求y 与x 之间的函数关系式,并指出x 取何值时,四边形
ABPN 的面积最大,最大面积是多少.
解:(1)过D 作DQ ⊥BC 于Q ,则四边形ABQD 为平行四边形 DQ=AB=3,BQ=AD=1 ∴QC=DQ △DQC 中∠C=∠QDC =45° ∴Rt △NPC 为等腰Rt △ ………………(4分) (2)∵ABM V ≌MPN V MP=AB=3, BM=NP ∵△NPC 为等腰Rt △
∴PC=NP= x ∴BM=BC -MP -PC=1-x ∴1- x= x ∴ x=
2
1
∴当ABM V ≌MPN V 时,x =
2
1
………………(8分) (3)ABPN S 四边形=
21(AB+NP ) BP=21(3+ x )(4-x )=-212x +21 x+ 6=-21( x-2
1
)+6.125(11分) ∴当x 取
2
1
时,四边形ABPN 面积最大,最大面积为6.125. ………………(14分) 5.(2012宝应模拟)在直角坐标系中,O 为坐标原点,点A 的坐标为(2,2),点C 是线段OA 上的一个动点(不运动至O ,A 两点),过点C 作CD ⊥x 轴,垂足为D ,以CD 为边在右侧作正方形CDEF. 连接AF 并延长交x 轴的正半轴于点B ,连接OF,设OD =t. ⑴ 求tan ∠FOB 的值;
⑵用含t 的代数式表示△OAB 的面积S ;
⑶是否存在点C, 使以B ,E ,F 为顶点的三角形与△OFE 相似,若存在,请求出所有满足要求
的B 点的坐标;若不存在,请说明理由.
(1)作AH ⊥x 轴于H ,交CF 于P ∵A(2,2) ∴AH=OH=2 ∴∠AOB=45° ∴CD=OD=DE=EF=t ∴1
tan 22
t FOB t ∠== ……………………3分 (2)∵CF ∥OB ∴△ACF ∽△AOB ∴
AP CF AH OB = 即22t t
OB
-=
∴22t OB t =
- ∴12(02)22OAB t
S OB AH t t
?=?=<<- ………………6分 (3)要使△BEF 与△OFE 相似,∵∠FEO=∠FEB=90° ∴只要
OE EF EB EF =或OE EF EF EB
= 即:2BE t =或1
2
EB t =
① 当2BE t =时, 4BO t =, ∴
242t t t
=- ∴0t =(舍去)或3
2t = ∴B(6,0) ……………………8分
② 当1
2
EB t =
时, (ⅰ) 当B 在E 的右侧时,52
OB OE EB t =+=
, ∴
2522
t t t =- ∴0t =(舍去)或6
5t = ∴B(3,0) …………………10分
(ⅱ) 当B 在E 的左侧时,如图,32
OB OE EB t =-=
, ∴
2322
t t t =- ∴0t =(舍去)或2
3t = ∴B(1,0) ……………………12分
6.(2012广东预测)(本小题满分12分)如图,抛物线的顶点坐标是??
? ??892
5
,-,且经过点
) 14 , 8 (A .
(1)求该抛物线的解析式;
(2)设该抛物线与y 轴相交于点B ,与x 轴相交于C 、D 两点(点C 在点D 的左边), 试求点B 、C 、D 的坐标;
(3)设点P 是x 轴上的任意一点,分别连结AC 、BC . 试判断:PB PA +与BC AC +的大小关系,并说明理由.
解:(1)(4分)设抛物线的解析式为89252
-??? ?
?
-=x a y ………………………1分
∵抛物线经过)14,8(A ,∴89258142
-??? ?
?
-a =,解得:21=a …………2分
∴8
9
25212
-??? ??-=x y (或225212+-=x x y ) …………………………1分
(2)(4分)令0=x 得2=y ,∴)2,0(B ……………………………………1分
(第24题图)
令0=y 得
022
5
212=+-x x ,解得11=x 、42=x ………………………2分 ∴)0 , 1(C 、) 0, 4(D …………………………………………………………1分 (3)(4分)结论:BC AC PB PA +≥+ …………………………………1分
理由是:①当点C P 与点重合时,有BC AC PB PA +=+ ………………………………1分
②当时异于点点C P ,∵直线AC 经过点)14,8(A 、)0,1(C ,∴直线AC 的解析式为
22-=x y ………3分
设直线AC 与y 轴相交于点E ,令0=x ,得2-=y , ∴)2,0(-E ,
则)2,0()2,0(B E 与点-关于x 轴对称 ∴EC BC =,连结PE ,则PB PE =, ∴AE EC AC BC AC =+=+, ∵在APE ?中,有AE PE PA >+
∴BC AC AE PE PA PB PA +=>+=+…………………………………1分 综上所得BC AC BP AP +≥+………………………………………………1分
7..如图,已知二次函数y =-x 2
+bx +c 的图象经过A (-2,-1),B (0,7)两点. (1)求该抛物线的解析式及对称轴; (2)当x 为何值时,y >0?
(3)在x 轴上方作平行于x 轴的直线l ,与抛物线交于C 、D 两点(点C 在对称轴的左侧),过点
C 、
D 作x 轴的垂线,垂足分别为F 、
E .当矩形CDE
F 为正方形时,求C 点的坐标.
解:解:(1)把A (-2,-1),B (0,7)两点的坐标代入
y =-x 2+bx +c ,得
??
? -4-2b +c =-1c =7,解得?
??
b =2
c =7. 所以,该抛物线的解析式为y =-x 2
+2x +7,
又因为y =-x 2
+2x +7=-(x -1)2+8,所以对称轴为直线x =1. (2)当函数值y =0时, -x 2
+2x +7=0的解为x =1±2 2,
结合图象,容易知道1-2
2 2时,y >0. (3)当矩形CDEF 为正方形时,设C 点的坐标为(m ,n ), 则n =-m 2 +2m +7,即CF =-m 2 +2m +7. 因为C 、D 两点的纵坐标相等, 所以C 、D 两点关于对称轴x =1对称, 设点D 的横坐标为p ,则1-m =p -1, 所以p =2-m ,所以CD =(2-m )-m =2-2m . 因为CD =CF ,所以2-2m =-m 2 +2m +7, 整理,得m 2 -4m -5=0,解得m =-1或5. 因为点C 在对称轴的左侧,所以m 只能取-1. 当m =-1时, n =-m 2+2m +7=-(-1)2+2×(-1)+7=4. 于是,点C 的坐标为(-1,4). 8.如图,在△ABC 中,已知AB =BC =CA =4cm ,AD ⊥BC 于D ,点P 、Q 分别从B 、C 两点同时出发,其中点P 沿BC 向终点C 运动,速度为1cm/s ;点Q 沿CA 、AB 向终点B 运动,速度为2cm/s ,设它们运动的时间为x(s)。 ⑴ 求x 为何值时,PQ ⊥AC ; ⑵ 设△PQD 的面积为y(cm 2 ),当0<x <2时,求y 与x 的函数关系式; ⑶ 当0<x <2时,求证:AD 平分△PQD 的面积; ⑷ 探索以PQ 为直径的圆与AC 的位置关系,请写出相应位置关系的x 的取值范围(不要求写出过程)。 Q D C B A P O 解:⑴∵当Q 在AB 上时,显然PQ 不垂直于AC 。 当Q 在AC 上时,由题意得:BP =x ,CQ =2x ,PC =4-x , ∴AB =BC =CA =4,∠C =600 , 若PQ ⊥AC ,则有∠QPC =300,∴PC =2CQ ∴4-x =2×2x ,∴x =4 5 , ∴当x =4 5 (Q 在AC 上)时,PQ ⊥AC ; ⑵ 当0<x <2时,P 在BD 上,Q 在AC 上,过点Q 作QH ⊥BC 于H , ∵∠C =600 ,QC =2x ,∴QH =QC ×sin600 =3x ∵AB =AC ,AD ⊥BC ,∴BD =CD =1 2 BC =2 ∴DP =2-x ,∴y =12 PD ·QH =12 (2-x)·3x =-32x 2 +3x ⑶ 当0<x <2时,在Rt △QHC 中,QC =2x ,∠C =600 , ∴HC =x ,∴BP =HC ∵BD =CD ,∴DP =DH , ∵AD ⊥BC ,QH ⊥BC ,∴AD ∥QH , ∴OP =OQ ∴S △PDO =S △DQO , ∴AD 平分△PQD 的面积; ⑷ 显然,不存在x 的值,使得以PQ 为直径的圆与AC 相离 当x =45或16 5 时,以PQ 为直径的圆与AC 相切。 当0≤x <45或45<x <165或16 5 <x ≤4时,以PQ 为直径的圆与AC 相交。 9.已知抛物线22(1)2y x k x k =-+-++与x 轴交于A 、B 两点,且点A 在x 轴的负半轴 上,点B 在x 轴的正半轴上. (1)求实数k 的取值范围; (2)设OA 、OB 的长分别为a 、b ,且a ∶b =1∶5,求抛物线的解析式; (3)在(2)的条件下,以AB 为直径的⊙D 与y 轴的正半轴交于P 点,过P 点作⊙D 的 切线交x 轴于E 点,求点E 的坐标。 解:(1)设点A (1x ,0),B (2x ,0)且满足1x <0<2x 由题意可知()0211<+-=?k x x ,即2->k (2)∵a ∶b =1∶5,设a OA =,即a x =-1,则a OB 5=,即a x 52=,0>a ∴???-=?-=?=+-=+2 21215545a a a x x a a a x x ,即()()???-=+-=-252412a k a k ∴12+=a k ,即03252 =--a a ,解得11=a , 53 2- =a (舍去) ∴3=k ∴抛物线的解析式为 542 ++-=x x y (3)由(2)可知,当0542 =++-x x 时,可得11-=x ,52=x 即A (-1,0),B (5,0) ∴AB =6,则点D 的坐标为(2,0) 当PE 是⊙D 的切线时,PE ⊥PD 由Rt △DPO ∽Rt △DEP 可得DE OD PD ?=2 即DE ?=232 ∴ 29= DE ,故点E 的坐标为(29 - ,0) 10.如图,抛物线y =ax 2 +c (a >0)经过梯形ABCD 的四个顶点,梯形的底AD 在x 轴上,其中A (-2,0),B (-1, -3). (1)求抛物线的解析式; (2)点M 为y 轴上任意一点,当点M 到A 、B 两点的距离之和为最小时,求此时点M 的坐标; (3)在第(2)问的结论下,抛物线上的点P 使S △PAD =4S △ABM 成立,求点P 的坐标. 解:(1)、因为点A 、B 均在抛物线上,故点A 、B 的坐标适合抛物线方程 ∴403a c a c +=?? +=-? 解之得:14 a c =??=-?;故2 4y x =-为所求 ……4分 (2)如图2,连接BD ,交y 轴于点M ,则点M 就是所求作的点 设BD 的解析式为y kx b =+,则有20 3k b k b +=?? -+=-?, 1 2k b =??=-? , 故BD 的解析式为2y x =-;令0,x =则2y =-,故(0,2)M -……8分 (3)、如图3,连接AM ,BC 交y 轴于点N ,由(2)知,OM=OA=OD=2,90AMB ∠=? 易知BN=MN=1, 易求AM BM == 1 22 ABM S =?=V ;设2(,4)P x x -, 依题意有: 214422AD x -=?g ,即:21 44422 x ?-=?g 解之得:x =±,0x =,故 符合条件的P 点有三个: 1234),(4),(0,4)P P P -- ……12分 11.如图,在平面直角坐标系中,O 是坐标原点,点A 的坐标是(﹣4,0),点B 的坐标是 (0,b)(b>0).P是直线AB上的一个动点,作PC⊥x轴,垂足为C.记点P关于y轴的对称点为P′(点P′不在y轴上),连接PP′,P′A,P′C.设点P的横坐标为a. (1)当b=3时, ①求直线AB的解析式; ②若点P′的坐标是(﹣1,m),求m的值; (2)若点P在第一象限,记直线AB与P′C的交点为D.当P′D:DC=1:3时,求a的值;(3)是否同时存在a,b,使△P′CA为等腰直角三角形?若存在,请求出所有满足要求的a,b的值;若不存在,请说明理由. 解:(1)①设直线AB的解析式为y=kx+3,把x=﹣4,y=0代入得:﹣4k+3=0,∴k=, ∴直线的解析式是:y=x+3,……3分 ②由已知得点P的坐标是(1,m),∴m=×1+3=;……4分 (2)∵PP′∥AC,△PP′D∽△ACD,∴=,即=,∴a=;……6分 (3)以下分三种情况讨论. ①当点P在第一象限时, 1)若∠AP′C=90°,P′A=P′C(如图1) 过点P′作P′H⊥x轴于点H. 初三数学 二次函数 知识点总结 一、二次函数概念: 1.二次函数的概念:一般地,形如2y ax bx c =++(a b c ,,是常数,0a ≠)的函数,叫做二次函数。 这里需要强调:和一元二次方程类似,二次项系数0a ≠,而b c ,可以为零.二次函数的定义域是全体实数. 2. 二次函数2y ax bx c =++的结构特征: ⑴ 等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2. ⑵ a b c ,,是常数,a 是二次项系数,b 是一次项系数,c 是常数项. 二、二次函数的基本形式 1. 二次函数基本形式:2y ax =的性质: a 的绝对值越大,抛物线的开口越小。 2. 2y ax c =+的性质: 上加下减。 3. ()2 y a x h =-的性质: 左加右减。 4. ()2 y a x h k =-+的性质: a 的符号 开口方向 顶点坐标 对称轴 性质 0a > 向上 ()00, y 轴 0x >时,y 随x 的增大而增大;0x <时,y 随 x 的增大而减小;0x =时,y 有最小值0. 0a < 向下 ()00, y 轴 0x >时,y 随x 的增大而减小;0x <时,y 随x 的增大而增大;0x =时,y 有最大值0. a 的符号 开口方向 顶点坐标 对称轴 性质 0a > 向上 ()0c , y 轴 0x >时,y 随x 的增大而增大;0x <时,y 随x 的增大而减小;0x =时,y 有最小值c . 0a < 向下 ()0c , y 轴 0x >时,y 随x 的增大而减小;0x <时,y 随x 的增大而增大;0x =时,y 有最大值c . a 的符号 开口方向 顶点坐标 对称轴 性质 0a > 向上 ()0h , X=h x h >时,y 随x 的增大而增大;x h <时,y 随x 的增大而减小;x h =时,y 有最小值0. 0a < 向下 ()0h , X=h x h >时,y 随x 的增大而减小;x h <时,y 随x 的增大而增大;x h =时,y 有最大值0. 九年级数学上册 圆 几何综合(提升篇)(Word 版 含解析) 一、初三数学 圆易错题压轴题(难) 1.如图,二次函数y=x 2-2mx+8m 的图象与x 轴交于A 、B 两点(点A 在点B 的左边且OA≠OB ),交y 轴于点C ,且经过点(m ,9m ),⊙E 过A 、B 、C 三点。 (1)求这条抛物线的解析式; (2)求点E 的坐标; (3)过抛物线上一点P (点P 不与B 、C 重合)作PQ ⊥x 轴于点Q ,是否存在这样的点P 使△PBQ 和△BOC 相似?如果存在,求出点P 的坐标;如果不存在,说明理由 【答案】(1)y=x 2 +2x-8(2)(-1,- 72)(3)(-8,40),(-15 4,-1316),(-174 ,-25 16 ) 【解析】 分析:(1)把(),9m m 代入解析式,得:22289m m m m -+=,解这个方程可求出m 的值; (2)分别令y =0和x =0,求出OA ,OB ,O C 及AB 的长,过点E 作EG x ⊥轴于点 G ,EF y ⊥轴于点F ,连接CE ,AE ,设OF =GE =a ,根据AE CE = ,列方过程求出a 的值, 从而求出点E 的坐标; (3)设点P (a , a 2+2a -8), 则2 28,2PQ a a BQ a =+-=-,然后分PBQ ∽CBO 时 和PBQ ∽BCO 时两种情况,列比例式求出a 的值,从而求出点P 的坐标. 详解:(1)把(),9m m 代入解析式,得:22289m m m m -+= 解得:121,0m m =-=(舍去) ∴228y x x =+- y x O 二次函数中的动点问题(二) 平行四边形的存在性问题 一、技巧提炼 1、二次函数y=ax 2 +bx+c 的图像和性质 a >0 a <0 图 象 开 口 对 称 轴 顶点坐标 最 值 当x = 时,y 有最 值是 当x = 时,y 有最 值是 增减 性 在对称轴左侧 y 随x 的增大而 y 随x 的增大而 在对称轴右侧 y 随x 的增大而 y 随x 的增大而 2、平行四边形模型探究 如图1,点A ()11,x y 、B ()22,x y 、C ()33,x y 是坐标平面内不在同一直线上的三点。平面直角坐标系中是否存在点D ,使得以A 、B 、C 、D 四点为顶点的四边形为平行四边形,如果存在,请求出点D 的坐标。 A B C x y 图1 图2 如图2,过A 、B 、C 分别作BC 、AC 、AB 的平行线,则以不在同一直线上的三点为顶点的平行四边形有三个。 由已知的三点坐标可根据图形平移的坐标性质,直接写出第四个顶点的坐标。 3、平面直角坐标系中直线和直线l2: 当l1∥l2时k1= k2; 4、二次函数中平行四边形的存在性问题: 解题思路:(1)先分类(2)再画图(3)后计算 二、精讲精练 1、已知抛物线y=ax2+bx+c与x轴相交于A、B两点(A、B分别在原点的左右两侧),与y轴正半轴相交于C 点,且OA:OB:OC=1:3:3,△ABC的面积为6,(如图1) (1)求抛物线的解析式; (2)坐标平面内是否存在点M,使得以点M、A、B、C为顶点四边形是平行四边形若存在,请求出点M的坐标;若不存在,请说明理由; (3)如图2,在直线BC上方的抛物线上是否存在一动点P,△BCP面积最大如果存在,求出最大面积,并指出此时P点的坐标;如果不存在,请简要说明理由. 初三数学二次函数经典题型 二次函数单元检测 (A) 姓名___ ____ 一、填空题: 1、函数2 1 (1)21m y m x mx +=--+是抛物线,则m = . 2、抛物线2 23y x x =--+与x 轴交点为 ,与y 轴交点为 . 3、二次函数2 y ax =的图象过点(-1,2),则它的解析式是 , 当x 时,y 随x 的增大而增大. 4.抛物线2)1(62 -+=x y 可由抛物线262 -=x y 向 平移 个单位得到. 5.抛物线342 ++=x x y 在x 轴上截得的线段长度是 . 6.抛物线() 422 2-++=m x x y 的图象经过原点,则=m . 7.抛物线m x x y +-=2 ,若其顶点在x 轴上,则=m . 8. 如果抛物线c bx ax y ++=2 的对称轴是x =-2,且开口方向与形状与抛物线 相同,又过原点,那么a = ,b = ,c = . 9、二次函数2 y x bx c =++的图象如下左图所示,则对称轴是 ,当函数值0y <时, 对应x 的取值范围是 . 10、已知二次函数2 1(0)y ax bx c a =++≠与一次函数2(0)y kx m k =+≠的图象相交于点 A (-2,4)和 B (8,2),如上右图所示,则能使1y 2y >成立的x 的取值范围 . 二、选择题: 11.下列各式中,y 是x 的二次函数的是 ( ) A .2 1xy x += B . 2 20x y +-= C . 2 2y ax -=- D .2 2 10x y -+= 2 2 3x y -= 12.在同一坐标系中,作2 2y x =、2 2y x =-、2 12 y x = 的图象,它们共同特点是 ( ) A . 都是关于x 轴对称,抛物线开口向上 B .都是关于y 轴对称,抛物线开口向下 B . 都是关于原点对称,顶点都是原点 D .都是关于y 轴对称,顶点都是原点 13.抛物线12 2+--=m mx x y 的图象过原点,则m 为( ) A .0 B .1 C .-1 D .±1 14.把二次函数122 --=x x y 配方成为( ) A .2 )1(-=x y B . 2)1(2--=x y C .1)1(2 ++=x y D .2)1(2 -+=x y 15.已知原点是抛物线2 (1)y m x =+的最高点,则m 的范围是( ) A . 1- 二次函数的动点问题 1.如图①,正方形ABCD 的顶点A B ,的坐标分别为()()01084,,,,顶点C D ,在第一象限.点P 从点A 出发,沿正方形按逆时针方向匀速运动,同时,点Q 从点()40E ,出发,沿x 轴正方向以相同速度运动.当点P 到达点C 时,P Q ,两点同时停止运动,设运动的时间为t 秒. (1)求正方形ABCD 的边长. (2)当点P 在AB 边上运动时,OPQ △的面积S (平方单位)与时间t (秒)之间的函数图象为抛物线的一部分(如图②所示),求P Q ,两点的运动速度. (3)求(2)中面积S (平方单位)与时间t (秒)的函数关系式及面积S 取最大值时点P 的坐标. (4)若点P Q ,保持(2)中的速度不变,则点P 沿着AB 边运动时,OPQ ∠的大小随着时间t 的增大而增大;沿着BC 边运动时,OPQ ∠的大小随着时间t 的增大而减小.当点P 沿着这两边运动时,使90OPQ =o ∠的点P 有 个. (抛物线()2 0y ax bx c a =++≠的顶点坐标是2424b ac b a a ?? -- ??? ,. [解] (1)作BF y ⊥轴于F . ()()01084A B Q ,,,, 86FB FA ∴==,. 10AB ∴=. (2)由图②可知,点P 从点A 运动到点B 用了10秒. 又1010101AB =÷=Q ,. P Q ∴,两点的运动速度均为每秒1个单位. (3)方法一:作PG y ⊥轴于G ,则PG BF ∥. GA AP FA AB ∴ =,即610 GA t =. 35GA t ∴=. 3 105OG t ∴=-. 4OQ t =+Q , ()113410225S OQ OG t t ? ?∴= ??=+- ?? ?. 二次函数与圆的专题复习 4.(2014?黑龙江哈尔滨)将抛物线y=﹣2x 2+1向右平移1个单位,再向上平移2个单位后所得到的抛物线为( ) A . y=﹣2(x+1)2﹣1 B . y ﹣2(x+1)2+3 C . y=﹣2(x ﹣1)2+1 D . y=﹣2(x ﹣1)2+3 5.(2014?舟山)当﹣2≤x ≤1时,二次函数y =﹣(x ﹣m )2+m 2+1有最大值4,则实数m 的值为( ) A . B . 或 C . 2或 D . 2或﹣或 6.(2014?毕节地区)抛物线y =2x 2,y =﹣2x 2,共有的性质是( ) A.开口向下 B.对称轴y 轴 C.都有最低点 D.y 随x 的增大而减小 7.(2014·台湾)已知a 、h 、k 为三数,且二次函数y =a (x ﹣h )2+k 在坐标平面上的图形通过(0,5)、(10,8)两点.若a <0,0<h <10,则h 之值可能为下列何者?( ) A .1 B .3 C .5 D .7 8.(2014?浙江宁波)已知点A (a ﹣2b ,2﹣4ab )在抛物线y =x 2+4x +10上,则点A 关于抛物线对称轴的对称点坐标为( ) 9.(2014·浙江金华)如图是二次函数2y x 2x 4=-++的图象,使y 1≤成立的x 的取值范围是( ) A .1x 3-≤≤ B .x 1≤- C .x 1≥ D .x 1≤-或x 3≥ 10. (2014年湖北黄石) 二次函数y=ax 2+bx+c (a≠0)的图象如图,则函数值y >0时,x 的取值范围是( )A . x <﹣1 B . x >3 C .﹣1<x <3 D . x <﹣1或x >3 11.(2014?陕西)二次函数y=ax 2+bx+c (a≠0)的图象如图,则下列结论中正确的是( ) A .c >﹣1 B . b >0 C .2a+b≠0 D .9a+c >3b 第9题图 第10题图 第11题图 第12题图 函数解题思路方法总结: ⑴求二次函数的图象与x轴的交点坐标,需转化为一元二次方程; ⑵求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式; ⑶根据图象的位置判断二次函数ax2+bx+c=0中a,b,c的符号,或由二次函数中a,b,c的符号判断 图象的位置,要数形结合; ⑷二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与x 轴的一个交点坐标,可由对称性求出另一个交点坐标. ⑸与二次函数有关的还有二次三项式,二次三项式ax2+bx+c﹙a≠0﹚本身就是所含字母x的二次函数;下面以a>0时为例,揭示二次函数、二次三项式和一元二次方程之间的内在联系: 动点问题题型方法归纳总结 动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。) 动点问题一直是中考热点,近几年考查探究运动中的特殊性:等腰三角形、直角三角形、 相似三角形、平行四边形、梯形、特殊角或 其三角函数、线段或面积的最值。 下面就此问题的常见题型作简单介绍,解题方法、关键给以点拨。 二、 抛物线上动点 5、(湖北十堰市)如图①, 已知抛物线32++=bx ax y (a ≠0)与x 轴交于点A (1,0)和点B (-3,0),与y 轴交于点C . (1) 求抛物线的解析式; (2) 设抛物线的对称轴与x 轴交于点M ,问在对称轴上是否存在点P ,使△CMP 为等腰三角形?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由. (3) 如图②,若点E 为第二象限抛物线上一动点,连接BE 、CE ,求四边形BOCE 面积的最大值,并求此时E 点的坐标. 注意:第(2)问按等腰三角形顶点位置分类讨论画图再由图形性质求点P 坐标----①C 为顶点时,以C 为圆心CM 为半径画弧,与对称轴交点即为所求点P ,②M 为顶点时,以M 为圆心MC 为半径画弧,与对称轴交点即为所求点P ,③P 为顶点时,线段MC 的垂直平分线与对称轴交点即为所求点P 。 第(3)问方法一,先写出面积函数关系式,再求最大值(涉及二次函数最值); 方法二,先求与BC 平行且与抛物线相切点的坐标(涉及简单二元二次方程组),再求面积。 共同点: 最新初中数学二次函数单元汇编含解析(3) 一、选择题 1.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线. 不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表: 下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线 9 2 t ; ③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m. 其中正确结论的个数是() A.1 B.2 C.3 D.4 【答案】B 【解析】 【分析】 【详解】 解:由题意,抛物线的解析式为y=ax(x﹣9),把(1,8)代入可得a=﹣1, ∴y=﹣t2+9t=﹣(t﹣4.5)2+20.25, ∴足球距离地面的最大高度为20.25m,故①错误, ∴抛物线的对称轴t=4.5,故②正确, ∵t=9时,y=0,∴足球被踢出9s时落地,故③正确, ∵t=1.5时,y=11.25,故④错误,∴正确的有②③, 故选B. 2.二次函数y=x2+bx的对称轴为直线x=2,若关于x的一元二次方程x2+bx﹣t=0(t为实数)在﹣1<x<4的范围内有解,则t的取值范围是() A.0<t<5 B.﹣4≤t<5 C.﹣4≤t<0 D.t≥﹣4 【答案】B 【解析】 【分析】 先求出b,确定二次函数解析式,关于x的一元二次方程x2+bx﹣t=0的解可以看成二次函数y=x2﹣4x与直线y=t的交点,﹣1<x<4时﹣4≤y<5,进而求解; 【详解】 解:∵对称轴为直线x=2, ∴b=﹣4, ∴y=x2﹣4x, 关于x的一元二次方程x2+bx﹣t=0的解可以看成二次函数y=x2﹣4x与直线y=t的交点, 二次函数知识点归纳及相关典型题 第一部分 基础知识 1.定义:一般地,如果c b a c bx ax y ,,(2 ++=是常数,)0≠a ,那么y 叫做x 的二次函数. 2.二次函数2 ax y =的性质 (1)抛物线2 ax y =的顶点是坐标原点,对称轴是y 轴. (2)函数2 ax y =的图像与a 的符号关系. ①当0>a 时?抛物线开口向上?顶点为其最低点; ②当0a 时,开口向上;当0