
求解线性卷积、循环卷积的课上例题
例:}1,1,1{)()(3==n R n x ,20≤≤n ;}1,2,3,4{)()4()(4=-=n R n n h ,30≤≤n ,
求线性卷积)(*)()(n h n x n y =和L 点循环卷积。 线性卷积:)(*)()(n h n x n y =∑∞
-∞
=-=
m m n h m x )
()(∑∞
-∞
=-=
m m n x m h )()(
1
y (n )={4, 7, 9, 6, 3, 1},50≤≤n ,非零数据长度6=4+3-1 ()(n h 长度为N ,)(n x 长度为M ,y (n )长度为1-+M N )
2)移位加权和法(以n 为变量) ∑=-=
2
1
)
()()(m m m m n h m x n y )2()2()1()1()()0(-+-+=n h x n h x n h x ,其中}1 1, ,1{)(=m x ,20≤≤m
y (n )={4, 7, 9, 6, 3, 1}50≤≤n
L 点循环卷积:)())(()()(1
n R m n h m x n y L L m L c ∑-=-=)())(()(1
n R m n x m h L L m L ∑-=-=
1)矩阵方程法(以m 为变量)
先将x (n )、h (n )补零到L 点长;再将其中一个序列周期延拓、翻褶、取主值区间的值、循环右移构成方阵,将另一个序列写成列矩阵,二者做矩阵乘法运算。
以用x (n )构成方阵为例。方阵第一行的构成:x (0)不动,将其它值从后往前倒过来写。下面各行依次对上一行循环右移一位,共L 行。
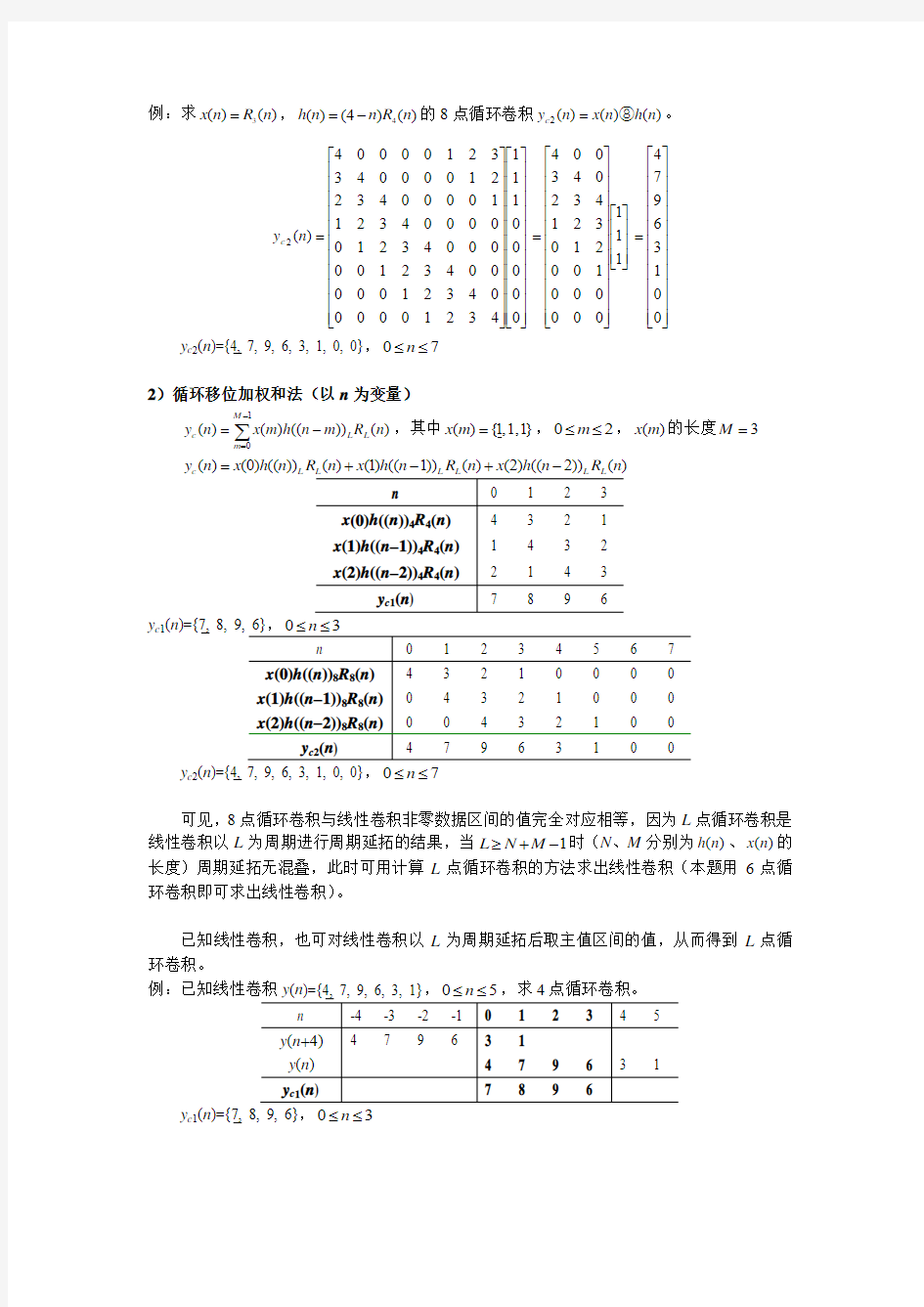
例:求)()(3n R n x =,)()4()(4n R n n h -=的4点循环卷积)()()(1n h n x n y c ④=。
????
??????=????????????????????=????????????????????=6987011143
21
14322143321
4123411
10
01111011110
1)(1n y c y c 1(n )={7, 8, 9, 6},30≤≤n
例:求)()(3n R n x =,)()4()(4n R n n h -=的8点循环卷积)()()(2n h n x n y c ⑧=。
??????????????????????????????????????????????
??????=0000011143
210000
04321000004321000004321000004321
10000432210000433210000
4)(2n y c ???????????????????
?
????????
???
?????=111000000100210321432043004??
??
??
?
?????
?
?????????????=
00136974 y c 2(n )={4, 7, 9, 6, 3, 1, 0, 0},70≤≤n
2)循环移位加权和法(以n 为变量)
)())(()()(10
n R m n h m x n y L M m L c ∑-=-=
,其中}1 1, ,1{)(=m x ,20≤≤m ,)(m x 的长度3=M
)())2(()2()())1(()1()())(()0()(n R n h x n R n h x n R n h x n y
L c -+-+=
y c 1(n
)={7, 8, 9, 6}y c 2(n )={4, 7, 9, 6, 3, 1, 0, 0}70≤≤n
可见,8点循环卷积与线性卷积非零数据区间的值完全对应相等,因为L 点循环卷积是线性卷积以L 为周期进行周期延拓的结果,当1-+≥M N L 时(N 、M 分别为)(n h 、)(n x 的长度)周期延拓无混叠,此时可用计算L 点循环卷积的方法求出线性卷积(本题用6点循环卷积即可求出线性卷积)。
已知线性卷积,也可对线性卷积以L 为周期延拓后取主值区间的值,从而得到L 点循环卷积。
y c 1(n )={7, 8, 9, 6}30≤≤n
第一章 1.什么是信号? 是信息的载体,即信息的表现形式。通过信号传递和处理信息,传达某种物理现象(事件)特性的一个函数。 2.什么是系统? 系统是由若干相互作用和相互依赖的事物组合而成的具有特定功能的整体。3.信号作用于系统产生什么反应? 系统依赖于信号来表现,而系统对信号有选择做出的反应。 4.通常把信号分为五种: ?连续信号与离散信号 ?偶信号和奇信号 ?周期信号与非周期信号 ?确定信号与随机信号 ?能量信号与功率信号 5.连续信号:在所有的时刻或位置都有定义的信号。 6.离散信号:只在某些离散的时刻或位置才有定义的信号。 通常考虑自变量取等间隔的离散值的情况。 7.确定信号:任何时候都有确定值的信号 。 8.随机信号:出现之前具有不确定性的信号。 可以看作若干信号的集合,信号集中每一个信号 出现的可能性(概率)是相对确定的,但何时出 现及出现的状态是不确定的。 9.能量信号的平均功率为零,功率信号的能量为无穷大。 因此信号只能在能量信号与功率信号间取其一。 10.自变量线性变换的顺序:先时间平移,后时间变换做缩放. 注意:对离散信号做自变量线性变换会产生信息的丢失! 11.系统对阶跃输入信号的响应反映了系统对突然变化的输入信号的快速响应能 力。(开关效应) 12.单位冲激信号的物理图景: 持续时间极短、幅度极大的实际信号的数学近似。 对于储能状态为零的系统,系统在单位冲激信号作 用下产生的零状态响应,可揭示系统的有关特性。
例:测试电路的瞬态响应。 13.冲激偶:即单位冲激信号的一阶导数,包含一对冲激信号, 一个位于t=0-处,强度正无穷大; 另一个位于t=0+处,强度负无穷大。 要求:冲激偶作为对时间积分的被积函数中一个因子, 其他因子在冲激偶出现处存在时间的连续导数. 14.斜升信号: 单位阶跃信号对时间的积分即为单位斜率的斜升信号。 15.系统具有六个方面的特性: 1、稳定性 2、记忆性 3、因果性 4、可逆性 5、时变性与非时变性 6、线性性 16.对于任意有界的输入都只产生有界的输出的系统,称为有界输入有界输出(BIBO )意义下的稳定系统。 17.记忆系统:系统的输出取决于过去或将来的输入。 18.非记忆系统:系统的输出只取决于现在的输入有关,而与现时刻以外的输入无关。 19.因果系统:输出只取决于现在或过去的输入信号,而与未来的输入无关。 20.非因果系统:输出与未来的输入信号相关联。 21.系统的因果性决定了系统的实时性:因果系统可以实时方式工作,而非因果系统不能以实时方式工作. 22.可逆系统:可以从输出信号复原输入信号的系统。 23.不可逆系统:对两个或者两个以上不同的输入信号能产生相同的输出的系统。 24.系统的时变性: 如果一个系统当输入信号仅发生时移时,输出信号也只产生同样的时移,除此之外,输出响应无任何其他变化,则称该系统为非时变系统;即非时变系统的特性不随时间而改变,否则称其为时变系统。 25.检验一个系统时不变性的步骤: 1. 令输入为 ,根据系统的描述,确定此时的输出 。 1()x t 1()y t
一、 实验目的 1. 理解卷积的概念及物理意义; 2. 通过实验的方法加深对卷积运算的图解方法及结果的理解。 二、实验设备 1.信号与系统实验箱 1台 2.双踪示波器 1台 三、实验原理 卷积积分的物理意义是将信号分解为冲激信号之和,借助系统的冲激响应,求解系统对任意激励信号的零状态响应。设系统的激励信号为)t (x ,冲激响应为)t (h ,则系统的零状态响应为)(*)()(t h t x t y =?∞∞ --=ττd t h t x )()(。 对于任意两个信号)t (f 1和)t (f 2,两者做卷积运算定义为: ?∞∞--=ττd t f t f t f )(2 )(1)(=)t (f 1*)t (f 2=)t (f 2*)t (f 1。 1. 两个矩形脉冲信号的卷积过程 两信号)t (x 与)t (h 都为矩形脉冲信号,如图9-1所示。下面由图解的方法(图9-1)给出两个信号的卷积过程和结果,以便与实验结果进行比较。 0≤<∞-t 2 10≤ ≤t 1 ≤≤t 4 1≤ ≤t ∞ <≤t 212 4 τ (b)(a)(c) (d)(e) (f) (g) (h)(i)2卷积结果
2. 矩形脉冲信号与锯齿波信号的卷积 信号)t (f 1为矩形脉冲信号,)t (f 2为锯齿波信号,如图9-2所示。根据卷积积分的运算方法得到)t (f 1和)t (f 2的卷积积分结果)t (f ,如图9-2(c)所示。 图9-2 矩形脉冲信号与锯齿脉冲信号的卷积积分的结果 3. 本实验进行的卷积运算的实现方法 在本实验装置中采用了DSP 数字信号处理芯片,因此在处理模拟信号的卷积积分运算时,是先通过A/D 转换器把模拟信号转换为数字信号,利用所编写的相应程序控制DSP 芯片实现数字信号的卷积运算,再把运算结果通过D/A 转换为模拟信号输出。结果与模拟信号的直接运算结果是一致的。数字信号处理系统逐步和完全取代模拟信号处理系统是科学技术发展的必然趋势。图9-3为信号卷积的流程图。 图9-3 信号卷积的流程图 四、实验内容 1. 检测矩形脉冲信号的自卷积结果 用双踪示波器同时观察输入信号和卷积后的输出信号,把输入信号的幅度峰峰值调节为4V ,再调节输入信号的频率或占空比使输入信号的时间宽度满足表中的要求,观察输出信号有何变化,判断卷积的结果是否正确,并记录表9-1。 实验步骤如下: (a) (b) (c)
连续时间信号的卷积运算的MATILAB实现 薛皓20091453 例1:已知两连续时间信号如图9-3所示,试用matlab求f(t)=f1(t)*f2(t),并绘出f(t)的时域波形图。 图1-1 连续时间信号波形图示例 实现上述过程的matlab命令如下: p=0.5; k1=0:p:2; f1=0.5*k1; k2=k1; f2=f1; [f,k]=sconv(f1,f2,k1,k2,p) 上述命令绘制的波形图也在图9-3中示出。图9-3中给出了抽样时间间隔p=0.5时的处理效果。而图9-4给出了抽样时间间隔p=0.01时的处理效果。
图1-2 例1的连续时间信号波形图 习题1:已知f1(t)=1(2t 1≤≤),f2(t)=1(3t 2≤≤),用matlab 实现其卷积并绘制出卷积曲线。 解:程序代码如下: >> p=0.01; k1=1:p:2; f1=ones(size(k1)).*(k1>1); k2=2:p:3; f2=ones(size(k2)).*(k2>2); f=conv(f1,f2); f=f*p; k0=k1(1)+k2(1); k3=k1(length(k1))+k2(length(k2)); subplot(2,2,1) plot(k1,f1) title('f1(t)') xlabel('t') ylabel('f1(t)') subplot(2,2,2) plot(k2,f2)
title('f2(t)') xlabel('t') ylabel('f2(t)') subplot(2,2,3) plot(k,f); h=get(gca,'position'); h(3)=2.5*h(3); 0 set(gca,'position',h) title('f(t)=f1(t)*f2(t)') xlabel('t') ylabel('f(t)') 绘制图形如图2-1所示。 图2-1 习题2:)1()2/1t ()t (2f ),1t ()t ()t (1f δ-+δ=-ε-ε=,求其卷积。 程序代码: p=0.01; t1=0:p:1; f1=ones(size(t1)).*(t1>0); t2=-0.5:p:1; f2=(t2==-0.5)-(t2==1); f=conv(f1,f2); f=f*p; t=-0.5:p:2;
1 信号与系统常用公式 一、周期信号的傅里叶级数 1.三角函数形式的傅里叶级数:0111()[cos()sin()]n n n f t a a n t b n t ωω∞ ==++∑,其中 01 011()t T t a f t dt T += ?,010112()cos()t T n t a f t n t dt T ω+=?,010112()sin()t T n t b f t n t dt T ω+=?。 2.指数形式的傅里叶级数:11()()jn t n f t F n e ωω∞ =-∞ =∑ ,其中0110 111()()t T jn t t F n f t e dt T ωω+-= ?。 二、傅里叶变换 1.傅氏正变换:()[()]()j t F F f t f t e dt ωω∞ --∞ ==? 2.傅氏逆变换:11()[()]()2j t f t F F F e d ωωωωπ ∞ --∞ ==? 3 1.拉氏正变换:0 ()[()]()st F s L f t f t e dt ∞ -==? 2.拉氏逆变换:11()[()]()2j st j f t L F s F s e ds j σσπ+∞ --∞ ==?
2 3 四、z 变换 1.z 正变换:0 ()[()]()k k X z Z x k x k z ∞ -===∑ 2.z 逆变换:111 ()[()]()2k C x k Z X z X z z dz j π--==? 3.z 变换的基本性质: 1.连续时间信号的卷积:121221()()()()()()f t f t f f t d f f t d ττττττ∞ ∞ -∞ -∞ *=-=-?? 2.离散时间信号的卷积:()()()()()()n n x k h k x n h k n h n x k n ∞ ∞ =-∞ =-∞ *=-=-∑∑ 3.卷积定理: (1)1212[()()]()()F f t f t F F ωω*=? (2)12121[()()]()()2F f t f t F F ωωπ?=* (3)1212[()()]()()L f t f t F s F s *=? (4)12121[()()]()()2L f t f t F s F s j π?=* (5)[()()]()()Z x k h k X z H z *= (6)1 [()()]()()2C z dv Z x k h k X v H j v v π?=?
已知x1(n)={2,3,2},x2(n)={1,2,3,4}(1)求出x2(m-n),当m=0,1,2,3时的序列;(2)计算出x1(n)与x2(n)的卷积;(3)用频域方法算出x1(n)与x2(n)的卷积 解:(1)m=0时,x(m-n)=x(-n) , x(-0)=x(-0+4)=1;x(-1)=x(-1+4)=4;x(-2)=3;x(-3)=2; 故x(-n)={1,4,3,2} 同理m=1时;x(m-n)=x(1-n)={2,1,4,3} 同理m=2时;x(m-n)=x(2-n)={3,2,1,4} 同理m=3时;x(m-n)=x(3-n)={4,3,2.1} (2)m=0时 3 =∑[{2,3,2,0}*{1,4,3,2}]=∑{2,12,6,0}=20 n=0 m=1时 3 =∑[{2,3,2,0}*{2,1,4,3}]=∑{4,3,8,0}=15 n=0 m=2时 3 =∑[{2,3,2,0}*{3,2,1,4}]=∑{6,6,2,0}=14 n=0
m=3时 3 =∑[{2,3,2,0}*{4,3,2.1}]=∑{8,9,4,0}=21 n=0 (3) x1(n)={2,3,2=}==> X1(k)={6, -2-2j, 2, 2j-2} x2(n)={1,2,3,4}==>X2(k)={10,-2+2j,-2,-2-2j} X1(k)?X2(k)={60, 8,- 4, 8} 令Y(k)=X1(k)·X2(k) y(n)=x1(n)x2(n) IDFT后 3 3 y(n)=(1/N )∑Y(k)e^(j(2π/4)kn)=(1/N )∑Y(k)(-j)^(kn) k=0 k=0 ={ 18,16,10,21}
卷积运算 信号的卷积运算是信号处理领域中最重要的运算之一。随着对信号与系统理论研究的深入,特别是计算机技术的不断发展,不仅使卷积方法在很我领域得到了很广泛的应用,而且卷积运算的逆运算---反卷积的问题也受到了越来越大的重视和应用。 比如,在语音识别、地震勘探、超声诊断、光学成像、系统辨识及其他诸多信号处理领域中,甚至可以说卷积与反卷积的问题无处不在,而且很多的问题,都是有待深入研究的课题。 所以,大家要切实理解和掌握好卷积分运算的各个方面,打好牢固的基础。下面,我们来看看卷积的定义是怎样的。 信号的卷积积分(简称卷积),定义为: 简记为,其中的星号是卷积运算符。注意不要与我们在编写计算机程序时所用的乘法的表示符号搞混了。在信号处理课程里,乘法往往是用居中的点来表示的,或者干脆不写居中的点,而直接将要进行乘积运算的信号(包括直流信号---它是一个常数)连在一起写。 信号的卷积运算对应着一定的物理背景,这要在我们进一步学习了关于系统的激励与响应的关系之后,才能更深入地理解。 不仅如此,信号的卷积运算还对应着一定的几何解释。从定义式我们可以看出:(1) 在积分式中,信号自变量改变了符号,这对应在几何波形上,就是将信号进行了反褶变换;(2) 并且,信号f2的波形 位置与积分变量的取值有关,积分变量在积分限内的不断变化,将导致信号的波形发生移动,即是对它不断进行平移操作;(3) 最后,每当信号处在一个新位置,都要与信号f1相乘,且依据积分的定义,要将这些乘积加起来,而其结果实际上对应着两信号波形相交部分的面积。所以,卷积运算可以用几何图解方式来直观求解。 下面我们来说明如何用它的几何意义来求解两信号的卷积。 将信号的自变量改为,信号变为。对任意给定的,卷积的计算过程为: (a) 将关于r进行反褶得到; (b) 再平移至t0得到; (c) 与相乘得到; (d) 对r进行积分得,即; 不断变化,就可以得到s(t)。
卷积积分与卷积 一、摘要: 近十年来,由于电子技术和集成电路工艺的飞速发展,电子计算机已为信号的处理提供了条件。信号与系统分析理论应用一直在扩大,它不仅应用于通信、雷达、自动控制、光学、生物电子学、地震勘探等多种领域,而且对社会和自然学科也具有重要的指导意义。 卷积运算是线性时不变系统的一个重要工具,随着信号与系统理论研究的深入,卷积运算得到了更广泛的应用。卷积运算有很多种解法,对于一般无限区间而言,可用定义法直接求解。而本文通过图解法、卷积性质法、简易算法对有限区间卷积积分和卷积和分别进行求解,最后进行了相关的比较。 二、关键词: 信号与系统;卷积;图解法;卷积性质法;简易算法 三、正文: 卷积在信号与系统理论分析中,应用于零状态响应的求解。对连续时间信号 的卷积称为卷积积分,定义式为: ∞ f t=f1τf2t?τdτ ?f1(t)?f2(t) ?∞ 对离散时间信号的卷积称为卷积和,定义式为: ∞ f n=f1m f2n?m ?f1(n)?f2(n) m=?∞ 1、卷积积分的解法 (1)图解法 图解法适合于参与卷积运算的两函数仅以波形形式给出,或者已知函数的波形易于画出的情况。利用图解法能够直接观察到许多抽象关系的具体情况,而且容易确定卷积积分的上、下限,是一种极有效的方法。
如果给定f 1 t 和f 2(t ),要求这两个函数的卷积积分f t =f 1(t )?f 2(t ),首先要改变自变量,即将f 1 t 和f 2(t )变成f 1 τ 和f 2(τ),这时函数图形与原来一样,只是横坐标变为了t ,然后再经过以下四个步骤: (1)反褶,即将f 2(τ)进行反褶,变为f 2(?τ); (2)时移,即将f 2(?τ)时移t ,变为f 2 t ?τ =f 2[?(τ?t )],当t >0时,将f 2(?τ)右移t ,而当t <0时,将f 2(?τ)左移t ; (3)相乘,即将f 1 t 与f 2 t ?τ 相乘得到f 1 t f 2 t ?τ ; (4)积分,即将乘积f 1 t f 2 t ?τ 进行积分,积分的关键是确定积分限。一般是将f 1 t f 2 t ?τ 不等于零的区间作为上下限,而当取不同的值时,不为零的区间有所变化,因此要分成不同的区间来求卷积。 例1、已知f 1 t 和f 2(t )的波形如图1-1所示,求f t =f 1(t )?f 2(t )。 图1-1 解:(1)变量代换,将变量f 1 t 和f 2(t )变成f 1 τ 和f 2(τ),此时波形不变; (2)将f 2(τ)进行反褶,变为f 2(?τ),图1-2; (3)时移,即将f 2(?τ)时移t ,图1-3; (4)相乘,即将f 1 t 与f 2 t ?τ 相乘得到f 1 t f 2 t ?τ ,图1-4~8; 图 1-3 图1-2 [τ] [τ]
信号与系统论文 卷积算法 姓名:曹九一 班级:电气10-9 学号:29号
卷积算法 摘要:卷积是在信号与线性系统的基础上或背景中出现的,脱离这个背景单独 谈卷积是没有意义的。卷积运算是一种有别于其他运算的新型运算,是信号处理领域中一种常用的重要工具。随着信号与系统理论的研究的深入及计算机技术发展,不仅使卷积方法在很多领域得到很广泛的应用,而且卷积运算的逆运算------反卷积的问题也越来越受重视和应用。在语言识别、现代地震勘测,超声诊断,光学诊断,光学成像,系统辨识及其他诸多信号处理领域中卷积和反卷积无处不在,而且许多都是有待深入开发研究的课题。用计算机来进行信号与系统分析,了解并灵活运用卷积运算去解决问题,提高自身的理论知识水平和动手能力,才是学习卷积运算的真正目的。 卷积运算的理论运算 1 卷积的概念及表达方式 卷积是信号处理中经常用到的运算。其离散型基本的表达式为: ∑=-=*=n m m n h n x n h n x n y 0 ) ()()()()( 其连续型基本的表达式为: ?+∞ ∞ -= *=τ ττd t h x t h t x t )-()()()()(y 换而言之,假设两个信号f 1(t)和f 2(t),两者做卷积运算定义为 f(t)d 做一变量代换不难得出: f(t)d=f 1(t)*f 2(t)=f 2(t)*f 1(t) 2 阶梯函数卷积 所谓阶梯函数,即是可以用阶梯函数u(t) 和u(t-1)的线性组合来表示的函数,可以看做是一些矩形脉冲的集合,图1-1给除了两个阶梯函数的例子
1—1 其中 3)-u(t -2)-2u(t -1)-u(t 2u(t)f(t)+=, 3)-3u(t -2)-2u(t 1)-u(t -2u(t) h(t)+=。 以图1—1中两个阶梯函数为例介绍本文提出的阶梯函数卷积算法。 根据卷积的性质(又称为杜阿美尔积分),上述f(t)与h(t)的卷积等于f(t)的导数与 h(t)的积分的卷积,即: ()t d h dt t d t h t ?+∞ ∞ -= )t *) (f )(*)(f ( 由于f(t)为阶梯函数,因此其导数也为冲击函数及其延时的线性组合, 如图1—2(a ) 所示。
2.1 选择题(每小题可能有一个或几个正确答案,将正确的题号填 入( )内) 1.系统微分方程式),()(),(2)(2)(t u t x t x t y dt t dy ==+若 3 4)0(=-y ,解得完全响应y (t )=)0(,13 12≥+-t e t 当 则零输入响应分量为——————————— ( 3 ) (1)t e 23 1- (2)21133t e -- (3)t e 23 4- (4)12+--t e 2.已知)()(),()(21t u e t f t u t f at -==,可以求得=)(*)(21t f t f ———— —( 3 ) (1)1-at e - (2)at e - (3))1(1at e a -- (4)at e a -1 3.线性系统响应满足以下规律————————————( 1、4 ) (1)若起始状态为零,则零输入响应为零。 (2)若起始状态为零,则零状态响应为零。 (3)若系统的零状态响应为零,则强迫响应也为零。 (4)若激励信号为零,零输入响应就是自由响应。 4.若系统的起始状态为0,在x (t )的激励下,所得的响应为—— —( 4 ) (1)强迫响应;(2)稳态响应;(3)暂态响应;(4)零状态响应。 2.2 是非题(下述结论若正确,则在括号内填入√,若错误则填入 ×)
1.零输入响应就是由输入信号产生的响应。 ( × ) 2.零状态响应是自由响应的一部分。 ( × ) 3.若系统起始状态为零,则系统的零状态响应就是系统的强迫响应 ( × ) 4.当激励为冲激信号时,系统的全响应就是冲激响应。 ( × ) 5.已知)2()1()(),1()1()(21---=--+=t u t u t f t u t u t f ,则f 1(t )*f 2 (t )的非零值区间为(0,3)。 ( √ ) 2.3 填空题 1.=-t e t *)(δt e - ()at t e δ-*=at e - 2.=+t t 0cos *)1(ωδ0cos (1)t ω+ =-)(cos *)(0τωδt t 0cos ()t ωτ- =--)2 (*)cos 1(πδt t 1cos()2t π-- 3.=)](*)([t u t u dt d ()u t =*)]()([t tu t u dt d ()tu t =?? ?????∞-t d u t u dt d λλ)(*)(()tu t =-)](*)([t u t u e dt d t ()t e u t - 4.已知),()1()(),1()()(21t u t u t f t u t u t f -+=--=则)(*)(21t f t f 的非 零值区间为( -1 ,1 )
卷积积分与卷积和初步分析 一、摘要: 近十年来,由于电子技术和集成电路工艺的飞速发展,电子计算机已为信号的处理提供了条件。信号与系统分析理论应用一直在扩大,它不仅应用于通信、雷达、自动控制、光学、生物电子学、地震勘探等多种领域,而且对社会和自然学科也具有重要的指导意义。 卷积运算是线性时不变系统的一个重要工具,随着信号与系统理论研究的深入,卷积运算得到了更广泛的应用。卷积运算有很多种解法,对于一般无限区间而言,可用定义法直接求解。而本文通过图解法、卷积性质法、简易算法对有限区间卷积积分和卷积和分别进行求解,最后进行了相关的比较。 二、关键词: 信号与系统;卷积;图解法;卷积性质法;简易算法 三、正文: 卷积在信号与系统理论分析中,应用于零状态响应的求解。对连续时间信号的卷积称为卷积积分,定义式为: 对离散时间信号的卷积称为卷积和,定义式为: 1、卷积积分的解法 (1)图解法 图解法适合于参与卷积运算的两函数仅以波形形式给出,或者已知函数的波形易于画出的情况。利用图解法能够直接观察到许多抽象关系的具体情况,而且容易确定卷积积分的上、下限,是一种极有效的方法。
如果给定 和 ,要求这两个函数的卷积积分 ,首先要改变自变量,即将 和 变成 和 ,这时函数图形与原来一样,只是横坐标变为了 ,然后再经过以下四个步骤: (1)反褶,即将 进行反褶,变为 ; (2)时移,即将 时移 ,变为 ,当 时,将 右移 ,而当 时,将 左移 ; (3)相乘,即将 与 相乘得到 ; (4)积分,即将乘积 进行积分,积分的关键是确定积分限。一般是将 不等于零的区间作为上下限,而当取不同的值时,不为零的区间有所变化,因此要分成不同的区间来求卷积。 例1、已知 和 的波形如图1-1所示,求 。 图1-1 解:(1)变量代换,将变量 和 变成 和 ,此时波形不变; (2)将 进行反褶,变为 ,图1-2; (3)时移,即将 时移 ,图1-3; (4)相乘,即将 与 相乘得到 ,图1-4~8; 图 1-3 图 1-2
x( t ) 或 x( τ ) t 或 h( -τ h( t - τ ) x( τ ) ? 实验 3 信号卷积实验 一、实验目的 1. 理解卷积的概念及物理意义; 2. 通过实验的方法加深对卷积运算的图解方法及结果的理解。 二、实验原理说明 卷积积分的物理意义是将信号分解为冲激信号之和,借助系统的冲激响应,求解系统对任意激励信号的零状态响应。设系统的激励信号为 x( t ) ,冲激响应为h( t ) ,则系统的零状 态响应为 y (t ) = x (t )* h (t ) = ∞ x (t )h (t - τ )d τ 。 -∞ 对于任意两个信号 f 1 ( t ) 和 f 2 ( t ) ,两者做卷积运算定义为: ∞ f (t ) = ?-∞ f (t ) f 2(t -τ )d τ = f 1 ( t ) * f 2 ( t ) = f 2 ( t ) * f 1 ( t ) 。 1 1. 两个矩形脉冲信号的卷积过程 两信号 x( t ) 与 h( t ) 都为矩形脉冲信号,如图 3-1 所示。下面由图解的方法(图 3-1)给 出两个信号的卷积过程和结果,以便与实验结果进行比较。 ) 1 (a) τ 1 (b) τ τ (c) τ τ (d) - ∞ < t ≤ 0 (e) 0 ≤ t ≤ 1 2 (f) 1 ≤ t ≤ 1 2 (g) 1 ≤ t ≤ 7 1 1 7 2 2 4 4 (h) 2 ≤ t < ∞ (i) 卷积结果 图 3-1 两矩形脉冲的卷积积分的运算过程与结果 2. 矩形脉冲信号与锯齿波信号的卷积 信号 f 1 ( t ) 为矩形脉冲信号, f 2 ( t ) 为锯齿波信号,如图 3-2 所示。根据卷积积分的运算 方法得到 f 1 ( t ) 和 f 2 ( t ) 的卷积积分结果 f ( t ) ,如图 3-2(c)所示。 h( t ) h( τ ) t 或 h( t - τ ) x( τ ) h( t - τ ) x( τ ) x( τ ) h( t - τ x( τ ) h( t - τ ) y( t ) = x( t )* h( t )
第三章信号的分解与合成 1、某周期偶函数f(t),其傅里叶级数中(含直流分量/不含正弦分量) 2、周期性冲激序列的傅里叶变换时(周期性冲激函数) 24、傅里叶级数(不适用非周期函数) 3、 4、 5、如图所示的傅里叶级数只包含(正弦分量/正弦分量的偶次谐波) 6、
7、若周期信号是奇函数,则其傅氏级数中不会含有(直流分量) 8、非周期的取样函数时间信号,其频谱是(频域的门函数) 9、 103/4 11、周期矩形脉冲的谱线幅度(与脉冲幅度有关/与脉冲周期有关) 12、周期矩形脉冲的谱线间隔与(脉冲宽度无关/脉冲幅度有关/脉冲周期有关) 13、以下不属于周期信号频谱特点的是(振幅频谱) 14、以下属于周期信号频谱特点的是(收敛频谱) 21、非周期的取样函数时间信号,其频谱是(频域的门函数) 22、周期信号的傅里叶系数(可正可负) 35、周期性时间信号的持续时间越长,其频带(越窄) 36、周期性时间信号的频带宽度与信号的持续时间成(反比) 27、周期性非正弦连续时间信号的频谱,其一般特点为(离散性,谐波性,收敛性) 35、连续周期信号的频谱的特点是(离散、非周期频谱) 15、周期矩形脉冲周期变大,谱线间隔(变密) 34、狄里赫利条件是傅里叶级数存在的(充分条件) 16、 17、 18、
19、 29、 20、 23、 25、其按段光滑,故可展开为傅里叶级数,由系数公式得bn=(0) 26、 28、
29、 30、 31、 37、 32、 33、 36、 第三章第四节傅里叶变换的性质与应用 1已知f t?Fφ,则f(±at)的傅里叶变换为(1 a F±φ a ) 2、设f t?Fφ,若f1t?1 a F±φ a e(±b)jω则f1t为(f±at+(±b)a)