
复旦版《2017年度中国医院排行榜》完整版
复旦版《2017年度中国医院排行榜》和《2017年度中国医院专科声誉和综合排行榜》今天正式发布。这是复旦大学医院管理研究所连续第九年发布“复旦版医院排行榜”。9年来,复旦大学医院管理研究所借鉴美国“最佳医院排行榜”的评价方法,以临床学科水平、专科声誉为核心,兼顾当年的科研产出。由于评价方法的科学性,排行榜的评选结果亦得到医疗行业广泛认可。评选专家库人数从去年的4175名提高至今年的4630名;与此同时,专家有效回执数也创历史新高,从去年的2657份提高到2964份,有效回复率从第一年的44.24%上升为64.1%。
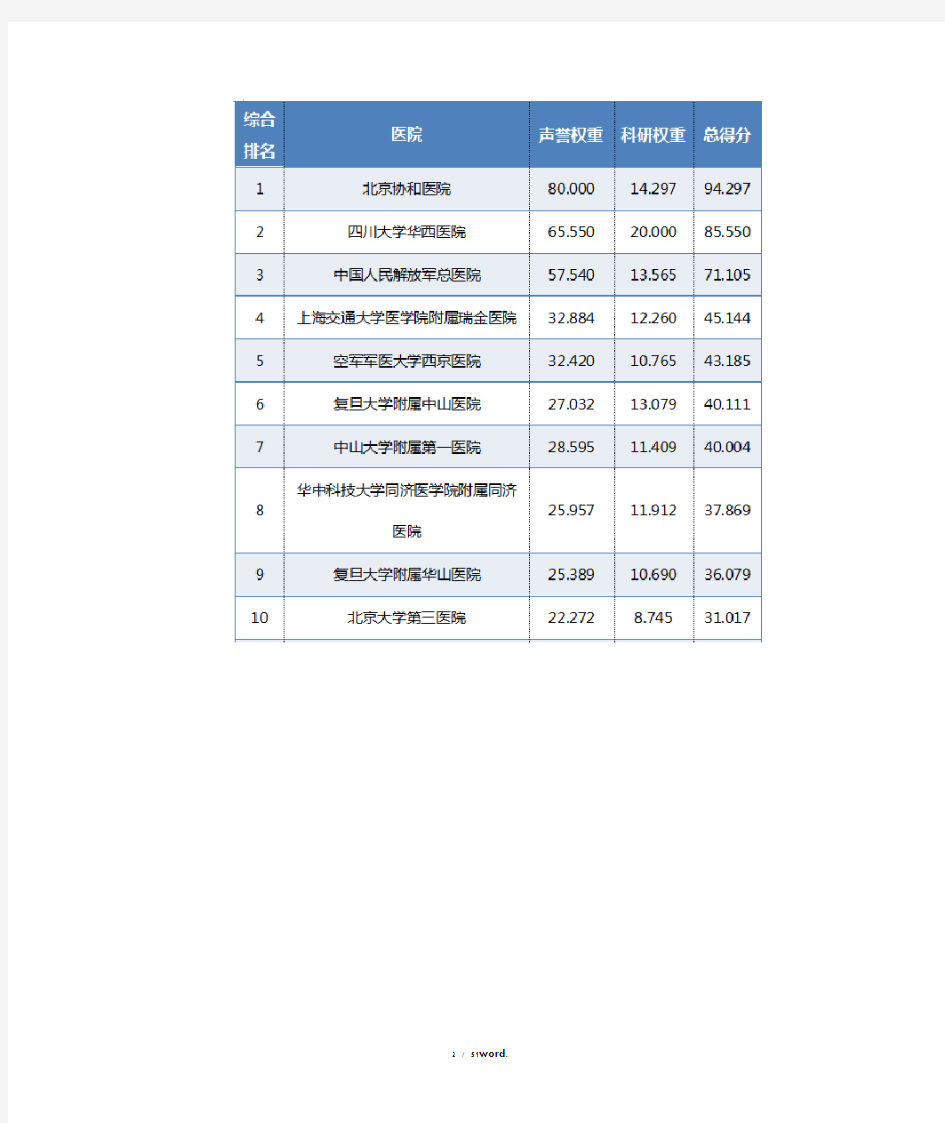
北京协和医院、四川大学华西医院和中国人民解放军总医院荣膺“2017年度中国医院排行榜(综合)”前三甲,这已是三家医院连续九年雄霸综合排名前三位。
作为医疗行业最受关注的榜单之一,复旦版医院排行榜今年有何亮点?
今年,为适应“健康中国”理念的深入人心和医院临床学科的不断发展,在评选中增加了生殖医学科、变态反应科和健康管理学科。
今年排行榜的另一个亮点是,以往仅在医院排名中计入“科研”分(即声誉占80%,科研占20%),而专科仅有声誉排名。今年40个专科除了声誉排名榜,另有一个专科综合排名榜,也就是说,由专家评审的声誉得分由100%权重调整为80%,剩余的20%权重被赋予该专业在2017年度进行的科学研究(由该学科在2017年度的国家自然科学基金、国家重大科研项目等科研投入和2017年度的科研论文、科技成果的科研产出构成)。
2017年度医院排行榜(综合)
复旦版《中国最佳医院排行榜》借鉴美国“最佳医院排行榜”的方法,坚持以临床学科水平、专科声誉为核心,兼顾当年的科研产出,充分结合中国的现实国情,采信符合中国国情的权威第三方数据这一方法学不会变,评选结果已被广泛认可!这与复旦版排行榜从诞生至今,实打实做到“以临床声誉为主要导向”这一不变目标有关。评议医院排名时,学科建设和临床能力在计分、计算时的权重达80%,科研成果权重为20%。
复旦大学医院管理研究所所长高解春表示,一个成功的顶尖医院或顶尖学科,临床声誉和科研能力是主要标志。一个不搞临床研究的临床学科不可能有创新、引领和大发展复旦大学医院管理研究所从2010年8月开始,以同行评议的方式,启动了全国首家也是唯一的《中国医院专科声誉排行榜》和《中国医院排行榜》评比工作。复旦版医院排行榜将继续坚持以学科建设为特色,临床能力为根本,始终把临床专科声誉排名作为其主要核心。
1. 解: (1)相等. 因为两函数的定义域相同,都是实数集R ; x =知两函数的对应法则也相同;所以两函数相等. (2)相等. 因为两函数的定义域相同,都是实数集R ,由已知函数关系式显然可得两函数的对应法则也相同,所以两函数相等. (3)不相等. 因为函数()f x 的定义域是{,1}x x x ∈≠R ,而函数()g x 的定义域是实数集R ,两函数的定义域不同,所以两函数不相等. 2. 解: (1)要使函数有意义,必须 400x x -≥?? ≠? 即 40x x ≤?? ≠? 所以函数的定义域是(,0)(0,4]-∞U . (2)要使函数有意义,必须 30lg(1)010x x x +≥?? -≠??->? 即 301x x x ≥-?? ≠??
线性代数课后习题答案 习题一 1.2.3(答案略) 4. (1) ∵ (127435689)415τ=+= (奇数) ∴ (127485639)τ为偶数 故所求为127485639 (2) ∵(397281564)25119τ=+++= (奇数) ∴所求为397281564 5.(1)∵(532416)421106τ=++++= (偶数) ∴项前的符号位()6 11-=+ (正号) (2)∵325326114465112632445365a a a a a a a a a a a a = (162435)415τ=+= ∴ 项前的符号位5(1)1-=- (负号) 6. (1) (2341)(1)12n n τ-?L L 原式=(1)(1)!n n -=- (2)()((1)(2)21) 1(1)(2)21n n n n n n τ--??---??L L 原式=(1)(2) 2 (1) !n n n --=- (3)原式=((1)21) 12(1)1(1) n n n n n a a a τ-?--L L (1) 2 12(1)1(1)n n n n n a a a --=-L 7.8(答案略) 9. ∵162019(42)0D x =?-?+?--?= ∴7x = 10. (1)从第2列开始,以后各列加到第一列的对应元素之上,得 []11(1)1110 01(1)1110 (1)1 1 (1)1 1 1 x x n x x x n x x x n x x n x x +-+--==+-+--L L L L L L L L L L L L L L L L L L L L L []1(1)(1)n x n x -=+-- (2)按第一列展开: 11100000 (1)(1)0 0n n n n n y x y D x x y x y x y -++=?+-=+-L L L L L L L L
206 习题十 1. 根据二重积分性质,比较 ln()d D x y σ +?? 与 2 [ln()]d D x y σ +?? 的大小,其中: (1)D 表示以(0,1),(1,0),(1,1)为顶点的三角形; (2)D 表示矩形区域{(, )|35,02}x y x y ≤≤≤≤. 解:(1)区域D 如图10-1所示,由于区域D 夹在直线x +y =1与x +y =2之间,显然有 图10-1 12x y ≤+≤ 从而 0l n ()1 x y ≤+< 故有 2 l n ()[l n ()] x y x y +≥+ 所以 2 l n ()d [l n ()]d D D x y x y σσ+≥ +?? ?? (2)区域D 如图10-2所示.显然,当(,)x y D ∈时,有3x y +≥ . 图10-2 从而 ln(x +y )>1 故有 2 l n ()[l n ()] x y x y +<+ 所以 2 l n ()d [l n ()]d D D x y x y σσ+< +?? ?? 2. 根据二重积分性质,估计下列积分的值: (1 ),{(,)|02,02}D I D x y x y σ==≤≤≤≤??; (2)2 2 sin sin d ,{(,)|0π,0π}D I x y D x y x y σ==≤≤≤≤??; (3)2 2 2 2 (49)d ,{(,)|4}D I x y D x y x y σ= ++=+≤?? . 解:(1)因为当(, )x y D ∈时,有02x ≤≤, 02y ≤≤
207 因而 04xy ≤≤. 从而 2≤≤故 2d d d D D σσσ≤ ≤ ?? ?? ?? 即 2d d D D D σσσ ≤ ≤???? 而 d D σσ =?? (σ为区域D 的面积),由σ=4 得 8D σ≤ ≤?? (2) 因为2 2 0sin 1,0sin 1x y ≤≤≤≤,从而 2 2 0sin sin 1x y ≤≤ 故 22 0d sin sin d 1d D D D x y σσσ ≤ ≤ ?? ?? ?? 即2 2 sin sin d d D D x y σσσ ≤ ≤ =?? ?? 而2 π σ= 所以222 0sin sin d π D x y σ≤ ≤?? (3)因为当(,)x y D ∈时,2 2 04x y ≤+≤所以 2 2 2 2 9494()925x y x y ≤++≤++≤ 故 22 9d (49)d 25d D D D x y σσσ ≤ ++≤ ?? ?? ?? 即 2 2 9(49)d 25D x y σσσ ≤ ++≤?? 而 2 π24πσ=?= 所以 22 36π(49)d 100πD x y σ≤ ++≤?? 3. 根据二重积分的几何意义,确定下列积分的值: (1 ) 222 (, {(,)|};D a D x y x y a σ- =+≤?? (2 ) 2 2 2 , {(,)|}.D D x y x y a σ=+≤?? 解:(1 ) (, D a σ-?? 在几何上表示以D 为底,以z 轴为轴,以(0,0,a )为顶点的圆锥的体积,所以
线性代数(低分数版) 习题一 1.2.3(答案略) 4. (1) ∵ (奇数) ∴为偶数 故所求为 (2) ∵(奇数) ∴所求为397281564 5.(1)∵ (偶数) ∴项前的符号位(正号) (2)∵ ∴项前的符号位(负号) 6. (1) (2) (3)原式= 7.8(答案略) 9. ∵ ∴ 10. (1)从第2列开始,以后各列加到第一列的对应元素之上,得 (2)按第一列展开: (3) 习题二 1.2.3.4.5(答案略) 6. 设为与可交换的矩阵,则有 即 解之得 7. (1),记为 ,记为
(2)即 8(答案略) 9. 10.(1) (2) = 11. ∵ ∴ 反之若 , 则 ,即 12. (1) 设∵∴ 又∵∴ 又 当时,有 ∴ (2)设,则 ∵∴ 当时,有 故即 13.(1) ∵∴为对称矩阵 同理也为对称矩阵 (2)∵ ∴为对称矩阵 又∵ ∴为反对称矩阵 (3)∵ 由(2)知,为对称矩阵,为反对称矩阵 故可表示成一个对称矩阵与一个反对称矩阵的和。 14. (1)必要性:∵ ∴ 充分性:∵ ∴ (2) 必要性:∵ ∴ 充分性:∵ ∴ (3) 必要性:∵ ∴ 即 充分性:∵ ∴ 15(答案略) 16. ∵ ∴可逆。
且 17. ∵ ∴可逆,且 18.(答案略) 19. ∵,若可逆,则 ∴故可逆,且 20.设,∵是对称矩阵∴记,则 ,即为对称矩阵,又∵ , ∴为对称矩阵。 21.(1)设,则 (2)∵∴ 又∵ ∴ 于是即 (3)∵∴ 于是 (4) (注意加条件:可逆) ∵可逆∴ ∴ 22. ∵∴ 23. 24.(答案略) 25. ∵∴ ∴可逆,且 26. ∵∴ 又∵, , ∴ 27(答案略) 28. ∵∴ 又∵∴ 故 29. ∵∴ ∴ 30.(答案略) 31.(1) (2) 32. 33. (1) ∵ ∴ (2) ∵
第一章课后答案 一、 1. 5)1(122211 2=-?-?=-; 2. 1)1)(1(1 1123222 2 --=-++-=++-x x x x x x x x x x ; 3. b a ab b a b a 222 2 -= 4.5361582732559841 31 11=---++= 5.比例)第一行与第三行对应成(,00 000 0=d c b a 6.1866627811 32213 3 21=---++=。 二.求逆序数 1. 55 1243 1 2 2 =↓↓↓↓↓ τ即 2. 52 134 2 3 =↓↓↓↓τ即 3. 2 ) 1(12)2()1(1 2)1(0 1 ) 2() 1(-= +++-+-=-↓↓-↓-↓n n n n n n n n ΛΛ τ即 4. 2 )1(* 2]12)2()1[()]1(21[2 4)22()2()12(310 1 2 1 1 1 -=+++-+-+-+++=--↓↓-↓-↓-↓↓↓n n n n n n n n n n n ΛΛΛ Λ τ 三.四阶行列式中含有2311a a 的项为4234231144322311a a a a a a a a +- 四.计算行列式值
1. 071 108517002 02145 9001577 1 1 202150202142701047 110 0251020214214 43412321=++------r r r r r r r r 2. 310 0100001 0111130 11110111101111130 1131013110311130 1111011110111104 321-=---?=? =+++c c c c 3.abcdef adfbce ef cf bf de cd bd ae ac ab 4111 111 1 11=---=--- 4. d c d c b a d c b a 10 10 1110 11 110 1 10011001--------按第一行展开 ad cd ab d c d a d c ab +++=-+ ---=)1)(1(11 1111 5. b a c c b c a b a a c b a c c b c a b a a b b a c c c b c a b b a a a b a c c c b c a b b a a c b a --------------=------202022202022222222222222 其中
261 习题十一 3.计算下列对坐标的曲线积分: (1)() 22d -?L x y x ,其中L 是抛物线y =x 2上从点(0,0)到点(2,4)的一段弧; (2)d L xy x ? 其中L 为圆周(x -a )2+y 2=a 2(a >0)及x 轴所围成的在第一象限内的区域的整个边界(按逆时针方向绕行); (6)()322d 3d d x x zy y x y z Γ++-?,其中Γ是从点(3,2,1)到点(0,0,0)的一段直线; 解:(1)L :y =x 2,x 从0变到2, ()()2 22224 35001156 d d 3515 L x y x x x x x x ??-=-=-=-?????? (2)如图11-1所示,L =L 1+L 2.其中L 1的参数方程为 图11-1 cos 0πsin x a a t t y a t =+?≤≤?=? L 2的方程为y =0(0≤x ≤2a ) 故 ()()()()() 12 π 200π32 0π π322003 d d d 1+cost sin cos d 0d sin 1cos d sin d sin dsin π 2L L L a xy x xy x xy x a a t a a t t x a t t t a t t t t a =+'=?++=-+=-+=-???????? (6)直线Γ的参数方程是32=??=??=?x t y t z t t 从1→0.
262 故()()3220322103 10 4 1 d 3d d 27334292d 87d 187487 4x x zy y x y z t t t t t t t t t Γ++-??=?+??+-???==?=-??? 7.应用格林公式计算下列积分: (1)()()d d 24356+-++-? x y x y x y Γ , 其中L 为三顶点分别为(0,0),(3,0)和(3,2)的三角形正向边界; 解:(1)L 所围区域D 如图11-4所示,P =2x -y +4, Q =3x +5y -6,3Q x ?=?,1P y ?=-?,由格林公式得 ()()d d 24356d d 4d d 4d d 14322 12 L D D D x y x y x y Q P x y x y x y x y +-++-????-= ????? ===???=??????? 8.利用曲线积分,求下列曲线所围成的图形的面积: (1)星形线x = a cos 3t ,y = a sin 3t ; 解:(1) ()()()()()2π 3202π2π242222002π20 2π202π202d sin 3cos d sin 33sin cos d sin 2sin d 4 3d 1cos 41cos 2163d 1cos 2cos 4cos 2cos 416 312π+d cos 2cos61623π8L A y x a t a t t t a t t t a t t t a t t t a t t t t t a t t t a =-=-?-==?= --=--+??=+????=??????? 9.证明下列曲线积分与路径无关,并计算积分值: (2)()()()()3,423221,2d d 663x y xy y x y xy +--? ; (3)()() 1,22 1,1d d x y x x y -?沿在右半平面的路径;
第十章 多元函数积分学(Ⅰ) 一元函数积分学中,曾经用和式的极限来定义一元函数()f x 在区间[a,b]上的定积分,并且已经建立了定积分理论,本章我们将推广到多元函数,建立多元函数积分学理论。 第一节 二重积分 教学目的: 1、熟悉二重积分的概念; 2、了解二重积分的性质和几何意义,知道二重积分的中值定理; 3、掌握二重积分的(直角坐标、极坐标)计算方法; 4、能根据积分区域和被积函数正确选择积分顺序 教学重点: 1、二重积分的性质和几何意义; 2、二重积分在直角坐标系下的计算 教学难点: 1、二重积分的计算; 2、二重积分计算中的定限问题 教学容: 一、二重积分的概念 1. 曲顶柱体的体积 设有一立体, 它的底是xOy 面上的闭区域D , 它的侧面是以D 的边界曲线为准线而母线平行于z 轴的柱面, 它的顶是曲面z =f (x , y ), 这里f (x , y )≥0且在D 上连续. 这种立体叫做曲顶柱体. 现在我们来讨论如何计算曲顶柱体的体积. 首先, 用一组曲线网把D 分成n 个小区域?σ 1, ?σ 2, ? ? ? , ?σ n .分别以这些小闭区域的边界曲线为准线, 作母线平行于z 轴的柱面, 这些柱面把原来的曲顶柱体分为n 个细曲顶柱体. 在每个?σ i 中任取一点(ξ i , η i ), 以f (ξ i , η i )为高而底为?σ i 的平顶柱体的体积为 f (ξ i , η i ) ?σi (i =1, 2, ? ? ? , n ). 这个平顶柱体体积之和 i i i n i f V σηξ?≈=∑),(1 . 可以认为是整个曲顶柱体体积的近似值. 为求得曲顶柱体体积的精确值, 将分割加密, 只需取极限, 即 i i i n i f V σηξλ?==→∑),(lim 1 0. 其中λ是个小区域的直径中的最大值.
线性代数课后习题答案-复旦大学出版社-熊维玲
第一章 3.如果排列n x x x 2 1是奇排列,则排列1 1 x x x n n 的奇偶 性如何? 解:排列 1 1x x x n n 可以通过对排列 n x x x 21经过 (1)(1)(2)212 n n n n L 次邻换得到,每一次邻换都 改变排列的奇偶性,故当2)1( n n 为偶数时,排列 1 1x x x n n 为奇排列,当2)1( n n 为奇数时,排列1 1 x x x n n 为 偶排列。 4. 写出4阶行列式的展开式中含元素13 a 且带负 号的项. 解:含元素13a 的乘积项共有13223144 (1)t a a a a ,13223441 (1)t a a a a , 13213244 (1)t a a a a ,13213442 (1)t a a a a ,13243241 (1)t a a a a ,13243142 (1)t a a a a 六项, 各项列标排列的逆序数分别为(3214)3t , (3241)4t , (3124)2 t , (3142)3 t , (3421)5t ,(3412)4 t , 故所求为13223144 1a a a a , 132134421a a a a , 13243241 1a a a a 。 5.按照行列式的定义,求行列式 n n 0 000100200100 的
值. 解:根据行列式的定义,非零的乘积项只有 1,12,21,1(1)t n n n nn a a a a L , 其中(1)(2) [(1)(2)21]2 n n t n n n L ,故行列式的值等于: (1)(2) 2 (1) ! n n n 6. 根据行列式定义,分别写出行列式x x x x x 1 11 1231112 1 2 的 展开式中含4 x 的项和含3 x 的项. 解:展开式含4 x 的乘积项为 4 11223344 (1)(1)22t a a a a x x x x x 含3 x 的乘积项为13 12213344 (1)(1)1t a a a a x x x x 8. 利用行列式的性质计算下列行列式: 解 : (1) 41 131123421 1234 1111 1 1 1 1 410234123410121 10310 ()341234120121 2412341230321 r r r r r r r r r r r
线性代数习题及答案(复旦版)[] 线性代数习题及答案 习题一 1. 求下列各排列的逆序数. (1) 341782659;(2) 987654321; (3) n(n?1)…321;(4) 13…(2n?1)(2n)(2n?2)…2. 【解】 (1) τ(341782659)=11; (2) τ(987654321)=36; (3) τ(n(n?1)…32221)= 0+1+2 +…+(n?1)=; (4) τ(13…(2n?1)(2n)(2n?2)…2)=0+1+…+(n?1)+(n?1)+(n?2)+…+1+0=n(n?1). 2. 略.见教材习题参考答案. 3. 略.见教材习题参考答案. 4. 本行列式的展开式中包含和的项. 解:设,其中分别为不同列中对应元素的行下标,则展开式中含项有 展开式中含项有 . 5. 用定义计算下列各行列式. (1);(2). 【解】(1) D=(?1)τ(2314)4!=24; (2) D=12. 6. 计算下列各行列式. (1);(2) ; (3);(4) . 【解】(1) ; (2) ; 7. 证明下列各式. (1) ; (2) ; (3) (4) ; (5) . 【证明】(1) (2) (3) 首先考虑4阶范德蒙行列式:
从上面的4阶范德蒙行列式知,多项式f(x)的x的系数为 但对(*)式右端行列式按第一行展开知x的系数为两者应相等,故 (4) 对D2n按第一行展开,得 据此递推下去,可得 (5) 对行列式的阶数n用数学归纳法. 当n=2时,可直接验算结论成立,假定对这样的n?1阶行列式结论成立,进而证明阶数为n时结论也成立. 按Dn的最后一列,把Dn拆成两个n阶行列式相加: 但由归纳假设 从而有 8. 计算下列n阶行列式. (1) (2) ; (3). (4)其中; (5). 【解】(1) 各行都加到第一行,再从第一行提出x+(n?1),得 将第一行乘(?1)后分别加到其余各行,得 (2) 按第二行展开 (3) 行列式按第一列展开后,得 (4)由题意,知 . (5) . 即有 由得 . 9. 计算n阶行列式. 【解】各列都加到第一列,再从第一列提出,得 将第一行乘(?1)后加到其余各行,得
习题七 1. 在空间直角坐标系中,定出下列各点的位置: A(1,2,3); B(-2,3,4); C(2,-3,-4); D(3,4,0); E(0,4,3); F(3,0,0). 解:点A在第Ⅰ卦限;点B在第Ⅱ卦限;点C在第Ⅷ卦限; 点D在xOy面上;点E在yOz面上;点F在x轴上. 2. xOy坐标面上的点的坐标有什么特点?yOz面上的呢?zOx面上的呢? 答: 在xOy面上的点,z=0; 在yOz面上的点,x=0; 在zOx面上的点,y=0. 3. x轴上的点的坐标有什么特点?y轴上的点呢?z轴上的点呢? 答:x轴上的点,y=z=0; y轴上的点,x=z=0; z轴上的点,x=y=0. 4. 求下列各对点之间的距离: (1)(0,0,0),(2,3,4);(2)(0,0,0),(2,-3,-4); (3)(-2,3,-4),(1,0,3);(4)(4,-2,3),(-2,1,3). 解:(1)s= (2) s== (3) s== (4) s== 5. 求点(4,-3,5)到坐标原点和各坐标轴间的距离. 解:点(4,-3,5)到x轴,y轴,z轴的垂足分别为(4,0,0),(0,-3,0),(0,0,5). 故 02 s= x s== y s== 5 z s==. 6. 在z轴上,求与两点A(-4,1,7)和B(3,5,-2)等距离的点. 解:设此点为M(0,0,z),则 222222 (4)1(7)35(2) z z -++-=++-- 解得 14 9 z=
即所求点为M (0,0, 149 ). 7. 试证:以三点A (4,1,9),B (10,-1,6),C (2,4,3)为顶点的三角形是等腰直角三角形. 证明:因为|AB |=|AC |=7.且有 |AC |2+|AB |2=49+49=98=|BC |2. 故△ABC 为等腰直角三角形. 8. 验证:()()++=++a b c a b c . 证明:利用三角形法则得证.见图 7-1 图7-1 9. 设2, 3.=-+=-+-u a b c v a b c 试用a , b , c 表示23.-u v 解: 232(2)3(3) 2243935117-=-+--+-=-++-+=-+u v a b c a b c a b c a b c a b c 10. 把△ABC 的BC 边分成五等份,设分点依次为D 1,D 2,D 3,D 4,再把各分点与A 连接,试以AB =c ,BC =a 表示向量1D A ,2D A ,3D A 和4D A . 解:1115D A BA BD =-=-- c a 222 5D A BA BD =-=--c a 333 5D A BA BD =-=--c a 444 .5 D A BA BD =-=--c a 11. 设向量OM 的模是4,它与投影轴的夹角是60°,求这向量在该轴上的投影. 解:设M 的投影为M ',则 1 Pr j cos604 2.2 u OM OM =?=?= 12. 一向量的终点为点B (2,-1,7),它在三坐标轴上的投影依次是4,-4和7,求这向量的起点A 的坐标. 解:设此向量的起点A 的坐标A (x , y , z ),则 {4,4,7}{2,1,7}AB x y z =-=----
线性代数复旦大学出版社练习题答案习题一 1.2.3 4. ∵ ∴ 为偶数 故所求为 ∵ ∴所求为397281564 5.∵ ∴项前的符号位 ∵ ∴ 项前的符号位 6. 原式= 7.8 9. ∵ ∴ 10. 从第2列开始,以后各列加到第一列的对应元素之上,得 按第一列展开:
习题二 1.2.3.4.5 6. 设为与可交换的矩阵,则有 即 解之得 7. ,记为 ,记为 即 8 9. 10. = 11. ∵ ∴ 反之若 , 则 ,即 12. 设∵∴ 又∵∴ 又 当时,有 ∴ 设,则
∵∴ 当时,有 故即 13. ∵∴为对称矩阵 同理也为对称矩阵 ∵ ∴为对称矩阵 又∵ ∴ 为反对称矩阵 ∵ 由知,为对称矩阵,为反对称矩阵 故可表示成一个对称矩阵与一个反对称矩阵的和。 14. 必要性:∵ ∴ 充分性:∵ ∴ 必要性:∵ ∴ 充分性:∵ ∴ 必要性:∵ ∴
即 充分性:∵ ∴ 15 16. ∵ ∴ 可逆。 且 17. ∵ ∴ 可逆,且 18. 19. ∵,若可逆,则 ∴故可逆,且 20.设,∵是对称矩阵∴ 记,则 ,即为对称矩阵,又∵ , ∴ 为对称矩阵。 21.设,则 ∵ ∴ 又∵ ∴ 于是即 ∵ ∴ 于是
∵ 可逆∴ ∴ 22. ∵∴ 23.4. 25. ∵ ∴ ∴ 可逆,且 26. ∵ ∴ 又∵, , ∴ 27 28. ∵ ∴ 又∵∴ 故 29. ∵∴ ∴ 30. 31. 32. 33. ∵ ∴
∵ ∴ 习题三 1.2.3.4 5. ∵ 不能由线性表示 ∴线性方程组无解 不妨假设能由线性表示,则存在一组数,使 从而 此式与方程组无解矛盾。 故不能由的任何部分组线性表示 6. 依题意 所以 即 7. ∵ ∴ 令∵ ∴可逆,于是 即 8. 9.当即当或时,线性相关 否则线性无关。 10 .设 则
复旦大学数学科学学院 2008~2009学年第二学期期末考试试卷 A 卷 B 卷 课程名称:__高等数学B _________ 课程代码: MATH120004.02.03__ 开课院系:__数学科学学院 _____________ 考试形式:闭卷 姓 名: 学 号: 专 业: 题 号 一 二 三 四 五 六 七 八 总 分 得 分 (以下为试卷正文) ( 装 订 线 内 不 要 答 题 )
注意:答题应写出文字说明、证明过程或演算步骤。 一、简单计算(每题4分,共40分) 1. 写出函数y x x u +=arccos 的定义域。 2. 求( )2 20 1ln lim y x e x y y x ++→→。 3. 设f 是一个三元可微函数,() xy y x y x f u 2,,2 222-+=,求 y u ??。 4. 设()y x z z ,=是由方程()0,,=+xz z y xy F 所确定的隐函数,且F 具有连续的一阶偏导数,求 x z ??。 5. 交换二次积分 ()? ? 20 32 ,y y dx y x f dy 的积分顺序。
6. 求级数()() ∑ ∞ =+-113231 k k k 的和。 7. 判别级数∑∞ =1 3sin 2n n n π 的收敛性。 8. 求幂级数() ∑∞ =--1 1 21n n n n n x 的收敛域。 9. 求方程() 042 =-+dy x x dx y 的通解。 10. 求方程023=+'-''y y y 的通解。 ( 装 订 线 内 不 要 答 题 )
二、 设 ()333,y x y x f +=,判断()y x f ,在()0,0处是否可微,为什么?(6分) 三、 计算二重积分( )dxdy xe y I D y ??+=2 ,其中D 是由1=y ,2 x y =及0=x 所围成的 有界闭区域。(6分)
第十章多元函数积分学(Ⅰ) f x在区间[a,b]上的定积分,并且已经建立 一元函数积分学中,曾经用和式的极限来定义一元函数() 了定积分理论,本章我们将推广到多元函数,建立多元函数积分学理论。 第一节二重积分 教学目的: 1、熟悉二重积分的概念; 2、了解二重积分的性质和几何意义,知道二重积分的中值定理; 3、掌握二重积分的(直角坐标、极坐标)计算方法; 4、能根据积分区域和被积函数正确选择积分顺序 教学重点: 1、二重积分的性质和几何意义; 2、二重积分在直角坐标系下的计算 教学难点: 1、二重积分的计算; 2、二重积分计算中的定限问题 教学内容: 一、二重积分的概念 1曲顶柱体的体积 设有一立体它的底是xOy面上的闭区域D它的侧面是以D的边界曲线为准线而母线平行于z轴的柱面它的顶是曲面z f(x y)这里f(x y)0且在D上连续这种立体叫做曲顶柱体现在我们来讨论如何计算曲顶柱体的体积 首先用一组曲线网把D分成n个小区域 1 2n分别以这些小闭区域的边界曲线为准线作母线平行于z轴的柱面这些柱面把原来的曲顶柱体分为n个细曲顶柱体在每个i中任取一点(i i)以f (i i)为高而底为i的平顶柱体的体积为
f ( i i ) i (i 1 2 n ) 这个平顶柱体体积之和 i i i n i f V σηξ?≈=∑),(1 可以认为是整个曲顶柱体体积的近似值 为求得曲顶柱体体积的精确值 将分割加密 只需取极限 即 i i i n i f V σηξλ?==→∑),(lim 1 其中是个小区域的直径中的最大值 2 平面薄片的质量 设有一平面薄片占有xOy 面上的闭区域D 它在点(x y )处的面密度为(x y ) 这里 (x y )0且在D 上连续 现在要计算该薄片的质量M 用一组曲线网把D 分成n 个小区域 1 2 n 把各小块的质量近似地 看作均匀薄片的质量 ( i i ) i 各小块质量的和作为平面薄片的质量的近似值 i i i n i M σηξρ?≈=∑),(1 将分割加细 取极限 得到平面薄片的质量 i i i n i M σηξρλ?==→∑),(lim 1 其中是个小区域的直径中的最大值 定义 设f (x y )是有界闭区域D 上的有界函数 将闭区域D 任意分成n 个小闭区域 1 2 n 其中 i 表示第i 个小区域 也表示它的面积 在每个 i 上任取一点( i i ) 作和 i i i n i f σηξ?=∑),(1 如果当各小闭区域的直径中的最大值趋于零时 这和的极限总存在 则称此极限为函数f (x y )在 闭区域D 上的二重积分 记作 σ d y x f D ??),( 即
习题十三 1. 求下列函数在所示点的导数: (1)()sin cos t f t t ??= ???,在点π4t =; 解:( )π4f ?? ?'= - ? (2)()22,x y g x y x y +??= ? ?+?? ,在点()(),1,2x y =; 解:()111,224g ??= ??? (3)sin cos u v u T u v v v ???? ?= ? ??? ??? ,在点π1u v ????= ? ?????; 解:1010101T -???? ?'=- ? ?π?? ??? (4)2222232u x y v x x y w x y y ?=-?=-??=-? 在点()3,2-. 解:6 26 6362-?? ?- ? ?--?? 2. 设()()(),,,,,,w f x y z u g x z v h x y ===,求,,w w w x y z ??????. 解:,w w w v w w u w v w w u x x v x y u y v x z u z ????????????=+=+=????????????, 3. 若r =()()21,,,,3n r r f r r n r ?????≥. 解: ()()()()()()()2231111,,,2,,,,,,,,,,,n n r x y z r x y z x y z f r f r x y z r nr x y z r r r r -'?=?=?=?=?=
4. 求22224428u x y z x y x y z =+++-+-在点,,,1,1,1,1,1,1(000)()()O A B ---的梯度,并求梯度为零的点. 解:()()()() 54,2,8,2,10,6,10,6,10,3,,42------- 5. 证明本章关于梯度的基本性质(1)~(5). 证明:略 6. 计算下列向量场A 的散度与旋度: (1)()222222,,y z z x x y =+++A ; 解:()0,2,,y z z x x y --- (2)()222,,x y z x y z x y z =A ; 解:()()()()2222226,,,xy x z y y x z z y x --- (3),,y x z y z z x x y ?? = ???A . 解:111yz zx xy ++,2222221,,y y z z x x xyz z y x z y x ??--- ??? 7. 证明: 本章关于散度的基本性质(1)~(3). 解:略。 8. 证明: 本章关于旋度的基本性质(1)~(3)(可应用算符?推导) 解:略。 9. 证明:场()()()()2,2,2y z x y z x z x y z x y x y z =++++++A 是有势场,并求其势函数. 解:略。 10. 若流体流速()222,,x y z =A ,求单位时间内穿过18球面,22210,0,0x y z x y z ++=>>>的流量. 解:38 π 11. 设流速(),,y x c =-A (c 为常数),求环流量: (1)沿圆周221,0x y z +==; 解:2π (2)沿圆周()2251,0x y z -+==. 解:2π
第一章 3.如果排列n x x x 21是奇排列,则排列11x x x n n 的奇偶性如何? 解:排列11x x x n n 可以通过对排列n x x x 21经过(1) (1)(2)212 n n n n L 次邻换得到,每一次邻换都改变排列的奇偶性,故当2 ) 1( n n 为偶数时,排列11x x x n n 为奇排列,当 2 ) 1( n n 为奇数时,排列11x x x n n 为偶排列。 4. 写出4阶行列式的展开式中含元素13a 且带负号的项. 解:含元素13a 的乘积项共有13223144(1)t a a a a ,13223441(1)t a a a a ,13213244(1)t a a a a , 13213442(1)t a a a a ,13243241(1)t a a a a ,13243142(1)t a a a a 六项,各项列标排列的逆序数分别 为(3214)3t ,(3241)4t ,(3124)2t ,(3142)3t ,(3421)5t , (3412)4t , 故所求为132231441a a a a ,132134421a a a a ,132432411a a a a 。 5.按照行列式的定义,求行列式n n 0 000010020 0100 的值. 解:根据行列式的定义,非零的乘积项只有1,12,21,1(1)t n n n nn a a a a L , 其中(1)(2) [(1)(2)21]2 n n t n n n L ,故行列式的值等于: (1)(2) 2 (1) !n n n 6. 根据行列式定义,分别写出行列式 x x x x x 111 1231112 12 的展开式中含4x 的项和含3 x 的项. 解:展开式含4 x 的乘积项为0411223344(1)(1)22t a a a a x x x x x 含3 x 的乘积项为1312213344(1)(1)1t a a a a x x x x
194 习题九 1. 求函数u =xy 2+z 3-xyz 在点(1,1,2)处沿方向角为πππ ,,343 αβγ===的方向导数。 解: (1,1,2)(1,1,2) (1,1,2)cos cos cos u u u u y l x z αβγ????=++???? 22(1,1,2)(1,1,2)(1,1,2)πππ cos cos cos 5.(2)()(3)343 xy xz y yz z xy =++=--- 2. 求函数u =xyz 在点(5,1,2)处沿从点A (5,1,2)到B (9,4,14)的方向导数。 解:{4,3,12},13.AB AB == AB 的方向余弦为 4312cos ,cos ,cos 131313 αβγ= == (5,1,2) (5,1,2) (5,1,2)(5,1,2) (5,1,2)(5,1,2) 2105 u yz x u xz y u xy z ?==??==??==? 故 4312982105.13131313 u l ?=?+?+?=? 3. 求函数222 21x y z a b ?? =-+ ??? 在点处沿曲线22221x y a b +=在这点的内法线方向的方向导数。 解:设x 轴正向到椭圆内法线方向l 的转角为φ,它是第三象限的角,因为 2222220,x y b x y y a b a y ''+==- 所以在点处切线斜率为 2.b y a a ' ==-
195 法线斜率为cos a b ?=. 于是tan sin ??== ∵ 2222,,z z x y x a y b ??=-=-?? ∴ 2222z l a b ??=- -= ?? 4.研究下列函数的极值: (1)z =x 3+y 3-3(x 2+y 2); (2)z =e 2x (x +y 2+2y ); (3)z =(6x -x 2)(4y -y 2); (4)z =(x 2+y 2)2 2() e x y -+; (5)z =xy (a -x -y ),a ≠0. 解:(1)解方程组2 2 360 360 x y z x x z y y ?=-=??=-=?? 得驻点为(0,0),(0,2),(2,0),(2,2). z xx =6x -6, z xy =0, z yy =6y -6 在点(0,0)处,A =-6,B =0,C =-6,B 2-AC =-36<0,且A <0,所以函数有极大值z (0,0)=0. 在点(0,2)处,A =-6,B =0,C =6,B 2-AC =36>0,所以(0,2)点不是极值点. 在点(2,0)处,A =6,B =0,C =-6,B 2-AC =36>0,所以(2,0)点不是极值点. 在点(2,2)处,A =6,B =0,C =6,B 2-AC =-36<0,且A >0,所以函数有极小值z (2,2)=-8. (2)解方程组22 2e (2241)0 2e (1)0x x x y z x y y z y ?=+++=??=+=?? 得驻点为1,12??- ??? . 22224e (21)4e (1)2e x xx x xy x yy z x y y z y z =+++=+= 在点1 ,12??- ??? 处,A =2e,B =0,C =2e,B 2-AC =-4e 2<0,又A >0,所以函数有极小值e 1,122z ?? =-- ??? . (3) 解方程组2 2 (62)(4)0 (6)(42)0x y z x y y z x x y ?=--=??=--=?? 得驻点为(3,2),(0,0),(0,4),(6,0),(6,4). Z xx =-2(4y -y 2), Z xy =4(3-x )(2-y )
线性代数课后习题答案 习题一 1、2、3(答案略) 4、 (1) ∵ (127435689)415τ=+= (奇数) ∴ (127485639)τ为偶数 故所求为127485639 (2) ∵(397281564)25119τ=+++= (奇数) ∴所求为397281564 5、(1)∵(532416)421106τ=++++= (偶数) ∴项前的符号位()6 11-=+ (正号) (2)∵325326114465112632445365a a a a a a a a a a a a = (162435)415τ=+= ∴ 项前的符号位5(1)1-=- (负号) 6、 (1) (2341)(1)12n n τ-?L L 原式=(1)(1)!n n -=- (2)()((1)(2)21) 1(1)(2)21n n n n n n τ--??---??L L 原式=(1)(2) 2 (1) !n n n --=- (3)原式=((1)21) 12(1)1(1) n n n n n a a a τ-?--L L (1) 2 12(1)1(1)n n n n n a a a --=-L 7、8(答案略) 9、 ∵162019(42)0D x =?-?+?--?= ∴7x = 10、 (1)从第2列开始,以后各列加到第一列的对应元素之上,得 []11(1)1110 01(1)1110 (1)1 1 (1)1 1 1 x x n x x x n x x x n x x n x x +-+--==+-+--L L L L L L L L L L L L L L L L L L L L L []1(1)(1)n x n x -=+-- (2)按第一列展开: 11100000 (1)(1)0 n n n n n y x y D x x y x y x y -++=?+-=+-L L L L L L L L